
Inferring Causality from Noisy Time Series Data
A Test of Convergent Cross-Mapping
Dan Mønster
1,2,∗
, Riccardo Fusaroli
2,3
, Kristian Tyl
´
en
3,2
, Andreas Roepstorff
2
and Jacob F. Sherson
4,5
1
Department of Economics and Business Economics, Aarhus University, Fulglesangs All
´
e 4, 8210 Aarhus V, Denmark
2
Interacting Minds Centre, Aarhus University, Jens Chr. Skous Vej 4, 8000 Aarhus C, Denmark
3
Center for Semiotics, Aarhus University, Jens Chr. Skous Vej 2, 8000 Aarhus C, Denmark
4
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
5
AU Ideas Center for Community Driven Research, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
Keywords:
Convergent Cross-Mapping, Causality, Logistic Map, Noise, Time Series Analysis.
Abstract:
Convergent Cross-Mapping (CCM) has shown high potential to perform causal inference in the absence of
models. We assess the strengths and weaknesses of the method by varying coupling strength and noise levels in
coupled logistic maps. We find that CCM fails to infer accurate coupling strength and even causality direction
in synchronized time-series and in the presence of intermediate coupling. We find that the presence of noise
deterministically reduces the level of cross-mapping fidelity, while the convergence rate exhibits higher levels
of robustness. Finally, we propose that controlled noise injections in intermediate-to-strongly coupled systems
could enable more accurate causal inferences. Given the inherent noisy nature of real-world systems, our
findings enable a more accurate evaluation of CCM applicability and advance suggestions on how to overcome
its weaknesses.
1 INTRODUCTION
The ability to infer causality from the relation between
two variables is an intensely researched area. Com-
mon approaches involve having both a model of the
system being studied and a series of measurements
of that same system (Pearl, 2009). In many cases,
however, we do not have an adequate model of the
system, or face several conflicting models. Complex
natural, technical and social systems are prime exam-
ples, including ecosystems, brains, the climate and
the global financial system. In such cases, inferring
whether one part has a causal influence on another part
has to rely on model-free methods. Convergent Cross-
Mapping (CCM) (Sugihara et al., 2012) is a relatively
new method that promises to ‘distinguish causality
from correlation’ in time series data (ibid., p. 496).
CCM was introduced as an alternative to other meth-
ods that detect causality between two time series, prin-
cipally Granger causality (Granger, 1969).
Granger causality has been developed to assess eas-
ily separable linear systems, whereas CCM is primarily
suited for weakly coupled components of non-linear
dynamic systems. Accordingly, they have slightly di-
verging notions of causality. Therefore, the statement
‘
X
causes
Y
’ would more accurately be phrased as ‘
X
Granger causes
Y
’ or ‘
X
CCM causes
Y
’. Sugihara
et al. (2012) refer to the type of causality captured
by CCM as dynamic causation, reminiscent of what
Lakoff (2010) terms systemic causation. For a system
with several variables, for which time series data are
available, the CCM method produces a causal network
structure describing which variables are causally con-
nected, including the direction of causality. Like mu-
tual information (Fraser and Swinney, 1986), transfer
entropy (Schreiber, 2000) and cross-recurrence quan-
tification (Webber and Zbilut, 1994; Marwan et al.,
2007) CCM is a state space method relying on time-
delayed embedding of the time series data in a higher
dimensional space.
CCM has already been used in a wide range of
different fields for different kinds of data (McBride
et al., 2015; BozorgMagham et al., 2015; McCracken
and Weigel, 2014), and it has been noted (McCracken
and Weigel, 2014) that CCM results are not always
consistent with theoretical intuitions. McCracken and
Weigel (2014) extended CCM to pairwise asymmetric
inference (PAI), which they demonstrated to give re-
sults that are in better accordance with the intuitively
expected outcomes for several physical systems. Re-
48
Mønster, D., Fusaroli, R., Tylén, K., Roepstorff, A. and Sherson, J.
Inferring Causality from Noisy Time Series Data - A Test of Convergent Cross-Mapping.
In Proceedings of the 1st International Conference on Complex Information Systems (COMPLEXIS 2016), pages 48-56
ISBN: 978-989-758-181-6
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
cently Ma et al. (2014) developed cross-map smooth-
ness (CMS)—a method related to CCM—which has
the advantage of requiring fewer points in the time
series. Notice, however, that in this paper we focus on
CCM, leaving the analysis of developments such as
PAI and CMS for future work.
Given the interest and relevance of CCM, it is im-
portant to better understand its strengths and limita-
tions. Accordingly, in this article we will present re-
sults of an in-depth study of a simple model system,
the coupled logistic map, with particular emphasis on
how the CCM results reflect the model input, vary-
ing strength of coupling, and levels of noise. We will
briefly describe how CCM is applied to the model.
Then we look at how the choice of coupling affects the
CCM results, and finally we report on results of adding
noise to the system. Although noise in real-world data
is ubiquitous, the inclusion of noise in model investiga-
tions has been largely neglected. We find that noise can
dramatically change the strength of causal inferences.
Crucially, we also observe that the appropriate injec-
tion of noise into the dynamics can be used as means
of inferring the relative strengths of the coupling (to
the extent that the system can be controlled).
2 MODEL SYSTEM
The logistic map has long been a model system of non-
linear dynamics displaying regular periodic behavior
as well as deterministic chaos (May, 1976). A sys-
tem of two coupled logistic maps has been used as a
simple model of chemical reaction dynamics (Ferretti
and Rahman, 1988) and population dynamics (Lloyd,
1995). This makes it an ideal model system for testing
CCM. We follow Sugihara et al. (2012) and study two
logistic maps coupled through linear terms
x
t+1
= x
t
(r
x
(1 − x
t
) − β
xy
y
t
)
y
t+1
= y
t
(r
y
(1 − y
t
) − β
yx
x
t
)
(1)
The two variables
x
and
y
have a nonlinear de-
pendence on their own past values parameterized by
the growth rates
r
x
,r
y
, and are coupled to each other
through linear terms with coupling constants that pa-
rameterize the strength of the coupling from
x
to
y
(β
yx
)
and from
y
to
x (β
xy
)
. Times series for
x
and
y
are shown in Figure 1 for a particular choice of the
parameters in the model.
A single logistic map has well-known domains
of periodic behavior controlled by the growth rate
r
. As
r
becomes larger, increasingly frequent period-
doublings occur, which ultimately give way to chaotic
behavior at
r ≈ 3.57
. This well-known phase diagram
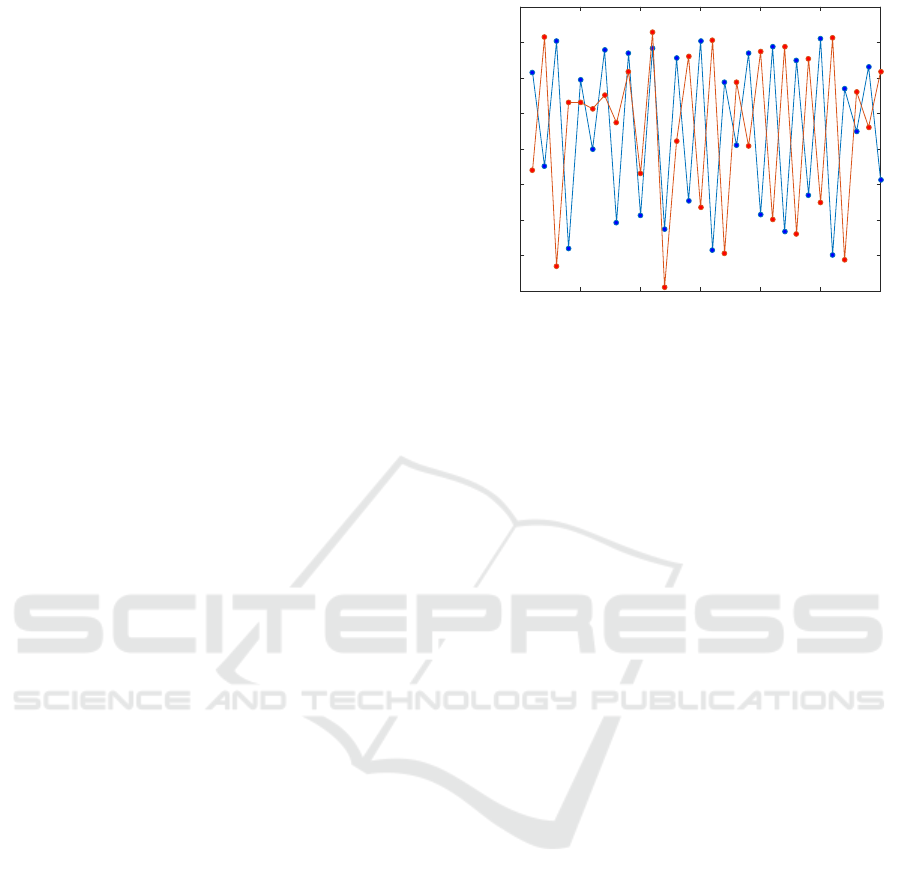
300 305 310 315 320 325 330
n
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
x
n
, y
n
Figure 1: Plot of the time series of
x
(shown in blue) and
y
(shown in red) after the initial 300 time steps. Note that
β
xy
= 0
, so there is no coupling from
y
to
x
and the causality
is therefore unidirectional from
x
to
y (β
yx
= 0.05)
. Both
r
x
= 3.65
and
r
y
= 3.77
are chosen to be in a chaotic regime
of the logistic map.
or bifurcation diagram is shown in the bottom panel
of Figure 2, representing the
x
variable. The top panel
shows the phase diagram for another logistic map rep-
resenting the
y
variable. In order to illustrate the effect
of coupling between two logistic maps the growth rate
for the
y
variable
r
y
is related to
r
x
by the equation
r
x
+ r
y
= 6.5
. This is the equation for a line in the
(r
x
,r
y
)
-plane with a slope of
−1
. The middle panel
in Figure 2 illustrates the phase diagram of
y
for a
family of two coupled logistic maps along this line in
the
(r
x
,r
y
)
-plane as described by Eq. 1 with
β
xy
= 0
and β
yx
= 0.2.
The middle and lower panels show the effect of
unidirectional coupling between two logistic maps. It
is evident that the dynamics of
x
leaves an imprint on
y
as indicated by the fixed points. For low
r
y
(high
r
) where the isolated system (top panel) is stationary,
the effect of coupling from the chaotic dynamics of
x
induces chaotic dynamics in
y
, albeit with a much
smaller amplitude. For high
r
y
(low
r
) where the iso-
lated system is chaotic, the coupling from
x
which is
in the stationary domain has the effect of stabilizing
the periodic phases of
y
which persist to higher values
of r
y
than in the isolated system.
2.1 Noise
Real-world systems present varying degrees of envi-
ronmental and measurement noise and the application
of the method to such systems thus critically depends
on the method’s ability to cope with noise. We there-
fore also consider the model with added noise terms:
x
t+1
= x
t
(r
x
(1 − x
t
) − β
xy
y
t
) + ε
x,t
y
t+1
= y
t
(r
y
(1 − y
t
) − β
yx
x
t
) + ε
y,t
(2)
Inferring Causality from Noisy Time Series Data - A Test of Convergent Cross-Mapping
49
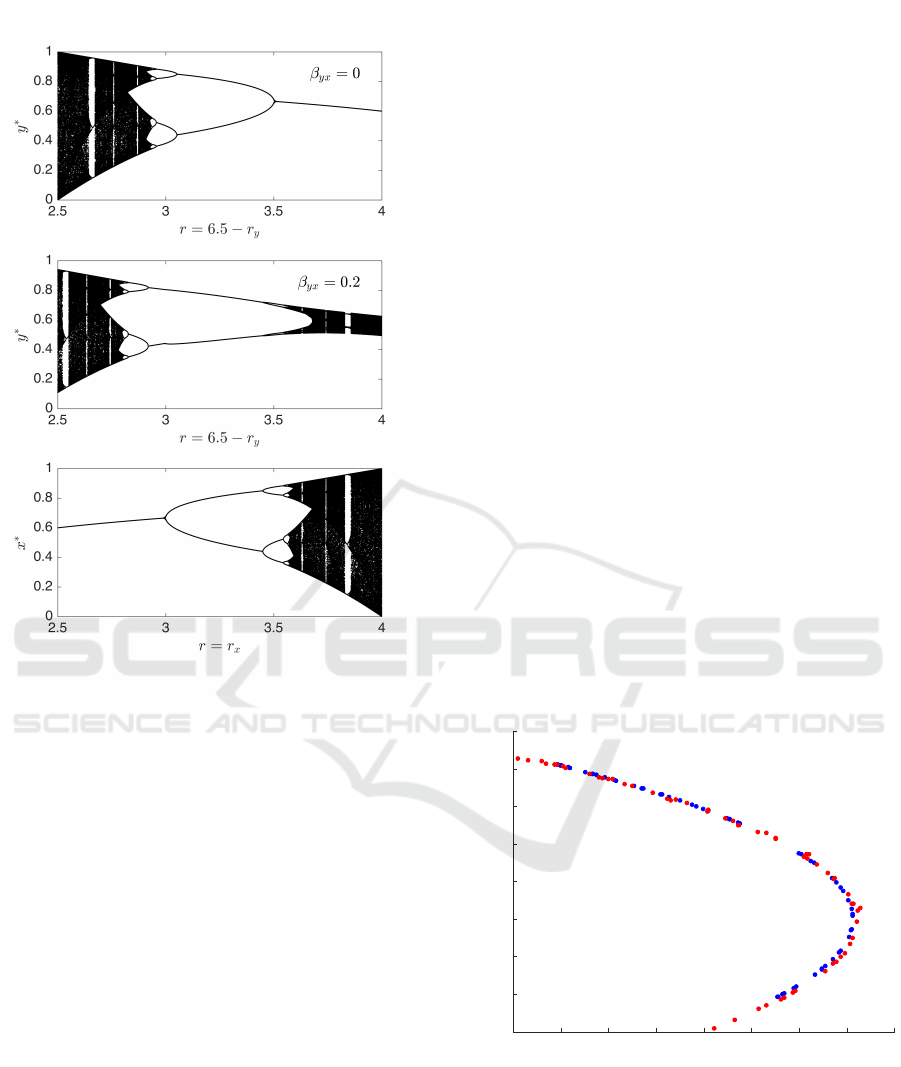
Figure 2: Phase diagram for the coupled logistic map in Eq. 1
for
β
xy
= 0
. The growth rates
r
x
,r
y
are parameterized by the
variable
r
on the horizontal axis as
r
x
= r
and
r
y
= 6.5 − r
.
For each value of
r
the plots represent a different pair of
parameters
r
x
,r
y
. The bottom panel shows the fixed points
x
∗
as a function of the growth rate, and the top panel
(β
yx
= 0)
shows the fixed points
y
∗
. The center panel shows the fixed
points for β
yx
= 0.2.
Here
ε
x,t
and
ε
y,t
are the noise terms on
x
and
y
which we model as stochastic variables sampled from
normal distributions
N (0, σ
2
)
with zero mean and
standard deviation
σ
. We will refer to
σ
as the noise
level. Note that noise in either variable in Eq. 2 prop-
agates to later values of the variable and to the other
variable through the coupling terms. Hence, the noise
terms in this model represent perturbations from the
environment rather than noise from the measurement
process.
3 METHOD
Convergent cross-mapping is a state space method
that relies on Takens’ theorem (Takens, 1981) to re-
construct the underlying dynamics of a system in a
model-free fashion, by using time-delayed embed-
ding to reconstruct its attractor landscape (see, e.g.,
Abarbanel (1996)). Our model system in Eq. 1 can
be described by its attractor, that is, the trajectory
consisting of consecutive points in two-dimensional
Euclidean space given by the Cartesian coordinates
(x
0
,y
0
),(x
1
,y
1
),...,(x
N
,y
N
)
resulting from the dy-
namics described by Eq. 1. We discard the first 300
points to avoid transient behavior of the model from
affecting our results. According to Takens’ theorem
we can approximately reconstruct the attractor from
one of the variables
x
or
y
alone using time-delayed
embedding of the points in one of the time series, say
x
, where each point in
E
-dimensional space is given
by
x
t
= (x
t
,x
t−τ
,x
t−2τ
,...x
t−(E−1)τ
)
. The embedding
thus depends on two parameters: the time delay
τ
and the dimension
E
of the space in which the recon-
structed attractor is embedded. Since we know that
there are only two independent variables in our model
system we choose
E = 2
, but estimating the embed-
ding dimension from the times series obtained from
Eq. 1 using the false nearest neighbor method (Abar-
banel, 1996) gives the same result. The time delay
for the embedding was set to
τ = 1
based on the aver-
age mutual information criterion (Kantz and Schreiber,
1997). The reconstructed attractors, referred to as
shadow manifolds by Sugihara et al. (2012), are shown
in Figure 3.
The two key ingredients of the CCM method are
the concept of cross-mapping and the convergence
property that are explained in the following sections.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x
t
, y
t
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
x
t−1
, y
t−1
Figure 3: The shadow manifolds based on the time series
displayed in Figure 1, embedded using
E = 2
and
τ = 1
. A
total of 60 points
x
t
= (x
t
,x
t−1
)
in
M
x
are shown in blue and
the points y
t
= (y
t
,y
t−1
) in M
y
are shown in red.
3.1 Cross-mapping
The time series data from each variable—in our case
x
and
y
—can be used to construct shadow manifolds—
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
50
M
x
and
M
y
—that are approximations to the true attrac-
tor. Given the non-separability of the system, Taken’s
theorem demonstrates that when two different vari-
ables represent different parts of the same dynamical
system their shadow manifolds are diffeomorphic to
the true attractor and therefore to each other. Intu-
itively the two variables are connected because they
are part of the same dynamical system as evidenced
by the fact that they both represent a dimension in
the state space. So, if
x
has a causal influence on the
dynamics of
y
then
x
will influence the dynamics of
y
.
This ‘imprint’ of
x
on
y
means that knowledge of the
shadow manifold M
y
obtained from the time series of
y
can be used to estimate values of
x
. This estimate is
called the cross-map and is denoted ˆx|M
y
.
To find the cross-mapped estimate
ˆx
t
|M
y
of
x
t
we
start by identifying the corresponding point
y
t
in
M
y
.
Since
M
y
is diffeomorphic to
M
x
, a small region around
y
t
will map to a small region around
x
t
and this can
be used to estimate
x
t
. To form a bounding simplex
around
y
t
at least
E + 1
points are needed (Sugihara
and May, 1990), so the
E + 1
nearest neighbors of
y
t
in
M
y
are found. Sorted from the closest to the farthest
point from
y
t
we call these
y
t
1
,y
t
2
,...,y
t
E+1
. We use
the points in the time series for
x
at the corresponding
times, i.e., x
t
1
,x
t
2
,...,x
t
E+1
to estimate x
t
as
ˆx
t
|M
y
=
E+1
∑
i=1
w
i
x
t
i
(3)
The weights
w
i
are exponentially weighted with the
Euclidean distance between
y
t
and the nearest neigh-
bor points:
w
i
= u
i
E+1
∑
j=1
u
j
, u
i
= exp
−
k
y
t
− y
t
i
k
k
y
t
− y
t
1
k
(4)
where
k
·
k
is the Euclidean norm in R
E
.
Estimating one point alone is not sufficient to show
how well
ˆx
t
|M
y
estimates the true value
x
t
. A library
consisting of
L
points from
M
y
is therefore used to
provide estimates of
L
points in the time series for
x
.
The Pearson correlation coefficient ρ
x ˆx
between the L
true values from
x
and the
L
cross-mapped estimates is
an indicator of how much the dynamics of
x
influences
the dynamics of
y
. Scatter plots of observed values
and cross-mapped estimates of
x
and
y
are shown in
Figure 4.
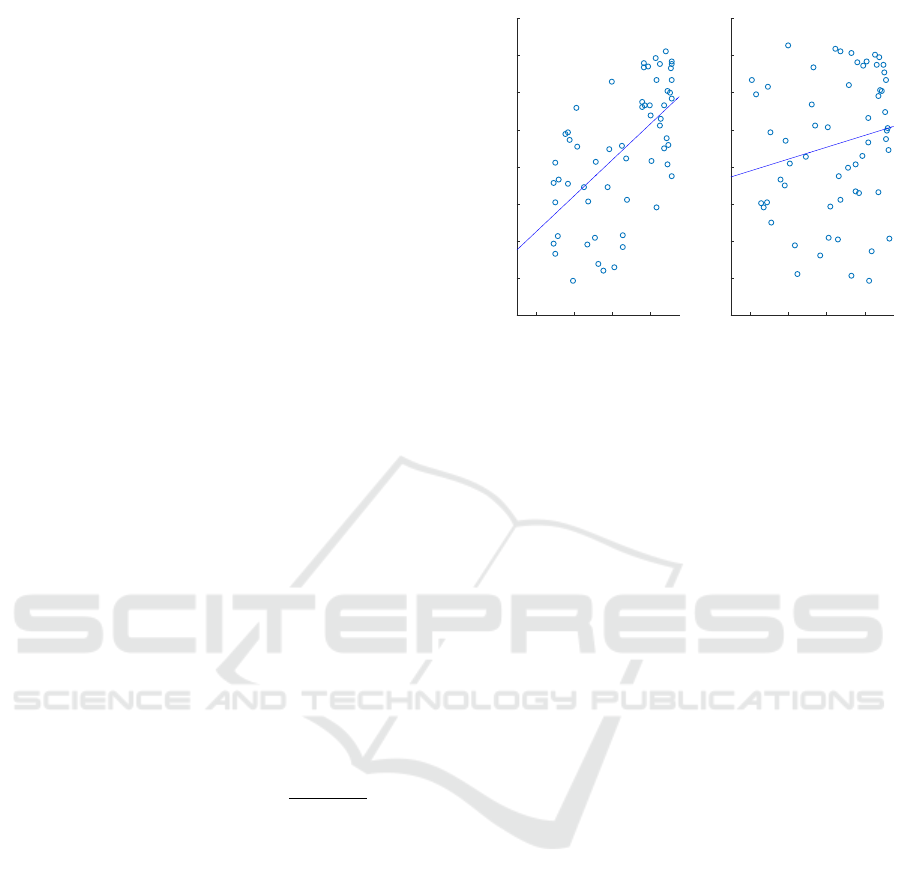
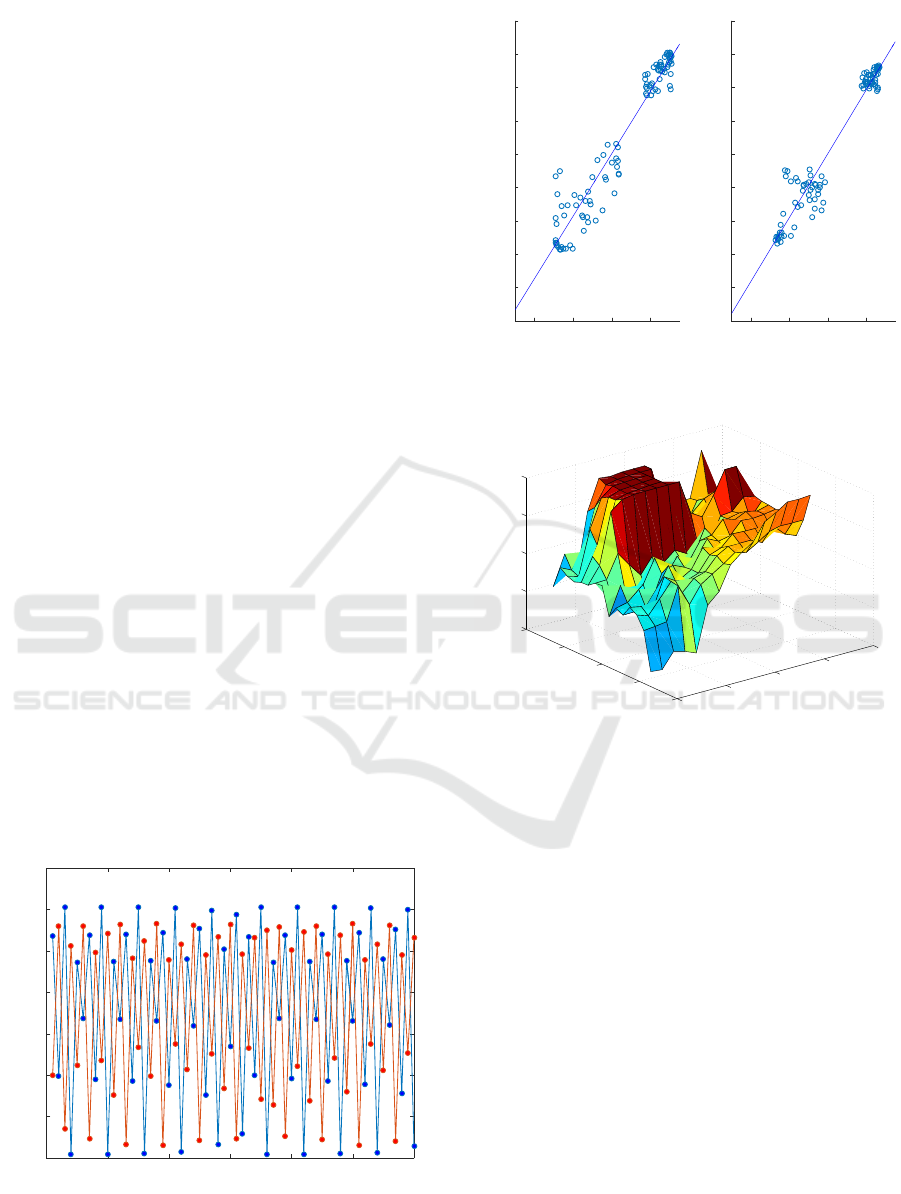
The results indicate that the cross-mapped esti-
mates of
x
obtained from
M
y
(ρ
x ˆx
≈ 0.6)
are better
than the cross-mapped estimates of
y
obtained from
M
x
(ρ
y ˆy
≈ 0.2)
. It is therefore tempting to conclude
that
x
causes
y
, but, although correct in this case, such a
conclusion is potentially misleading. Indeed, A slight
variation in the parameters, can produce results that
0.2 0.4 0.6 0.8
x
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
ˆx|M
y
ρ
x,ˆx
= 0.6
0.2 0.4 0.6 0.8
y
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
ˆy|M
x
ρ
y,ˆy
= 0.19
Figure 4: Scatter plot of pairs of observed values of
x
and
estimated values
ˆx|M
y
(left panel) and the equivalent for
y
(right panel). The cross-mapped estimates were computed
according to Eq. 3 and were based on the shadow manifolds
in Figure 3.
would lead to the opposite conclusion. The additional
criterion of convergence is crucial to correctly infer
the direction and relative strength of causality.
Cross-mappings were performed with XMAP
(Mønster, 2013) which was developed in MATLAB
and validated by reproducing the results by Sugihara
et al. (2012) and by comparing with an independently
developed algorithm (Jespersen, 2013). A small reg-
ularizing term
δ
is added to the denominator in the
argument to the exponential function in Eq. 4 in or-
der to avoid floating point overflow in cases where
y
t
1
= y
t
.
3.2 Convergence
The convergence properties of the correlation between
observed values and cross-mapped estimates as a func-
tion of the library length
L
is the second key ingredient
in CCM. If
x
causes
y
then the estimate of
x
obtained
from
M
y
should improve as the number of points
L
sampled from
M
y
becomes larger, since the library of
samples will become a better and better representation
of the attractor, and the nearest neighbor points will be
closer and closer to y
t
.
This convergence phenomenon is illustrated in Fig-
ure 5 where correlations derived from the data shown
in Figure 4 have been computed for increasing values
of the library length. Figure 5 shows that
ρ
x ˆx
converges
toward a much higher value than
ρ
y ˆy
does. This is evi-
dence that
M
y
enables much better estimates for
x
than
M
x
does for
y
. Note that cross-mapped estimation skill
is from y to x when x causes y.
Inferring Causality from Noisy Time Series Data - A Test of Convergent Cross-Mapping
51
0 50 100 150 200 250 300 350 400
L
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
ρ
Figure 5: The correlation coefficient
ρ
x, ˆx
(blue circles) and
ρ
y, ˆy
(red circles) as a function of library length
L
. Fits to
the function in Eq. 5 are shown as solid lines. For
x
the
converged value is
ρ
∞
= 0.71
, and for
y
it is
ρ
∞
= 0.096
.
Parameter values:
r
x
= 3.65
,
r
y
= 3.77
,
β
xy
= 0
,
β
yx
= 0.05
.
3.2.1 Fitting the Convergence
Rather than relying only on the value of the correlation
coefficient for the largest obtained value of
L
we fit
the computed values of
ρ
as a function of
L
to the
following function
ρ(L) = αe
−γL
+ ρ
∞
. (5)
This function, containing three constants
α
,
γ
and
ρ
∞
,
is in accordance with the computed values of the corre-
lation coefficient. It can be interpreted as convergence
toward the value
ρ
∞
as
L → ∞
where the speed of con-
vergence is given by the constant
γ
. The third constant
α
is necessary to obtain a good fit, but does not provide
additional interpretive value.
The solid lines in Figure 5 represent the fitted cor-
relation coefficients to the function in Eq. 5 using the
same parameters as in Figure 1. The fitted value for
ρ
x ˆx
is
ρ
∞
= 0.71 ±0.046
(95% CI), and the fitted value
for ρ
y ˆy
is ρ
∞
= 0.096 ± 0.024.
4 RESULTS
The previous section introduced CCM and demon-
strated how to apply the method on the model system
using a particular choice of parameter values as an ex-
ample. Sugihara et al. (2012) summarize their results
for different values of the coupling constants
β
xy
and
β
yx
with
r
x
and
r
y
chosen uniformly from the interval
[3.6,4]
in Figure 3B of their manuscript. This figure
indicates that CCM gets the direction of the coupling
right, but also indicates that for some choices of the
coupling constants the method may give results that
100 200 300
L
0.2
0.4
0.6
0.8
1
ρ
β
yx
= 0.1
100 200 300
L
0.2
0.4
0.6
0.8
1
ρ
β
yx
= 0.2
100 200 300
L
0.2
0.4
0.6
0.8
1
ρ
β
yx
= 0.5
100 200 300
L
0.2
0.4
0.6
0.8
1
ρ
β
yx
= 2
Figure 6: Correlations between observed and cross-mapped
estimates of
x
(blue) and
y
(red) for four different values of
β
yx
. Thin lines are the computed correlations and thick lines
are fits to Eq. 5. For
β
yx
= 0.2
and
β
yx
= 2
a good fit is not
possible, and no fits are shown.
are hard to distinguish from symmetric coupling, even
when β
xy
β
yx
or vice versa.
To investigate this further, we will look at what
happens for a particular choice of
r
x
and
r
y
when the
coupling between the two variables is manipulated.
4.1 Effect of Weak and Strong Coupling
To study how CCM causality estimates depend on the
strength of the coupling between the two variables we
fix
r
x
= 3.625
and
r
y
= 3.77
. To keep things simple,
we will set
β
xy
= 0
as in the previous example, and
only vary
β
yx
. The correlation coefficients
ρ
x ˆx
and
ρ
y ˆy
are shown in Figure 6 for β
yx
= 0.1, 0.2, 0.5, 2.0.
For
β
yx
= 0.05
, a plot very similar to that displayed
in Figure 5 is produced (not shown in Figure 6), which
is consistent with a coupling from
x
to
y
, but no cou-
pling from y to x.
For
β
yx
= 0.1
,
ρ
x, ˆx
is seen to converge toward
ρ
∞
=
0.89
, whereas
ρ
y, ˆy
fluctuates around 0.36. This lack
of convergence as a function of the library size is an
indication that there is no coupling from y to x.
For
β
yx
= 0.5
, the convergence of
ρ
x ˆx
is toward
the higher value
ρ
∞
= 0.96
, and convergence is faster,
indicating a stronger coupling. Here we also see con-
vergence of
ρ
y ˆy
toward
ρ
∞
= 0.43
, and although the
value is much smaller than for
x
, this could indicate a
coupling from
y
to
x
. We know that this is not the case,
since
β
xy
= 0
, so instead this is most likely due to the
fact that
x
is driving
y
, and that the two time series are
becoming more synchronized.
For an intermediate
β
yx
value of 0.2 something
unexpected happens: both
ρ
x ˆx
and
ρ
y ˆy
quickly increase
to values close to 1, already for very low values of
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
52
L
. Furthermore for
L . 100
,
ρ
y ˆy
> ρ
x ˆx
. Naively this
could be seen as an indication that there is a strong
bidirectional coupling between
x
and
y
. Alternatively
both signals could be driven by a common external
variable—the Moran effect (Moran, 1953)—or one of
the variables is driving the other so strongly that they
synchronize (Boccaletti et al., 2002; Pikovsky et al.,
2003). We know, however, that neither the Moran
effect, nor synchronization can be the explanation here,
so a different explanation must be found. We return to
this in section 4.1.1, but note here that (i) for both
x
and
y
the correlation is uniformly high, i.e., there is not
much evidence of convergence, and (ii) the function in
Eq. 5 is not a good fit to the data.
For
β
yx
= 2
we again see very high correlation
coefficients for both
x
and
y
, but clearly
ρ
x ˆx
> ρ
y ˆy
.
There is not much evidence of convergence for
ρ
x ˆx
and
ρ
y ˆy
fluctuates around a value close to 0.8. This
is consistent with synchronization due to the strong
coupling from
x
to
y
and inspection of the time series
confirms this. Again we note that
ρ(L)
from Eq. 5 is
not a good fit to the data.
4.1.1 Near-periodicity and Bunching
We now return to the case in the upper right panel
in Figure 6. For
r
x
= 3.625
and
r
y
= 3.77
both logis-
tic maps—considered in isolation—are in the chaotic
phase, cf. Figure 2. But for
β
yx
= 0.2
the dynamics of
y become nearly periodic as illustrated in Figure 7.
Nonlinear dynamic systems are known to display
intermittency (Ott, 2002), where periods of chaos are
interspersed with periods of nearly periodic behavior.
Intermittency, however, does not seem to be the cause
here, since the phenomenon persists no matter how
many points are discarded as transient before starting
300 310 320 330 340 350 360
n
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
x
n
, y
n
Figure 7: Plot of the time series of
x
(shown in blue) and
y
(shown in red) displaying nearly periodic behavior. Parame-
ter values: r
x
= 3.625, r
y
= 3.77, β
xy
= 0, β
yx
= 0.2.
0.2 0.4 0.6 0.8
x
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
ˆx|M
y
ρ
x,ˆx
= 0.96
0.2 0.4 0.6 0.8
y
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
ˆy|M
x
ρ
y,ˆy
= 0.97
Figure 8: Cross-mapped estimates vs. observed values of
x
and
y
. Parameter values:
r
x
= 3.625
,
r
y
= 3.77
,
β
xy
= 0
,
β
yx
= 0.2.
0
0.2
0.4
0.6
0.8
3.5
3.6
3.7
3.8
3.9
−1
−0.5
0
0.5
1
β
yx
r
y
ρ(y)
Figure 9: Surface plot of
ρ
y ˆy
for
L = 400
as a function of
r
y
and
β
yx
. Note that
r
x
is also varied, since
r
x
+ r
y
= 7.3984
.
β
xy
= 0 throughout.
to sample. Instead, it seems, that
y
becomes partially
synchronized with
x
because the range of
x
-values lies
within several relatively narrow intervals. An example
of cross-mapped estimates for
x
and
y
are shown in
figure 8.
Near-periodicity results in
ρ
y ˆy
becoming higher
than
ρ
x ˆx
at low
L
, and ‘bunching’ of the points leads to
‘fast non-convergence’, i.e., high correlations, that are
not reminiscent of the convergence behavior expected
in CCM, evidenced by the fact that the fits to
ρ(L)
in
Eq. 5 fail.
To see whether this is an isolated point in parameter
space, resulting in pathological behavior, we calculate
cross-mapped estimates
ˆy|M
x
of
y
for a range of param-
eter values
r
x
,
r
y
and
β
yx
. For each value we discard
the first 1000 points in the time series and sample
the next 400 points after that to construct the shadow
manifolds. The result is shown in Figure 9.
There is a clear plateau in Figure 9 that corresponds
Inferring Causality from Noisy Time Series Data - A Test of Convergent Cross-Mapping
53
to the ‘bunching’ observed in Figure 7, indicating that
the issue is not confined to a few isolated parameter
combinations. Whether similar issues affect the use of
CCM for other models or when applied to empirical
data is a topic for future research.
4.2 Effects of Noise
Since all empirical data contain a certain level of noise
it is important to study what effect noise, as included
in Eq. 2, has on CCM results. We consider the simple
case of unidirectional coupling from
x
to
y
, i.e.,
β
xy
= 0
.
In this case the noise term
ε
x,t
propagates directly to
the variable
y
, and therefore does not affect the cross-
mapped estimates of
x
based on
M
y
(a fact that has
been verified by numerical simulations). On the other
hand, noise in
y
is not coupled back into
x
and could
potentially be detrimental to the reconstruction. Hence,
we will make the simplifying assumption of setting
ε
x,t
= 0
. This leaves
r
x
,r
y
,β
yx
and the noise level
σ
y
as
free parameters of the model in Eq. 2. We fix
r
x
= 3.8
and
r
y
= 3.5
, so that
x
is in the chaotic regime and the
dynamics of
y
is governed by a period-4 attractor for
β
yx
= 0
, but as illustrated in Figure 2 the dynamics of
y
will become increasingly chaotic as
β
yx
increases. We
present results for three different values of
β
yx
ranging
from weak to strong coupling. At low noise levels
CCM gives the correct result for all three values of the
coupling strength, namely that x causes y.
When the noise level
σ
y
is increased the cross-
mapped estimates of
x
from
M
y
deteriorate, and as a
result
ρ
x ˆx
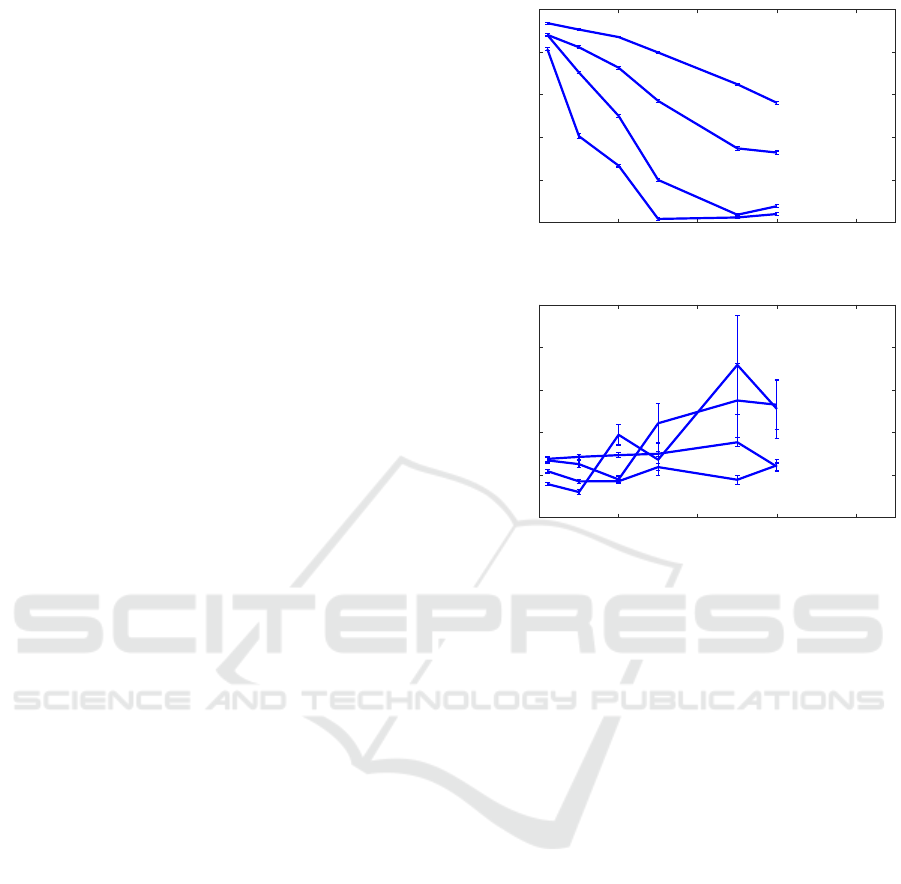
decreases. Figure 10 shows the fitted values
ρ
x,∞
that
ρ
x ˆx
converges to as a function of the noise
level (top panel).
We see that
ρ
x,∞
decreases in a roughly linear fash-
ion as
σ
y
is increased until the correlation becomes
very low
(0 . ρ
x,∞
. 0.2)
where the curve becomes
flat. For systems corresponding to the flat part of the
curves
ρ
x,∞
is very low and at about the same level as
ρ
y,∞
, so, effectively, the system is too noisy for CCM
to extract the direction of causality from the converged
value of ρ
x ˆx
.
The bottom panel shows that the rate of conver-
gence
γ
x
from Eq. 5 is relatively unaffected by the
noise level, except when
ρ
x ˆx
≈ 0
, where CCM is not
applicable under any circumstances. But for combi-
nations of coupling strength and noise level that lie
on the linear decline of the curves in the top panel of
Figure 10 the fitted rate of convergence
γ
x
seems to
be a better indicator that
ρ
x ˆx
converges than
ρ
x,∞
; and
hence also a better predictor of causality.
0 0.01 0.02 0.03 0.04
σ
y
0
0.2
0.4
0.6
0.8
1
ρ
x,∞
β
yx
= 0.05
β
yx
= 0.1
β
yx
= 0.2
β
yx
= 0.4
0 0.01 0.02 0.03 0.04
σ
y
0
0.02
0.04
0.06
0.08
0.1
γ
x
β
yx
= 0.05
β
yx
= 0.1
β
yx
= 0.2
β
yx
= 0.4
Figure 10: The effect of the noise level
σ
y
on the converged
value
ρ
x,∞
of
ρ
x ˆx
(top panel) and on the rate of convergence
γ
x
of
ρ
x ˆx
(bottom panel). In all cases
r
x
= 3.8
,
r
y
= 3.5
and
β
xy
= 0
. The coupling
β
yx
was varied as shown in the figure.
The error bars represent 95% confidence intervals on the
fitted values.
4.2.1 Estimating Coupling from Noise
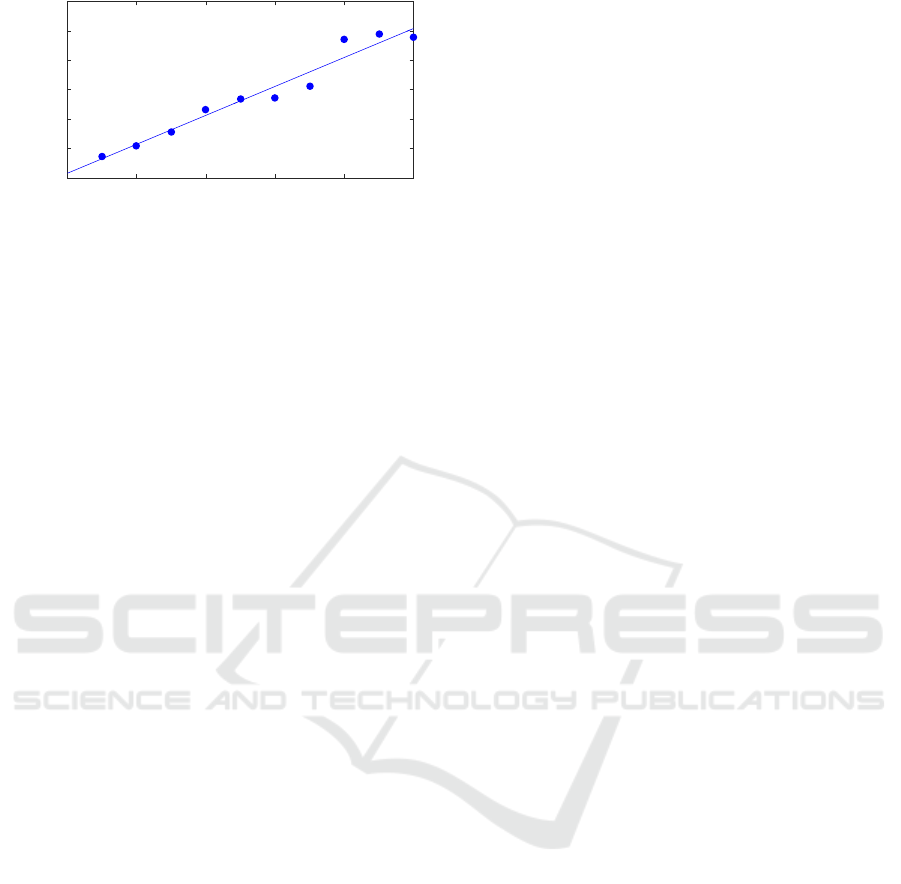
As noted above, we observe from Figure 10 that
ρ
x,∞
decreases linearly as a function of noise. We further
note that the inverse of the slope depends linearly on
the strength of the coupling, as shown in Figure 11.
For the particular example studied here this has the
implication that we can determine the strength of the
coupling from
x
to
y
by controlled injection of noise
into the system. Whether this results generalizes to
other systems is a question for future research that has
practical implications for measuring the interaction
between different parts of complex dynamic systems.
5 DISCUSSION
Methods for reliable inference of causality between
two or more variables are of great interest to many
fields of research. Convergent Cross-Mapping (CCM)
shows great potential in this regard. However, based
on the systematic assessments presented in the previ-
ous sections, we conclude that the method can give
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
54
0 0.1 0.2 0.3 0.4 0.5
β
yx
0
0.02
0.04
0.06
0.08
0.1
−1/q
Figure 11: The inverse negative slope
−1/q
of the linear
portion of the curves in the top panel of Figure 10 as a
function of the coupling.
erroneous results. It was noted already by Sugihara
et al. (2012) that CCM does not correctly predict the
direction of causality when the coupling is so strong
that it results in synchronization of variables, as we
have also seen above. Further, our study shows that
the method seems very sensitive to the particular dy-
namics of the model system, and CCM also fails to
correctly predict the direction of causality in cases
where the coupling is weak to moderate. Interestingly,
we have shown that both types of cases where CCM
fails is associated with a failure to fit the observed val-
ues of cross-mapped correlations to the function
ρ(L)
in Eq. 5. It would therefore seem that the failure to
produce a good fit to
ρ(L)
is an indicator that CCM is
not applicable to the data.
Another aspect of CCM performance concerns con-
ditions of noise. Generally, we observe that CCM is
fairly robust to random noise and makes reliable infer-
ences at varying degrees of coupling under conditions
of lower noise levels. However, for higher levels of
noise CCM correlations drop linearly as a function
of added noise. For systems subject to noise our re-
sults suggest that the rate of convergence is a more
robust indicator of cross-mapping convergence and
hence of causality. In applications where noise can
be controlled, injecting noise into the system at differ-
ent noise levels presents an opportunity to gauge the
strength of coupling between variables.
Together our results warrant caution in the applica-
tion of CCM to real-world data for purposes of causal
inference, and care must be taken to look in detail at
the convergence properties of the correlations between
observed data and cross-mapped estimates. Our re-
sults suggest that fitting the correlation coefficients
as a function of library length can give an indication
of the applicability of CCM. When applied under the
right circumstances, the method has the potential not
only to inform the researcher about the causal direc-
tion of dynamics between coupled variables, but by
controlled injection of noise, we can also infer the
coupling strength between the variables.
ACKNOWLEDGEMENTS
We would like to acknowledge the Interacting Minds
Centre, Aarhus University, for providing the ideal en-
vironment for the authors’ collaboration.
REFERENCES
Abarbanel, H. (1996). Analysis of Observed Chaotic Data.
Springer New York.
Boccaletti, S., Kurths, J., Osipov, G., Valladares, D. L., and
Zhou, C. S. (2002). The synchronization of chaotic
systems. Physics Reports, 366(1–2):1–101.
BozorgMagham, A. E., Motesharrei, S., Penny, S. G., and
Kalnay, E. (2015). Causality Analysis: Identifying
the Leading Element in a Coupled Dynamical System.
PLOS ONE, 10(6):e0131226.
Ferretti, A. and Rahman, N. K. (1988). A study of coupled
logistic map and its applications in chemical physics.
Chemical Physics, 119(2–3):275–288.
Fraser, A. M. and Swinney, H. L. (1986). Independent coor-
dinates for strange attractors from mutual information.
Physical Review A, 33(2):1134–1140.
Granger, C. W. J. (1969). Investigating Causal Relations
by Econometric Models and Cross-spectral Methods.
Econometrica, 37(3):424–438.
Jespersen, S. N. (2013). Personal communication.
Kantz, H. and Schreiber, T. (1997). Nonlinear Time Series
Analysis. Cambridge University Press, New York,USA.
Lakoff, G. (2010). Why it Matters How we Frame the Envi-
ronment. Environmental Communication,4(1):70–81
Lloyd, A. L. (1995). The coupled logistic map: a sim-
ple model for the effects of spatial heterogeneity on
population dynamics. Journal of Theoretical Biology,
173(3):217–230.
Ma, H., Aihara, K., and Chen, L. (2014). Detecting Causality
from Nonlinear Dynamics with Short-term Time Series.
Scientific Reports, 4:7464.
Marwan, N., Carmen Romano, M., Thiel, M., and Kurths, J.
(2007). Recurrence plots for the analysis of complex
systems. Physics Reports, 438(5–6):237–329.
May, R. M. (1976). Simple mathematical models with very
complicated dynamics. Nature, 261(5560):459–467.
McBride, J. C., Zhao, X., Munro, N. B., Jicha, G. A.,
Schmitt, F. A., Kryscio, R. J., Smith, C. D., and Jiang,
Y. (2015). Sugihara causality analysis of scalp EEG for
detection of early Alzheimer’s disease. NeuroImage:
Clinical, 7:258–265.
McCracken, J. M. and Weigel, R. S. (2014). Conver-
gent cross-mapping and pairwise asymmetric inference.
Physical Review E, 90(6):062903.
Mønster, D. (2013). XMAP. https://github.com/danm0nster
/xmap.
Moran, P. (1953). The statistical analysis of the Canadian
Lynx cycle. Australian Journal of Zoology, 1(3):291–
298.
Inferring Causality from Noisy Time Series Data - A Test of Convergent Cross-Mapping
55

Ott, E. (2002). Chaos in Dynamical Systems. Cambridge
University Press, Cambridge, U.K. ; New York, 2 edi-
tion edition.
Pearl, J. (2009). Causal inference in statistics: An overview.
Statistics Surveys, 3:96–146.
Pikovsky, A., Rosenblum, M., and Kurths, J. (2003). Syn-
chronization: A Universal Concept in Nonlinear Sci-
ences. Cambridge University Press.
Schreiber, T. (2000). Measuring Information Transfer. Phys-
ical Review Letters, 85(2):461–464.
Sugihara, G., May, R., Ye, H., Hsieh, C.-h., Deyle, E., Foga-
rty, M., and Munch, S. (2012). Detecting Causality in
Complex Ecosystems. Science, 338(6106):496–500.
Sugihara, G. and May, R. M. (1990). Nonlinear forecasting
as a way of distinguishing chaos from measurement
error in time series. Nature, 344(6268):734–741.
Takens, F. (1981). Detecting strange attractors in turbulence.
Lecture Notes in Mathematics, 898:366–381.
Webber, C. L. and Zbilut, J. P. (1994). Dynamical assess-
ment of physiological systems and states using recur-
rence plot strategies. Journal of Applied Physiology,
76(2):965–973.
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
56
