Combining Harvesting Operation Optimisations using Strategy-based

Simulation

Luis Diogo Couto

, Peter W. V. Tran-Jørgensen

and Gareth T. C. Edwards

Department of Engineering, Aarhus University, Aarhus, Denmark

Agro Inteligence ApS, Aarhus, Denmark

Keywords:

Harvesting Operations, Optimisation, Strategy Pattern, Design Patterns, VDM, Formal Methods, Model

Architecture.

Abstract:

Modelling and simulation assist in decision support or planning activities by allowing efﬁcient exploration

of multiple scenarios in a situation where testing in a real setting is impractical. This exploration is often

done by varying numerical parameters in the model such as physical dimensions or speed in order to ﬁnd

the optimal conﬁguration. However, for certain problems, in order to ﬁnd optimal solutions it is beneﬁcial to

vary the algorithms that are used to implement the behaviour of the model. For example, when calculating

optimised routes for harvesters and other vehicles in a harvest operation, the choice of optimisation algorithms

is an important part of the problem. Traditional modelling and simulation techniques do not allow us to

vary algorithms across simulations effectively. In this paper, we address this issue by applying the strategy

pattern from software engineering to the construction of a formal model that enables different combinations of

harvest optimisation algorithms to be analysed effectively. This approach can be generalised to other planning

activities where multiple algorithms need to be considered.

1 INTRODUCTION

There are various steps to calculating optimised solu-

tions for harvest operations. These steps include par-

titioning of the ﬁeld and calculating optimised cov-

erage plans for harvesters and route plans for other

vehicles. One approach to the problem often involves

the use of various optimisation algorithms that pro-

duce coverage plans for the harvesters (Spekken and

de Bruin, 2013; Edwards et al., 2013). However, plan-

ning of harvester routes is just one part of the har-

vest operation planning. Path planning for wagons (or

similar) that service the harvesters must often also be

developed. Algorithms exist for optimising service

plans (Jensen et al., 2012) but they are independent

from those of harvesters. This independence makes

it difﬁcult to explore in detail how the various types

of algorithms interact and combine to produce a com-

plete solution for the harvest operation.

As an example, little research has previously been

conducted into how harvesting and loading algo-

rithms can affect operational execution times of har-

vesting operations. Examples of planning tools for

operations often employ a single algorithm; such as

in-ﬁeld unloading (Oksanen and Visala, 2009) or sin-

gle point unloading (Edwards et al., 2015). Farmers

will generally choose a plan with which they are fa-

miliar without considering alternatives.

In this paper, we seek to explore how different op-

timization algorithms can be combined. We will ex-

plore this using a formal model in combination with

the strategy pattern from software engineering. The

strategy pattern is used in the model to encode differ-

ent optimization algorithms. A novel aspect here is

that the strategies representing the different kinds of

algorithms (harvest routing and wagon path planning)

co-exist and collaborate to produce the ﬁnal solution.

From an operational research perspective, the

harvest operation is an example of an output ma-

terial ﬂow (OMF) operation where material is re-

moved from the ﬁeld and transported to another lo-

cation (Bochtis and Sørensen, 2009). The machinery

utilised within the OMF operation can be divided into

two groups; Primary Units (PUs) which perform the

main task i.e. harvesting the crop, and Service Units

(SUs) which service the PUs by receiving harvested

material and transporting it away. The capacity of the

PU is many times smaller than the expected yield of

the ﬁeld, and therefore a PU unloads either to a nearby

SU or directly to an out of ﬁeld storage point.

Couto, L., Tran-Jørgensen, P. and Edwards, G.

Combining Harvesting Operation Optimisations using Strategy-based Simulation.

DOI: 10.5220/0005932900250032

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 25-32

ISBN: 978-989-758-199-1

The planning of the tasks of the PUs and SUs are

often considered separately (Jensen, 2014), with cov-

erage plans being developed for PUs (Spekken and

de Bruin, 2013; Edwards et al., 2013) and path plans

being developed for SUs (Jensen et al., 2012). How-

ever, the tasks are spatially and temporally depen-

dant on one another, so in order for efﬁcient plans

to be produced the plans must be developed concur-

rently (Scheuren et al., 2013).

To assist with the planning of in-ﬁeld operations,

ﬁelds can be decomposed into a number of tracks or

rows. Many methods have been proposed for the de-

composition of ﬁelds (Oksanen and Visala, 2009; Jin

and Tang, 2010; Zandonadi, 2012; Hameed et al.,

2013). Fields are typically divided into headlands

which encircle the ﬁeld and can be used for turning

and working rows which transect the main area of the

ﬁeld. By conﬁning all ﬁeld trafﬁc to drive along these

predeﬁned rows, the trafﬁcked area of the ﬁeld can

be limited which has been shown to produce beneﬁts

on increased yield and better soil structure (Tullberg,

2010).

In the above mentioned approaches, the planning

for the various kinds of vehicles is performed inde-

pendently, as is the decomposition of the ﬁeld. In our

work, we consider all vehicles simultaneously when

planning, although ﬁeld decomposition is still done

separately.

A different approach to optimisation was car-

ried out in a EU project called DESTECS. In this

project design space exploration is performed by

sweeping parameters of models of cyber-physical

systems (Fitzgerald et al., 2014). Among other

things, the DESTECS project proposes methodolog-

ical guidelines for modelling fault-tolerant cyber-

physical systems, which also involve the use of the

strategy pattern to model faulty behaviour as well

guarding against it (Broenink et al., 2012). This is

similar to the presented approach, in that the strategy

pattern is used in the DESTECS project to explore

different behaviours of a system. However, while the

DESTECS project used the strategy pattern to make

a system more fault-tolerant, in this work the strategy

pattern is used to help ﬁnd optimised solutions to use

in a harvest operation.

The strategy pattern is a design pattern (Gamma

et al., 1995) with two key features. First, the strat-

egy pattern allows selection of different algorithms to

be done at execution time and; secondly, it deﬁnes

a family of interchangeable algorithms. Essentially

this allows one to execute the same functionality in

different ways. Broadly speaking, the strategy pat-

tern consists of a contract that deﬁnes the functions

of a strategy in terms of their inputs and outputs in-

cluding the properties that these functions may have.

Given this contract, a speciﬁc strategy must provide

an implementation of the functions that obeys the in-

put and output properties of the contract, but which is

free to use whatever algorithms are desired.

The remainder of this paper is structured as fol-

lows: in section 2 we present the architecture of the

formal model of the harvest operation based on the

strategy pattern. The technologies that have been used

to implement the model are described in section 3.

Next, the execution of the model is demonstrated in

section 4. Following that, in section 5, we report the

results of applying the model to a case study of a real

ﬁeld. The results are then discussed in section 6. We

conclude the paper in section 7.

2 MODEL ARCHITECTURE

2.1 Model Overview

The model was developed according to the structure

shown in Figure 1. The Execution Engine is respon-

sible for coordinating the simulation and is connected

to both the State and the three Strategy classes. The

State contains the physical entities involved in the har-

vest operation. The harvesters are the PUs of the

operation. Coverage plans and coordinated service

points are developed for the harvesters by the em-

ployed strategies. The SUs are tractors with grain

wagons whose main objective within the harvest op-

eration is to convey material from the harvesters to

the out-of-ﬁeld storage. The service points coordinate

when and where the SUs must meet the PUs in order

for material to be passed between the two.

Both the harvesters and the grain wagons are

modelled by their physical parameters such as their

working/non-working speed, storage capacity and

material ofﬂoad rate. These parameters are speciﬁed

in the initialisation of the model. The storage point

is the out-of-ﬁeld storage where all material from the

ﬁeld must be transported to in order for the harvest

operation to be completed. This too is modelled by

its capacity.

The strategy classes deﬁne how certain aspects of

the harvest operation are executed. In Figure 1 these

strategies are represented by the Route Strategy, De-

conﬂict Strategy and Load Strategy classes.

2.1.1 Route Strategy

A route strategy is responsible for constructing the

routes for harvesters. The routes direct the harvester

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

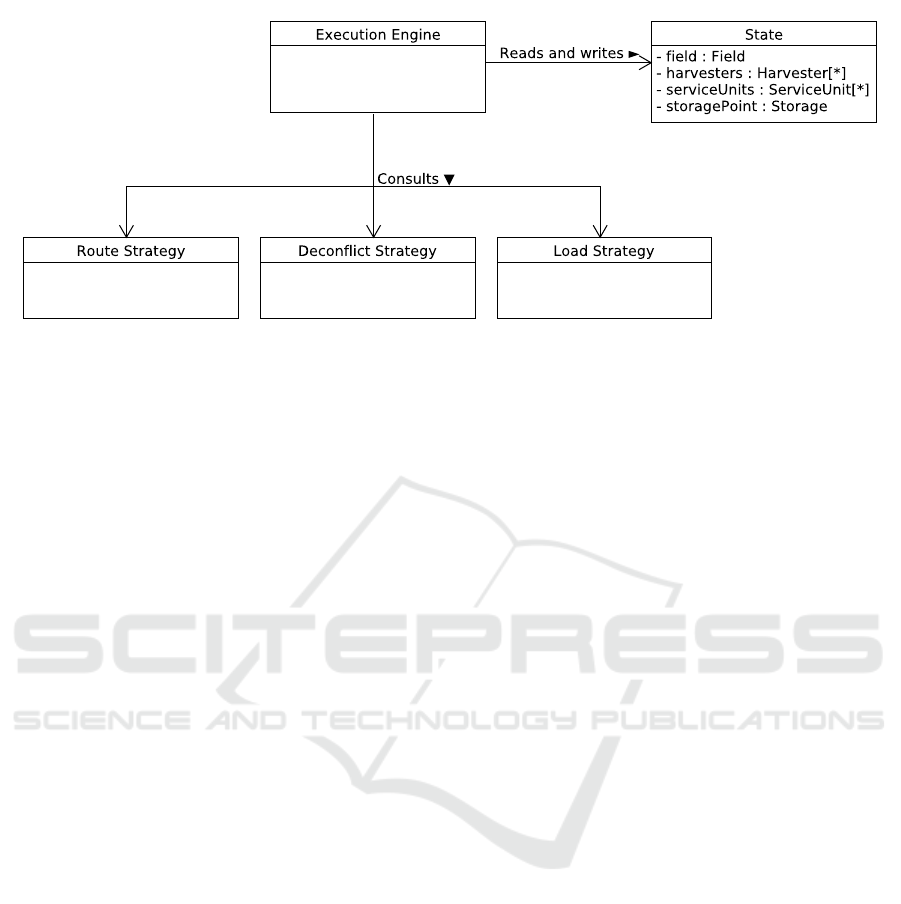
Figure 1: Model structure realised as a UML class diagram.

from its location to a point where it will next re-

quire a service. A similar approach to the planning

of routes for harvesters was also utilised in (Oksanen

and Visala, 2009). In this way the routes for multiple

harvesters can be constructed in a consecutive man-

ner.

As already stated, the construction of routes for

the harvester and grain wagon are dependent on one

another, therefore the route strategy must call func-

tions from the loading strategy to ensure that the har-

vester is able to be serviced at the end of the route.

The route strategies are allowed to produce more than

one possible route for the harvester, these are later dis-

tinguished by the load strategy as appropriate.

Two route strategies have been implemented

within the model: Predeﬁned Route strategy and

Greedy Route strategy.

The Predeﬁned Route strategy enables the model

to execute coverage plans that have been developed

externally, provided they are represented as a se-

quence of rows to harvest. This strategy receives the

assignment of a sequence of rows to a harvester as an

input. A route is constructed which navigates the har-

vester along the sequence of rows, inserting service

points where they are needed.

The Greedy Route strategy employs a search al-

gorithm on the ﬁeld to create a route for the harvester

which will end with the harvester being as full as pos-

sible and in a position where it can be serviced. An

extra constraint is also implemented within the strat-

egy that every row must be harvested in its entirety

and that all headland rows must be harvested before

work rows.

2.1.2 Deconﬂict Strategy

A deconﬂict strategy is responsible for determining

if a vehicle can move along its route, or calculating

new routes if this is not possible. In the Simple De-

conﬂict strategy a vehicle to reroute is chosen non-

deterministically.

A deconﬂict strategy is responsible for the inﬁeld

coordination of the vehicles. It is possible that con-

ﬂicts can arise when a vehicle may block the path of

another vehicle. In this case the deconﬂict strategy is

employed to determine what course of action (such as

planning a new route, or waiting for the obstruction to

pass) is to be taken.

The Simple Deconﬂict strategy ensures that two

vehicles cannot travel towards each other either along

the same row or along two adjacent rows.

2.1.3 Load Strategy

A load strategy is responsible for assisting the route

strategy to ﬁnd a location where the harvester can

be serviced and for constructing a route for the grain

wagon from its current position to the service point

and then to the out of ﬁeld storage.

This is done through three functions

of the load strategy that are called by the

route strategy: isDoneExtendingRoute(),

isRouteServiceable(), and finaliseRoute().

isDoneExtendingRoute() checks if it is possi-

ble to extend a harvesters route. A common reason

why it would not be possible to extend a harvester’s

route is if there are no more remaining rows in the

ﬁeld to be harvested, or if the harvester is full.

finaliseRoute() modiﬁes a harvester’s route to

ensure the ﬁnal position of the harvester is valid. For

example if harvesting the full length of the ﬁnal row

of a harvester’s route will cause the harvester to ex-

ceed its capacity, the route is modiﬁed so that a ser-

vice point is required at some point along the length

of the ﬁnal row.

isRouteServiceable() checks that a grain

wagon is able to converge on the service point that

is required by the harvester’s route, for example that

Combining Harvesting Operation Optimisations using Strategy-based Simulation

there is a previously harvested row adjacent to the ser-

vice point in which the grain wagon can move.

Four different versions of the load strategy have

been developed in the model. These cover the four

basic ways in which harvesters are unloaded during

grain harvests.

The Single Point Unload version requires the har-

vester to transport material directly to the out of ﬁeld

storage point without using a grain wagon. It is im-

portant that the harvester must avoid the event of be-

coming full without a navigable path to the out of ﬁeld

storage. This strategy limits the amount of trafﬁc in

the ﬁeld, which could offer beneﬁts when reducing

soil compaction.

The Headland Unload version limits the grain

wagon to only travelling in the headland areas of the

ﬁeld. The harvester must avoid becoming full in the

middle of the ﬁeld as a grain wagon would not be

able to meet it, therefore service points must be co-

ordinated before the harvester becomes full while it is

turning in the headland area.

The Inﬁeld Static Unload version allows the grain

wagons to drive in the working areas of the ﬁeld in or-

der to meet the harvester. Service points are planned

for the latest possible moment to ensure that the har-

vester is full when it passes its load.

The Inﬁeld Moving Unload version is similar to

the Inﬁeld Static Unload strategy, however the har-

vester and the grain wagon are both moving when the

load is being passed. As the machines remain in mo-

tion it is imperative that the grain wagon is travelling

in the same direction as the harvester when they meet

at the service point.

The Route, Load and Deconﬂict strategies are rep-

resented in Figure 1 by their contracts. The various

concrete versions of each strategy must conform to

these contracts. Figure 2 shows how the various load

strategies are realised based on the ILoadStrategy

class that deﬁnes the contract. Whenever the model

is executed, a concrete strategy of each kind must be

provided to the Execution Engine.

Not all versions of a strategy can be used in all sit-

uations. In order to cope with this, a notion of strategy

feasibility has been introduced. The strategy feasibil-

ity check is implemented as a function in each of the

strategies and invoked at the beginning of model exe-

cution in order to check if the ﬁeld meets the require-

ments of the strategy conﬁguration. The advantage of

this approach is that the feasibility of each version of

a strategy is encapsulated in that version itself, so the

remaining parts of the model need not be aware of its

speciﬁc details.

The concrete versions of strategies can be used to

model different optimisation algorithms and therefore

vary in implementation detail as well as the restric-

tions they impose on the harvest operation.

3 MODEL IMPLEMENTATION

The model drives the development of a harvest plan-

ning system, which is developed using the Vienna

Development Method (VDM) and implemented us-

ing code generation. VDM is one of the longest-

established formal methods for the development of

computer-based systems. This method focuses on

the development and analysis of a system model ex-

pressed in a formal language.

The strategy pattern is based on object-oriented

(OO) features (Meyer, 1988), as enabled by the

VDM++ formal modelling language (Fitzgerald et al.,

2005). VDM++ is the OO dialect of VDM. Broadly

speaking, a VDM++ model consists of a series of def-

initions for types, functions, operations, etc. The OO

features of VDM++ allow for structuring the model

into classes and provide standard OO mechanisms

such as inheritance.

In addition to allowing for an effective imple-

mentation of the strategy pattern, the OO features

of VDM++ have other useful beneﬁts, including the

ability to add new versions of a strategy that reuse

parts of an existing strategy by changing only those

parts that must be different. Additionally, object-

orientation facilitates modularity and encapsulation

which, while not essential to develop the model, make

it easier to do so.

There are several reasons for choosing a formal

language such as VDM++ over an OO implemen-

tation language such as Java or C++. The use of

VDM++ promotes a high-level approach that ab-

stracts away details that are of little importance to

harvesting operations. The formal semantics under-

pinning the VDM language allow us to have conﬁ-

dence in the results and that there are no errors in the

language and tool that can “contaminate” the result.

Additionally, VDM has features that enable us to de-

scribe the properties of the model and its functions,

and these properties are constantly checked during

model execution. For example, in the model the ca-

pacity is expressed as a ﬂoating point number, which

must always be positive and smaller than 1. VDM

invariants allow us to attach such a property to the ca-

pacity variable in order to ensure that the model never

violates this. While that is a simple example, VDM

allows us to express any arbitrary property that can

be described in terms of ﬁrst-order logic. Many of

the beneﬁts of using VDM cannot be achieved using

implementation languages, which operate at a lower

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Figure 2: Load strategy hierarchy realised as a UML class diagram.

level of abstraction. In particular implementation lan-

guages must take things such as the underlying hard-

ware platform into account. Use of VDM allows us

to focus solely on the development of the strategies,

which is our primary concern.

4 MODEL EXECUTION

In order to execute the model, it is ﬁrst necessary to

conﬁgure the harvest operation by loading both the

ﬁeld and the resources, i.e. the State, and also one of

each class of strategy to guide the Execution Engine

during the simulation. Once this is done, the model is

executed and whenever the Execution Engine reaches

a point where it needs to make a decision that depends

on a strategy, it will consult whatever strategy it has

loaded and the output of the strategy will be used to

further progress execution of the model. As an ex-

ample, consider Figure 3. In this ﬁgure, the Execu-

tion Engine needs to know what vehicles are mov-

able at a given point in time. One particular version

of the strategy may allow the harvesters to move be-

cause they can ofﬂoad in the work rows. Another ver-

sion may not allow the harvesters to move because

they can only ofﬂoad in the headlands and they cannot

fully harvest the next work row.

In this way, differ-

ent versions of a strategy lead to different outcomes

in the model.

One of the key features of the model is the abil-

ity to explore strategy combinations and how their in-

teractions affect the performance of the harvest op-

eration. One way to do this is by ﬁxing two kinds

of strategies and varying the remainder (for example,

load strategies) thus investigating how a particular as-

pect of optimisation affects the overall harvest oper-

ation. Conversely, if external restrictions dictate the

In both of these examples, the route strategy consults the

load strategy as part of its calculation of movable vehicles.

Figure 3: Strategy dispatching realised as a UML sequence

diagram.

use of a particular strategy, then the other strategies

may be manipulated to ﬁnd the best solution within

the restrictions. For a small number of strategies, test-

ing the different scenarios of interest can be done with

manually written tests. However, when the number

of scenarios to be tested is large then an automated

combinatorial testing feature for VDM can be used

to concisely specify the various combinations and au-

tomatically generate and execute the corresponding

tests (Larsen et al., 2010).

Combining Harvesting Operation Optimisations using Strategy-based Simulation

4.1 Simulation Visualisation

As part of model execution, a log of all the important

events in the harvest operation is produced. Logged

events include vehicle movement, harvesting of a row,

passing load between harvesters and grain wagons,

etc. Once execution is completed, this log can be in-

spected in order to get a full understanding of the har-

vest operation outcome. This log can also be seen as a

harvest plan since it contains detailed instructions of

when and where the different vehicles must go.

In order to better understand what occurred during

the simulation, the log can also be analysed. However,

as manual inspection of the log is difﬁcult, a proof-of-

concept visualization tool was developed to analyse

the log and replay the simulation as shown in Fig-

ure 4. The ﬁgure shows a representation of the ﬁeld

partitioned into work rows and headlands. The black

square represents the harvester, the circle represents

the grain wagon and the square at the bottom repre-

sents the storage point. As the log is processed, the

visualiser displays an animation of the vehicles mov-

ing along the ﬁeld.

Figure 4: Simulation visualisation.

5 RESULTS

This section demonstrates the approach by report-

ing results of executing various simulations with the

model in order to explore the interactions between all

possible combinations of the strategies described in

section 2.1. Every execution was performed with the

same resources and on the same ﬁeld. The focus is

not on changing the parameters of the simulation such

as number of harvesters or harvester capacity but in

changing the strategy versions used in each simula-

tion.

The simulations were carried out on a repre-

sentation of a real ﬁeld located in the vicinity of

the Research Center at Foulum, Denmark (56°29’N,

9°35’E).

The yield of the ﬁeld is simulated and is

lower for headland rows than for working rows, as is

typical in real ﬁelds (due to excess soil damage, lower

nutrients, etc.). The yield is further constrained such

that a complete lap of the ﬁeld can be made without

exceeding the harvester capacity, and no single work-

ing row can exceed the capacity of the harvester. The

ﬁeld, partitioned into rows, is shown in Figure 5.

Figure 5: Agro Park ﬁeld.

The results of the simulations are summarised in

table 1. Each row in the table represents a particular

simulation, indexed by the Sim. (Simulation) column.

The Route and Load columns identify the combina-

tion of strategies used in each particular simulation

(the same deconﬂict strategy – Simple Deconﬂict – is

used for all simulations). The Op. Time (Operational

Time) column reports the duration of the harvest op-

eration in seconds and serves as an indication of how

well a combination of strategies performs. Finally the

Exec. Time (Execution Time) column reports the ac-

tual, physical time in seconds it takes to execute the

simulation.

The simulation was executed using a Java 7

code generated version of the model on a Fujitsu

LIFEBOOK U772 laptop with a 1.7GHz Intel Core

i5 processor and 8Gb of memory running a Windows

7 Professional Edition operating system.

The model has been applied to representations of various

other ﬁelds, both real and invented. However, these results

are not reported here as the focus of this paper is on strat-

egy interaction and not ﬁeld analysis.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Table 1: Results summary.

Sim. Route Load Op. Time [s] Exec. Time [s]

1 Greedy Headlands 425.558 12.619

2 Predeﬁned Headlands 497.38 13.417

3 Greedy In Field Static 420.694 12.319

4 Predeﬁned In Field Static 463.484 13.912

5 Greedy In Field Moving 410.298 7.056

6 Predeﬁned In Field Moving 446.854 7.25

7 Greedy Single Point 679.498 26.977

8 Predeﬁned Single Point 623.347 4.421

6 DISCUSSION

Table 1 shows that for the ﬁeld subject to analysis,

for most of the unloading strategies the Greedy Route

strategy produces a better solution, than the Prede-

ﬁned Route strategy as indicated by the operational

time. This is due to the harvesters route used as an in-

put for the Predeﬁned Route strategy being developed

as a coverage plan that ignores the coordination of the

service units. As the Greedy Route strategy was able

to enquire the constraints of the unloading strategy

while developing the harvesters route, the ﬁnal solu-

tion is more integrated and allows for more efﬁcient

operations. This indicates that it may be advantageous

to use optimisation approaches that consider both har-

vesters and service units when developing routes.

The Inﬁeld Moving Unloading strategy offers the

best operational times for both of the routing strate-

gies. This unloading strategy is likely to offer the best

solution as it allows the harvester to be completely full

when it ofﬂoads and does not require the harvester to

stop. It is also worth noting that the model allows this

hypothesis to be further conﬁrmed by adding addi-

tional route strategies and checking the resulting op-

erational times.

In terms of actual execution times, most combina-

tions yield similar results for Greedy and Predeﬁned

strategies. The exception is for the Single Point Un-

load strategy, where the Greedy version has a signif-

icantly higher execution time. This is mostly due to

the fact that many more routes have to be computed

for this particular combination, which makes it signif-

icantly slower than its Predeﬁned Route counterpart.

7 CONCLUSIONS AND FUTURE

WORK

In this paper, it has been shown how optimisation al-

gorithms for different aspects of the harvest operation

can be combined. This was achieved using a com-

bination of the strategy pattern and formal modelling

and simulation. The model can be executed with dif-

ferent strategy combinations, yielding harvest times

that can be used to compare the combinations. More

detailed analysis is also enabled by analysing a log

ﬁle that is generated for each execution, and which

contains all major events for that particular harvest.

The execution of the model has been demonstrated

on a representation of a real ﬁeld and a comparison

for the ﬁeld under analysis has been made based on

the results for 8 strategy combinations.

These results can be generalised to other kinds of

problems where there is a need to combine and com-

pare multiple algorithms for the same operation, but

where there is a signiﬁcant amount of data and com-

putation required in order to produce meaningful re-

sults.

Looking forward, the work presented in this pa-

per can be taken further by moving the harvest con-

trol to a distributed setting. The current version of

the model assumes a global view of the harvest op-

eration and directly controls the harvest participants

in a sequential manner. In the future, the system can

be moved to a distributed setting where the harvest

participants operate independently and must coordi-

nate and exchange information with each other in or-

der to carry out the harvest plan. This work can be

supported by the use of VDM-RT, a dialect of VDM

that extends VDM++ with support for modelling of

distributed systems (Verhoef, 2009).

Another avenue of future work lies in improving

the performance and scalability of the solution. Al-

though VDM is well suited for modelling and analy-

sis of object-oriented systems, it is not performance-

oriented and therefore the current solution does not

scale well enough to ﬁelds of larger sizes (10+ rows).

One potential way to address this is to move some

of the more computationally intensive operations to

a pure Java implementation and utilise the Overture

VDM-Java bridge (Nielsen et al., 2012) to connect

Combining Harvesting Operation Optimisations using Strategy-based Simulation

that implementation to the model.

ACKNOWLEDGEMENTS

A previous version of this paper appears in the ﬁrst

author’s PhD thesis. The work described in this paper

was partially carried out in the context of the Danish

High Technology Foundation research project Off-

line and on-line logistics planning of harvesting pro-

cesses. We would like to thank all our colleagues on

the project for their valuable contributions and feed-

back, particularly Peter Gorm Larsen, Claus Grøn

Sørensen, Dionysis Bochtis and Morten Bilde. We

also thank Kun Zhou for his assistance with the har-

vest visualisation.

REFERENCES

Bochtis, D. and Sørensen, C. (2009). The vehicle routing

problem in ﬁeld logistics part i. Biosystems Engineer-

ing, 104(4):447–457.

Broenink, J. F., Fitzgerald, J., Gamble, C., Ingram, C.,

Mader, A., Marincic, J., Ni, Y., Pierce, K., and Zhang,

X. (2012). Methodological guidelines 3. Technical

report, The DESTECS Project (INFSO-ICT-248134).

Edwards, G., Christiansen, M. P., Bochtis, D. D., and

Sørensen, C. G. (2013). A test platform for planned

ﬁeld operations using lego mindstorms nxt. Robotics,

2(4):203–216.

Edwards, G., Jensen, M. A. F., and Bochtis, D. D. (2015).

Coverage planning for capacitated ﬁeld operations un-

der spatial variability. International Journal of Sus-

tainable Agricultural Management and Informatics,

1(2):120–129.

Fitzgerald, J., Larsen, P. G., Mukherjee, P., Plat, N., and

Verhoef, M. (2005). Validated Designs for Object–

oriented Systems. Springer, New York.

Fitzgerald, J., Larsen, P. G., and Verhoef, M., editors

(2014). Collaborative Design for Embedded Systems

– Co-modelling and Co-simulation. Springer.

Gamma, E., Helm, R., Johnson, R., and Vlissides, R.

(1995). Design Patterns. Elements of Reusable

Object-Oriented Software. Addison-Wesley Profes-

sional Computing Series. Addison-Wesley Publishing

Company.

Hameed, I., Bochtis, D., Sørensen, C., Jensen, A. L., and

Larsen, R. (2013). Optimized driving direction based

on a three-dimensional ﬁeld representation. Comput-

ers and electronics in agriculture, 91:145–153.

Jensen, M. A. F. (2014). Operations planning for agricul-

tural machinery under capacity constraints. PhD the-

sis, Aarhus University.

Jensen, M. A. F., Bochtis, D., Sørensen, C. G., Blas, M. R.,

and Lykkegaard, K. L. (2012). In-ﬁeld and inter-ﬁeld

path planning for agricultural transport units. Com-

puters & Industrial Engineering, 63(4):1054–1061.

Jin, J. and Tang, L. (2010). Optimal coverage path planning

for arable farming on 2d surfaces. Transactions of the

ASABE, 53(1):283.

Larsen, P. G., Lausdahl, K., and Battle, N. (2010). Combi-

natorial Testing for VDM. In Proceedings of the 2010

8th IEEE International Conference on Software Engi-

neering and Formal Methods, SEFM ’10, pages 278–

285, Washington, DC, USA. IEEE Computer Society.

ISBN 978-0-7695-4153-2.

Meyer, B. (1988). Object-oriented Software Construction.

Prentice-Hall International.

Nielsen, C. B., Lausdahl, K., and Larsen, P. G. (2012).

Combining VDM with Executable Code. In Derrick,

J., Fitzgerald, J., Gnesi, S., Khurshid, S., Leuschel,

M., Reeves, S., and Riccobene, E., editors, Abstract

State Machines, Alloy, B, VDM, and Z, volume 7316

of Lecture Notes in Computer Science, pages 266–

279, Berlin, Heidelberg. Springer-Verlag.

Oksanen, T. and Visala, A. (2009). Coverage path planning

algorithms for agricultural ﬁeld machines. Journal of

Field Robotics, 26(8):651–668.

Scheuren, S., Stiene, S., Hartanto, R., Hertzberg, J., and

Reinecke, M. (2013). Spatio-temporally constrained

planning for cooperative vehicles in a harvesting sce-

nario. KI-K

unstliche Intelligenz, 27(4):341–346.

Spekken, M. and de Bruin, S. (2013). Optimized routing

on agricultural ﬁelds by minimizing maneuvering and

servicing time. Precision agriculture, 14(2):224–244.

Tullberg, J. (2010). Tillage, trafﬁc and sustainabilitya chal-

lenge for istro. Soil and Tillage Research, 111(1):26–

32.

Verhoef, M. (2009). Modeling and Validating Distributed

Embedded Real-Time Control Systems. PhD thesis,

Radboud University Nijmegen.

Zandonadi, R. S. (2012). Computational Tools for Improv-

ing Route Planning in Agricultural Field Operations.

PhD thesis, University of Kentucky.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications