Database Buffer Cache Simulator to Study and Predict Cache

Behavior for Query Execution

Chetan Phalak

, Rekha Singhal

and Tanmay Jhunjhunwala

Performance Engineering Research Center, Tata Consultancy Services, Andheri, Mumbai, India

Department of Mathematics and Computing, Delhi University, Delhi, India

Keywords: Database Buffer Cache, Data Blocks, Index Blocks, LRU, Simulator, Cache Hit, Cache Miss.

Abstract: Usage of an electronic media is increasing day by day and consequently the usage of applications. This fact

has resulted in rapid growth of an application's data which may lead to violation of service level agreement

(SLA) given to its users. To keep applications SLA compliance, it is necessary to predict the SQL query

response time before its deployment. The SQL query response time comprises of two elements, computation

time and IO access time. The latter includes time spent in getting data from disk subsystem and

database/operating system (OS) cache. Correct prediction of a SQL query performance needs to model

cache behavior for growing data size. The complex nature of data storage and data access pattern by queries

brings in difficulty to use only mathematical model for cache behavior prediction. In this paper, a Database

Buffer Cache Simulator has been proposed, which mimics the behavior of the database buffer cache. It can

be used to predict the cache misses for different types of data access by a SQL query. The simulator has

been validated using Oracle 11g and TPC-H benchmarks. The simulator is able to predict cache misses with

an average error of 2%.

1 INTRODUCTION

Cache plays a very crucial role in improving the

performance of any query/system. A good cache can

reduce I/O operations and lead to higher CPU

utilization. Accurately predicting the behavior of a

cache prior to the execution of a SQL query will

help us to predict the execution time and resources

that would be required. This paper is focused on

building database buffer cache simulator, which can

predict the behavior of the database buffer cache in

terms of cache misses on SQL query execution for

larger database size.

A cost based optimizer database provides an

execution plan of a query before its execution.

Execution plan shows different types of operations

occurred on tables participated in a query, for

example the Full Table Scan or Index Scan. Full

Table Scan accesses the data sequentially while the

Index Scan accesses data blocks using an index

created on one or more data field(s). Buffer cache

behavior for query execution strongly depends on

the type of data access and relative order of accessed

data. A query accessing data through index scan

require fetching of two types of blocks from storage

system. First data blocks that contains the address of

actual data and second, index blocks that contains

the address of associated data blocks.

Use of only mathematical model to simulate

working of the database buffer cache does not

capture the complexity in data access pattern. This

inability to create mathematical model forces the

adaption of programmatic approach. The proposed

simulator mimics the behavior of the database buffer

cache, which can be used to predict the cache misses

for different types of data access by a query. Both

data and index blocks are taken into account while

developing and validating the database buffer cache

simulator. Input to the simulator is various data

access patterns from the storage subsystem while

being transparent to the architecture of the storage

subsystem. The simulator provides database buffer

and OS cache hits, misses of blocks as output, which

is useful to judge the behavior of cache. Studying

the pattern of misses with respect to various data

patterns can lead to detection of miss reason and

optimization potentialities.

The simulator needs several inputs, which

include size of database buffer cache and OS cache,

numbers of rows reside in each data block, numbers

Phalak, C., Singhal, R. and Jhunjhunwala, T.

Database Buffer Cache Simulator to Study and Predict Cache Behavior for Query Execution.

DOI: 10.5220/0005936800710078

In Proceedings of the 5th International Conference on Data Management Technologies and Applications (DATA 2016), pages 71-78

ISBN: 978-989-758-193-9

of indices reside in each index block, data storage

pattern on disk and data access pattern. The

simulator provides output in the form of buffer

cache misses and OS cache misses. The simulator

output is validated with actual cache misses

perceived by a query during its execution. The

validation is performed by comparing cache misses

collected from query execution plan with cache

misses obtained from the simulator. For validation

purpose, custom queries on TPC-H benchmark

schema are used. The simulator can predict cache

misses with an average 2% of prediction error.

This paper is organized as follows. Section 2

reviews the prior work on cache simulation. The

design of database buffer simulator is presented in

Section 3. It describes how database cache works,

how simulation works and types of data access

patterns which had been taken into account while

building the simulator. Section 4 follows with

elaboration of the validation process in simulation

along with its results. The conclusion is given in

Section 5. References are mentioned in last section.

2 RELATED WORK

Simulation is a well-established technique for

studying the computer hardware and predicting the

system performance. Over the years, many

simulation systems with the goal of providing a

general tool for such studies have been developed.

Several works have been carried out related with

operating system’s cache simulation (Tao and

Weidendorfer, 2004; Tao and Karl, 2006; Holliday,

1992; Sugumar and Abraham, June 1993). Jie Tao

and Wolfgang Karl have simulated cache in detail to

detect bottleneck, reasons of misses and

optimization potentialities (Jie and Wolfgang, 2006).

Rabin A. Sugumar and Santosh G. Abraham have

modified the OPT algorithm with variety and came

up with efficient algorithm using which miss

characterization can be performed via reasonable

simulation resources (Sugumar and Abraham, 1993).

Several methods for cache simulation have been

developed; for example, use of address reference

traces (Holliday, 1992), use of runtime

instrumentation of applications (Tao and

Weidendorfer, 2004).

Along with OS cache, lot of work in the past few

years has been carried out in web cache simulation

as well (Cárdenas et al., 2005; Cárdenas et al.,

2004). L.G. Cárdenas and team have developed new

techniques for proxy cache simulation (Cárdenas et

al., 2004). In addition, L.G. Cárdenas has also

proposed a proxy-cache platform to check the

performance of a web object based on the multi-key

management techniques and algorithms. The

proposed platform developed in a modular way,

which allows the implementation of new algorithms

or policy proposals in an easy and robust manner

(Cárdenas et al., 2005).

There has been work done in literature on

simulating functional behaviour of database buffer

cache however they do not simulate cache misses for

larger data sizes. Daniel Moniz and Paul Fortier

have done the simulation analysis of a real time

database buffer manager (Moniz and Fortier 1996).

The authors have analysed the buffer management

policies and presented two new algorithms for page

replacement. However, they have not focussed on

database cache hits and misses of data as well as

index blocks for larger data size. Rekha Singhal and

Manoj Nambiar has talked about estimation of IO

access time on larger data size for various disk

access patterns during SQL query execution, but

does not include the delay in IO access time due to

effect of cache behaviour on larger data size

(Singhal and Nambiar, 2013). The simulator

proposed in this paper is about deriving database

cache hits and misses depending on the data access

pattern, which is not been analysed earlier.

3 DATABASE CACHE

SIMULATION

When a query is executed on the database, to locate

and retrieve any row in any table, several access

paths can be used. For example, Full Table Scan,

Row-id Scans Operation, Index Scans. When

database server performs a full table scan, it reads

blocks sequentially, while for index scan it first

needs to get an address of data block from index

block, hence reads blocks randomly. Thus for each

row, two physical blocks are demanded. Both these

blocks are first looked in the database buffer cache

and otherwise demanded from the OS. The OS then

itself looks for the blocks in its own cache and if still

not found, fetches them from the disk or physical

storage by calling an I/O operation. An important

thing to note is that index blocks can store a much

larger number of indices than the number of rows

stored in a data block. This means that the

probability of repetitive access of an index block is

always significantly higher than the probability of

repetitive access of a data block.

The relative order of data access block and data

storage location impacts the cache behavior.

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

Table 1: Varieties of data access and storage patterns.

Sr. No. Data Access Pattern Data Storage Pattern Repetition in storage Sorting in storage Uniformity in storage

1 Ordered

Ordered

(1,2,3,4,5,6…)

NO YES YES

2 Ordered

Ordered

(1,1,1,2,2,2,3,3,3…)

YES YES YES

3 Ordered

Ordered

(1,1,2,2,2,2,3,3,4…)

YES YES NO

4 Ordered

Ordered

(1,2,3,4,1,2,3,4…)

YES (Range) YES YES

5 Ordered

Pseudo-random

(1,21,41,2,22,42,3…)

YES (Pattern) NO YES

6 Random

Random

(5,9,1,5,2,9,12,5…)

YES NO NO

7 Random

Ordered

(any order)

NO NO NO

8 Random

Random

(4,9,1,2,7,12,19,3…)

NO NO NO

Table 1 shows, few types of data access pattern,

data storage pattern along with their specifications.

Due to variation in data access patterns, sequence of

blocks demanded to cache is also variable; hence,

cache behaves differently for different data access

pattern. Though cache behavior is mainly depends

on data access patterns, there are few other

parameters which affect the cache behavior. The

parameter list includes size of database buffer cache

and OS cache. As cache is larger, it can

accommodate more blocks and this will reduce the

number of misses, hence number of misses is

inversely proportional to the cache size. Along with

these, number of rows reside in each data block and

number of indices reside in each index block is also

important. Though data block size is constant, due to

variable length of row in table, number of rows

reside in data block varies from table to table.

Similarly, number of indices reside in each index

block also depends on width and depth of the tree

structures used to store the particular index. As more

number of data rows corresponds to single block,

less number of misses will occur. Finally, data

storage pattern on disk and data access pattern also

affect the quantity of misses. Therefore, these six

parameters need to be provided as inputs to the

cache simulator. Moreover, we can judge the cache

behavior from buffer cache misses of data and index

blocks; hence, these will be outputs of the simulator

as shown in Figure 1.

Figure 1: Database Buffer Cache Simulator.

Initially, a mathematical approach had been tried

to develop a simulator. Inputs to a model, other than

data access pattern and storage pattern are single

number, which can easily be taken as input.

However, for patterns the mathematical function was

needed to be generated. Such functions were

generated for sorted and uniformly distributed data,

for e.g. pattern number 1, 2 and 4 in Table 1.

Nevertheless, incorporating all previously discussed

patterns resulted in complexity. Difficulties in

creating a mathematical model resulted in

elimination of this approach. Later, a programmatic

Database Buffer Cache Simulator to Study and Predict Cache Behavior for Query Execution

approach has been followed. Incorporating all

patterns mentioned in Table 1 can be fulfilled by

developing a code to build the simulator.

The aim of this simulation is to mimic the actual

working of a database cache. The first step is to

virtually realize a file system made up of blocks,

which will contain all the data. It has been achieved

by writing a function that will calculate block

number from the data value. As this functionality

was different for various data storage patterns,

unique functions were written for every data storage

pattern. The cache developed will fetch these blocks

when requested. Data stored in these blocks may

have some pattern or complete random fashion. The

next step is to build a cache on this file system that

follows the Least Recently Used (LRU) policy. This

requires a queue that maintains the blocks present in

the cache in the order by which they have been

accessed and moves them according the

specifications of LRU replacement policy. Linked

List was the best suitable option to implement cache

in this case. Various operative functions were

written to add, update and delete entry in Linked

List, means cache, to maintain LRU policy. The max

size of this queue is predefined; actually, this will be

buffer cache size. Along with it, we need to provide

simulator the number of data rows per data block

and number of keys per index block as input.

Number of data rows per data block was calculated

by dividing total number of rows of table by the

number of blocks used by same table while, number

of keys per index block was calculated by dividing

total number of rows in the index by the number of

leaf blocks in the same index. In Oracle, the values,

number of rows and blocks of table, were collected

from USER_TABLES view (USER_TABLES),

while number of rows and leaf blocks in the index

were collected from USER_INDEXES view

(USER_INDEXES). These views are generated and

maintained by Oracle itself. These values must be

read only after execution of gather statistics

command on the schema.

Once this cache is in place, it acts as a black-box

which takes all required inputs and gives output in

the form of block hits and misses. This black-box is

a very strong tool as any type of query, be it single

table, multiple table or even many simultaneous

queries running over many tables; any type of access

can be described as a block access order. Once this

order learnt accurately black-box is expected to map

this order to the exact number of hits and misses.

Thus, a major task is to build functions that convert

data access pattern in any query to a corresponding

block access pattern.

4 SIMULATION VALIDATION

This simulation validation was conducted on a Linux

machine, having 4GB RAM and 400GB SAN Hard

disk, using Oracle 11G and TPC-H benchmark. The

Simulator was developed in java using JDK 1.6

version on Windows 8 Platform.

The validation of simulation is carried out for

different custom queries as shown in Table 2. The

queries may require unique or repeated access,

ordered or random access, complete or partial

access. In addition, the storage order of the data

blocks may be variable. The data could be sorted or

random, it could be in single or multiple instances,

where these instances could be arranged in various

different fashions. Hence, for validation purpose

queries were selected, which consequently created

data access patterns described in Table 1. This list of

queries, mentioned in Table 2, generates first five

data access patterns described in Table 1.

In each case, it was made sure that the column

accessed has an index built on it. First, row-ids will

be fetched from this index block and then the exact

row will be returned. Furthermore, special focus was

on getting accurate results for the index hits and

misses. The task was to write the exact function that

will map the data elements to their corresponding

blocks. Then, the block access patterns returned to

the cache were fed to predict hits and misses. Along

with it, the exact query fired on an Oracle database

and the actual numbers of physical reads were noted

from the query plan. Comparisons of these numbers

Table 2: Varieties of data access and storage patterns.

Access Pattern Query

1 select /*+ index(orders pk_orders) */ o_custkey from orders where o_orderkey >0;

2 select /*+ index(ps pk_partsupp) */ * from partsupp ps where ps_partkey>=0;

3 select /*+ index(lineitem pk_lineitem) */ l_quantity from lineitem where l_orderkey>=0;

4 select /*+ index(s supp_nk) */ * from supplier s where s_nationkey>=0;

5 select /*+ index(ps partsupp_sk) */ ps_partkey from partsupp ps where ps_suppkey>=0;

(Note: First column of Table 2 corresponds to the serial number of first column of Table 1)

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

can be used to calculate the error percentage. The

results, errors and possible reasons for the errors

have been discussed in the following sections.

4.1 Ordered Access and Data Storage

In this section, the first five access patterns

mentioned in Table 1 have been discussed. In these

cases, the location of each data element is precisely

known. It means that, all the blocks that need to be

fetched for every element are known. Hence, it was

easy to write the exact mathematical function to

mimic these access patterns.

For each of these patterns, the exact blocks

where each element is present are known. Thus, the

order in which blocks are going to be accessed is

known. This block access pattern can be fed to the

buffer cache simulator to predict the data and index

misses.

This validation was conducted on three data sizes

(see Table 3). Efficient synthetic data generator

(Phalak and Singhal, 2016) is been used to generate

data of various sizes. The simulator works almost

perfectly for all these patterns and negligible error

(approx 1%-2%) had been observed.

It can be seen from Table 3, a few errors are over

3%. However, these occur only when the data size is

very small and thus can be ignored. The other errors,

though very small, are arising because the number of

rows per block is taken as a constant number.

However, this number is actually the average

number of rows per block rounded off to the nearest

integer. For example, if this number comes out to be

43.458 for the customer table then, the simulator

will assume each block to contain 43 rows and will

predict the total number of blocks to be much greater

than the actual value. This is the reason behind the

1% to 2% error in the above validation.

4.2 Un-ordered Access and Unknown

Data Storage Order

The previous section shows that the cache simulator

can give excellent predictions, when it has

knowledge about the access pattern and data storage

pattern. In this section, the performance when data is

not accessed in any particular order or when it is not

stored on the disk in any particular order or both is

analyzed. In other words, it can be said that the

query will demand blocks in a pattern that is

completely random. At start, queries that randomly

access ordered data are considered.

For the first test case, a query that repeatedly and

randomly selects the entries in the custkey column of

customer table is designed. To achieve this, a nested

loop is forced on this column in the order of custkey

present in orders table. As orders table is 10 times

larger than the customer table each custkey will be

demanded 10 times. In addition, this table is sorted

by orderkey, thus, the custkey column is unsorted.

This is the case of a repeated random access on the

ordered data. It is simulated by generating random

numbers up to 10 times the range and then dividing

them by 10. Later, the calculated number fed to the

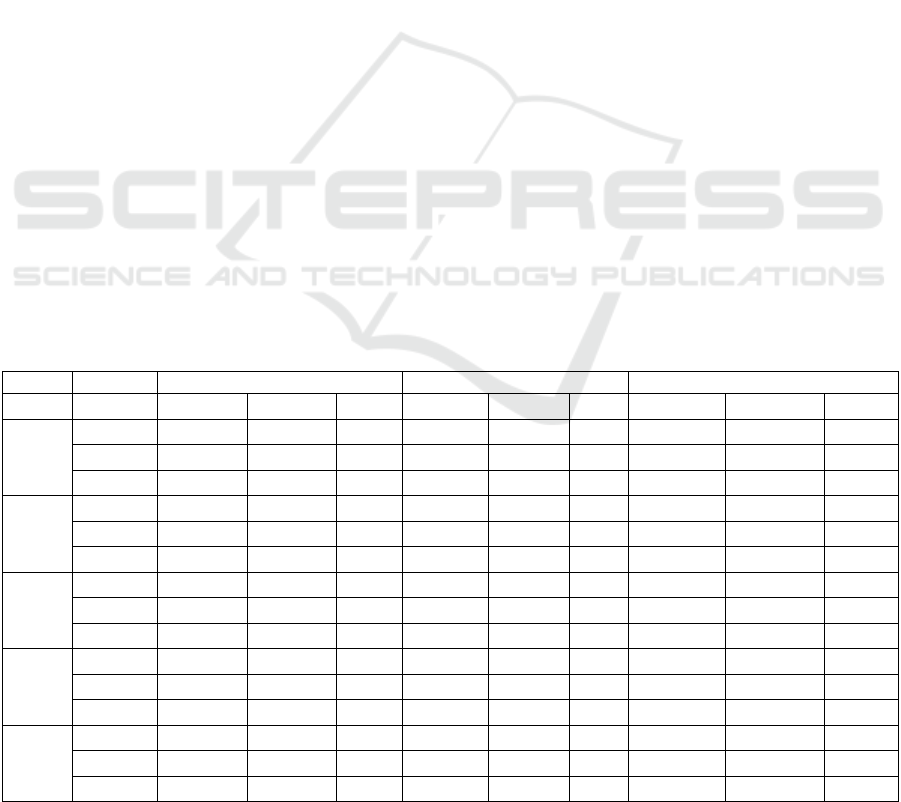
Table 3: Validation results for ordered access and known data patterns.

Pattern DB SIZE DB-MISS DB-index MISS OS-MISS

Predicted Actual Error Predicted Actual Error Predicted Actual Error

1GB 24194 24046 0.615 3304 3309 -0.15 439968 445280 -1.193

4GB 96775 95669 1.156 13334 13331 0.02 1761744 1771776 -0.5662

128GB 3147541 3132000 0.496 450705 451000 -0.07 57571936 57492768 0.1377

1GB 16667 16459 1.264 2111 2112 -0.05 300448 304968 -1.4821

4GB 66667 66135 0.804 8816 8811 0.06 1207728 1214248 -0.537

128GB 2133334 2137000 -0.172 302065 301000 0.35 38966384 39173264 -0.5281

1GB 109091 108245 0.782 15790 15755 0.22 1998096 2008648 -0.5253

4GB 436364 436585 -0.051 63493 63415 0.12 7997712 8041528 -0.5449

128GB 14222223 13875000 2.503 2127424 2125000 0.11 261594352 262564352 -0.3694

1GB 223 209 6.699 20 21 -4.76 3888 5744 -32.312

4GB 852 834 2.158 78 79 -1.27 14880 17340 -14.187

128GB 27235 26728 1.897 2496 2495 0.04 475696 476496 -0.1679

1GB 16667 16459 1.264 1674 1674 0 36682 37128 -1.2012

4GB 266748 263973 1.051 7033 7027 0.09 147400 164249 -10.258

128GB 8533416 8548000 -0.171 231152 231000 0.07 17529136 17588470 -0.3373

(Note: First column of Table 3 corresponds to the serial number of first column of Table 1)

Database Buffer Cache Simulator to Study and Predict Cache Behavior for Query Execution

cache after mapping to its corresponding block and

the results are shown in Table 4.

Table 4: Validation results of randomly accessed ordered

data.

DB SIZE TYPE Predicted Actual Error

128 GB

DB-MISS 160659873 170000000 -5.49

DB-index MISS 36878380 6616000 457.4

From Table 4, it can be seen that prediction of

index misses is erroneous with huge margin. What

could be the reason of such large error?

4.2.1 Skewness in Data

After the study of custkey column in orders table, it

can be seen that custkey columns entries are highly

skewed. They are not even close to being uniform as

in the assumption during the simulation. It was

assumed that each custkey must occur exactly ten

times at some random places in the orders table. The

truth however is that one-third of the total number of

custkeys is not even present in this column!

Furthermore, the custkeys which are present are not

uniformly repeated as well with their repetition

ranging from 1 to 25. It is a perfect example of a

highly skewed data, i.e. data where certain elements

in the range are more frequent than others.

It is a well-known fact that caches perform much

better, if there is even a slight amount of skew in the

data. This is because if there are some blocks that

are more frequently accessed than others, then there

is a higher chance of them being in the cache and

causing cache hits. Whereas if the data is completely

uniform, then all the blocks compete for a position

in the cache leading to much lower cache hits. This

effect on index blocks is much higher as each block

store large number of indices. Thus, the skewness in

data blocks gets magnified for index blocks.

Therefore, the reason of difference between

predicted results and that of the actual ones is that a

highly skewed data is assumed to be uniform. As

expected, the simulation returned much higher

number of misses than what actually were observed.

To confirm this, the next test case was taken, where

the data actually was accessed uniformly.

In this test case, the orderkey column in lineitem

is accessed in a random order. To achieve this, the

oracle (with help of hints) is forced to select

orderkey from orders table by taking a hash join of

custkey columns in customer and orders table. This

returns all the orderkeys exactly once but in a

random order. Then, the oracle is asked to select

orderkey from lineitem in this order. The exact

query:

select /*+USE_NL(l) ORDERED

USE_HASH(c o) */ c.c_custkey,

c.c_name,o.o_totalprice,l.l_return

flag, o.o_orderkey from customer

c, orders o, lineitem l where

o.o_orderkey=l.l_orderkey and

c.c_custkey = o.o_custkey;

In the code, it is simulated by using a random

number generator to return a random value of

orderkey. This value is converted into its

corresponding blocks and then given as an input to

the simulator. The results are shown in Table 5.

As expected, the predictions are much closer to

the actual values, especially in the case of index

misses. This was expected as index hit rates are the

ones that are highly affected by any kind of skew in

the data. However, the error is still very high and

there must be more factors to be understood.

4.3 Order in Randomness – Pseudo

Randomness

The next major source of error comes from the fact

that every random sequence is unique in itself and

cannot be equivalent to the other. This is because

after any random sequence is being generated it is

always possible that there are some hidden

undetectable patterns running through it. Thus, there

is no magnitude that can be associated with

randomness and all random patterns are actually

pseudo random.

Table 5: Validation results of randomly accessed ordered

data (Uniformly distributed data).

DB SIZE TYPE Predicted Actual Error

128 GB

DB-MISS 195799034 182000000 7.582

DB-index MISS 183175650 103000000 77.84

In the last test case, the random order in which

lineitem table is accessed can be derived from the

hash join between two other tables. The random

order, used for simulation is obtained from an

algorithm that makes use of the random number

generator, which is inbuilt in the java. Thus, these

two sequences, though both random, cannot be

assumed to be equivalent. The process of hash join

is giving rise to certain internal patterns, patterns

that can never arise from the entirely different

algorithm that the java inbuilt random number

generator uses. Thus, assuming these two to be

equivalent is also one of the sources of the error we

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

observed. Again, the effect is more on index blocks

as any pattern in data access will give rise to a more

compact pattern in index access.

To verify the entire idea, the next test case is

considered where there is random access to

randomly arranged data. This is with the hope that

any patterns left after the hash join will be destroyed

now when they are mapped to their corresponding

block. For this, a hash join between partkey columns

in part and partsupp table is taken. This returns all

the partkeys in some random order. These partkeys

are mapped to the partkey column in lineitem table

in the same order with the help of a forced nested

loop. As lineitem is sorted by the orderkey column,

the partkey column is arranged completely

randomly. Thus, in this case there is random access

on randomly arranged data. For simulating this

query, first a random number generator is used to get

the order of access. Then another generator is used

to determine the location of the data requested in the

table. This location is divided by block size to get

the block in which it is present, which is given as

input to the cache. The results obtained are displayed

in Table 6.

Table 6: Validation results of randomly accessed random

distributed data.

DB SIZE TYPE Predicted Actual Error

4 GB

DB-MISS 18871831 19000000 - 0.675

DB-index MISS 710390 645000 10.1

As seen, the error has now gone down from

77.8% to 10.1% for index blocks and from 7.5% to

0.6% for data blocks. Thus, the thinking that there

must be some hidden patterns in the random

sequence returned by hash join was probably

correct. Mapping that sequence to another random

pattern may have lead to reduction in its impact on

cache hits. In all, it can be concluded that different

random sequences can lead to very different

response from the cache.

To see this practically, a little change is made in

the way the random block of any element was

calculated. A random number generator used to

determine the element location. However, to get the

corresponding block the modulus of this number is

calculated with the total number of blocks. The

sequence now generated is also a random sequence

and is fed into the cache. Table 7 describes the

results.

Table 7: Validation results of randomly accessed data with

known location.

DB SIZE TYPE Predicted Actual Error

4 GB

DB-MISS 17899324 19000000 -5.793

DB-index MISS 705675 645000 9.41

It can be seen; there is significant change both in

the data and index misses predicted. This shows that

the choice of an algorithm for generating the

required random sequence can have an impact on the

accuracy of the predicted result. It is required that a

random sequence must be chosen which would be

closest to the one actually generated. This task is

difficult and sometimes impossible, as many local or

global patterns may exist in the access patterns

which are unknown. This is the shortcoming of this

simulation that without proper information about

block access pattern, approximating it is difficult

and sometimes impossible.

However, expecting the simulator to work on

random queries is like expecting the correct answer

without giving out the proper problem statement! On

the better side, it can be concluded that once proper

information about the type of access is known, the

proposed cache simulator will give almost 100%

accurate results. To show this practically, one last

validation was carried out. Here, the exact order of

access is extracted from a query and then given to

the simulator. Now that the code knows the exact

random order in which the table was accessed

accurate predictions are expected about the hits and

misses for both data and index blocks. This same

process was carried out on four different tables. The

results are shown in Table 8.

Thus, proposed cache simulator has handled the

case of random access accurately. This accuracy is

possible because the simulator has knowledge of the

exact order of access of the rows in table.

Table 8: Validation results of randomly accessed data with exact known location of blocks.

Query type DB SIZE DB-MISS DB-index MISS

Predicted Actual Error Predicted Actual Error

12345678… 1GB 24194 23963 0.964 3304 3313 -0.27

exactly 11112222…. 1GB 16667 16400 1.628 2111 2115 -0.19

almost 11112222… 1GB 550421 546000 0.81 16301 15880 2.65

appox. 1234512345… 1GB 3334 3413 -2.315 300 294 2.04

Database Buffer Cache Simulator to Study and Predict Cache Behavior for Query Execution

Hence it is safe to state that errors observed in

the other test cases, where randomness was

involved, arise only due to lack of information about

the ‘kind’ of random pattern being dealt with. Once

this gap is filled, the simulator definitely gives

accurate results for any type of query.

5 CONCLUSIONS

A simulator is discussed to mimic the behavior of

buffer cache during query execution. It is used to

predict cache misses perceived by the query

execution on a given data size. Various types of data

access and storage patterns are discussed which

plays a significant role in deciding the cache misses.

The cache simulator built, works with negligible

errors for the cases, where we have complete

information about the query access pattern and the

data distribution pattern. In these cases, approximate

2% error prediction was observed. Hence, the

simulator can handle any query as long as most of

the dynamics of the query are known. In case of

random queries, where we have no information

about data access and distribution pattern, the

simulator has difficulty in making predictions, thus,

simulator cannot be used for such queries. The error

that arises from this lack of information is higher in

magnitude for index blocks than for data blocks.

REFERENCES

Tao, Jie and Weidendorfer, Josef 2004. ‘Cache Simulation

Based on Runtime Instrumentation for OpenMP

Applications Reasoning about naming systems’,

Proceedings of the 37th annual symposium on

Simulation, pages 97-104.

Tao, Jie and Karl, Wolfgang 2006. ‘Detailed Cache

Simulation for Detecting Bottleneck, Miss Reason and

Optimization Potentialities’, Proceedings of the 1st

international conference on Performance evaluation

methodologies and tools, Article No. 62, ACM

1-59593-504-5/06/10.

Cárdenas, LG, Gil, JA, Domènech, J, Sahuquillo, J and

Pont, A 2005, ‘Performance Comparison of a Web

Cache Simulation Framework’, Proceedings of the

international conference on Advance Information

Networking and Applications, Pages 281-284, vol 2.

Cárdenas, LG, Sahuquillo, J, Pont, A and Gil, JA 2004,

‘The Multikey Web Cache Simulator: a Platform for

Designing Proxy Cache Management Techniques’,

Proceedings of the 12th Euromicro Conference on

Parallel, Distributed and Network-Based Processing,

Pages 390-397.

Holliday, Mark 1992, ‘Techniques for Cache and Memory

Simulation Using Address Reference Traces’,

International Journal of Computer Simulation.

Available from: https://www.researchgate.net/

publication/2811661_Techniques_for_Cache_and_Me

mory_Simulation_Using_Address_Reference_Traces.

Sugumar, Rabin and Abraham, Santosh June 1993,

‘Effective Simulation of Caches under Optimal

Replacement with Applications to Miss

Characterization’, Proceedings of the 1993 ACM

SIGMETRICS conference on Measurement and

modelling of computer systems, Pages 24-35.

Moniz, Daniel and Fortier, Paul 1996, ‘Simulation

analysis of a real-time database buffer manager’,

Proceedings of the 29th Annual Simulation

Symposium, Pages 252-259.

Phalak, Chetan and Singhal, Rekha November 2016,

‘Efficient Synthetic Data Generator for structured

Data’, Proceedings of CMG imPACT 2016.

Singhal, Rekha and Nambiar, Manoj November 2013,

‘Measurement Based Model to Study the Affect of

Increase in Data Size on Database Query Response

Time’, Proceedings of the Performance and Capacity

CMG 2013.

USER_TABLES. Available from: http://docs.oracle.com/

cd/B12037_01/server.101/b10755/statviews_2666.htm

USER_INDEXES. Available from: http://docs.oracle.com/

cd/B14117_01/server.101/b10755/statviews_2534.htm

DATA 2016 - 5th International Conference on Data Management Technologies and Applications