Scalable Versioning for Key-Value Stores

Martin Haeusler

University of Innsbruck, Department of Computer Science, Technikerstaße 21a, Innsbruck, Austria

Keywords:

Key-Value Store, Versioning, Historization, Persistence.

Abstract:

Versioning of database content is rapidly gaining importance in modern applications, due to the need for re-

liable auditing, data history analysis, or due to the fact that temporal information is inherent to the problem

domain. Data volume and complexity also increase, demanding a high level of scalability. However, imple-

mentations are rarely found in practice. Existing solutions treat versioning as an add-on instead of a ﬁrst-class

citizen, and therefore fail to take full advantage of its beneﬁts. Often, there is also a trade-off between perfor-

mance and the age of an entry, with newer entries being considerably faster to retrieve. This paper provides

three core contributions. First, we provide a formal model that captures and formalizes the properties of the

temporal indexing problem in an intuitive way. Second, we provide an in-depth discussion on the unique

beneﬁts in transaction control which can be achieved by treating versioning as a ﬁrst-class citizen in a data

store as opposed to treating it as an add-on feature to a non-versioned system. We also introduce an index

model that offers equally fast access to all entries, regardless of their age. The third contribution is an open-

source implementation of the presented formalism in the form of a versioned key-value store, which serves as

a proof-of-concept prototype. An evaluation of this prototype demonstrates the scalability of our approach.

1 INTRODUCTION

In recent years, the importance of versioning and his-

torization concepts has increased considerably. Mod-

ern applications face many challenges in the imple-

mentation of features involving temporal data, such as

auditing, traceability of changes and data history anal-

ysis, which are very difﬁcult to implement on appli-

cation level without dedicated support from the stor-

age backend. There are also concrete problems where

time is an inherent aspect of the processed data, such

as in Geo Information Systems for road planning (Shi

and Shibasaki, 2000) and spatio-temporal tracking of

wildlife (Urbano and Cagnacci, 2014).

In order to meet these requirements, much ef-

fort has been put into the inclusion of temporal as-

pects in databases. Early work in this area dates back

about 30 years when Snodgrass published his book

Temporal Databases (Snodgrass, 1986). Up until

now, several authors have proposed numerous, some-

times radically different, approaches (Ramaswamy,

1997), (Lomet et al., 2006), (Felber et al., 2014).

In 2012, IBM conducted an internal study (Saracco

et al., 2012), discovering that development time of a

business application that incorporates temporal infor-

mation decreases by up to 90% if a database with ver-

sioning capabilities is used. However, even though

the SQL 2011 Standard (ISO, 2011) introduced ex-

plicit support for versioning and temporal features,

few database vendors actually implement them. The

few existing implementations usually come as an add-

on, as for example in SQL Server (Lomet et al.,

2006), or by using trigger-based workarounds on reg-

ular non-versioned tables. Existing approaches can-

not take full advantage of versioning, due to the

fact that they were designed as non-versioned stores.

Also, performance often deteriorates considerably

when historical data instead of current information is

requested (Lomet et al., 2006). As we are going to

show in this paper, implementing versioning as a ﬁrst-

class citizen offers many advantages which cannot be

achieved by treating it as an extension to an existing,

non-versioned database. Furthermore, our approach

offers the same performance for all data items, regard-

less of their timestamps.

In this paper, we present a generic approach

for transaction time versioning (Jensen et al., 1998)

(sometimes also referred to as system time versioning

(ISO, 2011)), covering the entire end-to-end process,

from formal foundations to implementation

. Our

proof-of-concept prototype is called ChronoDB and is

This work was partially funded by the research project QE

LaB - Living Models for Open Systems (FFG 822740).

Haeusler, M.

Scalable Versioning for Key-Value Stores.

DOI: 10.5220/0005938700790086

In Proceedings of the 5th International Conference on Data Management Technologies and Applications (DATA 2016), pages 79-86

ISBN: 978-989-758-193-9

presented in detail in Section 3. We work with a key-

value data model, as it is a simple format that doesn’t

distract from the versioning concepts. Just like the

popular B-Tree structure, it is generic and expressive

enough to be used as a backing store for many record

formats, including tables, documents or graphs. How-

ever, as we are going to explain in more detail in Sec-

tion 6, the intended usage of ChronoDB is to act as a

storage backend for a graph database.

The remainder of this paper is structured as follows.

In Section 2, we provide the formal foundations of our

approach. Section 3 contains implementation consid-

erations for the formalism. We continue with an eval-

uation of the presented material in Section 4 and a

discussion on related work in Section 5, before con-

cluding the paper with an outlook to future work in

Section 6 and a summary in Section 7.

2 FORMAL FOUNDATION

Salzberg and Tsotras identiﬁed three key capabilities

which have to be supported by a data store in or-

der to provide the full temporal feature set (Salzberg

and Tsotras, 1999), restricted to timestamps instead

of time ranges:

• Pure-Timeslice Query: Given a point in time

(e.g. date & time), ﬁnd all keys that existed at

that time.

• Range-Timeslice Query: Given a set of keys and

a point in time, ﬁnd the value for each key which

was valid at that time.

• Pure-Key Query: Given a set of keys, for each

key ﬁnd the values that comprise its history.

We use these three core capabilities as the functional

requirements for our formalization approach. For

practical reasons, we futhermore require that inserted

entries never have to be modiﬁed again. In this way,

we can achieve a true append only store. In order to

maintain the traceability of changes over time (e.g.

for auditing purposes), we also require that the his-

tory of a key must never be altered, only appended.

The key idea behind our formalism is based on the

observation that temporal information always adds an

additional dimension to a dataset. A key-value for-

mat has only one dimension, which is the key. By

adding temporal information, the two resulting di-

mensions are the key, and the time at which the value

was inserted. Therefore, a matrix is a very natural

ﬁt for formalizing the versioning problem, offering

the additional advantage of being easy to visualize.

The remainder of this section consists of deﬁnitions

which deﬁne the formal semantics of our solution, in-

terleaved with ﬁgures and (less formal) textual expla-

nations.

Deﬁnition 1. Temporal Data Matrix

Let T be the set of all timestamps with T ⊆ N. Let S

denote the set of all non-empty strings and K be the

set of all keys with K ⊆ S . Let B deﬁne the set of all

binary strings with B ⊆ {0, 1}

∗

∪ {null} and ε ∈ B be

the empty binary string with ε 6= null. We deﬁne the

Temporal Data Matrix D ∈ B

∞×∞

as:

D : T × K → B

We deﬁne the initial value of a given Temporal Data

Matrix D as:

t,k

:= ε ∀t ∈ T, ∀k ∈ K

In Deﬁnition 1 we deﬁne a Temporal Data Matrix,

which is a key-value mapping enhanced with tempo-

ral information. Note that the number of rows and

columns in this matrix is inﬁnite. In order to retrieve

a value from this matrix, a key string and a timestamp

are required. We refer to such a pair as a Temporal

Key. The matrix can contain a bit array in every

cell, which can be interpreted as the serialized rep-

resentation of an arbitrary object. The formalism is

therefore not limited to any particular value type. The

dedicated null value (which is different from all other

bitstrings and also different from the ε values used to

initialize the matrix) will be used as a marker that in-

dicates the deletion of an element later in Deﬁnition 3.

In order to guarantee the traceability of changes,

entries in the past must not be modiﬁed, and new en-

tries may only be appended to the end of the history,

not inserted at an arbitrary position. We use the notion

of a dedicated now timestamp for this purpose.

Deﬁnition 2. Now Operation

Let D be a Temporal Data Matrix. We deﬁne the func-

tion now : B

∞×∞

→ T as:

now(D) = max({t|k ∈ K, D

t,k

6= ε} ∪ {0})

Deﬁnition 2 introduces the concept of the now time-

stamp, which is the largest (i.e. latest) timestamp at

which data has been inserted into the store so far, ini-

tialized at zero for empty matrices. This particular

timestamp will serve as a safeguard against temporal

inconsistencies in several functions. We continue by

deﬁning the temporal counterparts of the put and get

operations of a key-value store.

Deﬁnition 3. Temporal Write Operation

Let D be a Temporal Data Matrix. We deﬁne the func-

tion put : B

∞×∞

× T × K × B → B

∞×∞

as:

put(D, t, k, v) = D

with v 6= ε, t > now(D) and

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

i, j

(

v if t = i ∧ k = j

i, j

otherwise

The write operation put replaces a single entry in a

Temporal Data Matrix by specifying the exact coordi-

nates and a new value for that entry. All other entries

remain the same as before. Please note that, while v

must not be ε in the context of a put operation (i.e.

a cell cannot be “cleared”), v can be null to indicate

a deletion of the key k from the matrix. Also, we re-

quire that an entry must not be overwritten. This is

given implicitly by the fact that each put advances

the result of now(D), and further insertions are only

allowed after that timestamp. Furthermore, write op-

erations are not permitted to modify the past in order

to preserve consistency and traceability, which is also

asserted by the condition on the now timestamp. This

operation is limited in that it allows to modify only

one key at a time. In the implementation, we will

generalize it to allow simultaneous insertions in sev-

eral keys via transactions.

Deﬁnition 4. Temporal Read Operation

Let D be a Temporal Data Matrix. We deﬁne the func-

tion get : B

∞×∞

× T × K → B as:

get(D,t, k) :=











t,k

if D

t,k

6∈ {ε, null}

u,k

if D

t,k

∈ {ε, null}∧ ∃u ≥ 0

ε otherwise

with t ≤ now(D) and

u := max({x|x ∈ T, x < t, D

x,k

6∈ {ε, null}}∪ {−1})

The function get ﬁrst attempts to return the value at

the coordinates speciﬁed by the key and timestamp.

If that position is empty, we scan for the entry

in the same row with the highest timestamp and

a non-empty value, considering only entries with

lower timestamps than the request timestamp. In the

formula, we have to add −1 to the set from which u is

chosen to cover the case where there is no other entry

in the row. If there is no such entry (i.e. u = −1),

we return the empty binary string, otherwise we re-

turn the entry with the largest encountered timestamp.

This process is visualized in Figure 1. In this ﬁg-

ure, each row corresponds to a key, and each column

to a timestamp. The depicted get operation is work-

ing on timestamp 5 and key ’d’. As D

5,d

is empty, we

attempt to ﬁnd the largest timestamp smaller than 5

where the value for the key is not empty, i.e. we move

left until we ﬁnd a non-empty cell. We ﬁnd the result

in D

1,d

and return v1. This is an important part of the

versioning concept: a value for a given key is assumed

to remain unchanged until a new value is assigned to

it at a later timestamp. This allows any implementa-

tion to conserve memory on disk, as writes only occur

time

keys

0 1 2 3 4 5 6 7

...

get t=5, k='d'

ε ε ε ε ε ε ε ε

ε ε ε ε ε ε ε

ε ε ε ε εε

ε ε ε ε ε ε

ε ε ε ε ε ε ε ε

ε ε ε ε ε ε ε

Figure 1: Performing a get operation on a Temporal Data

Matrix.

if the value for a key has changed (i.e. no data dupli-

cation is required between identical revisions). Also

note that we do not need to update existing entries

when new key-value pairs are being inserted, which

allows for pure append only storage. In Figure 1, the

value v1 is valid for the key ’d’ for all timestamps be-

tween 1 and 5 (inclusive). For timestamp 0, the key

’d’ has value v0. Following this line of argumentation,

we can generalize and state that a row in the matrix,

identiﬁed by a key k ∈ K, contains the history of k.

This is formalized in Deﬁnition 5. A column, iden-

tiﬁed by a timestamp t ∈ T , contains the state of all

keys at that timestamp, with the additional considera-

tion that value duplicates are not stored as they can be

looked up in earlier timestamps. This is formalized in

Deﬁnition 6.

Deﬁnition 5. History Operation

Let D be a Temporal Data Matrix, and t be a time-

stamp with t ∈ T,t ≤ now(D). We deﬁne the function

history : B

∞×∞

× T × K → 2

as:

history(D, t, k) := {x|x ∈ T, x ≤ t, D

x,k

6= ε}

In Deﬁnition 5, we deﬁne the history of a key k up

to a given timestamp t in a Temporal Data Matrix D

as the set of timestamps less than or equal to t that

have a non-empty entry for key k in D. Note that the

resulting set will also include deletions, as null is a

legal value for D

x,k

in the formula. The result is the

set of timestamps where the value for the given key

changed. Consequently, performing a get operation

for these timestamps with the same key will yield dif-

ferent results, producing the full history of the tempo-

ral key.

Deﬁnition 6. Keyset Operation

Let D be a Temporal Data Matrix, and t be a time-

stamp with t ∈ T,t ≤ now(D). We deﬁne the function

keyset : B

∞×∞

× T → 2

as:

keyset(D,t) := {x |x ∈ K, get(D,t, x) 6= ε}

Scalable Versioning for Key-Value Stores

time

keys

0 1 2 3 4 5 6 7

...

ε ε ε ε ε ε ε

ε ε ε ε ε

ε ε ε εε

ε ε ε ε ε

ε ε ε ε ε ε ε ε

ε ε ε ε ε ε ε

null

keyset / version at t=5

v1 v2

Figure 2: Performing a keyset or version operation on a

Temporal Data Matrix.

As shown in Deﬁnition 6, the key set in a Tempo-

ral Data Matrix changes over time. We can retrieve

the key set at any desired time by providing the ap-

propriate timestamp t. Note that this works for any

timestamp in the past, in particular we do not require

that a write operation has taken place precisely at t

in order for the corresponding key(s) to be contained

in the key set. In other words, the precise column of t

may consist only of ε entries, but the key set operation

will also consider earlier entries which are still valid

at t. The version operation introduced in Deﬁnition

7 operates in a very similar way, but returns tuples

containing keys and values, rather than just keys.

Deﬁnition 7. Version Operation

Let D be a Temporal Data Matrix, and t be a time-

stamp with t ∈ T,t ≤ now(D). We deﬁne the function

version : B

∞×∞

× T → 2

K×B

version(D, t) := {hk, vi|

k ∈ keyset(D,t), v = get(D,t, k)}

Figure 2 illustrates the key set and version operations

by example. In this scenario, the key set (or version)

is requested at timestamp t = 5. We scan each row

for the latest non-ε entry, and add the corresponding

key of the row to the key set, provided that a non-ε

right-most entry exists (i.e. the row is not empty) and

is not null (value was not removed). In this example,

keyset(D,5) would return {a, c, d}, assuming that

all non-depicted rows are empty. b and f are not in

the key set, because their rows are empty (up to and

including timestamp 5), and e is not in the set because

its value was removed at timestamp 4. If we would

request the key set at timestamp 3 instead, e would

be in the key set. The operation version(D, 5) returns

{ha, v0i, hc, v2i, hd, v4i} in the example depicted in

Figure 2. The key e is not represented in the version

because it did not appear in the key set.

Table 1: Mapping capabilities to operations.

Capability Realization in formalism

Pure-Timeslice Equivalent to keyset operation

Range-Timeslice One get operation per given key

Pure-Key One history operation per given key

With the given set of operations, we are able to an-

swer all three kinds of temporal queries identiﬁed by

Salzberg and Tsotras (Salzberg and Tsotras, 1999), as

indicated in Table 1. Due to the restrictions imposed

onto the put operation (see Deﬁnition 3), data cannot

be inserted before the now timestamp (i.e. the his-

tory of an entry cannot be modiﬁed). Since the valid-

ity range of an entry is determined implicitly by the

empty cells between changes, existing entries never

need to be modiﬁed when new ones are being added.

The formalization therefore fulﬁlls all requirements

stated at the beginning of this section.

3 IMPLEMENTATION

We implemented the concepts presented in Section

2 in a prototype called ChronoDB. It is a fully

ACID-compliant, process-embedded, temporal key-

value store written in Java. The intended use of

ChronoDB is to act as the storage backend for a graph

database, which is the main driver behind numerous

design and optimization choices. The full source code

is freely available under a GPL license

3.1 Implementing the Matrix

As the formal foundation includes the concept of a

matrix with inﬁnite dimensions, a direct implemen-

tation is not feasible. However, a Temporal Data

Matrix is typically very sparse. Instead of storing a

rigid, inﬁnite matrix structure, we focus exclusively

on the non-empty entries and expand the underlying

data structure as more entries are being added.

There are various approaches for storing ver-

sioned data on disk (Lomet and Salzberg, 1989; Eas-

ton, 1986; Nascimento et al., 1996). We reused ex-

isting, well-known and well-tested technology for our

prototype instead of designing custom disk-level data

structures. The temporal store is based on a regular

-Tree (Salzberg, 1988). We make use of the imple-

mentation of B

-Trees provided by MapDB

. In order

to form an actual index key from a Temporal Key, we

concatenate the actual key string with the timestamp

https://github.com/MartinHaeusler/chronos/tree/master/

chronodb

http://www.mapdb.org/

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

(left-padded with zeros to achieve equal length), sep-

arated by an ’@’ character. Using the standard lexi-

cographic ordering of strings, we receive an ordering

as shown in Table 2. This implies that our B

-Tree

is ordered ﬁrst by key, and then by timestamp. The

advantage of this approach is that we can quickly de-

termine the value of a given key for a given timestamp

(i.e. get is reasonably fast), but the keyset (see Deﬁni-

tion 6) is more expensive to compute.

Table 2: Ascending Temporal Key ordering by example.

Order Temporal Key Key String Timestamp

0 a@0123 a 123

1 a@0124 a 124

2 a@1000 a 1000

3 aa@0100 aa 100

4 b@0001 b 1

5 ba@0001 ba 1

The put operation appends the timestamp to the

user key and then performs a regular B

-Tree inser-

tion. The temporal get operation requires retrieving

the next lower entry with the given key and time-

stamp. This is similar to regular B

-Tree search, ex-

cept that the acceptance criterion for the search in the

leaf nodes is “less than or equal to” instead of “equal

to”, provided that nodes are checked in descending

key order. MapDB already provides this functionality.

After ﬁnding the next lower entry, we need to apply

a post-processing step in order to ensure correctness

of the get operation. Using Table 2 as an example, if

we requested aa@0050, the result of the “next lower

search” is a@1000. The key string in this temporal

key (a) is different from the one which was requested

(aa). In this case, we can conclude that the key aa did

not exist up to the requested timestamp (50), and we

return null instead of the retrieved result.

Due to the way we set up the B

-Tree, adding a

new revision to a key (or an entirely new key) has

the same runtime complexity as inserting an entry

into a regular B

-Tree. Temporal search also has the

same complexity as regular B-Tree search, which is

O(log(n)), where n is the number of entries in the

tree. From the formal foundations onward, we assert

by construction that our implementation will scale

equally well when faced with one key and many ver-

sions, many keys with one revision each, or any dis-

tribution in between. This is also consistent with our

experimental results, which will be presented in Sec-

tion 4. An important property of our data structure

setup is that, regardless of the versions-per-key dis-

tribution, the data structure never degenerates into a

list, maintaining an access complexity of O(log(n))

by means of regular B

-Tree balancing without any

need for additional algorithms.

Server OLAP clientOLTP client

query

result

query

result

start TX

end TX

start TX

delay

modify

result

Server OLAP clientOLTP client

query+ts

result

query+ts

result

start TX

end TX

start TX

modify+ts

delay

result

end TX

No versioning, pessimistic locking With versioning & pessimistic locking

Figure 3: Transaction control with and without versioning.

3.2 Transaction Control

Consistency and reliability are two major goals in

ChronoDB, therefore we offer full ACID transactions

with the highest possible read isolation level (serial-

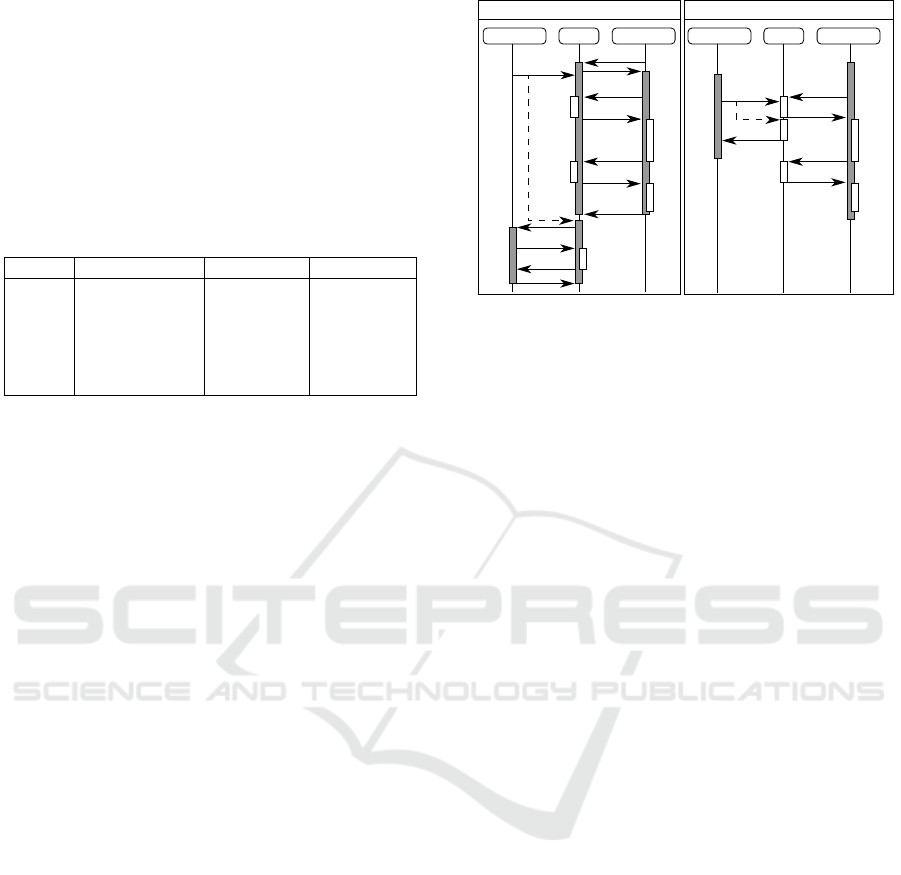
izable, see (ISO, 2011)). Figure 3 shows an example

with two sequence diagrams with identical transac-

tion schedules. A database server is communicating

with an Online Analytics Processing (OLAP (Codd

et al., 1993)) client that owns a long-running transac-

tion (indicated by the gray bars). The process involves

messages (arrows) sending queries with timestamps

and computation times (blocks labeled with “c”) on

both machines. Then, a regular Online Transaction

Processing (OLTP) client wants to make changes to

the data which is analyzed by the OLAP client. The

left ﬁgure shows what happens in a non-versioned

scenario with pessimistic locking. The server needs

to lock the relevant contents of the database for the

entire duration of the OLAP transaction, otherwise

we risk inconsistencies due to the incoming OLTP

update. We need to delay the OLTP client until

the OLAP client releases the transaction. Modern

databases use optimistic locking and data duplication

techniques to mitigate this issue, but the core problem

remains: the server needs to dedicate resources (e.g.

locks, RAM. . . ) to client transactions over their en-

tire lifetime. With versioning, the OLAP client sends

the query plus the request timestamp to the server.

This is a self-contained request, no additional infor-

mation or resources are needed on the server, and yet

the OLAP client achieves full isolation over the en-

tire duration of the transaction, because it always re-

quests the same timestamp. While the OLAP client

is processing the results, the server can safely al-

low the modiﬁcations of the OLTP client, because it

is guaranteed that a valid modiﬁcation will only ap-

pend to the history. The data at timestamp on which

the OLAP client is working is immutable. Client-

Scalable Versioning for Key-Value Stores

side transactions are merely containers for transient

change sets and metadata, most notably the timestamp

on which the transaction is working. Security con-

siderations aside, they can be created (and disposed)

without involving the server. This does not solve the

problem of write conﬂicts on the same key-value pair

and timestamp, which we currently resolve in a “ﬁrst

come ﬁrst served” fashion, rejecting the other con-

ﬂicting transaction.

3.3 Disadvantages & Open Issues

A disadvantage of our approach (which we share with

many other techniques, such as (Lomet et al., 2006)

and (Ramaswamy, 1997)) is that each get query, even

though it returns a single value, shares many char-

acteristics with range queries. Therefore, we can-

not make use of techniques that would allow for bet-

ter performance, but are applicable only for point

searches (e.g. hashing techniques). We are restricted

to tree structures that allow for quick identiﬁcation

of neighboring nodes. Therefore, the actual perfor-

mance of our versioning concept implementation is

tied very closely to the performance of the underly-

ing tree structure. Storing all entries in a single tree

provides many advantages, but also implies that the

search time for a key will increase as new versions are

added to other keys, because the tree as a whole grows

larger. We intend to mitigate this problem in the fu-

ture by splitting the key set into segments, where each

segment is represented by its own tree. We aknowl-

edge the fact that the keyset operation is very costly

in our data structure, as its general direction (given a

version ﬁnd all keys) is exactly opposed to our index

structure (given a key ﬁnd a version). We are cur-

rently investigating the possibility of applying sec-

ondary indices to alleviate this problem, as the abil-

ity to query entries by attributes (e.g. ﬁnd all per-

sons where the attribute “name” contains “Eva”) in

many cases replaces the need for the keyset opera-

tion. Range queries on the timestamp are expensive

as well, which is a direct consequence of the design,

as the system was built to handle interactions on sin-

gle timestamps as transparently as possible.

4 EVALUATION

In Section 2 we provided an argumentation why the

distribution of temporal entries over keys and ver-

sions does not have an impact on performance. In

other words, our implementation performs equally

well when faced with 1 key with many versions, many

keys with one version each, or any other distribution

Figure 4: Distribution of entries over Keys and Versions.

in between these two extremes.

Figure 4 shows a box plot for 5 such distributions.

For this experiment, a dataset of 100.000 entries was

generated randomly, subject to the distributions indi-

cated on the X-Axis. The corner case with V : 0%

implies that all keys have exactly one revision each.

K : 0% means that there is exactly one key, and all

other entries represent revisions of that key. On the

resulting state, 1000 temporal get operations were ex-

ecuted, which were random in both the requested key

and the associated timestamp (within the bounds of

the dataset). The aggregated execution time of these

operations is depicted on the Y-Axis. The experiment

was repeated 500 times for each distribution, result-

ing in the given box plots. The entire process was ex-

ecuted without any caching in ChronoDB itself. The

box plots clearly show that there is no deﬁnitive re-

lationship between the distribution of entries and the

access time of read operations, in particular there is

no consistent linear growth in any direction. We at-

tribute the existing minor differences to implementa-

tion details of the underlying B

-Tree, disk caches on

the hardware and operating system level, as well as

operating system background processes.

Figure 5: Access times for increasing number of Versions.

We claimed earlier that our versioning approach

is scalable for a large number of keys, but also for a

large number of versions. Based on the results pre-

sented in Figure 4, we argue that our versioning tech-

nique is as scalable as the underlying B

-Tree struc-

ture. What is still left to be discussed is the progres-

sion of the increase in access time, as more versions

are being added to a key. Figure 5 displays this par-

ticular scenario. A single key-value pair was inserted

into the store, and revisions were added gradually.

DATA 2016 - 5th International Conference on Data Management Technologies and Applications

The X-Axis displays the number of versions in the

store for that particular key. The Y-Axis shows the

time for 1000 get calls on that key, at random times-

tamps (within the range of the dataset), at the base

(i.e. initial) revision, and at the head revision, re-

spectively. The experiment was repeated 500 times

for each data point. The results clearly indicate the

logarithmic growth in access time, as the number of

versions increases. In particular, the access time does

not increase linearly with the number of versions. In

contrast to the approach presented in (Lomet et al.,

2006), there is almost no difference in response times

when different versions are requested, regardless of

the timestamp. Head and base revisions are retrieved

faster on average is due to the fact that their timestamp

is known precisely, whereas for random timestamps,

the next-lower search in the B

-Tree may trigger an

additional disk access. These results are consistent

with Figure 4, as they represent a more detailed view

on a similar scenario as the right-most box plot.

All presented results were measured on a ma-

chine running Windows 10 (64bit) with an Intel Core

i7-5820K processor (3.30GHz), a Crucial MX200

500GB SATA SSD drive and 2GB of RAM avail-

able to the Java Virtual Machine, provided by JDK

1.8.0 66.

5 RELATED WORK

Our work is inspired by the publication by Ra-

maswamy (Ramaswamy, 1997). Both our and Ra-

maswamy’s work solve the same problems. We even

make use of the same data structure, a B

-Tree, and

employ a similar approach for constructing the keys

for the tree. In contrast to Ramaswamy, we do not ex-

plicitly index time ranges on disk. The time range

in which a value is valid for a given key is deter-

mined implicitly in our approach, as a value for a key

is valid until it is overwritten by another value. Un-

like Ramaswamy, we do not need to modify existing

entries in our data structure when new entries are be-

ing added. Also, deletions of entries do not impact

our data structure in any different way than inserts or

modiﬁcations, which was an issue in Ramasway’s so-

lution.

The work of Felber et al. (Felber et al., 2014) is

a recent representative of techniques that use explicit

version identiﬁers. For each key, a list of versions is

stored as the value. Using the version identiﬁer (i.e.

the index in the list), any version can be accessed.

While this approach is acceptable for cases where the

data stored in each key is unrelated from other keys

(e.g. documents), it is not possible to reconstruct a

consistent view of all key-value pairs at a given ver-

sion, because version lists grow independently of each

other. By using timestamps, we are able to corellate

histories of different keys. Due to the way we laid

out our B

-Tree, our approach never degenerates into

linear search on disk, even in cases with extremely

unbalanced distributions of keys and versions.

The project ImmortalDB is an effort to integrate

transaction time versioning concepts into Microsoft

SQL Server (Lomet et al., 2006). This is done by

linking each entry with its predecessor using point-

ers, creating a history chain in the process. The bene-

ﬁt of this implementation is that the performance of

queries on the latest version is almost the same as

for an unversioned table, but it degenerates in a linear

fashion as the requested timestamp is moved further

into the past, because the history chain has to be tra-

versed linearly. This is the exact opposite behaviour

of ChronoDB, which offers equal performance on all

versions without linear search, but has lower perfor-

mance on the head revision when a large history is

present. Because of the fact that SQL Server was de-

signed as a non-versioned store, ImmortalDB cannot

take advantage of the beneﬁts in transaction manage-

ment identiﬁed in Section 3.

Database systems like Cassandra (Lakshman and

Malik, 2010) and Dynamo (DeCandia et al., 2007)

also incorporate temporal aspects. These systems use

temporal information to resolve conﬂicts in the data

that arise from the principle of eventual consistency.

They do not allow to explicitly query past states of the

stored data, and we therefore do not consider them to

be versioned stores. However, implementing our for-

malism on top of them in a middleware layer may be

feasible and will be subject to future research.

6 FUTURE WORK

Our implementation of the concepts presented in Sec-

tion 2 provides scalable versioning in a key-value

store. Such a store is conceptually simple, but of-

ten inconvenient for programmers to use when com-

plex data structures have to be mapped to a key-value

representation in application code. For that reason,

we started developing a graph computing frontend

for ChronoDB, which implements the popular Apache

TinkerPop API

and will be the ﬁrst implementation

to feature versioning support, named ChronoGraph.

Projects such as Titan

have already demonstrated

that persisting graphs into a key-value store back-

end is a feasible way to achieve high performance.

https://tinkerpop.incubator.apache.org/

http://thinkaurelius.github.io/titan/

Scalable Versioning for Key-Value Stores

With Gremlin, the integrated query language provided

by TinkerPop, we can also provide a powerful query

mechanism to client developers, completely hiding

the key-value store in the background. With Chrono-

Graph, it will be possible for the ﬁrst time in any Tin-

kerPop implementation to analyze the history of any

given graph element (vertex or edge), as well as run-

ning a given Gremlin query on any past graph state.

Further research on ChronoDB will include how

caching with temporal aspects can be implemented.

We are also investigating potential opportunities for

taking advantage of our versioning concept in order

to distribute the content of our store over several ma-

chines. Secondary indexing in a versioned environ-

ment is also a subject of our ongoing research, as well

as lightweight branching (as seen in traditional ver-

sion control systems, e.g. Git or SVN).

7 SUMMARY & CONCLUSION

In this paper we presented a concept for scalable ver-

sioning in key-value stores. We motivated the prob-

lem at hand by pointing out concrete use cases found

in literature such as road planning in Global Informa-

tion Systems and wildlife tracking, as well as describ-

ing the advantages to be gained from versioned data

stores in general software engineering. Our ﬁrst con-

tribution is the formalization of the transaction time

versioning problem in the form of a Temporal Data

Matrix, which provides precise semantics of all oper-

ations and an intuitive way of visualizing even com-

plex temporal scenarios. We also provided a map-

ping to the three kinds of temporal queries found

in (Salzberg and Tsotras, 1999), demonstrating that

our set of operations is comprehensive. The sec-

ond contribution of this paper is the in-depth discus-

sion on the practical aspects of the presented the-

ory, in particular with respect to an implementation,

index structures and transaction management. The

third and ﬁnal contribution is the open-source project

ChronoDB which implements the presented concepts,

serving as a proof-of-concept prototype. We also used

ChronoDB to evaluate the practical feasibility of the

presented concepts through experiments.

REFERENCES

Codd, E. F., Codd, S. B., and Salley, C. T. (1993). Providing

olap (on-line analytical processing) to user-analysts:

An it mandate. Codd and Date, 32.

DeCandia, G., Hastorun, D., Jampani, M., Kakulapati,

G., Lakshman, A., Pilchin, A., Sivasubramanian,

S., Vosshall, P., and Vogels, W. (2007). Dynamo:

amazon’s highly available key-value store. In ACM

SIGOPS Operating Systems Review, volume 41, pages

205–220. ACM.

Easton, M. C. (1986). Key-sequence data sets on indelible

storage. IBM Journal of Research and Development,

30(3):230–241.

Felber, P., Pasin, M., Riviere, E., Schiavoni, V., Sutra, P.,

Coelho, F., et al. (2014). On the Support of Versioning

in Distributed Key-Value Stores. In 33rd IEEE SRDS

2014, Nara, Japan, October 6-9, 2014, pages 95–104.

ISO (2011). SQL Standard 2011 (ISO/IEC 9075:2011).

Jensen, C. S., Dyreson, C. E., B

ohlen, M., Clifford, J.,

Elmasri, R., Gadia, S. K., et al. (1998). Tempo-

ral Databases: Research and Practice, chapter The

consensus glossary of temporal database concepts —

February 1998 version, pages 367–405. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Lakshman, A. and Malik, P. (2010). Cassandra: a decen-

tralized structured storage system. ACM SIGOPS Op-

erating Systems Review, 44(2):35–40.

Lomet, D., Barga, R., Mokbel, M., and Shegalov, G. (2006).

Transaction time support inside a database engine. In

Proceedings of the 22nd ICDE, pages 35–35.

Lomet, D. and Salzberg, B. (1989). Access Methods for

Multiversion Data. SIGMOD Rec., 18(2):315–324.

Nascimento, M., Dunham, M., and Elmasri, R. (1996). M-

IVTT: An index for bitemporal databases. In Wag-

ner, R. and Thoma, H., editors, Database and Expert

Systems Applications, volume 1134 of Lecture Notes

in Computer Science, pages 779–790. Springer Berlin

Heidelberg.

Ramaswamy, S. (1997). Efﬁcient indexing for con-

straint and temporal databases. In Database Theory-

ICDT’97, pages 419–431. Springer.

Salzberg, B. (1988). File Structures: An Analytic Approach.

Prentice-Hall, Inc., Upper Saddle River, NJ, USA.

Salzberg, B. and Tsotras, V. J. (1999). Comparison of ac-

cess methods for time-evolving data. ACM Computing

Surveys (CSUR), 31(2):158–221.

Saracco, C., Nicola, M., and Gandhi, L. (2012). A matter

of time: Temporal data management in DB2 10. IBM

developerWorks.

Shi, Z. and Shibasaki, R. (2000). GIS Database Revision–

The Problems and Solutions. International Archives of

Photogrammetry and Remote Sensing, 33(B2; PART

2):494–501.

Snodgrass, R. T. (1986). Temporal databases. IEEE Com-

puter, 19:35–42.

Urbano, F. and Cagnacci, F. (2014). Spatial Database

for GPS Wildlife Tracking Data: A Practical Guide

to Creating a Data Management System with Post-

greSQL/PostGIS and R. Springer Science & Business

Media.

DATA 2016 - 5th International Conference on Data Management Technologies and Applications