
Accessibility Profiles
Measuring Vulnerability and Amendability of Transportation Network
Wojciech Pomianowski
Institute of Geography and Spatial Organization, Polish Academy of Sciences, Warszawa, Poland
1 STATE OF THE ART
Gravity and potential-based models have a long
standing tradition in geographic studies of
interactions. With the incorporation of graph data
structures, these models have undergone a
substantial improvement in terms of distance (or
generalised cost) component, which can be
calculated with realistic accuracy and with account
for real-life transportation network issues. Combined
graph-potential models are primary tool in two
domains: transportation studies and geography, with
the focus on slightly different questions. The
former’s interest is mostly in traffic volume, its
variability and correlation to areal units assigned as
origin and destination (Erlander and Stewart, 1990).
Models have been developed starting from pioneer
Chicago Area Transportation Study (CATS, 1960)
and nowadays highly sophisticated software tools
are available commercially (e.g. PTV 2013).
In the context of geography, the focus is less on
exact volume of flows and more on the impact of
transportation on territory, its population and
economy. One of the key concepts here is
accessibility – the “potential of opportunities for
interaction”, as originally formulated by Hansen
(1959), which can be re-stated as the ability of
certain place to provide good transportation for its
inhabitants and businesses (or, alternatively, the
property of a place to be easily accessed by the
outside inhabitants or businesses). Measures of
potential-based accessibility invariably stem from
potential formula (Isard W., 1960, owing to earlier
work of J.Q. Stewart):
,
(1)
where i-th point in space receives a sum of
influences of all other objects (indexed by j) of the
analysed system. Each influence is proportional to
the “mass” m
j
of a remote object and inversely
proportional to the distance to this object. To express
diminishing effect of distance on interaction, many
different functional forms have been employed
(Taylor, 1971) and this component is usually
elaborated separately under the name of distance-
decay function or impedance function. Except for
power function with negative β parameter, like
above, the exponent function exp (-βd
ij
) is widely
used today.
Contemporary general formula (e.g. Geurs and
Ritsema van Eck, 2001)
(2)
replaces distance with a generalized cost notion,
where travel time, distance or monetary cost can be
substituted. Accessibility of i-th object in a system is
a sum of influences of all other objects (indexed by
j). Each influence is a product of D
j
(j-th object
attractiveness) and c
ij
– the cost of travel between i
and j reduced by distance decay function F.
Depending on study objective, many variables may
be used as attractiveness, from specific like
healthcare provision indices to general like
population or GDP.
Accessibility gives much better insight into
transportation network role in socio-economic
system then other measures like gross infrastructure
density indices (e.g. road density), or isochrone
surfaces (op cit.). Compared to first group, it does
relate the demand for travel to the supply of
infrastructure and even particular topology of
infrastructure. Compared to second, it does
incorporate distance decay concept and accounts for
all possible travel destinations (or origins). Also, it
has the property of additiveness, so values obtained
for singular objects may be legitimately aggregated
to wider areal units or the whole system (country) by
simple or weighted summation.
A notable feature of potential-based accessibility
is that it does, like no other measure, answer the
question of quality of the transportation system and
it does it in most direct way. In contrast to some
other policy-related terms like sustainability or
equity, the logic of accessibility computation is close
to commonsense semantics and the meaning is
20
Pomianowski, W.
Accessibility Profiles - Measuring Vulnerability and Amendability of Transportation Network.
In Doctoral Consortium (DCGISTAM 2016), pages 20-24
unequivocal – high accessibility is good, low is bad.
Thus, potential-based accessibility is a perfect
candidate for strategic goal setting, a benchmark or
evaluation criterion. Possibly, it can be tied to
investment effectiveness appraisal.
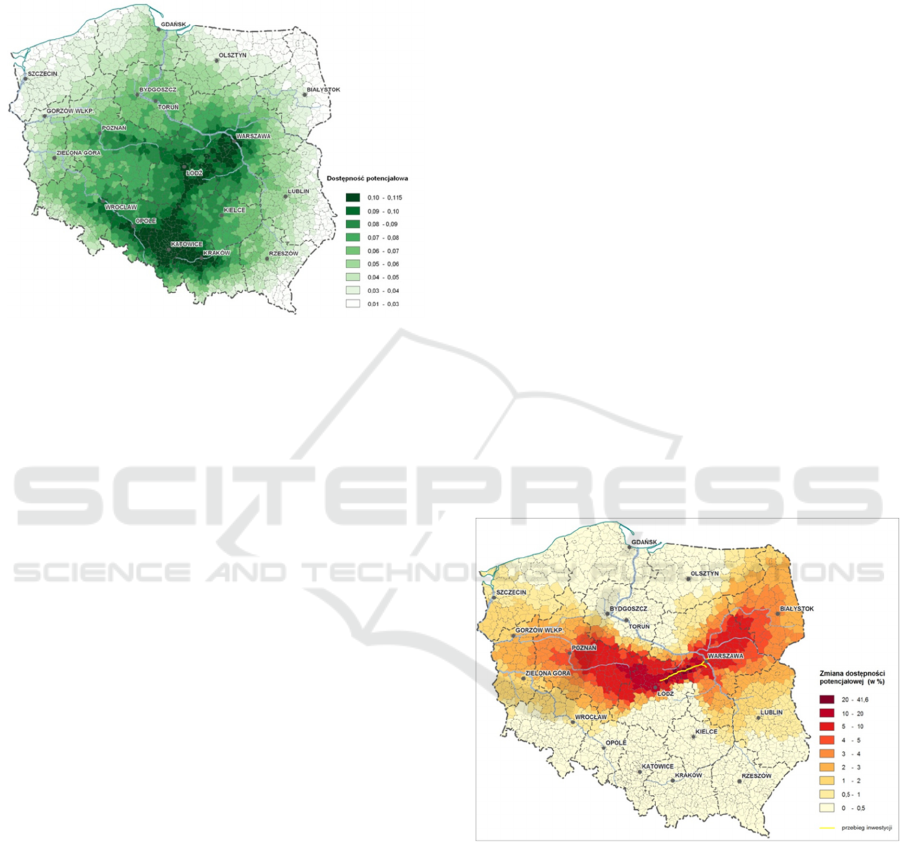
Figure 1: An example of potential-based accessibility in
road transportation. Source: IGiPZ website.
Starting in 2008, Ministry of Regional
Development of Poland become interested in a
methodological advances and a software tool
capable of evaluating the effects of EU-funded
transportation investments. The task was
accomplished with the help of tailor-made software
for graph-based potential accessibility computation.
Shortly after, the next software system OGAM –
Open Graph Accessibility Model (Pomianowski,
2012) was developed with significantly extended
architecture and features. The system accepts
arbitrary graph data set in ESRI shapefile format and
allows for formula-based specification of 1)
attracting masses, 2) velocity engine and 3) distance
decay function. Travel speeds are calculated
according to velocity engine specification and used
to assign the travel times to graph edges. Then a
shortest path algorithm finds the paths for every
node-node pair. O-D (origin-destination) matrix
found this way is fed into potential calculations. This
approach assumes that a transportation network is
unsaturated (no alternative paths or traffic load), so
the model is applicable only to regional or
countrywide level. Total accessibility is computed
with weighting, an extra feature is addition of self-
potential (see Appendix for explanations).
The most frequently used data and parameter set
used in OGAM was designed for private car road
transportation modeling and will be referred to as
OGAM Base Model. OGAM Base Model for
December 2014 is comprised of a network of 14400
edges of total length of 65525 km and 2321 nodes
corresponding to municipality administrative units
(LAU-2) plus 8884 auxiliary nodes (joins,
crossings). An attraction mass variable is census
population, which also serves as a weighting factor
for total (countrywide) accessibility computation.
Two exponential distance decay functions are in use,
with β parameter of 0.023105 for so called short
trips (everyday activity including commuting) with
mean of 30 min and 0.005775 for long trips
(business, leisure) with mean of 120 min. Travel
cost variable is equal to the travel time and is
derived from edge length and travel velocity. Travel
velocity is based on three factors: road category,
road inclination and surrounding population density,
combined by a
minimum()
function.
2 RESEARCH PROBLEM
OGAM system has been subsequently used in a
series of projects with different networks and
parameters. A lot of activity is directed towards
tracking accessibility improvement resulting from
adding new sections to ever increasing network of
motorways in Poland or upgrades made to existing
roads (e.g. Rosik and Stepniak, 2013).
Figure 2: Accessibility change after Warszawa-Lodz
motorway construction. Source: IGiPZ website.
The system performs well, giving numerical
results for pre-change and post-change state of
accessibility, which are then imported into GIS and
used for map production.
Individual simulations give good view of
particular event in network’s lifetime and reveal
some truth about the role of single edge or group of
edges in network connectivity. The scheme is as
follows: a change in edge’s travel cost (time) gives a
Accessibility Profiles - Measuring Vulnerability and Amendability of Transportation Network
21

response in accessibility measure, both locally (for
individual network nodes) and globally.
However, the results lack generality. We are able
to test a single improvement by changing a travel
time, but we may suspect that other, untested
changes on the analysed edge yield different and
unexpected changes in accessibility. Though the
monotonic relation between travel time and
accessibility seems to be beyond discussion, the
exact magnitude and shape of this relation in
different parts of the network is unexplored. Also, in
the current practice, only positive changes have been
tested, but exactly the same procedure could be used
to simulate negative changes. What is needed is
general characteristics of a network edge over the
whole range of travel time variability. With fixed
edge length this translates to the range of travel
speeds. Due to complex formulation and graph
involvement, no analytic solution exists to simply
derive a range of accessibility values from a single,
base value. The only solution is numerical simulation.
In above circumstances, a strong, unifying
concept was necessary and it appeared as a
accessibility response profile (explained in
METHODOLOGY section). The other need is of
technical nature: existing OGAM software was not
designed to run multiple simulations in a systematic
way because the complete dataset must be modified
and model must be run again for each simulation.
3 METHODOLOGY
Figure 3 illustrates the concept of accessibility
response profile. X-axis runs along speed dimension,
from 0 value (no traffic) up to maximum allowed
speed (in case of Polish Traffic Code, 130 km/h). A
special point v
base
corresponds to actual, current
Figure 3: Generic accessibility response profile (exact
shape irrelevant).
value of speed on the link in the base model. Y-axis
runs along accessibility dimension. A special point
A
base
is actual, current value of accessibility
computed in the base model. A generic profile runs
from zero speed to maximum speed with ever
increasing A value and always crosses v
base
position.
Two parts of the profile may be distinguished
(see Figure 4): left part corresponds to negative
change usually related to congestion, accident
blocking, construction works or even complete
exclusion from traffic. This is the vulnerability area.
The bigger the area, the worse traffic disruption
occurs in case of negative event.
Figure 4: Profile functional structure.
The right part corresponds to improvements
resulting in increased speed due to construction (e.g.
surface or width improvement) or regulatory action
(higher speed limit, vehicle-type restrictions). This is
the amendability area. The bigger the are, the better
results may be achieved. A base point is neutral and
corresponds to current state of affairs. Please note,
that this “attachment” point for the profile is actually
not located in the middle, but on the right side for a
good road or left side for poor road. Thus, low speed
segments have small vulnerability area and cannot
do much harm to the network in case of failure. High
speed segments have small amendability area and
cannot give much improvement (in many cases they
have no amendability area at all).
Actual profiles given by series of simulations are
not smooth. They are approximated by nine speed
points, spread evenly across 0 – 130 km/h range.
Extra tenth value comes from the base model itself
and is computed once only. The test run results are
illustrated on Figure 5.
Observations on the shape, inclination and
attachment point give a complete information about
road segment’s importance and it’s influence on the
network. We may choose to observe the influence on
whole system or on particular node. This is why two
kinds of profiles will be computed:
DCGISTAM 2016 - Doctoral Consortium on Geographical Information Systems Theory, Applications and Management
22

Figure 5: A sample of response profiles from test run.
• global profile with Y-axis describing the
accessibility response of the whole system,
and
• local profiles describing the accessibility
responses of a single nodes.
4 OBJECTIVES AND EXPECTED
OUTCOME
A series of descriptive and analytical procedures will
cover following topics:
1. Assessment of magnitude of influence across
segments (global accessibility).
2. Assessment of profile shapes and
categorization.
3. Ranking of segments according to global
influence, with mapping.
4. Mapping of global vulnerability and
amendability (see Figure 6 and Figure 7 for
preliminary maps).
5. Comparing global vulnerability and
amendability, seeking and summarizing
coincidences and differences.
6. Exploring the “foot” shaped profile
phenomenon (see Figure 5), which suggests a
redundancy of connectivity.
7. Comparing local accessibility magnitudes with
global effects.
8. Observing the relation of high-impact segments
to high-traffic segments. Challenging the thesis
that these always coincide (evidence exists).
9. Observing and quantifying the distance
between high-impact segment and it’s target
node (the node being influenced), based on
local accessibility. Supporting the thesis on far-
reaching influence.
Figure 6: Vulnerability (L-mean) map of road segments.
4.1 Challenges
Data Volume
Major objective of the first phase of analysis is
taming the sheer volume of data. Simulation of
global accessibility response brings 14400 profiles.
Simulations of local (node-related) accessibility
brings another 2321⨯ 14400 = over 33 million
profiles. Each profile is composed of 10 values. An
analysis should keep the profile data as a series and
not a unordered set or independent dimensions.
Time series analysis tools seem to be inappropriate
because the length of a series is limited.
Synthetic Measures
Two kinds of measures are necessary: one capturing
the magnitude of accessibility change, the other –
the structure (shape) of the profile. So far, for testing
and demonstration purposes, two simple magnitude
measures were computed (see Figure 4): R-mean, a
mean of amendability area under the right side of the
profile and L-mean - a mean value of vulnerability
area above left side of the profile. These are not
capable of capturing the variability of the width of
the profile and probably will be dropped in favour of
integral-based (surface) measures.
Mapping
Very detailed structure of the network must be
preserved to distinguish objects and this precludes
varying line widths and use of symbols. Colour
alone does not give good readability, especially for
paper medium.
Accessibility Profiles - Measuring Vulnerability and Amendability of Transportation Network
23

Figure 7: Amendability (R-mean) map of road segments.
5 STAGE OF THE RESEARCH
New software – OGAM Lab – has been developed
to complement OGAM capabilities with massive
simulation. Both programs share code responsible
for core functionality (reading network data, model
specification, shortest path algorithm etc.). Currently
OGAM Lab performs two tasks, and these have been
already completed for proper 2014 data:
• computation of path matrices (14400 files
totalling 130GB of data)
• computation of accessibility cube: a data file
with dimensions: nodes x edges x no.
simulations = 2321 x 14400 x 10.
The architecture allows for seamless inclusion of
next jobs, and these will be focused on accessibility
cube analytics.
REFERENCES
CATS, 1960. Chicago Area Transportation Study Vol. I-
III. https://archive.org/details/chicagoareatrans01chic
(accessed 19.11.2014).
Erlander S., Stewart, N., 1990. The Gravity Model in
Transportation Analysis – Theory and Extensions.
VSP BV Utrecht.
Geurs, K.T., Ritsema van Eck, J.R., 2001. Accessibility
Measures: Review and Applications. RIVM Report
408505 006. National Institute of Public Health and
the Environment, Bilthoven.
IGiPZ Accessibility Website. Maps by Marcin Stepniak.
<http://www.igipz.pan.pl/accessibility/pl/mapy.html>
(accessed 2.03.2016).
Isard, W., 1960. Methods of Regional Analysis: an
Introduction to Regional Science. The Technology
Press MIT, John Wiley & Sons Inc., New York –
London.
Pomianowski, W., 2012. OGAM – Open Graph
Accessibility Model. <http://www.igipz.pan.pl/access
ibility/pl/ogam> (accessed 12.02.2016).
PTV, 2013. Visum 13 Fundamentals. PTV AG, Karlsruhe.
Rosik, P., Stepniak, M., 2013. Accessibility improvement,
territorial cohesion and spillovers: a multidimensional
evaluation of two motorway sections in Poland.
Journal of Transport Geography 31, pp.154–163.
Taylor, P., 1971. Distance Transformation and Distance
Decay Functions, Geographical Analysis Vol. 3, Issue
3, July 1971, p. 221-238.
APPENDIX
Total accessibility
Summary countrywide accessibility computed as a
weighted total of node’s values. The weighting
occurs by node population P
j
raw or fraction.
,
(3)
Self potential
Self potential that is a measure of extra interaction
occurring within a node. It is based on assumption
that a great deal of transportation activity is released
for very short trips, confined to immediate node
vicinity. As this activity occurs below model
resolution, it must be accounted for in special way.
Compared to formula (2), an extended formula
(4)
includes the front term with c
ii
– the mean internal
cost (time) of travel within a node. This variable is
provided externally and is based on administrative
unit size.
DCGISTAM 2016 - Doctoral Consortium on Geographical Information Systems Theory, Applications and Management
24
