Mode Combining and -Splitting in Optical MIMO Transmission using

Photonic Lanterns

Andreas Ahrens and Steffen Lochmann

Hochschule Wismar, University of Technology, Business and Design,

Philipp-Müller-Straße 14, 23966 Wismar, Germany

Keywords:

Multiple-Input Multiple-Output System, Singular-Value Decomposition, Photonic Lantern, Optical MIMO

Transmission.

Abstract:

Within the last years the multiple-input multiple-output (MIMO) technology has revolutionized the optical

ﬁbre community. Theoretically, the concept of MIMO is well understood and shows some similarities to wire-

less MIMO systems. However, practical implementations of optical components are in the focus of interest

of substantial research. Optical couplers have long been used as passive optical components also being able

to combine or split SISO (single-input single-output) data transmission. They have been proven to be well

suited for the optical MIMO (multiple-input multiple-output) transmission despite their insertion losses and

asymmetries. Nowadays, next to optical couplers, Photonic Lanterns (PLs) have attracted a lot of attention in

the research community as they offer the beneﬁt of a low loss transition from the input ﬁbers to the modes

supported by the waveguide at its output. Therefore they seem to be highly beneﬁcial for optical MIMO com-

munication. In this contribution mode coupling and splitting devices such as PLs and fusion couplers have

been analysed in a testbed with regard to their respective MIMO suitability. Based on the obtained results, a

simpliﬁed time-domain MIMO simulation model including PLs for mode-combining at the transmitter side as

well as mode-splitting at the receiver side is elaborated. Our results obtained by the simulated bit-error rate

(BER) performance show that PLs are well suited for the optical MIMO transmission.

1 INTRODUCTION

The growing demand of bandwidth particularly

driven by the developing Internet has been satisﬁed

so far by optical ﬁbre technologies such as Dense

Wavelength Division Multiplexing (DWDM), Polar-

ization Multiplexing (PM) and multi-level modula-

tion. These technologies have now reached a state

of maturity (Winzer, 2012). The only way to fur-

ther increase the available data rate is now seen in the

area of spatial multiplexing (Richardson et al., 2013),

which is well-established in wireless communications

(Tse and Viswanath, 2005; Kühn, 2006). Nowa-

days several novel techniques such as Mode Group

Diversity Multiplexing (MGDM) (Franz and Bülow,

2012) or Multiple-InputMultiple-Output (MIMO) are

in the focus of interest (Singer et al., 2008). Among

these techniques, the concept of MIMO transmission

(Kühn, 2006; Foschini, 1996) over multi-mode ﬁbers

has attracted increasing interest in the optical ﬁber

transmission community, targeting at increased ﬁber

capacity (Singer et al., 2008; Aust et al., 2012). The

ﬁber capacity of a multi-mode ﬁber is limited by the

modal dispersion compared to single-mode transmis-

sion where no modal dispersion except for polariza-

tion exists. The description of the optical MIMO

channel has attracted attention and reached a state of

maturity (Singer et al., 2008; Hsu et al., 2006; Bülow

et al., 2011).

However, the realization of the optical MIMO

channel requires substantial further research regard-

ing mode combining, mode maintenance and mode

splitting (Schöllmann and Rosenkranz, 2007; Schöll-

mann et al., 2008). Hence, Photonic Lanterns (PLs)

have attracted a lot of attention in the research com-

munity (Leon-Saval et al., 2014; Huang et al., 2015;

Fontaine et al., 2013). Compared to other passive de-

vices used for mode combining and mode splitting

such as optical couplers, PLs offer the beneﬁt of a low

loss transition from the input ﬁbers to the modes sup-

ported by the waveguide at its output which makes

such devices very attractive for optical MIMO com-

munication.

In this contribution mode coupling and splitting

devices such as PLs and fusion couplers have been

analysed in a testbed with regard to their respective

Ahrens, A. and Lochmann, S.

Mode Combining and -Splitting in Optical MIMO Transmission using Photonic Lanterns.

DOI: 10.5220/0005944600890096

In Proceedings of the 6th International Joint Conference on Pervasive and Embedded Computing and Communication Systems (PECCS 2016), pages 89-96

ISBN: 978-989-758-195-3

MIMO suitability. Based on the obtained results, a

simpliﬁed time-domain MIMO simulation model in-

cluding PLs for mode-combining at the transmitter

side as well as mode-splitting at the receiver side is

elaborated. Our results obtained by the simulated

BER performance show that PLs are well suited for

the optical MIMO transmission.

The remaining part of this paper is structured as

follows: Section 2 introduces the practical issues of

optical MIMO. The newly developed concept of the

PL and the resulting system model are analyzed in

section 3. The associated performance results are pre-

sented and interpreted in section 4. Finally, section 5

provides some concluding remarks.

2 PRACTICAL ISSUES OF

OPTICAL MIMO

An optical MIMO system can be formed by feeding

different sources of light into the ﬁber. These sources

of light activate different optical modes. Theoreti-

cally, it can be done by using two single-mode ﬁbers

(Ahrens and Lochmann, 2013) as shown in Fig. 1.

Practically, a possible solution for feeding different

sources of light into the ﬁbre can be provided by op-

tical couplers (see Fig. 2). It is well known that op-

tical couplers may show a strong mode selective be-

havior. In general this behavior depends on the fab-

rication technique. Although the term ’mode selec-

tivity’ is usually referred to the unwanted coupling

ratio’s dependency on the launching conditions, we

can make use of this parameter to control or better to

maintain the mode groups within such a device. Dif-

ferent kinds of couplers have been studied in (Ahrens

Figure 1: Transmitter side conﬁguration with center and

offset light launch condition.

(low order mode path)

(high order mode path)

Figure 2: Transmitter-side coupler for launching different

sources of light into the multi-mode ﬁbre (MMF).

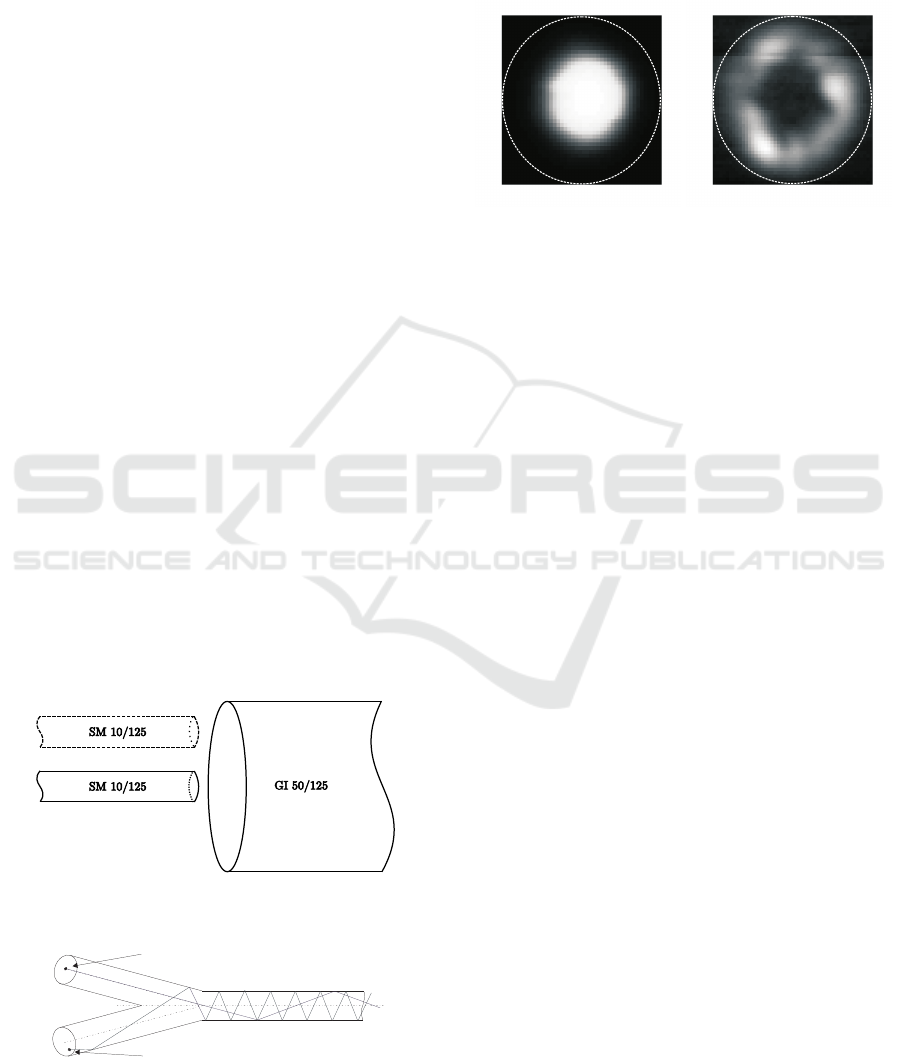
and Lochmann, 2013). A measured mean power dis-

tribution pattern of an asymmetric fusion coupler at

the coupler output is depicted in Fig. 3. Here, dif-

ferent launching conditions were used for creating in-

dividual modes, which are subsequently combined by

the coupler. As shown in Fig. 3 the fundamental mode

Figure 3: Measured mean power distribution pattern as a

function of the light launch position at an operating wave-

length of λ = 1550nm (left: eccentricity δ = 0µm, right: ec-

centricity δ = 15µm); the dotted line represents the 50µm

core size.

as well as the higher-order mode groups are spatially

well separated. Using these couplers for mode com-

bining at the transmitter side and mode splitting at the

receiverside, a simple MIMO direct detection scheme

can be formed. However, the demand for higher data

rates requires high-level modulation formats, which

are not feasible by direct detection receivers.

Photonic Lanterns, which have attracted a lot of

attention in the research community, may overcome

this disadvantage. Besides using integrated optical

chips they are mostly produced by fusing and tapering

single-mode ﬁbres (Leon-Saval et al., 2014; Huang

et al., 2015; Fontaine et al., 2013), which are placed

in a low refractive index capillary. The process is

controlled in such a way that the taper matches the

dimensions of the following few-mode ﬁbre (FMF).

Now, the input single-mode ﬁbre channels create indi-

vidual mode-patterns at the output of the PL. Having

an ideal FMF channel, these individual mode-patterns

are re-transformed into the independent single-mode

ﬁbre (SMF) channels.

Fig. 4 shows exemplarily three measured mean

power distribution patterns at the output of the PL as

an example of the investigated 6-port PL. Thereby,

the creation of the different mode patterns capable

of carrying individual data channels has been veri-

ﬁed. Since the FMF dimension supports only four

modes, the obtained patterns must consist of super

positioned modes as demonstrated in (Huang et al.,

2015) or (Fontaine et al., 2013), too.

In comparison to the fusion coupler shown in

Fig. 3 the PL does not show well separated mode

patterns. However, the concept of activating individ-

ual modes offers the possibility of coherent transmis-

sion combined with high-level modulation schemes

SPCS 2016 - International Conference on Signal Processing and Communication Systems

Figure 4: Measured mean power distribution patterns at the output of the PL using different input SMFs at an operating

wavelength of λ = 1550nm; the dotted line represents the 30µm core size.

such as 16-QAM (quadrature amplitude modulation)

or 256-QAM.

Table 1: Comparison of the investigated asymmetric fusion

coupler and the PL with respect to insertion losses (in dB).

Insertion Loss Fusion Coupler Photonic Lantern

0,1 6,7

8,1 6,7

−− 4,2

−− 4,1

−− 7,0

−− 4,1

For the evaluation of the whole MIMO concept,

the component dependent losses play an important

role and must be characterized. Tab. 1 compares the

investigated asymmetric fusion coupler and the PL

with respect to their insertion losses.

Although the fusion coupler may form well sepa-

rated mode patterns, its insertion losses exhibit a high

asymmetry. However, the PL which may theoretically

achieve a 0 dB insertion loss, shows notable vari-

ations, too. Further technology improvements may

overcome these variations.

Now, the carried out measurements form the basis

for the development of a time domain MIMO simu-

lation model, which takes the mode combining and

mode splitting components into account.

3 TIME-DOMAIN SIMULATION

MODEL

In this section the MIMO transmission scheme is in-

troduced. For simpliﬁcation a (2×2) MIMO scheme

is analyzed. Here, an ideal (2×2) PL is considered,

where SMFs are connected with the respective inputs

Tx−1 as well as Tx−2 as shown in Fig. 5. The map-

ping of the incoming LP

modes by the PL can be

described by the corresponding coupling matrix



1 0

0 1



(1)

Photonic Lantern

Tx-1

Tx-2

Rx-1

Rx-2

ℓ

Figure 5: Multi-mode MIMO transmission using Photonic

Lantern for mode combining and splitting.

resulting in the mode LP

at the output 1 as well as

in the mode LP

at the output 2 (see Fig. 6). Further-

more, in this work it is assumed that the coupling ma-

trix of the receiver side PL equals the coupling matrix

of the transmitter side, i. e., K

= K

. The corre-

sponding system model is depicted in Fig. 6.

Here, it is worth noting that under practical as-

sumptions the output of the PL in Fig. 6, the LP

and LP

mode may appear as superposition modes

as highlighted in section 2.

In the time-domain, the impulse responses of the

FMF channel are given as follows

(t) = k

δ(t) g

(t) = k

δ(t −∆τ/2)

(t) = k

δ(t −∆τ/2) g

(t) = k

δ(t −∆τ)

describing the mode-coupling of the underlying chan-

nel. Herein, the parameter ∆τ describes the differen-

tial mode delay between the fundamental mode LP

and the mode LP

, which is identiﬁed to be ∆τ = 200

ps for the considered ﬁbre length of 2 km. The opti-

cal ﬁeld coupling coefﬁcients of the underlying FMF

Photonic Lantern

Tx-1

Rx-1

Tx-2

Rx-2

ℓ/2

∆τ/2

1 1

2 2

2 1

1 2

Figure 6: Underlying MIMO-based System Model of the

ﬁbre length ℓ.

Mode Combining and -Splitting in Optical MIMO Transmission using Photonic Lanterns

channel, describing the coupling from the mode LP

to the mode LP

and from the mode LP

to the

mode LP

, are given by the coupling matrix K





, (2)

with the parameter k

νµ

to be determined. Since no

power-loss is assumed, the coupling coefﬁcients have

to fulﬁll the following condition for the considered

(2×2) MIMO system

∑

ν=1

νµ

= 1 for µ = 1,2,... , L and L = 2 .

(3)

Finally, the effect of the chromatic dispersion is not

analyzed in this contribution since the focus of this

simulation is on the MIMO characteristic. However,

it can be taken into account by a simple convolution

of the impulse responses g

νµ

(t) with a Gaussian dis-

tribution modelling the chromatic dispersion.

The mode-coupling along the optical channel to-

gether with the PL at the transmitter as well as the

receiver side is forming a MIMO system, as given in

Fig. 7. Here, each optical input within the multi-mode

ﬁber is fed by a system with identical mean proper-

ties with respect to transmit ﬁlter and pulse frequency

= 1/T

. Rectangular pulses are used for transmit

and receive ﬁltering, i. e. g

(t) and g

(t) in order to

form the overall impulse response g

(νµ)

(t) as follow

(νµ)

(t) = g

(t) ∗g

νµ

(t) ∗g

(t) . (4)

The MIMO block diagram of the transmission model

is shown in Fig. 8. When considering a frequency-

selective MIMO link, composed of n

optical in-

puts and n

optical outputs, the resulting electrical

discrete-time block-oriented system can be modelled

u = H·c+ w . (5)

In (5), c is the (N

×1) transmitted signal vector con-

taining the input symbols transmitted over n

optical

inputs in K consecutive time slots, i. e., N

= Kn

TX 1

(t)

TX 2

(t)

RX 1

(t)

RX 2

(t)

Figure 7: Electrical (2×2) MIMO system model.

transmit vector

receive vector

noise vector

Figure 8: Transmission system model.

This vector can be decomposed into n

transmitter-

speciﬁc signal vectors c

according to

c =



,... ,c



. (6)

In (6), the (K × 1) input-speciﬁc signal vector c

transmitted by the optical input µ (with µ = 1,.. ., n

)

is modelled by



1µ

,... ,c

kµ

,... ,c

Kµ



. (7)

The (N

× 1) received signal vector u, deﬁned in

(5), can again be decomposed into n

output-speciﬁc

signal vectors u

(with ν = 1,.. ., n

) of the length

K + L

, i.e., N

= (K + L

, and results in

u =



,... ,u



. (8)

By taking the (L

+ 1) non-zero elements of the re-

sulting symbol rate sampled overall channel impulse

response g

(νµ)

(t) between the µth input and νth out-

put into account, the output-speciﬁc received vector

has to be extended by L

elements, compared to

the transmitted input-speciﬁc signal vector c

deﬁned

in (7). The ((K + L

) × 1) signal vector u

received

by the optical output ν (with ν = 1,... ,n

) can be

constructed, including the extension through the mul-

tipath propagation, as follows



1ν

2ν

,... ,u

(K+L

)ν



. (9)

Similarly, in (5) the (N

×1) noise vector w results in

w =



,... ,w



. (10)

The vector w of the additive, white Gaussian noise

(AWGN) can still be decomposed into n

transmitter-

speciﬁc signal vectors w

(with ν = 1,... ,n

) accord-

ing to



1ν

2ν

,... ,w

(K+L

)ν



. (11)

Finally, the (N

×N

) system matrix H of the block-

oriented system model, introduced in (5), results in

H =







... H

··· H







, (12)

and consists of n

single-input single-output

(SISO) channel matrices H

νµ

(with ν = 1, ... ,n

and

SPCS 2016 - International Conference on Signal Processing and Communication Systems

replacements

1 k

2 k

1 k

2 k

1 k

2 k

1 k

2 k

Figure 9: SVD-based layer-speciﬁc transmission model.

µ = 1,... ,n

). Every of these matrices H

νµ

with the

dimension ((K + L

) × K) describes the inﬂuence of

the channel from transmitter µ to receiver ν including

transmit and receive ﬁltering, i.e. g

(νµ)

(t). The chan-

nel convolution matrix H

νµ

between the µth input and

νth output is obtained by taking the (L

+ 1) non-zero

elements of resulting symbol rate sampled overall im-

pulse response g

(νµ)

(t) into account and results in:

νµ







0 0 ··· 0

0 ···

··· 0

. h

··· h

. h

··· h

0 h

. ··· h

0 0 h

···

0 0 0 ··· h







. (13)

The interference, which is introduced by the off-

diagonal elements of the channel matrix H, requires

appropriate signal processing strategies. A popular

technique is based on the singular-value decomposi-

tion (SVD) of the system matrix H, which can be

written as H = S · V· D

, where S and D

are uni-

tary matrices and V is a real-valued diagonal matrix

of the positive square roots of the eigenvalues of the

matrix H

H sorted in descending order

. The SDM

(spatial division multiplexing) MIMO data vector c is

now multiplied by the matrix D before transmission.

In turn, the receiver multiplies the received vector u

by the matrix S

. Thereby neither the transmit power

nor the noise power is enhanced. The overall trans-

mission relationship is deﬁned as

y = S

(H·D·c+ w) = V·c+ ˜w. (14)

As a consequence of the processing in (14), the

channel matrix H is transformed into independent,

non-interfering layers having unequal gains (Pankow

et al., 2011; Raleigh and Ciofﬁ, 1998).

In MIMO communication, singular-value decom-

position (SVD) has been established as an efﬁcient

The transpose and conjugate transpose (Hermitian) of

D are denoted by D

and D

, respectively.

concept to compensate the interferences between the

different data streams transmitted over a dispersive

channel: SVD is able to transfer the whole sys-

tem into independent, non-interfering layers exhibit-

ing unequal gains per layer as highlighted in Fig. 9,

where as a result weighted additive, white Gaussian

noise (AWGN) channels appear.

Analyzing the considered (2×2) MIMO system,

the data symbols at the time k (with k = 1,2,. . .,K),

i. e. c

and c

are weighted by the positive square

roots of the eigenvalues of the matrix H

H, i. e.

and

. Finally, some noise is added,

i. e. w

and w

. Here it is worth noting that the

the number of readily separable layers is limited by

min(n

). Therefore in this work the maximum

number of layers is given by L = 2.

In general the quality criterion for transmission

systems can be expressed by using the signal to noise

ratio (SNR) at the detector input as follows

ρ =

(half vertical eye opening)

noise power

)

, (15)

where U

and P

correspond to one quadrature com-

ponent. Considering a layer-based MIMO system

with a given SNR ρ

(ℓ,k)

for each layer ℓ (with ℓ =

1,2, . ..,L) and time k (with k = 1,2,. ..,K) and a M-

ary quadrature amplitude modulation (QAM), the bit-

error rate (BER) probability is given by

(ℓ,k)

BER

log

ℓ



1−

√

ℓ



er fc





(ℓ,k)





(16)

This BER is averaged over all time slots and activated

layers taking different modulation sizes at each layer

into account. For QAM modulated signals the aver-

age transmit power per layer can be expressed as

s,ℓ

ℓ

−1) . (17)

Intuitively the total available transmit power P

equally split between the L activated layers, and hence

the layer-speciﬁc transmit power is given by P

s,ℓ

/L, inﬂuencing the half-level transmit amplitude

s,ℓ

for each MIMO layer.

Considering the SVD layer model, the noise

power is unchanged at the receiver. However, the

half vertical eye openings U

at each time slot k

(with k = 1,2,.. . ,K) and layer ℓ (with ℓ = 1,2, . .., L)

are inﬂuenced by the singular values so that U

(ℓ,k)

ℓ,k

s,ℓ

holds and the corresponding SNR values

are given by

(ℓ,k)

SVD

ℓ,k

s,ℓ

3ξ

ℓ,k

L(M

ℓ

−1)

, (18)

Mode Combining and -Splitting in Optical MIMO Transmission using Photonic Lanterns

with E

being the transmit symbol energy and the pa-

rameter N

describing the noise power spectral den-

sity. The overall bit-error rate of the uncoded MIMO

system is largely determined by the layer with the

highest BER. In order to balance the bit-error rates,

the mean of choice is to equalize the SNR values ρ

(ℓ,k)

SVD

over all layers and time-slots. This is clearly not the

optimal solution for minimizing the overall BER but

it is easy to implement and not far away from the

optimum as shown in (Ahrens and Benavente-Peces,

2009). Therefore, the half-level transmit amplitude

s,ℓ

is adjusted on each layer by multiplying it with

√

ℓ,k

in order to apply the power allocation (PA)

scheme. Consequently, the half vertical eye opening

of the received symbols becomes

(ℓ,k)

A,PA

√

ℓ,k

s,ℓ

. (19)

With this adjustment the SNR values are resulting in

(ℓ,k)

= p

ℓ,k

(ℓ,k)

SVD

. (20)

In the SVD-based model the singular values are vary-

ing for each time slot. Consequently, power alloca-

tion should be able to balance the BER’s on all layers

L and given time slots per block K. Therefore, the

overall transmit power after PA needs to be the same

as without PA and thus

∑

k=1

∑

ℓ=1

ℓ,k

·P

s,ℓ

∑

k=1

∑

ℓ=1

ℓ,k

(21)

has to be guaranteed, resulting in the condition

K ·L =

∑

ℓ=1

∑

k=1

ℓ,k

(22)

for the total available transmit power. As a result, the

power allocation factors for layer and time-based PA

in SVD systems can be calculated as follows

(LT−SVD)

ℓ,k

ℓ

−1)

ℓ,k

K ·L

∑

ν=1

∑

κ=1

−1)

ν,κ

(23)

and guarantee the above mentioned equal-SNR sce-

nario for all activated layers and time slots per trans-

mitted block (Ahrens et al., 2015). An illustration of

the resulting SNRs of the proposed PA schemes for

SVD systems is depicted in Fig. 10.

4 PERFORMANCE ANALYSIS

For comparing the different MIMO conﬁgurations, a

ﬁxed transmission bit rate is analysed. Furthermore,

for numerical analysis it is assumed, that each optical

layer ℓ

time k

layer ℓ

time k

Figure 10: Illustration of the remaining SNRs in SVD sys-

tems without applying PA (left) and with combined layer

and time PA (right). The color black refers to high and white

to low SNR values.

input within the multi-mode ﬁber is fed by a system

with identical mean properties with respect to trans-

mit ﬁltering and pulse frequency f

= 1/T

. Rectan-

gular pulses are used for transmit and receive ﬁlter-

ing. The average transmit power is supposed to be

= 1V

. This equals 1 W at a linear and constant

resistance of 1Ω. As an external disturbance a white

Gaussian noise with power spectral density N

is as-

sumed (Pankow et al., 2011). Tab. 2 highlights the

different transmission modes to be investigated when

minimizing the overall BER at a ﬁxed data rate.

Table 2: Parameters for bitloading: Investigated QAM

transmission modes for ﬁxed transmission bit rate.

throughput layer 1 layer 2

4 bit/s/Hz 16 0

4 bit/s/Hz 4 4

In order to transmit at a ﬁxed data rate while main-

taining the best possible integrity, i. e. bit-error rate

(BER), an appropriate number of MIMO layers has

to be used, which depend on the speciﬁc QAM con-

stellation size as well as the layer-speciﬁc weighting

factors, i.e.

and

The optical ﬁeld coupling coefﬁcients of the un-

derlying FMF channel shall be given as follows



0,83 0,54

0,54 0,83



(24)

and



0,94 0,31

0,31 0,94



, (25)

with the coupling matrix K

deﬁning 30% crosstalk

and the matrix K

deﬁning 10% channel crosstalk.

For a given MIMO conﬁguration the correspond-

ing BER performance is depicted in Fig. 11. The pa-

rameters are chosen as follows: the pulse frequency

equals f

= 5.00 GHz and the differential mode de-

lay is identiﬁed to be ∆τ = 200 ps for the considered

ﬁbre length of 2 km.

As shown by the BER results, the achievable per-

formance of the MIMO system is strongly affected by

the channel crosstalk. Using SVD, the singular val-

ues are ordered in descending order. Thereby only the

strongest layer should be used for the data transmis-

sion with appropriate QAM modulation levels in the

SPCS 2016 - International Conference on Signal Processing and Communication Systems

5 10 15

−6

−4

−2

10 ·log

) (indB) →

bit-error rate →

, 30% crosstalk

, 10% crosstalk

Figure 11: BER performance when activating two layers

(dotted line) as well as one layer (solid line) and using the

transmission modes introduced in Tab. 2 at different channel

couplings.

5 10 15

−6

−4

−2

10 ·log

) (indB) →

bit-error rate →

= 1,00 GHz

= 5,00 GHz

Figure 12: BER performance when activating two layers

(dotted line) as well as one layer (solid line) and using the

transmission modes introduced in Tab. 2 at the channel cou-

pling K

case of high crosstalk conditions. However, in prac-

tical implementations ﬁbres usually show only small

crosstalk values. Thus, activating two MIMO layers

becomes more and more beneﬁcial.

Analyzing different pulse frequencies, the result-

ing BER performance is highlighted in Fig. 12 and

Fig. 13 for different parameters of the channel cou-

pling. However, considering a ﬁxed differential mode

delay, at low pulse frequencies less intersymbol inter-

ference appears and the BER performance improves

even under high crosstalk conditions.

5 CONCLUSIONS

In this contribution mode coupling and splitting de-

5 10 15

−6

−4

−2

10 ·log

) (indB) →

bit-error rate →

= 1,00 GHz

= 5,00 GHz

Figure 13: BER performance when activating two layers

(dotted line) as well as one layer (solid line) and using the

transmission modes introduced in Tab. 2 at the channel cou-

pling K

vices such as PLs and fusion couplers have been

analysed in a testbed with regard to their respec-

tive MIMO suitability. The established time-domain

MIMO simulation model proven to be a versatile tool

for the optimization of the overall MIMO transmis-

sion system shows that PLs are well suited for optical

MIMO communications.

ACKNOWLEDGEMENTS

This work has been funded by the German Ministry

of Education and Research (No. 03FH016PX3).

REFERENCES

Ahrens, A. and Benavente-Peces, C. (2009). Modulation-

Mode and Power Assignment in Broadband MIMO

Systems. Facta Universitatis (Series Electronics and

Energetics), 22(3):313–327.

Ahrens, A. and Lochmann, S. (2013). Optical Couplers in

Multimode MIMO Transmission Systems: Measure-

ment Results and Performance Analysis. In Interna-

tional Conference on Optical Communication Systems

(OPTICS), pages 398–403, Reykjavik (Iceland).

Ahrens, A., Sandmann, A., Lochmann, S., and Wang, Z.

(2015). Decomposition of Optical MIMO Systems us-

ing Polynomial Matrix Factorization. In 2nd IET In-

ternational Conference on Intelligent Signal Process-

ing, London (United Kingdom).

Aust, S., Ahrens, A., and Lochmann, S. (2012). Channel-

Encoded and SVD-assisted MIMO Multimode Trans-

mission Schemes with Iterative Detection. In Interna-

tional Conference on Optical Communication Systems

(OPTICS), pages 353–360, Rom (Italy).

Mode Combining and -Splitting in Optical MIMO Transmission using Photonic Lanterns

Bülow, H., Al-Hashimi, H., and Schmauss, B. (2011).

Coherent Multimode-Fiber MIMO Transmission with

Spatial Constellation Modulation. In European Con-

ference and Exhibition on Optical Communication

(ECOC), Geneva, Switzerland.

Fontaine, N. K., Leon-Saval, S. G., Ryf, R., Salazar-Gil,

J. R., Ercan, B., and Bland-Hawthorn, J. (2013).

Mode-Selective Dissimilar Fiber Photonic-Lantern

Spatial Multiplexers for Few-Mode Fiber. In 39th Eu-

ropean Conference and Exhibition on Optical Com-

munication (ECOC 2013), pages 1–3, London, United

Kingdom.

Foschini, G. J. (1996). Layered Space-Time Architecture

for Wireless Communication in a Fading Environment

when using Multiple Antennas. Bell Labs Technical

Journal, 1(2):41–59.

Franz, B. and Bülow, H. (2012). Experimental Evaluation

of Principal Mode Groups as High-Speed Transmis-

sion Channels in Spatial Multiplex Systems. IEEE

Photonics Technology Letters, 24:1363–1365.

Hsu, R. C. J., Tarighat, A., Shah, A., Sayed, A. H., and

Jalali, B. (2006). Capacity Enhancement in Coherent

Optical MIMO (COMIMO) Multimode Fiber Links.

IEEE Communications Letters, 10(3):195–197.

Huang, B., Fontaine, N. K., Ryf, R., Guan, B., Leon-Saval,

S. G., Shubochkin, R., Sun, Y., Lingle Jr, R., and Li,

G. (2015). All-Fiber Mode-Group-Selective Photonic

Lantern using Graded-Index Multimode Fibers. Op-

tics Express, 23(1):224–234.

Kühn, V. (2006). Wireless Communications over MIMO

Channels – Applications to CDMA and Multiple An-

tenna Systems. Wiley, Chichester.

Leon-Saval, S. G., Fontaine, N. K., Salazar-Gil, J. R., Er-

can, B., Ryf, R., and Bland-Hawthorn, J. (2014).

Mode-Selective Photonic Lanterns for Space-Division

Multiplexing. Optics Express, 22(1):1–9.

Pankow, J., Aust, S., Lochmann, S., and Ahrens, A. (2011).

Modulation-Mode Assignment in SVD-assisted Op-

tical MIMO Multimode Fiber Links. In 15th Inter-

national Conference on Optical Network Design and

Modeling (ONDM), Bologna (Italy).

Raleigh, G. G. and Ciofﬁ, J. M. (1998). Spatio-Temporal

Coding for Wireless Communication. IEEE Transac-

tions on Communications, 46(3):357–366.

Richardson, D. J., Fini, J., and Nelson, L. (2013). Space

Division Multiplexing in Optical Fibres. Nature Pho-

tonics, 7:354–362.

Schöllmann, S. and Rosenkranz, W. (2007). Experimen-

tal Equalization of Crosstalk in a 2 x 2 MIMO Sys-

tem Based on Mode Group Diversity Multiplexing

in MMF Systems @ 10.7 Gb/s. In 33rd European

Conference and Exhibition on Optical Communica-

tion (ECOC), Berlin.

Schöllmann, S., Schrammar, N., and Rosenkranz, W.

(2008). Experimental Realisation of 3 x 3 MIMO Sys-

tem with Mode Group Diversity Multiplexing Limited

by Modal Noise. In Optical Fiber Communication

Conference (OFC), San Diego, California.

Singer, A. C., Shanbhag, N. R., and Bae, H.-M. (2008).

Electronic Dispersion Compensation– An Overwiew

of Optical Communications Systems. IEEE Signal

Processing Magazine, 25(6):110–130.

Tse, D. and Viswanath, P. (2005). Fundamentals of Wireless

Communication. Cambridge, New York.

Winzer, P. (2012). Optical Networking beyond WDM.

IEEE Photonics Journal, 4:647–651.

SPCS 2016 - International Conference on Signal Processing and Communication Systems