The Mathematical Foundations for Mapping Policies to Network Devices

Dinesha Ranathunga

, Matthew Roughan

, Phil Kernick

and Nick Falkner

ARC Centre of Excellence for Mathematical and Statistical Frontiers,

School of Mathematical Sciences, University of Adelaide, Adelaide, Australia

CQR Consulting, Unley, Australia

School of Computer Science, University of Adelaide, Adelaide, Australia

Keywords:

Network-security, Zone-Conduit Model, Security Policy, Policy Graph.

Abstract:

A common requirement in policy speciﬁcation languages is the ability to map policies to the underlying net-

work devices. Doing so, in a provably correct way, is important in a security policy context, so administrators

can be conﬁdent of the level of protection provided by the policies for their networks. Existing policy lan-

guages allow policy composition but lack formal semantics to allocate policy to network devices.

Our research tackles this from ﬁrst principles: we ask how network policies can be described at a high-level,

independent of vendor and network minutiae. We identify the algebraic requirements of the policy-mapping

process and propose semantic foundations to formally verify if a policy is implemented by the correct set of

policy-arbiters. We show the value of our proposed algebras in maintaining concise network-device conﬁgu-

rations by applying them to real-world networks.

1 INTRODUCTION

Managing modern-day networks is complex, tedious

and error-prone. These networks are comprised of a

wide variety of devices, from switches and routers to

middle-boxes like ﬁrewalls, intrusion detection sys-

tems and load balancers. Conﬁguring these heteroge-

neous devices with their potentially complex policies

manually, box-by-box is impractical.

A better approach is a top-down conﬁguration

where device conﬁgurations are derived from a high-

level user speciﬁcation. Such speciﬁcations raise the

level of abstraction of network policies above device

and vendor-oriented APIs (e.g., Cisco CLI, Open-

Flow). Doing so, provides a single source of truth,

so, security administrators for instance, can easily de-

termine who gets in and who doesn’t (Howe, 1996).

In recent years, several research groups have pro-

posed high-level policy speciﬁcation languages for

both Software Deﬁned Networking (SDN) (Soul

et al., 2014; Reich et al., 2013; Foster et al., 2010;

Prakash et al., 2015) and traditional networks (Bartal

et al., 2004; Guttman and Herzog, 2005). A com-

mon requirement in these languages is the ability to

map the abstract policies to the underlying physical

network. Doing so accurately, is essential to

• enforce policy correctly; and

• track policy changes per network device, so, re-

dundant policy updates can be avoided.

But, mapping policies to the physical network devices

has challenges

• policy needs to be decoupled from the network. A

policy shouldn’t need to change with vendor, or

every time IP address changes occur;

• the mapping must be formally veriﬁable. Precise

and unambiguous mathematical semantics elimi-

nate wishful thinking pitfalls in deploying policies

to networks. So, security administrators have as-

surance, for instance, that their intended policies

are enforced by the correct ﬁrewalls; and

• policies can have complex semantics including

node and link properties.

We propose a generic framework to map policies

to network devices algebraically. We illustrate it’s

use by considering security policies, because incor-

rect deployment of these policies in domains such as

Supervisory Control and Data Acquisition (SCADA)

networks can result in catastrophic outcomes includ-

ing the loss of human lives! However, the principles

involved, can easily be extended to policies involving

trafﬁc measurement, QoS, load balancing and so on.

In developing our algebras, we have derived

the properties and constraints of sequentially- and

Ranathunga, D., Roughan, M., Kernick, P. and Falkner, N.

The Mathematical Foundations for Mapping Policies to Network Devices.

DOI: 10.5220/0005946201970206

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 197-206

ISBN: 978-989-758-196-0

197

parallelly-composed policies for various policy con-

texts. These policy-composition semantics must be

preserved, when mapping policy to devices, to ensure

correct deployment. Using an algebraic framework

also makes the policy-mapping process efﬁcient.

We will demonstrate the use of our proposed al-

gebras in deploying security policies on real SCADA

networks. Particularly, we will show it’s value in

maintaining a clear, concise set of ﬁrewall conﬁgura-

tions. Our approach allows administrators to conduct

“what if” analysis by changing policy and/or network

topology and observe their effect on the network de-

vices required to implement the changes.

2 BACKGROUND AND RELATED

WORK

“The advantages of implicit deﬁnition over construc-

tion are roughly those of theft over honest toil.”

Bertrand Russel

The quote is salient because network installa-

tions are commonly built from the bottom-up, i.e., a

network-device is purchased, and conﬁgurations writ-

ten. The policy is the result of the conﬁguration,

which is the consequence of a purchasing decision.

So, the policy is implicitly deﬁned as a result of many

small decisions that interact in complex ways. In-

stead, best-practice guides (e.g., Byres et al., 2005)

suggest designing the policy ﬁrst, and only then de-

termining how to implement it.

Solutions that employ a top-down network conﬁg-

uration have been proposed (e.g., Soule et al., 2014;

Anderson et al., 2014; Bartal et al., 2004). They allow

management of a single network-wide policy (i.e.,

source of truth). These policies should be high-level:

i.e., decoupled from network and vendor intricacies,

to capture policy intent and not the implementation.

Capturing intent has several beneﬁts: policy can

be distinguished from network to assist with change

management; accurate comparison of organisational

policies to industry best-practices can be made to

evaluate compliance; and policy semantics can be ex-

pressed without network minutiae like IP addresses.

But, most research towards high-level policy lan-

guages (Bartal et al., 2004; Cisco Systems Inc., 2014;

Soul

e et al., 2014), still requires these minutiae to be

speciﬁed in-policy, to implement policy on a network.

If the high-level policy deﬁnition is built on formal

mathematical constructions, then there are no implicit

properties and it provides a truly sound foundation

for everything that follows. The formalism would al-

low construction of complex and ﬂexible policies and

support reasoning about the policies. For instance,

we could precisely compare a deﬁned policy with in-

dustry best-practices in (Byres et al., 2005) for com-

pliance and reduce network vulnerability to cyber at-

tacks (Ranathunga et al., 2016a).

It is equally important to map policy to devices us-

ing a formal approach. For instance, we can be conﬁ-

dent of the blanket of protection provided for our net-

work if and only if we could prove that an intended

security policy is implemented by the correct set of

network ﬁrewalls. Some top-down conﬁguration lan-

guages (Bartal et al., 2004; Prakash et al., 2015; Cisco

Systems Inc., 2014) allow creation of network-wide

high-level policies, but lack means to allocate policy

to network devices in provably correct way.

NetKAT (Anderson et al., 2014) is a SDN pro-

gramming language for specifying and reasoning

about network behaviour. An implementation has

been developed for NetKAT to handle high-level poli-

cies based on virtual network topologies (Smolka

et al., 2015). The implementation uses an extension

of Binary Decision Diagrams to generate OpenFlow

table entries from high-level policy. In another ap-

proach, the SOL framework (Heorhiadi et al., 2016)

uses a path-based abstraction to capture optimisation

requirements of SDN applications. The abstraction

allows deﬁnition of valid paths via predicates (e.g.,

those that include a ﬁrewall). In contrast to these

works, our aim is to develop an algebraic framework

to map high-level policy to network-devices in both

SDN and traditional networks.

We have proposed (Ranathunga et al., 2016a) a

high-level security policy speciﬁcation that is network

and vendor independent for top-down conﬁguration

of ﬁrewalls. The language semantics allow these poli-

cies to be easily understood by humans. We investi-

gate here, the underlying requirements for mapping

these policies to network devices.

3 ABSTRACT POLICIES

Abstractions are key to constructing high-level poli-

cies. A good policy abstraction should capture the

underlying concepts naturally and concisely. For in-

stance, a policy may be arbitrated using one or more

network devices. A good abstraction should decouple

what is arbitrated from how it is arbitrated.

A simple abstraction that is commonly used to de-

couple policy from the network is (endpoint-group,

edge) (Bartal et al., 2004; Prakash et al., 2015). An

endpoint groups elements with common physical or

logical properties: e.g., a subnet, a user-group, a col-

lection of servers, etc. An edge speciﬁes the rela-

tionship between the endpoints, i.e., it describes what

SECRYPT 2016 - International Conference on Security and Cryptography

198

communication is allowed between the endpoints.

Consider the example network in Figure 1(a), our

high-level policy might be “we want to measure all

HTTPS ﬂows from S1 to S4”. This intent can be ex-

pressed using the (endpoint-group, edge) abstraction

as p:=S1 → S4 : collect https, where p ∈ P is

an element of the possible space P of policies.

We now want to map the policy to enforcing de-

vices (i.e., arbiters). It looks naively easy. Just imple-

ment the policy on arbiter F. However, the problem is

in general more complicated. For example, consider

policy from S1 to S2. If arbiter A captures ﬂows de-

scribed by policy p

and likewise p

, then the combi-

nation is p

A∩B

because the policy expresses that ﬂows

be collected but load balancing across the two paths

could result in either being used by a given packet.

For another example, consider policy from S2 to

S3. If arbiters C and D capture ﬂows described by

policy p

and p

respectively, then the combination

would yield their union because both arbiters in the

path are used for ﬂow collection. So, when mapping

policies to network devices, they must be composed in

a way that preserve the topology-speciﬁc semantics.

We will, in general, denote the policy composition

resulting from parallel routes as p

⊕ p

and that re-

sulting from serial routes as p

⊗ p

. In this example,

⊕ p

= p

A∩B

and p

⊗ p

= p

C∪D

. Note though,

the meaning of ⊕, ⊗ are policy-context dependent.

The problem of mapping our high-level policy p

(from S1 to S4) to network devices, may be even more

complicated than simply implementing the policy on

F. What happens if F fails? Surely we would still

want to collect HTTPS ﬂows that traverse the redun-

dant paths from S1 and S4 (e.g., path via S2 and S3).

So, p must also be mapped to the policy arbiters along

the path S1 − S2 − S3 − S4, to cater for this redun-

dancy. But then, should we map the policy to all of

these arbiters or a subset of them?

Given the parallel routes between S1 and S2 it is

easy to see that we need to map p to both A and B to

preserve the semantics of ⊕. But, when arbiters are in

series (e.g., C, D) we have the choice of mapping pol-

icy to both or just one to preserve the semantics of ⊗.

Mapping to both may be unnecessary and inefﬁcient

and arbiters may have limits on their capabilities.

The policy arbiters may not always be in series

or parallel. As we have outlined in our earlier work

(Ranathunga et al., 2015), when a star-topology is in-

volved, the question of how to map policy to topol-

ogy gets interesting. Loosely mapping policy to ar-

biters using a hyper-edge adds to the complexity of

the policy-graph and decreases it’s precision. For in-

stance, it allows a 1 : n relationship between hyper-

edges and policies, so, we must track the policy be-

(a) Network topology. (b) Policy graph of (a).

Figure 1: Example network consisting of four endpoints

(S1 − S4) and six policy arbiters A, B, ..., F (a). The corre-

sponding policy graph is shown in (b) with these endpoints

and policy edges (E1, E2, ..., E6) between them.

tween every endpoint-pair in a hyper-edge to correctly

map it’s policy to network devices.

We can overcome these issues using a simple-edge

mapping instead (Ranathunga et al., 2015). The pol-

icy graph is then simpliﬁed and it’s precision is in-

creased. The 1 : 1 relationship between edges and

policies now implies we need to only track a single

policy per edge, to map policy accurately to devices.

We may also need to consider paths that consist

of one or more intermediate endpoints, when im-

plementing policy between an endpoint pair. For

instance, consider implementing a security policy

f :=S1 → S3: http in the network in Figure 1(a).

Once implemented on the arbiters (i.e., ﬁrewalls), the

policy should allow HTTP trafﬁc ﬂow from S1 to S3.

But, the policy can only be deployed correctly if end-

points S2,S4 can route or forward HTTP trafﬁc.

This ability of an endpoint to route or forward

trafﬁc can be restrictive. For instance, in a security

policy context, an endpoint can group systems (e.g.,

hosts) with similar security requirements (ANSI/ISA-

62443-1-1, 2007). So, high-risk systems can be

grouped in to one endpoint and only safe trafﬁc that

originate and/or terminate at the endpoint is permit-

ted by the security policy. Enabling this endpoint to

transit-trafﬁc could potentially expose the high-risk

systems within to cyber attacks. So, an endpoint’s

trafﬁc transitivity capability must be considered in

constructing valid device-paths and must be captured

explicitly in the mapping process.

The intent of our high-level policy p is to col-

lect HTTPS ﬂow data from S1 to S4. Similarly, traf-

ﬁc measurement policies can be deﬁned between any

pair of endpoints in the network, so the correspond-

ing (endpoint-pair,edge) tuples collectively construct

a policy-graph (Figure 1(b)). Each (logical) edge in

this graph maps to a physical network path compris-

ing of policy arbiters and zero or more intermediate

endpoints. For instance, policy-edge E4 in Figure

1(b) implements our policy p.

The Mathematical Foundations for Mapping Policies to Network Devices

199

So far, we have described several key require-

ments of a policy-to-device mapping process. Next,

we illustrate these using more detailed examples in-

volving policies found in practice.

3.1 Quality of Service (QoS) Policies

QoS policies can provide bandwidth guarantees for

certain types of trafﬁc. The policy arbiters here would

be QoS capable routers or switches. Imagine we need

to provision a minimum bandwidth of 100MB/s for

HTTP trafﬁc ﬂow from S1 to S4 in Figure 1(a). The

high-level policy intent can be expressed as min(S1

→ S4 : http, 100MB/s). Similarly, QoS policies

between any endpoint-pair can be expressed using the

policy-graph in Figure 1(b).

Parallel and serial (QoS-device) topologies also

have an impact on the end QoS policy. Consider the

parallel topology between S1 and S2 in Figure 1(a), if

we assume p

and p

provide bandwidth guarantees

of B1 and B2 respectively, then with load balancing,

the resultant QoS policy (p

) can provide a total band-

width guarantee p

= p

⊕ p

= sum(B1, B2).

When the devices are in series, the resultant policy

provides a bandwidth guarantee given by p

⊗ p

min(B3, B4) where B3, B4 are the bandwidth guaran-

tees provided by p

and p

3.2 Security Policies

We consider here access-control policies in a network.

The policy arbiters would be trafﬁc ﬁltering devices

(e.g., ﬁrewalls, SDN switches). The endpoints could

be zones or user groups. Imagine we want to enable

only SSH trafﬁc from S1 to S4 (Figure 1(a)). The

high-level policy can be expressed as S1 → S4: ssh

with an implicit deny-all in place.

When the trafﬁc ﬁltering devices are in parallel

(e.g., topology between S1 and S2 in Figure 1(a)),

the resultant security policy (p

), has meaning — all

packets that can possibly be allowed through — and

is the union of the packet sets allowed by the indi-

vidual devices. We take union conservatively because

intrusions and attacks are usually carried out through

permitted trafﬁc. So, if p

and p

allows packet sets

Q and T respectively, then p

= p

⊕ p

= p

Q∪T

When the devices are in series, the resultant pol-

icy permits the intersection of the packet sets V,W

allowed by the policies of C, D respectively, i.e.,

= p

⊗ p

= p

V ∩W

With security policies, it is often useful to have

endpoints that group systems with similar security re-

quirements. Doing so, allows to deﬁne a single pol-

icy for all members of an endpoint: a clean and con-

cise abstraction of network security. But, a generic

(endpoint-pair, edge) abstraction cannot capture such

network-security speciﬁc concepts precisely.

So, we need concrete deﬁnitions for what an end-

point and an edge means for each policy context to

capture policy-speciﬁc intricacies. We will show later

how to deﬁne these concretely for security policies.

3.3 Trafﬁc Measurement Policies

Trafﬁc measurement policies help implement, for in-

stance, NetFlow (v9) on the network in Figure 1(a).

The policy arbiters A,B, ..., F here, would be NetFlow

capable devices (usually routers or switches). The

endpoints could be subnets or zones in the network.

When we considered the parallel routes between

S1 and S2, the resultant policy (p

) has meaning —

the ﬂows that are guaranteed to be captured by the

topology (without sampling) — and constitutes of the

intersection of the packet sets of A and B. So, if p

and p

capture packet sets Q and T respectively, then

= p

⊕ p

= p

Q∩T

We also showed when the devices are in series, the

resultant policy captures the union of the packet sets,

i.e., p

= p

⊗ p

= p

V ∪W

Thus, policies can be composed using the generic

semantics ⊕ and ⊗ in different policy contexts. The

actual meaning of these operators is policy-type de-

pendant. For instance, with QoS policies, ⊗ repre-

sented minimum while here it has meaning of union.

Policy Mapping Vs Routing: Our discussion above

on mapping policies to network devices, relates to

network paths or routes. This is no accident. Our

target problem has many parallels with routing.

But, the aim in routing is to determine the path

that optimises a given path-metric (e.g., shortest-path

routing ﬁnds a minimum-distance path between end-

points). Our target problem is different: we need to

determine the arbiters in a network a given policy

should be implemented on. So, constructing all fea-

sible paths is crucial because, for instance, a security

policy between two endpoints can only be correctly

implemented (e.g., to block all Telnet trafﬁc) if all re-

dundant paths between them are taken into account.

In routing, the number of endpoints (e.g., individ-

ual gateways) can be high for a large network, so,

distributed means to computing a solution is essen-

tial (requiring de-centralised protocols like OSPF and

BGP). In contrast, we expect a relatively low num-

ber of endpoint groups when mapping policies to de-

vices. As we will show in 5, a low endpoint-count

makes our policy-mapping algorithm computation-

ally tractable. So, a logically-centralised implemen-

tation can be considered.

SECRYPT 2016 - International Conference on Security and Cryptography

200

Current meta-routing algebras (Dynerowicz and

Grifﬁn, 2013), allow to provably choose paths that op-

timise various path-metrics. These algebras support

speciﬁcation of link properties, but, not the speciﬁca-

tion of node properties such as trafﬁc transitivity.

We described earlier, the need to deﬁne endpoints and

edges concretely to incorporate the intricacies in each

policy context. We illustrate the idea next using se-

curity policies and their concretised (endpoint-pair,

edge) abstraction: the Zone-Conduit model.

The Zone-Conduit Model: Lack of internal-network

segmentation is a key contributor to the fast prop-

agation of threats and attacks in a network (Byres

et al., 2005). So, ANSI/ISA have proposed the Zone-

Conduit model as a way of segmenting and isolat-

ing the various sub-systems in a SCADA network

(ANSI/ISA-62443-1-1, 2007).

A zone is a logical or physical grouping of an

organisation’s systems with similar security require-

ments so that a single policy can be deﬁned for all

zone members. A conduit provides the secure com-

munication path between two zones, enforcing the

policy between them (ANSI/ISA-62443-1-1, 2007).

A conduit could consist of multiple links and ﬁrewalls

but, logically, is a single connector.

The Zone-Conduit model is a concrete instance

of the (endpoint-pair, edge) abstraction for high-level

security policy speciﬁcation. Zones and conduits de-

ﬁne endpoints and edges concretely. These deﬁnitions

allow important network-security characteristics such

as a single zone-policy, to be captured concisely.

The ISA Zone-Conduit model in its original de-

scription lacks precision for policy speciﬁcation. We

use the extensions proposed in (Ranathunga et al.,

2015) to increase its precision, e.g., we add Firewall-

Zones to specify ﬁrewall-management policies.

Zone-Conduit Policies: A conduit policy is an or-

dered set of rules [p

, p

, ..., p

] that act on packet

sequences to accept, deny, or in some cases, modify

them. In our related work (Ranathunga et al., 2016a),

we have identiﬁed properties and constraints required

in a Zone-Conduit based policy description to make

the rules implementation- and order-independent.

To summarise, we adopt a security whitelisting

model, i.e., we restrict policies to express positive

abilities

and deny all inter-zone ﬂows that are not ex-

plicitly allowed (Ranathunga et al., 2015). Doing so,

renders the rule order irrelevant and allows consistent

conversion of policy to heterogeneous ﬁrewalls. Thus

the underlying vendor can change without requiring

policy alterations. By being explicit, we also prevent

services being accidentally enabled implicitly.

Refers to the ability to initiate or accept a trafﬁc service.

Directed- vs Undirected-Conduit Policy: The policy

on an undirected-conduit can be expressed using two

directed-conduit policies. Directed-conduits are im-

portant in understanding how policy should be imple-

mented on device interfaces. For instance, an undi-

rected conduit can only map a security policy to a ﬁre-

wall interface. But, to implement the policy correctly,

we additionally need to know if it should be imple-

mented inbound or outbound on these interfaces. A

directed-conduit provides this directionality.

However, analysis using directed-conduits can

also lead to problems. For instance, directed-conduit

paths that may seem feasible may require trafﬁc to

traverse a ﬁrewall interfaces twice (illustrated in de-

tail in the longer version of the paper). We inval-

idate such directed-conduit paths via a mapping h :

F → W where F = {directed f irewalls} and W =

{ f irewalls}. A directed-ﬁrewall in the Zone-Conduit

graph G = (Z,C) is deﬁned as

Deﬁnition 1 (Directed ﬁrewall). A directed ﬁrewall

i j

is a ﬁrewall t ∈ W that ﬁlters trafﬁc on directed-

conduit (i, j) ∈ C.

Then we can check if the directed-ﬁrewalls in a path

map to the same physical ﬁrewall (i.e., h(A

) =

h(A

) = A) and deem that path invalid.

4 MAPPING ALGEBRA

We outline here, our proposed algebra to map policy

to network devices by ﬁrst making the distinction be-

tween primary and secondary policy-edges.

4.1 Firewall-path Construction

A policy-edge can be classiﬁed as primary or sec-

ondary based on how it arbitrates policy. A primary-

edge enforces policy using arbiters (e.g., ﬁrewalls)

only. A secondary-edge enforces policy using arbiters

and one or more endpoints (e.g., a zone).

We demonstrate the idea using the simple Zone-

Conduit graph G = (Z,C) in Figure 2(a). The ﬁrewall

composition of each primary-conduit in the model is

shown (Figure 2(b)). The example secondary-conduit

ﬁlters trafﬁc ﬂow from zone 1 to 3, using several

directed-ﬁrewalls and transit zones 2, 4. The set of all

directed-conduits are given by DC = {C

i j

| (i, j) ∈ C}.

A policy-graph is essentially an automation that

moves trafﬁc packets from one endpoint to another us-

ing policy-edges. So, regular expressions (the natural

language of ﬁnite automata), can capture the packet-

processing behaviour of this model; a path encoding

is a concatenation of directed-devices (i.e., policy-

arbitration steps pq) and a set of paths is encoded as

The Mathematical Foundations for Mapping Policies to Network Devices

201

a union of paths. Past work (Anderson et al., 2014)

has shown, all single-path encodings stem from the

Kleene star operator (*) on the set of directed-devices.

In a security policy context, the automation means

that a single ﬁrewall-path encoding is a concatenation

of directed-ﬁrewalls. Each path depicts a sequence of

trafﬁc ﬁltering steps and is an element of F

∗

But, the Zone-Conduit model is a logical repre-

sentation, so, every ﬁrewall-path encoding in F

∗

may

not be valid. We deﬁne single ﬁrewall-path concate-

nation to ﬁlter-out invalid paths

Deﬁnition 2 (Single ﬁrewall-path concatenation).

Take a ∈ F

∗

s.t. a = t

...t

n+1

where

∈ F. Also take b ∈ F

∗

s.t. b =

...s

m+1

where s

∈ F. Then

ﬁrewall-path concatenation from F

∗

× F

∗

→ F

∗

ab =











...t

n+1

...s

m+1

if d

n+1

= g

and g

6= d

; ∀i, j, i > 1

and h(t

) 6= h(s

); ∀i, j, k, l

φ, otherwise.

and aφ = φa = φ; ∀a ∈ F

∗

Concatenation deﬁned above is a binary operation

that constructs only elementary ﬁrewall-paths. These

paths do not allow trafﬁc to traverse a particular ﬁre-

wall interface more than once and also prohibit trafﬁc

ﬂow through a non-transit zone (e.g., Firewall-Zone).

Consider two directed-ﬁrewalls X,Y with policies

and p

that accept packet sets R and T . The re-

sultant policy of the concatenated ﬁrewall-path XY

is that of sequential ﬁrewalls and can be denoted as

⊗ p

)(s) = p

R∩T

(s) where s is a packet sequence.

This result is policy-context dependent, for instance,

with trafﬁc measurement policies, the outcome is sim-

ilar to that of serial arbiters: i.e., p

⊗ p

= p

R∪T

We deﬁne a set of directed-ﬁrewall paths as a

union of elements in F

∗

. Again, consider our

directed-ﬁrewalls X,Y from before. If these described

two distinct paths, then the resultant policy of the

path union X ∪ Y is that of parallel ﬁrewalls, i.e.,

⊕ p

)(s) = p

R∪T

(s) where s is a packet sequence.

This result is also context dependent, so, for trafﬁc

measurement policies, the outcome is similar to that

of parallel arbiters, i.e., p

⊕ p

= p

R∩T

We also extend concatenation in Deﬁnition 2 to

S = {Power-set of F

∗

}

Deﬁnition 3 (Multiple ﬁrewall-path concatena-

tion). Take a, b ∈ S s.t. a = {a

, a

..., a

}, b =

, b

, ..., b

} where a

, b

∈ F

∗

. Then ﬁrewall-path

concatenation from S × S → S is given by

ab = {a

}; ∀i j

Deﬁnition 3 allows to construct all possible ﬁrewall-

path sets from the union of elements in S. Then

(S, ∪, ·,

1) is an idempotent semiring with

0 = φ; empty set; and

1 = {ε}; empty-string set where ε is the identity

element of the concatenation operation.

The properties of the operators ∪ and · actually dic-

tate rules for ﬁrewall-path construction. So, these se-

mantics must be preserved when composing ﬁrewall-

paths. For instance, ∪ is commutative while · is not.

So, the order of the directed-ﬁrewalls matter, when

constructing a single ﬁrewall-path, but, are irrelevant

when constructing multiple paths.

Similarly, we can construct single and multiple

device-paths for other policy contexts and obtain the

semiring result for (S, ∪, ·,

1) per security policies.

4.2 Mapping Policy to Arbiters

We described how the semiring (S, ∪, ·,

1) con-

structs sets of device-paths between policy-graph end-

points. The sequential (i.e., ⊗) and parallel (i.e., ⊕)

policy-composition operators in 3 can now construct

the policies of these paths. Assume we have to im-

plement a high-level policy p

i j

on arbiters q

that lie

in the paths from i to j. All applicable device-paths

from i to j can be constructed as per 4.1 and given by

i j

= {q

...q

n−1

, ....., q

...q

m−1

Then, the high-level policy p

i j

derived from the in-

dividual arbiter policies p

i j

= (p

⊗ p

... ⊗ p

n−1

)

⊕ (....................................)

⊕ (p

⊗ p

... ⊗ p

m−1

). (1)

Mapping the intended high-level policy p

i j

to the

arbiters is now a matter of ﬁnding p

i j

for all arbiters

such that p

i j

= p

i j

. But deriving such a mapping is

non trivial because ⊕ and ⊗ have policy-context de-

pendent meanings. For instance, with security poli-

cies ⊕ means union and ⊗ means intersection. So, a

simple solution that supports defence in depth would

be to implement the access-control policy p

i j

on ev-

ery sequential ﬁrewall across all paths.

For another instance, ⊕ means summation and

⊗ means minimum in QoS policies. So, a required

bandwidth guarantee p

i j

can be split across multiple

paths with sequential arbiters in each path guarantee-

ing only a portion of the total bandwidth.

Irrespective of the policy context, the underlying

requirement when mapping policy to network devices

is to adhere to the semantics of 1.

4.3 Computation of All Firewall-paths

We reduced the policy-to-device mapping problem to

the semantics of 1 in the previous section. We now

SECRYPT 2016 - International Conference on Security and Cryptography

202

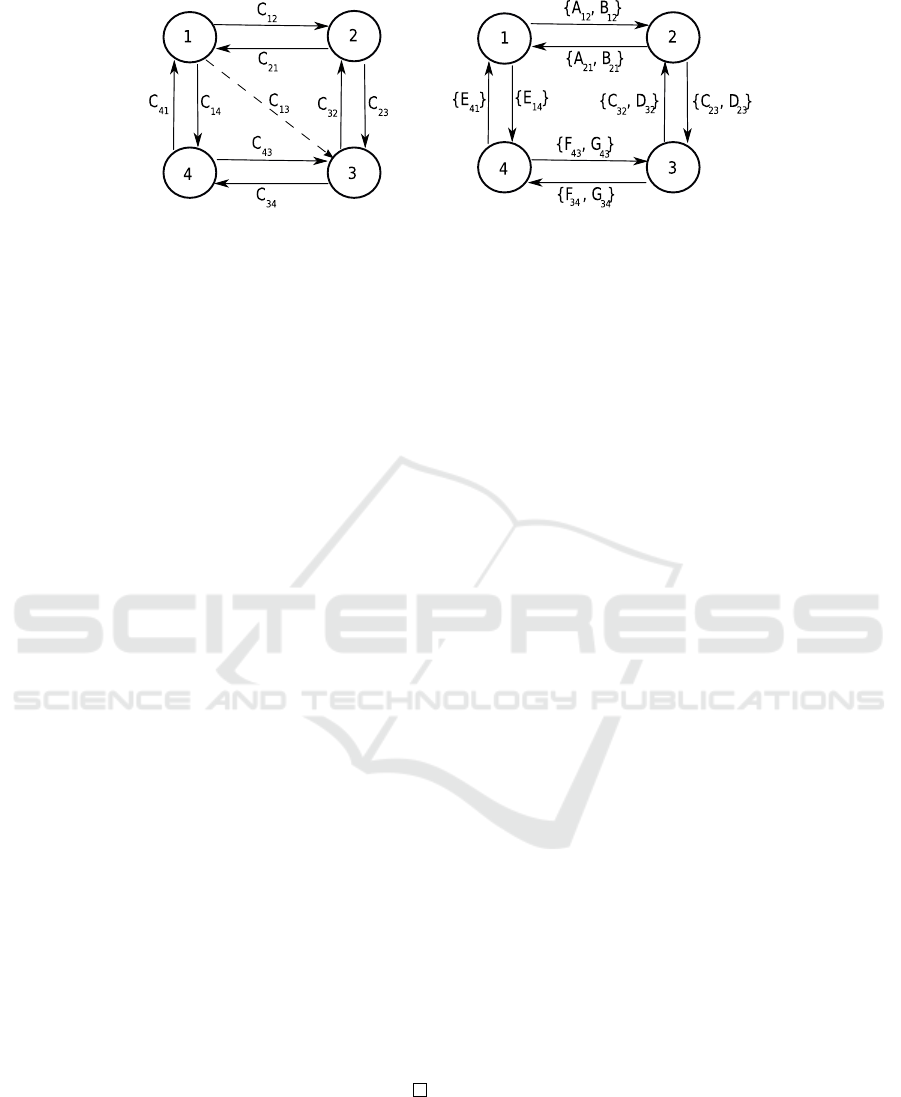
(a) Zone-Conduit model with pri-

mary and secondary conduits.

(b) Firewall-paths of the primary-conduits

in (a).

Figure 2: Zone-Conduit model depicting primary-conduits C

i j

and a secondary-conduit C

enabled by the transit zones 2 and

4 are shown in (a). The ﬁrewall-paths of the primary-conduits are shown in (b).

develop an algorithm to compute the device-paths of

1 efﬁciently. Again, we demonstrate the idea using

security policies and the Zone-Conduit model.

We can represent the primary-conduit ﬁrewall-

paths using a generalised Adjacency matrix A. Here,

A(i, j) is the ﬁrewall-path of primary conduit C

i j

∈

DC. For our example in Figure 2(b), A =







z}|{

{ε}

z }| {

, B

}

z}|{

}

, B

} {ε} {C

, D

} φ

φ {C

, D

} {ε} {F

, G

}

} φ {F

, G

} {ε}







(2)

Given such a matrix A, the solution to the problem

of ﬁnding the set of all valid ﬁrewall-paths between

zones is a matrix A

∗

such that

∗

(i, j) = {valid primary- and secondary-conduit

ﬁrewall-paths from zone i to j} (3)

We developed the following theorem to compute

∗

, inspired by algorithms in meta-routing (Dynerow-

icz and Grifﬁn, 2013).

Theorem 4 (A

∗

calculation). A

∗

can be calculated us-

ing the right iteration algorithm

<k+1>

= (A

<k>

T ∪ I)A where A

<0>

= I.

T and I are the zone-transitivity matrix and

the multiplicative-identity matrix (of semiring

(S, ∪, ·,

1)) respectively.

Proof. See the longer version (Ranathunga et al.,

2016b) of this paper.

The zone-transitivity matrix T is deﬁned as

T (i, j) =

(

{ε} if i = j and transitivity(i) = 1

φ, otherwise.

(4)

and I is the multiplicative-identity matrix

I(i, j) =

(

1 if i = j

0, otherwise.

(5)

For bounded semirings we only iterate n −1 times

to converge to A

∗

, where n is the number of nodes in

the Zone-Conduit model, i.e., A

∗

= A

<n−1>

We have deﬁned T , A

∗

and the right-iteration al-

gorithm for a security-policy context, but these can

equally be deﬁned for other policy contexts.

If we apply our algorithm in 4 to the example in

Figure 2(b), n = 4, so, A

∗

= A

<3>

and for simplicity

assume that all zones are transitive, then

T =







{ε} φ φ φ

φ {ε} φ φ

φ φ {ε} φ

φ φ φ {ε}







(6)

and we see that I = T in this instance.

We calculate A

∗

= A

<3>







{ε} η κ θ

µ {ε} ν β

γ λ {ε} ρ

ξ δ ζ {ε}







(7)

where for instance

κ = {A

, A

, B

, E

} (8)

All valid ﬁrewall-paths from zone 1 to 3 are in κ.

Let’s now assume that zone 4 is non-transitive,

then transitivity(4) = 0, we re-calculate A

∗







{ε} {A

, B

} η θ

, B

} {ε} {C

, D

} µ

γ {C

, D

} {ε} ρ

ξ δ ζ {ε}







(9)

where for instance

η = {A

, A

, B

} (10)

The Mathematical Foundations for Mapping Policies to Network Devices

203

Figure 3: Policy to network-device mapping process.

The updated ﬁrewall-paths from 1 to 3 are in η. In

comparison to 8, we see that the paths via zone 4 (i.e.,

, E

) have now been removed as the zone

is no longer transitive. A

∗

can similarly be calculated

for other policy contexts to determine all valid device-

paths between endpoint pairs.

We describe next our implementation of the algorithm

in 4. The implementation allows the use of these al-

gebras to map policy to real network devices.

5 IMPLEMENTATION

Our policy mapping system is depicted in 3, and we

outline it’s details below. The system is currently im-

plemented in Python, and allows mapping of high-

level policies written in our own policy speciﬁcation

language, to network devices. We will make the sys-

tem open source in the near future.

High-level Security Policy: The topology-

independent policy input ﬁle created using our

high-level policy speciﬁcation language.

Network Topology: The input network topology

described in the XML-based graph ﬁle format

GraphML. The ﬁle holds information of all devices

in the network and their interconnections. The crucial

aspects are the details of the topology near the policy

arbiters (e.g., ﬁrewalls).

Map Policy to Network: Compiles high-level policy

to an Intermediate-Level (IL), generates the policy

graph (e.g., Zone-Conduit model) of the input net-

work and computes A

∗

as per 4.3 to map high-level

policy to the devices (e.g., ﬁrewalls) in the network.

Policy-to-device Map: The primary output depicting

policy breakdown by device, interface and direction.

Veriﬁcation Output: Secondary output speciﬁcally

suited for veriﬁcation (e.g., policy errors).

Our system implements a high-level policy on a net-

work instance by coupling the two. We outline here,

the computation of A

∗

to map policy to network de-

vices (see the longer paper version for a detailed im-

plementation). We illustrate our system using security

policies and the Zone-Conduit model, but it can like-

wise be used in other policy contexts.

5.1 A

∗

Calculation

We compute A

∗

using the algorithm in 4. A cen-

tralised implementation is used (given typically low

n), but, it could be distributed across multiple nodes

performing parallel computations.

Our implementation algorithm has time complex-

ity O(n

) (Ranathunga et al., 2016b). So, specify-

ing policy per individual host (i.e., large n) in top-

down conﬁguration makes policy mapping extremely

inefﬁcient. More efﬁcient is to create network groups

(e.g., by subnet) and specify policy between them, so,

a reasonably low value can be maintained for n. For

instance, we will see in 6 that in a SCADA network

typically n < 25.

We considered all valid paths between zone-pairs

in calculating A

∗

. The decision allows us to per-

mit or block trafﬁc along all possible communication

paths between a zone pair, providing redundancy and

defence-in-depth in the network. We also map pol-

icy uniformly to every ﬁrewall in a single-path, fur-

ther boosting defence-in-depth. These decisions col-

lectively create a robust defence against cyber attacks.

But, in other policy contexts, it may be useful to

select a subset of all valid paths or just a single path

(e.g., shortest path) instead. Doing so, could improve

the time complexity of the algorithm in 4 (e.g., short-

est paths yield O(n

)). This path pruning can be done,

for instance, by incorporating a sparse matrix in the

algorithm. In some contexts, it can be efﬁcient to ap-

ply policy only on edge arbiters of a path (e.g., when

enabling trafﬁc measurements).

6 A SERIES OF CASE STUDIES

We now show the use of our developed algebras,

through real SCADA-ﬁrewall conﬁguration case stud-

ies summarised in 1. The data was provided by the

authors of (Ranathunga et al., 2015).

The seven Systems Under Consideration (SUCs),

involve various ﬁrewall architectures and models. We

use them to demonstrate several properties, most no-

tably that the computational complexity of our policy-

to-device mapping algorithm is tractable.

An important feature depicted in 1 is the number

of security zones in each network. This number is

SECRYPT 2016 - International Conference on Security and Cryptography

204

Table 1: SCADA case study summary adapted from (Ranathunga et al., 2015) (# ACL rule allocation error).

SUC Fire-

walls

Zones Cond-

uits

Max.

hosts

ACLs Average

rules

per ACL

Incorrect

ﬁrewall

Incorrect

interface

Incorrect

direction

Run-

time

(s)

1 3 7 11 67580 8 237 15 13 19 40

2 6 21 81 2794 12 16 3 2 5 70

3 4 10 17 886 8 6 2 1 4 43

4 3 9 16 2038 3 80 5 12 13 61

5 3 12 19 2664 12 677 15 8 26 47

6 3 13 21 3562 8 1034 21 15 19 63

7 6 15 22 3810 17 724 9 5 17 49

small (i.e., ≤ 21) relative to the maximum (potential)

number of hosts per network (i.e., ≤ 67580).

This is to be expected, a zone groups a set of hosts

or subnets with identical policies. If every host had a

distinct policy then a large number of ﬁrewalls would

be needed to enforce a real separation between the

hosts, making it impractical. By grouping hosts into

zones, we reduce policy complexity, so their speciﬁ-

cation becomes easier and less error-prone.

We identiﬁed incorrectly assigned ACL rules in

each case study by parsing the ﬁrewall conﬁgurations

as per (Ranathunga et al., 2015). We then classed the

errors into three groups: incorrect-ﬁrewall, incorrect-

interface and incorrect-direction errors (1). Incorrect-

ﬁrewall errors are ACL rules that are assigned to the

wrong ﬁrewall to begin with, i.e., the desired trafﬁc

ﬁltering could not be achieved by placing the ACL

rule in any of that ﬁrewall’s interfaces. Incorrect-

interface errors are ACL rules that are assigned to

the correct ﬁrewall but to the wrong ﬁrewall-interface,

i.e., the desired trafﬁc ﬁltering could not be achieved

by assigning the rule inbound or outbound of that

ﬁrewall-interface. Incorrect-direction errors comprise

of ACL rules that are assigned to the correct ﬁrewall

and ﬁrewall-interface, but in the wrong direction (e.g.,

outbound instead of inbound).

As (1) suggests, on average there were 10 ACL

rules allocated to the wrong ﬁrewall, 8 rules allocated

to the wrong ﬁrewall-interface and 15 rules allocated

in the wrong interface-direction, per case study. We

automatically mapped the high-level policy in each

case to it’s network using our system. There were

zero incorrectly allocated policy rules, when the pol-

icy was mapped to the ﬁrewalls using our algebras!

Through correct policy deployment, we reduce vul-

nerability of these SCADA networks to cyber attack,

preventing potentially-catastrophic outcomes.

7 CONCLUSIONS

There are various obstacles that hinder the precise

mapping of policies to network devices. Most promi-

nent is the lack of decoupling between policy and

network which makes policy sensitive to network-

intricacies and vendor changes. To compound the

problem, policies can also have complex semantics

including node and link properties.

Our research addresses these challenges and pro-

poses a mathematical foundation for mapping policies

to network-devices. We use it to deploy real-world se-

curity policies to network ﬁrewalls provably correctly,

so, that administrators can be conﬁdent of the protec-

tion provided by their policies for their networks.

ACKNOWLEDGEMENTS

This project was supported by an Australian Post-

graduate Award, Australian Research Council Link-

age Grant LP100200493 and CQR Consulting.

REFERENCES

Anderson, C. J., Foster, N., Guha, A., Jeannin, J.-B., Kozen,

D., Schlesinger, C., and Walker, D. (2014). NetKAT:

Semantic foundations for networks. ACM SIGPLAN

Notices, 49(1):113–126.

ANSI/ISA-62443-1-1 (2007). Security for industrial au-

tomation and control systems part 1-1: Terminology,

concepts, and models.

Bartal, Y., Mayer, A., Nissim, K., and Wool, A. (2004).

Firmato: A novel ﬁrewall management toolkit. ACM

TOCS, 22(4):381–420.

Byres, E., Karsch, J., and Carter, J. (2005). Good practice

guide on ﬁrewall deployment for SCADA and process

control networks. NISCC.

The Mathematical Foundations for Mapping Policies to Network Devices

205

Cisco Systems Inc. (2014). Cisco Virtual Security Gateway

for Nexus 1000V Series Switch Conﬁguration Guide.

San Jose, CA 95134-1706, USA.

Dynerowicz, S. and Grifﬁn, T. G. (2013). On the forward-

ing paths produced by Internet routing algorithms. In

ICNP, pages 1–10.

Foster, N., Freedman, M. J., Harrison, R., Rexford, J.,

Meola, M. L., and Walker, D. (2010). Frenetic: a

high-level language for OpenFlow networks. In ACM

PRESTO, pages 21–27.

Guttman, J. D. and Herzog, A. L. (2005). Rigorous auto-

mated network security management. IJIS, 4:29–48.

Heorhiadi, V., Reiter, M. K., and Sekar, V. (2016). Sim-

plifying software-deﬁned network optimization using

SOL. In USENIX NSDI, pages 223–237.

Howe, C. D. (1996). What’s Beyond Firewalls? Forrester

Research, Incorporated.

Prakash, C., Lee, J., Turner, Y., Kang, J.-M., Akella, A.,

Banerjee, S., Clark, C., Ma, Y., Sharma, P., and Zhang,

Y. (2015). PGA: Using graphs to express and automat-

ically reconcile network policies. In ACM SIGCOMM,

pages 29–42.

Ranathunga, D., Roughan, M., Kernick, P., and Falkner, N.

(2016a). Malachite: Firewall policy comparison. In

IEEE ISCC.

Ranathunga, D., Roughan, M., Kernick, P., and

Falkner, N. (2016b). The mathematical foun-

dations for mapping policies to network devices,

http://arxiv.org/abs/1605.09115. Technical Report.

Ranathunga, D., Roughan, M., Kernick, P., Falkner, N., and

Nguyen, H. (2015). Identifying the missing aspects

of the ANSI/ISA best practices for security policy. In

ACM CPSS, pages 37–48.

Reich, J., Monsanto, C., Foster, N., Rexford, J., and Walker,

D. (2013). Modular SDN programming with Pyretic.

USENIX login, 38(5).

Smolka, S., Eliopoulos, S., Foster, N., and Guha, A. (2015).

A fast compiler for NetKAT. In ACM SIGPLAN,

pages 328–341.

Soul

e, R., Basu, S., Marandi, P. J., Pedone, F., Kleinberg,

R., Sirer, E. G., and Foster, N. (2014). Merlin: A

language for provisioning network resources. In ACM

CoNEXT, pages 213–226.

SECRYPT 2016 - International Conference on Security and Cryptography

206