The Sourcing Problem

Energy Optimization of a Multisource Elevator

Chlo

e Desdouits

1,2,3

, Mazen Alamir

, Rodolphe Giroudeau

and Claude Le Pape

Strategy Technology, Schneider Electric Industries SAS,

38 TEC, 37 quai Paul-Louis Merlin, 38050 Grenoble Cedex 09, France

Control Systems Department, GIPSA-lab,

UMR 5216 CNRS - Grenoble INP - Universit

e Joseph Fourier - Universit

e Stendhal,

11 rue des Math

ematiques - Grenoble Campus - BP46, 38402 Saint Martin d’H

eres Cedex, France

Computer Science Department, LIRMM,

UMR 5506 - Universit

e Montpellier 2, CC477,

161 rue Ada, 34095 Montpellier Cedex 5, France

Keywords:

Energy Optimization, Control of Dynamic Systems, Linear Programming, Rule-based Algorithms.

Abstract:

As the interest in regulating energy usage and in the demand-response market is growing, new energy man-

agement algorithms emerge. In this paper, we propose a formalization of “the sourcing problem” and its

application to a multisource elevator. We propose a linear formulation that, coupled with a low level rule-

based controller, can solve this problem. We show in the experiments that a compromise between reducing

consumption peaks and minimizing the energy bill has to be reached.

1 INTRODUCTION

Reducing energy consumption is a major issue nowa-

days; not only in order to restrain the ecological im-

pact on the planet, but also to both respect building

norms and minimize industrial and residential activ-

ities’ energy bill. In order to achieve this goal, one

can act on energy consumption by optimizing the

amount of energy consumed, or by shifting consump-

tion during the day. But one can also control one’s

energy consumption impact, by adding renewable en-

ergy sources and storage units. Thus, an “energy hub”

is created.

If one chooses this second possibility, a new op-

timization problem arises. The energy hub has to de-

cide which energy source to be used at which mo-

ment. We call this problem “the sourcing problem”

and formalize it in Section 2.

In this paper, we solve the sourcing problem for a

multisource elevator, as the newest generations of el-

evators are equipped with energy storage to ensure a

minimum autonomy in case of power failure. This is

crucial for safety (e.g. to evacuate people with re-

duced mobility) and energy storage may also offer

ﬂexibility in power management. In Section 3, the

reader is given an glimpse of what can be done for

dealing with energy sourcing issues of those multi-

source elevators.

Section 4 gives details on our solution to solve the

sourcing problem. First by describing interactions be-

tween our two coupled controllers. Then by explain-

ing the linear formulation used to compute a sourcing

strategy. And ﬁnally by giving some details on how

our low-level rule-based controller takes strategy into

account.

Afterwards, experiments are conducted in Sec-

tion 5 to highlight advantages and drawbacks of that

method, as well as parameters inﬂuencing its achieve-

ments.

Finally, Section 6 concludes the paper and intro-

duces future work.

2 THE SOURCING PROBLEM

We call “prosumers”, entities that consume and/or

produce energy. An energy hub allows each prosumer

to consume power produced by all other prosumers at

the same time.

Deﬁnition 1. Let P be a set of n

prosumers, all con-

nected to the same energy hub h.

Desdouits, C., Alamir, M., Giroudeau, R. and Pape, C.

The Sourcing Problem - Energy Optimization of a Multisource Elevator.

DOI: 10.5220/0005947600190030

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 19-30

ISBN: 978-989-758-198-4

We differentiate three kinds of prosumers: the set

S of storage units, the set P of controllable producers

and the set E of the others. Thus, these sets form a

partition of the whole set of prosumers.

Deﬁnition 2. Let S = {π

, . . . , π

} be the set of stor-

age units, P = {π

, . . . , π

} be the set of controllable

producers or consumers, and E = {π

, . . . , π

} be

the set of the other prosumers. Then, P = S ∪ P ∪ E.

Each prosumer can consume and/or produce

power, depending on its physical capabilities.

Deﬁnition 3. For a given prosumer π

∈ P , let p

min

≤

0 (resp. p

max

≥ 0) be the minimum (resp. maximum)

instantaneous power of π

. Then, at a given time t, let

min

≤ p

[t] ≤ p

max

be the instantaneous power pro-

duced by π

if p

[t] is positive, or consumed by π

[t] is negative

A system composed of an energy hub and its pro-

sumers can be represented by a star oriented graph.

Deﬁnition 4. Let G = (P ∪ h,A) be a star oriented

graph rooted in h where P ∪ h are the nodes of the

graph and A are the weighted arcs. There is an arc

(π

, h) if p

max

> 0 and the weight of the arc is p

max

In the same way, there is an arc (h,π

) if p

min

< 0 and

the weight of the arc is p

min

We suppose that time can be sampled in a regular,

uniform way.

Deﬁnition 5. Let τ ∈ R be the sampling period (ex-

pressed in hours), and H ∈ N be the number of peri-

ods considered. Then time-steps are expressed in the

following way: t

= t

l−1

+ τ = l × τ, ∀l ∈ {0, . . . , H}.

Finally, each controllable producer has an energy

cost function that gives the price associated to an en-

ergy consumption or production of this prosumer.

Deﬁnition 6. ∀π

∈ P, let cost

: [p

min

, p

max

] → R be

the energy cost function associated to π

Then, we can deﬁne sourcing problems:

Instance: a set of prosumers P = P ∪ S ∪ E,

a graph G = (P ∪ h, A),

a period τ ∈ R,

a time horizon H ∈ N,

a set of cost functions:

{cost

, ∀π

∈ P}

Solution: S, a n

× H matrix of p

[t]

Power is expressed in Watts and energy in Watt hours.

Quest. 1: given p

max

hub

∈ R the allowed residual

power of the energy hub, does a ma-

trix S exist such that:

∀l ∈ {0, . . . , H −1},

− p

max

hub

≤

∑

i=1

] ≤ p

max

hub

(1)

Can the energy hub be autonomous?

Quest. 2: given p

max

∈ R the allowed power

peak of controllable producers, does

a matrix S exist such that:

∀l ∈ {0, . . . , H −1},

max

∈P

] ≤ p

max

(2)

Can power peaks purchased from

controllable producers stay below a

given value?

Quest. 3: given cost

max

hub

∈ R the allowed energy

bill, does a matrix S exist such that:

H−1

∑

l=0

∑

∈P

cost

] × τ)

≤ cost

max

hub

(3)

Can the energy bill stay below a

given value?

These three objectives are sometimes antagonis-

tic.

In this paper, we consider the following applica-

tion of the sourcing problem. The set P of prosumers

is composed of: an elevator π

, that can get energy

from a battery π

, a supercapacitor π

, the grid π

and

Energy

hub

Elevator

Solar

panels

Grid

Battery

Supercapacitor

Dissipation

resistor

min

max

min

max

min

max

min

Figure 1: The elevator sourcing problem.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

a solar panel π

. The supercapacitor is here to absorb

power peaks above the maximum power capability of

the battery. But the former is more expensive than the

latter. Moreover, energy can be recovered from the

elevator when the brakes are applied. Finally, energy

can be dissipated in a resistor π

if there is too much.

The partition of P is the following: E = {π

, π

P = {π

, π

}, S = {π

, π

}. An illustration of the ele-

vator sourcing problem is given in Figure 1.

As it is a real-life application, the three objectives

corresponding to questions above have to be achieved

simultaneously. The goal is to minimize power peaks

purchased from the grid and the energy bill while en-

suring that the hub is autonomous.

3 STATE OF THE ART

Energy optimization systems have been widely stud-

ied in the literature, especially in the past few years.

In the following state of the art, we present research

works dedicated to energy sourcing of multisource el-

evators.

A very comprehensive work on energy systems

for elevators is proposed by (Paire et al., 2010).

They have designed a physical multi-source system

to power an elevator. In the paper, rules are used to

charge or discharge batteries depending on whether

the electrical current is below or above a given refer-

ence. This control method may be reduced to a simple

“if, then, else” structure achieved by physical compo-

nents.

Likewise, (Tominaga et al., 2002) presents three

rule-based methods to control a battery coupled with

an elevator. This method takes into account peak/off-

peak tariffs and reduces energy consumption cost by

storing energy recovered from the elevator.

These methods allow controlling very reactively

the system, but cannot take into account optimally ex-

ternal considerations such as the electricity tariff or

battery state of health. Therefore, these control meth-

ods may not be efﬁcient regarding economical objec-

tives.

On the other hand, (Bilbao and Barrade, 2012)

have proposed a General Energy and Statistical De-

scription (GESD) of the possible missions of an ele-

vator and an energy manager based on dynamic pro-

gramming. Their energy manager is inspired by stock

management theory and minimizes the sum of en-

ergy (i) absorbed from the grid, (ii) dissipated in the

braking resistor and (iii) not provided to the elevator.

The optimization is done off-line. This method de-

duces economically optimal solutions from consump-

tion probabilities. But elevator usage is unpredictable

by nature and there is no given alternative when the

strategy is not applicable.

Finally, in (Sachs, 2005), authors summarize dif-

ferent ways to optimize choices of elevator physical

components (motor, drive, etc). An appropriate sizing

of these components is a way to optimize energy con-

sumption but it should be coupled with a good control

algorithm of multiple sources of energy.

From these observations, we have decided to pro-

pose a two-layer optimization that can achieve reac-

tive control of low-level equipment as well as com-

pute economically optimal sourcing strategy. As part

of the European Arrowhead project, we published a

ﬁrst description of a linear program to solve the mul-

tisource elevator problem in (Desdouits et al., 2015).

We also described, in (Boutin et al., 2014), the inter-

actions between our control method and partner com-

ponents. In the current paper, we formalize the sourc-

ing problem, improve our linear formulation and give

details on Local Controllers. More accurate experi-

mental results than before are additionally given.

4 PROPOSED SOLUTION

In this section, we give a centralized rule-based algo-

rithm for the energy hub controller, but we also could

overlay another controller already implemented. We

call these controllers “Local Controllers”, and we ab-

breviate LC. They have to be embedded and highly

reactive, thus they cannot compute the best sourcing

strategy on a long time-frame. Therefore, we decided

to compute a sourcing strategy with a “Strategic Op-

timizer” (abbreviated SO), and to send next strategic

instructions to LC regularly.

Deﬁnition 7. Let us call the plan computed by SO a

strategy, and the set-point computed by LC a tactic.

Hereafter, we start by presenting data that feed

components and interactions between them.

4.1 Data and Interactions

In this sub-section, we ﬁrst describe how we draw

samples of elevator usage. Then we explain how we

compute forecasts used by SO. Finally, we show com-

ponents interactions and their dynamic.

4.1.1 Elevator Usage Description

The building considered is a business tower with nine

ﬂoors and the elevator has the following characteris-

tics: standby consumption: 50 W, cabin mass: 750

kg, counterweight mass: 850 kg, nominal velocity:

1.0 ms

−1

The Sourcing Problem - Energy Optimization of a Multisource Elevator

We simulate user calls to the elevator with a statis-

tical model. This model distinguishes multiple types

of travels: morning and afternoon arrivals and depar-

tures, lunch breaks, inter-ﬂoor travels, arrivals and de-

partures of external visitors. Statistical laws are iden-

tiﬁed based on historical data. For each travel type

and relevant pair of ﬂoors, these laws provide infor-

mation on the number of people moving during the

day (depending on day-of-week, week-of-year, etc.),

the distribution of their weights, the distribution of the

times of the people movements during the day, and the

probability that two similar movements are grouped

(e.g., several people going to lunch together). A ran-

dom generator is used on this basis to generate sce-

narios.

Moreover, we have implemented a tactic to an-

swer user calls to the elevator. That tactic considers

calls in chronological order to choose the destination

of the elevator. But, it stops the elevator along the way

if another call destination is on this way. That seems

to be the tactic implemented in the biggest part of the

elevators.

On the other hand, we have an energy model of

the elevator that allows us to compute energy con-

sumption regarding the chosen travel and the weight

of passengers. The data used in this model include

the weight of the cabin and counterweight, the length

and weight of the cable, the elevator’s base power and

nominal speed, the altitude of the departure and ar-

rival ﬂoors, and efﬁciency for both energy-consuming

and energy-producing travels.

4.1.2 Forecasts

SO is fed by a forecast f, that is a |P ∪ E| × H ma-

trix, with H the number of periods considered by SO.

For prosumers in P, the tariff is forecasted, while for

prosumers in E, the produced and consumed quantity

is forecasted. In this paper, forecasts are considered

exact (issues concerning robustness to forecasts un-

certainties will be considered in a future paper).

In our use case, a forecast is composed of: (i) the

predicted amount of energy consumed / produced by

the elevator, (ii) the predicted solar production, (iii)

the predicted grid energy tariff. Dissipation is as-

sumed to have no cost.

The ideal solar production prediction uses pre-

dicted irradiance data of a typical sunny day. We con-

sider that 2 square meters of solar panels are installed

on the roof top of the building, and are dedicated to

the elevator. These solar panels are supposed well ori-

ented towards the sun and having a yield of 15%.

The electricity tariff considered in the experiments

is a typical peak / off-peak French tariff: 0.00015 /

0.00010 e/Wh.

Regarding the elevator, we use data described in

sub-section 4.1.1 to simulate several daily scenarios

and compute the average energy production or con-

sumption for each SO period. An alternative could

be to use standard machine learning techniques to di-

rectly forecast energy production or consumption for

each SO period.

4.1.3 Interactions and Dynamic

LC has to be highly reactive. For the multisource el-

evator application, we estimate a relevant time-step

is one second, iterated every seconds. On the other

hand, SO has to consider sufﬁciently long time-steps

to get relevant forecasts, and a sufﬁciently long hori-

zon to take into account energy price variations. Thus,

a ﬁfteen minutes period with a 24h horizon is relevant

for the multisource elevator, and the problem is re-

solved every hours. The dynamic of interactions is

illustrated on Figure 2.

In a real product, LC would probably be embed-

ded into the energy hub. While SO could be proposed

as a web service. We can see on the ﬁgure that LC

and SO are separated components that communicate

only through a strategic instruction. An instruction is

composed of a target time, and an array of n

cells:

one per prosumer connected to the energy hub. For

storage units, an instruction is expressed as a target

state of charge. For controllable producers, an in-

struction is expressed as mean power. For the other

prosumers (that are supposed non controllable), in-

structions are empty. An instruction can be sent over

a network or shared by components running into the

same computer. That allows ﬂexible business models.

Moreover, SO needs to know the current state of

charge of every storage units and the current availabil-

ity of controllable producers.

Finally, LC applies the computed tactic that is a

vector of n

power values, on the multisource system.

LC is fed with solar radiation, electricity tariff and

users’ calls to the elevator.

Runs every hour

Runs every second

Strategic

Optimizer

Local

Controller

Multisource

system

strategy for the

next hour

Power set-point

for all prosumers

Current state

and ﬂexibilities

Current

state

forecast f (15 mn

timestep, 24 h horizon)

Figure 2: Software components interactions.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

4.2 Strategic Optimizer

The problem solved by SO consists of ﬁnding the best

sources of energy to be used, factoring in the storage

capacities, during a long time frame. The goal is to

minimize costs related to energy purchasing and bat-

tery usage within the time frame, while ensuring the

hub is autonomous.

4.2.1 A Generic Formulation Depending on

Prosumers Kind

Let us suppose that the optimization period is a con-

stant τ, and that the number of periods in the opti-

mization horizon is denoted H.

Deﬁnition 8. Let e

[t] = p

[t] × τ be the energy

amount produced by prosumer π

over a period τ.

Thereafter decision and state variables are deﬁned,

depending on prosumers kind:

• Storage units: ∀π

∈ S,

– ∀l ∈ {0, . . . , H − 1}, 0 ≤ e

] ≤ −p

min

× τ

(resp. 0 ≤ e

dis

] ≤ p

max

× τ) the amount of

energy charged into (resp. discharged from)

the prosumer π

(that is a storage unit) between

time t

and time t

l+1

= t

+ τ. Thus e

] =

dis

] − e

– ∀l ∈ {0, . . . , H}, 0 ≤ x

] ≤ 1 the state of charge

of the prosumer π

at time t

• Controllable producers: ∀π

∈ P,

– ∀l ∈ {0, . . . , H − 1}, 0 ≤ e

purch

] ≤ p

max

× τ

(resp. 0 ≤ e

sold

] ≤ −p

min

× τ) the amount

of energy purchased from (resp. sold to) the

prosumer π

(that is a controllable producer)

between time t

and time t

l+1

= t

+ τ. Thus

] = e

purch

] − e

sold

• Non-controllable prosumers: ∀π

∈ E,

– ∀l ∈ {0, . . . , H − 1}, p

min

× τ ≤ e

] = f

] ≤

max

× τ the forecasted production (if positive)

or consumption (if negative) of the prosumer π

between time t

and time t

l+1

= t

+ τ. These

are not decision variables but constant data

given by an external forecast.

Remark: Although storage units charge and dis-

charge could be modeled as a single variable e

, two

variables (e

and e

dis

) are used in our model, be-

cause there are two different yields that impact the

charge and the discharge. However, we do not want

to charge and discharge the same storage unit at the

same time, thus both variables are minimized in the

objective function.

Lemma 4.1. In all optimal solutions,

∀l ∈ {0, . . . , H −1}, ∀π

∈ S, e

] = 0 ∨ e

dis

] = 0.

Proof. Assume

e, an optimal solution, such that there

exists 0 ≤ l ≤ H −1 where both ˆe

] and ˆe

dis

] are

strictly positive. Then, let us consider another so-

lution e

where all decision variables have the same

value except that:

] = ˆe

] − min( ˆe

], ˆe

dis

])

dis

] = ˆe

dis

] − min( ˆe

], ˆe

dis

])

As e

] and e

dis

] are both penalized in the objec-

tive function, then solution e

admits a lower cost than

solution

e that was optimal by assumption.

The following constraints must be taken into account:

• A minimum energy amount must be kept into stor-

age units.

∀π

∈ S, ∀l ∈ {0, . . . , H},

] + ρ

minSOC

] ≥ c

minSOC

, (4)

For this constraint, a new slack variable is deﬁned:

0 ≤ ρ

minSOC

] ≤ c

minSOC

is the percentage of stor-

age unit state of charge under a given minimum

value c

minSOC

at time t

. Then, c

minSOC

is the ratio

of the storage unit state of charge that the energy

hub needs to ensure security in case of grid fail-

ure. The ρ

minSOC

variables must be null except in

the case of grid failure, so they are penalized in

the objective function (cf Equation (9) ).

• The energy-related equation of the energy hub

must be satisﬁed: the sum of consumed and pro-

duced energy between time t

and time t

l+1

= t

+τ

must be equal.

∀l ∈ {0, . . . , H − 1},

∑

i∈P

]) = 0 (5)

• The state of charge of storage units must be up-

dated at each time-step with the energy charged

and discharged.

∀π

∈ S, ∀l ∈ {0, . . . H −1},

l+1

] = x

] +

× e

]

−

× c

× e

dis

] (6)

where c

is the energy capacity of the storage unit

and c

(resp. c

) is the charging (resp. discharg-

ing) yield of the storage unit. Yields are normal-

ized between 0 and 1.

The Sourcing Problem - Energy Optimization of a Multisource Elevator

• Let a new slack variable ∀l ∈ {0, . . . H − 1}, 0 ≤

stab

] ≤ p

max

− p

min

be the difference between

the amount of energy purchased from a control-

lable producer π

at time t

and the amount of en-

ergy purchased from the same controllable pro-

ducer at time t

l−1

. This value has to be penal-

ized in the objective function. The associated con-

straints are:

∀π

∈ P,∀l ∈ {0, . . . H −1},

l−1

] − e

] − ρ

stab

] ≤ 0 (7)

] − e

l−1

] − ρ

stab

] ≤ 0 (8)

Please note that, for the ﬁrst period, e

l−1

] is set

to the instruction computed for prosumer π

dur-

ing SO last run. If the current execution is the ﬁrst

one, e

l−1

] is set to zero.

• Depending on the exact use case, cyclical con-

straints (or additional cost factors), such as requir-

ing the battery to be full at the beginning of the

morning can be added.

Given those constraints, our economical objective

function is given by Equation (9).

Minimize

H−1

∑

l=0

∑

∈P

−c

sold

] × e

sold

] + c

purch

] × e

purch

]

+ min

min

∈P

purch

])

min

∈S

aging

)

× ρ

stab

]

∑

∈S

aging

× e

] +

aging

× e

dis

]

+ 2 × max

∈P

purch

]) × ρ

minSOC

]

(9)

where c

purch

] is the electricity buying price at time

and c

sold

] is the electricity selling price at time t

thus −c

sold

] × e

sold

] + c

purch

] × e

purch

] is the

electricity bill for the l

period and prosumer π

These constants are given by the cost function cost

which is considered linear in the current formulation.

On the other hand, c

aging

is a coefﬁcient that al-

lows to have a linear approximation of the impact of

the storage unit usage on its aging: c

aging

inve

cye

×c

the constant c

inve

represents the investment cost of the

storage unit; c

is the energy capacity of the storage

unit and c

cye

is the mean number of cycles that the

storage unit can bear.

Remark: As the battery aging cost is just a way to

discourage the controller from using the battery, a ﬁrst

order approximation was chosen. In reality, “small”

charges and discharges further impact storage units

but we ignore this effect here. This cost could be

tuned depending on the results of long-term simula-

tions (typically several years) of the controller and its

impact on the battery lifetime. On the other hand,

auto-discharge of storage units is neglected for the

moment.

Moreover, a minimum energy amount must be

kept into storage units in order to ensure autonomy

in case of grid failure. We cannot ensure that with

a hard constraint because we need to allow consum-

ing this reserve during a grid failure. Thus, we use

the soft constraint (4) with a slack variable ρ

minSOC

that is minimized in the objective function. We could

have considered that, in case of grid failure, a different

operating mode that allows violating this constraint

would be set. But a soft constraint, with a soundly

chosen penalization, does the same job in a simpler

way.

Finally, in order to reduce the chattering of the en-

ergy purchased from controllable producers, we min-

imize a slack variable called ρ

stab

Note that all variables are weighted with a fraction

of the energy tariff in order to ensure the right setting

of the objective (reserve for grid failure, electricity

cost, . . . ).

The overall linear formulation is then:

Minimize (9)

Subject to (4) − (8)

4.2.2 The Multisource Elevator Formulation

In the elevator context, we choose to set c

minSOC

0.2 and c

minSOC

to 1.0 because the super-capacitor

has to be fully charged in case of grid failure and a

20% charged battery can supply the super-capacitor

for several travels. Moreover, the battery is a lead-

acid battery with an energy capacity of 3000 Wh, an

investment cost of 300 e and a maximum power of

2880 W. The super-capacitor has an energy capacity

of 120 Wh, an investment cost of 2400 e and a max-

imum power of 57600 W. Thus, storage units aging

costs are the following ones:

aging

inve

cye

× c

300

20000 × 3000

= 0.000005

aging

inve

cye

× c

2400

20000 × 120

= 0.001

Table 1 shows the linear program applied to the

multisource elevator case, in vector form. Variables

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

Table 1: A linear formulation for the multi-source elevator

sourcing problem.

Minimize

−c

purch

 e

purch

+5 × 10

−6

× e

+ 0.001 × e

+2 × c

purch

 ρ

minSOC

+ 2 × c

purch

 ρ

minSOC

+min



purch

, 0.0005



 ρ

stab

∑

i=1

= 0

sold−

− e

sold

− ρ

stab

≤ 0

sold

− e

sold−

− ρ

stab

≤ 0

− x

] + Ae

+ Be

dis

= 0

−x

− ρ

minSOC

≤ −0.2

− x

] + A

+ B

dis

= 0

−x

− ρ

minSOC

≤ −1.0

0 ≤ e

≤ −p

min

× τ ,∀π

∈ S

0 ≤ ρ

stab

0 ≤ e

dis

≤ p

max

× τ ,∀π

∈ S

0 ≤ e

purch

≤ 50000 × τ

0 ≤ x

≤ 1 ,∀π

∈ S

0 ≤ e

0 ≤ ρ

minSOC

≤ 0.2 ,∀π

∈ S

in bold are column vectors of dimension H, and ma-

trices. Let A, B, A

and B

be H × H-matrices:

A = diag



−

= −

0.9

3000



B = diag



×c

0.9×3000



= diag



−

= −

0.9

120



= diag



×c

0.9×120



Moreover, the symbol  states for the Hadamard

product (element-wise product).

As we choose 15 minutes periods (τ = 0.25) and a

24 hours horizon, H = 24 ÷ 0.25 = 96. That gives us

a linear program with 96 periods. In practice, we have

12 vectors of H decision variables each and 10 con-

straints per time step. Thus every hour we solve a lin-

ear problem with 1152 variables and 960 constraints.

Building and solving the problem with GLPK (GNU,

2014) takes about one second.

4.3 Local Controller

Our LC is a centralized rule-based controller that

computes, in real-time and for a single time-step, a

sourcing tactic. The tactic depends on: 1) the relative

priority associated to every prosumers, 2) current ﬂex-

ibilities of every prosumers, 3) the current strategic

instruction if any, or a default instruction otherwise.

As SO is based on energy forecasts, some strategic

instructions may be infeasible at some points, and LC

has to ﬁnd the best trade-of between instruction and

current situation.

4.3.1 Principles of the Rule-based Algorithm

Each prosumer connected to the energy hub is as-

sociated with a priority number. A priority list is

deﬁned as a permutation of the prosumers set P :

(π

, . . . , π

), ordered by decreasing priority num-

bers. A priority number represents the importance of

satisfying a prosumer relatively to the others.

Moreover each prosumer has a list of ﬂexibilities,

that can be discrete power values:

, p

, . . . , p

)

or power intervals:

([p

1,min

, p

1,max

], . . . , [p

m,min

, p

m,max

])

Flexibilities are ordered by decreasing preference or-

der of the prosumer. The preference order of the pro-

sumer is linked to its quality of service.

Example: If an elevator π

is stopped and empty, it

can move to a higher ﬂoor (ﬂexibility p

), or move

to a lower ﬂoor (ﬂexibility p

), or stay still and con-

sume standby power (ﬂexibility p

). The preferred

ﬂexibility p

of the elevator is to go to the ﬂoor that

corresponds to the ﬁrst user call.

On the other hand, some prosumers have no dis-

crete ﬂexibilities but a set of possible intervals. For

example, a battery can consume or produce a power

value bounded by its minimum and maximum power

bound.

The third, and last, parameter that inﬂuences LC

is the strategic instruction. If there is no strategic in-

struction available, LC decides itself of a default in-

struction. That allows LC to work alone if its link

with SO is broken. Setting the default instruction in-

ﬂuences performances of the tactic.

Given these three inputs, LC builds a decision tree

for the current time step. The decision tree has a level

per prosumer, ordered by decreasing priority order. In

a given level, every node has as many children as the

number of ﬂexibilities of the prosumer corresponding

to the next level. A tactic is obtained by a depth-ﬁrst

search in the tree, and composed of a power value per

prosumer.

During the depth ﬁrst search, when the node holds

a single power value, this value is chosen. Else, a de-

fault value is chosen in the given interval. When a

strategic instruction is available for the current pro-

sumer, the value in the interval, nearest to the in-

struction value is chosen; else the value, in the in-

terval, nearest to zero is chosen. When a leaf is

The Sourcing Problem - Energy Optimization of a Multisource Elevator

Table 2: Three LCs and their parameters.

(a) Priority orders.

MinPeaks Opportunistic Secure

P 3 3 1

4 4 3

2 2 4

1 1 2

E 5 5 5

(b) Default instructions.

MinPeaks Opportunistic Secure

P standby cons 0 W 0 W

minSOC

100% x

100%

100% x

reached, the algorithm checks if the sum of the chosen

power values is equal to zero. If not, the difference

is compensated, as much as possible, by each node

through backtracking in the tree. When the tree root is

reached, if the sum of the control vector is null, the so-

lution is kept. If not, the depth ﬁrst search continues.

That way, the ﬁrst found solution is the best one re-

garding the prosumers priority order, the preferences

of each prosumer and the strategic instruction.

4.3.2 Parameters Values and Objectives

This rule-based algorithm can be tuned depending

on the objective, through parameters value described

above. We cannot inﬂuence prosumers ﬂexibilities

but we can choose priority order and default instruc-

tion. There are three versions of LC:

MinPeaks. The ﬁrst controller considered seeks to

minimize power peaks purchased from control-

lable producers.

Opportunistic. The second controller considered

seeks to minimize dissipated energy and thus the

energy bill.

Secure. The third controller considered seeks to min-

imize storage units usage while guaranteeing that

storage units will be ready in case of grid failure.

Note that the Opportunistic LC’s behavior is com-

parable to a classical rule-based controller.

Priority order and default instruction associated

with each of these three controllers are shown in Ta-

ble 2. For that purpose, storage units are classiﬁed in

three categories:

• those under their minimum state of charge S

{π

∈ S|x

< c

minSOC

• those usable to absorb power peaks S

= {π

∈

S \ S

max

≥ max

∈E

(−p

min

• the others S

= S \ (S

∪ S

5 RESULTS

In order to evaluate the proposed solution, we need

to compare SO plans with the results obtained by LC

following the instructions. Then, we have to compare

the different tactics between them, without strategic

instructions.

For the simulation purpose, we developed in Mat-

lab (The MathWorks Inc., 2015) a simulation engine

with dynamic time steps depending on events occur-

ring.

5.1 A Typical Strategy

Results obtained by SO, during a typical day, are il-

lustrated on Figure 3. The ﬁrst sub-ﬁgure is an energy

layers plot where positive power represents power

that is injected in the energy hub (produced by pro-

sumers) and negative power represents power that is

taken from the energy hub (consumed by prosumers).

The second sub-ﬁgure presents the storage units state

of charge and the grid tariff. We can see that, when the

electricity is cheap (before 09:00), the energy is pur-

chased from the grid (in red), and stored in the battery

(in green). After 09:00, no more energy is purchased

and the energy needed is discharged from the battery.

In this situation, SO tries to take advantage of

the off-peak tariff to charge the battery and avoid to

purchase energy from the grid during the peak tariff.

We can see that the battery is charged just enough to

achieve this goal (about 40% at 09:00).

Figure 3: A typical strategic plan.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

5.2 Strategic Controller Error Induced

by Aggregating Periods

In this sub-section, the point is to characterize the er-

ror made by SO when computing the objective value

(i.e. energy bill and aging costs). This error is eval-

uated (on a typical day) by comparing results of the

MinPeak LC following the strategy with results com-

puted by SO before the beginning of the day.

The plan computed before the day by SO is the

same as on Figure 3 and the corresponding MinPeaks

tactic is illustrated on Figure 4. The ﬁrst sub-ﬁgure

represents the power consumption and production of

the different prosumers. We can see that the consump-

tion peaks of the elevator (in blue; that reaches 8 kW)

are absorbed by storage units (in green). While in ev-

ery cases, the maximum power peak purchased from

the grid is under 400 W, that is far less than 8 kW. The

second sub-ﬁgure shows the evolution of the storage

units state of charge and the grid tariff. In brown, we

can see the strategic instructions that are quite well

followed by the battery.

Now, let us compare numeric results of LC and

SO. As the accuracy of SO depends on 1) charging

and discharging yields of storage units, and 2) fore-

casts accuracy. We decided to consider ideal yields

(100 % and realistic yields (90 %). On the other hand,

forecasts are exact as described in sub-section 4.1.2.

Table 3 summarizes the results obtained by SO and by

the MinPeaks LC following the instructions, in three

cases.

When storage units yields are ideal, the energy bill

and the amount of energy purchased obtained by the

strategy are very close to ones obtained by the tac-

tic. Both values are less than 3 % higher with tactic

than with strategy. Though all parameters are ideal,

this small error is due to the energy aggregation in

15 mn periods into forecasts. Indeed, when sum-

ming positive and negative energy values over a pe-

riod, only the difference is kept. Then, SO take into

account only this small amount of energy to purchase

(or discharge). In reality, if production occurs be-

fore consumption, produced energy is stored and dis-

Figure 4: MinPeaks LC following strategy.

charged later to supply consumption. But, if con-

sumption occurs before production, the energy has to

be found elsewhere before the production could be

stored. When yields are ideal and storage units not

empty, that has no impact on the energy bill. But

when storage units are empty the energy has to be

purchased and that explains the small differences ob-

served above. On the other hand, the aging cost com-

puted by LC is far bigger than those estimated by the

SO because the latter did not take into account power

peaks. Indeed, to achieve instructions at the end of

a strategic period, LC cannot always charge storage

units with average power computed from the instruc-

tion. It has to absorb consumption and production

peaks, and thus to charge and discharge storage units

many times within the period. The amount of energy

charged into and discharged from storage units is thus

far bigger (about 14 times in this case) than computed

by SO.

Now let us look at the impact of realistic yields

on these results. We can see that, in the three met-

rics, results are worse than before. The reason is that

non ideal yields drive non null energy losses. Thus,

the above mentioned discrepancy due to aggregation

is emphasized in presence of non ideal yield.

In order to make SO take into account almost

all energy has to transit through storage units, we

integrate the impact of storage units yield into

consumption forecasts of prosumers in E. The strat-

egy becomes pessimistic because not all energy goes

through storage units. But the yield taken into account

in forecasts becomes a tunable parameter for the pes-

simistic prediction. Moreover, re-computing a strat-

egy every hour prevents LC to deviate too far away

from the target, even if the strategy is not perfectly

accurate. In this experiment, we choose a yield value

of 0.9, that is the real storage units yield. We can see

that the error of SO is really reduced compared to the

previous experiment. That also improves LC results,

especially on aging costs.

The last thing that has to be explained in the table

is: why do tactic aging costs are higher when yields

are ideal than when yields are realistic and when fore-

casts take yields into account? Aging costs are higher

in the former because, the battery is emptied at the be-

ginning of some periods and the supercapacitor has to

supply the elevator before being reﬁlled by produced

energy. On the other hand, when the strategy is pes-

simistic, this situation occurs less frequently. Since

supercapacitors are much more expensive than regu-

lar batteries, aging costs in the ﬁrst experiment are

higher than in the third one.

The Sourcing Problem - Energy Optimization of a Multisource Elevator

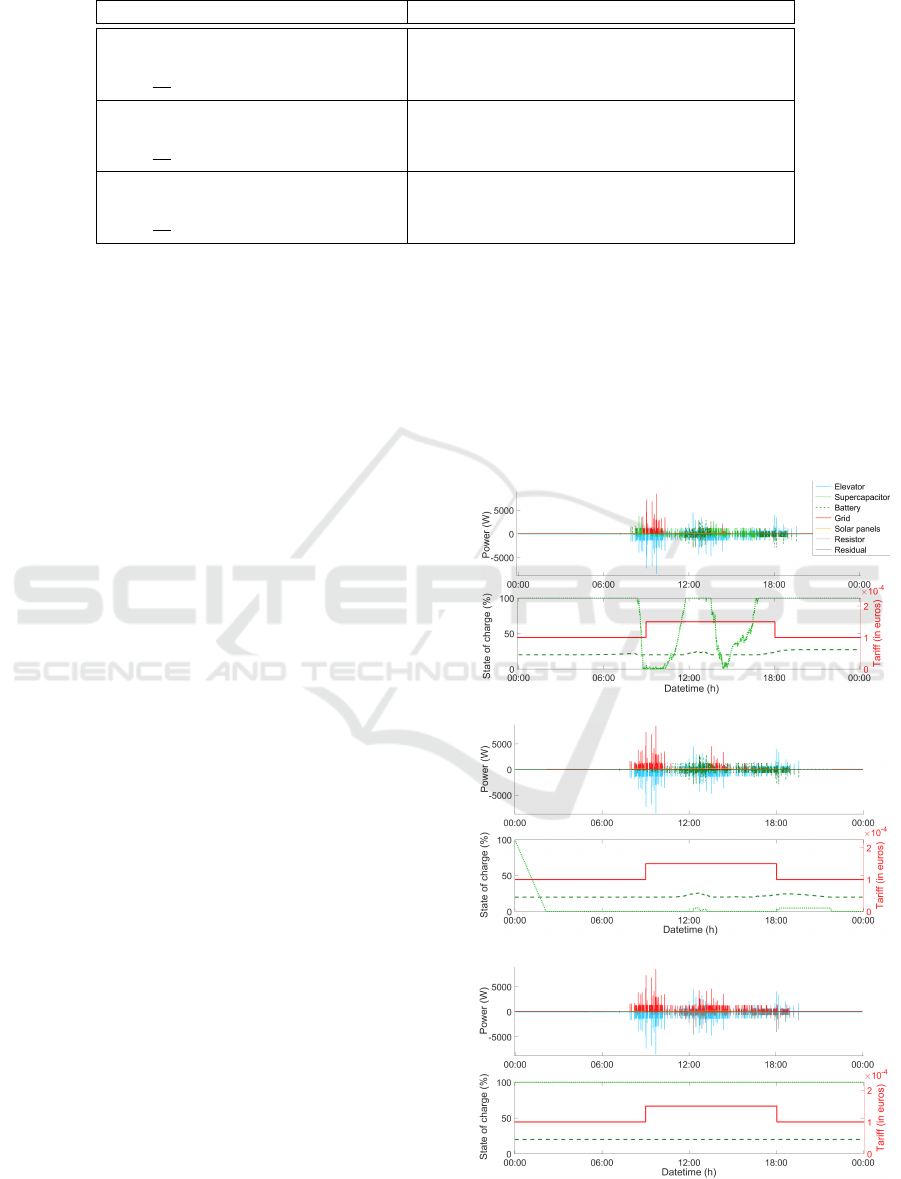
Table 3: Strategical and tactical results with different yields.

view point yield forecast energy bill aging costs energy purchased

SO 100 % exact 0.1164 e 0.0097 e 1164.3 Wh

LC 100 % exact 0.1198 e 0.1318 e 1187.8 Wh

ratio

100 % exact 1.03 13.59 1.02

SO 90 % exact 0.1382 e 0.0104 e 1382.2 Wh

LC 90 % exact 0.1745 e 0.3285 e 1640.5 Wh

ratio

90 % exact 1.26 31.59 1.19

SO 90 % exact + yield 0.1706 e 0.0117 e 1705.7 Wh

LC 90 % exact + yield 0.1655 e 0.1015 e 1654.5 Wh

ratio

90 % exact + yield 0.97 8.67 0.97

5.3 Three Tactics, One Strategy

Let us compare results of the different LCs, averaged

over ﬁfty elevator usage samples drawn. For this pur-

pose, we use an additional Key Performance Indica-

tor (KPI) that is the net daily gain g

net

. Let: c

ebill

the energy bill of the whole day, c

be the energy bill

that would have been obtained without storage units,

aging

be the aging cost associated to the storage units

usage that have been done during the day. Moreover,

the initial state of charge of storage units are: 20%

for the battery and 100% for the supercapacitor. But

depending on the controller, ﬁnal states of charge can

be different. Then we note c

soc

the cost associated

to reﬁll (or empty) storage units to match their ini-

tial state of charge. We consider that corresponding

energy is purchased (or sold) during off-peak hours.

Then, g

net

= −(c

ebill

− c

+ c

aging

+ c

soc

) is an addi-

tional KPI for the following experiments.

First of all, let us look at Figures 5(a), 5(b) and

5(c) that allow us to compare the three different tac-

tics, without any strategy.

Figure 5(a) corresponds to the MinPeaks LC and

we can see that there are a few power peaks from the

grid at the beginning of the day. This is because not

enough energy was produced before consumption, so

energy had to be purchased to supply the elevator.

Moreover at the end of the day, the battery is not at

its minimum state of charge and the supercapacitor is

full.

Figure 5(b) corresponds to the Opportunistic LC.

With this tactic, all available energy is used as soon as

possible, thus the supercapacitor supplies the elevator

at the beginning of the day and is emptied. Then, there

are many power peaks purchased from the grid in the

morning and in the middle of the afternoon.

Figure 5(c) corresponds to the Secure LC. This

tactic purchases from the grid all energy needed to

preserve storage units from aging. The supercapaci-

tor, that allows the elevator to travel during grid fail-

ures, is maintained full. The battery, that has to sup-

ply supercapacitor during grid failures, is maintained

at its minimum state of charge.

Now, let us look at numerical results of these

three tactics and of the MinPeaks Controller follow-

ing strategy. The latter is illustrated on Figure 4.

Please note that a LC on its own does not take into

account electricity tariff at all. The c

value, in this

example, corresponds to the c

bill

value of the Secure

(a) MinPeaks LC.

(b) Opportunistic LC.

Figure 5: LC on their owns.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

Table 4: Net daily gain of different tactics.

SO LC p

max

ebill

aging

soc

net

X MinPeaks 317.7 0.13 0.12 0.00 0.00

7 MinPeaks 7839 0.19 0.51 -0.03 -0.42

7 Opport. 8627 0.12 0.07 0.01 0.04

7 Secure 8775 0.24 0.00 0.00 0.00

LC: c

= 0.24 e.

On simulated days, we can see that the only ef-

ﬁcient way to reduce the maximum power peak pur-

chased from the grid is the MinPeaks Controller fol-

lowing the strategy. That way, the purchasing peak is

less than 5% of the maximum possible power peak.

The tactics on their own do not absorb power peaks,

because a predictive strategy is necessary to achieve

such a goal. On the other hand, the MinPeaks Con-

troller following the strategy only succeeds to com-

pensate aging costs by a gain on the energy bill. Thus,

its net daily gain is null in this context. Please note

that, if the gap between on- and off-peak hourly cost

grows, the net daily gain of this tactic following the

strategy also increases.

If the MinPeaks LC is on its own (for example

during a long network failure), the net daily gain be-

comes negative but the number of (and the maximum)

power peaks stays below the other controllers alone.

However, if the goal is only to minimize the net

daily gain, without taking into account power peaks,

the Opportunistic LC alone is the best (as far as the

ratio between the high/low prices is moderate).

Finally, the Secure tactic does not use storage

units at all and thus, has a higher energy bill, but a

null aging cost.

6 CONCLUSIONS

In this paper we formalize what we call the sourc-

ing problem and its application to a multisource ele-

vator. We give a method to solve it, composed of a

Local Controller coupled with a Strategic Optimizer.

That allows us to tackle real-time issues while taking

into account long-term objectives based on forecasts.

A linear formulation allows us to compute a strategy

and a centralized rule-based algorithm gives us a tac-

tic. Three Local Controller parametrizations are il-

lustrated, and one will choose the most adapted to its

studied energy hub.

A legitimate criticism of this work could be that

gains in euros are very low. First, let us recall that

these results are for a unique elevator, while in prac-

tice several elevators could share the same battery.

Second, reducing power consumption peaks could be

very useful to be demand-response aware and to re-

spect future energy limitation laws. In those cases,

minimizing the energy bill is only an appreciable ad-

dition to the consumption peaks minimization. For

the multisource elevator use case, having storage units

allows the elevator to evacuate disabled people in case

of ﬁre. Using these storage units to minimize the en-

ergy bill could amortize the investment. Third, en-

ergy prices are going to increase in future years, as

will storage units performances. That will also in-

crease the beneﬁt of this solution. Finally, the pro-

posed solution can be applied to other multisource

systems where it can be much more proﬁtable. In fact,

as the consumption increases, the proﬁtability also in-

creases, especially if reselling energy is possible.

On the other hand, we will have to compare the

cost of maintaining our rather complex solution, re-

garding the customer value in each use case. If the

maximum power peak purchased from the grid is not

an issue and the energy tariff considered is a typi-

cal French peak/off-peak tariff, the Opportunistic LC

(or a similar classical rule-based controller) should be

used.

As future work, we will study our method robust-

ness to forecast uncertainties. This is a critical issue

and studying it could allow us to give performance

guarantees to potential customers. A sensibility study

of controller parameters will also be conducted. Fi-

nally, a real-life experiment, in a building equipped

with a BMS, would worth being conducted.

ACKNOWLEDGEMENTS

This work has been conducted as part of the Arrow-

head European project and has been partially funded

by the Artemis/Ecsel Joint Undertaking, supported by

the European Commission and French Public Author-

ities, under grant agreement number 332987.

REFERENCES

Bilbao, E. and Barrade, P. (2012). Optimal energy man-

agement of an improved elevator with energy storage

capacity based on dynamic programming. In Energy

Conversion Congress and Exposition (ECCE), 2012

IEEE, page 3479–3484.

Boutin, V., Desdouits, C., Louvel, M., Pacull, F., Vergara-

Gallego, M. I., Yaakoubi, O., Chomel, C., Crignon,

Q., Duhoux, C., Genon-Catalot, D., Lefevre, L.,

Pham, T. H., and Pham, V. T. (2014). Energy optimi-

sation using analytics and coordination, the example

of lifts. In Emerging Technology and Factory Automa-

tion (ETFA), 2014 IEEE, pages 1–8. IEEE.

Desdouits, C., Alamir, M., Boutin, V., and Pape, C. L.

(2015). Multi-source elevator energy optimization

The Sourcing Problem - Energy Optimization of a Multisource Elevator

and control. In European Control Conference (ECC),

EUCA 2015. EUCA.

GNU (2014). GNU Linear Programming Kit, version 4.54.

http://www.gnu.org/software/glpk/glpk.html.

Paire, D., Simoes, M. G., Lagorse, J., and Miraoui, A.

(2010). A real-time sharing reference voltage for hy-

brid generation power system. In Industry Applica-

tions Society Annual Meeting (IAS), 2010 IEEE, pages

1–8. IEEE.

Sachs, H. M. (2005). Opportunities for elevator energy ef-

ﬁciency improvements. Technical report, American

Council for an Energy-Efﬁcient Economy Washing-

ton, DC.

The MathWorks Inc. (2015). Matlab 2015b. The Math-

Works Inc., Natick, Massachusetts, United States.

Tominaga, S., Suga, I., Araki, H., Ikejima, H., Kusuma, M.,

and Kobayashi, K. (2002). Development of energy-

saving elevator using regenerated power storage sys-

tem. In Power Conversion Conference, 2002. PCC-

Osaka 2002. Proceedings of the, volume 2, pages

890–895. IEEE.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics