
Polynomial Matrix SVD Algorithms for Broadband Optical MIMO
Systems
Andreas Ahrens
1
, André Sandmann
1
, Zeliang Wang
2
and John G. McWhirter
2
1
Hochschule Wismar, University of Technology, Business and Design, Philipp-Müller-Straße 14, 23966, Wismar, Germany
2
School of Engineering, Cardiff University, Queen’s Buildings, The Parade, Cardiff, CF24 3AA, Wales, U.K.
Keywords:
Polynomial Matrix SVD, Broadband MIMO, Optical MIMO, Bit Allocation, Power Allocation.
Abstract:
Polynomial matrix singular value decomposition (PMSVD) plays a very important role in broadband multiple-
input multiple-output (MIMO) systems. It can be used to decompose a broadband MIMO channel matrix in
order to recover the transmitted signals corrupted by the channel interference (CI) at the receiver. In this
contribution newly developed singular value decomposition (SVD) algorithm for polynomial matrices are
analyzed and compared in the application of decomposing optical MIMO channels. The bit-error rate (BER)
performance is evaluated and optimized by applying bit and power allocation schemes. For our simulations,
the specific impulse responses of the (2× 2) MIMO channel, including a 1.4 km multi-mode fiber and optical
couplers at both ends, are measured for the operating wavelength of 1576 nm.
1 INTRODUCTION
An explosive development of MIMO technology has
been witnessed in wireless communication systems
over the last decade. Compared to single-input single-
output (SISO) systems, MIMO systems are capable of
achieving higher data rates and transmission reliabili-
ties. Aiming to increase the fiber capacity, the concept
of MIMO in optical transmission systems has also
attracted intensive research interests (Singer et al.,
2008; Winzer and Foschini, 2011; Sandmann et al.,
2016).
Theoretical investigations have shown that simi-
lar capacity increases are possible compared to wire-
less MIMO systems (Kühn, 2006; Tse and Viswanath,
2005). The basis for this approach is the exploitation
of the different optical mode groups. However, the
practical implementation has to cope with many tech-
nological obstacles such as mode multiplexing and
management. This includes mode combining, mode
maintenance and mode splitting. In order to improve
existing simulation tools practical measurements are
needed. That is why in this contribution a whole opti-
cal transmission testbed is characterized by its respec-
tive impulse responses obtained by high-bandwidth
measurements.
In broadband MIMO systems, the channel is char-
acterized by frequency-selective fading. In order to
recover the transmitted data sequence corrupted by
channel interference (CI), a conventional method is to
combine the spatio-temporal vector coding (STVC)
(Raleigh and Cioffi, 1998; Raleigh and Jones, 1999)
with the SVD based equalization technique (Haykin,
2002). However, there are some existing papers (Ta
and Weiss, 2007; Sandmann et al., 2015c) which dis-
cussed an alternative signal pre- and post-processing
method used in broadband MIMO systems. Basically
this method consists of two steps. The first step is
based on the PMSVD which is used to remove the CI
by decomposingthe frequency-selectiveMIMO chan-
nel into a number of independent frequency-selective
SISO channels, and the second step involves re-
moving the remaining inter-symbol interference (ISI),
which can be implemented by further equalization
techniques, such as zero-forcing (ZF) equalization or
maximum likelihood sequence estimations (MLSE).
Whereas STVC-based approaches require guard in-
tervals between consecutive data blocks, they can be
avoided when PMSVD-based approaches are applied
(Raleigh and Cioffi, 1998; McWhirter and Baxter,
2004; Wang et al., 2016).
The PMSVD method in most of the existing liter-
ature is computed by an iterative polynomial matrix
eigenvalue decomposition (PEVD) algorithm, called
the second order sequential best rotation (SBR2) al-
gorithm (McWhirter et al., 2007). However, there are
some other PEVD algorithms which have been devel-
oped recently, including the sequential matrix diago-
Ahrens, A., Sandmann, A., Wang, Z. and McWhirter, J.
Polynomial Matrix SVD Algorithms for Broadband Optical MIMO Systems.
DOI: 10.5220/0005949400350042
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 3: OPTICS, pages 35-42
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
35

nalization (SMD) algorithm (Redif et al., 2015), mul-
tiple shift maximum element SMD (MSME-SMD) al-
gorithm (Corr et al., 2014), and multiple shift SBR2
(MS-SBR2) algorithm (Wang et al., 2015) etc. All
these PEVD algorithms can provide much faster con-
vergence than the SBR2 algorithm.
The contribution of this paper is to investigate dif-
ferent PEVD algorithms in computing the PMSVD
for broadband optical MIMO systems. The resulting
CI after decomposition, which is indicated by the di-
agonalization level, is also examined among different
PEVD algorithms. In particular, the possible errors
caused by the proposed PMSVD method are also dis-
cussed. In addition, transmission and power alloca-
tion schemes are employed to bring further improve-
ment in BER performance. Our simulations are im-
plemented based on a measured (2×2) optical MIMO
channel which comprises a 1.4 km multi-mode fiber
and optical couplers at both ends, and the channel im-
pulse responses are measured for the operating wave-
length of 1576 nm (Sandmann et al., 2015a; Sand-
mann et al., 2015c).
The rest of the paper is structured as follows. The
MIMO channel model with polynomial matrix repre-
sentation is introduced in Sec. 2. In Sec. 3 we de-
scribe the concept of broadband MIMO channel de-
composition, i. e. PMSVD. Sec. 4 presents some ex-
isting iterative PEVD algorithms for calculating the
PMSVD. The underlying MIMO testbed is presented
in Sec. 5. Simulation results and conclusions are
shown in Sec. 6 and Sec. 7, respectively.
2 MIMO CHANNEL MODEL
Given a frequency selective optical MIMO link with
n
T
optical inputs and n
R
optical outputs, the channel
can be modelled as a polynomial matrix with an inde-
terminate variable z
−1
given by
C
(z) =
T
∑
τ=0
C(τ)z
−τ
=
c
11
(z) ··· c
1n
T
(z)
.
.
.
.
.
.
.
.
.
c
n
R
1
(z) ··· c
n
R
n
T
(z)
,
(1)
where C(τ) ∈ C
n
R
×n
T
denotes the polynomial coeffi-
cient matrix at time lag τ and c
νµ
(z) is the polynomial
matrix entity which represents the channel impulse re-
sponse between the µ-th optical input and the ν-th op-
tical output. It takes the form of
c
νµ
(z) =
T
∑
τ=0
c
νµ
(τ)z
−τ
, (2)
where c
νµ
(τ) denotes a non-zero element of the sym-
bol rate sampled overall channel impulse response at
the τ-th lag. In this case there are T + 1 lags in total
for each SISO channel.
Throughout this paper, polynomial matrices and
vectors are denoted as underscored boldface letters.
Finally, the resulting MIMO system model can be de-
scribed in polynomial matrix notation as follows
x
(z) = C(z)s(z) + n(z), (3)
where x
(z), s(z) and n(z) represent the received sig-
nal, the source signal and the noise signal in z-domain
respectively (Sandmann et al., 2015c).
3 BROADBAND MIMO CHANNEL
DECOMPOSITION VIA PMSVD
Given the MIMO channel matrix C
(z) as shown
in (1), the CI can be removed by performing the
PMSVD, which can be expressed as (McWhirter and
Baxter, 2004)
C
(z) =
e
U(z)Σ
Σ
Σ(z)V(z) =
e
U(z)
Γ
Γ
Γ
(z)
0
V
(z), (4)
where we assume n
R
≥ n
T
, and Γ
Γ
Γ(z) is a diagonal
polynomial matrix with n = n
T
diagonal elements, s.t.
Γ
Γ
Γ
(z) = diag{γ
1
(z),γ
2
(z),··· , γ
n
(z)}.
e
U
(z) and V(z)
are paraunitary polynomial matrices with dimension
n
R
× n
R
and n
T
× n
T
respectively, s.t.
e
U
(z)U(z) =
U
(z)
e
U(z) = I
n
R
and
e
V
(z)V(z) = V(z)
e
V(z) = I
n
T
.
Here the notation eover the polynomial matrix U
(z)
denotes the paraconjugate operation which is com-
puted by performing Hermitian transpose {·}
H
of all
the polynomial coefficient matrices U(τ) and time-
reversing all entries inside, i.e.
e
U(z) = U
H
(1/z).
Note that
e
U
(z) and V(z) are acting as the mul-
tichannel all-pass filters which can transform the
frequency-selective MIMO channel into a number of
independent frequency selective SISO channels while
still preserving the total signal energy (Vaidyanathan,
1993).
In this paper, the PMSVD in (4) is implemented
by calculating the PEVD of two polynomial matrices
C
(z)
e
C(z) and
e
C(z)C(z), which take the form as
[C
(z)
e
C(z)]
n
R
×n
R
=
e
U
(z)Σ
Σ
Σ(z)
e
Σ
Σ
Σ(z)U(z), (5)
and
[
e
C(z)C(z)]
n
T
×n
T
=
e
V
(z)
e
Σ
Σ
Σ(z)Σ
Σ
Σ(z)V(z). (6)
Further details about PEVD algorithms will be dis-
cussed in the following section. To eliminate the CI,
the transmit data vector s
(z) is pre-multiplied by
e
V(z)
OPTICS 2016 - International Conference on Optical Communication Systems
36

at the transmitter, and pre-multiplied by U(z) at the
receiver, which results in
x
(z) = Σ
Σ
Σ(z)s(z) + w(z), (7)
where w(z) = U(z)n(z). Note that neither the transmit
power is increased, nor the channel noise is enhanced
here.
Unlike the conventional SVD-based method, each
diagonal element (also called layer) in Σ
Σ
Σ
(z) is
frequency-selective and hence ISI occurs. In order
to remove the ISI, layer-specific T-spaced zero forc-
ing equalizers (Sandmann et al., 2015c) are adopted
in this paper.
4 ITERATIVE PEVD
ALGORITHMS
As mentioned above, the PEVD method can be used
to formulatethe PMSVD problem in equation (4), and
the idea of PEVD has been generalized as (McWhirter
et al., 2007)
H
(z)R(z)
e
H(z) ≈ D(z), (8)
where R(z) is assumed to be a M × M input para-
Hermitian matrix, such that
e
R
(z) = R(z), H(z) is a
paraunitary matrix which aims to diagonalize R
(z) by
means of paraunitary similarity transformation, and
D
(z) is (ideally) a diagonal matrix.
This is an iterative process which transforms all
the off-diagonal elements in R
(z) onto the diagonal
subject to the pre-specified stop condition. For the
remaining part of this section, different PEVD algo-
rithms are briefly reviewed.
4.1 The SBR2 Algorithm
At the i-th iteration, the SBR2 algorithm (McWhirter
et al., 2007) starts by locating the maximum off-
diagonal element r
(i)
jk
(τ). To find the maximum
off-diagonal element, we define a matrix S
(i)
(τ),
which contains only the upper triangular elements in
R
(i−1)
(τ) with the remaining elements set to zero.
Thus the location of r
(i)
jk
(τ), ( j < k) found at i-th it-
eration satisfies
{ j
(i)
,k
(i)
,τ
(i)
} = argmax
j,k,τ
kS
(i)
(τ)k
∞
, (9)
where j
(i)
, k
(i)
and τ
(i)
are the corresponding row, col-
umn and time lag index. An elementary delay matrix
P
(i)
(z) and Jacobi rotation Q
(i)
are applied to bring
r
(i)
jk
(τ) and its complex conjugate r
(i)
kj
(−τ) onto the
zero-lag (τ = 0) coefficient matrix R
(i−1)
(0), and then
rotate its energy onto the diagonal. This results in
R
(i)
(z) given by
R
(i)
(z) = Q
(i)
P
(i)
(z)R
(i−1)
(z)
e
P
(i)
(z)Q
H(i)
. (10)
Then the elementary paraunitary matrix E
(i)
(z) can be
expressed as
E
(i)
(z) = Q
(i)
P
(i)
(z). (11)
The algorithm continues its iterative process until all
the off-diagonal elements are smaller than a given
threshold ε which can be set to a very small value to
achieve sufficient accuracy. Assuming that the algo-
rithm has converged at the N-th iteration, the diago-
nalized para-Hermitian matrix in (8) takes the form
of
D
(z) = diag{d
1
(z),d
2
(z),··· ,d
M
(z)}, (12)
and the generated paraunitary polynomial matrix is
given by
H
(z) =
N
∏
i=1
E
(i)
(z) = E
(N)
(z)··· E
(2)
(z)E
(1)
(z). (13)
4.2 The SMD Algorithm
Unlike the SBR2 algorithm, the sequential matrix di-
agonalization (SMD) algorithm (Redif et al., 2015)
requires a initialization step to diagonalize the zero-
lag coefficient matrix R
(0)
(0) before all iterations.
This is implemented by computing a full EVD to
R
(0)
(0) and then applying the corresponding modal
matrix to the rest of coefficient matrices R
(0)
(τ),τ 6=
0. For the i-th iteration, it starts by locating the col-
umn that contains the maximum off-diagonal energy,
and then according to the location information k
(i)
and
τ
(i)
, it shifts the corresponding row and column pair
onto the zero-lag coefficient matrix. As to the rotation
step, rather than just using a single Jacobi rotation as
with SBR2, the SMD algorithm computes a full EVD
for the shifted zero-lag coefficient matrix R
′(i)
(0).
4.3 The MSME-SMD Algorithm
The MSME-SMD algorithm (Corr et al., 2014) in-
troduced a distinguishing search and shift strategy,
which can transfer more off-diagonal elements than
both SBR2 and SMD onto the diagonal at each itera-
tion. For each iteration, more than one maximum off-
diagonal element is found by using a reduced search
space strategy. Every row and column pair containing
a maximum off-diagonal element will then be shifted
to the zero-lag coefficient matrix. This is different to
Polynomial Matrix SVD Algorithms for Broadband Optical MIMO Systems
37
the way the SMD algorithm operates. The SMD algo-
rithm always shifts the row and column pair contain-
ing the maximum off-diagonal energy rather than the
maximum off-diagonal element as in MSME-SMD.
At the rotation step, the MSME-SMD algorithm fol-
lows the same procedure as the SMD algorithm trans-
ferring all the off-diagonal elements in R
′(i)
(0) onto
the diagonal.
4.4 The MS-SBR2 Algorithm
The MS-SBR2 algorithm (Wang et al., 2015) is an
improved version of the SBR2 algorithm in terms of
the algorithm convergence speed. Basically it adopts
the advantages of less computational cost from SBR2
and the faster convergence from MSME-SMD, which
seems to provide a compromise between the SBR2
and the SMD algorithm family. The MS-SBR2 al-
gorithm uses a distinguishing search strategy of the
off-diagonal elements which is akin to that of the
MSME-SMD algorithm, so that it can achieve the di-
agonalization with less iterations than the SBR2 algo-
rithm. For the i-th iteration, the MS-SBR2 algorithm
involves multiple shifts operations
b
P
(i)
(z), followed
by a sequence of Jacobi rotations
b
Q
(i)
. Therefore, the
resulting para-Hermitian matrix is computed by
R
(i)
(z) =
b
Q
(i)
b
P
(i)
(z)R
(i−1)
(z)
e
b
P
(i)
(z)
b
Q
H(i)
, (14)
where
b
P
(i)
(z) =
∏
L
(i)
l=1
P
(l,i)
(z),
b
Q
(i)
=
∏
L
(i)
l=1
Q
(l,i)
and
L
(i)
denotes the total number of off-diagonal elements
shifted to the zero-lag coefficient matrix at the i-th it-
eration. Accordingly the elementary paraunitary ma-
trix can be expressed as
b
E
(i)
(z) =
b
Q
(i)
b
P
(i)
(z). Note
that when L
(i)
= 1, the MS-SBR2 algorithm is identi-
cal to the SBR2 algorithm.
Different PEVD algorithms are assessed in terms
of the normalized remaining off-diagonal energy at
the i-th iteration. This is defined as
η
(i)
=
∑
τ
∑
M
m,n=1,m6=n
|r
(i)
mn
(τ)|
2
∑
τ
kR(τ)k
2
F
, (15)
where the notation k·k
F
denotes the Frobenius norm.
The comparison among different PEVD algo-
rithms is calculated via Monte Carlo simulations over
an ensemble of 100 different (6 × 6) para-Hermitian
matrices R
(z) of order 13, which is generated from
matrices A(z) ∈ C
6×6
of order 7 with i.i.d. zero mean
unit variance complex Gaussian entries, s.t. R
(z) =
A
(z)
e
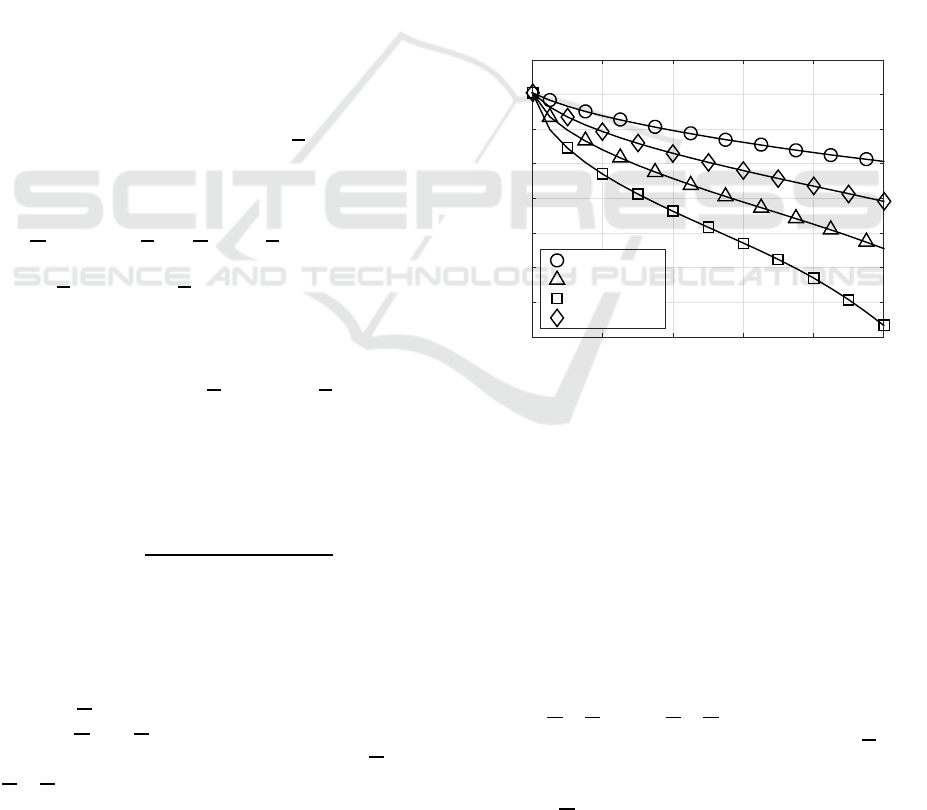
A(z). Fig. 1 shows the normalized remaining
off-diagonal energy η
(i)
versus iteration index i for
each PEVD algorithm. Obviously, both the SMD and
MSME-SMD algorithms outperform SBR2 and MS-
SBR2 in terms of eliminating the off-diagonalenergy.
This is due to the fact that a full EVD operation is
applied in SMD algorithm family at each iteration,
which can transform more off-diagonal elements onto
diagonal. However, this is also one of the factors
which causes the SMD algorithm family much higher
computational cost than the SBR2 algorithm. Obvi-
ously the MS-SBR2 algorithm requires much fewer
iterations than the conventional SBR2 algorithm to
achieve the same level of diagonalization. However,
it should also be noticed that each iteration within
MS-SBR2 involves more rotation steps, which means
the computational costs between them are compara-
ble. Nonetheless, the MS-SBR2 algorithm has been
found to converge faster than SBR2 especially when
decomposing high dimension para-Hermitian polyno-
mial matrices. For further details of the algorithm,
including numerical examples and proof of conver-
gence, see (Wang et al., 2015).
0 20 40 60 80 100
-16
-14
-12
-10
-8
-6
-4
-2
0
iteration index i →
5 · l og
10
E{η
(i)
} (indB) →
SBR2
SMD
MSME-SMD
MS-SBR2
Figure 1: Comparisons of normalized off-diagonal energy
among different PEVD algorithms, showing ensemble av-
erages versus iterations.
As shown by the simulation results, the off-
diagonal energy with the use of the investigated
PEVD algorithms becomes neglectable small at a suf-
ficiently high number of iterations.
4.5 Accuracy of the Decomposition
There are two main factors which can affect the accu-
racy of the decomposition. Firstly, since the decom-
position is performed upon the two para-Hermitian
matrices C
(z)
e
C(z) and
e
C(z)C(z) as shown in equa-
tions (5) and (6), the resulting diagonal matrix Σ
Σ
Σ(z)
might be less accurate than that found by the way of
operating the decomposition directly upon the chan-
nel matrix C
(z).
Secondly, for the broadband MIMO application,
OPTICS 2016 - International Conference on Optical Communication Systems
38

a strictly diagonalized channel matrix is required.
However, the proposed PMSVD method can only
generate an approximately diagonal matrix subject to
the pre-specified stop condition of the algorithm, so
there will be errors when assuming all off-diagonal
elements of the matrix Σ
Σ
Σ
(z) are equal to zero. In ad-
dition, due to the fact that the orders of the polyno-
mial matrices increase as the iteration goes through-
out the PEVD process, proper truncations are usually
required for the matrices U
(z), Σ
Σ
Σ(z), and V(z) in or-
der to keep orders as small as possible and reduce the
computational cost of the algorithm. This can cause
a very small proportion of the total Frobenius norm
of the matrix being eliminated, which also can bring
errors.
5 OPTICAL MIMO TESTBED
An optical MIMO system can be formed by feeding
different sources of light into the fibre, which can ac-
tivate different optical mode groups. This can be car-
ried out by using centric and eccentric light launching
conditions and subsequent combining of the activated
different mode groups with a fusion coupler as shown
in Fig. 2 (Sandmann et al., 2014).
(low order mode path)
(high order mode path)
1
2
3
Figure 2: Transmitter side fusion coupler for launching dif-
ferent sources of light into the MMF.
Different sources of light lead to different power
distribution patterns at the fibre end depending on the
transmitter side light launch conditions. Fig. 3 high-
lights the measured mean power distribution pattern
at the end of a 1.4 km multi-mode fibre (MMF). Here,
for splitting the different mode groups a similar fusion
coupler is used.
The measurement setup depicted in Fig. 4 shows
the testbed with the utilized devices for measuring
the system properties of the optical MIMO channel
in form of its specific impulse responses needed for
modelling the MIMO data transmission.
A picosecond laser unit is chosen for generating
the 25 ps input pulse. This input pulse is used to mea-
sure separately the different SISO channels within the
MIMO system. Since the used picosecond laser unit
doesn’t guarantee a fully flat frequency spectrum in
the region of interest, the captured signals have to be
deconvolved (Sandmann et al., 2013). The obtained
impulse responses are forming the base for modelling
Figure 3: Measured mean power distribution pattern when
using the fusion coupler at the transmitter side (left: cen-
tric mode excitation; right: eccentric mode excitation); the
dotted line represents the 50 µm core size.
the MIMO transmission system. Fig. 5 highlights the
resulting electrical MIMO system model.
6 SIMULATION RESULTS
In this work, the BER quality is studied by using fixed
transmission modes with a spectral efficiency of 8
bit/s/Hz. The analyzed quadrature amplitude modu-
lation (QAM) constellations, equivalent to how many
bits are allocated to each layer, are shown in Tab. 1.
Table 1: Transmission Modes.
throughput layer 1 layer 2
8 bit/s/Hz 256 0
8 bit/s/Hz 64 4
8 bit/s/Hz 16 16
The channel, studied in this contribution, is a mea-
sured (2× 2) optical MIMO channel.
Here, the measurement results within a 1.4 km
(2× 2) optical MIMO channel at an operating wave-
length of 1576 nm, depicted in Fig. 6, have been used
(Sandmann et al., 2015b). The graphs clearly show
the effect of chromatic dispersion being characteristic
at this operating wavelength in a standard fiber.
Applying PMSVD to this frequency-selective
MIMO channel results in layers having a time-
dispersive characteristic and hence ISI occurs on each
layer. The ISI is removed by applying a T-spaced zero
forcing (ZF) equalizer and therefore this equalization
scheme is entitled T-PMSVD. The equalizers mod-
ify the noise power on each layer differently, which
is expressed by the weighting factors θ
ℓ
, with ℓ de-
noting the layer index. These factors determine the
layer specific SNRs and hence also the total BER per-
formance (Sandmann et al., 2015c). Calculating the
PMSVD of the optical MIMO channel using differ-
ent PEVD algorithms shows that the weighting fac-
tors θ
ℓ
listed in Tab. 2 are identical. This implies
Polynomial Matrix SVD Algorithms for Broadband Optical MIMO Systems
39
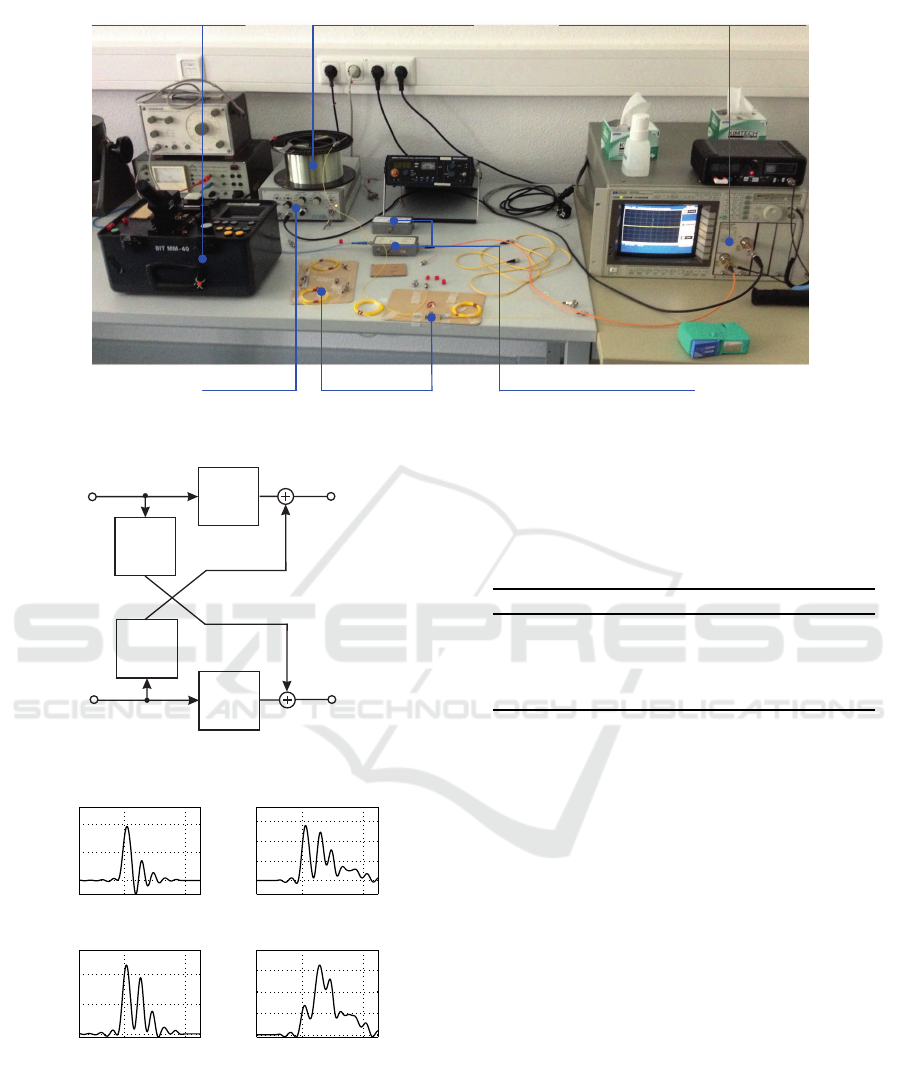
Light Launching Unit (splicer) 1.4 km multi-mode fibre channel Sampling Oscilloscope with MSM Photo Detector
Picosecond Laser Laser-diode ( ≈ 1.3 μm or 1.55 µm)Fusion Couplers
Figure 4: Measurement setup for determining the MIMO specific impulse responses.
u
s 1
(t)
u
s 2
(t)
u
k 1
(t)
u
k 2
(t)
g
11
(t)
g
21
(t)
g
12
(t)
g
22
(t)
Figure 5: Electrical (2× 2) MIMO system model (example:
n
R
= n
T
= 2).
2 4
0.0
0.5
1.0
2 4
0
0.1
0.2
0.3
2 4
0
0.1
0.2
2 4
0
0.05
0.1
0.15
t (inns) →t (inns) →
t (inns) →t (inns) →
T
s
g
1 1
(t) →
T
s
g
1 2
(t) →
T
s
g
2 1
(t) →
T
s
g
2 2
(t) →
Figure 6: Measured electrical MIMO impulse responses
with respect to the pulse frequency f
T
= 1/T
s
= 620 MHz
at 1576 nm operating wavelength.
that the achievable BER is independent of the ap-
plied PEVD algorithms for the studied (2× 2) MIMO
channel. In addition, the remaining off-diagonal en-
ergy ε =
∑
τ
kC(τ)k
2
F
−
∑
τ
kΣ
Σ
Σ(τ)k
2
F
is negligibly small,
Table 2: Comparisons of remaining off-diagonal energy ε
and noise amplification factor θ
ℓ
among different PEVD
algorithms, showing that different PEVD algorithms can
achieve exactly the same BER performance subject to the
same stop criterion of the PEVD algorithms, i.e. the thresh-
old of the off-diagonal element ε = 10
−4
.
algorithms ε θ
1
θ
2
SBR2 1.26× 10
−6
37.22 4243.46
SMD 1.26× 10
−6
37.22 4243.46
MSME-SMD 1.26×10
−6
37.22 4243.46
MS-SBR2 1.26× 10
−6
37.22 4243.46
which means that the CI has been significantly elimi-
nated.
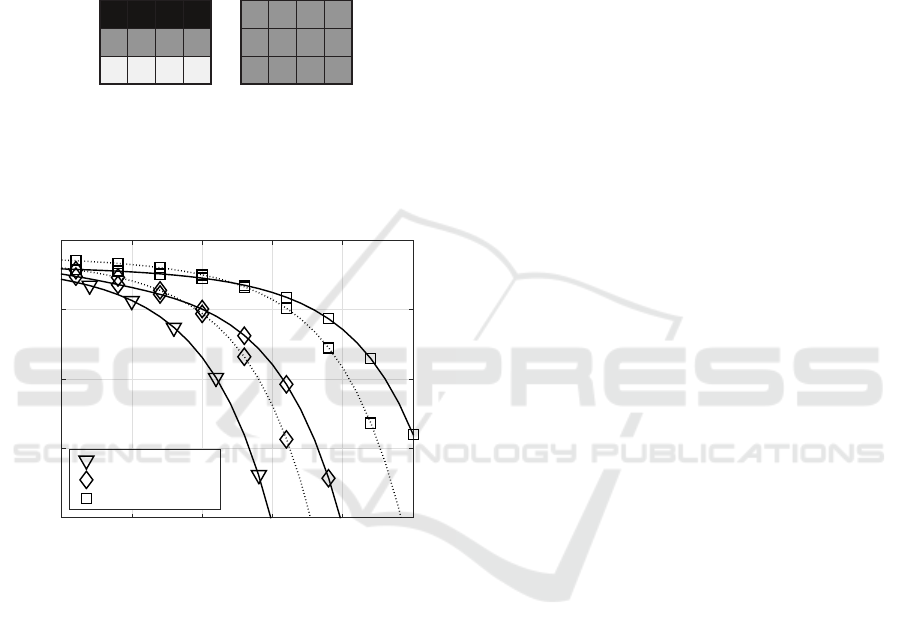
The BER performance results, obtained by apply-
ing the SBR2 algorithm for calculating the PMSVD,
are depicted in Fig. 8 for the different QAM constel-
lation sizes. The (256, 0) transmission scheme shows
the best performance results suggesting that not all
layers should be activated when optimizing the BER
performance.
Based on the unequal weighting of the layers, PA
can be used to balance the bit-error probabilities in
the different numbers of activated MIMO layers. Re-
garding the channel quality, the BER performance is
affected by the layer-specific weighting factors, the
chosen QAM-constellation size as well as the layer-
specific noise power. Since optimal PA solutions
are notably computationally complex to implement,
a suboptimal solution which concentrates on the ar-
gument of the complementary error function is inves-
tigated in this work (Ahrens et al., 2015).
By applying T-PMSVD the ISI is fully removed
by the equalizer and thus for each layer the half ver-
tical eye opening of the receive signal equals the
OPTICS 2016 - International Conference on Optical Communication Systems
40
half-level amplitude of the transmitted symbols. The
drawback of the T-PMSVD is that the noise and hence
the noise power is weighted differently on each layer
by the equalizer coefficients expressed by the factors
θ
1
and θ
2
as shown in Tab. 2. The proposed PA al-
gorithm distributes the available transmit power such
that the layer specific SNRs are equal (Sandmann
et al., 2015c; Ahrens et al., 2015). The resulting SNRs
for the proposed PA scheme in T-PMSVD systems are
visualized in Fig. 7.
layer ℓ
time k
layer ℓ
time k
Figure 7: Illustration of the remaining SNRs in T-PMSVD
systems without applying PA (left) and with layer-based PA
(right). The color black refers to high and white to low SNR
values.
35 40 45 50 55 60
10
-8
10
-6
10
-4
10
-2
10
0
P
BER
→
10 · log
10
(E
s
/N
0
) (indB) →
(256,0) QAM
(64,4) QAM
(16,16) QAM
Figure 8: BER with PA (dotted line) and without PA
(solid line) by applying the T-PMSVD equalization scheme,
showing the comparisons among different transmission
modes when transmitting over the optical (2 × 2) MIMO
channel.
7 CONCLUSION
We have investigated the PMSVD technique in the
application of decomposing the channel matrix of a
measured (2×2) optical MIMO system, and different
iterative PEVD algorithms have been utilized for the
calculation of PMSVD. Despite the different number
of iterations needed to minimize the off-diagonal ele-
ment below a given threshold, all investigated PEVD
algorithms show the same BER performance.
ACKNOWLEDGEMENTS
This work has been funded by the German Ministry
of Education and Research (No. 03FH016PX3).
REFERENCES
Ahrens, A., Sandmann, A., Lochmann, S., and Wang, Z.
(2015). Decomposition of Optical MIMO Systems us-
ing Polynomial Matrix Factorization. In 2nd IET In-
ternational Conference on Intelligent Signal Process-
ing (ISP), London (United Kingdom).
Corr, J., Thompson, K., Weiss, S., McWhirter, J. G., Redif,
S., and Proudler, I. K. (2014). Multiple Shift Maxi-
mum Element Sequential Matrix Diagonalisation for
Parahermitian Matrices. In IEEE SSP Workshop,
pages 312–315, Gold Coast (Australia).
Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,
New Jersey.
Kühn, V. (2006). Wireless Communications over MIMO
Channels – Applications to CDMA and Multiple An-
tenna Systems. Wiley, Chichester.
McWhirter, J. G. and Baxter, P. D. (2004). A Novel Tech-
nique for Broadband Singular Value Decomposition.
In 12th Annual ASAP Workshop, MA (USA).
McWhirter, J. G., Baxter, P. D., Cooper, T., Redif, S.,
and Foster, J. (2007). An EVD Algorithm for Para-
Hermitian Polynomial Matrices. IEEE Trans. SP,
55(5):2158–2169.
Raleigh, G. G. and Cioffi, J. M. (1998). Spatio-Temporal
Coding for Wireless Communication. IEEE Transac-
tions on Communications, 46(3):357–366.
Raleigh, G. G. and Jones, V. K. (1999). Multivariate
Modulation and Coding for Wireless Communication.
IEEE Journal on Selected Areas in Communications,
17(5):851–866.
Redif, S., Weiss, S., and McWhirter, J. G. (2015). Sequen-
tial Matrix Diagonalization Algorithms for Polyno-
mial EVD of Parahermitian Matrices. IEEE Trans. SP,
61(1):81–89.
Sandmann, A., Ahrens, A., and Lochmann, S. (2013).
Signal Deconvolution of Measured Optical MIMO-
Channels. In XV International PhD Workshop OWD,
pages 278–283, Wisla, Poland.
Sandmann, A., Ahrens, A., and Lochmann, S. (2014). Ex-
perimental Description of Multimode MIMO Chan-
nels utilizing Optical Couplers. In ITG-Fachbericht
248: Photonische Netze, pages 125–130, Leipzig
(Germany). VDE VERLAG GmbH.
Sandmann, A., Ahrens, A., and Lochmann, S. (2015a).
Modulation-Mode and Power Assignment in SVD-
Assisted Broadband MIMO Systems using Polyno-
mial Matrix Factorization. Przeglad Elektrotech-
niczny, 04/2015:10–13.
Sandmann, A., Ahrens, A., and Lochmann, S. (2015b). Per-
formance Analysis of Polynomial Matrix SVD-based
Polynomial Matrix SVD Algorithms for Broadband Optical MIMO Systems
41

Broadband MIMO Systems. In Sensor Signal Pro-
cessing for Defence Conference (SSPD), Edinburgh
(United Kingdom).
Sandmann, A., Ahrens, A., and Lochmann, S. (2015c).
Resource Allocation in SVD-Assisted Optical MIMO
Systems using Polynomial Matrix Factorization. In
ITG-Fachbericht 257: Photonische Netze, pages 128–
134, Leipzig (Germany). VDE VERLAG GmbH.
Sandmann, A., Ahrens, A., and Lochmann, S. (2016). Ex-
perimental Evaluation of a (4x4) Multi-Mode MIMO
System Utilizing Customized Optical Fusion Cou-
plers. In ITG-Fachbericht 249: Photonische Netze,
pages 101–105, Leipzig (Germany). VDE VERLAG
GmbH.
Singer, A. C., Shanbhag, N. R., and Bae, H.-M. (2008).
Electronic Dispersion Compensation– An Overwiew
of Optical Communications Systems. IEEE Signal
Processing Magazine, 25(6):110–130.
Ta, C. and Weiss, S. (2007). A Design of Precoding
and Equalisation for Broadband MIMO Systems. In
Asilomar Conf. Signals, Systems & Computers, pages
1616–1620, Pacific Grove, (CA).
Tse, D. and Viswanath, P. (2005). Fundamentals of Wireless
Communication. Cambridge, New York.
Vaidyanathan, P. P. (1993). Multirate Systems and Filter
Banks. Prentice Hall, New Jersey.
Wang, Z., McWhirter, J. G., Corr, J., and Weiss, S. (2015).
Multiple Shift Second Order Sequential Best Rotation
Algorithm for Polynomial Matrix EVD. In 23rd EU-
SIPCO, pages 849–853, Nice (France).
Wang, Z., Sandmann, A., McWhirter, J., and Ahrens, A.
(2016). Multiple Shift SBR2 Algorithm for Calculat-
ing the SVD of Broadband Optical MIMO Systems.
In 39th International Conference on Telecommunica-
tions and Signal Processing (TSP), Vienna (Austria).
Winzer, P. J. and Foschini, G. J. (2011). MIMO Ca-
pacities and Outage Probabilities in Spatially Multi-
plexed Optical Transport Systems. Optics Express,
17(19):16680–16696.
OPTICS 2016 - International Conference on Optical Communication Systems
42
