Numerical Research on Water Hammer in Propellant Filling Pipeline
based on Spectral Method
Youhuan Xiang, Ping Zhang, Jianguo Pang, Hui Zhang and Quansheng He
Technical Department, Taiyuan Satellite Launch Center, Taiyuan, China
Keywords: Filling System, Water Hammer, Spectral Method, Characteristic Line Method.
Abstract: In order to research the water hammer problem in the filling pipeline during the rocket propellant filling
process for the spaceflight launch site, improved schemes are proposed. Chebyshev spectral method is
adopted to solve the water hammer problem in the paper. The law of pressure change is analyzed when
water hammer occurs, and the results calculated by the spectral method are compared with the results
calculated by the characteristic line method and the experimental results. The results show that the proposed
schemes can effectively weaken the water hammer in the pipeline during the filling process, improve the
reliability and security of the filling system, and verify the feasibility that adopting the Chebyshev spectral
method to solve the water hammer problem in the filling pipeline.
1 INTRODUCTION
The rockets propellant filling system is an important
part of the spaceflight launch site, and the filling
pipeline is a key assembly in the filling system.
Accurately grasp the work state of the filling
pipeline in the rocket propellant filling process is
very important for the filling accuracy and the
reliability and security of the system (Xiang, 2015).
The filling pipeline in the launch site can provide
routeway for the propellant transporting from the
storehouse horizontal tank to the rocket tank. It’s
stability, reliability and security is very important for
the success of the spaceflight launch. The water
hammer is a water power phenomena in the pipeline
that the water flow rate changed suddenly, leading to
the pressure rise and fall sharply, caused by some
external reasons, such as the valve suddenly open or
close. In the process of rocket propellant filling in
the spaceflight launch site filling system, it often
takes place the phenomena that the pressure of the
filling pipeline is far higher than the designed
pressure, and it is far more than the normal working
pressure range. It is a potential danger for the
system.
The water hammer can damage equipment,
increase the fault probability of the system. It also
can cause violent vibration of the filling pipeline,
result in measurement error for the vortex-shedding
flowmeter. It will reduce the actual propellant filling
precision. Therefore, it requires numerical research
on water hammer problem in the filling system, and
proposes effectively improved schemes. It is very
important for improving the filling precision and
guaranteeing the success of rocket launch.
The rest parts of the paper are organized as
follows: Section 2 introduces the related work.
Section 3 adopts the spectral method to solve the
water hammer problem. The experimental results are
compared and analyzed in section 4. Section 5
makes the conclusions.
2 RELATED WORK
The characteristic line method is widely applied for
solving the water hammer problem. (Liu, 2005)
Firstly it changes the partial differential equation
into ordinary differential equation along the
characteristic line, and then changes it into first order
finite difference equation. The method can solve the
water hammer problem of complicated piping
system with boundary conditions, and the calculation
accuracy of the method is high.
In literature (Yan, 2012), Yan Zheng researches
the water hammer problem of the spacecraft
propulsion system in the processes of priming and
shutdown. On the basic of the established simulation
Xiang, Y., Zhang, P., Pang, J., Zhang, H. and He, Q.
Numerical Research on Water Hammer in Propellant Filling Pipeline based on Spectral Method.
DOI: 10.5220/0005949803930398
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 393-398
ISBN: 978-989-758-198-4
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
393

model of the spacecraft propulsion system, the
simulation research was conducted and the
suppression effect of water hammer for the orifice
and bent duct was analyzed. In literature (Lin, 2008),
Lin Jing-song studies the fluid transients of the
propellant pipes after the liquid rocket engine shut
down, and carries out numerical simulation of water
hammer in shutting liquid rocket engine based on the
method of characteristic line. The correctness of the
simulation results was approved by comparison with
the experiment data. In literature (Nie, 2003), Nie
Wan-sheng researches the pressure and the flow
transients characteristic when the liquid rocket
engine system shut down based on the method of
finite difference characteristic line. In literature (Liu,
2010), Liu Zhao-zhi analyzes the water-hammer
problem based on the characteristic line method for
the actual pipeline structure in the liquid hydrogen
filling system, and the useful measures are proposed
to reduce peak pressure of the water-hammer.
The following are the steps that using the
characteristic line to solve the water hammer
problems. The first step: the partial differential
equation that can’t directly to solve should be
changed into a specific form of ordinary differential
equation, namely characteristic line equation. The
second step: carrying through integral calculus for
the ordinary differential equations, getting the
approximate algebraic integral formula, namely
finite difference equation. The third step: according
to the finite difference equation and bound condition
equation of piping system to calculate. However,
when adopting the spectral method to solve water
hammer in the filling pipeline, the boundary
conditions are complicated, the coordination of time
step is difficult, and the nonlinear iterative
convergence is slow.
The spectral method is discrete method for a kind
of partial differential equation. It is a calculation
method that takes orthogonal function or inherent
function as the approximate function. The spectral
approximation contains two approximate ways, that
is function approximation and equation
approximation (Wang, 2001). On the way of
function approximation, the spectral method contains
three methods: the Fourier method, the Chebyshev
method and the Legendre method. The former is
suitable for the periodic problem, and the latter is
suitable for aperiodic problem. On the way of
equation approximation, the spectral method
contains Collocation method, Galerkin method and
Pseudo-spectral method. The Collocation method is
suitable for the nonlinear problem in the physical
space. The Galerkin method is suitable for the linear
problem in the spectral space. The Pseudo-spectral
method is suitable for nonlinear term processing in
the combination of physical space and spectral
space.
The main characteristic of the spectral method is
fast convergence speed, no phase error, higher
precision and global. It makes the spectral method be
widely adopted in high precision calculation. In
literature (Chen, 2012), Chen Hong-yu proposes a
new algorithm that adopting the Fourier spectral
method to solve the nonlinear hyperbolic partial
differential equations for governing the fluid
transient. By adopting the method, it solves the water
hammer and pressure oscillation formed in the
pipeline when the valve is shut down. It proves the
credibility of the method. In literature (Chen, 2013),
Chen Hong-yu proposes the Chebyshev spectral
method to solve the nonlinear hyperbolic partial
differential equations for governing the fluid
transient in the propellant pipelines. It solves the
water hammer problem in the pipeline when the
valve is shut down by the method, and proves the
feasibility of the method.
In order to further analyzing the generating
mechanism of water hammer problem in the filling
pipeline and the water hammer change law
influenced by the control process of filling system,
and researching the scheme weakening the water
hammer problem in the filling pipeline, the
Chebyshev spectral method is adopted to solve the
water hammer problem in the filling system in the
paper.
3 SOLVE THE WATER HAMMER
PROBLEM BASED ON THE
CHEBYSHEV SPECTRAL
METHOD
3.1 Basic Differential Equation of
Water Hammer
The theoretical basic of the water hammer basic
equation is the mechanics law and continuous
principle of water flow movement. It includes the
motion equation and the continuity equation which
expressed in differential equation. It reflects the flow
velocity of instability flow and the changing rule of
water head in the process of hydraulic transient
(Xiang, 2015), (Lin, 2007).
The continuous differential equation of water
hammer is:
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
394

0sin
2









s
v
g
c
v
s
h
v
t
h

(1)
The motion differential equation of water hammer is:
0
2









vv
D
f
s
v
v
t
v
s
h
g
(2)
In the equation, v is the flow velocity of water
hammer, h is the piezometric head of water hammer.
D is the pipe diameter, f is the pipe friction
coefficient, g is the acceleration of gravity. θ is the
angle between pipeline and horizontal plane, c is the
wave velocity of water hammer, s is the distance,
and t is the time.
The basic differential equation of water hammer
is a first order quasilinear hyperbolic partial
differential equations thanks to considering the loss
of the frictional head. The equations contains two
dependent variables and two independent variables.
It is difficult to accurately solve the equations.
3.2 Solve the Problem by the
Chebyshev Spectral Method
The basic differential equation of Water Hammer is
solved based on the Chebyshev spectral method in
this paper. Chebyshev spectral method takes the
Chebyshev polynomial as the basis function. The
function defined in the computational domain can be
go to approximation by the basis function. Then the
partial differential equation can be solved through
the weighted residual method.
When adopting the Chebyshev spectral method,
firstly we take N+1 Chebyshev-Gauss-Lobatto (CLG
for short) (Yang, 2015) points in the interval of [-1,1].
Namely,
n
N
n

 cos
，n=0,1,2,…,N.
Then the Chebyshev polynomial is as follow:
)]arccos(cos[)(
nnm
mT



, m=0,1,2,…,N
(3)
The approximate values of state variable and control
variable for the basic differential equation of water
hammer are:



N
k
kkN
hhh
0
)()()()( 
(4)



N
k
kkN
vvv
0
)()()()( 
(5)
For k=0,1,2, … ,N, the N-order Lagrange
polynomial is as follow:
k
N
k
k
k
T
cN









)(')1(
)1(
)(
2
2
1
(6)
In the above equation,
)('

N
T
is the derivative of
)(

N
T
which is the N-order Chebyshev polynomial,
and parameter
k
c satisfy the following condition:






111
,02
Nk
Nk
c
k
, and
)('
jkjk
D



.
jk
D
is
the Chebyshev differential matrix, the expression
is as follow:

























Nkj
N
kj
N
Nkj
kj
c
c
D
j
j
kj
kj
k
j
jk
,
6
12
0,
6
12
11,
)1(2
,
)1(
2
2
2



(7)
The water hammer problem has discontinuous
solutions, and larger oscillation can be produced near
the discontinuity point. In order to solve the problem,
the viscous term is introduced in the equation (Chen,
2013), (Ma, 2006). For the continuous differential
equation, the viscous term is
N
ss
hQ
21
)1(

 
. For
the motion differential equation, the viscous term is
N
ss
vQ
21
)1(

 
. In the viscous term,

is the
viscous amplitude,
Q
is the viscous operator, and
s
CN
21
 
,





2
1 Q
.
The calculation formula of water hammer wave
velocity is (Xu, 2012):
 

DEK
K
c


1
. In the
formula, K is the fluid bulk modulus,
ρ is the fluid
density, E is the piping materials elastic modulus, D
is the pipe diameter,

is the pipe wall thickness.
According to the calculation formula of water
hammer wave velocity, the water hammer wave
velocity of oxidant pipeline in the propellant filling
system can be get through calculation, c=850m/s.
4 EXPERIMENTAL RESULT
ANALYSIS
The pipeline model for the rocket propellant filling
system is established as Fig.1. In the Fig, the rocket
Numerical Research on Water Hammer in Propellant Filling Pipeline based on Spectral Method
395

tank is vertically located on the launch pad and on
one horizontal plane. Except that, the equipments
such as pump, flowmeter, valve and pressure gauges,
are all located in the pump room of the filling
storehouse and on the same horizontal plane. The
height from the 125# valve to the filling port of the
rocket oxidizer tank is 30 meter or so, and they are
connected together through the filling pipeline.
Pressure
Gauge
P1
Flowmeter
L1
Pump
Flowmeter
L2
Flowmeter
L3
Flowmeter
L4
125#
124#
Rocket tank
Outlet
134#
Inlet
DT4
121#
122#
Figure 1: Pipeline model for the filling system.
The fluid in the pipeline is N
2
O
4
, and the physical
parameter of N
2
O
4
at the temperature of 20℃ is: the
density ρ=1.446g/cm
3
, the viscosity
μ=0.4189×10
-3
Pa·s, the saturation pressure
Ps=0.096MPa, the fluid bulk modulus K=1.27GPa.
Before water hammer in the filling pipeline occurs,
the initial state is: the opening of electric control
valve is 30%, the frequency of pump inverter is 50Hz,
the state of the 121# 124# and 134# valve is open,
and the state of the 122# and 125# valve is close.
In order to verify the validity of adopting the
Chebyshev spectral method to solve water hammer
problem in the filling pipeline, the following four
experiments that reduce water hammer in the pipeline
are calculated. The results calculated by the
Chebyshev spectral method are compared with the
results calculated by the characteristic line method
and the experimental results.
Experiment 1: According to the existing filling
process, that is: open up 125# valve, delay of 1
second, at the same time close 124# and 134# valve,
the pump speed is 50Hz, the opening of electric
control valve DT4 is 30%. The calculation results
are shown in Fig. 2.
Fig. 2 shows the comparison and pressure change
law when water hammer happens under the existing
process.
024681012
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Pressure (MPa)
Time (s)
characteristic line method
experimental data
spectral method
Figure 2: Comparison and pressure change law under the
existing process.
The ordinate shows the pressure, and the abscissa
shows the test time. The read curve shows the results
calculated by the Chebyshev spectral method, the
black curve shows the results calculated by the
characteristic line method, and the blue curve shows
the real experimental data. From the Fig we can
know, before water hammer happens, the pressure of
the filling pipeline is 0.25MPa. When water hammer
happens, the pressure increases rapidly, and the peak
pressure calculated by the Chebyshev spectral
method is as high as 3.22MPa. The pressure in the
pipeline has changed dramatically, and there is 13
times difference of the pressure when water hammer
happens.
024681012
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
characteristic line method
experimental data
spectral method
Pressure (MPa)
Time (s)
Figure 3: Comparison and pressure change law after
changing the sequential.
Experiment 2: On the basis of the above
experiment, we change the closed sequential of the
related valve when water hammer happens. The
closed sequential of the related valve are changed as
follow: close the 124# valve, 1 second later close the
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
396

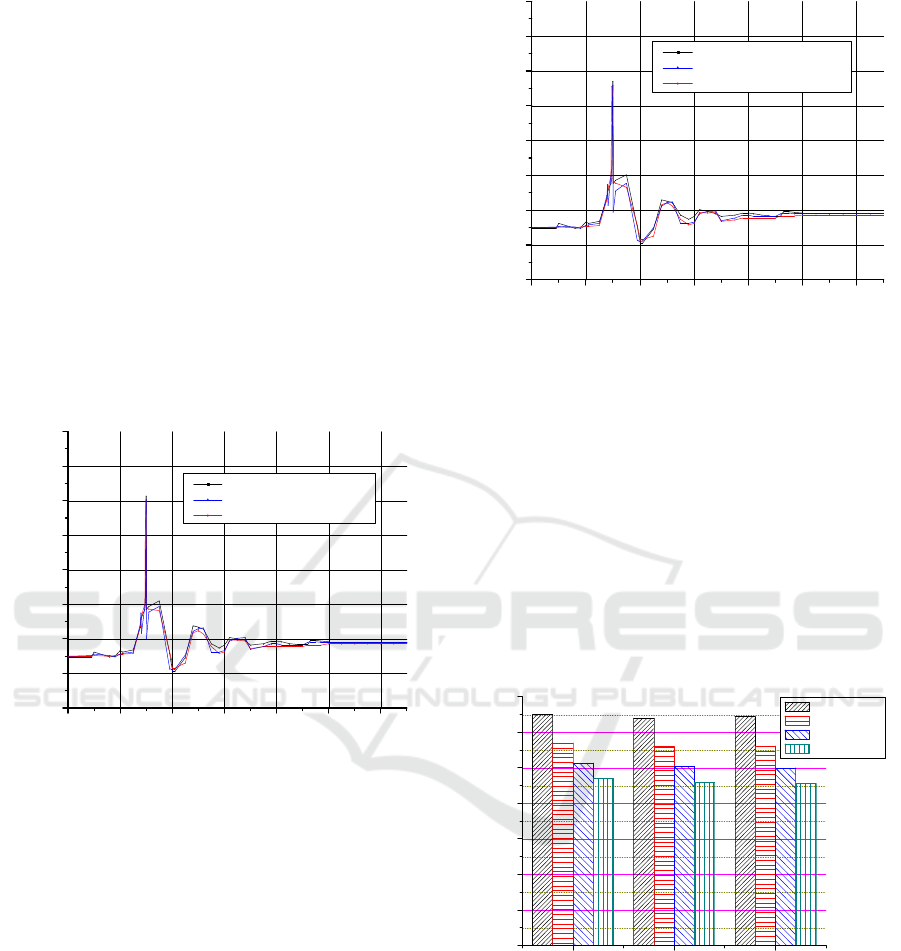
134# valve. The calculation results are shown in
Fig.3.
Fig. 3 shows the comparison and pressure change
law when water hammer happens after changing the
sequential. The ordinate shows the pressure, and the
abscissa shows the test time. Through comparing
Fig.2 and Fig.3, we can know that the scheme which
changing the closed sequential of the related valve
can effectively weaken the water hammer problem in
the filling pipeline. Compared with the results in
experiment 1, the peak pressure calculated by the
Chebyshev spectral method is reduced from 3.22MPa
to 2.81MPa, reduced by 12.7%.
Experiment 3: On the basis of the above
experiment, we change the speed of the filling pump
when water hammer happens. The speed of the filling
pump is changed from 50Hz to 40Hz. The calculation
results are shown in Fig.4.
024681012
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
characteristic line method
experimental data
spectral method
Pressure (MPa)
Time (s)
Figure 4: Comparison and pressure change law after
changing the pump speed.
Fig. 4 shows the comparison and pressure change
law when water hammer happens after changing the
speed of the filling pump. The ordinate shows the
pressure, and the abscissa shows the test time.
Through comparing Fig.3 and Fig.4, we can know
that the scheme which changing the speed of the
filling pump can effectively weaken the water
hammer problem in the filling pipeline. Compared
with the results in experiment 2, the peak pressure
calculated by the Chebyshev spectral method is
reduced from 2.81MPa to 2.5MPa, reduced by 11%.
Experiment 4: On the basis of the above
experiment, we change the opening of the electric
control valve DT4 when water hammer happens. The
opening of the electric control valve DT4 is changed
from 30% to 60%. The calculation results are shown
in Fig. 5.
024681012
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
characteristic line method
experimental data
spectral method
Pressure (MPa)
Time (s)
Figure 5: Comparison and pressure change law after
changing the opening of electric control valve.
Fig. 5 shows the comparison and pressure change
law when water hammer happens after changing the
opening of electric control valve DT4. The ordinate
shows the pressure, and the abscissa shows the test
time. Through comparing Fig.4 and Fig.5, we can
know that the scheme which changing the opening of
electric control valve can effectively weaken the
water hammer problem in the filling pipeline.
Compared with the results in experiment 3, the peak
pressure calculated by the Chebyshev spectral
method is reduced from 2.5MPa to 2.28MPa, reduced
by 8.8%.
123
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
spectral
method
characteristic line
method
Pressure (MPa)
experimental
data
experiment 1
experiment 2
experiment 3
experiment 4
Figure 6: Comparison of water hammer peak pressure
under different experimental conditions.
The comparison of water hammer peak pressure
under different experimental conditions is show in
Fig.6. From the Fig, we can know that the water
hammer peak pressure in experiment 1 is the highest,
it decreased gradually in experiment 2, 3 and 4, and
the water hammer peak pressure in experiment 4 is
the lowest. There is little difference among the three
peak pressures.
Numerical Research on Water Hammer in Propellant Filling Pipeline based on Spectral Method
397

Overall, when adopting the spectral method to
solve water hammer problem, boundary conditions is
simple and computational efficiency is high. The
results calculated by the spectral method under
different experiments are well consistent with the
results calculated by the characteristic line method
and the experimental results. It shows that the
spectral method can well solve the water hammer
problem in propellant filling pipeline as well as the
characteristic line method.
5 CONCLUSION
This paper researches the water hammer problem in
the rocket propellant filling pipeline under the filling
process of the spaceflight launch site, and analyzes
the effects of filling process on water hammer. The
law of pressure change is analyzed when water
hammer happens. Improved schemes are proposed to
weaken the water hammer in the filling pipeline. We
adopt the Chebyshev spectral method to solve the
water hammer problem, and present the calculation
results. We can come to the following conclusions:
(1) The Chebyshev spectral method can well solve
the water hammer problem in propellant filling
pipeline. (2) The proposed schemes can effectively
weaken water hammer in the pipeline during the
filling process, and improve the reliability and
security of the filling system. Through numerical
analysis for the different experiments, it can provide
theoretical basis and data support for weakening
water hammer problem in the filling system and
optimizing filling process.
REFERENCES
Xiang Youhuan, Zhang ping, Zhang Hui. Numerical
Analysis on Water Hammer Characteristics of Rocket
Propellant Filling Pipeline[C]. SIMULTECH 2015-5th
International Conference on Simulation and Modeling
Methodologies, Technologies and Applications. July
21-23, 2015:337-343.
Liu Deyou, Suo Lisheng. Rigid Model of Transient
Analysis for Multiple-characteristic Long Pipeline
with Trapped Air Mass[J]. Journal of Hydrodynamics.
Ser. A, Vol.20, No.1 Jan, 2005:44-49.
Yan Zheng, Peng Xiao-hui, Cheng Yu-qiang, Wu Jian-jun.
Research of water hammer and its suppression
methods for spacecraft propulsion system[J]. Journal
of Aerospace Power. Sep.2012, Vol.27
No.9:2028-2034.
Lin Jingsong, Wang Pingyang, Gao hong. Numerical
Simulation of Water Hammer in Shutting Liquid
Rocket Engine[J]. Aerospace Shanghai. No.3
2008:53-57.
Nie Wansheng, Dai Haide, Xia Peng. Transient
Characteristics during shutdown operation of liquid
feed line for attitude control propulsion system[J].
Journal of Propulsion Technology. 2003, 24(1):6-8.
Liu Zhaozhi, Ding Pengfei, Tian Qingya. Numerical
Analysis on Water-hammer of Liquid Hydrogen
Loading System[J]. Missiles and Space Vehicles. No.4
2010, Sum No.408:10-12.
Wang Jian-ping. Fundamental problems in spectral
methods and finite spectral method[J]. Acta
Aerodynamica Sinica. Jun.2001, Vol.19,
No.2:161-170.
Chen Hong-yu, Liu Hong-jun, Liu Shang. Spectral-Fourier
method for water hammer[J]. JOURNAL OF ROCKET
PROPULSION[J]. Jun.2012, Vol.38, No.3:7-11.
Chen Hong-yu, Liu Hong-jun, Liu Shang. Solution of
transient flow in propellant pipelines by Chebyshev
spectral collocation method[J]. Journal of Rocket
Propulsion. Aug.2013, Vol.39, No.4:24-29.
Lin Jing-song. Numerical Simulation of Water Hammer in
Shutting Liquid Rocket Engine[D]. Shanghai Jiaotong
University. 2007.
Yang Xixiang, Yang Huixin, Wang Peng. Overview of
pseudo-spectral method and its application in
trajectory optimum design for flight vehicles[J].
Journal of National University Of Defense
Technology. Aug.2015, Vol.37, No.4:1-8.
Ma H P, Li H Y. Super spectral viscosity method for
nonlinear conservation laws[J]. Journal of Shanghai
University (English Edition). 2006, 10(1):9-14.
Xu Feng, Liu Ying-yuan, Chen Hai-feng. Numerical
simulation analysis of water-hammer pressure of
rocket engine[J]. Journal of Rocket Propulsion.
Feb.2012, Vol.38, No.1: 72-75.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
398