
FPGA Implementation of HS1-SIV
Gerben Geltink and Sergei Volokitin
Institute for Computing and Information Sciences, Radboud University, Toernooiveld 212, Nijmegen, The Netherlands
Keywords:
HS1-SIV, CAESAR, Authenticated Encryption, FPGA, VHDL.
Abstract:
This work describes a hardware implementation of HS1-SIV with regular cipher parameter settings for the
second round of the CAESAR competition. The implementation encompasses both the HS1-SIV hardware
implementation, which is conforming to the specifications of the authenticated cipher, as well as a hardware
API. The implemented API is conforming to the specifications of the GMU Hardware API for authenticated
ciphers. On the target device Xilinx Virtex-7, using Xilinx XST High Level Synthesis, we achieved a through-
put of 122.20 Mbit/s and an area of 103,214 LUTs with the data length of the message and the associated data
set at 64 bytes and the data length of the key set at 32 bytes. Our performance results suggest that the area
overhead of the API is between 8% (8-byte data length) and 15% (2048-byte data length) in comparison the
the cipher-core.
1 INTRODUCTION
Due to the reason that encryption algorithms only pro-
vide confidentiality of the encrypted data, real life ap-
plications of encryption require the use of additional
mechanisms to provide integrity and authenticity of
messages. Although it is possible to build an au-
thenticated encryption scheme using an encryption al-
gorithm and a message authentication code (MAC),
such an approach is often less computationally effi-
cient. Authenticated encryption schemes are designed
to perform encryption of the message and provide
a message authentication code. Additionally, Au-
thenticated encryption with associated data (AEAD)
not only provides an authentication code of the se-
cret message but also authenticates the associated data
which is often a header.
As part of the second round of the Competition
for Authenticated Encryption: Security, Applicabil-
ity, and Robustness (CAESAR), candidates have to
submit a hardware implementation of their authenti-
cated cipher (Bernstein, 2016). The competition was
announced in 2013 at the Early Symmetric Crypto
workshop in Mondorf-les-Bains, Luxembourg. Simi-
larly to AES (Daemen and Rijmen, 1999), eSTREAM
(Babbage et al., 2008), SHA-3 (Keccak (Bertoni et al.,
2011)) and PHC (Argon2 (Biryukov et al., 2015)),
CAESAR seeks to select a portfolio of algorithms
which most likely will include a number of encryp-
tion algorithms. With this portfolio, the confidence in
the security, applicability and robustness of authenti-
cated encryption ciphers will be improved.
Although functional software requirements have
been set for the CAESAR candidates, details of the
hardware Application Programming Interface (API)
have not yet been specified. However, the GMU
Hardware API, which was introduced to provide a ba-
sis for benchmarking the hardware implementations
of the CAESAR candidates, is considered as a stan-
dard amongst the hardware implementers of the CAE-
SAR candidates (Homsirikamol et al., 2015). This
API provides specifications for the interface (AEAD-
core) of the authenticated cipher-core as well as the
communication protocol needed.
Implementing HS1-SIV is not trivial due to a
number of reasons. First, HS1-SIV is designed to be
efficient on 32-bit architectures, which means that the
numerous amount of multiplications and modulo op-
erations have to be implemented thoughtfully. Sec-
ond, the computation of the hashes require the en-
tire input message, which means that the architecture
needs to be implemented such that these continuous
computations are supported.
We describe the first effort to implement HS1-SIV
(Krovetz, 2014) with regular security parameter set-
tings (hereafter called HS1-SIV-MED) on a Field Pro-
grammable Gate Array (FPGA). Regular security set-
tings of the cipher include:
• the number of bytes used by the hashing algo-
rithm, which is equal to 64 bytes;
• the collision level of the hashing algorithm, which
Geltink, G. and Volokitin, S.
FPGA Implementation of HS1-SIV.
DOI: 10.5220/0005950100410048
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 41-48
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
41

is equal to 4 bytes;
• the number of internal rounds of the steam cipher,
which is equal to 12 bytes;
• the byte length of synthetic IV, which is equal to
16 bytes.
The structure of the paper is as follows.
In Section 2, we describe the authenticated encryp-
tion cipher HS1-SIV-MED and its subroutines. Sec-
tion 3 describes the related work. Section 4 describes
our contributions. In Section 5, we describe the hard-
ware design of the HS1-SIV-MED cipher-core. In
Section 6, we present the performance results of the
implementation. Section 7 describes some topics for
future research. And finally, Section 8 concludes the
paper.
2 HS1-SIV
HS1-SIV is an abbreviation for “Hash-Stream 1 -
Synthetic Initialization Vector”. As the name suggests
the algorithm of HS1-SIV uses HS1 as a Pseudo-
Random Function (PRF) to provide deterministic au-
thenticated encryption with Rogaway and Shrimp-
ton’s SIV mode (Rogaway and Shrimpton, 2007).
Specifically, HS1-SIV is composed of six subrou-
tines: HS1-SIV-Encrypt, HS1-SIV-Decrypt, HS1,
HS1-Hash, HS1-Subkeygen and ChaCha. This sec-
tion describes these subroutines for HS1-SIV-MED
using Python pseudocode. The subroutines in the
pseudocode contain comments about the required in-
puts and provided outputs.
2.1 HS1-SIV-Encrypt
HS1-SIV-Encrypt is the main algorithm which en-
crypts a message using a key, an initialization vector
and associated data. The algorithm uses the HS1 and
HS1-Subkeygen subroutines.
def HS1_SIV_ENCRYPT(K, M, A, N):
# K, a list containing up to 32 bytes
# M, A, a list containing up to 2**64 bytes
# N, a list containing 12 bytes
# T, a list of 16 bytes
# C, a list of len(M) bytes
k = HS1_SUBKEYGEN(K)
A_ = pad(64,A)
M_ = pad(16,M)
A_len = pad(8,[len(A)])
M_len = pad(8,[len(M)])
M_prime = (A_ + M_ + A_len + M_len)
T = HS1(k, M_prime, N, 16)
C_ = HS1(k,T,N,64+len(M))[64:64+len(M)]
C = map(xor, M, C_)
return (T,C)
2.2 HS1-SIV-Decrypt
HS1-SIV-Decrypt is the main algorithm which can
decrypt a cipher-text using a key, an initialization vec-
tor, an authenticator for the associated data and the as-
sociated data itself. The algorithm uses the HS1 and
the HS1-Subkeygen subroutines.
def HS1_SIV_DECRYPT(K, (T,C), A, N):
# K, a list containing up to 32 bytes
# T, a list of 16 bytes
# C, A, a list containing up to 2**64 bytes
# N, a list containing 12 bytes
# M, a list of len(C) bytes
k = HS1_SUBKEYGEN(K)
M_ = HS1(k,T,N,64+len(C))[64:64+len(C)]
M = map(xor, C, M_)
A_ = pad(64, A)
M_ = pad(16, M)
A_len = pad(8, [len(A)])
M_len = pad(8, [len(M)])
M_prime = A_ + M_ + A_len + M_len
T_prime = HS1(k, M_prime, N, 16)
if T == T_prime:
return M
else:
return []
2.3 HS1
HS1 is the algorithm for HS1-SIV’s PRF, it uses four
results from HS1-Hash to supply as a key for ChaCha
(Bernstein, 2008).
def HS1(k, M, N, y):
# k, a list [K_S, k_N, k_P] containing
# K_S, a list of 32 bytes
# k_N, is a list of 28 integers
# k_N, is a list of 4 integers
# M, a list containing any number of bytes
# N, a list containing 12 bytes
# y, an integer
K_S = k[0]
k_N = k[1]
k_P = k[2]
a = []
s = [0x00]*y
for i in range(4):
a += HS1_HASH(k_N[4*i:4*i+16],k_P[i],M)
a = pad(32, a)
key = map(xor, a, K_S)
Y = CHACHA(12, key, 0, N, s)
return Y
2.4 HS1-Hash
HS1-Hash is the subroutine to produce the hash of
a message using several sub-keys produced by HS1-
Subkeygen. It also uses the NH-function in order to
produce NH hashes.
SECRYPT 2016 - International Conference on Security and Cryptography
42

def HS1_HASH(k_N, k_P, M):
# k_N, a list of 16 integers
# k_P, an integer
# M, a list containing any number of bytes
# Y, a list of 8 bytes
n = int(max(math.ceil(len(M)/(64.0)),1))
h = k_P**n
for i in range(n):
M_i = M[i*64:i*64 + 64]
m_i = toInts(4, pad(16,M_i))
a_i =(NH(k_N,m_i)+(len(M_i)%16))%2**60
h += (a_i * k_P ** (n - i - 1))
h %= (2**61-1)
Y = toStr(8,h)
return Y
def NH(v1, v2):
# v1, v2 a list of a multiple of 4 integers
n = min(len(v1), len(v2))
res = 0
for i in range(1, n/4+1):
res += (
((v1[4*i-4]+v2[4*i-4]) % 2**32) *
((v1[4*i-2]+v2[4*i-2]) % 2**32) +
((v1[4*i-3]+v2[4*i-3]) % 2**32) *
((v1[4*i-1]+v2[4*i-1]) % 2**32)
)
return res % 2**64
2.5 HS1-Subkeygen
HS1-Subkeygen is the subroutine to produce the sub-
keys, it uses the ChaCha subroutine.
def HS1_SUBKEYGEN(K):
# K, a list containing up to 32 bytes
# k, a list [K_S, k_N, k_P] containing
# K_S, a list of 32 bytes
# k_N, is a list of 28 integers
# k_N, is a list of 4 integers
K_ = K
while len(K_) < 32:
K_ += K_
K_prime = K_[:32]
N = (
[len(K), 0x00, 0x10, 0x00] +
[0x0c, 0x04, 0x40] + [0x00] * 5
)
T = CHACHA(12, K_prime, 0, N, [0x00]*152)
K_S = T[:32]
k_N = toInts(4,T[32:128])
k_P_ = toInts(8,T[128:152]
m = 2**60
k_P = map(mod, k_P_, [m, m, m, m])
k = (K_S, k_N, k_P)
return k
2.6 ChaCha
ChaCha is HS1-SIV’s stream cipher to encrypt inter-
mediate results. For details on the setState, round
and addStates we encourage the reader to consult
(Nir and Langley, 2015).
def CHACHA(r, K, b, N, M):
# r, b, an integer
# K, a list of 32 bytes
# N, a list of 12 bytes
# M, a list containing any number of bytes
Y = []
n = int(max(math.ceil(len(M)/64.0),1))
for j in range(n):
s = setState(K, N, b)
b += 1
ws = s[:]
for i in range(r/2):
ws = round(ws)
state = addStates(s, ws)
Y += serialize(s)
Y = map(xor,Y[0:len(M)],M)
return Y
3 RELATED WORK
As mentioned in the introduction there is a lot of on-
going research in the area of authenticated encryption
schemes with associated data. There were 57 submit-
ted ciphers in the first round of the CEASAR com-
petition and 29 of them were selected for the second
round. With the beginning of the second round the
focus of research shifted from the analysis of the al-
gorithms in general to the study of hardware and soft-
ware implementations and their optimizations.
In a recent paper (Kotegawa et al., 2016) a number
of hardware implementations of CAESAR candidate
ciphers were optimized and their performance was an-
alyzed. The paper focuses on implementation and op-
timization of four CAESAR candidates, namely AES-
OTR, SILC, AES-COPA and POET. In the results
section we compare the performance of these ciphers
with our performance.
One paper (Morawiecki et al., 2014) presents ICE-
POLE, a high-speed hardware-oriented authenticated
encryption algorithm which also made it to the sec-
ond round of the CAESAR competition. The algo-
rithm was designed initially to be efficient when im-
plemented on hardware. The paper states that the ba-
sic iterative architecture reaches 41 Gbit/s throughput.
The paper describing the API for hardware imple-
mentations (Homsirikamol et al., 2015) also presents
the performance results and API overhead for eight
CAESAR candidates. This presented data will be dis-
cussed in details in the results section.
Although there is a lot of research in the area of
hardware implementations of authenticated encryp-
tion algorithms there are no published results on HS1-
SIV implementations and its optimizations.
FPGA Implementation of HS1-SIV
43
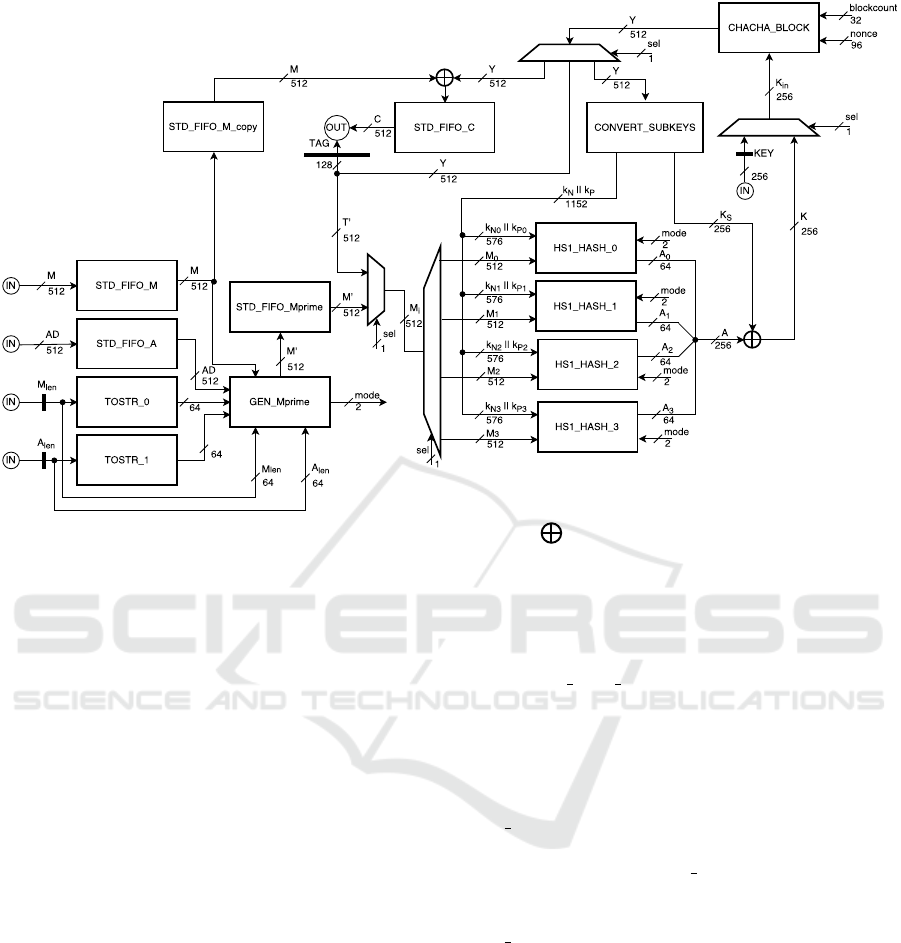
Figure 1: Hardware architecture of HS1-HS1-MED. denotes a bitwise XOR.
4 CONTRIBUTION
The main contribution of this paper is presenting the
first effort to implement HS1-SIV with regular param-
eter settings including an API on a FPGA such that it
can be used as a reference implementation in further
research. To our best knowledge, there are no other
hardware implementations of HS1-SIV yet.
5 DESIGN
This section describes the hardware design of HS1-
SIV-MED. All hardware descriptions are written in
VHSIC Hardware Description Language (VHDL)
and synthesized using Xilinx ISE 14.7.
We implemented HS1-SIV-MED using the hard-
ware architecture illustrated in Figure 1 and a state-
machine. For clarification purposes of this paper, the
figure only illustrates the general outline of the archi-
tecture. That means that the selection signals (sel),
blockcount, nonce and mode signals are controlled
by the state-machine. Also, in the architecture, IN and
OUT denotes that signals communicate through the IO
buffers of HS1-SIV-MED. Apart from these signals
and the standard clock and reset signal, the imple-
mentation acts on an input instruction signal indicat-
ing the kind of data that is on the input, an input signal
indicating encryption or decryption and an output sig-
nal indicating that the encryption or decryption is fin-
ished. The block also contains a generic which speci-
fies the MAX DATA SIZE of either the message/cipher-
text or the associated data which is needed to reserve
memory for the FIFOs.
Upon encryption the state-machine first loads the
message, the associated data, the nonce and the
key, before computing the sub-keys. Then, using
GEN Mprime, the algorithm pads and stores the as-
sociated data, the message and both their lengths
in the Mprime FIFO. GEN Mprime also produces a
mode signal which indicates the amount of data of
the last 64 byte block in Mprime (this is needed for
HS1 HASH). Following, the algorithm computes the
tag using Mprime and stores it in a register. When the
tag is computed, the cipher-text is produced using this
tag and stored in the C FIFO. Finally, the cipher-text
and the tag are ready to be unloaded.
Upon decryption, all previously mentioned inputs
and the tag are loaded before the sub-keys are com-
puted. Then, the cipher-text is being decrypted and
stored in the C FIFO. Following, the tag is being com-
puted using the resulting decrypted cipher-text and
compared to the loaded tag. If the computed tag is
equal to the loaded tag, the resulting decrypted cipher-
text is ready to be unloaded.
The hardware implementation includes five FI-
SECRYPT 2016 - International Conference on Security and Cryptography
44

Figure 2: Hardware architecture of HS1 HASH. v
n−>m
denotes bits n (MSB) to m (LSB) of v where n > m and 0 ≤ n, m < |v|
(if n+m < |v|−1 then v is padded with zeros at the MSB), denotes an addition in GF(2
64
) and denotes a multiplication
in GF(2
128
).
FOs, two TOSTR blocks, a GEN Mprime block, four
HS1 HASH blocks, a CONVERT SUBKEYS block, a
CHACHA BLOCK block, several registers and several
multiplexers. The remaining paragraphs of this sec-
tion describe the hardware architectures of these
blocks in more detail.
5.1 Generate Mprime
GEN Mprime pads the associated data and message up
to respectively 64 bytes and 16 bytes and stores this
in STD FIFO Mprime before concatenating them with
their lengths. The behavior of this block is given in
Formula 1.
M = pad(64, A) || pad(16, M) ||
toStr(8, |A|) || toStr(8, |M|)
(1)
Each clock cycle, 64 bytes are stored into
STD FIFO Mprime.
Because the last message fragment can either be
16 bytes, 32 bytes, 48 bytes or 64 bytes, a mode
signal is generated by the block as an indication for
HS1 HASH.
5.2 HS1 Hash
Figure 2 illustrates the hardware architecture of
HS1 HASH. The HS1 hash block implements the hash-
ing functionality of the cipher. With regular parame-
ter settings for HS1-SIV, HS1 hash acts on message
fragments of 64 bytes up to the last message frag-
ment. Hence, our input message length for the HS1
hash block is 64 bytes. The last message fragment can
either be 16 bytes, 32 bytes, 48 bytes or 64 bytes. De-
pending on which of these four modes the HS1 hash
block operates, the results of the NH function blocks
are added up.
Also note that the HS1 hash block modifies the in-
termediate result h on each clock/input until the block
is being reset again.
Figure 3: Hardware architecture of the NH (4x4) func-
tion. v
n−>m
denotes bits n (MSB) to m (LSB) of v where
n > m and 0 ≤ n, m < n
max
, m
max
, denotes an addition
in GF(2
32
) and denotes a multiplication in GF(2
64
).
5.2.1 NH Function
Figure 3 shows the hardware architecture of NH 4x4.
Because there are four different message fragment
lengths, it is convenient to split the NH function block
into four blocks that each act on two vectors of four
4-byte integers (NH 4x4). Depending on the mode of
HS1 hash, the result of all four, the first three or the
first two NH function blocks are added up and re-
turned or the result of the first NH function block is
returned.
FPGA Implementation of HS1-SIV
45
5.3 Convert Subkeys
The convert sub-keys block is needed to convert the
ChaCha output into usable sub-keys. For this, the im-
plementation uses a block to convert the streams into
4-byte little-endian integers (for kN) and 8-byte little-
endian integers (for kP).
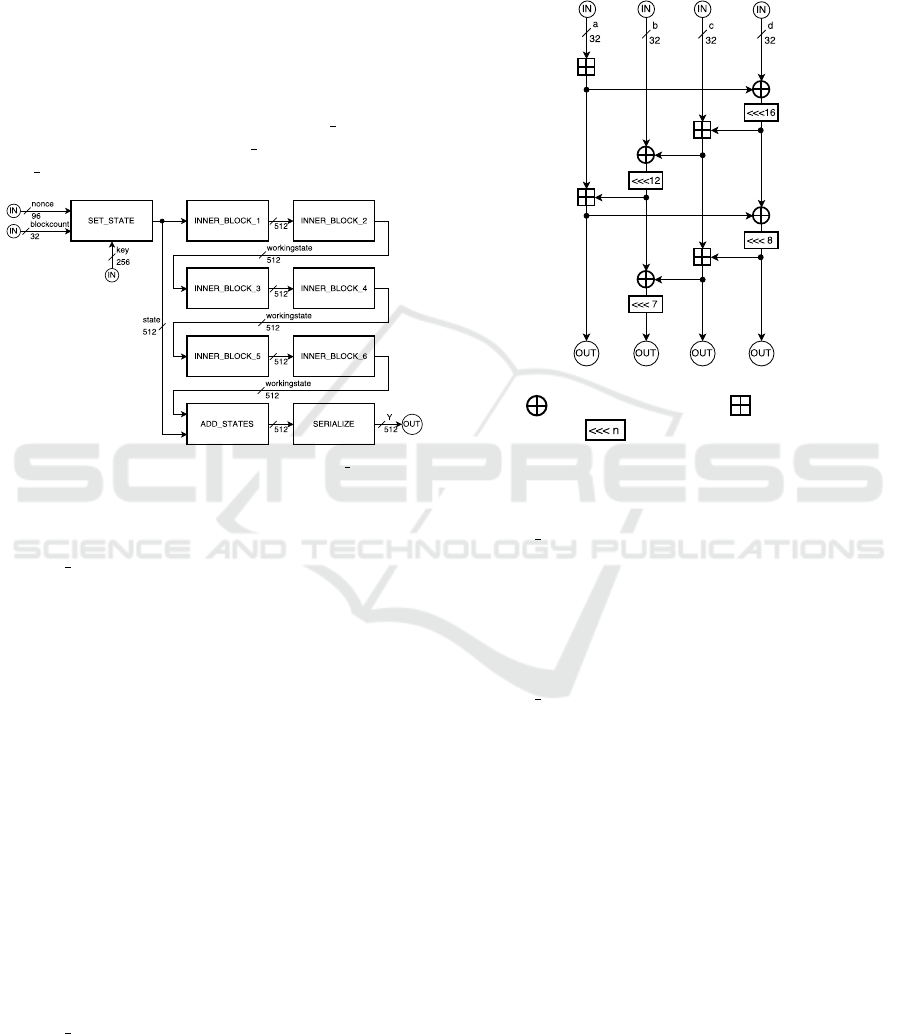
5.4 ChaCha Block
The hardware architecture of the ChaCha block
is illustrated in Figure 4. CHACHA
BLOCK has
four different sub-blocks, SET STATE, INNERBLOCK,
ADD STATES and SERIALIZE.
Figure 4: Hardware architecture of CHACHA BLOCK.
5.4.1 Setstate
CHACHA SETSTATE rewires the key, block-count and
nonce into a signal of 512 bits that represents the
ChaCha state. This 512-bit state is composed of 16
words of 32 bit long. The ChaCha state is initialized
as follows:
• The first four words (indexed 0-3) are con-
stants: 0x61707865, 0x3320646e, 0x79622d32,
0x6b206574.
• The next eight words (indexed 4-11) are taken
from the 256-bit key by reading the bytes in little-
endian order, in 4-byte chunks.
• Word 12 is a block counter.
• Words 13-15 are a nonce. The 13th word is the
first 32 bits of the input nonce taken as a little-
endian integer, while the 15th word is the last 32
bits.
5.4.2 Innerblock
CHACHA INNERBLOCK contains the logic for two
ChaCha rounds. As a result, the ChaCha block
contains six of these blocks (HS1-SIV-MED has 12
ChaCha rounds). The inner block contains four
quarter-round blocks that represent the ‘column’
ChaCha round and four quarter-round blocks that rep-
resent the ‘diagonal’ ChaCha round. The architecture
of the quarter-round is depicted in Figure 5. Here, de-
pending on the round, a, b, c and d are 32-bit words
drawn from the ChaCha state.
Figure 5: Hardware architecture of the ChaCha quarter-
round. denotes a bitwise XOR, denotes an addition
in GF(2
64
) and denotes a left-rotation over n bits.
5.4.3 Addstates
CHACHA ADDSTATES contains the logic to add the
working state to the current state. For this, the in-
put words are added up with the output words from
the working state.
5.4.4 Serialize
CHACHA SERIALIZE contains the logic to return the
serialized output of the ChaCha block. For this, the
words are sequenced one-by-one in little-endian or-
der.
6 RESULTS
This section describes the analysis of the performance
of HS1-SIV-MED’s AEAD-core. Table 1 shows the
performance results of HS1-SIV-MED’s AEAD-core
using Xilinx XST High Level Synthesis (HLS) on a
Virtex-7 device. These results have been achieved by
restricting the use of Block RAM and DSP. Moreover,
the optimization goal is set on Area and the optimiza-
tion effort on Normal. The key length was fixed to
32 bytes. We found out that the area overhead of
the AEAD-core is between 8% (8-byte data length)
SECRYPT 2016 - International Conference on Security and Cryptography
46
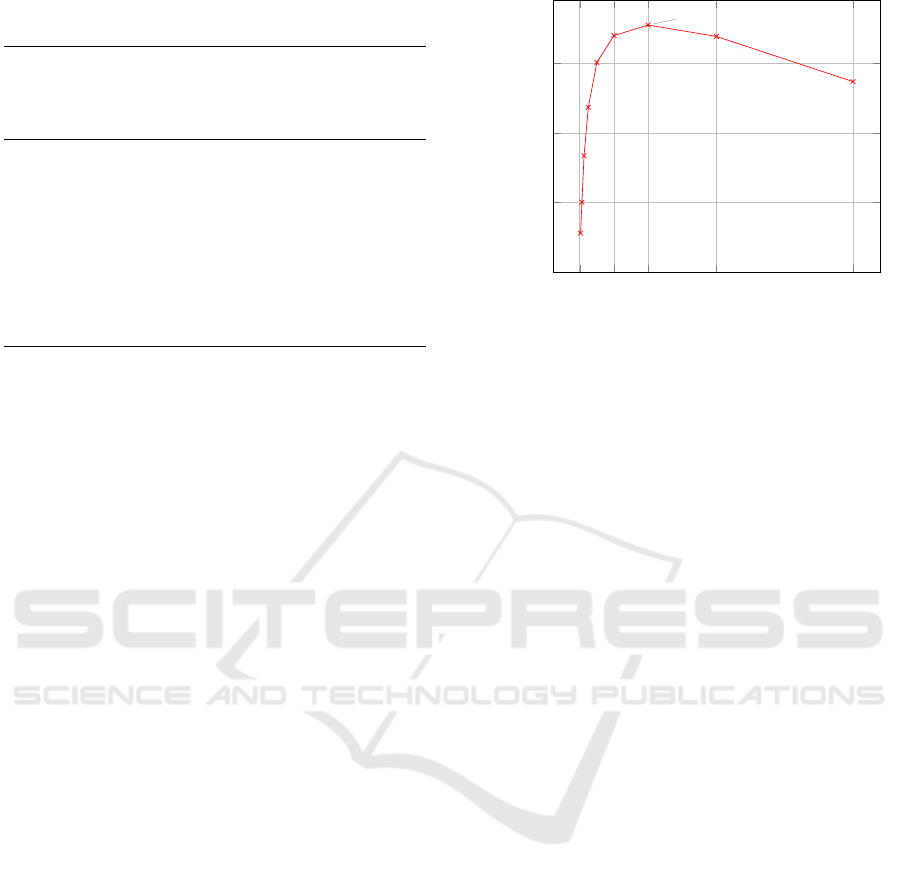
Table 1: Performance results of HS1-SIV-MED’s AEAD-
core using Xilinx XST HLS on a Virtex-7 device.
Data Area Throughput Throughput
length [LUT] [Mbit/s] /Area
[bytes] [(Kbit/s)
/LUT]
8 100,397 28.039 0.279
16 100,925 50.539 0.501
32 101,004 84.406 0.836
64 103,214 122.200 1.184
128 103,967 156.697 1.507
256 107,325 182.449 1.700
512 111,919 198.784 1.776
1024 122,813 208.100 1.694
2048 155,666 213.093 1.369
and 15% (2048-byte data length) in comparison to the
cipher-core.
In the table, Data length corresponds to both the
length of the associated data as well as the length of
the message. The difference in area is mainly because
of the memory that needs to be reserved for the FI-
FOs.
The performance results of the throughput-to-area
ratio is also given in Figure 6. This figure shows that
the optimal data length is at 512 bits. At 512 bits, the
AEAD-core has a throughput of 198.784 Mbit/s, an
area of 111,919 LUTs and an throughput-to-area ratio
of 1.776 (Kbit/s)/LUT. In comparison to the ATHENa
Database of Results (Cryptographic Engineering Re-
search Group (CERG) at GMU, 2016), the perfor-
mance of this hardware implementation of HS1-SIV-
MED is not as good as some other ciphers. For ex-
ample, the area required by the HS1-SIV-MED im-
plementation takes over 8 times more than the AES-
COPA implementation.
The performance results of AES-OTR, SILC,
AES-COPA and POET high level synthesis is pre-
sented in the paper (Kotegawa et al., 2016) with op-
timization goal on Area are 122 Mbit/s, 126 Mbit/s,
117 Mbit/s and 124 Mbit/s respectively. It is clear
to see that our implementation of HS1-SIV outper-
forms all of those implementation in throughput. Un-
fortunately, direct comparison of the area that is being
used by the ciphers to the area that is being used by
HS1-SIV is not possible because the paper presents
the area of the ciphers in logic slices whereas the HS1-
SIV area is measured in LUTs. The ICEPOLE cipher
(Morawiecki et al., 2014) basic iterative implementa-
tion achieved 41 Gbit/s throughput on FPGA Virtex-
6 without usage of any dedicated resources such as
Block RAM or DSP. The presented performance re-
sults are much higher than other published results on
hardware implementation performances of CAESAR
0
256
512
1,024 2,048
0
0.5
1
1.5
(512, 1.776)
Data length in bytes
Throughput/Area in (Kbit/s)/LUT
Figure 6: Performance results of the throughput-to-area ra-
tio of HS1-SIV-MED’s AEAD-core using Xilinx XST HLS
on a Virtex-7 device.
candidates. It is not possible to compare performance
results of ICEPOLE and HS1-SIV because the ICE-
POLE implementation presented in the paper does not
include an API which highly likely will cause some
overhead. Despite the fact it is obvious that ICE-
POLE cipher has higher throughput by a few orders of
magnitude. One of the reasons only moderate perfor-
mance results of HS1-SIV are achieved in comparison
to the ICEPOLE cipher is that the design of HS1-SIV
was optimized to be efficient running on x86 archi-
tecture and other 32-bit platforms, whereas ICEPOLE
was initially designed to provide a high throughput on
hardware. A larger area required for the implementa-
tion of HS1-SIV can be explained by the bigger input
sizes of the message and the nonce. For instance, the
ICEPOLE cipher takes 128-bit inputs whereas HS1-
SIV operates on 64-byte long blocks.
7 FUTURE WORK
We have seen that the cipher uses quite a lot of FPGA
resources. Although we have not focused on opti-
mizing the implementation, we think that this is also
an unfortunate characteristic of HS1-SIV. Future im-
provements that focus on optimizing the operations
and the number of instructions should confirm this
prediction. The paper proposed by At et al. (At et al.,
2014) provides a good basis for optimizing ChaCha.
Also, our paper only describes the hardware im-
plementation of HS1-SIV with regular parameter set-
tings, different parameter settings will have different
results. For HS1-SIV on high parameter settings, in
general, the intermediate keys get larger and more
ChaCha rounds need to be executed. On the other
hand, HS1-SIV on low parameter settings requires
FPGA Implementation of HS1-SIV
47

less ChaCha rounds and uses smaller intermediate
keys.
Another possible future improvement is to sim-
plify the implemented architecture. Now, the AEAD-
core does not contain a pre- and post-processor,
meaning that upon unloading the results, no new data
can be loaded. Also, the HS1-HASH function in-
cludes four blocks which in our implementation are
executed in parallel. Each HS1 HASH block requires
approximately 1500 LUTs, thus a serial computa-
tion of these blocks might decrease the area by up to
4500 LUTs. The same holds for the NH 4x4 blocks
in HS1 HASH, the INNER BLOCK blocks in ChaCha and
the quarter-rounds in ChaCha’s INNER BLOCK.
Finally, the state-machines in both the AEAD-
core as well as the cipher-core are very large, a fu-
ture study towards a new hardware architecture with
a reduced number of states could reveal whether the
overall performance can be optimized.
8 CONCLUSIONS
In this paper, we have presented the first effort to im-
plement HS1-SIV with regular parameter settings in-
cluding the API on hardware. With this hardware im-
plementation, the requirement of the second round of
the CAESAR competition has been met for HS1-SIV.
Future improvements, analysis and study should indi-
cate whether HS1-SIV on hardware provides enough
security, applicability and robustness.
ACKNOWLEDGMENTS
We would like to thank Ted Krovetz for answering our
questions regarding HS1-SIV. Also, our thanks go out
to Antonio de la Piedra and Kostas Papagiannopoulos
for their support and technical expertise.
REFERENCES
At, N., Beuchat, J.-L., Okamoto, E., San, I., and Yamazaki,
T. (2014). Compact Hardware Implementations of
ChaCha, BLAKE, Threefish, and Skein on FPGA.
Circuits and Systems I: Regular Papers, IEEE Trans-
actions on, 61(2):485–498.
Babbage, S., Canniere, C., Canteaut, A., Cid, C., Gilbert,
H., Johansson, T., Parker, M., Preneel, B., Rijmen, V.,
and Robshaw, M. (2008). The eSTREAM portfolio.
eSTREAM, ECRYPT Stream Cipher Project.
Bernstein, D. J. (2008). ChaCha, a variant of Salsa20. In
Workshop Record of SASC: The State of the Art of
Stream Ciphers, volume 8.
Bernstein, D. J. (2016). CAESAR: Competition for Au-
thenticated Encryption: Security, Applicability, and
Robustness. http://competitions.cr.yp.to/caesar.html.
Bertoni, G., Daemen, J., Peeters, M., and Van Assche, G.
(2011). The keccak sha-3 submission. Submission to
NIST (Round 3), 6(7):16.
Biryukov, A., Dinu, D.-D., and Khovratovich, D. (2015).
Argon and Argon2.
Cryptographic Engineering Research Group (CERG)
at GMU (2016). ATHENa Database of Results.
https://cryptography.gmu.edu/athenadb/fpga auth cip
her/rankings view.
Daemen, J. and Rijmen, V. (1999). AES proposal: Rijndael.
Homsirikamol, E., Diehl, W., Ferozpuri, A., Farahmand, F.,
Sharif, M. U., and Gaj, K. (2015). GMU Hardware
API for Authenticated Ciphers. Cryptology ePrint
Archive, Report 2015/669. http://eprint.iacr.org/.
Kotegawa, M., Iwai, K., Tanaka, H., and Kurokawa, T.
(2016). Optimization of hardware implementations
with high-level synthesis of authenticated encryption.
Bulletin of Networking, Computing, Systems, and
Software, 5(1):26–33.
Krovetz, T. (2014). HS1-SIV (v2). CAESAR 2nd Round,
competitions.cr.yp.to/round2/hs1sivv2.pdf.
Morawiecki, P., Gaj, K., Homsirikamol, E., Matusiewicz,
K., Pieprzyk, J., Rogawski, M., Srebrny, M., and
W
´
ojcik, M. (2014). Icepole: high-speed, hardware-
oriented authenticated encryption. In Cryptographic
Hardware and Embedded Systems–CHES 2014, pages
392–413. Springer.
Nir, Y. and Langley, A. (2015). ChaCha20 and Poly1305
for IETF Protocols. Technical report, RFC 7539,
DOI 10.17487/RFC7539, May 2015, http://www. rfc-
editor. org/info/rfc7539.
Rogaway, P. and Shrimpton, T. (2007). Deterministic
Authenticated-Encryption A Provable-Security Treat-
ment of the Key-Wrap Problem.
SECRYPT 2016 - International Conference on Security and Cryptography
48
