Control of Uncertain Robot Manipulators using Integral Backstepping

and Time Delay Estimation

Yassine Kali

, Maarouf Saad

, Khalid Benjelloun

and Mohammed Benbrahim

Ecole Mohammadia d’Ingenieurs, Mohammed V University, Rabat, Morocco

Ecole de Technologie Superieure, Quebec University, Montreal, Canada

Sciences Faculty, SMBA University, Fez, Morocco

Keywords:

Integral Backstepping, Time Delay Control, Trajectory Tracking, Robot Manipulators.

Abstract:

In this paper, a novel controller is proposed and applied for high accuracy tracking trajectory in the workspace

of robot manipulators in presence of uncertainties and external disturbances. Most of nonlinear controllers are

based on the mathematical model of robot manipulator, but a lot of robotic systems do not have exact model.

This novel approach which consists on designing an Integral Backstepping with Time Delay Control (IBTDC)

can estimate uncertainties and keep high tracking performance. The proposed controller is able to stabilize

the robot system, and also to drive the trajectory tracking errors to converge in ﬁnite time. Furthermore,

experimental results are given to illustrate the effectiveness of the proposed method applied to the 7-DOF

ANAT robot arm.

1 INTRODUCTION

Control of robot manipulators, has received wide at-

tention and is a topic of great research interest. These

research works have focused on tracking control prob-

lems in the joint and task space. In literature, we can

ﬁnd many nonlinear techniques such as Sliding Mode

Control (SMC) (Utkin et al., 1999), Feedback Lin-

earization (Park and Cho, 2007), Backstepping (H.-

J.Shieh and C.-H.Hsu, 2008). However, the robot

manipulators are uncertain Multiple-Input Multiple-

Output (MIMO). They suffer from the plant uncer-

tainties due to uncertain parameters, load variations

and external disturbances, which may seriously de-

grade the performance of the tracking control and/or

deteriorate the controlled system.

The backstepping approach is a recursive Lya-

punov procedure, proposed in the beginning of 1990s.

This approach was introduced ﬁrst in (P.V. Kokotovic,

1995). The basic idea of this technique is to design a

controller by selecting appropriate stabilization func-

tions for some state variables chosen as virtual con-

trols (Slotine and Li, 1991; Lewis et al., 1993). This

allows, in addition to the control objective for which

the technique is developed (tracking and/or stabiliza-

tion), to ensure, at all times, the stability of the con-

trolled system. Therefore, Backstepping provides ro-

bust and high-accuracy solutions. However, one main

restriction remains. Nonlinear backstepping is sensi-

tive to uncertainties and external disturbances, other-

wise, the control may easily cause unacceptable prac-

tical complications.

To cope with the aforementioned problem, some

works proposed adaptive backstepping (H.-J.Shieh

and C.-H.Hsu, 2008; Zhou and Wen, 2008) which

provide an adaptation of the control to be sufﬁciently

robust to eliminate the effect of uncertain nonlinear

dynamics and unexpected disturbances but this over-

parametrization may cause inequality of the num-

ber of parameter estimates and the number of un-

known parameters. Other works proposed a combi-

nation of backstepping and intelligent control tech-

niques (neural-network or fuzzy logic) (Jagannathan

and Lewis, 1998; Weisheng et al., 2015; Yoo and

Ham, 2000; Su et al., 2015). These controllers have

the merit to estimate uncertain dynamics and unex-

pected disturbances but they introduce fuzzy rules in

case of fuzzy logic or a large number of parameters

in case of neural-network that may make implemen-

tation impossible.

A possible solution to consider is a combination

of Integral Backstepping (Tan et al., 2000; Skjetne

and Fossen, 2004) and Time Delay Control (TDC)

Kali, Y., Saad, M., Benjelloun, K. and Benbrahim, M.

Control of Uncertain Robot Manipulators using Integral Backstepping and Time Delay Estimation.

DOI: 10.5220/0005950201450151

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 145-151

ISBN: 978-989-758-198-4

145

(Youcef-Toumi and Ito, 1990; Hsia and Gao, 1990).

TDC can estimate unknown dynamics and exter-

nal disturbances simply and effectively using time-

delayed information provided from control inputs sig-

nals and the states variables without a prior exact

knowledge of robot model. When the TDC is applied,

a so-called TDE error appear that can be reduced us-

ing integral backstepping, else, the system will lead

with a large steady state error. As a consequence it

can be expected that the system can be stabilized even

in presence of uncertainties and external disturbances.

The paper is organized in ﬁve sections. In Section

2, the dynamics of serial n-link rigid robot manip-

ulators is presented with sufﬁcient property and as-

sumptions. In Section 3, the design of the controller

called integral backstepping with time delay control

is described with stability analysis using Lyapunov

function. In Section 4, experimental results of the

proposed method applied to the 7-DOF ANAT robot

are presented and comparison with nonlinear back-

stepping and Sliding Mode with Time Delay Con-

trol (SMTDC) is discussed. Finally, the conclusion

is drawn in section 5.

2 PROBLEM FORMULATION

The dynamic model expressed in joint space coor-

dinates according to the Lagrange theory of n-joint

robot manipulator is given by:

M(q) ¨q+C(q, ˙q) ˙q+ G(q) + F( ˙q) − τ

= τ (1)

where q ∈ R

, ˙q ∈ R

and ¨q ∈ R

are the joint po-

sitions, velocities and accelerations vectors, respec-

tively, M(q) ∈ R

n×n

is the symmetric positive-deﬁnite

inertia matrix, C(q, ˙q) ˙q ∈ R

is the centrifugal and

Coriolis vector, G(q) ∈ R

is the gravitational vec-

tor, F( ˙q) ∈ R

is the viscous/static friction torque at

the joints vector, τ

∈ R

denotes disturbance vector

and τ ∈ R

is the torque input vector. The inertia ma-

trix can be written into two parts, without loss of any

generality:

M(q) = M

(q) + ∆M(q) (2)

where M

(q) is the nominal part while ∆M(q) denotes

the uncertain part. Then, we can rewrite the model

given in Eq.1 as:

(q) ¨q+ H(q, ˙q, ¨q) = τ (3)

where

H(q, ˙q, ¨q) = ∆M(q) ¨q+C(q, ˙q) ˙q+ G(q) + F( ˙q) − τ

For ease of control design, let’s denote M

= M

(q)

and H = H(q, ˙q, ¨q).

The objective in this paper is to design a robust

controller able to ensure that the joint position q tracks

a desired trajectory q

with high accuracy even if the

dynamics is uncertain and in presence of external dis-

turbances. To this end, we will design the controller

and carry out its stability analysis based on the fol-

lowing property and assumptions:

• Property 1. The nominal part of inertia ma-

trix M

(q) is positive-deﬁnite symmetrical and

bounded such that:

I ≤ M

(q) ≤ m

where m

and m

are two known positive con-

stants (Spong et al., 2005).

• Assumption 1. The joint position states and its

ﬁrst time derivative are measurable.

• Assumption 2. H is a globally lipschitz function.

3 IBTDC

3.1 Controller Design

For the development of this method, we consider the

robot system given by Eq.3. As said before, the con-

trol objective is to track a desired trajectory with high

accuracy even in the presence of nonlinear unknown

dynamics and external disturbancesby designing a ro-

bust control. The closed-loop system is represented in

Fig.1.

Figure 1: Block diagram of the proposed controller.

For the development of IBTDC, we deﬁne the po-

sition tracking error e:

e = q− q

(4)

where q

∈ R

is the desired position trajectory vec-

tor. Now, let’s select the regulated variable ε

as fol-

lows:

= e + λ

edt (5)

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

146

where λ = diag(λ

) for i = 1,· ·· ,n is a positive con-

stant gain matrix. Its time derivative is:

= ˙e+ λe

= ˙q− ˙q

+ λe (6)

Choosing ˙q as virtual control variable, we select the

following stabilizing function as:

= ˙q

− λe− K

(7)

where K

= diag(k

) for i = 1,· ·· , n is a positivecon-

stant diagonal gain matrix that are in direct relation

with the convergence rate. Deﬁning now the error

obtained by the difference between the stabilizing

function and virtual control in Eq.6 as:

= ˙q− α

= ˙q− ˙q

+ λe+ K

+ K

(8)

Thus in terms of Eq.8, we can rewrite Eq.6 as follows:

= ε

− K

(9)

Therefore, differentiating Eq.8 with respect to time

leads to:

= ¨q−

= ¨q− ¨q

+ λ˙e+ K

= M

−1

[τ− H] − ¨q

+ λ˙e+ K

(10)

According to the Lyapunov stability analysis, we

choose:

= −K

− ε

(11)

where K

= diag(k

) for i = 1,· ·· , n is a positivecon-

stant diagonal gain matrix. Then, we obtain:

τ = M

u+ H (12)

where u = ¨q

− λ˙e− K

− K

− ε

The control performance is affected since H is un-

certain. Then, if Assumption 2 given in Section 2 is

veriﬁed we can estimate H(t) using a TDE (Youcef-

Toumi and Ito, 1990; Hsia and Gao, 1990) as:

H(t)

∼

H(t − L)

= τ(t − L) − M

(t − L) ¨q(t − L) (13)

where L is the estimation time delay. Clearly the ac-

curacy of

H(t) improves as L decreases. In practice,

the smallest estimation time delay L is chosen to be

the sampling period which means that the unknown

dynamics are identiﬁed every L times. Then, the pro-

posed integral backstepping with time delay control is

obtained as:

τ = M

= τ(t − L) − M

(t − L) ¨q(t − L) + M

u (14)

As ¨q(t − L) may not be at our disposal, we use:

¨q(t − L) =

(q(t) − 2q(t − L) + q(t − 2L)).

3.2 Stability Analysis

To prove the stability of the overall system, the fol-

lowing Lyapunov function candidate is used:

V =



+ ε



(15)

Taking time derivative gives:

V = ε

+ ε

= ε

(ε

− K

)

+ε



−1

[τ− H] − ¨q

+ λ ˙e+K



= −ε

+ ε

+ε



−1

[τ− H] − ¨q

+ λ ˙e+K



(16)

Using Property 1 given in Section 2 and replacing

the IBTDC given in Eq.14 in the Lyapunov function

derivative given in Eq. 16, we obtain:

V = −ε

+ ε

− ε

+ε



−1

[

H − H] − K



= −ε

+ ε



−1

∆H − K



≤ −ε

− ε

+ ε

∆H

≤

∑

i=1

−k

− |ε



|ε

| −

|∆H



(17)

where ∆H =

H − H is the TDE error and I

∈ R

n×n

denotes the identity matrix. To ensure

V is a negative-

deﬁnite function, the following condition must be ful-

ﬁlled:

|∆H

||ε

−1

(18)

Otherwise, using Assumption 2, we have:

|∆H

| = |

− H

= |H

(t − L) − H

(t)|

≤ l

|(t − L) − (t)|

≤ l

L (19)

where l

> 0 is the Lipschitz constant. Then, the con-

dition given in Eq. (18) becomes:

|ε

−1

(20)

Therefore, the Lyapunov function derivative is

negative deﬁnite

V < 0, i.e, the error e and its deriva-

tives go to zero, hence the stability of the closed loop

system is proven.

Control of Uncertain Robot Manipulators using Integral Backstepping and Time Delay Estimation

147

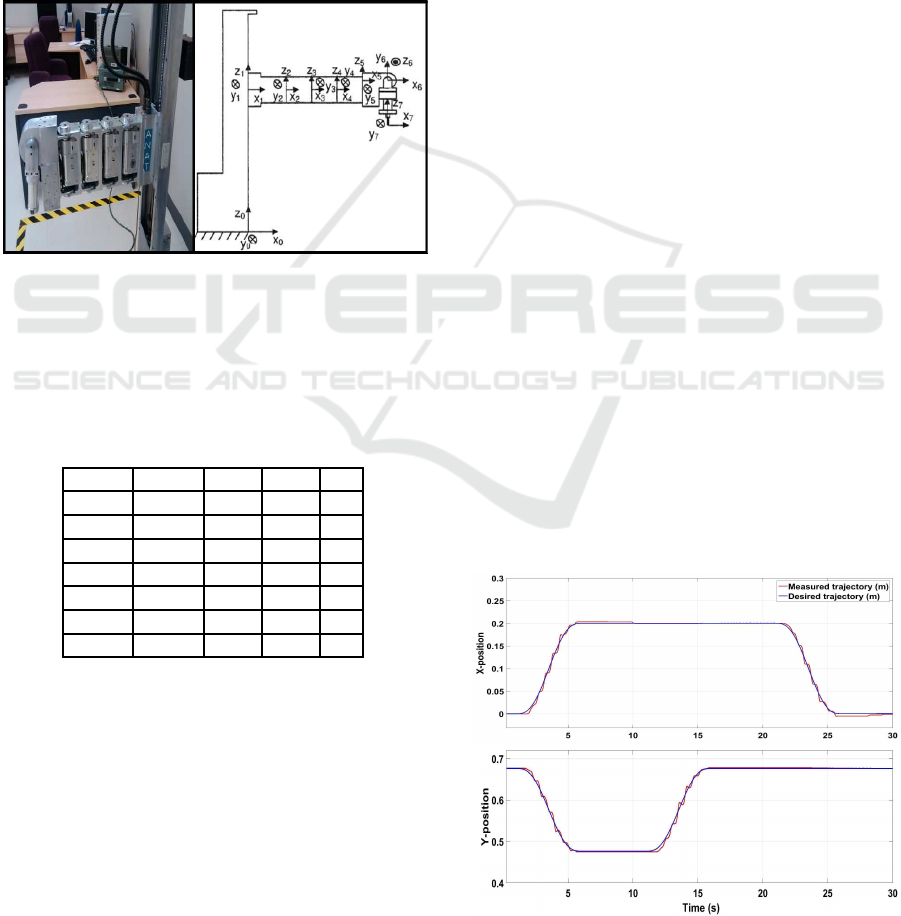
4 CASE STUDY

To illustrate the effectiveness of the proposed con-

troller, the IBTDC is implemented on the ANAT robot

shown in Fig.2 using Simulink with Real-Time Work-

shop (RTW). ANAT robot is a 7-DOF hyper redun-

dant articulated nimble adaptable trunk: the ﬁrst joint

is prismatic (joint 1), followed by three redundant ro-

tational joints (joints 2, 3, and 4) and ﬁnally three ro-

tational joints (joints 5, 6, and 7), the end-effector is

mounted on the last joint (Fareh et al., 2012). For sim-

plicity, three joints are locked during the experimental

tests (joints 1, 6 and 7).

Figure 2: ANAT robot arm and D-H frames.

For the ANAT robot, modiﬁed Denavit-

Hartenberg (D-H) convention (Dombre and Khalil,

2007) is used for selecting frames of references as

shown in Fig.2. The D-H parameters of the ANAT

robot are given in Tab.1.

Table 1: D-H parameters of 7-DOF ANAT robot.

Joints α

i−1

1 0 0 q

2 0 L

0 q

3 0 L

0 q

4 0 L

0 q

5 0 L

6 π/2 L

0 q

7 −π/2 0 −L

The initial position of the end-effector in task

space is x(0) = [0.6764 0 − 0.196] while the ini-

tial joint positions and joint velocities are 0 rad and

0 rad/sec, respectively. The objective here is to fol-

low a desired triangle deﬁned in XY plane of the task

space of the ANAT robot. For our robot, assuming

that the desired trajectory is away from singular con-

ﬁguration, the desired accelerations in joint space and

the desired accelerations and velocities in task space

are linked by:

¨q

= J

¨x

− J

˙x

(21)

where J denotes the Jacobian matrix, J

= J

(JJ

)

−1

denotes the generalized inverse, ¨q

is the desired joint

acceleration vector, ¨x

is the desired workspace ac-

celeration vector, ˙x

is the desired workspace velocity

vector. The desired joint velocity ˙q

is obtained from

desired joint acceleration using an integrator while the

desired joint position q

is obtained from desired joint

velocity using another integrator.

During the experiment, we placed a load of 2.25kg

on the 5

joint at t = 10s. In addition, a disturbances

was added to the torque input representing 10% of

maximum value of the torque as:







0.15e

−5(t−5)

sin(2πt)

0.15e

−5(t−5)

sin(3πt)

0.03e

−13(t−13)

sin(4πt)

0.025e

−18(t−18)

sin(5πt)







In Section 3, the development of IBTDC for un-

certain robot manipulators is given in Eq.14 where

the controller gains are tuned to achieve the optimal

performance such as the stability is guaranteed and

the condition given in Eq (20) is veriﬁed: λ = 5 ∗ I

= 5∗ I

and K

= 7∗ I

. The estimation time delay

is selected as the smallest sampling period L = T

0.03s.

4.1 Experimental Results

The experimental results are shown in Fig.3 to Fig.7:

workspace tracking, joint space tracking, joint space

tracking error and control torque input obtained by us-

ing the proposed integral backstepping with time de-

lay controller.

It is obvious that the proposed controller ensures

good tracking trajectory even in presence of uncer-

Figure 3: Workspace tracking trajectory.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

148

Figure 4: Workspace tracking error.

Figure 5: Joint space tracking trajectory.

tainties as shown in Fig.5 and conﬁrmed by the small

tracking errors as depicted in Fig.6. In addition, using

the direct kinematics, we can notice that the controller

ensures also a good tracking in task space as shown

in Fig.3 and Fig.4. However, using integral backstep-

ping cause a small overshoot. From Fig.7, we observe

Figure 6: Joint space tracking error.

that the control inputs evolves continuously with ac-

ceptable values for the motors of the ANAT robot.

To show the effectiveness of the proposed IBTDC,

it is compared with the nonlinear backstepping (Zhou

and Wen, 2008) and the SMTDC (?) in terms of

energy and stability by using the root-mean-squared

(RMS) errors and torque inputs as:

kτk

RMS

∑

kτ(k)k

, kek

RMS

∑

ke(k)k

where N denotes the number of sampling steps of

the experimentation. the quantitative analysis is pre-

sented in Tab.2

Table 2: Controllers comparison.

Controller kτk

RMS

kek

RMS

Backstepping 1.72 4.9∗ 10

−2

SMTDC 1.31 2.75∗ 10

−2

IBTDC 1.253 9.8∗ 10

−3

From the above comparison, we can notice that

IBTDC stabilizes the system even in presence of un-

Control of Uncertain Robot Manipulators using Integral Backstepping and Time Delay Estimation

149

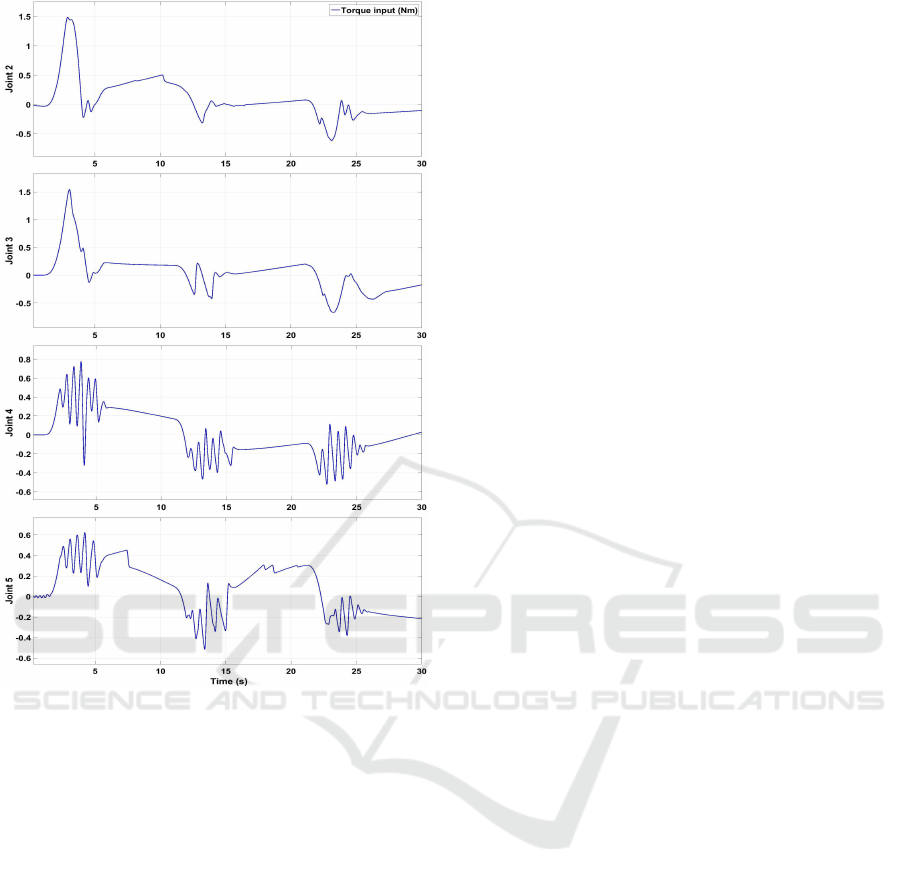
Figure 7: Control torque input.

certainties and external disturbances in ﬁnite time

with the best tracking and less energy.

5 CONCLUSIONS

For a class of uncertain n-link robot systems, an inte-

gral backstepping with time delay controller which is

a combination of integral backstepping and TDC, is

presented. TDC is used to estimate uncertain nonlin-

ear dynamics and to cancel the effect of external dis-

turbances while integral backstepping is used to elim-

inate the TDE error. Experimental results on the 7-

DOF ANAT robot showed the merit of IBTDC, par-

ticularly regarding the uncertain dynamics, external

disturbances and ﬁnite time convergence. Otherwise,

using integral backstepping may cause a large over-

shoot known as windup phenomenon. Further re-

search should be pursued in the direction to overcome

this phenomenon. We will also implement the pro-

posed controller on other nonlinear systems.

ACKNOWLEDGEMENTS

This work was supported in part by Automatic and In-

dustrial Informatics Laboratory, Ecole Mohammadia

d’Ingenieurs, Mohammed V University, Rabat, Mo-

rocco and Ecole de technologie superieure, Montreal,

Canada.

REFERENCES

Dombre, E. and Khalil, W. (2007). Modeling, Performance

Analysis and Control of Robot Manipulators. Wiley-

ISTE.

Fareh, R., Saad, M., and Saad, M. (2012). Workspace track-

ing trajectory for 7-dof anat robot using a hierarchi-

cal control strategy. In 20th Mediterranean Confer-

ence on Control and Automation, July 3-6. p. 122-127.

Barcelona, Spain.

H.-J.Shieh and C.-H.Hsu (2008). An adaptive

approximator-based backstepping control approach

for piezoactuator-driven stages. IEEE Transactions

On Industrial Electronics, 55:1729–1738.

Hsia, T. and Gao, L. (1990). Robot manipulator control

using decentralized linear time-invariant time-delayed

joint controllers. IEEE International Conference on

Robotics and Automation, 3:2070–2075.

Jagannathan, S. and Lewis, F. (1998). Robust backstep-

ping control of robotic systems using neural networks.

Journal of Intelligent and Robotic Systems, 23:105–

128.

Lewis, F., Abdallah, C., and Dawson, D. (1993). Control

of Robot Manipulators. Macmillan Publishing Com-

pany.

Park, C.-W. and Cho, Y.-W. (2007). Robust fuzzy feed-

back linearization controllers for takagi sugeno fuzzy

models with parametric uncertainties. Control Theory

Appl., IET, 1:1242–1254.

P.V. Kokotovic, M. Krstic, I. K. (1995). Nonlinear and adap-

tive control design. In Wiley, New York.

Skjetne, R. and Fossen, T. (2004). On integral control in

backstepping: Analysis of different techniques. In

Proceedings of the 2004 American Control Confer-

ence, Boston, Massachusetts.

Slotine, J. and Li, W. (1991). Applied nonlinear control.

Printice-Hall international.

Spong, M., Hutchinson, S., and Vidyasagar, M. (2005).

Robot Modeling and Control. John Wiley and Sons,

Inc.

Su, C.-Y., Li, G., Li, Z., and Su, H. (2015). Fuzzy

approximation-based adaptive backstepping control

of an exoskeleton for human upper limbs. IEEE Trans-

actions on Fuzzy Systems, 23:555–566.

Tan, Y., Chang, J., Tan, H., and Jun, H. (2000). Integral

backstepping control and experimental implementa-

tion for motion system. In IEEE International Con-

ference on Control Applications, Anchorage, AK.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

150

Utkin, V., Guldner, J., and Shi, J. (1999). Sliding mode

control in electromechanical systems. Taylor-Francis.

Weisheng, C., Ge, S., Jian, W., and Maoguo, G. (2015).

Globally stable adaptive backstepping neural network

control for uncertain strict-feedback systems with

tracking accuracy known a priori. IEEE Transactions

on Neural Networks and Learning Systems, 26:1842–

1854.

Yoo, B. K. and Ham, W. C. (2000). Adaptive control of

robot manipulator using fuzzy compensator. IEEE

Transactions on Fuzzy Systems, 8:186–199.

Youcef-Toumi, K. and Ito, O. (1990). A time delay con-

troller for systems with unknown dynamics. ASME

Journal of Dynamic System, Measurement ans Con-

trol, 112:133–141.

Zhou, J. and Wen, C. (2008). Adaptive Backstepping Con-

trol of Uncertain Systems. Springer.

Control of Uncertain Robot Manipulators using Integral Backstepping and Time Delay Estimation

151