Hardware Accelerator for Stream Cipher Spritz

Debjyoti Bhattacharjee and Anupam Chattopadhyay

School of Computer Science and Engineering, Nanyang Technological University, Singapore, Singapore

Keywords:

Stream Cipher, Hardware Accelerator, Spritz.

Abstract:

RC4, the dominant stream cipher in e-commerce and communication protocols such as, WEP, TLS, is being

considered for replacement due to the series of vulnerabilities that have been pointed out in recent past. After

a thorough analysis of the possible weaknesses, Spritz, a new stream cipher is proposed to that effect by

the author of RC4. The design of Spritz is based on Cryptographic Sponge construction, which permits

Spritz to be used in different modes, and therefore, makes it an attractive design choice for security protocols.

Initial software performance analysis of Spritz shows that it fares poorly compared to the state-of-the-art hash

functions and stream ciphers. In this paper, we extend the analysis to the hardware performance. We propose

a fully customized accelerator design for Spritz and identify the highest achievable runtime performance for

ASIC and FPGA technology. Our results show that the Spritz accelerator is signiﬁcantly faster in encryption

compared to the software implementation (32.38× speed-up for the SQUEEZE and 64.07× speed-up for the

ABSORB function), though fares weakly against hardware implementation of state-of-the-art hash functions

and stream ciphers in terms of area-efﬁciency.

1 INTRODUCTION

Spritz is a new RC4-like stream cipher, proposed by

Ron Rivest and Jacob Schuldt (Rivest and Schuldt,

2014). RC4 (Paul and Maitra, 2012) is one of the

most well-recognized stream ciphers being part of

communication standards like Wired Equivalent Pri-

vacy (WEP), Wi-Fi Protected Access (WPA), Secure

Sockets Layer (SSL) and Transport Layer Security

(TLS). Due to a series of vulnerabilities (Paul and

Maitra, 2007) pointed out in recent times, it was pro-

hibited from all the versions of TLS in 2015. In

parallel to RC4, there were numerous other propos-

als for stream ciphers, primarily driven by the eS-

TREAM project (est, 2015), which listed a total of

seven stream ciphers in its ﬁnal portfolio - four in

software proﬁle and three in hardware proﬁle, respec-

tively. Intense scrutiny of these ciphers are currently

taking place, in terms of cryptographic weaknesses

and efﬁcient implementations.

Given the successful stint of RC4, many re-

searchers have also attempted to address the weak-

nesses of the basic algorithm and proposed different

variants (Paul and Maitra, 2012). In a recent such ef-

fort, Spritz was proposed, which, however, is based

on the “sponge-like” construction. Sponge construc-

tion was proposed in (Bertoni et al., 2007) and then

gained stronghold with applications in different cryp-

tographic primitives (Bertoni et al., 2010; Bertoni

et al., 2011), including the standardization of SHA-

3 (sha, 2015). Spritz is based on this construction,

which offers signiﬁcant ﬂexibility for the stream ci-

pher to be used for encryption, pseudo-random num-

ber generation, hash function, message authentica-

tion codes and authenticated encryption. Naturally,

this ﬂexibility brings in added advantage for Spritz

to be deployed in different communication and se-

curity protocols. However, the basic performance

analysis of Spritz shows that it falls short in perfor-

mance (Rivest and Schuldt, 2014). While the distin-

guisher proposed in (Banik and Isobe, 2016), poses a

real attack threat in the scenario of broadcast, it can

be easily avoided by dropping the ﬁrst 2 bytes of the

pseudo-random bitstream, as also indicated by the au-

thors.

All the values in Spritz are modulo-N. By de-

fault, N is 256 which makes Spritz byte-oriented. The

state Q

of Spritz consists of six one byte registers

i, j, k, w, z and a along with array S of length N,

which stores a permutation of Z

= {0,1,...,N − 1}.

The cryptographic key K is a byte-array of length L.

INITIALIZESTATE initializes the state of Spritz to a

standard state. ABSORB takes a variable length in-

put I and updates the state of Spritz based on the in-

put. For every b

c nibbles absorbed, SHUFFLE is in-

voked which whips, crushes, whips, crushes and ﬁ-

Bhattacharjee, D. and Chattopadhyay, A.

Hardware Accelerator for Stream Cipher Spritz.

DOI: 10.5220/0005951302150222

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 215-222

ISBN: 978-989-758-196-0

215

nally whips again. ABSORBSTOP absorbs a special

stop symbol, is used to separate various inputs be-

ing absorbed. SQUEEZE, the main output function of

Spritz, produces r-output bytes, where r is an input

to the function. By using these top level functions,

Spritz can operate in one of the many operating modes

speciﬁed in (Rivest and Schuldt, 2014).

1.1 Motivation and Contribution

Although the cryptographic designs are often guarded

within premise of software-centric or hardware-

centric design (est, 2015), it reveals a limited per-

spective regarding the end usage. For example, efﬁ-

cient hardware implementations for RC4, a primarily

software-oriented design have been extensively stud-

ied (Kitsos et al., 2003; Gupta et al., 2013). SOSE-

MANUK (Berbain et al., 2008), a software proﬁle

stream cipher from eSTREAM, is touted to be suit-

able for hardware implementation as well. Indeed,

a custom instruction designed for a cipher requires

a dedicated hardware functional unit, although it is

being run on a software platform (Constantin et al.,

2012). Therefore, the most efﬁcient implementation

of a cipher gives key design insights that can be under-

taken for software optimization as well. This factor,

besides Spritz being a promising candidate for RC4

replacement, forms the motivation of our work. The

major contributions of this paper are the following.

• An in-depth analysis of the constituent functions

for Spritz to derive the most efﬁcient architecture.

• Performance evaluation with ASIC and FPGA

technology mapping.

• Benchmarking against state-of-the-art hash func-

tions and stream ciphers.

The main content of the paper is organized in four

sections. Section 2 presents the cycle-per-byte(cpb)

analysis assuming a naive implementation of con-

stituent functions. Section 3 explores various de-

sign choices, and presents the cpb analysis of the

cipher, corresponding to the design choices. Sec-

tion 4 presents the implementation of hardware accel-

erator for the cipher and compares the performance

with other existing stream cipher designs. Section 5

presents the summary of the paper.

2 THEORETICAL ANALYSIS

FOR IMPROVING

CYCLES-PER-BYTE

We kindly refer reader to (Rivest and Schuldt, 2014)

for a detailed speciﬁcation of Spritz. The structure di-

agram of Spritz is presented in Figure 1. It is possible

to construct different cryptographic primitives using

the top level functions of Spritz, namely KEYSETUP,

ABSORB, ABSORBSTOP and SQUEEZE, which are

called from inside ENCRYPT or HASH, for example.

SPRITZ

KEYSETUP

ABSORB

SQUEEZE

ABSORBSTOP

ABSORBBYTE

ABSORBNIBBLE

SHUFFLE

WHIPCRUSH

DRIP

UPDATE

OUTPUT

INITIALIZESTATE

Figure 1: Structure diagram of Spritz.

To enable a clear analysis of the dependencies, we

begin with a study of each of the Spritz algorithmic

blocks and deﬁne a quantitative parameter R, which

approximates the upper bound on the number of op-

erations that each of the blocks execute, with the as-

sumption that each operation is executed in a single

clock cycle. Afterwards, we will attempt to model the

architecture in a way to satisfy the best-case assump-

tion for the number of cycles.

Spritz performs encryption by key setup using the

key K, followed by performing squeeze on the mes-

sage M to generate the cipher stream C.

• UPDATE(): In UPDATE, 4 operations are per-

formed. Thus R(UPDATE) = 4.

• WHIP(r): In WHIP(r), UPDATE gets called r times and

an operation is performed to update state register w.

R(WHIP(r))

= r × R(UPDATE)+1

= 4r + 1

• CRUSH(): In CRUSH, at most

swaps are per-

formed and assuming each swap is a single operation,

R(CRUSH) =

• SHUFFLE(): There are three calls to WHIP with param-

eter 2N, two calls to CRUSH and a single operation to

set state register a to 0.

R(SHUFFLE)

= 3 × R(WHIP(2N)) + 2 ×R(CRUSH)+ 1

= 3 × (8N + 1) + 2 ×(N/2) + 1

= 24N + 5 + N +1 = 25N + 6

• ABSORBNIBBLE(x): The conditional Shufﬂe call in

ABSORBNIBBLE is accounted for during calcula-

tion of R(ABSORB). There are two operations in

ABSORBNIBBLE irrespective of the value of x and

hence R(ABSORBNIBBLE) = 2.

• ABSORBBYTE(b): There are two calls to

ABSORBNIBBLE irrespective of the value of b, hence

R(ABSORBBYTE) = 2 ×R(ABSORBNIBBLE) = 4.

• ABSORB(M): There are M.length calls to

ABSORBBYTE, which in turn makes two call to

SECRYPT 2016 - International Conference on Security and Cryptography

216

ABSORBNIBBLE. In each call of ABSORBNIBBLE, the

value of state register a is incremented by 1, thereby

after every N/2 calls to ABSORBNIBBLE, there will

be a call to SHUFFLE, with the assumption that a is

initially 0. Assuming N is greater than 10,

R(Absorb(M))

= M.length × R(AbsorbByte) +

(M.length/(N/2)) ×R(Shu f f le)

= M.length × 4 +2 × M.length × (25N + 6)/N

= M.length(54 + 12/N)

• OUTPUT() : There is nested access of memory, and

with the assumption that the results of memory request

is obtained in the next cycle, it will require 3 cycles for

the accesses, hence R(OUTPUT) = 3.

• DRIP() : Each call to DRIP requires a call to UPDATE

and OUTPUT, and hence R(Drip) = 4 + 3 = 7.

• SQUEEZE(r) : There are r calls to DRIP and at most one

call to SHUFFLE. Thus, R(SHUFFLE) = r × R(DRIP)+

R(SHUFFLE) = 7r +25N + 5.

• INITIALIZESTATE() : Assuming each initialization of

each register or memory location is a single operation,

R(INITIALIZESTATE) = 6 + N.

• KEYSETUP() : Assuming that the key is byte array K

and K.length <

R(KEYSETUP) = R(INITIALIZESTATE) + K.length ×

R(ABSORBBYTE)

= 6 + N + 4K.length

The above discussion presents the number of cy-

cles required for execution for a na

ıve implementation

of constituent functions of Spritz, with the assumption

that each operation requires a single cycle to complete

execution. In the following section, we analyze the

various design points of accelerator design of Spritz.

The key challenge in the design phases is ﬁrst, to iden-

tify an optimized architecture for a given function and

second, to accommodate and adjust the same architec-

ture to include all the different functions.

3 DESIGN DECISIONS FOR

IMPLEMENTATION OF

ACCELERATOR

We begin designing the key constituent functions as

shown in structure diagram of Spritz, in Figure 1. The

design of each constituent function is presented in the

following subsections. We conclude this section by

presenting estimated cpb of Spritz with the chosen de-

sign decisions in subsection 3.9.

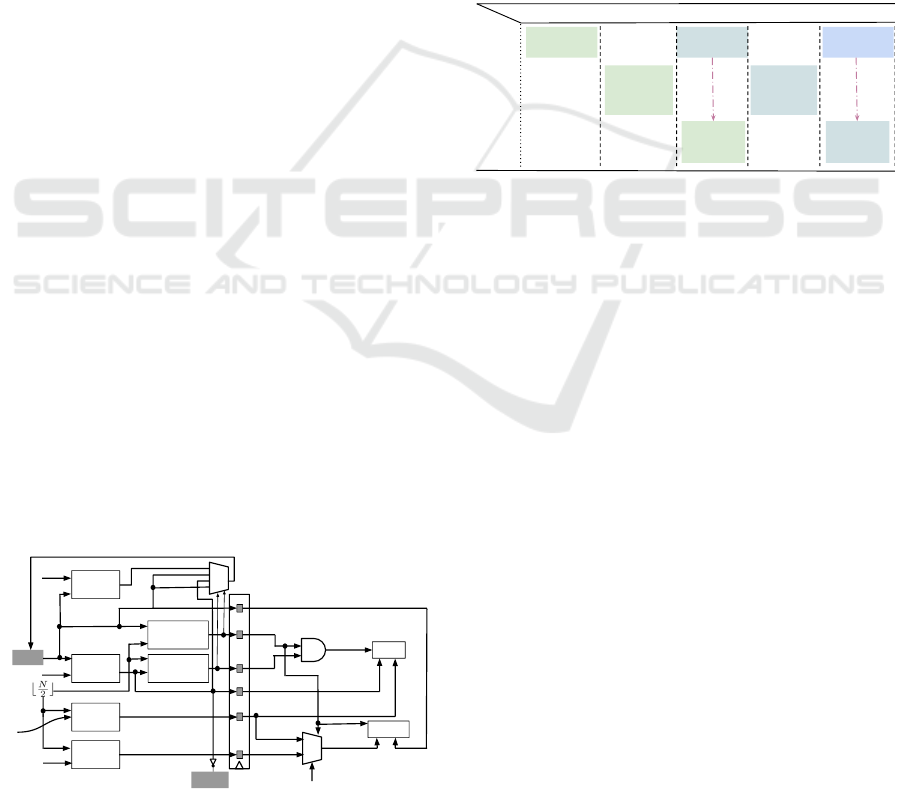
3.1 ABSORBBYTE(b)

The architecture for ABSORBBYTE(b), is shown

in Figure 2. LOW(b) and HIGH(b) repre-

sent the lower order 4 bits and higher order

4 bits of the byte b respectively. We im-

plement both the ABSORBNIBBLE(LOW(b)) and

ABSORBNIBBLE(HIGH(b)) simultaneously in a sin-

gle clock cycle. The target address for the swaps in

the corresponding ABSORBNIBBLE(x) is computed

along with incrementing the value of state register a.

We perform the two swaps simultaneously when no

call to SHUFFLE() is involved. We present three cases

related to the operation of ABSORBBYTE(b)-

1. If a == b

c, we set a register shu f f leOn to True

and do not perform any other operation, for invok-

ing SHUFFLE() in the next cycle.

2. If a + 1 == b

c, we set a register shu f f leOn

to True (for invoking SHUFFLE() in the next

cycle) and swap the contents of S[a] and

S[b

+LOW(b)c]. Once SHUFFLE() has com-

pleted, we assert Resume signal to high for

performing swap the contents of S[a] and

S[b

+HIGH(b)c]. In the next cycle, the Resume

signal is set to low to continue with ordinary op-

eration of ABSORBBYTE(b). During both these

operations, we increment a by 1.

3. Otherwise, we perform a double swap operation

taking into account the data dependencies that

might be present amongst the memory locations

and increment the value of a by 2. The data depen-

dencies are resolved using the register-to-register

transfer addresses shown in Table 1 and explained

below.

Case 1: a

6= b

& b

6= a

& b

6= b

Symbolically, the data transfers can be represented by

the following permutation on the state array S -





7→





It involves four simultaneous data transfers.

S[b

] ← S[a

],S[a

] ← S[b

],S[a

] ← S[b

] and

S[b

] ← S[a

Case 2: a

6= b

& b

6= a

& b

= b

In this case, permutation of the state array is





7→





This involves three data transfers. S[a

] ← S[a

S[b

] = S[b

] ← S[a

], and S[a

] ← S[b

Case 3: a

6= b

& b

= a

& b

6= b

In this case, permutation of the state array is





7→





This involves three data transfers : S[b

] ← S[a

S[a

] = S[b

] ← S[a

], and S[a

] ← S[b

Hardware Accelerator for Stream Cipher Spritz

217

Case 4: a

6= b

& b

= a

& b

= b

In this case, permutation of the state array is





7→





This involves two data transfers : S[a

] ← S[a

], and

S[a

] = S[b

] ← S[a

Case 5: a

= b

& b

6= a

& b

6= b

In this case, permutation of the state array is





7→





This involves three data transfers : S[b

] ← S[a

S[b

] = S[a

] ← S[b

], and S[a

] ← S[b

Case 6: a

= b

& b

6= a

& b

= b

In this case, permutation of the state array is





7→





This involves two data transfers : S[b

] = S[a

] =

S[b

] ← S[a

], and S[a

] ← S[b

Case 7: a

= b

& b

= a

& b

6= b

In this case, permutation of the state array is





7→





This is an identity permutation and hence it does not

involve data transfer.

Case 8: a

= b

& b

= a

& b

= b

This case cannot occur, since it implies a

= a

which

is not feasible, as a

= a

+ 1.

We do not implement higher number of

ABSORBNIBBLE(x) operations in a single clock

cycle, since the amount of control circuit needed for

resolving dependencies amongst the swaps would

be high and negatively impact the critical path of

the entire circuit. In addition, we would also require

a higher number of ports to read from and write

simultaneously to the register array S, which would

also contribute to the area of the circuit.

2 input

adder

2 input

adder

2 input

adder

HIGH(b)

LOW (b)

Comparator

(0 if equal)

Comparator

(0 if equal)

Swap

Resume

2 input

adder

shuffleOn

Figure 2: Pipeline structure for ABSORBBYTE.

3.2 UPDATE()

We propose a three stage pipeline for the implemen-

tation of UPDATE, with the schedule shown in Figure

3. In Stage 1, we compute the new value of state reg-

ister i and a temporary variable t

which is used in

next stage for computation of j. In Stage 2, we com-

pute the updated value of state register j and another

temporary variable t

required for computation state

memory locations i and j respectively and also com-

pute the new value of state register k. Since Stage 1

of the pipeline uses the updated value of stage regis-

ter j that is available in Stage 3 and also has a data

dependency with stage 3 for the swap of the previ-

ous iteration of UPDATE, a single cycle delay in the

pipeline is introduced into the pipeline.

= i

+ w

= j

+ S[i

+w]

= k

+ t

= k

+ i

= S[i

]

= S[k

+ t

]

S[j

] = t

S[i

] = t

= t

+ t

= i

+ w

= j

+ S[i

+w]

= k

+ t

= k

+ i

= S[i

]

= S[k

+ t

]

S[j

] = t

S[i

] = t

= t

+ t

= i

+ w

= j

+ S[i

+w]

Cycle 1 Cycle 2 Cycle 3 Cycle 4 Cycle 5

Stage 1

Stage 2

Stage 3

Figure 3: Pipeline structure for UPDATE.

3.3 DRIP()

The pipeline schedule for DRIP is shown in Figure

4. The ﬁrst three stages for DRIP are identical to

that for UPDATE operation and hence these two con-

stituent functions can run on the same physical hard-

ware pipeline. The last three stages of the pipeline

from stage 4 to 6 is used for accessing memory loca-

tions related to update of state register z and complet-

ing operation OUTPUT. Stage 4 of the pipeline has a

data dependency with Stage 6 of the pipeline, since

stage 4 of the next iteration uses the updated value of

z, that is available in Stage 6 of the previous iteration

of DRIP. Hence, we require at least two cycle stalls to

account for this data dependency. We should note that

we cannot access a memory location and use the data

at the memory in the same cycle for accessing another

memory location. Given this limitation, the current

pipeline schedule offers the best throughput possible

for hardware implementation of operation DRIP.

3.4 WHIP(x)

For the operation WHIP(x), we perform x iterations

of operation UPDATE following the pipeline schedule

presented in subsection 3.2. In the subsequent cycle,

SECRYPT 2016 - International Conference on Security and Cryptography

218

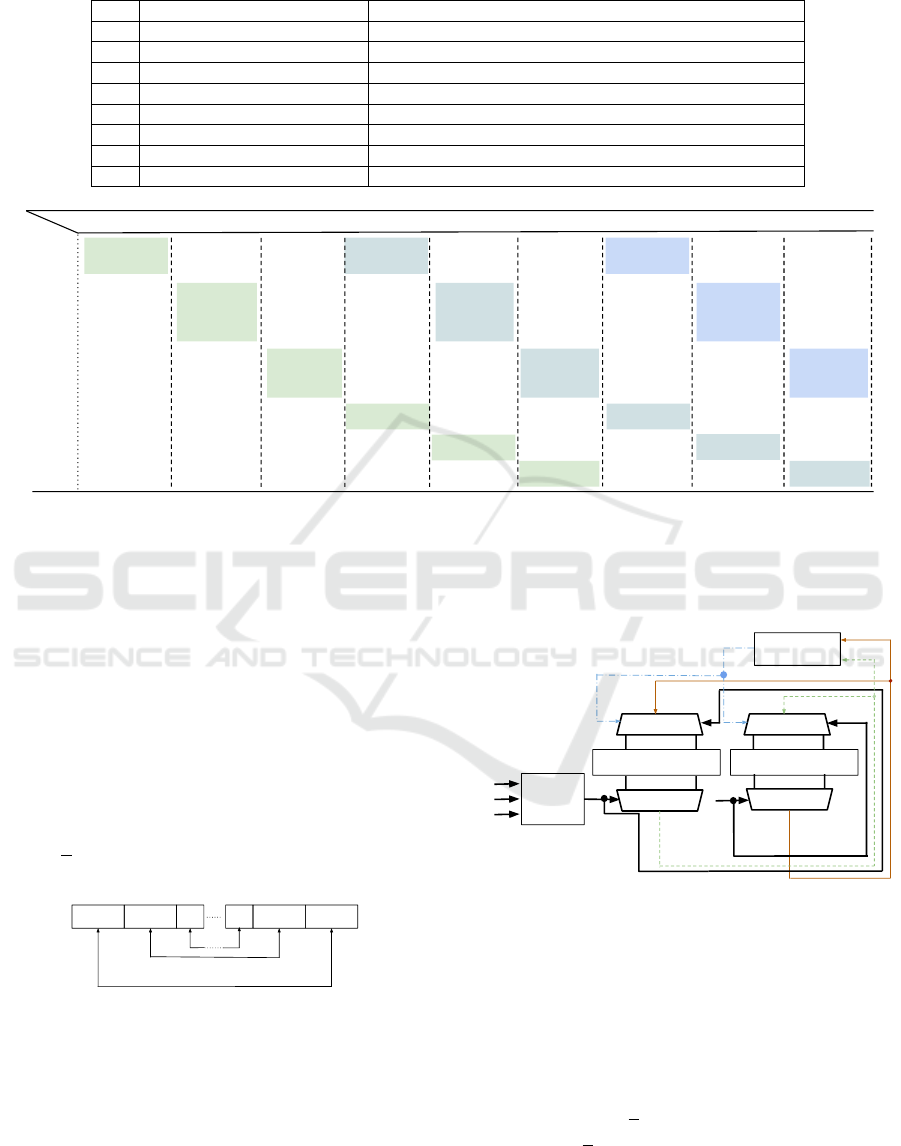
Table 1: Register-to-Register transfers issued to resolve Read-After-Write (RAW) dependencies.

Sl# Condition Register-to-Register transfers for Double Swap

1 a

6= b

& b

6= a

& b

6= b

S[b

] ← S[a

],S[a

] ← S[b

],S[a

] ← S[b

],S[b

] ← S[a

]

2 a

6= b

& b

6= a

& b

= b

S[a

] ← S[a

],S[b

] = S[b

] ← S[a

],S[a

] ← S[b

]

3 a

6= b

& b

= a

& b

6= b

S[b

] ← S[a

],S[a

] = S[b

] ← S[a

],S[a

] ← S[b

]

4 a

6= b

& b

= a

& b

= b

S[a

] ← S[a

],S[a

] = S[b

] ← S[a

]

5 a

= b

& b

6= a

& b

6= b

S[b

] ← S[a

],S[b

] = S[a

] ← S[b

],S[a

] ← S[b

]

6 a

= b

& b

6= a

& b

= b

S[b

] = S[a

] = S[b

] ← S[a

],S[a

] ← S[b

]

7 a

= b

& b

= a

& b

6= b

Identity permutation, no data transfer

8 a

= b

& b

= a

& b

= b

Impossible, as it implies a

= a

+ 1

= i

+ w

= j

+ S[i

+w]

= k

+ t

= k

+ i

= S[i

]

= S[k

+ t

]

S[j

] = t

S[i

] = t

= t

+ t

= i

+ S[z

]

= j

+ S[t

]

= i

+ w

= j

+ S[i

+w]

= k

+ t

= k

+ i

= S[i

]

= S[k

+ t

]

S[j

] = t

S[i

] = t

= t

+ t

= i

+ S[z

]

= j

+ S[t

]

= i

+ w

= j

+ S[i

+w]

= k

+ t

= k

+ i

= S[i

]

= S[k

+ t

]

S[j

] = t

S[i

] = t

= t

+ t

Cycle 1 Cycle 2 Cycle 3 Cycle 4 Cycle 5 Cycle 6 Cycle 7

Stage 1

Stage 2

Stage 3

Stage 4

Stage 5

Stage 6

= S[t

]

Cycle 8 Cycle 9

= S[t

]

Figure 4: Pipeline structure for UPDATE and DRIP.

we increment state register w by 2, since N is a power

of 2 to complete the operation WHIP(x).

3.5 CRUSH()

The data at location S[v] is swapped with data at loca-

tion S[N − 1 − v], where N is a parameter of Spritz if

the condition S[v] > S[N − 1 − v] is satisﬁed. We can

observe that CRUSH has follows a well deﬁned pat-

tern in regard to the locations that might be swapped,

as shown in Figure 5. There are no data dependencies

between the iterations of the loop in the CRUSH func-

tion and hence theoretically, we can unroll the loop

up to b

c to complete the loop operation in a single

clock cycle.

S[0] S[1] S[N-2] S[N-1]

Figure 5: Swap operation locations in CRUSH.

During hardware implementation, the unroll fac-

tor would be determined by the number of ports that

are available concurrently for reads and writes. In our

design, we limit ourselves to using four read ports and

four write ports for the register ﬁle. We propose the

following implementation of CRUSH as shown in Fig-

ure 6 for one swap operation. We use two such cir-

cuits to achieve an unroll factor of two - the ﬁrst one

swaps locations v and N − 1 − v, while the second cir-

cuit swaps v+1 and N −2−v, subject to the condition

speciﬁed in operation CRUSH.

-v

3 input

adder

-1

256 to 1 MUX

1 to 256 DeMUX

Comparator

(1 if D

> D

)

Figure 6: Circuit for swap in operation CRUSH.

3.6 SHUFFLE()

SHUFFLE operation is performed by the following se-

quence of operations:-

1. Invoke UPDATE 2N times following the pipeline

schedule shown in Figure 3. Thereafter, incre-

ment w by 2.

2. Invoke CRUSH

times, with parameter v ranging

from 0 to

, incremented by two in each iteration.

3. Same as Step 1

4. Same as Step 2

Hardware Accelerator for Stream Cipher Spritz

219

5. Same as Step 1

6. Set state register a to 0 in the cycle immediately

after the cycle in which w has been incremented

by 2 in Step 4.

3.7 SQUEEZE()

At the start of SQUEEZE, we set register shu f f leOn

to the result of the condition, a > 0. If shu f f leOn

is high, then we invoke SHUFFLE. Once SHUFFLE

has completed, pipeline for DRIP as per the schedule

speciﬁed in Figure 4 is executed. We should note that

if a > 0, SHUFFLE is invoked causing a to be set to

0, hence we do not need to check for a > 0 during

execution of the DRIP pipeline.

3.8 INITIALIZESTATE

Assuming 4 write ports, the state array S can be ini-

tialized in

cycles. Simultaneously, the state reg-

isters i, j,k,z,a can be initialized to zero while state

3.9 Estimated cpb of Spritz with the

Chosen Design Decisions

In this subsection, we analyze the cpb of the com-

ponent functions of Spritz based on the chosen de-

sign decisions, presented in the immediately previ-

ous subsections. It should be noted that KEYSETUP,

ABSORB, ABSORBSTOP and SQUEEZE are the top

level functions of Spritz that are used required for

construction of different cryptographic primitives.

• WHIP(2N) : 2 × 2N + 2 = 4N + 2 cycles

• CRUSH : b

c cycles

• SHUFFLE : 3×WHIP+ 2×CRUSH

= 12N + 6 +b

= 12.25N +6 cycles

• ABSORBBYTE(b) : 1 cpb

• ABSORB(k): We can absorb one byte per cycle.

However, after every

bytes absorbed, SHUFFLE

has to be invoked. For absorbing k bytes, the num-

ber of cycles and cycles per byte for ABSORB is

shown in Equation 1 and Equation 2 respectively.

Abosrb

cycles

(k) =

(

k(25.5 +

) k ≥

k k <

(1)

ABSORB

cpb

(k) =

(

25.5 +

k ≥

1 k <

(2)

• SQUEEZE(m) : Assuming SHUFFLE is invoked at

the start of operation SQUEEZE, the number of cy-

cles per byte for SQUEEZE for a message of length

m bytes is presented in the following equation 3.

SQUEEZE

cpb

(m) = 3 +

12.25N +6

(3)

• INITIALIZESTATE :

cycles

• KEYSETUP :

+ ABSORB

cycles

(K.length) cy-

cles, where K is the key used for encryption.

Compared to the naive implementation presented in

Section 2, it can be observed that the design deci-

sions made by us, help in gaining considerable im-

provements in terms of number of cycles for all the

constituent functions.

4 ACCELERATOR

IMPLEMENTATION

We have implemented the proposed design of Spritz

stream cipher using Verilog description. The array S,

of size 256 bytes, which forms part of the state Q

Spritz, has been implemented as an array of master-

slave ﬂip-ﬂops. The top level schematic of the imple-

mented design is shown in Figure 7. The input bus

f unc sel is used to choose the operation to be per-

formed while data in is used to supply required data

to the accelerator. The output port shu f f le on is set to

high when SHUFFLE has be invoked in the next cycle.

The input port resume is used to ﬂag that operation

ABSORBBYTE has resumed after SHUFFLE.

Spritz

Core

clock

reset

resume

func_sel

data_in

shuffle_on

data_out

Figure 7: Block diagram of SPRITZ hardware accelerator.

4.1 Hardware Performance

The Verilog code for the accelerator has been synthe-

sized and evaluated with Synopsys Design Compiler

version J-2014.09, using 65nm Faraday library. De-

tailed performance results (pre-layout) are presented

in Table 2. Unless mentioned otherwise, a 16-byte

key is set up followed by encryption of a 10 kilo-

byte message to compute the throughput. We also

synthesized the code using Xilinx ISE 14.7 for a

FPGA-based implementation. The results of the Xil-

inx Virtex-7 (device: xc7vx330t-3ffg1157) FPGA im-

plementation is also shown in Table 2. The maximum

SECRYPT 2016 - International Conference on Security and Cryptography

220

Table 2: Performance Summary: Spritz Accelerator Core.

ASIC FPGA

Clock frequency(MHz) 1150 Frequency(MHz) 64.72

Throughput(Mbps) 2780.14 Throughput(Mbps) 156.46

Combinatorial Area(KGE) 119.52 #slice registers 2197

Non-combinatorial Area(KGE) 11.19 #slice LUTS 23103

Total Area (KGE) 130.71 #occupied slices 7146

Area Efﬁciency(Mbps/KGE) 21.27

Energy Efﬁciency(pJ/bits) 5.834

clock frequency was determined by the Xilinx static

timing analysis tool.

In Table 2, the reported throughput is for en-

cryption. For comparing with the software im-

plementation, we separately report the throughput

achieved by ABSORB and SQUEEZE functions. The

keystream generation rates for SQUEEZE, for the

ASIC and FPGA implementations, are 3066.67 Mbps

and 172.6 Mbps, respectively. The processing rates

for ABSORB when large amounts of data is passed,

are 360.122 Mbps and 20.24 Mbps for ASIC and

FPGA implementations respectively. In compar-

ison, the unoptimized software implementation of

SQUEEZE and ABSORB reported a throughput of

94.69 Mbps and 5.62 Mbps respectively [1]. Con-

sidering our best achieved implementations, we ob-

tain a 32.38× speed-up for the SQUEEZE and 64.07×

speed-up for the ABSORB function, in comparison

with the software implementation.

4.2 Area-Throughput Comparison with

Existing Designs

In (Rivest and Schuldt, 2014), authors have com-

pared the throughput of the SQUEEZE function with

the keystream generation speed of prominent stream

ciphers and the throughput of the ABSORB func-

tion with that of the hash functions. Following

the same approach, we provide a performance list-

ing of accelerators for prominent stream ciphers

and hash functions in Table 3, where the perfor-

mances are obtained from state-of-the-art implemen-

tations (Gurkaynak et al., 2006; Good and Benaissa,

2007; Gupta et al., 2013; Paul and Chattopadhyay,

2015; Henzen et al., 2010). For a different technol-

ogy node, the performance is scaled.

Table 3: Stream Cipher and Hash Function Accelerators.

Cipher

Technology Area Throughput TpA

Node (nm) (KGE) (Gbps) (Gbps/KGE)

Sosemanuk (Berbain et al., 2008) 130 95.74 66.56 0.695

RC4 (Paul and Maitra, 2012) 130 59.93 10.0 1.667

Grain128 (Hell et al., 2008) 130 3.2 14.48 4.525

MICKEY (Babbage and Dodd, 2008) 130 5.0 0.41 0.082

Trivium (De Canni

ere, 2006) 130 4.9 22.3 4.551

Keccak256 (Bertoni et al., 2009) 130 50.0 43.01 0.860

Spritz fares rather poorly in comparison to the

lightweight stream ciphers as well as high-speed

stream cipher candidates (e.g., Sosemanuk). Al-

though Spritz is capable of operating in multiple

modes due to its Sponge construction, its large

area overhead due to the state array S and nested

memory accesses required for computation of UP-

DATE and OUTPUT, makes it implementation-wise a

weak candidate compared to block ciphers like AES,

PRESENT, which can also operate in different modes.

4.3 Throughput Comparison with

Existing Designs for Large Messages

It might be noted that the cpb of ABSORB reaches

25.5 for large N (refer equation 2), which is 2.3×

slower compared to the SHA-3 standard hash func-

tion Keccak and 16× faster compared to the software

implementation of Spritz (Rivest and Schuldt, 2014).

In the same manner, compared to the best reported

implementation of RC4 (Gupta et al., 2013), which

reports a cpb of 0.5, for arbitrarily long messages, the

cpb of SQUEEZE function reaches a value of 3 (refer

equation 3), which is 6× slowdown. This slowdown

is directly caused by the nested calls to the storage for

the output function of Spritz.

Table 4: cpb Performance Summary of Stream Ciphers.

Cipher/Machine Intel Core i5-6600 ARM Cortex-A9

Chacha8 0.56 3.06

AES-128 Counter Mode 0.67 21.85

Salsa20 1.34 8.14

HC-128 1.65 -

Trivium 1.92 -

Sosemanuk 2.57 -

Snow 2.0 2.57 -

A direct comparison of cpb across different archi-

tectures and technologies is biased, since the under-

lying clock frequency and number of cores may dif-

fer. For example, in (eba, 2015), performance bench-

marking of multiple stream ciphers are presented. For

a quad-core Intel Core i5-6600, running at 3.31 GHz,

cpb of prominent stream ciphers are listed in the fol-

lowing Table 4. The same table also lists the perfor-

mances reported by those stream ciphers for a single-

core Cortex-A9 processor with NEON extensions,

running at 1.2 GHz, which shows that cycles/byte for

Spritz is comparable to the fastest stream ciphers re-

ported. From this perspective, it is interesting to study

the parallelization options of Spritz for an optimized

software implementation.

5 CONCLUSION

Spritz is a new stream cipher proposed as a replace-

ment for RC4, which is part of several standards. So

far, no optimized hardware/software implementation

Hardware Accelerator for Stream Cipher Spritz

221

of Spritz has been reported. We explored the de-

sign points of Spritz considering a high performance,

custom hardware architecture to minimize its cycles

per byte. The implementation results on ASIC and

FPGA technology reveal signiﬁcant speed-up com-

pared to the basic, un-optimized software implemen-

tation. However, in terms of area-efﬁciency, Spritz

fares worse compared to the prominent stream ciphers

and hash functions.

REFERENCES

(2015). eBACS: ECRYPT Benchmarking of Cryptographic

Systems. In http://bench.cr.yp.to/results-stream.html,

Accessed: 2015-11-24.

(2015). eSTREAM: the ECRYPT Stream Cipher Project.

http://www.ecrypt.eu.org/stream/. Accessed: 2015-

11-23.

(2015). NIST Releases SHA-3 Cryptographic Hash Stan-

dard. http://www.nist.gov/itl/csd/201508 sha3.cfm.

Accessed: 2015-11-23.

Babbage, S. and Dodd, M. (2008). The mickey stream

ciphers. In Robshaw, M. and Billet, O., editors,

New Stream Cipher Designs, volume 4986 of Lecture

Notes in Computer Science, pages 191–209. Springer

Berlin Heidelberg.

Banik, S. and Isobe, T. (2016). Cryptanalysis of the full

spritz stream cipher. Cryptology ePrint Archive, Re-

port 2016/092. http://eprint.iacr.org/.

Berbain, C., Billet, O., Canteaut, A., Courtois, N., Gilbert,

H., Goubin, L., Gouget, A., Granboulan, L., Lau-

radoux, C., Minier, M., Pornin, T., and Sibert, H.

(2008). Sosemanuk, a fast software-oriented stream

cipher. In Robshaw, M. and Billet, O., editors,

New Stream Cipher Designs, volume 4986 of Lecture

Notes in Computer Science, pages 98–118. Springer

Berlin Heidelberg.

Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.

(2007). Sponge functions. Ecrypt Hash Workshop

2007.

Bertoni, G., Daemen, J., Peeters, M., and Assche,

G. V. (2009). Keccak speciﬁcations version 2.

http://keccak.noekeon.org/.

Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.

(2010). Sponge-based pseudo-random number gener-

ators. In CHES, pages 33–47.

Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.

(2011). Duplexing the sponge: single-pass authenti-

cated encryption and other applications. In Selected

Areas in Cryptography (SAC).

Constantin, J., Burg, A., and Gurkaynak, F. K. (2012). In-

vestigating the potential of custom instruction set ex-

tensions for sha-3 candidates on a 16-bit microcon-

troller architecture. Cryptology ePrint Archive, Re-

port 2012/050. http://eprint.iacr.org/.

De Canni

ere, C. (2006). Trivium: A stream cipher con-

struction inspired by block cipher design principles.

In Katsikas, S., L

opez, J., Backes, M., Gritzalis, S.,

and Preneel, B., editors, Information Security, volume

4176 of Lecture Notes in Computer Science, pages

171–186. Springer Berlin Heidelberg.

Good, T. and Benaissa, M. (2007). Hardware results for

selected stream cipher candidates. Technical Re-

port 2007/023, eSTREAM, ECRYPT Stream Cipher

Project.

Gupta, S., Chattopadhyay, A., Sinha, K., Maitra, S., and

Sinha, B. (2013). High-performance hardware imple-

mentation for rc4 stream cipher. Computers, IEEE

Transactions on, 62(4):730–743.

Gurkaynak, F., Luethi, P., Bernold, N., Blattmann, R.,

Goode, V., Marghitola, M., Kaeslin, H., Felber,

N., and Fichtner, W. (2006). Hardware Evalua-

tion of eSTREAM Candidates: Achterbahn, Grain,

MICKEY, MOSQUITO, SFINKS, Trivium, VEST,

ZK-Crypt. From: eSTREAM: the ECRYPT Stream Ci-

pher Project, 15:2006.

Hell, M., Johansson, T., Maximov, A., and Meier, W.

(2008). The grain family of stream ciphers. In Rob-

shaw, M. and Billet, O., editors, New Stream Cipher

Designs, volume 4986 of Lecture Notes in Computer

Science, pages 179–190. Springer Berlin Heidelberg.

Henzen, L., Gendotti, P., Guillet, P., Pargaetzi, E., Zoller,

M., and G

urkaynak, F. K. (2010). Developing a hard-

ware evaluation method for sha-3 candidates. In Man-

gard, S. and Standaert, F.-X., editors, Cryptographic

Hardware and Embedded Systems, CHES 2010, vol-

ume 6225 of Lecture Notes in Computer Science,

pages 248–263. Springer Berlin Heidelberg.

Kitsos, P., Kostopoulos, G., Sklavos, N., and Koufopavlou,

O. (2003). Hardware implementation of the rc4 stream

cipher. In Circuits and Systems, 2003 IEEE 46th Mid-

west Symposium on, volume 3, pages 1363–1366 Vol.

Paul, G. and Chattopadhyay, A. (2015). Three snakes in one

hole: The ﬁrst systematic hardware accelerator design

for sosemanuk with optional serpent and snow 2.0

modes. Computers, IEEE Transactions on, PP(99).

Paul, G. and Maitra, S. (2007). Permutation after rc4 key

scheduling reveals the secret key. In Proceedings of

the 14th International Conference on Selected Areas

in Cryptography, SAC’07, pages 360–377.

Paul, G. and Maitra, S. (2012). RC4 Stream Cipher and Its

Variants. CRC Press.

Rivest, R. L. and Schuldt, J. C. N. (2014). Spritz—a spongy

RC4-like stream cipher and hash function. Presented

at Charles River Crypto Day (2014-10-24).

SECRYPT 2016 - International Conference on Security and Cryptography

222