
Motion Error Compensation for Quad-rotor Miniature Unmanned
Aerial Vehicle SAR Imaging
Song Zhou, Lei Yang, Gang Xu and Guoan Bi
School of Electrical and Electronic Engineering (EEE), Nanyang Technological University, Singapore, 639798, Singapore
Keywords:
Quad-rotor Miniature Unmanned Aerial Vehicle (QMUAV), Synthetic Aperture Radar (SAR), Motion Error
Compensation.
Abstract:
Quad-rotor miniature unmanned aerial vehicle (QMUAV) synthetic aperture radar (SAR) is an ultra-small
airborne SAR system. Because of lowing flying altitude and small size constraints, the motion errors of
QMUAV-SAR are very complicated which introduces difficulty to the QMUAV-SAR imaging processing. To
deal with this problem, an effective motion compensation approach for QMUAV-SAR is proposed. By es-
tablishing the relationship between the motion errors and the Doppler parameters of SAR echoes, the motion
errors of QMUAV platform are extracted from the estimated Doppler rates. After the majority of the motion
error being properly compensated, phase gradient autofocusing (PGA) is employed to estimate and compen-
sate the residual phase errors to further improve the focusing quality of the SAR image. Experimental results
are provided and the image quality is evaluated to demonstrate the ability of achieving well focused image and
high spacial resolutions of the proposed method.
1 INTRODUCTION
Quad-rotor miniature unmanned aerial vehicle
(QMUAV) is a special kind of ultra-small unmanned
aerial vehicle (UAV) that can be easily launched and
landed in a space-constrained environment. There-
fore, QMUAV has significant potentials in many
practical applications, such as battlefield awareness,
disaster monitoring and traffic control (Dydek et al.,
2013; Lara et al., 2010; Zhao et al., 2015). Because
synthetic aperture radar (SAR) is a microwave remote
sensing technology with the capability of working
all day and all weather, it has attracted growing
interests in recent years. With current hardware
technology, the antenna and the digital processor
can be compacted into a very small and cheap flying
platform for QMUAV SAR imaging. Being equipped
with a SAR sensor on the UAV, high-resolution
microwave images of the observed scene can be
obtained to enhance its sensing capability under
various environmental conditions (Coker and Tewfik,
2011; Zeng et al., 2015; Yang et al., 2015; Sun et al.,
2013; Zhou et al., 2011).
For QMUAV SAR imaging, it is common that the
flying path is easily and frequently disturbed by the
atmospheric turbulence because of low flying altitude
and small size constraints. The unknown motion er-
ror or the flying path deviation is usually significant
enough to result in both serious defocusing and geo-
metric distortion in the SAR image (Moreira, 1990).
It is necessary to properly deal with the motion error
problem to obtain a well focused image (Wahl et al.,
1994; Xu et al., 2013; Zhang et al., 2012).
The motion errors can be measured and com-
pensated by using on-board measurement equipment,
such as the global positioning system (GPS) and the
inertial navigation system (INS). With accurate fly-
ing path information, the impact of the motion error
can be effectively reduced for obtaining desirable fo-
cusing quality of SAR image. Unfortunately, it is
not possible to make use of accurate and expensive
GPS and INS on board of the QMUAVs due to its
constrains on size, weight and costs of the device.
The motion error problem has appeared to be a dif-
ficult problem in the QMUAV SAR signal process-
ing. In this paper, autofocusing techniques are used
to extract the motion error information from the SAR
echoes. With the estimated motion error information,
the motion compensation is accordingly carried out
to improve the focusing quality of the final SAR im-
age (Yang et al., 2013; Zhao et al., 2014; Zhou et al.,
2013).
In this paper, experiment results of Ku-band
QMUAV SAR are presented and the focusing quality
38
Zhou, S., Yang, L., Xu, G. and Bi, G.
Motion Error Compensation for Quad-rotor Miniature Unmanned Aerial Vehicle SAR Imaging.
DOI: 10.5220/0005952000380044
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 5: SIGMAP, pages 38-44
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
X
H
Z
Y
R
B
R
,,
n n n n
P x y z
Actual path
Ideal path
A
O
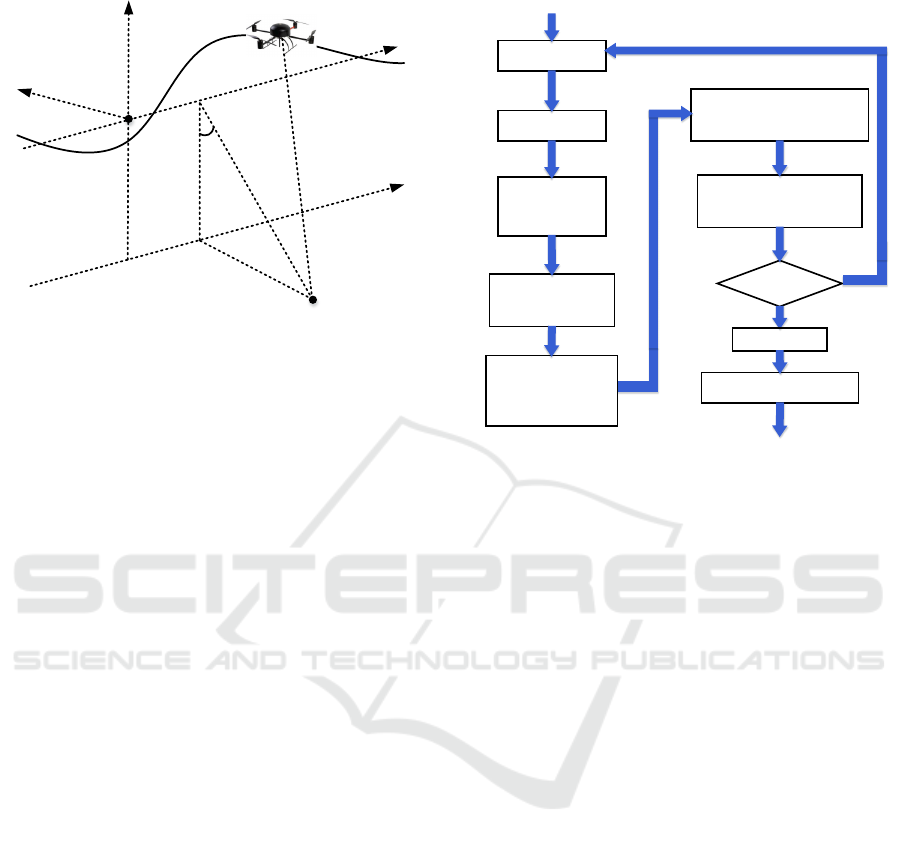
Figure 1: QMUAV SAR geometry.
of the QMUAV SAR image is evaluated. The paper
is organized as follows. The QMUAV geometry and
signal model are briefly introduced in section 2. The
motion error of QMUAV and the impact are analysed
in section 3. Then, the processing diagram integrated
with autofocusing techniques is briefly described in
section 4. In section 5, the QMUAV SAR system
used in our experiment is briefly introduced and the
experimental results are analyzed to demonstrate the
validity of our motion error compensation algorithm.
Finally, conclusion is provided in section 6.
2 SIGNAL MODEL
The geometry of the QMUAV SAR system is shown
in Fig. 1. The radar is mounted on a QMUAV plat-
form and is operated in strip-map mode. In ideal case,
the antenna phase centre (APC) is supposed to move
along a straight line (X axis) with a constant velocity,
as indicated by the dashed line. The SAR echo signal
can be expressed as the spectral form (Munson et al.,
1983):
S (k, t) =
∑
i∈S
C
A
i
exp[− jkR
i
(t)] (1)
where A
i
is the backscattering coefficient, t is the az-
imuth time, and k is the wavenumber variable. The
spectrum is the summation of echos from all scatter-
ers (S
C
) within the SAR antenna beam. R
i
(t) denotes
i-th scatterer’s range history during the QMUAV SAR
flying along the expected path. When the QMUAV
flies along the designateded path, the SAR image can
be obtained by using the back projection as (Desai and
Jenkins, 1992)
Azimuth Blocking
Raw radar data
Range Blocking
Doppler Rate
estimation for
each range block
Reduce estimating
error by using
Linear fitting
Extract the cross track
motion error and
forward motion error
Phase error compensation
and range cell compensation
for full aperture
Calculating full aperture
phase error by using the
estimated motion error
Iteration End?
Back projection processing
Final SAR image
PGA processing
Figure 2: Main processing steps of the QMUAV SAR sys-
tem.
I (x, y) =
t
max
Z
t
min
k
max
Z
k
min
S (k, t) dkdt . (2)
Because of the atmospheric turbulence in pratice, the
trajectory of the QMUAV platform seriously deviates
from the designated path, as indicated by the solid
curve. In this case, the range history R
i
(t) becomes
R
i
(t) + ∆R
i
(t), and an additional phase modulation
will be in S (k, t). The error ∆R
i
(t) will cause the
SAR image degradation, such as smearing and defor-
mation (Huang et al., 2011; Bao et al., 2012; Liao
et al., 2013).
3 MOTION ERROR ANALYSIS
In the SAR processing, the range error and the mo-
tion error are closely related to the Doppler param-
eters of the SAR echoes. Because the quadratic co-
efficient of phase error is closely related the motion
error of the QMUAV, we first consider the Doppler
rate parameter of the SAR echoes and establish the
relation between motion error and the Doppler rate.
Let β be the looking angle, as shown in Fig. 1. The
ideal and the actual APC positions at t are (v
0
t, 0, 0)
and (x (t) , y(t) , z (t)), respectively, where v
0
is the
ideal velocity. Then, the motion error can be denoted
as (x (t) − v
0
t, y (t), z (t)), with x (t) − v
0
t being the
along-track motion error. y (t) and z(t) are the motion
Motion Error Compensation for Quad-rotor Miniature Unmanned Aerial Vehicle SAR Imaging
39

errors along Y axis and Z axis. For an arbitrary scat-
tering point P
n
(x
n
, y
n
, z
n
), the range history R(t) from
the actual APC position to P
n
is given by
R(t) =
q
(x (t) − x
n
)
2
+ (y (t) − y
n
)
2
+ (z (t) − z
n
)
2
.
(3)
The main problem in the analysis is that the along-
track and cross-track motion errors are coupled to-
gether in (3). To facilitate the following discussion
and derivation, the range history R (t) is expanded into
Taylor series with high order terms being ignored as
follows (Xing et al., 2009)
R(t) ≈ R
n
+
1
2R
n
(x (t) − x
n
)
2
+ R
r
(t) (4)
where R
n
=
p
y
n
2
+ z
n
2
is the closest range of P
n
with
respect to the ideal trajectory. R
r
(t) = y (t)sinβ +
z(t) cos β is the cross-track motion error. In a SAR
system, the phase modulation of the echoed signal
arises from the range variation between radar and il-
luminated target and the corresponding phase history
can be deduced. Let λ be the radar wavelength and
the instantaneous phase of the echoed signal from P
n
can be written as
ϕ(t) = −
4π
λ
R(t) . (5)
By taking double derivation to (5), the instantaneous
Doppler rate γ(t) of the echoed signal can be derived
as
γ(t) = −
2v
2
(t)
λR
n
−
2a(t)
λR
n
(x (t) − x
n
) −
2a
r
(t)
λ
(6)
where v (t) is the instantaneous forward velocity,
a
r
(t) is the instantaneous cross-track acceleration and
a(t) is the instantaneous forward acceleration. Ow-
ing to the mechanical inertia of the airborne platform,
the variation of the forward velocity is usually small
and the impact of a (t) on the Doppler rate can be ne-
glected (Xing et al., 2009). γ (t) can be approximated
as
γ(t) ≈ −
2v
2
(t)
λR
n
−
2a
r
(t)
λ
. (7)
Equation (7) reveals the relationship between Doppler
rate and motion errors of the QMUAV platform. By
using the estimated Doppler rate, the motion error can
be calculated and the motion compensation can be im-
plemented accordingly.
4 PROCESSING ALGORITHM
In the QMUAV experiments, it is impossible to mount
an expensive INS/GPS equipment on board due to the
small size and limited payload of the platform. Thus,
autofocusing technique is used to estimate the motion
error from the SAR echoes and the main steps of the
processing processing are shown in Fig. 2.
4.1 Doppler Rate Estimation and
Compensation
As mentioned in section 3, the motion error is closely
related to the Doppler rate that can be estimated from
the SAR echoes. However, because the motion er-
ror of the QMUAV platform is much more severe
than a general aircraft, additional technique needs to
be utilized to improve the accuracy of the estimated
Doppler rate. As shown in (7), the Doppler rate is
varying along the range direction. Thus the range
variation of γ(t) will be considered by reformulating
(7) into
γ(t) R
n
= −
2v
2
(t)
λ
−
2a
r
(t)
λ
R
n
. (8)
From (8), it can be seen that γ(t) R
n
can be regarded as
a linearly variant component. Thus, in our QMUAV
SAR processing, the SAR data are divided into sev-
eral range blocks. Generally, it is assumed that when
the range size of each block is small, the Doppler
rate is regarded as constant along range direction.
Meanwhile, the linear variation of γ (t) R
n
can be ob-
served from different range blocks. Then, linear fit-
ting technique is applied to the estimated Doppler rate
from different range blocks to improve the estimat-
ing accuracy. Iteration of the above discribed process
is performed to refine the accuracy of the estimated
Doppler rate.
With the estimated Doppler rate, the cross track
motion a
r
(t) and the forward velocity v (t) can be
separated by using the kinetic characteristic of the
QMUAV platform. Generally, the frequency of the
forward velocity is very low while the frequency
of the cross track acceleration a
r
(t) is much higher
(Moreira, 1990). Thus, the first and the second terms
of (7) can be separated based on their spectral distri-
bution in the frequency domain. Then, both a
r
(t) and
v(t) can be accordingly calculated.
The map-drift (MD) technique (Carrara et al.,
1995; Cumming and Wong, 2005) is employed for
the Doppler rate estimation. As reported in (Car-
rara et al., 1995), the MD can directly estimate the
quadratic coefficient of the phase error. Then the ob-
tained estimates are used to apply a one-dimensional
correction function to the phase history. Generation
and application of the correction function can be read-
ily established once the quadratic error coefficient,
corresponding to the Doppler rate of the echoes, is
SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications
40

Table 1: QMUAV SAR Parameters.
Wave Band Ku Band
Bandwidth 300 MHz
Pulse Repetition Frequency (PRF) 1000 Hz
Synthetic Time Duration about 20 seconds
Range Centre 150 m
Forward Velocity 4-8 m/s
Flying Altitude below 100 m
known. Because the MD generally uses the fact that
a quadratic phase error (QPE) across the full process-
ing aperture has a differential functional form across
two half-length sub-apertures, the full aperture SAR
data need to be divided into small data blocks along
azimuth direction for MD application.
Because the motion error of the QMUAV is large,
the size of the data block along azimuth is usually set
to be very small, i.e., about 0.25s. In this case, it can
be assumed that the Doppler rates of the two adjacent
sub-apertures are identical, denoted as γ
n
. Then, the
signals from these two adjacent data blocks are for-
mulated as
s
1
(t) = a
t −
T
2
exp
jπγ
n
t −
T
2
2
s
2
(t) = a
t +
T
2
exp
jπγ
n
t +
T
2
2
(9)
By applying FFT to (9), we have
S
1
( f ) =
T
/
2
R
−T
/
2
s
1
(t)exp(−j2π f t) dt =
ˆ
S
1
f +
γ
n
T
2
S
2
( f ) =
T
/
2
R
−T
/
2
s
2
(t)exp(−j2π f t) dt =
ˆ
S
2
f −
γ
n
T
2
(10)
For small data blocks, it can be assumed that (Car-
rara et al., 1995)
|
S
1
( f )
|
2
=
|
S
2
( f )
|
2
. (11)
By cross-correlating the two sub aperture signals, the
location of the cross correlation peak can be used to
measure the relative shift to obtain the quadratic coef-
ficient.
With the estimated Doppler rate, the motion er-
ror can be extracted and combined to form the full-
aperture function for the motion error compensation.
Both phase error and motion induced range cell mi-
gration (RCM) are considered in the imaging process.
Iterations are also utilized to improve the estimating
accuracy.
4.2 PGA Processing
After the quadratic phase error being compensated
by Doppler rate estimation, the residual high order
phase error needs to be considered to improve the fo-
cusing quality of the final image. In the processing,
we employ phase gradient autofocusing (PGA) which
is very useful for high order phase error estimation
(Wahl et al., 1994; De Macedo et al., 2008). The
success of the technique relies upon four fundamen-
tal signal processing steps (Wahl et al., 1994): centre
shifting, windowing, phase gradient estimation, and
iterative correction. It has been proved that excellent
results can be obtained over a wide variety of scene
content, and phase error function is achievable if and
only if all of the four steps are included in the process-
ing. By following the idea of weighted phase estima-
tion, a weighted ML kernel is employed in the phase
gradient estimation (Ye et al., 1999). Weighting tech-
nique is based on the contribution adjustments of dif-
ferent samples according to their SCR, which encour-
ages the contribution of high SCR samples in phase
gradient estimate. If so, the selection of samples can
be much more relaxed and fast convergence can be
obtained. The weighted maximum likelihood (WML)
kernel is given by
ˆ
φ
W ML
e
(h) = arg
K
∑
k=1
w
k
[con j [s (k, h)]s (k, h + 1)]
K
∑
j=1
w
j
(12)
where
ˆ
φ
W ML
e
is the estimated phase-error gradient, K
is the number of selected range bins, J + 1 denotes
the azimuth length of samples, con j denotes the con-
jugate operator, and w
k
is the weight of the kth range
bin. In the PGA estimation, we also use blocking,
linear fitting and iterative processing to improve the
estimation accuracy (Zhang et al., 2012). After the
residual high order phase error being removed, back
projection processing is implemented to obtain a well
focused SAR image.
5 EXPERIMENTAL RESULTS
AND ANALYSIS
In this section, the QMUAV-SAR experimental re-
sults are presented and analyzed. Because the size of
QMUAV is very small (length: 1.2m, height: 0.5m),
it is very convenient for launching and landing in a
space-constrained environment. A low accurate GPS
system is mounted on the top of the QMUAV for
navigation. Its measurement accuracy is about 0.1m,
Motion Error Compensation for Quad-rotor Miniature Unmanned Aerial Vehicle SAR Imaging
41

Azimuth
Range
Entropy: 13.7839
Azimuth
Range
Entropy: 14.2273
(d)
Azimuth
Range
Entropy: 13.4562
(b)
Corner reflector
Azimuth
Range
Google earth image
(a)
Corner reflector
Corner reflector
(c)
Figure 3: Google earth image and SAR images. (a) Google earth image. (b) QMUAV-SAR image without motion error
compensation. (c) QMUAV-SAR image from conventianal motion error compensation. (d) QMUAV-SAR image from the
proposed method.
Figure 4: 3D responses of the corner reflector.
which can not meet the requirement of motion error
compensation. Therefore, all the motion errors of the
QMUAV are to be estimated from the SAR echoes.
The above described motion error compensation al-
gorithm is used in the process of SAR imaging for-
mation. Hamming windows are used in the range and
the azimuth processing for side lobe suppressions.
Fig. 3 presents the Google earth image and the
QMUAV-SAR images. The focusing result without
motion error compensation is shown in Fig. 3 (b)
showing that the image has serious defocusing and ge-
ometrical distortion with an entropy value of 14.2273.
With conventional motion error compensation (Mor-
eira, 1990; Xing et al., 2009), the SAR image in Fig.
3 (c) still has some defocusing and geometric dis-
tortion with an entropy value of 13.7839. Fig. 3
(d) presents the SAR image obtained from the pro-
posed method that has much reduced defocusing and
geometric distortion with a reduced entropy value of
13.4562. From Fig. 3 (d), it can be easily seen that
the roads, the round shape objects and the edges of the
buildings in the scenario can be easily distinguished
in QMUAV SAR image.
To evaluate the focusing quality of the SAR im-
age, the responses of the corner reflector are particu-
larly analyzed. Fig. 4 is the responses of the corner
reflector in the SAR image domain. From Fig. 4, it
can be seen that the corner reflector is highly focused
with well separated main lobe and side lobes. Fig. 5
presents the azimuth and range response of the cor-
ner reflector. It is seen that all the side lobes of the
response are under 20dB. The shape of the responses
of the corner reflector demonstrates the high focusing
quality of our QMUAV SAR experiment.
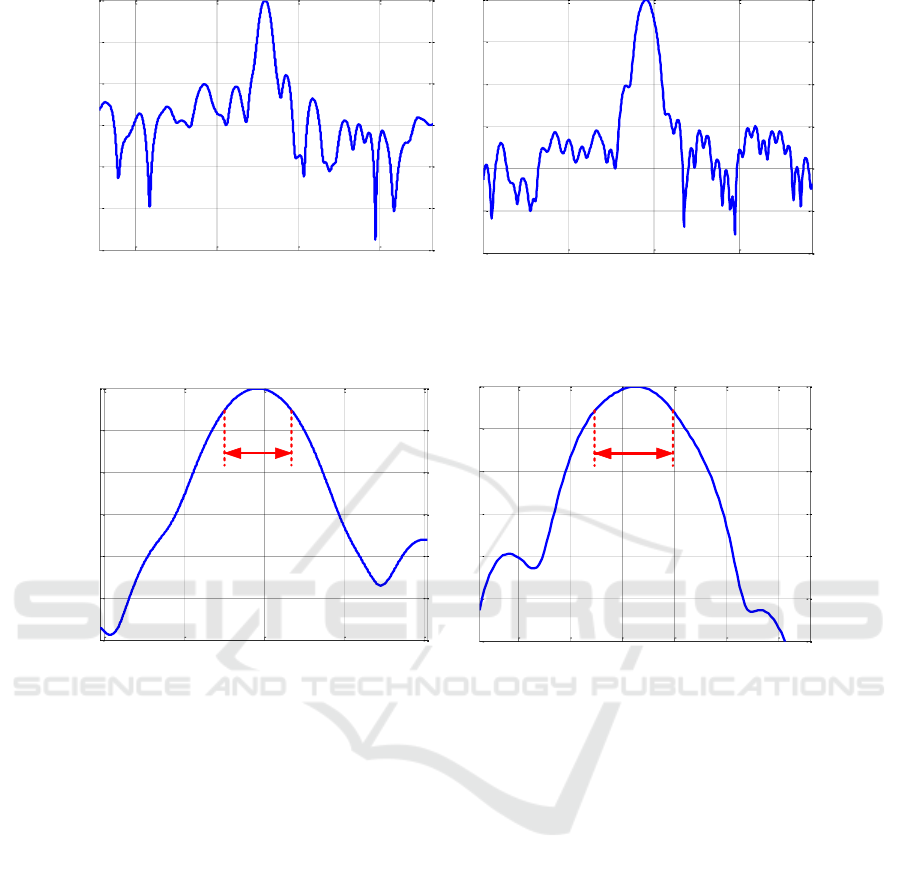
To further examine the spatial resolutions of our
QMUAV SAR system, the zoomed azimuth and range
responses of the corner reflector are particularly an-
alyzed, as shown in Fig. 6. From the zoomed re-
sponses, the azimuth and range resolutions can be
evaluated and they are very close to the theoretic val-
ues (The theoretic azimuth resolution is 0.15m and the
theoretic range resolution is 0.44m), which demon-
strates the ability of achieving high spacial resolution
of our QMUAV SAR system.
6 CONCLUSION AND FUTURE
WORK
This paper presents a motion error compensation al-
gorithm for SAR imaging system on the platform of
quad-rotor miniature unmanned aerial vehicle. Be-
cause of the severe motion error and the absence of
high accurate INS/GPS system on board, we estimate
the motion errors from the SAR echoes for compen-
sation. The focusing results are evaluated by the data
collected by our real hardware implementationed sys-
tem to show that the proposed error compensation al-
gorithm is effective to achieve high quality SAR im-
ages. It should be pointed that the presented image is
obtained by the off-line processing mode, i.e., the col-
SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications
42
0 1.75 3.50 5.25
-60
-50
-40
-30
-20
-10
0
Azimuth (m)
Amplitude (dB)
(a)
3.0 6.0 9.0
-60
-50
-40
-30
-20
-10
0
Range (m)
Amplitude (dB)
(b)
Figure 5: Azimuth response and range response. (a) Azimuth response. (b) Range response.
-0.4 -0.2 0 0.2 0.4
-30
-25
-20
-15
-10
-5
0
Azimuth (m)
Amplitude (dB)
3dB width
0.198m
-0.6 -0.3 0 0.3 0.6 0.9
-30
-25
-20
-15
-10
-5
0
Azimuth (m)
Amplitude (dB)
3dB width
0.47m
Range (m)
(a)
(b)
Figure 6: Zoomed responses. (a) Zoomed azimuth response. (b) Zoomed range response.
lected echo data are recorded in an on-board storage
and processed on a workstation computer. Develop-
ment of real-time algorithm and processing system on
the QMUAV platform will be our future work.
ACKNOWLEDGEMENTS
The work reported herein was supported by
TL@NTU, Singapore. The authors would like
to thank the TL@NTU for the flight trials and data
support.
REFERENCES
Bao, M., Xing, M., and Li, Y. (2012). Chirp scaling algo-
rithm for geo sar based on fourth-order range equa-
tion. Electronics letters, 48(1):41–42.
Carrara, W. G., Goodman, R. S., and Majewski, R. M.
(1995). Spotlight synthetic aperture radar- signal
processing algorithms(book). Norwood, MA: Artech
House, 1995.
Coker, J. and Tewfik, A. (2011). Performance synthesis of
uav trajectories in multistatic sar. Aerospace and Elec-
tronic Systems, IEEE Transactions on, 47(2):848–
863.
Cumming, I. G. and Wong, F. H.-c. (2005). Digital process-
ing of synthetic aperture radar data: algorithms and
implementation. Artech house.
De Macedo, K. A. C., Scheiber, R., and Moreira, A. (2008).
An autofocus approach for residual motion errors with
application to airborne repeat-pass sar interferometry.
Geoscience and Remote Sensing, IEEE Transactions
on, 46(10):3151–3162.
Desai, M. D. and Jenkins, W. K. (1992). Convolution back-
projection image reconstruction for spotlight mode
synthetic aperture radar. Image Processing, IEEE
Transactions on, 1(4):505–517.
Dydek, Z., Annaswamy, A., and Lavretsky, E. (2013).
Adaptive control of quadrotor uavs: A design trade
study with flight evaluations. Control Systems Tech-
nology, IEEE Transactions on, 21(4):1400–1406.
Motion Error Compensation for Quad-rotor Miniature Unmanned Aerial Vehicle SAR Imaging
43

Huang, L., Qiu, X., Hu, D., and Ding, C. (2011). Focus-
ing of medium-earth-orbit sar with advanced nonlin-
ear chirp scaling algorithm. Geoscience and Remote
Sensing, IEEE Transactions on, 49(1):500–508.
Lara, D., Romero, G., Sanchez, A., Lozano, R., and Guer-
rero, A. (2010). Robustness margin for attitude control
of a four rotor mini-rotorcraft: Case of study. Mecha-
tronics, 20(1):143–152.
Liao, Y., Xing, M.-d., Zhang, L., and Bao, Z. (2013). A
novel modified omega-k algorithm for circular tra-
jectory scanning sar imaging using series reversion.
EURASIP Journal on Advances in Signal Processing,
2013(1):1–12.
Moreira, J. (1990). A new method of aircraft motion error
extraction from radar raw data for real time motion
compensation. Geoscience and Remote Sensing, IEEE
Transactions on, 28(4):620–626.
Munson, D. C., O’Brien, J. D., and Jenkins, W. K. (1983). A
tomographic formulation of spotlight-mode synthetic
aperture radar. Proceedings of the IEEE, 71(8):917–
925.
Sun, G., Xing, M., Xia, X.-G., Wu, Y., and Bao, Z. (2013).
Robust ground moving-target imaging using deramp–
keystone processing. Geoscience and Remote Sens-
ing, IEEE Transactions on, 51(2):966–982.
Wahl, D., Eichel, P., Ghiglia, D., and Jakowatz, C.V.,
J. (1994). Phase gradient autofocus-a robust tool
for high resolution sar phase correction. Aerospace
and Electronic Systems, IEEE Transactions on,
30(3):827–835.
Xing, M., Jiang, X., Wu, R., Zhou, F., and Bao, Z. (2009).
Motion compensation for uav sar based on raw radar
data. Geoscience and Remote Sensing, IEEE Transac-
tions on, 47(8):2870–2883.
Xu, G., Xing, M., Zhang, L., and Bao, Z. (2013). Ro-
bust autofocusing approach for highly squinted sar
imagery using the extended wavenumber algorithm.
Geoscience and Remote Sensing, IEEE Transactions
on, 51(10):5031–5046.
Yang, L., Bi, G., Xing, M., and Zhang, L. (2015). Air-
borne sar moving target signatures and imagery based
on lvd. Geoscience and Remote Sensing, IEEE Trans-
actions on, 53(11):5958–5971.
Yang, L., Xing, M., Wang, Y., Zhang, L., and Bao, Z.
(2013). Compensation for the nsrcm and phase er-
ror after polar format resampling for airborne spot-
light sar raw data of high resolution. Geoscience and
Remote Sensing Letters, IEEE, 10(1):165–169.
Ye, W., Yeo, T. S., and Bao, Z. (1999). Weighted least-
squares estimation of phase errors for sar/isar autofo-
cus. Geoscience and Remote Sensing, IEEE Transac-
tions on, 37(5):2487–2494.
Zeng, T., Li, Y., Ding, Z., Long, T., Yao, D., and Sun,
Y. (2015). Subaperture approach based on azimuth-
dependent range cell migration correction and az-
imuth focusing parameter equalization for maneuver-
ing high-squint-mode sar. Geoscience and Remote
Sensing, IEEE Transactions on, 53(12):6718–6734.
Zhang, L., Qiao, Z., Xing, M.-d., Yang, L., and Bao, Z.
(2012). A robust motion compensation approach for
uav sar imagery. Geoscience and Remote Sensing,
IEEE Transactions on, 50(8):3202–3218.
Zhao, B., Xian, B., Zhang, Y., and Zhang, X. (2015). Non-
linear robust adaptive tracking control of a quadro-
tor uav via immersion and invariance methodol-
ogy. Industrial Electronics, IEEE Transactions on,
62(5):2891–2902.
Zhao, L., Wang, L., Bi, G., and Yang, L. (2014). An aut-
ofocus technique for high-resolution inverse synthetic
aperture radar imagery. Geoscience and Remote Sens-
ing, IEEE Transactions on, 52(10):6392–6403.
Zhou, S., Bao, M., Zhou, P., Xing, M.-D., and Bao,
Z. (2011). An imaging algorithm for missile-
borne sar with downward movement based on az-
imuth nonlinear chirp scaling. Dianzi Yu Xinxi Xue-
bao(Journal of Electronics and Information Technol-
ogy), 33(6):1420–1426.
Zhou, S., Xing, M., Xia, X.-G., Li, Y., Zhang, L., and
Bao, Z. (2013). An azimuth-dependent phase gradi-
ent autofocus (apga) algorithm for airborne/stationary
bisar imagery. Geoscience and Remote Sensing Let-
ters, IEEE, 10(6):1290–1294.
SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications
44
