Synthetic Workload Generation of Broadcast Related HEVC Stream

Decoding for Resource Constrained Systems

Hashan Roshantha Mendis and Leandro Soares Indrusiak

Real-time Systems Group, Department of Computer Science, University of York, York, U.K.

Keywords:

HEVC, Decoding, Workload Characterisation, Synthetic Workload Generation.

Abstract:

Performance evaluation of platform resource management protocols, require realistic workload models as in-

put to obtain reliable, accurate results. This is particularly important for workloads with large variations, such

as video streams generated by advanced encoders using complex coding tools. In the modern High Efﬁciency

Video Coding (HEVC) standard, a frame is logically subdivided into rectangular coding units. This work

presents synthetic HEVC decoding workload generation algorithms classiﬁed at the frame and coding unit

levels, where a group of pictures is considered as a directed acyclic graph based taskset. Video streams are

encoded using a minimum number of reference frames, compatible with low-memory decoders. Characteristic

data from several HEVC video streams, is extracted to analyse inter-frame dependency patterns, reference data

volume, frame/coding unit decoding times and other coding unit properties. Histograms are used to analyse

their statistical characteristics and to ﬁt to known theoretical probability density functions. Statistical proper-

ties of the analysed video streams are integrated into two novel algorithms, that can be used to synthetically

generate HEVC decoding workloads, with realistic dependency patterns and frame-level properties.

1 INTRODUCTION

HEVC (H.265) as well as its predecessor, H.264,

both utilise advanced video coding techniques to ef-

ﬁciently compress highly dynamic and diverse video

streams. Advanced compression techniques such as

the use of hierarchical B-frame structures (Sullivan

et al., 2012), random-access proﬁles (Chi et al., 2013)

and scene-change detection (Eom et al., 2015), makes

video decoding workloads highly variable and com-

plex. As video streaming workloads become more

sophisticated, efﬁcient platform resource manage-

ment mechanisms and optimised scheduling of tasks

and are required at the decoder to optimise perfor-

mance. Input workloads highly inﬂuence the sim-

ulation based evaluation of these resource manage-

ment protocols, therefore it is crucial to achieve an

analytical, tractable and realistic, model or abstrac-

tion of the actual application. For example, in re-

search where workload properties such as task ex-

ecution costs are assumed to be Uniform/Gaussian

distributed (e.g.(Yuan and Nahrstedt, 2002; Mendis

et al., 2015)), the performance evaluation might sig-

niﬁcantly deviate from the results obtained using a re-

alistic workload with a non-uniform distribution (e.g.

skewed/long-tailed).

HEVC frames are logically structured as coding

tree blocks (CTB) and each CTB is recursively sub-

partitioned into coding units (CU) in a quad-tree man-

ner (illustrated in Figure 1). The CU deﬁnes a re-

gion sharing the same prediction mode (e.g., intra and

inter). This work, analyses traces from real HEVC

decoding workloads at the group of pictures (GoP),

frame and CU levels. Workload generation algo-

rithms are presented, that use statistical distribution

models that closely represent video decoding work-

load characteristics. Frame decoding time is derived

in a bottom-up manner by utilising CU-level charac-

teristics.

Novel Contributions: This work introduces algo-

rithms, that can be used to generate directed acyclic

graph (DAG) based HEVC decoding workloads, with

statistical properties closely matching real HEVC

video streams. These synthetically generated, abstract

workloads can then valuable in simulation-based de-

sign space exploration research (such as in (Mendis

et al., 2015; Kreku et al., 2010)), to investigate timing

and performance properties more accurately. To our

knowledge this is the ﬁrst work to characterise HEVC

decoding workloads at the block-level as well as cap-

turing the properties of GoP-level task graphs depen-

dency patterns, for different types of video streams.

Mendis, H. and Indrusiak, L.

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems.

DOI: 10.5220/0005953200520064

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 5: SIGMAP, pages 52-64

ISBN: 978-989-758-196-0

64x64

32x32

16x16

8x8

CU-level information extraction:

* Prediction type (I/P/B/Skip)

* Size distribution

* Decoding execution cost

* Reference data dependency

B B

GoP-level characteristics:

* Distribution of P, B frames

* Hierarchical B-frame structure

* Scene change rate

* Inter-prediction reference distance

Inter-task communication:

* Frame-level reference data volume

* Memory read/write volume

B B

GoP

Sequence of open GoPs within the video stream

B B

GoP

B B

GoP

B B

GoP

Figure 1: Task-graph based HEVC decoding workload.

Workload characterisation at different levels: taskset (GoP),

task (frame) and inter-task communication (reference data).

A group of pictures (GoP), represented via a

DAG based application model is shown in Figure 1.

There are essentially three kinds of frames in a GoP:

I-frames (intra-predicted), P-frames (uni-directional,

inter-predicted) and B-frames (bi-directional, inter-

predicted). Inter-predicted, P and B frames use ref-

erence data from other frames in the GoP to construct

the current frame. In this work, a task-graph (TG)

refers to the graph derived from the GoP structure,

where nodes in a TG refers to HEVC frame decoding

tasks and edges in a graph represents inter-prediction

frame data-dependencies. For example, the weight

of edge P ← I represent the overall decoded I-frame

data that is referenced by the P-frame. Video decod-

ing workloads are increasingly dynamic with highly

varying frame decoding execution costs and depen-

dency relationships based on the temporal and spatial

characteristics of the video streams. Most specially in

HEVC each inter-predicted frame can have up to 16

reference frames. Hence for example in a 35 frame

GoP, there could be up to 35×16 edges in the TG and

buffer requirements would vary greatly as well.

This work explores the following workloads char-

acteristics of different video streams:

• Taskset/GoP Characteristics: number of P and

B frames in a GoP, TG dependency characteris-

tics, scene-changes, reference frame distribution.

• Task/Frame and CU Level Characteristics: de-

coding time and frame-to-CU relationship analy-

sis, CU-size and type distributions.

• Inter-task Communication Characteristics:

reference data volume per frame/CU-type (i.e.

task communication trafﬁc) and encoded frame

size analysis (i.e. task memory read trafﬁc)

2 RELATED WORK

In previous research, video decoding workloads have

primarily been characterised at the functional level.

Functional computation units of the video decoder

such as entropy decoding, motion compensation, ﬁl-

tering, inverse quantisation etc. are identiﬁed and

considered as tasks with data dependencies. A com-

prehensive discussion of the computation cost of the

HEVC decoding functional units on ARM and x86

platforms have been given by Bossen et al. (Bossen

et al., 2012). They show that motion compensation

and entropy decoding dominate the decoding time of

a random-access video stream. Holliman et al. (Hol-

liman and Chen, 2003), analyse MPEG-2 and H.264

decoding workloads from a system architecture per-

spective by investigating how CPU branch predic-

tions, cache and main memory hierarchy effects ex-

ecution time. An abstract workload model of a paral-

lel H.264 decoder is introduced in the MCSL bench-

mark framework (Liu et al., 2011). They specify the

decoder functional unit execution cost and inter-task

communication trafﬁc as actual traces obtained from

recorded real video streams as well as data derived

from statistical properties of trace-data. However,

their workload properties such as execution cost, re-

lease patterns, inter-task trafﬁc volumes are assumed

to be Gaussian distributed, which may not be accurate

with the real underlying distribution.

Video decoding workloads have also been anal-

ysed at the data-level, where a task can be consid-

ered as decoding video streams at at different lev-

els of granularity (e.g. GoP/frame/slice/block etc.).

The data communication between the tasks represent

reference data. Encoded frame sizes have been as-

sumed to follow a Gamma, Lognormal or Weibull dis-

tribution (Mashat, 1999; Krunz et al., 1995). Tanwir

et al.(Tanwir and Perros, 2013) in their survey pa-

per, show that wavelet-based models offer a reason-

able compromise between complexity and accuracy

to model frame sizes, and the model prediction re-

sults can vary signiﬁcantly based on the type of en-

coding. Frame decoding time is assumed to have a

linear relationship with the frame size (Bavier et al.,

1998). However, Isovic et al. (Isovic et al., 2003)

show that there is a large variance in the decoding

time for the same frame size. Roitzsch et al. (Roitzsch

and Pohlack, 2006) estimates the total decoding time

of a frame by adding macroblock and frame-level

metrics into video stream headers at the encoder-end.

In more recent work, Benmoussa et al. (Benmoussa

et al., 2015) uses a linear regression model to illustrate

the relationship between bit rate and frame decoding

time. High variability in decoding times are seen for

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

FastFurous5

LionWildlife Football

ObamaSpeech BigBuckBunny ColouredNoise

Figure 2: Video sequence snapshots.

I/P/B frame-types due to different coding tools in

each type and memory access patterns (Alvarez et al.,

2005). Therefore, classiﬁcation based on frame type

need to be addressed in the model in order to obtain an

accurate representation of video decoding workloads.

To our knowledge this is the ﬁrst work to present

characterisation and analysis of HEVC decoding at

the CU-level, for different types of video streams. Un-

like previous work, we analyse the reference frame

patterns within a GoP as well as frame/block level de-

coding times. We provide algorithms that construct

HEVC GoPs and frames using a bottom-up method-

ology by using characteristics derived at the CU-level.

3 VIDEO SEQUENCE AND

CODEC TOOL SELECTION

The video sequences under investigation has been

chosen to represent varying levels of spatial and tem-

poral video characteristics. Below are the video se-

quences selected for this study (snapshots presented

in Figure 2):

• FastFurious5 (Action, 720p, 30fps, 15mins):

Heavy panning/camera movement, frequent scene

changes.

• LionWildlife (Documentary, 720p, 30fps,

15mins): Natural scenery, medium move-

ment scenes, fade in/out, grayscale to colour

transitions.

• Football (Sport, 720p, 30fps, 15mins): camera

view mostly on ﬁeld, camera panning, occasional

close-ups on players/spectators. Large amounts of

common single colour background, combined text

and video.

• ObamaSpeech (Speech footage, 720p, 24fps,

10mins): Constant, non-uniform background;

uni-camera and single person perspective, head-

/shoulder movement.

• BigBuckBunny (CGI/Animation, 480p, 25fps,

9mins): Wide range of colours, moderate scene

changes.

• ColouredNoise (Pseudo Random coloured pix-

els, 720p, 25fps, 10mins): Low compression, use-

ful for analysing worst-case characteristics of a

codec.

3.1 Encoder and Decoder Settings

The video streams were encoded using the open

source x265 encoder (v1.7) (Multicoreware, 2015).

x265 has shown to produce a good balance between

compression efﬁciency and quality (Zach and Slan-

ina, 2014; Naccari et al., 2015), by incorporating sev-

eral advanced coding features such as adaptive, hi-

erarchical B-frame sequences. The default settings

of x265 (Multicoreware, 2015) are complimented

with additional settings (Listing 1), to suit resource-

constrained decoding platforms (e.g. set-top box,

smart phone), targeted at broadcast/video streaming

applications. Main memory data trafﬁc of dependent

picture buffer (DPB) access has shown to impact real-

time display of high deﬁnition (HD) video sequences

(Soares et al., 2013). Furthermore, multiple refer-

ence frames can linearly increase the memory usage

of the decoder (Saponara et al., 2004). Therefore,

inter-prediction has been restricted to 1 forward and 2

backward references. Higher number of B-frames in

a GoP offers better compression but decreases inter-

frame compression and quality (Wu et al., 2005). To

strike a balance, the encoder was conﬁgured to use a

maximum of 4 contiguous B-frames.

Listing 1: x265-encoder and OpenHEVC-decoder

command-line arguments.

Encoder:

x2 65 -- i npu t vid_ raw . yuv - o v i d_ enc . bin -I 35

-- b - a da pt 2 - - b fr ame s 4 --no - we i gh tp --no -

we i gh tb

-- no - ope n - g op --b - i nt ra -- r ef 2 -- csv - log - l ev el

2 -- csv v i d_s tat s . cs v - - log - le vel 4

Decoder:

oh ev c -i v id_ en c . bi n - f 1 -o vid_ dec . yuv - p 1 -n

Key-frames (random access-points in the

video) provide the ability to move (e.g. fast-

forward/pause/rewind) within a video stream. x265

by default treats all I-frames as key-frames if the

closed-GoP (self-contained/independent GoPs) set-

ting is chosen. Closed-GoPs offer less compression

than open-GoPs, but reduce error propagation during

data losses, hence more suited for broadcast video.

To ensure a balance between compression and

random-access precision, maximum I-frame interval

of 35 frames was chosen. Weighted prediction

was disabled to increase decoder performance and

B-frames were allowed to have intra-coded blocks in

order to be efﬁcient during high motion/scene-change

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

0 100 200 300 400 500 600 700 800

GoP index

Inter-predicted

frames ratio (P/B)

Football goal scored

Goal replay

Ball goes out of ﬁeld,

play restart

Normal

game play

Figure 3: Ratio of P:B frames within a GoP for (Football

video).

b28

B14

b15

b13

B10 b9

b11

P27

P30

B29

B32

b31

b33

P12

P16

P17 P18 P19 P20

P34

P23 P24

P25 P26P21 P22

b28

b26

b23

b21

B12 b11

b16

B31

b30

b32

P10 P13

b14

P17

B15

b18

b19

B20

P22

P33

P34

B27

P29

B24

P25

Hierarchical

B-Frames

Long sequence of P-frames

(high motion video sequence)

I-frame

B-frame

P-frame

Figure 4: Example structure of a GoP (from BigBuck-

Bunny). Top: low number of P-frames, Bottom: high num-

ber of P-frames. (NB: edges and nodes are unweighted).

sequences.

Decoding execution trace data was obtained us-

ing the open source, OpenHEVC (Opensource, 2015;

Hamidouche et al., 2014) decoder with the minimal

settings (Listing 1). In order to eliminate any inter-

thread communication and synchronisation latencies

which might affect decoding time data capture, for

this work, multi-threading has been disabled. The

platform used for decoding was a laptop with Intel

Core i7-4510U 2.00GHz CPU, 4MB L3-cache and

8GB of DDR3 RAM.

4 GoP STRUCTURE MODEL

The GoP structure is directly related to the scene

changes and motion in the video. For example, the ra-

tio of the number of P and B frames per GoP (denoted

as P/B ratio) of the Football changes with respect

to high-motion scenes/scene-changes (Figure 3). We

measure the scene change rate as 1/GoP

di f f

, where

GoP

di f f

refers to the mean number of GoPs between

scene change events. The scene change rate in each

tested video stream is given in Table 1. This met-

ric gives a notion of how often the GoP structure

changes with respect to time. FastFurious5 has the

highest scene change rate while the Football video has

the lowest. P-frames give higher compression than

I-frames, hence during scene changes, the x265 en-

coder increases the P/B ratio, whilst keeping the GoP

length constant. Figure 4 shows two example GoPs

from the BigBuckBunny video; the bottom GoP refers

a high-motion scene (more P-frames).

4.1 Distribution of Different Frame

Types

The number of P and B frames in a GoP for each video

sequence is shown as a histogram in Figure 5. The

number of P-frames in a GoP (denoted nP) is mod-

elled as an exponentiated-Weibull (exp-Weibull) dis-

tribution (Mudholkar et al., 1995), where the proba-

bility density function (PDF) of the exp-Weibull dis-

tribution is given as Eq. 1 with shape parameters a

and c. Additional scale and location parameters de-

ﬁnes the relative size and position of the PDF; they

are speciﬁc to the statistics package used (i.e. SciPy).

f (x) = ac (1 −exp −x

)

a−1

exp−x

c−1

(1)

Gamma and Gumbel PDFs provided inaccurate

ﬁts to the distributions, motivating the use of exp-

Weibull distribution due to its long-tail, right-skewed

density and ﬂexibility in shape. From Figure 5, it

is clear that most of the video sequences ﬁt the exp-

Weibull distribution except for the case of Coloured-

Noise, where no variation in the number of P or B

frames is seen. Due to the constant GoP length N,

the number of B-frames nB = (N − 1) − nP, giving

us an inverted distribution. For low-motion videos

such as ObamaSpeech with no scene changes (Ta-

ble 1), the P,B distributions show less variation and

do not overlap; furthermore high values of c and a

are seen. Video sequences with large variation in mo-

tion, long-tailed distributions are seen (e.g. BugBuck-

Bunny), with a low c,a.

4.2 Contiguous B-frames & Reference

Distance

The maximum number of contiguous B-frames

(nB

max

) in a GoP is an encoder parameter, which is

set to 4 in our study. Figure 6 shows the proportion of

different contiguous B-frames in a GoP. Low-motion

videos (e.g. ObamaSpeech), show a high level of

contiguous B-frames, while high motion videos (e.g.

FastFurious5), the proportions are uniform. The pro-

portion of contiguous B-frames have a direct impact

to the reference distance of a frame. Reference dis-

tance (RFD) is the absolute difference between the

GoP index of the current frame and its parent/depen-

dent frame(s). Larger reference distances correlate

with higher contiguous B-frames in a GoP. Higher av-

erage reference distances in a video stream, means the

decoder has to keep a decoded frame longer in the

DPB, which would result in high buffer occupancy

and hence a larger main memory requirement.

Generally, P-frames do not refer to B-frames and

if the encoder is restricted to have only 1 reference

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

Table 1: Scene change rate for all video sequences. GoP

di f f

refers to the mean number of GoPs between scene-changes.

VidName Scene change rate (1/GoP

di f f

)

FastFurious5 0.45

BigBuckBunny 0.30

LionWildlife 0.20

Football 0.05

ObamaSpeech 0.00

Figure 5: P,B frame histogram for all video sequences (dis-

tributions ﬁtted to the exp-Weibull PDF with shape param-

eters (a,c), location=0, scale=1.5).

frame for the forward direction, then a P frame refers

to the closest previous I/P frame. B-frames referred to

past and future I/P/B frames with a RFD characteris-

tic as shown in Figure 7. A highest B-frame RFD of 3

is seen as we restricted the maximum number of con-

tiguous B-frames in the GoP to 4. Further analysis

showed that a contiguous sequence of B-frames re-

ferred only to I/P-frames in close temporal proximity;

therefore long edges in the task graph are not present.

A correlation exists between the RFD ratios shown

in Figure 7 and the number of contiguous B-frames

shown in Figure 6. For example, less than 10% of

of contiguous B-frames in LionWildlife are of size 4,

which leads to a very low number of frames having a

RFD of 3.

4.3 GoP Structure Generation

Construction of a synthetic GoP structure can be done

in two stages as per Algorithm. 1. Firstly, a GoP

sequence (in temporal decoding order) is generated,

taking into account the exp-Weibull distributed P,B

frames. The position of the B-frames within the GoP

are uniformly distributed, but the selection of con-

tiguous B-frame sizes are derived from the ratio rela-

tionships observed from the trace results (Figure 6).

Lines 12-19 generate B-frame groups (Hierarchical

B-frames) and inject them at random positions in the

GoP. In phase II of the algorithm, each inter-predicted

frame is assigned reference frames as per the anal-

ysis in Section 4.2. The number of reference frame

Figure 6: Number of contiguous B-frames in a GoP.

Figure 7: Reference distances for B-frames in different

video sequences.

per temporal direction is an algorithm parameter. P

frames are assigned the immediate previous I/P frame

in the GoP. B-frames are assigned multiple refer-

ence frames (past and future) as per the RFD ratios

seen in Figure 7. Lines 28, 34 and 36 derive possi-

ble and legal reference frames within the GoP. The

RAND.CHOICE function, generates a random sample

from the given possible reference frame set, according

to the speciﬁed probabilities (derived from the distri-

butions).

The parameter N in Algorithm 1 can be varied to

obtain different GoP lengths. nBmax and W

can be

varied to obtain different numbers of B and P frames

within a GoP. rB

f wd

max

,rB

bwd

max

and rP

f wd

max

can be used to

provide more reference frames to P and B frames, this

would in turn increase the number of edges in the TG.

prob

r f d

is representative of the length of the edges in

the TG and also gives a notion of the number of pos-

sible reference frames for a B-frame.

5 DERIVING A FRAME-LEVEL

TASK MODEL

HEVC frames are logically partitioned into CTBs and

each CTB is sub-partitioned into CUs (Figure 1). The

objective of this work is to analyse the video prop-

erties at the CU granularity in order to understand

and derive a frame decoding model. For example,

when modelling an I-frame, a higher proportion of

smaller CU sizes may need to be used, while hav-

ing no P/B/Skip-CUs. A ﬁne-grain workload charac-

terisation can also facilitate exploration of CU/wave-

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

front/tile level task models as seen in (Roitzsch and

Pohlack, 2006; Chi et al., 2012).

5.1 CU Sizes, Types and Decoding Time

HEVC CUs can be of the size 64x64, 32x32, 16x16,

8x8, 4x4 (intra only) and can use either intra (I-

CU) or inter (P/B/Skip-CU) prediction. I-CUs refer

to other CUs within the same frame and P/B/Skip-

CUs refer to CUs in other frames. Skip-CUs are

those which do not have a residual or motion vector,

hence a reference-CU is copied directly, resulting in

reduced computation complexity at the decoder and

higher compression efﬁciency. Analysis of the CUs

by size and type is necessary to derive a coarse-grain

frame-level model. Figure 8 shows that intra and in-

ter predicted frame types differ signiﬁcantly in the us-

age of different CU sizes. There are a higher number

of smaller CUs in detailed scene background videos

(e.g.ObamaSpeech and Football) than others because.

Overall, 64x64 CUs are least used than other sizes,

however inter-frames seem to use signiﬁcantly more

64x64 CUs than intra-frames. The encoder has failed

to use small CU sizes for the ColouredNoise video.

As seen in Figure 9, except for ColouredNoise, all

other videos contain a large proportion of Skip-CUs.

The number of intra-predicted CUs (I-CU) seem to

be higher in video sequences with high-motion. The

inverse is true of Skip-CUs; for example in Oba-

Figure 8: Proportion of CU sizes within each video se-

quence (per Intra/Inter frame type).

Figure 9: Proportion of CU types within each video se-

quence (per Inter frame type).

Algorithm 1: Pseudo-code for GoP structure con-

struction.

1 Phase I - Construct GoP sequence

/* Parameter definition */

2 N = GoP length;

3 nB

max

= max. sequential B-frames;

4 assert((N − 1)%(nB

max

+ 1) == 0), validate parameters;

5 nP

min

= (N − 1)/(nB

max

+ 1);

6 nP

max

= (N − 1), max. P-frames;

/* Contiguous B-frame probs. - Figure 6 */

7 B

prob

seq

= [p

..p

(nB

max

)

];

/* exp. Weibull distributed num. P,B-frames */

8 W

= exp-Weibull PDF shape params: a, c, scale,loc

nP = EXPWEIBULL(W

).SAMPLE(nP

min

, nP

max

);

9 nB = (N −1) − nP;

10 nB

sizes

= [1..nB

max

], contiguous B-fr lengths;

/* main data structures */

11 B

f r

= {} /* hash table of positions and B-frame

numbers */

12 GOP

f r

= “I” + (“P” ∗ nP);

/* get contigous B-fr positions in the GoP */

13 while

∑

f r

.values() < nB do

14 pos = RAND.CHOICE([1..nP], prob=’UNIFORM’);

15 tmpB

f r

= RAND.CHOICE(nB

size

,prob=B

prob

seq

);

16 if (B

f r

[pos].value + tmpB

f r

) <= nB

max

then

17 B

f r

[pos]+ = tmpB

f r

;

18 end

19 end

20 GOP

f r

← B

f r

/* Put B-frames into GoP */

21 Phase II - Construct GoP frame references;

/* maximum frame references */

22 rB

f wd

max

,rB

bwd

max

= max. forward and backward B-frame refs.;

23 rP

f wd

max

= max. forward P-frame refs.;

24 vs

prob

r f d

: ref. dist. ratios;

/* hash table of inter-fr references */

25 f r

re f s

= {}

26 for f r

, f r ∈ GOP

f r

/* P-frames depend on prev. I/P frs */

27 if f r == “P” then

28 r

all f wd

POCs

= GOP

f r

[POC < f r

∩ (r

≤

max

) ∩ ¬“B”];

29 re f s

f wd

= RAND.CHOICE(r

all f wd

POCs

,size = rP

f wd

max

30 prob=vs

prob

r f d

);

31 f r

re f s

[ f r

] = re f s

f wd

32 else if f r == “B” then

/* B-fr depend on prev/future I/P/B frs */

33 r

all f wd

POCs

= GOP

f r

[POC < f r

∩ (r

≤ r

max

)];

34 r

all bwd

POCs

= GOP

f r

[POC > f r

∩ (r

≤ r

max

)];

35 re f s

f wd

= RAND.CHOICE(r

all f wd

POCs

,size = rB

f wd

max

36 prob=vs

prob

r f d

);

37 re f s

bwd

= RAND.CHOICE(r

all bwd

POCs

,size = rB

bwd

max

38 prob=vs

prob

r f d

);

39 f r

re f s

[ f r

] = {re f s

f wd

,re f s

bwd

};

41 end

maSpeech, the amount of Skip-CUs are between 80-

93%. Overall the number of P-CUs seem to be 2-

3 times the amount of B-CUs, and P-frames have

a higher amount of I-CUs than B-frames. The en-

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

coder has failed to use inter-prediction to compress

the ColouredNoise, where 99% of the video has been

coded using intra-CUs. BigBuckBunny has lower

amount of frame data because of the lower video res-

olution (480p).

The distributions of CU-level decoding time are

given in Figure 10. I,P and B-CUs are ﬁtted with

a exp-Weibull distribution (parameters given in Ta-

ble 2). Skip-CUs could belong to either P or B frames,

and could have 1 or 2 reference CUs; hence, the Skip-

CU decoding times appear to be multi-modal. They

are ﬁtted with a high-order polynomial function (co-

efﬁcients given in Table 3). The large coefﬁcient val-

ues in the model presents a risk of over ﬁtting the data;

however, we do not use the model to predict the de-

coding times, but randomly sample the distribution to

generate new workloads. As future work, regularisa-

tion can be used to prevent over ﬁtting.

High B-CU decoding times are due to complex

transformations, in bidirectional inter-prediction. B-

Figure 10: Normalised CU-level decoding time histogram

per video sequence. I/P/B-CUs distributions ﬁtted to a exp-

Weibull PDF (dashed line; parameters given in Table 2);

polynomial function ﬁtted to Skip-CUs (parameters given

in Table 3). (NB: Subﬁgures use different scales, share axes

and distribution tails are cropped in order to assist visuali-

sation).

Figure 11: Normalised frame-level decoding time distribu-

tion histogram for each video sequence.

Table 2: I/P/B-CU decoding time distribution, exp-Weibull

ﬁt shape parameters. (default location=0).

CU type a c scale

FastFurious5

I-CU 1.77E+01 6.56E-01 3.05E-06

P-CU 7.47 1.28 8.42E-06

B-CU 1.38 2.55 4.51E-05

LionWildlife

I-CU 9.24 7.43E-01 5.06E-06

P-CU 3.29 1.57 1.58E-05

B-CU 1.38 2.78 5.78E-05

Football

I-CU 2.87E+03 3.21E-01 1.02E-08

P-CU 9.12E+02 4.46E-01 1.44E-07

B-CU 7.13 1.35 1.99E-05

ObamaSpeech

I-CU 1.23E+03 3.25E-01 2.09E-08

P-CU 8.07E+02 3.93E-01 1.08E-07

B-CU 6.54 1.14 2.49E-05

BigBuckBunny

I-CU 6.56E+02 3.08E-01 1.93E-08

P-CU 3.47E+01 5.62E-01 1.49E-06

B-CU 4.74 9.47E-01 1.91E-05

CUs decoding times are about 2-3 times larger than

I and P-CUs. The CU decoding time is dependent on

the CU-size and content of the video sequence. This is

evident in the Football B-CU decoding times, where

compared to others has a lower variance in decoding

times, because of a higher proportion of inter-frame

8x8 CUs in the video stream. Furthermore, in Li-

onWildlife a high amount of 16x16,32x32,64x64 CU

sizes is seen, which could give rise to larger CU de-

coding times. Larger CU-sizes could lead to higher

decoding times due to bottlenecks at the memory sub-

systems (Kim et al., 2012). A trend can be seen in

the I-CU decoding time and the exp-Weibull shape

parameters; where high-motion, high scene-change

videos such as FastFurious5 and LionWildlife have

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

a lower a and higher c, leading to wider distribu-

tions. Overall Skip-CUs have the lowest decoding

time compared with the other CU-types.

The I-CU decoding time in ColouredNoise gave

the highest execution time out of all the videos; giv-

ing an observed worst-case CU decoding time of

4.94×10

−4

s. Football shows the lowest Skip-CU de-

coding time (1.08×10

−6

s), which indicates that de-

coding CUs can have two orders of magnitude vari-

ation, depending on the type of video and CU-type

and size. The CU-level decoding time data in Fig-

ure 10 correlates with the frame-level decoding time

shown in Figure 11. Overall in every video stream,

> t

where the terms t

, t

and t

denote I,P,B

frame decoding times. This is mainly due to the num-

ber of Skip-CUs in a frame. E.g. a B-frame primarily

contains Skip-CUs (Figure 9), and Skip-CUs decod-

ing times are lower than other CU types, resulting in

relatively lower overall B-frame decoding times. In

ObamaSpeech, I-frame decoding is approx. 2-3 times

larger than P,B-frame decoding. In FastFurious5 there

is low variation between average P and I frame de-

coding times, this is because 45% of P-frame CUs

are intra-coded. As expected it takes about 2-3 times

longer to decode ColouredNoise when compared to

the other streams, because about 99% of the stream

consists of I-CUs.

5.2 Inter-task Communication Volume

In Section 4.2 the inter-frame dependency pattern in a

GoP was discussed. This section investigates the vol-

ume of reference data required for inter-prediction,

which is essentially the weight of each arc in the

GoP-level TG. Apart from reference frame-data, the

encoded frame also needs to be loaded from main

memory in order to perform the decoding operations;

hence this data trafﬁc also forms part of the commu-

nication volume in the application.

The reference data is the pixel data of a decoded

frame; the maximum amount of data a P-frame can

reference is ( f r

size

= (h×w)×bpp), where h and w rep-

resents the frame dimensions and bpp is bytes per

pixel. For B-frames this upper bound is doubled due

to bi-directional prediction. Figure 12 shows the dis-

tribution of reference data categorised by direction of

reference; for example P ← I refers to the data ref-

erenced by a P-frame from an I-frame in the GoP.

Considering the distributions and their sample sizes

for each video stream, overall all inter-frames have

a preferred reference probability of: p

> p

where for example p

denotes the probability of a

frame obtaining data from an I-frame. This observa-

tion is true because B-frames have the lowest decoded

Figure 12: Distribution of frame reference data for all video

sequences. E.g. P ← I refers to the data referenced by a

P-frame from an I-frame. Sample-size of the distribution

given as n.

Figure 13: Distribution of frame compression ratio (en-

coded frame size as a % of the uncompressed frame size).

Distribution ﬁtted to Exp-Weibull PDF (dashed-line, pa-

rameters given in Table 4). (NB: Subﬁgures use different

scales in order to assist visualisation).

frame data accuracy due to bi-directional prediction,

and I-frames have the highest accuracy due only us-

ing intra-prediction. In a synthetic frame-level task

generator, probabilities of reference frame selection

is only required when the encoder allows the use of

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

more than 1 reference frame per direction. Further

observations showed that when considering the total

amount of referenced data per frame-type, B-frames

referenced twice the amount of data than P-frames.

The reference data distributions are highly depen-

dent on the reference frame distance (Figure 7), the

number of contiguous B-frames (Figure 6) and the

distribution of frame types (Figure 5) in a GoP. This is

also the reason for the wide variation of reference data

in the B ← P distribution. The data trafﬁc variation

seems to be higher in videos with high rate of scene-

change (e.g. FastFurious5), while the mean amount

of data volume is higher in largely static videos (e.g.

ObamaSpeech). ColouredNoise has very low refer-

ence data because a majority of the CUs are I-CUs.

The distribution of frame compression ratio are

given in Figure 13; this data represents the size of

an encoded frame. The distributions are ﬁtted with

a exp-Weibull distribution (parameters given in Ta-

ble 4). Unlike in (Krunz et al., 1995) where a Log-

normal distribution gave the best ﬁt for frame-size,

a right skewed distribution such as ObamaSpeech,

does not ﬁt a Lognormal distribution well. Overall,

> s

, where s

denote I/P/B encoded

frame sizes. However, the long-tailed distributions

tell us that there may be extreme-case scenarios where

this may not always be true (further veriﬁed in (Iso-

vic et al., 2003)). It can be observed that variation in

the distribution is relative to the motion/scene-change

rate of the video streams. Low-motion videos such as

ObamaSpeech have a much lower encoded P/B frame

size than high-motion videos. The distributions cor-

relate with the distribution of CU-sizes and CU-types

in a frame (Figure 8 and Figure 9). B-frame sizes

have very long-tailed distributions compared to I or

P-frames due to the variation in the number of Skip-

CUs in the frame; because Skip-CUs do not contain

a residual, the amount of data encoded is relatively

small. In general I-frame sizes have less variation

than inter-predicted frames.

5.3 Frame-level Task Generation

Algorithm 2 illustrates the frame-generation algo-

rithm pseudocode. The algorithm builds up the frame-

level task in a hierarchical bottom-up manner, by ﬁrst

iterating through each CTU in the frame (line 13) and

then constructing a set of CUs per CTU (lines 15-32).

The frame decoding time is calculated as the sum-

mation of the CU decoding time (C

) of all CUs in

the frame. Videos of different resolutions can be gen-

erated by changing the N

CTU

parameter accordingly;

h,w in line 2 is the resolution of the video. For each

CU in a CTU an appropriate value for the CU-type

Algorithm 2: Pseudo-code for frame construction, us-

ing CU-level properties.

/* Parameter definition */

1 CTU

max

= 64×64;

2 N

CTU

= (h×w)/CTU

max

,number of CTUs per frame;

3 CU

sizes

= 64,32, 16, 8,4;

4 CU

size

= CU size probabilities per frame type - Figure 8;

5 CU

types

= {I-CU, P-CU, B-CU, Skip-CU};

6 CU

types

= CU type probabilities - Figure 9;

7 W

= expWeibull parameters: a, c, scale,loc;

8 p

skip

= Skip-CU polynomial coefﬁcients;

9 dI

lim

,dP

lim

,dB

lim

,dSkip

lim

= min/max CU dec. cost;

/* Ref. frame selection params - Optional: if more

than 1 ref. frames per direction. */

10 f r

re f

= reference frames for current frame;

11 PB

r f

= Prob. of current fr referencing I/P/B frames;

/* Construct each CTU in the frame */

12 f r

CTUs

= /* empty CTU list in frame */

13 for each CTU ∈ [0..N

CTU

] do

14 px = 0;CTU

CUs

= {} /* init. data struct. */

/* get CU-level information */

15 while px < CTU

max

/* randomly select CU size */

16 C

= RAND.CHOICE(CU

sizes

,prob=C

);

17 if (px +C

) ≤ CTU

max

then

18 px+ = (C

)

;

/* randomly select CU type */

19 C

= RAND.CHOICE(CU

types

,prob=C

);

/* random dec. time per CU type */

20 if C

== “I-CU” then

21 C

EXPWEIBULL(W

).SAMPLE(dI

lim

);

22 else if C

== “P-CU” then

23 C

EXPWEIBULL(W

).SAMPLE(dP

lim

);

24 else if C

== “B-CU” then

25 C

EXPWEIBULL(W

).SAMPLE(dB

lim

);

26 else if C

== “Skip-CU ” then

27 C

POLYNOMIAL(p

skip

).SAMPLE(dSkip

lim

);

28 /* pick CU reference from reference

frame list */

29 C

r f

= RAND.CHOICE( f r

re f

,prob=PB

r f

);

/* append to CU list */

30 CU

in f o

= {C

r f

};

31 CTU

CUs

← CU

in f o

;

32 end

33 end

/* append to CTU list */

34 f r

CTUs

← CTU

CUs

;

35 end

(line 19), CU-size (line 16), CU decoding time (lines

20-27) and CU reference frame (line 28) is selected.

The selection process for these properties is facilitated

by the observations and derived PDFs at the CU/frame

level in Sections 5.1 and 5.2. A set of parameters

(lines 1-11) needs to be carefully chosen for the al-

gorithm, which are representative of the type of video

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

(e.g. high temporal activity with low number of ﬁne-

grain visual details) one intends to generate.

5.3.1 Limitations of the Workload Model

The CU type and size ratios given in Figure 10, 9 are

mean results obtained at the stream-level for differ-

ent frame types. In order to obtain variation of these

proportions between different individual frames, we

vary each percentage value according to a normal dis-

tribution. For example, when generating a frame for

FastFurious5, rather than taking the same value (31%

probability) for a SkipCU, we sample a normal distri-

bution with µ = 0.31 and σ = 0.05. The σ value needs

to be high enough to add a certain level of variation

between different frames of the same video stream,

but not too high such that the original proportions will

be masked. In real video streams however, the varia-

tion between frames would be complex and would not

ﬁt a theoretical distribution. A deeper analysis into

the distribution of the CU types and sizes of a distri-

bution of frames will need to be analysed, in order to

infer the variations between frames.

Secondly, the CU decoding time provided contain

latencies induced by the memory subsystems of the

platform. Hence, during our evaluation we noticed

the frame decoding time does not scale proportion-

ally to the number of different CUs. In order to ob-

tain a reasonable frame-level mode, the CU decod-

ing time model (Figure 10) needs to be scaled down.

Furthermore, the decoding time results shown in this

work are dependent on the decoder implementation

and our hardware architecture. The scale factors need

to be tuned appropriately to suit a platform with dif-

ferent memory and CPU characteristics. CUs that

require more memory transactions such as P/B/Skip

CUs would need to be scaled down more than I-CUs.

During evaluation of the generator we noticed a scale-

down factor of 0.02-0.03 for I/P/B-CUs and 0.002-

0.002 for Skip-CU decoding times gave satisfactory

results.

6 WORKLOAD GENERATOR

USAGE

As discussed in Section 1 the algorithms presented in

Algorithm 1 and 2 can be used in system-level sim-

ulations to facilitate evaluation of workload resource

management and scheduling techniques (e.g. (Mendis

et al., 2015; Kreku et al., 2010; Yuan and Nahrstedt,

2002)). For example in (Mendis et al., 2015), we see

a multi-stream video decoding application workload

that needs to be allocated to multiple processing el-

ements in order to maximise system utilisation. Fig-

ure 14 shows how the workload generators proposed

in this work can be integrated into system simulators.

The workload generators can be used to output task-

level information (e.g. dependency patterns, execu-

tion costs, communication costs, arrival times) of a

large quantity of video streams, into text-based data

ﬁles (e.g. XML/CSV format) and read back in by

the simulator to be used as input for system perfor-

mance evaluation. The bottom-up methodology fur-

ther adds ﬂexibility into the framework, such that the

CU-level information can also be used to generate

HEVC tile/wave-front (Chi et al., 2013) based work-

loads, in a similar manner to generating frames.

As illustrated in Figure 14, a video stream can be

generated by generating multiple GoPs using Algo-

rithm 1. Within each GoP a frame can be generated

using Algorithm 2. Likewise, any number of video

streams can be synthetically generated and fed into

a simulator. The GoP/frame-level model parameters

(e.g. exp-Weibull PDF shape parameters, CU size/-

type ratios), should be selected based on the type of

video. Variations of videos can be generated by mix-

ing/adapting the model parameters. For example, a

high-motion video with a ﬁne-detailed background

can be generated by using a high nP distribution sim-

ilar to LionWildlife (Figure 5) and using proportions

of CU-sizes similar to ObamaSpeech(Figure 8, high

4x4, 8x8 count).

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate GoP

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate GoP

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate GoP

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate GoP

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CUs

Generate Frame

Generate CTUs/CUs

Generate Frame

Generate GoP

(taskset with

dependencies)

Video stream (abstract workload)

System simulator

(e.g. multicore platform)

workload input

(pregenerated data ﬁles)

System evaluation

results

Scheduler

Resource manager

Processing elements

GoP/Frame/CU

generator

parameters

Proposed workload generator

Figure 14: Integration of the bottom-up workload generator

with a system simulator. (M=Number of GoPs).

Usage examples, implementation source code and

analysis data has been made open to the community

for reproducibility of the analyses/results and applica-

bility of the workload generation algorithms (Mendis,

2015).

7 EVALUATION

To evaluate the proposed video decoding workloads,

we synthetically generated 200 GoPs of the Lion-

Wildlife video stream and compared against the data

gathered from the real LionWildlife video. From Fig-

ure 15(a) we can see that the number of P-frames in

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

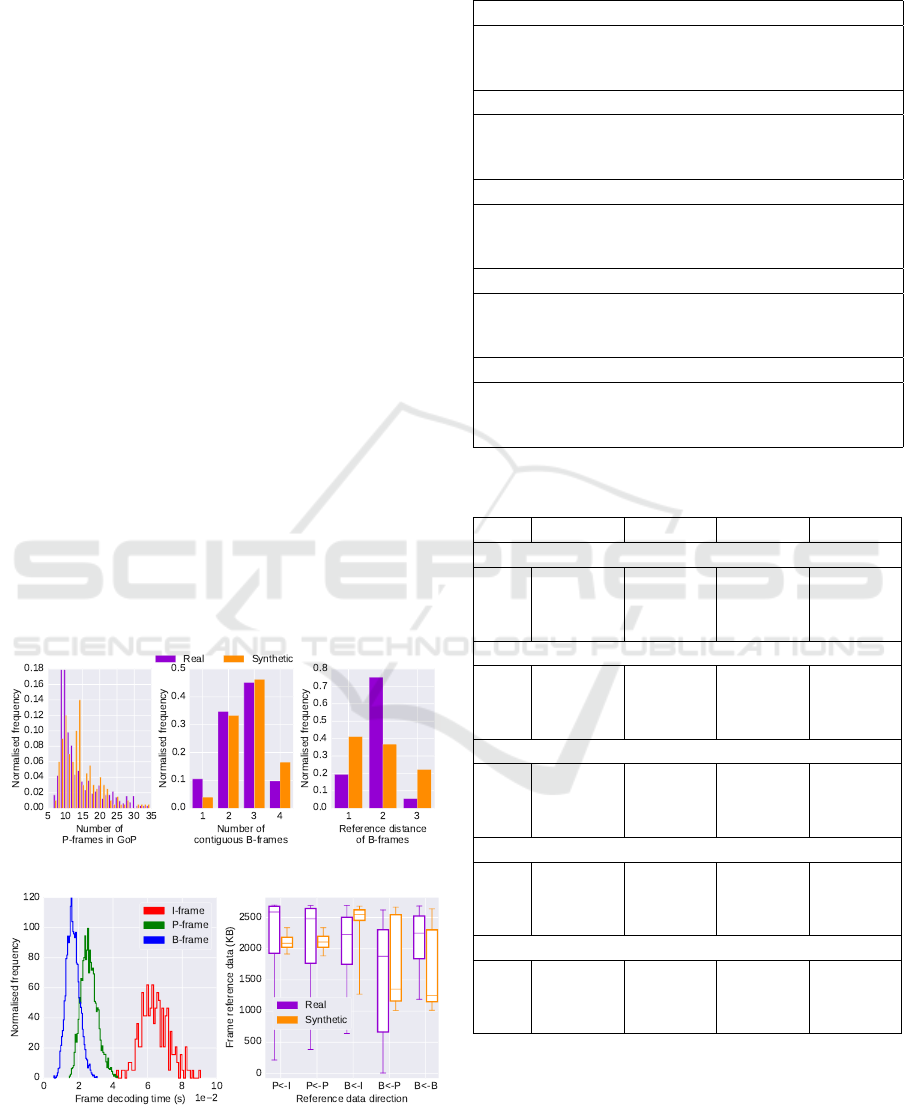
the generated GoPs follow a exp-Weibull distribution

as shown by the ﬁt in Figure 5. However, the distri-

bution is slightly shifted to the right causing a higher

number of 4 contiguous B-frames which in turn af-

fects the reference distance ratios. A reference dis-

tance of 3 is still the lowest, similar to the real video

stream.

Figure 15(b)(left) shows the decoding time distri-

butions of the synthetically generated frames; these

need to be evaluated against the data given in Fig-

ure 11(LionWildlife). Due to inaccurate representa-

tion of the frame-level variations (Section 5.3.1), the

distribution of the frame decoding times generated do

not exactly follow the same shape as the real video

stream. However, we can see that the decoding times

are approximately in the same region for P and B

frames (i.e between 1.0 − 4.0×10

−2

s), which is ma-

jority of the video stream; and a slightly larger I-

frame decoding time (4.0 − 8.5×10

−2

s) can be seen.

The difference in decoding times between P and

B frames follow a similar trend to the real video

stream, as P-frame decoding times are overall larger

than B-frames. The generated frame decoding times

show a narrower spread of values than the real video

stream. We also evaluate the reference data volume

distributions between the synthetically generated and

real video stream. Figure 15(b)(right) shows that the

P ← I and P ← P show a narrower spread of data

volume than the real video stream. B ← I results are

higher than the real video and B ← B show a slightly

(a) GoP structure comparison: Left

(b) Frame characteristics comparison: Left

Figure 15: Comparison of GoP and frame-level characteris-

tics of a real vs. synthetically generated video stream.

Table 3: Skip-CU decoding time distribution, polynomial

ﬁt coefﬁcients.

FastFurious5, f(x)=

2.34×10

− 4.62×10

x +3.87×10

− 1.78×10

4.84×10

− 7.63×10

+ 5.82×10

4.03×10

− 4.09×10

+ 2.45×10

− 2.99×10

LionWildlife, f(x)=

−8.75×10

+ 3.92×10

x −7.60×10

+ 8.35×10

−

5.71×10

+ 2.52×10

− 7.21×10

1.30×10

− 1.38×10

+ 7.40×10

− 9.15×10

Football, f(x)=

−8.54×10

+ 3.41×10

x −5.87×10

+ 5.71×10

−

3.43×10

+ 1.32×10

− 3.24×10

4.90×10

− 4.22×10

+ 1.75×10

− 1.82×10

ObamaSpeech, f(x)=

5.45×10

− 4.99×10

x −3.55×10

+ 7.47×10

−

4.81×10

+ 1.65×10

− 3.32×10

3.93×10

− 2.61×10

+ 8.51×10

− 9.65×10

BigBuckBunny, f(x)=

−1.13×10

+ 5.22×10

x −1.04×10

+ 1.16×10

−

8.05×10

+ 3.58×10

− 1.03×10

1.84×10

− 1.92×10

+ 9.95×10

− 1.16×10

Table 4: Encoded frame size distributions, exp-Weibull ﬁt

shape parameters.

Frame a c loc scale.

FastFurious5

I-Fr 4.76E+01 5.15E-01 5.81E-04 1.93E-04

P-Fr 1.57E+01 7.90E-01 2.71E-05 4.41E-04

B-Fr 1.29 7.38E-01 2.46E-05 3.08E-04

LionWildlife

I-Fr 1.31E+02 4.50E-01 0.00 1.52E-04

P-Fr 1.20E+01 5.07E-01 0.00 1.27E-04

B-Fr 1.17 7.79E-01 1.99E-05 2.47E-04

Football

I-Fr 6.05E-01 2.74E+00 2.74E-03 1.81E-02

P-Fr 4.15 9.49E-01 1.45E-04 1.56E-03

B-Fr 1.16 8.88E-01 1.92E-05 4.15E-04

ObamaSpeech

I-Fr 4.56E-01 6.21E+00 1.29E-02 3.69E-03

P-Fr 1.60 1.18E+00 3.79E-05 4.17E-04

B-Fr 8.45E+01 2.66E-01 2.31E-05 1.10E-07

BigBuckBunny

I-Fr 3.36 1.23 0.00 1.39E-02

P-Fr 5.51 4.59E-1 2.23E-05 1.70E-04

B-Fr 9.80E-01 7.34E-01 3.17E-05 2.57E-04

lower distribution. However the inter-quartiles of the

real and synthetic video distributions overlap, spe-

cially in the case of B ← P. These discrepancies are

also a result of the differences in B-frame reference

distances (Figure 15(a)(right)) and also the limitation

of getting an accurate view of the inter-frame CU vari-

ations.

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

8 CONCLUSION

The aim of this paper was to characterise the work-

load of HEVC decoding at the GoP, frame and CU

level. The state-of-the-art in video stream workload

modelling, either assumes Gaussian distributed ran-

dom properties such as frame decoding times and de-

pendent data volumes or tries to estimate the decoding

times with respect to frame sizes. Furthermore data

dependency patterns (i.e. GoP structure patterns) are

not addressed in the state-of-the-art. In this work, a

bottom-up workload generation methodology is pre-

sented where, block-level characteristics were used to

derive higher-level properties such as frame execution

costs and reference data volumes. This work attempts

to generate video decoding workloads with real sta-

tistical properties obtained from proﬁled video de-

coding tasks. It was found that frame-level decoding

time correlated well with the CU-level statistics ob-

tained. This work quantitatively shows that the inter-

frame dependency pattern of the GoPs are highly cor-

related with the level of activity or motion in the video

stream. Algorithms were presented to generate the

GoP sequence and structure as well as frame genera-

tion which satisfy the probability density of real video

streams.

The exponential Weibull distribution was ﬁt to the

distribution of the number of P/B frames in a GoP,

CU-level decoding time and encoded frame sizes. To

represent the multi-modal nature of Skip-CU decod-

ing times, higher-order polynomial functions were

chosen. Characteristics of different types of video

streams including high/low activity and coarse/ﬁne

level detail imagery was analysed. The workload gen-

eration algorithms presented can be used as an input

to system-level simulators. The evaluation of the pro-

posed technique showed that the workload generators

do not fully capture the extreme variations between

frames. However, the average-case properties of real-

video streams and synthetically generated streams are

comparable.

As future work, ﬁrstly, we hope to analyse the

frame-level variations and in more detail to improve

the accuracy of the synthetic workload. Secondly,

the relationship between the workload model and the

experimental platform (e.g. decoder conﬁguration,

memory and processor architecture etc.) will need to

be further analysed to derive a robust generator. Fur-

thermore, the workload generator would need to be

evaluated with higher resolution videos (e.g., 1080p

or 4k) and high frame rates (e.g. 60 fps).

ACKNOWLEDGEMENT

We would like to thank the LSCITS program

(EP/F501374/ 1), DreamCloud project (EU FP7-

611411) and RheonMedia Ltd.

REFERENCES

Alvarez, M., Salami, E., Ramirez, A., and Valero, M.

(2005). A performance characterization of high deﬁ-

nition digital video decoding using H.264/AVC, pages

24–33.

Bavier, A. C., Montz, A. B., and Peterson, L. L. (1998).

Predicting mpeg execution times. In ACM SIGMET-

RICS Performance Evaluation Review, pages 131–

140. ACM.

Benmoussa, Y., Boukhobza, J., Senn, E., Hadjadj-Aoul, Y.,

and Benazzouz, D. (2015). A methodology for perfor-

mance/energy consumption characterization and mod-

eling of video decoding on heterogeneous soc and its

applications. Journal of Systems Architecture, pages

49–70.

Bossen, F., Bross, B., Suhring, K., and Flynn, D.

(2012). HEVC complexity and implementation anal-

ysis. IEEE TCSTV, 22:1685–1696.

Chi, C. C., Alvarez-Mesa, M., Juurlink, B., Clare, G.,

Henry, F., Pateux, S., and Schierl, T. (2012). Paral-

lel scalability and efﬁciency of HEVC parallelization

approaches. IEEE TCSVT, 22:1827–1838.

Chi, C. C., Alvarez-Mesa, M., Lucas, J., Juurlink, B., and

Schierl, T. (2013). Parallel HEVC decoding on multi

and many-core architectures: A power and perfor-

mance analysis. Journal of Signal Processing Sys-

tems, 71:247–260.

Eom, Y., Park, S., Yoo, S., Choi, J. S., and Cho, S. (2015).

An analysis of scene change detection in HEVC bit-

stream. In IEEE ICSC, pages 470–474. IEEE.

Hamidouche, W., Raulet, M., and Deforges, O. (2014). Real

time SHVC decoder: Implementation and complexity

analysis. In IEEE ICIP, pages 2125–2129.

Holliman, M. and Chen, Y. K. (2003). Mpeg decoding

workload characterization. In CAECW Workshop.

Isovic, D., Fohler, G., and Steffens, L. (2003). Timing con-

straints of MPEG-2 decoding for high quality video:

misconceptions and realistic assumptions. In Euromi-

cro Conf. on Real-Time Sys., pages 73–82. IEEE.

Kim, I.-K., Min, J., Lee, T., Han, W.-J., and Park, J.

(2012). Block partitioning structure in the HEVC

standard. Circuits and Systems for Video Technology,

IEEE Transactions on, 22:1697–1706.

Kreku, J., Tiensyrja, K., and Vanmeerbeeck, G. (2010). Au-

tomatic workload generation for system-level explo-

ration based on modiﬁed GCC compiler. In DATE

Conf., pages 369–374.

Krunz, M., Sass, R., and Hughes, H. (1995). Statistical

characteristics and multiplexing of MPEG streams. In

INFOCOM, pages 455–462. IEEE.

Synthetic Workload Generation of Broadcast Related HEVC Stream Decoding for Resource Constrained Systems

Liu, W., Xu, J., Wu, X., Ye, Y., Wang, X., Zhang, W.,

Nikdast, M., and Wang, Z. (2011). A noc trafﬁc suite

based on real applications. In IEEE ISVLSI.

Mashat, A. S. (1999). VBR MPEG trafﬁc: characterisa-

tion, modelling and support over ATM networks. PhD

thesis, University of Leeds.

Mendis, H. R. (2015). Analysis data, sourcecode and

usage examples of proposed workload generator.

http://gdriv.es/hevcanalysisdata.

Mendis, H. R., Audsley, N. C., and Indrusiak, L. S. (2015).

Task allocation for decoding multiple hard real-time

video streams on homogeneous nocs. In INDIN conf.

Mudholkar, G. S., Srivastava, D. K., and Freimer, M.

(1995). The exponentiated weibull family: a reanal-

ysis of the bus-motor-failure data. Technometrics,

37:436–445.

Multicoreware (2015). x265 HEVC encoder/h.265 video

codec. http://x265.org/. [Online; accessed 26-

October-2015].

Naccari, M., Weerakkody, R., Funnell, J., and Mrak, M.

(2015). Enabling ultra high deﬁnition television ser-

vices with the hevc standard: The thira project. In

IEEE ICMEW conf.

Opensource (2015). Openhevc HEVC decoder.

https://github.com/openhevc/. [Online; accessed

26-October-2015].

Roitzsch, M. and Pohlack, M. (2006). Principles for the

prediction of video decoding times applied to MPEG-

1/2 and MPEG-4 part 2 video. In RTSS conf.

Saponara, S., Denolf, K., Lafruit, G., Blanch, C., and Bor-

mans, J. (2004). Performance and complexity co-

evaluation of the advanced video coding standard for

cost-effective multimedia communications. EURASIP

J. Appl. Signal Process., pages 220–235.

Soares, A. B., Bonatto, A. C., and Susin, A. A. (2013). De-

velopment of a soc for digital television set-top box:

Architecture and system integration issues. Interna-

tional Journal of Reconﬁgurable Computing.

Sullivan, G., Ohm, J., Han, W.-J., and Wiegand, T. (2012).

Overview of the high efﬁciency video coding (HEVC)

standard. IEEE TCSVT journal, 22(12):1649–1668.

Tanwir, S. and Perros, H. (2013). A survey of VBR video

trafﬁc models. IEEE Communications Surveys Tuto-

rials, pages 1778–1802.

Wu, H., Claypool, M., and Kinicki, R. (2005). Guidelines

for selecting practical MPEG group of pictures. In In

Proceedings of IASTED (EuroIMSA) conf.

Yuan, W. and Nahrstedt, K. (2002). Integration of dynamic

voltage scaling and soft real-time scheduling for open

mobile systems. In NOSSDAV workshop.

Zach, O. and Slanina, M. (2014). A comparison of

H.265/HEVC implementations. In ELMAR, 2014.

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications