Detecting Data Stream Dependencies on High Dimensional Data

Jonathan Boidol

1,2

and Andreas Hapfelmeier

Institute for Informatics, Ludwig-Maximilians University, Oettingenstr. 67, D-80538, Munich, Germany

Corporate Technology, Siemens AG, Otto-Hahn-Ring 6, D-81739, Munich, Germany

Keywords:

Sensor Application, Online Algorithm, Entropy-based Correlation Analysis.

Abstract:

Intelligent production in smart factories or wearable devices that measure our activities produce on an ever

growing amount of sensor data. In these environments, the validation of measurements to distinguish sensor

ﬂukes from signiﬁcant events is of particular importance. We developed an algorithm that detects dependencies

between sensor readings. These can be used for instance to verify or analyze large scale measurements. An

entropy based approach allows us to detect dependencies beyond linear correlation and is well suited to deal

with high dimensional and high volume data streams. Results show statistically signiﬁcant improvements in

reliability and on-par execution time over other stream monitoring systems.

1 INTRODUCTION

Large-scale wireless sensor networks (WSN) and

other forms of remote monitoring, reaching from

personal activity to surveillance of industrial plants

or whole ecological systems are advancing towards

cheap and widespread deployment. This progress has

spurred the need for algorithms and applications that

work on high dimensional streaming data. Stream-

ing data analysis is concerned with applications where

the records are processed in unbounded streams of in-

formation. Popular examples include the analysis of

streams of text, like in twitter, or the analysis of image

streams, like in ﬂickr. However, there is also an in-

creasing interest in industrial applications. The nature

and volume of this type of data make traditional batch

learning exceedingly difﬁcult, and ﬁt naturally to al-

gorithms that work in one pass over the data, i.e. in an

online-fashion. To achieve the transition from batch

to online algorithms, window-based and incremental

algorithms are popular, often favoring heuristics over

exact results.

Instead of relying only on single stream statis-

tics to e.g. detect anomalies or ﬁnd patterns in the

data, this paper is concerned with a setting where we

ﬁnd many sensors monitoring in close proximity or

closely related phenomena, for example temperature

sensors in close spacial proximity or voltage and ro-

tor speed sensors in large turbines. It appears obvi-

ous that we should be able to utilize the – in some

sense redundant, or rather shared – information be-

tween sensor pairs to validate measurements. The

task at hand becomes then to reliably and efﬁciently

compute and report dependencies between pairs or

groups of data streams. We can imagine such a sce-

nario in the context of smart homes or smart cities

with personal monitoring or automated manufactur-

ing that form the internet of things. A particular ap-

plication could be the validation of sensor readings in

the context of multiple cheap sensors where measure-

ments are possibly impaired by limited technical pre-

cision, processing errors or natural ﬂuctuations. Then,

unusual readings might either indicate actual changes

in the monitored system or be due to these measuring

uncertainties. Finding correlations helps differentiate

such cases.

The best known indicator for pairwise correla-

tion is Pearson’s correlation coefﬁcient ρ, essentially

the normalized covariance between two random vari-

ables. Direct computation of ρ, however, is pro-

hibitively expensive and, more problematic, it is only

a suitable indicator for linear or linear transformed re-

lationships (Granger and Lin, 1994). Non-linearity in

time-series has been studied to some extent and may

arise for example due to shifts in the variance (Fernan-

dez et al., 2002) or simply if the underlying processes

are determined by non-linear functions.

We propose an algorithm that is used to detect

dependencies in high volume and high dimensional

data streams based on the mutual information be-

tween time series. The three-fold advantages of our

approach are that mutual information captures global

dependencies, is algorithmically suitable to be calcu-

lated in an incremental fashion and can be computed

Boidol, J. and Hapfelmeier, A.

Detecting Data Stream Dependencies on High Dimensional Data.

DOI: 10.5220/0005953303830390

In Proceedings of the International Conference on Internet of Things and Big Data (IoTBD 2016), pages 383-390

ISBN: 978-989-758-183-0

383

efﬁciently to deal with high data volume without the

need for approximation short-cuts. This leads to a de-

pendency measure that is signiﬁcantly faster to calcu-

late and more accurate at the same time.

The remainder of this paper is organized as fol-

lows: We will present the background in information

theory for mutual information, introduce the termi-

nology to use it in a streaming algorithm and explain

our main algorithm called MID in section 2. Section

3 contains the experimental evaluations on one syn-

thetic and four real world datasets. We conclude and

suggest possible future work in section 4.

2 MUTUAL INFORMATION

DEPENDENCY

This section introduces the necessary background to

the concept mutual information and shows our adap-

tation into MID, a convenient, global measure to de-

tect dependencies between data streams.

2.1 Correlation and Independence

(Dionisio et al., 2004) argue that mutual information

is a practical measure of dependence between random

variables directly comparable to the linear correlation

coefﬁcient, but with the additional advantage of cap-

turing global dependencies, aiming at linear and non-

linear relationships without knowledge of underlying

theoretical probability distributions or mean-variance

models.

StatStream(Zhu and Shasha, 2002) and PeakSimi-

larity(Seliniotaki et al., 2014) are algorithms to moni-

tor stream correlation. Both employ variants of a dis-

crete fourier transformation (DFT) to detect similari-

ties based on the data compression qualities of DFT.

More speciﬁcally, they exploit that DFT compresses

most of a time series’ information content in few co-

efﬁcients and develop a similarity measure on these

coefﬁcients. The similarity measure for Peak Similar-

ity is deﬁned as

peak similarity(X,Y ) =

∑

i=1

1 −|

−

2 ·max(|

|,|

where X and Y are the time series we want to compare

and

the n coefﬁcients with the highest magnitude

of the respective Fourier transformations.

The similarity measure of Stat Stream is similarly

deﬁned on the DFT coefﬁcients as

stat stream(X,Y ) =

∑

i=1

(

−

)

but here

are the largest coefﬁcients of the re-

spective Fourier transformations of the normalized X

and Y .

StatStream also uses hashing to reduce execution

time, but the choice of hash functions is highly appli-

cation speciﬁc. PeakSimilarity relies on a similarity

measure specially deﬁned to deal with uncertainties in

the measurement, but requires in-depth apriori knowl-

edge of a cause-and-effect model to do so.

We develop our own measure based on mutual

information and compare its accuracy and execution

time to the DFT-based measures and the correlation

coefﬁcient.

2.2 Mutual Information

Mutual information is a concept originating from

Shannon information theory and can be thought of

as the predictability of one variable from another

one. We will exploit some of its properties for

our algorithm. Since the mathematical aspects are

quite well-known and described extensively else-

where, e.g. (Cover, 1991), we will review just the ba-

sic background and notation needed in the rest of the

paper. The mutual information between variables X

and Y is deﬁned as

I(X;Y ) =

∑

y∈Y

∑

x∈X

p(x,y)log



p(x,y)

p(x)p(y)



(1)

or equivalently as the difference between the

Shannon-entropy H(X ) and conditional entropy

H(X |Y ):

I(X;Y ) = H(Y ) −H(Y |X) (2)

= H(X )−H(X |Y ) (3)

= H(X )−H(X ,Y ) + H(Y ). (4)

Shannon-entropy and conditional entropy are de-

ﬁned as

H(X ) =

∑

x∈X

p(x)log



p(x)



(5)

H(X |Y ) =

∑

y∈Y

∑

x∈X

p(x,y)log



p(y)

p(x)p(y)



. (6)

I(X;Y ) is bounded between 0 and

max(H(X ),H(Y )) = log(max(|X|, |Y |)) so we

can deﬁne a normalized

I(X;Y ) which becomes 0 if

X and Y are mutually independent and 1 if X can be

predicted from Y and vice versa. This makes it easily

comparable to the correlation coefﬁcient and also

forms a proper metric.

I(X;Y ) = 1 −

I(X;Y )

log(max(|X|,|Y |))

. (7)

IoTBD 2016 - International Conference on Internet of Things and Big Data

384

Figure 1: Sliding window and pairwise calculation of

I for

a data stream with window size w = 5 and |S|= 3.

Next, we want to compute

I for pairs of streams

∈S at times t. The streams represent a measurement

series s

= (. ..,m

t+1

t+2

,...) without beginning

or end so we add indices s

t,w

to denote measurements

from stream s

from time t to t + w −1, i.e. a win-

dow of length w. |S| is the dimension of the overall

data stream S in the sense that every s

represents a

series of measurements of a different type and/or dif-

ferent sensor. We will drop indices where they are

clear from the context. Our goal is then to efﬁciently

calculate the stream dependencies D

for all points t

in the observation period t ∈ [0;inf)

= {

I(s

t,w

)|s

∈ S}. (8)

Figure 1 demonstrates the basic window approach for

a stream with three dimensions.

2.3 Estimation of PDFs

Two problems remain to determine the probability

distribution functions (PDFs) we need to calculate en-

tropy and mutual information. First, data streams of-

ten contain both nominal event data and real values.

Consequentially our model needs to deal with both

continuous and discrete data types. Second, the un-

derlying distribution of both single stream values and

of the joint probabilities is usually unknown and must

be estimated from the data.

There are three basic approaches to formulate a

probability distribution estimate: Parametric meth-

ods, kernel-based methods and binning. Parametric

methods need speciﬁc assumptions on the stochas-

tic process and kernel-based methods have a large

number of tunable parameters where sensible choices

are difﬁcult and maladjustment will lead to biased

or erroneous results.(Dionisio et al., 2004) Binning

or histogram-based estimators are therefore the safer

and more feasible choice for continuous data which

have been well studied (Paninski, 2003; Kraskov

et al., 2008), and a natural ﬁt for discrete data. They

have been used convincingly in different applica-

tions.(Dionisio et al., 2004; Daub et al., 2004; Sor-

jamaa et al., 2005; Han et al., 2015)

Quantization, the ﬁnite number of observations

and the ﬁnite limits of histograms – depending on

the speciﬁc application – might lead to biased re-

sults. However (Dionisio et al., 2004) argue that both

equidistant and equiprobable binning lead to a consis-

tent estimator of mutual information.

Of the two fundamental ways of discretization -

equal-width or equal-frequency - equal-width binning

is algorithmically slightly easier to execute, since it

is only necessary to keep track of the current min-

imum and maximum. Equal frequency binning re-

quires more effort, but has been shown to be the bet-

ter estimator for mutual information.(Bernhard et al.,

1999; Darbellay, 1999) We conﬁrmed this in a sepa-

rate set of experiments and consequentially use equal

frequency binning for our measure.

The choice of the number of bins b is a criti-

cal problem for a reliable method. (Hall and Mor-

ton, 1993) point out that histogram estimators may be

used to construct consistent entropy estimators for 1-

dimensional samples and describe an empiric method

for histogram construction depending on the num-

ber of data points n in the sample and the expected

range of values R. Their rule balances bias and vari-

ance components of the estimation error and reduces

to b ≥

−0.32

. Typical ranges and sample sizes in

our intended applications would result in a choice of

b ∈ [10,100].

For our algorithm, we discretize on a per-window-

basis. A window-wise discretization gives us a local

view on the data since it depends only on the prop-

erties of the data in the window but is also limited to

the data currently available in the window. We call

I(X;Y ) with per-window discretization MID – mu-

tual information dependency. For greater clarity, we

add pseudocode for MID as Algorithm 1.

The new incoming values possibly change the his-

togram boundaries in the window and therefore the

underlying empirical probability distribution at each

step which gives a runtime of O(w ·n) after n steps.

We evaluate MID on real-valued data in section 3.

Algorithm 1: Window-wise Computation of Dependencies.

1: procedure MID(data streams S)

2: for s

t,w

∈ S do

3: ˆs ← Discretize(s

t,w

)

4: P ← getPDF( ˆs)  generate PDFs

5: H ← entropy(P)

6: CH ← condEntropy(P)  for all pairs

I ← norm(H,CH) of streams

8: yield

9: end for

10: end procedure

Detecting Data Stream Dependencies on High Dimensional Data

385

3 EXPERIMENTAL EVALUATION

We evaluate MID against two other algorithms for

stream correlation monitoring ﬁrst on three synthetic

dataset and second on four real life datasets. The Re-

sults for the synthetic data is shown in Figure 2 and

for the real datasets are shown in Figures 3 to 6, Ta-

bles 1 and 2 show an overview to compare methods

with each other.

3.1 Synthetic Data

We created a synthetic datasets with four time series

of 6400 datapoints each. Each consists of a non-

linear function of the elapsed time t in the ﬁrst 3200

time steps and gaussian noise in the second half. The

functions are chosen similar to the ﬁrst Friedman data

set.(Friedman, 2001):

f (t,i) =











t mod 400, if i = 0.

sin(t) + sin(t/3 + 20), if i = 1.

t + t

, if i = 2.

√

1 −t

, if i = 3.

(9)

The advantage of the synthetic data is a clear

knowledge of the dependency (and predictability) in

the data which has to be inferred in other data without

prior knowledge. We call the resulting data set NL.

3.2 Stream Datasets

We use four datasets to evaluate our algorithm with

different numbers of time steps and dimensions, rang-

ing from 32.000 to 332 million measurements in to-

tal. They have been used to emulate the high volume

data streams consistently and allow comparison of the

methods.

NASDAQ (NA) contains daily course information

for 100 stock market indices from 2014 and 2015,

with 600 indicators (including e.g. open and high

course or trading volume) over 320 days in total.(The

NASDAQ Stock Market, 2015)

PersonalActivity (PA) is a dataset of motion cap-

ture where several sensors have been placed on ﬁve

persons moving around. The sensors record their

three-dimensional position. This dataset contains 75

data points each from 5.255 time steps.(Kalu

za et al.,

2010)

OFFICE (OL) is a dataset by the Berkley Re-

search Lab, that collected data about temperature, hu-

midity, light and voltage from sensors placed in a lab

ofﬁce. We use a subset of 32 sensors since there are

large gaps in the collection. The subset still contains

some gaps that have been ﬁlled in with a missing-

value indicator. In total this datasets contains 128

●

0.4 0.5 0.6 0.7 0.8 0.9 1.0

AUC

PeakSim

StatStream

Corr.Coeff.

MID

(a) AUC

●

0.7 0.8 0.9 1.0

PeakSim

StatStream

Corr.Coeff.

MID

(b) F1-score

Figure 2: (a) Area under ROC curve and (b) F1-value on NL

dataset.

measurements over 65.537 time steps.(Bodik et al.,

2004)

TURBINE (TU) contains measurements from 39

sensors in a turbine over half an hour with measure-

ments every quarter of a millisecond. This is the

largest of our datasets and contains 39 measurements

over about 8.5 million time steps.(Siemens AG, 2015)

3.3 Experimental Settings

Window size w determines the scale of correlation we

are interested in and eventually has to be chosen by

the user. For the purpose of this evaluation we set it

w = 80 for the synthetic data and equivalent to 1 sec-

ond for the turbine dataset, 30 seconds for the other

sensor datasets, and to 4 weeks for the stock market

dataset. The number of bins b for the discretization

needs to be small enough to avoid singletons in the

histogram but large enough to map the data distribu-

tion – we considered criteria for a sensible choice in

section 2.3. As a compromise we chose b = 20 for

IoTBD 2016 - International Conference on Internet of Things and Big Data

386

0.40 0.45 0.50 0.55 0.60 0.65 0.70

AUC

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(a) AUC

0.00 0.05 0.10 0.15 0.20 0.25

F1 max

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(b) F1-score

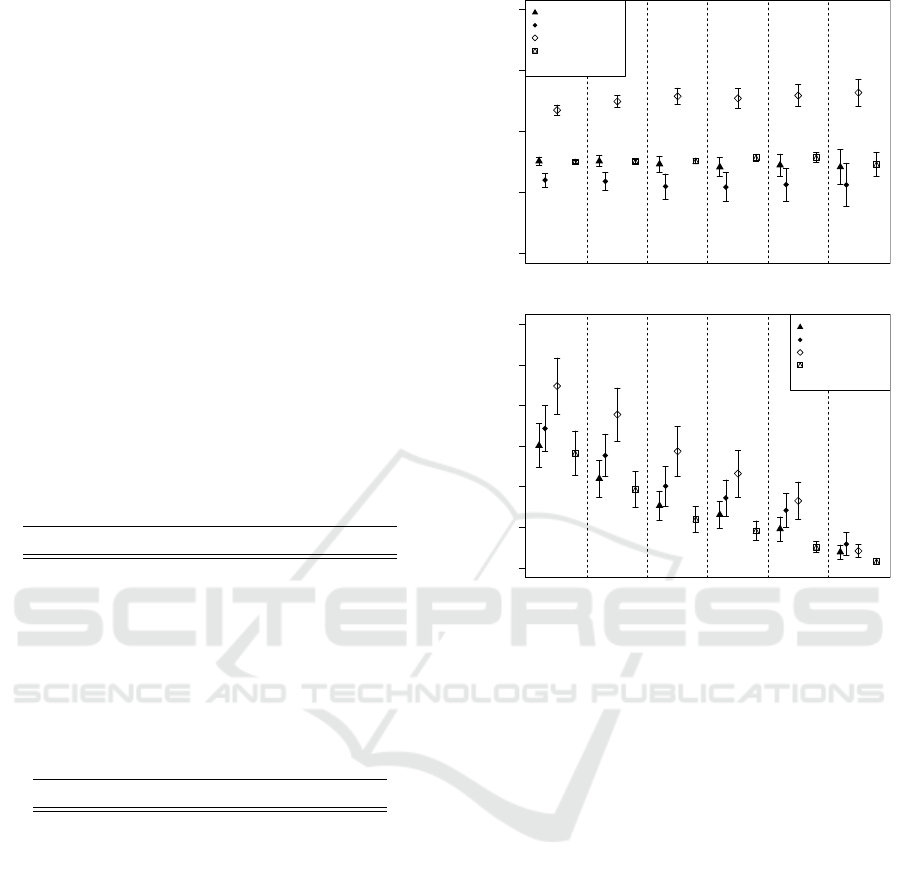
Figure 3: (a) Area under ROC curve and (b) maximum F1-

value on TU dataset. Areas separated by dashed ines show

performance at different levels of desired correlation.

the experiments. PeakSim and StatStream use a pa-

rameter n that determines the number of DFT-peaks

used, and inﬂuences runtime and memory in a similar

way b inﬂuences MID. Consequently we set n equal

to b, which is very close to the choice of n in (Zhu and

Shasha, 2002) and (Seliniotaki et al., 2014).

We calculate dependency of every dimension with

every other, e.g. voltage with temperature. So, for a

dataset n ×d i.e. with n steps and d dimensions we

calculate (n −w) ·





dependency scores. Statistical

signiﬁcance is determined with a standard two-sided

t-test.

3.4 Evaluation Criteria

For the synthetic dataset we provide the area under

ROC curve as classiﬁcation measure that is indepen-

dent from the number of true positives in the dataset:

AUC = P(X

> X

), (10)

where X

and X 2 are the scores for a positive and neg-

ative instance respectively.

0.4 0.5 0.6 0.7 0.8

AUC

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(a) AUC

0.0 0.1 0.2 0.3 0.4 0.5

F1 max

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(b) F1-score

Figure 4: (a) Area under ROC curve and (b) maximum F1-

value on OL dataset. Areas separated by dashed lines show

performance at different levels of desired correlation.

Also, we report the F1-measure, i.e. the harmonic

mean of precision and recall:

F1 = 2 ·

precision·recall

precision+recall

, (11)

precision =

T P

T P+FP

, (12)

recall =

T P

T P+FN

. (13)

As a positive in the evaluation we label every instance

as 1 if it is generated from a function, and as 0 if it

is generated by noise (c.f. 3.1). The ground truth to

achieve is then simply the mean of ones and zeros in

a window.

For the datasets where true dependencies are not

known, we chose to evaluate our algorithms at six lev-

els of correlations, from weak to strong correlation,

where we deem a windowed pair of streams with cor-

relation coefﬁcient above 0.66, 0.75, 0.85, 0.9, 0.95

and 0.99 respectively as dependent. Accordingly, we

classify each window as 0 or 1. For each level, we

report for each algorithm AUC and the maximum F1-

score, i.e. the highest F1-score along the precision re-

call curve generated by moving the threshold that sep-

arates predicted positives from predicted negatives.

Detecting Data Stream Dependencies on High Dimensional Data

387

This likely underestimates the number of positives

in the data but provides a lower bound for the perfor-

mance of our algorithm. We see in the synthetic data

how Pearsons’s correlation coefﬁcient underestimates

the dependency of the data streams but performs sur-

prisingly well through linear approximating.

3.5 Results

Figures 2 to 6 show F1-measure (± one standard de-

viation) and AUC (± one standard deviation) for the

ﬁve datasets. For the synthetic dataset NL we included

the Pearson’s correlation coefﬁcient. Random has

been determined for the non-synthetic datasets by al-

locating a random value uniformly chosen from [0, 1]

as dependency measure to each pair of stream win-

dows.

Table 1: Direct overview of all (non-synthetic) datasets: We

count signiﬁcant improvement in AUC (p-value < 0.1 in a

two-sided t-test) of row vs. column in 24 experiments. MID

scores a total of 48.

AUC improvement vs.

MID PkSim SStr

MID - 24 24

PeakSim 0 - 15

StatStream 0 1 -

Table 2: Direct overview of all datasets: We count signiﬁ-

cant improvement in F1 value (p-value < 0.1 in a two-sided

t-test) of row vs. column in 24 experiments. MID scores 33

wins.

F1 improvement vs.

MID PkSim SStr

MID - 19 14

PeakSim 0 - 1

StatStream 5 17 -

Between PeakSim and StatStream we see little

clear difference: PeakSim generally does better than

StatStream in AUC but worse if we look at recall

and precision. Both perform considerably worse than

MID. This holds for both the synthetic and the real

datasets.

In our synthetic data, MID shows close to per-

fect scores, improving signiﬁcantly (p < 0.1 in a two-

sided t-test) over the correlation- or DFT-based mea-

sures. In the other four datasets it also almost always

improves on the other compared methods.

Considering the area under the ROC curve, we

see our method in the window-based version clearly

outperforming the other correlation measures in all

datasets. Altogether MID signiﬁcantly outperforms

●

0.2 0.4 0.6 0.8 1.0

AUC

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(a) AUC

0.00 0.05 0.10 0.15 0.20 0.25 0.30

F1 max

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(b) F1-score

Figure 5: (a) Area under ROC curve and (b) maximum F1-

value on PA dataset. Areas separated by dashed lines show

performance at different levels of desired correlation.

the DFT-based methods in 48 out of 48 direct com-

parisons.

The maximum F1-value shows a similar picture:

We see MID outperforming the DFT-based methods

in 33 out of 48 cases. Table 2 shows the complete ma-

trix of pairwise comparisons for the F1-value. MID

performs well on all data sets, the difference however

tends to fall within the margin of error when higher

levels of correlation are examined where only few

positives are present in the data.

In summary, as proxy for the correlation coefﬁ-

cient, MID works signiﬁcantly better than DFT-based

methods based on AUC and F1-score.

3.6 Execution Time

All experiments have been performed on a PC with an

Intel Xeon 1.80GHz CPU and consumer grade hard-

ware, running a Linux with a current 64-bit kernel,

and implemented in python 3.4. Figure 7 shows exe-

cution times over 5 runs of different correlation mea-

sures.

Considering that the number of pairwise depen-

IoTBD 2016 - International Conference on Internet of Things and Big Data

388

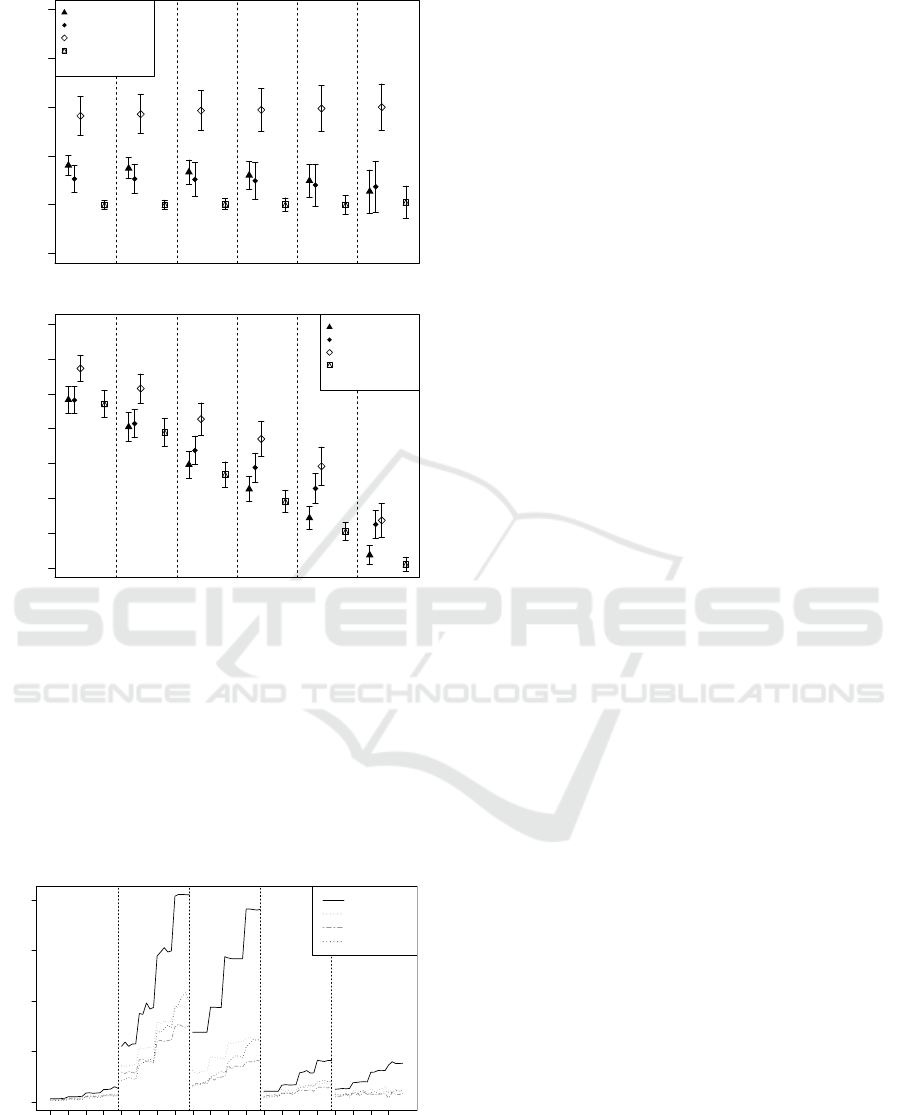
0.4 0.5 0.6 0.7 0.8 0.9

AUC

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(a) AUC

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

F1 max

0.66 0.75 0.85 0.9 0.95 0.99

PeakSim

StatStream

MID

Random

Correlation level

0.x

(b) F1-score

Figure 6: (a) Area under ROC curve and (b) maximum F1-

value on NA dataset. Areas separated by dashed lines show

performance at different levels of desired correlation.

dencies grows quadratic in the number of monitored

dimensions, computation speed is an essential factor

to deal with high dimensional data. Clearly, the di-

rect calculation of the correlation coefﬁcient is not

competitive for large datasets and higher data volume

within a window. MID appears about on par with

PeakSim and StatStream.

0 200 400 600 800

window length

time/s

20 40 80 120 20 40 80 120 20 40 80 120 20 40 80 120 20 40 80 120

CorrCoeff

PeakSim

StatStream

MID

Figure 7: Execution time averaged over 5 runs with increas-

ing window length on the (from left to right) NL, TU, OL,

PA and NA dataset.

4 CONCLUSION

We developed mutual information, a concept from in-

formation theory, into a metric that can help to eval-

uate sensor readings or other streaming data. We de-

scribe an incremental algorithm to compute our mu-

tual information based measure with time complexity

linear to the length of the data streams. The compet-

itive execution time is achieved with a suitable dis-

cretization technique. We evaluated our algorithm on

four real life datasets with up to 8.5 million records

and against two other algorithms to detect correlations

in data streams. It is as more accurate for detecting

dependencies in the data than other approximation al-

gorithms.

In future work we want to address the choice of

a suitable parameter value for the window length or

eliminate the static window altogether. Extending the

search for dependencies from pairwise to groups of

3 or more streams increases the computational com-

plexity but brings the potential to extend the analysis

to an entropy-based ad-hoc clustering.

Mutual information brings a different perspective

to stream analysis that is independent from assump-

tions on the distribution of or relationship between the

data streams.

REFERENCES

Bernhard, H.-P., Darbellay, G., et al. (1999). Performance

analysis of the mutual information function for non-

linear and linear signal processing. In Acoustics,

Speech, and Signal Processing, 1999. Proceedings.,

1999 IEEE International Conference on, volume 3,

pages 1297–1300. IEEE.

Bodik, P., Hong, W., Guestrin, C., Madden, S., Paskin,

M., and Thibaux, R. (2004). Intel lab data.

http://db.csail.mit.edu/labdata/labdata.html.

Cover, T. M. (1991). Ja thomas elements of information

theory.

Darbellay, G. A. (1999). An estimator of the mutual in-

formation based on a criterion for conditional inde-

pendence. Computational Statistics & Data Analysis,

32(1):1–17.

Daub, C. O., Steuer, R., Selbig, J., and Kloska, S.

(2004). Estimating mutual information using b-

spline functions–an improved similarity measure for

analysing gene expression data. BMC bioinformatics,

5(1):118.

Dionisio, A., Menezes, R., and Mendes, D. A. (2004). Mu-

tual information: a measure of dependency for nonlin-

ear time series. Physica A: Statistical Mechanics and

its Applications, 344(1):326–329.

Fernandez, D. A., Grau-Carles, P., and Mangas, L. E.

(2002). Nonlinearities in the exchange rates returns

Detecting Data Stream Dependencies on High Dimensional Data

389

and volatility. Physica A: Statistical Mechanics and

its Applications, 316(1):469–482.

Friedman, J. H. (2001). Greedy function approximation: a

gradient boosting machine. Annals of statistics, pages

1189–1232.

Granger, C. and Lin, J.-L. (1994). Using the mutual infor-

mation coefﬁcient to identify lags in nonlinear mod-

els. Journal of time series analysis, 15(4):371–384.

Hall, P. and Morton, S. C. (1993). On the estimation of

entropy. Annals of the Institute of Statistical Mathe-

matics, 45(1):69–88.

Han, M., Ren, W., and Liu, X. (2015). Joint mutual

information-based input variable selection for multi-

variate time series modeling. Engineering Applica-

tions of Artiﬁcial Intelligence, 37:250–257.

Kalu

za, B., Mirchevska, V., Dovgan, E., Lu

strek, M., and

Gams, M. (2010). An agent-based approach to care

in independent living. In Ambient intelligence, pages

177–186. Springer.

Kraskov, A., St

ogbauer, H., and Grassberger, P. (2008).

Estimating mutual information. Physical review E,

69(6):066138.

Paninski, L. (2003). Estimation of entropy and mutual in-

formation. Neural computation, 15(6):1191–1253.

Seliniotaki, A., Tzagkarakis, G., Christoﬁdes, V., and

Tsakalides, P. (2014). Stream correlation monitor-

ing for uncertainty-aware data processing systems.

In Information, Intelligence, Systems and Applica-

tions, IISA 2014, The 5th International Conference on,

pages 342–347. IEEE.

Siemens AG (2015). Gas turbine data. .

Sorjamaa, A., Hao, J., and Lendasse, A. (2005). Mutual in-

formation and k-nearest neighbors approximator for

time series prediction. Artiﬁcial Neural Networks:

Formal Models and Their Applications–ICANN 2005,

pages 752–752.

The NASDAQ Stock Market (2015). Nasdaq daily quotes.

http://www.nasdaq.com/quotes/nasdaq.

Zhu, Y. and Shasha, D. (2002). Statstream: Statistical mon-

itoring of thousands of data streams in real time. In

Proceedings of the 28th international conference on

Very Large Data Bases, pages 358–369. VLDB En-

dowment.

IoTBD 2016 - International Conference on Internet of Things and Big Data

390