Analytical Models for Evaluating Effectiveness of

Compressed File Transfers in Mobile Computing

Armen Dzhagaryan and Aleksandar Milenković

Electrical and Computer Engineering Department, The University of Alabama in Huntsville,

301 Sparkman Drive, Huntsville, AL, U.S.A.

Keywords: Mobile Sensing, Networks, Lossless Compression, Energy Efficiency, Performance Evaluation.

Abstract: The importance of optimizing data transfers between mobile computing devices and the cloud is increasing

with an exponential growth of mobile data traffic. Lossless data compression can be essential in increasing

communication throughput, reducing communication latency, achieving energy-efficient communication,

and making effective use of available storage. In this paper we introduce analytical models for estimating

effective throughput and energy efficiency of uncompressed data transfers and compressed data transfers

that utilize common compression utilities. The proposed analytical models are experimentally verified using

state-of-the-art mobile devices. These models are instrumental in developing a framework for seamless

optimization of data file transfers.

1 INTRODUCTION

Mobile computing devices such as smartphones,

tablets, and e-readers, have become the dominant

platforms for consuming digital information. On the

other side, Internet-of-Things (IoT) devices have

become an important source of digital information.

Data traffic initiated from mobile computing devices

and Internet-of-Things devices has been growing

exponentially over the last several years. A Cisco

report states that the global mobile data traffic grew

69% in 2014 relative to 2013, reaching 2.5 exabytes

per month (CISCO, 2015). This is an over 30-fold

increase relative to the total Internet traffic in 2000.

It is forecast that the global mobile data traffic will

grow nearly 10-fold from 2014 to 2019, reaching

24.3 exabytes per month.

Lossless data compression can increase

communication throughput, reduce latency, save

energy, and increase available storage. However,

compression introduces additional overhead that

may exceed any gains due to transferring or storing

fewer bytes. Compression utilities on mobile

computing platforms differ in compression ratio,

compression and decompression speeds, and energy

requirements. When transferring data, we would like

to have an agent to determine whether compressed

transfers are beneficial, and, if so, select the most

beneficial compression utility. A first step toward

designing such an agent is to obtain a good

understanding of various parameters impacting the

efficiency of data transfers.

Lossless data compression is currently being

used to reduce the required bandwidth during file

downloads and to speed up web page loads in

browsers. Google’s Flywheel proxy (Agababov et

al., 2015), Google Chrome (Google, 2014a),

Amazon Silk (Amazon, 2015), as well as the mobile

applications Onavo Extend (Onavo, 2015) and

Snappli (Snappli, 2014) use proxy servers to provide

HTTP compression for all pages during web

browsing. For file downloads, several Google

services, such as Gmail and Drive, provide zip

compression (zlib, 2015) of attachments and files

(Google, 2014b). Similarly, application stores such

as Google Play and Apple’s App Store use zip or

zip-derived containers for application distribution.

Several Linux distributions are also using common

compression utilities such as gzip, bzip2, and xz for

their software repositories.

The importance of lossless compression in

network data transfers has also been recognized in

academia (Barr and Asanović, 2003; 2006;

Dzhagaryan et al., 2013). Recent studies

(Dzhagaryan et al., 2015; Milenkovic et al., 2013b)

focused on a measurement-based experimental

evaluation of compressed and uncompressed file

transfers on the state-of-the-art mobile devices.

Dzhagaryan, A. and Milenkovi

c, A.

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing.

DOI: 10.5220/0005953700400051

In Proceedings of the 6th International Joint Conference on Pervasive and Embedded Computing and Communication Systems (PECCS 2016), pages 40-51

ISBN: 978-989-758-195-3

These studies showed that selected compressed

transfers over a WLAN and cellular interfaces

outperform corresponding uncompressed file

transfers. However, not a single combination of a

compression utility and a compression level

performs the best for all file transfers and network

conditions. A number of parameters may impact the

effectiveness of file uploads and downloads initiated

on a mobile device. These parameters include the

type of network interface (e.g., cellular, WLAN),

network connection throughput and latency, type

and size of transferred files, mobile device

performance, and energy characteristics.

In this paper, we propose analytical models for

estimating the effectiveness of uncompressed data

transfers and compressed data transfers that use

common compression utilities and their compression

levels. As a measure of effectiveness, we use the

effective upload and download throughputs

expressed in megabytes per second. In addition, we

consider energy efficiency expressed in megabytes

per Joule. The analytical models describe effective

upload and download throughputs and energy

efficiencies for uncompressed and compressed data

transfers as a function of parameters such as:

 Uncompressed (raw) file size;

 Local compression and decompression

throughput or energy efficiency;

 Compression ratio;

 Network parameters including network

connection throughput or energy efficiency, time

or energy to setup a network connection.

We experimentally verify the proposed models on

Google’s Nexus 4 and OnePlus One smartphones.

The proposed models are instrumental in developing

a framework for optimized data transfer between

mobile computing devices and the cloud. The

framework relies on agents running on mobile

devices and the cloud to select effective modalities

for file uploads and downloads.

The rest of this paper is organized as follows.

Section 2 presents background for our study. It gives

a system view of file transfers (2.1) and makes a

case for optimizing file transfers (2.2). Section 3

describes the design and verification of analytical

models for uncompressed file transfers. Section 4

describes the design and verification of analytical

models for compressed file transfers. Finally,

Section 5 summarizes our findings and draws

conclusions.

2 BACKGROUND

2.1 File Transfers in Mobile Cloud

Figure 1 illustrates file uploads and downloads that

are initiated from a mobile device. A data file can be

uploaded uncompressed or compressed. In a case of

uncompressed uploads, an uncompressed file (UF) is

uploaded over a network interface. In a case of

compressed uploads, the uncompressed file is first

compressed locally on the device, and then a

compressed file (CF) is uploaded over the network.

Similarly, a file can be downloaded from the cloud

uncompressed or compressed. In a case of

compressed downloads, a compressed version of the

requested file is downloaded from the cloud, and

then the compressed file is decompressed locally on

the mobile device. Compressed uploads and

downloads utilize one of the available compression

utilities. Each compression utility typically supports

a range of compression levels that allow us to trade

off speed for compression ratio. Lower levels favor

speed, whereas higher levels result in better

compression.

Figure 1: Uncompressed and compressed data flows

between mobile devices and the cloud.

In this paper for compressed transfers, we

consider six common compression utilities described

in Table. We have selected relatively fast gzip and

lzop utilities, as well as bzip2 and xz, which provide

a high compression ratio. We also consider pigz and

pbzip2, parallel version of gzip and bzip2,

respectively, because modern mobile devices

routinely include multicore processors. For each

utility, we consider at least three compression levels:

low (L), medium (M), high (H), as described in

Table 1.

To evaluate the effectiveness of a networked file

transfer we need to determine the total time to

complete the transfer. This time, in general, includes

the following components: (i) sender overhead time,

(ii) network connection setup time, (iii) file

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing

transmission time, and (iv) receiver overhead time.

To measure the effectiveness of data transfers we

use the effective throughput rather than the total

transfer time. The effective upload or download

throughput, measured in megabytes per second, is

defined as the ratio between the uncompressed file

size in megabytes and the time needed to complete

the file transfer. This metric thus captures the

system’s ability to perform a file transfer in the

shortest period of time regardless of a transfer mode.

Table 1: Compression Utilities.

Utility

Levels (Default)

[L, M, H]

Version Notes

gzip 1-9 (6) [1,6,9] 1.6

DEFLATE (Ziv-

Lempel, Huffman)

lzop 1-9 (6) [1,6,9] 1.03

LZO (Lempel-Ziv-

Oberhumer)

bzip2 1-9 (6) [1,6,9] 1.0.6

RLE+BWT+MTF+RL

E+Huffman

xz 1-9 (6) [1,6,9] 5.1.0a LZMA2

pigz 1-9 (6) [1,6,9] 2.3 Parallel gzip

pbzip2 1-9 (9) [1,6,9] 1.1.6 Parallel bzip2

Another metric of interest for networked file

transfers initiated on mobile devices is energy

efficiency. The energy consumed for compression

and decompression can be a decisive factor in

battery-powered mobile devices. Achieving a higher

compression ratio requires more computation and,

therefore, more energy, but better compression

reduces the number of bytes, thus saving energy

when transmitting the data. The energy efficiency,

measured in megabytes per Joule, is defined as the

ratio between the uncompressed file size in

megabytes and the total energy needed to complete

the file transfer. This metric thus captures the

system’s ability to perform a file transfer while

consuming the least energy.

The effective upload and download throughputs

and energy efficiencies depend on many factors,

including the file size and type, selected

compression utility, the compression level, network

characteristics such as latency and throughput, as

well as the smartphone’s performance and energy-

efficiency. Whereas previous studies showed that

compressed uploads and downloads can save time

and energy in many typical file transfers initiated

from smartphones (Dzhagaryan et al., 2015;

Dzhagaryan and Milenkovic, 2015; Milenkovic et

al., 2013b) there is not a single upload or download

file transfer method that works the best for all data

types and network conditions. To underscore this

problem, we conduct a measurement-based study

that evaluates the effectiveness of various data

transfer options under different network conditions.

For the evaluation, we use Google’s Nexus 4

(Google, 2014c, p. 4) and OnePlus One (OnePlus,

2015) smartphones and the measurement setup

described in (Dzhagaryan et al., 2016, 2015).

2.2 Why Optimize File Transfers?

In this section, we show the results of a

measurement-based study that evaluates the

effectiveness of uncompressed and compressed file

transfers initiated on a mobile device. We show that

a compression utility, compression level pair that

achieves the maximum throughput or energy

efficiency changes as a function of network

conditions and file size and type.

Upload Example. We consider uploading a text file

that contains a summary of user’s physiological state

captured every second by a wearable Zephyr

Technologies BioHarness 3 chest belt. The file

contains information about user’s heart rate,

breathing rate, activity level, and body posture. The

file is periodically uploaded to the cloud for future

analysis and long-term storage, e.g. in health

monitoring applications. The file size is 4.69 MB.

The experiment involves uncompressed and

compressed file uploads from an OnePlus One

smartphone to a remote server over the Internet. For

each type of a transfer, the time to upload the file

and energy consumed are measured to determine the

upload throughput and energy efficiency. To

demonstrate the impact of network connection

parameters, the measurements are performed when

the WLAN network throughput is set to 0.5 MB/s

(low) and 5 MB/s (high).

Table shows the effective upload throughputs

and the energy efficiencies for all types of file

uploads. The two bottom rows show speedups in the

effective throughput and energy efficiency when

comparing the best performing compressed upload

to the uncompressed upload [best/raw] and to the

compressed upload using gzip -6 [best/gzip-6],

which is considered a default compression mode.

The uncompressed upload on a 0.5 MB/s

network achieves the effective throughput of

0.51 MB/s and the effective energy efficiency of

0.88 MB/J. The compressed upload with gzip -6

achieves the effective throughput and energy

efficiency of 4.05 MB/s and 3.82 MB/J,

respectively. The best effective throughput of

4.83 MB/s is achieved with xz -0, while the best

energy efficiency of 4.55 MB/J is achieved with

gzip -1. Selecting the best compression mode

(utility, level) for throughput achieves 9.43- and

1.19-fold improvements over the uncompressed and

PEC 2016 - International Conference on Pervasive and Embedded Computing

the default compressed upload, respectively.

Selecting the best compression mode for energy

efficiency achieves 5.15 and 1.19-fold

improvements over the uncompressed and the

default compressed upload.

Table 2: Throughput and energy-efficiency for different

uploading modes of Summary.csv over WLAN.

Utility & Level CR

Effective

Throughput

[MB/s]

Energy

Efficiency

[MB/J]

Net Thr. [MB/s] - 0.5 5.0 0.5 5.0

gzip 1 7.05 2.97 9.25 4.55 11.24

gzip 6 10.60 4.05 6.07 3.82 5.42

gzip 9 11.69 2.15 2.24 1.39 1.40

lzop 1 5.14 2.20 7.98 3.58 11.68

lzop 6 5.14 2.25 8.46 3.95 10.60

bzip2 1 16.91 2.55 2.59 1.53 1.47

bzip2 6 17.48 1.79 1.83 1.07 1.08

bzip2 9 17.43 1.68 1.71 0.96 0.98

xz 0 13.66 4.83 7.66 4.45 6.29

xz 6 16.86 0.49 0.49 0.28 0.28

xz 9 16.86 0.48 0.49 0.28 0.27

pigz 1 7.06 2.92 8.05 4.34 8.42

pigz 6 10.61 4.12 10.73 4.27 6.73

pigz 9 11.69 4.19 6.59 1.66 1.92

raw - 1.00 0.51 3.16 0.88 2.99

[best/raw] - - 9.43 3.40 5.15 3.90

[best/gzip-6] - - 1.19 1.77 1.19 2.15

The uncompressed upload on a 5 MB/s network

achieves the effective throughput of 3.16 MB/s and

the effective energy efficiency of 2.99 MB/J. The

compressed upload with gzip -6 achieves the

effective throughput and energy efficiency of

6.07 MB/s and 5.42 MB/J, respectively. Selecting

the best compression mode for throughput achieves

3.4 and 1.77-fold improvements over the

uncompressed and the default compressed upload,

respectively. Selecting the best compression mode

for energy efficiency achieves 3.9 and 2.15-fold

improvements over the uncompressed and the

default compressed upload, respectively.

Download Example. In this example, we consider

downloading an Android executable file for the

Telegram application (telegram.tar). To prepare the

input file, the original apk file is extracted into an

uncompressed tar file. The file size is 22.34 MB.

The experiment involves uncompressed and

compressed file downloads initiated from the

OnePlus One smartphone. The server keeps the

uncompressed and compressed files available, so the

sender overhead is minimal. The total download

time includes the time needed to download and

decompress the requested file. The measurements

are performed when the WLAN network throughput

is set to 0.5 MB/s and 5 MB/s.

Table shows the effective download throughputs

and energy efficiencies. The two bottom rows show

speedups in the effective throughput and energy

efficiency when comparing the best performing

compressed download with the uncompressed and

with the compressed download using gzip -6.

Table 3: Throughput and energy-efficiency for different

downloading modes of Telegram.tar over WLAN.

Utility & Level CR

Throughput

[MB/s]

Energy

Efficiency

[MB/J]

WLAN Thr.[MB/s] - 0.5 5.0 0.5 5.0

gzip 1 1.87 0.90 7.91 1.65 7.61

gzip 6 1.95 0.98 8.28 1.74 7.58

gzip 9 1.95 0.96 8.11 1.80 7.76

lzop 1 1.56 0.73 6.89 1.38 8.31

lzop 6 1.56 0.77 6.93 1.46 8.03

bzip2 1 1.93 0.94 5.64 1.45 2.90

bzip2 6 1.93 0.97 4.98 1.37 2.52

bzip2 9 1.91 0.92 5.31 1.32 2.48

xz 0 2.13 1.07 8.16 1.76 4.77

xz 6 2.32 1.15 9.35 1.90 5.11

xz 9 2.32 1.10 9.56 1.82 5.06

pigz 1 1.93 0.92 8.12 1.69 9.04

pigz 6 1.93 0.92 8.29 1.72 9.34

pigz 9 1.91 0.98 7.30 1.87 8.36

raw - 1.00 0.48 4.55 0.92 5.35

[best/raw] - 2.41 2.10 2.07 1.75

[best/gzip-6] - 1.17 1.15 1.09 1.23

The uncompressed download on a 0.5 MB/s

network achieves the effective throughput of

0.48 MB/s and the energy efficiency of 0.92 MB/J.

The compressed download with gzip -6 achieves the

effective throughput of 0.98 MB/s and the energy

efficiency of 1.74 MB/J. The best effective

download throughput of 1.15 MB/s and the best

energy efficiency of 1.90 MB/J are achieved with xz

-6. Thus, xz -6 achieves 2.41 and 1.17 times better

throughput than the uncompressed download and the

compressed download with gzip -6, respectively.

Similarly, it achieves 2.07 and 1.09 times better

energy efficiency than the uncompressed and the

default compressed download, respectively.

The uncompressed download on a 5 MB/s

network achieves the effective throughput of

4.55 MB/s and the effective energy efficiency of

5.35 MB/J. The default compressed download

achieves the effective throughput and the energy

efficiency of 8.28 MB/s and 7.58 MB/J,

respectively. Selecting the best decompression mode

for throughput, xz -9, achieves 2.1 and 1.15-fold

improvement over the uncompressed and the default

compressed download, respectively. Selecting the

best decompression mode for energy efficiency, pigz

-6, achieves 1.75- and 1.23-fold improvements over

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing

the uncompressed and the default compressed

download, respectively.

These examples demonstrate that not a single

combination of a compression utility and level offers

the best throughputs and energy efficiencies in all

conditions. The file size, file type, device

performance, energy characteristics, and network

conditions, all impact the choice of the best

performing file upload or download combination.

However, these examples also show that the best

performing compression mode provides a substantial

increase in the effective throughput and energy

efficiency when compared to the uncompressed or

the default compressed data transfers.

Ideally, we would like to design a framework for

near optimal file transfers between mobile devices

and the cloud. The framework would autonomously

in real-time and with minimal overhead make a

selection of a near optimal file transfer mode while

taking into account all parameters discussed above.

In this paper, we describe analytical models for

uncompressed and compressed file transfers which

will serve as first steps in implementing the

framework for near optimal data transfers.

3 UNCOMPRESSED TRANSFERS

3.1 Modeling Uncompressed Transfers

The total time to perform a file transfer includes

sender overhead time, network connection setup

time, file transmission time, and receiver overhead

time. In a case of uncompressed file uploads, the

sender and receiver overheads can be ignored. Thus,

the total time of an uncompressed file upload,

T.UUP, includes the time to setup a network

connection, T.SC, and the file transmission time,

T.UP, as shown in Equation (1). If we know the

network upload throughput, Th.UP, the file

transmission time for upload can be calculated as the

ratio between the file size and the network upload

throughput, T.UP=US/Th.UP. Similarly, the total

time of an uncompressed file download, T.UDW,

includes T.SC and the file transmission time, T.DW,

as shown in Equation (2). The file transmission time

for download can be calculated as

Th.DW=US/Th.DW, where Th.DW is the network

download throughput.

The effective upload throughput is calculated as

the uncompressed file size in megabytes, US,

divided by the total time to upload the file,

Th.UUP=US/T.UUP. The effective download

throughput, Th.UDW, is calculated as the

uncompressed file size, US, divided by the total time

to download the file, Th.UDW=US/T.UDW.

Equations (3) and (4) show the expressions for the

effective upload and download throughputs,

respectively. The effective throughputs depend on

the file size, the time to set up the network

connection, and the network upload and download

throughputs. The effective throughputs, Th.UUP

[Th.UDW], reach the network throughputs, Th.UP

[Th.DW], when transferring very large files. In a

case of smaller files, the time to setup the network

connection limits the effective throughput.

...

(1)

...

(2)

.

.

1.∙./

(3)

.

.

1.∙./

(4)

...

(5)

...

(6)

.

.

1.∙./

(7)

.

.

1.∙./

(8)

The energy consumed by an uncompressed file

upload, ET.UUP, includes the energy spent while

setting up the network connection, ET.SC, and the

energy needed to upload the file, ET.UP, as shown

in Equation (5). If we know the energy-efficiency of

the network connection for uploads, EE.UP, we can

calculate ET.UP as ET.UP=US/EE.UP. Similarly,

the energy consumed by an uncompressed file

download, ET.UDW, includes the energy needed to

establish the connection and the energy needed to

download the file, ET.DW, as shown in Equation (6).

The effective upload energy efficiency, EE.UUP, is

calculated as the uncompressed file size in

megabytes, US, divided by the total energy needed

to upload the file, EE.UUP=US/ET.UUP. The

effective download energy efficiency, EE.UDW, is

calculated as the uncompressed file size, US, divided

by the total energy needed to download the file,

EE.UDW=US/ET.UDW. Equations (7) and (8) show

the expressions for the upload and download energy

efficiencies, respectively. They imply that the

effective energy efficiencies, EE.UUP [EE.UDW],

reach the network energy efficiencies, EE.UP

[EE.DW], when transferring very large files.

PEC 2016 - International Conference on Pervasive and Embedded Computing

3.2 Model Verification

To verify the models described by the equations

from above, we perform a set of measurement-based

experiments as follows. An OnePlus One

smartphone is used to initiate a series of file uploads

to a server and a series of file downloads from a

server. For each file transfer, the execution time and

the energy consumed are measured using a

measurement setup that involves a battery simulator

(Dzhagaryan et al., 2016, 2015). The smartphone is

connected to the Internet over its WLAN interface,

and file transfers take place over a secure shell (ssh),

an encrypted network protocol. The file sizes are set

to vary from 1 kB to 100 MB. The upload and

download experiments are repeated for four distinct

network throughputs set to Th.UP = Th.DW

= 0.5 MB/s, 2.0 MB/s, 3.5 MB/s, and 5.0 MB/s.

Figure 2: Measured effective throughput and energy

efficiency for file uploads.

Figure 2(a) shows the measured effective

throughput for uncompressed uploads as a function

of the file size, US, and the network connection

throughput for uploads, Th.UP. The plots show that

the effective throughput saturates for the larger files,

reaching the network connection throughput, i.e.,

Th.UUP=Th.UP. By using a curve fitting, we derive

an equation that models the effective throughput.

The dashed lines in Figure 2(a) illustrate the derived

equation for different network upload throughputs.

The derived equation matches the Equation (3) from

the proposed analytical model. The constant that

corresponds to the time to setup the connection for

our setup, T.SC, is 0.39 seconds.

Figure 2(b) shows the measured effective energy

efficiency for the same set of experiments. By using

the curve fitting, we derive an equation that matches

the one described in Equation (4). The constant that

corresponds to the energy consumed while setting up

the communication channel for out setup, ET.SC, is

0.14 Joules.

We Perform a similar set of measurement-based

experiments for uncompressed file downloads for

different network throughputs. The experiment

results confirm the correctness of the proposed

analytical models for the effective throughput and

energy efficiency for uncompressed file downloads.

Derived constants for T.SC and ET.SC match the

ones derived from the upload experiments.

3.3 Profiling Network Connection

The experimental verification of the models for the

effective throughput and energy efficiency requires a

series of uploads and downloads of data files of

different sizes. However, such an approach is not

practical in real conditions because it takes

considerable time and requires instrumentation of

smartphone for performing energy measurements.

Here we describe a practical approach for deriving

unknown network parameters using the verified

analytical model and a limited number of

experiments. Specifically, we describe practical

experiments that derive the following parameters:

 The network upload and download throughputs,

Th.UP [Th.DW], respectively;

 The network upload and download energy

efficiencies, EE.UP [EE.DW], respectively;

 The time and energy spent to setup the network

connection, T.SC [ET.SC].

The proposed method for deriving the network

parameters involves performing a two file upload or

download test. Two files of different sizes are

selected to be uploaded or downloaded over a

network connection with unknown parameters. The

time is measured during the transfers and used in

estimating energy consumption based on device

characteristics (using its idle current and the delta

current during file transfers). The calculated

throughputs or energy efficiencies are then used

within the models to derive the network parameters.

To demonstrate the derivation of network

parameters, we consider file uploads over an ssh

0.01

0.10

1.00

10.00

0.01 0.10 1.00 10.00 100.00

Th.UUP[MB/s]

US[MB]

Effectivethroughputforuploads

0.5MB/s 2.0MB/s 3.5MB/s 5.0MB/s

0.01

0.10

1.00

10.00

0.01 0.10 1.00 10.00 100.00

EE.UUP[MB/J]

US[MB]

Effectiveenergyefficiencyforuploads

0.5MB/s 2.0MB/s 3.5MB/s 5.0MB/s

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing

network connection that utilizes the smartphone’s

WLAN interface. The goal is to determine the T.SC

and Th.UP. We select two test files with sizes

US(s)=0.14 MB and US(l)=1.24 MB. The measured

effective throughputs are Th.UUP(s)=0.36 MB/s for

the 0.14 MB file and Th.UUP(l)=1.24 MB/s for the

1.24 MB file. Next, using Equation (9) for

calculating the effective network upload throughput,

we derive values of 5.167 MB/s and 0.362 seconds

for Th.UP and T.SC, respectively.

Figure 3 illustrates the proposed method for

characterizing network connection. The measured

upload throughputs for two selected files are marked

with a blue and a red diamond. By deriving Th.UP

and T.SC as described above, the model from

Equation (3) is plotted using a black dashed-dot

curve. The actual measurements of the effective

upload throughputs performed during the

verification phase are shown as blue circles. A visual

inspection shows that the model with parameters

extracted by just two measurements matches the

actual measurements performed during the

verification phase.

.

.

1.∙.



(9)

Figure 3: Extracting network parameters for uploads.

4 COMPRESSED TRANSFERS

A compressed upload of a data file to the cloud and

a compressed download from the cloud can be

performed in two ways, sequentially or with the use

of piping. In the former, for upload, the data file is

first compressed locally on the mobile device and

then compressed file is transferred to the cloud, with

no overlap between these two tasks. For download,

the compressed data file is downloaded on the

mobile device and then decompressed with no

overlap between these two tasks. In the later, for

upload and download, the file compression or

decompression times are partially or completely

hidden by the time to setup the network connection

and the file transmission time.

4.1 Performance Limits

The maximum compressed upload time shown in

Equation (10), T.CUP.max, includes the time to

perform the local compression of the file on the

mobile device, the time to setup network connection,

T.SC, and the time to transfer the compressed file,

T.CUP'. The time to transfer the compressed file can

be calculated as the compressed file size, which is

US/CR, where CR is the compression ratio, divided

by the network connection upload throughput

Th.UP. Instead of using the time to perform local

compression on a mobile device, T.C, we can use the

local compression throughput, Th.C, defined as the

uncompressed file size, US, divided by the time to

perform a local compression, T.C. This “higher is

better” metric captures ability of a mobile device to

perform local compression fast. The minimum

upload time shown in Equation (11), T.CUP.min,

includes the time to setup network connection, T.SC,

and the time to transfer the compressed file, T.CUP'.

.. ...′

(10)

.. ..′

(11)

..



∙.

1∙.∙









.





(12)

..



∙.

1∙.∙./

(13)

The minimum upload throughput, Th.CUP.min, is

calculated as the uncompressed file size in

megabytes, US, divided by the maximum time to

perform compressed upload, T.CUP.max. The

maximum upload throughput, Th.CUP.max, is

calculated as the uncompressed file size in

megabytes, US, divided by the minimum time to

perform compressed upload T.CUP.min. The final

expressions in Equations (12) and (13) show the

boundaries for the compressed upload throughputs

as a function of the network parameters, Th.UP and

T.SC, the file size, US, the compression ratio, CR,

and the local compression throughput, Th.C. From

these expressions, we can analytically estimate the

impact of changes in these parameters to the

effective throughputs. For example, the highest

compressed upload throughput that can be achieved

approaches the product of the compression ratio and

the network connection upload throughput, which is

possible in devices where local compression

0.00

0.01

0.10

1.00

10.00

0.00 0.01 0.10 1.00 10.00 100.00

Th.UUP[MB/s]

US[MB]

Extractingnetworkparametersforupload(througput)

Th.UUP(ActualMeasurements) 0.14MB 1.24MB Th.UP Th.UUP

PEC 2016 - International Conference on Pervasive and Embedded Computing

throughputs exceeds the network upload throughput

and when the size of a transferred file is sufficiently

large so that transfer time dwarfs the network

connection setup time.

The maximum total download time shown in

Equation (14), T.CDW.max, includes the time to

setup network connection, T.SC, the time to transfer

the compressed file, T.CDW', and the time to

perform the decompression of the received file on

the mobile device. The time to transfer the

compressed file can be calculated as the compressed

file size, US/CR, divided by the network connection

download throughput Th.DW. The time to perform

decompression on the mobile device, T.D, can be

used to determine the local decompression

throughput, Th.D, which is defined as the

uncompressed file size, US, divided by the time to

perform decompression. This metric thus captures

the mobile device’s ability to effectively perform

decompression. The minimum download time

shown in Equation (15), T.CDW.min, includes the

time to setup network connection, T.SC, and the time

to transfer the compressed file, T.CDW'.

.....′

(14)

....′

(15)

..



∙.

1∙.∙





.



.





(16)

..



∙.

1∙.∙./

(17)

The minimum effective compressed download

throughput, Th.CDW.min, is calculated as the

uncompressed file size in megabytes, US, divided by

the maximum time to perform compressed upload,

T.CDW.max. The maximum download throughput,

Th.CDW.max, is calculated as the uncompressed file

size in megabytes, US, divided by the minimum time

to perform the compressed download, T.CDW.min.

The final expressions in Equations (16) and (17)

show the boundaries for the compressed download

throughputs as a function of the network parameters,

file size, compression ratio, and the local

decompression throughput.

Figure 4 illustrates the estimated minimum and

maximum throughputs, Th.CUP.min [Th.CDW.min]

and Th.CUP.max [Th.CDW.max], respectively, as

well as the measured compressed upload and

download throughput, Th.CUP [Th.CDW], for

different modes of compressed file transfer. The

measurements are performed on a Nexus 4

smartphone with a 2.5 MB/s WLAN network

interface, Th.UP [Th.DW] =2.5 MB/s.

Figure 4: Effective compressed upload and download

throughputs.

For upload, the estimated lower and upper limits

for the compression throughput of gzip -1 are 3.9

MB/s and 6.2 MB/s, and the measured compression

throughput is 5.9 MB/s; in contrast, the estimated

bounds for bzip2 -1 are 1.8 MB/s and 8.1 MB/s and

the measured compression throughput is 2.04 MB/s.

The measured compressed upload throughput is

between the predicted minimum and maximum

throughputs. In cases when the local compression

throughput, Th.C, falls below the network

connection upload throughput, Th.UP, the effective

compressed upload throughput is closer to the

minimum throughput (e.g., for xz). In cases when

Th.C >> Th.UP, the effective compressed upload

throughput is closer to the expected maximum

throughput (e.g, for lzop).

For download, the estimated lower and upper

boundaries for the decompression throughput of

gzip -9 are 6.19 MB/s and 7.29 MB/s, and the

measured compression throughput is 7.16 MB/s. The

utilities with high local decompression throughputs

achieve the effective download throughputs close to

the upper boundaries when downloading large files

(e.g., gzip and lzop for all compression levels).

4.2 Energy Limits

The maximum energy for compressed upload shown

in Equation (18), ET.CUP.max, includes the energy

to perform the local compression of the file on the

mobile device, the energy to setup network

connection, ET.SC, and the energy to transfer the

compressed file, ET.CUP'. The energy to transfer

the compressed file can be calculated as the

compressed file size, US/CR, divided by the energy

efficiency of the network connection for uploads,

EE.UP. The energy to perform local compression on

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing

a mobile device, ET.C, can be used to determine the

local compression energy efficiency, EE.C, defined

as the uncompressed file size, US, divided by the

energy to perform a local compression, ET.C. This

metric captures the mobile device’s ability to

perform compression with the least amount of

energy. The minimum energy for uploads shown in

Equation (19), ET.CUP.min, includes the energy

overhead to perform the local compression of the

file on the mobile device, ET.C(0), the energy to

setup network connection, ET.SC, and the energy to

transfer the compressed file of size, ET.CUP', which

is calculated as described above. The energy

overhead, ET.C(0), excludes the energy needed to

run the platform when idle.

.....′

(18)

...





..



(19)

..



∙.

1∙.∙

.



.





(20)

..



∙.

1∙.∙

.0



.





(21)

The minimum upload energy efficiency,

EE.CUP.min, is calculated as the uncompressed file

size in megabytes, US, divided by the maximum

energy to perform compressed upload, ET.CUP.max.

The maximum upload energy efficiency,

EE.CUP.max, is calculated as the uncompressed file

size in megabytes, US, divided by the minimum

energy to perform compressed upload, ET.CUP.min.

The final expressions in Equations (20) and (21)

show the boundaries for the compressed upload

energy efficiencies as a function of the energy-based

network parameters, EE.UP, ET.SC, file size, US,

compression ratio, CR, and the local compression

energy efficiency, EE.C.

.....′

(22)

...





.

.



(23)

..



∙.

1∙.∙

.



.





(24)

..



∙.

1∙.∙

.0



.





(25)

The maximum energy for compressed downloads

shown in Equation (22), ET.CDW.max, includes the

energy to setup network connection, ET.SC, the

energy to transfer the compressed file, ET.CDW',

and the energy to perform the decompression of the

received file on the mobile device. The energy to

transfer the compressed file can be calculated as the

compressed file size, US/CR, divided by the network

connection download energy efficiency EE.DW. The

energy to perform decompression on the mobile

device, ET.D, can be used to determine the local

decompression energy efficiency, EE.D, which is

defined as the uncompressed file size, US, divided

by the energy to perform decompression. This

metric thus captures the mobile device’s ability to

effectively perform decompression. The minimum

energy for download shown in Equation (23),

ET.CDW.min, includes the energy to setup network

connection, ET.SC, and the energy to transfer the

compressed file, ET.CDW', and the overhead energy

to perform decompression, ET.D(0).

The minimum effective compressed download

energy efficiency, EE.CDW.min, is calculated as the

uncompressed file size in megabytes, US, divided by

the maximum energy to perform the compressed

download, ET.CDW.max. The maximum download

energy efficiency, EE.CDW.max, is calculated as the

uncompressed file size in megabytes, US, divided by

the minimum energy to perform the compressed

download, ET.CDW.min. The final expressions in

Equations (24) and (25) show the boundaries for the

compressed download energy efficiencies as a

function of the network parameters, file size,

compression ratio, and the local decompression

energy efficiency.

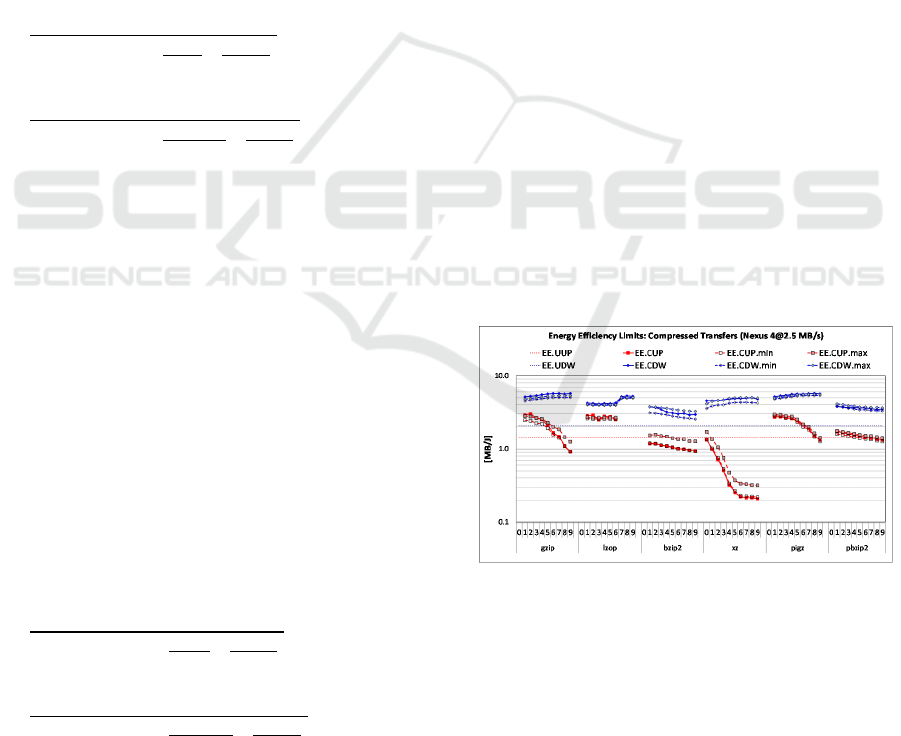
Figure 5: Effective compressed upload and download

energy efficiency.

Figure 5 illustrates the estimated energy

efficiency boundaries, EE.CUP.min [EE.CDW.min]

and EE.CUP.max [EE.CDW.max], and the measured

compressed upload and download energy efficiency,

EE.CUP [EE.CDW], for different modes of

compressed file transfer. The measurements are

performed on Nexus 4 smartphone with a 2.5 MB/s

WLAN network interface.

PEC 2016 - International Conference on Pervasive and Embedded Computing

For example, the estimated lower and upper

limits for the compression energy efficiency of

gzip -1 are 2.46 MB/J and 2.8 MB/J, and the

measured compression energy efficiency is

2.9 MB/J. The estimated lower and upper boundaries

for the decompression energy efficiency of gzip -9

are 5.06 MB/J and 5.36 MB/J, and the measured

compression energy efficiency is 5.72 MB/J. In both

cases, the utilities with high local (de)compression

energy efficiencies achieve the effective energy

efficiencies close to the upper boundaries when

transferring large files (e.g., gzip and lzop for all

compression levels).

4.3 Piping Model

Whereas we experimentally verified that we can

estimate the minimum and maximum compressed

transfer throughputs and energy efficiencies, the

distance between these boundaries for a particular

compression mode is often too wide, rendering them

insufficient to estimate the effective throughputs or

energy efficiencies. Ideally, we would like to be able

to devise models for accurate estimation of effective

upload and download throughputs and energy

efficiencies.

The use of piping when transferring data file is

beneficial as it increases the effective throughput

and energy efficiency. It allows for overlapping

local (de)compression tasks with the file transfer

tasks on mobile devices. In a case of compressed

upload, a degree of this overlap depends on the ratio

between the network upload throughput or energy

efficiency, Th.UP [EE.UP], and the local

compression throughput or energy efficiency, Th.C

[EE.C]. When the local compression throughput or

energy efficiency exceeds by far the corresponding

network upload throughput, the bottleneck is the

network. When the local compression throughput or

energy efficiency falls below the corresponding

network throughput, the compressed upload is not

beneficial. In a case of compressed downloads, a

degree of overlapping depends on the ratio between

the network download throughput or energy

efficiency, Th.DW [EE.DW], and the local

decompression parameter, Th.D [EE.D].

..

.

.

,..

1,..

(26)

..

∙.

1∙.∙

..

.



.





(27)

..

.

.

,..

1,..

(28)

..

∙.

1∙.∙

..

.



.





(29)

To derive the piping model for upload throughput,

the compression term from the lower throughput

limit is restricted using a corrective factor, described

in Equation (26). This factor lowers the impact of

the local compression term when the local

compression throughput exceeds the network

connection upload throughput. The final model for

the compressed upload throughput with the use of

piping is expressed in Equation (27). To derive the

piping model for download throughput, the

decompression term from the lower throughput limit

is restricted using a corrective factor, described in

Equation (28). The final model for compressed

download throughput is shown in Equation (29).

To derive the piping model for upload energy

efficiency, the compression term from the lower

energy efficiency limit is restricted using a

corrective factor, described in Equation (30). To

derive the piping model for the download energy

efficiency, the decompression term from the lower

energy efficiency limit is restricted using a

corrective factor, as described in Equation (32).

Effectively, the corrective factors restrict the energy

component of the local (de)compression that

includes the energy needed to run the platform,

which is ET.CET.C(0) for compression and

[ET.DET.D(0)] for decompression. The final

models for the compressed upload and download

energy efficiencies with piping are expressed in

Equations (31) and (33), respectively.

..

.

.

,..

1,..

(30)

..

∙.

1∙.∙



..

.



1..

.







.





(31)

..

.

.

,..

1,..

(32)

..

∙.

1∙.∙



..

.



1..

.







.





(33)

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing

Figure 6(a) shows the estimated compressed upload

(green dots) and download (green circles)

throughput and the measured compressed upload

(red squares) and download (blue triangles)

throughput for all considered compression modes.

Figure 6(b) shows the estimated compressed upload

and download energy efficiency and the measured

compressed upload and download energy

efficiencies for all considered compression modes.

The plots suggest a very high accuracy of the

proposed models for all compression utilities and

compression levels. This expression implies that if

we know the parameters of the network connection

(Th.UP [Th.DW] and T.SC or EE.UP [EE.DW] and

ET.SC), and if for a given uncompressed file of size

US we can predict the compression ratio, CR, and

local compression or decompression throughput or

energy efficiency for a given (utility, level) pair

(Th.C [Th.D] or EE.C [EE.D]) on a particular

mobile device, we can fairly accurately estimate the

expected compressed upload or download

throughput and energy efficiency.

Figure 6: Compressed Upload and Download with piping:

Throughput (a) and Energy Efficiency (b) Estimation.

The proposed models rely on three sets of

parameters: those that are readily available (e.g., file

size), those that can be determined using simple

experiments (T.SC [ET.SC], Th.UP [EE.UP],

Th.DW [EE.DW]), and those that are unknown such

as the compression ratio, CR, and compression or

decompression throughput, Th.C [Th.D], or energy

efficiency, EE.C [EE.D]. To be able to successfully

apply and use the proposed models, the compression

ratio, and the time or energy spent to perform

(de)compression of files has to be estimated. One

method which can provide estimation for

compression ratio and (de)compression throughput

and energy efficiency is the use of data tables filled

with historical data of prior data transfers and their

effectiveness for specific utility-level pairs.

5 CONCLUSIONS

This paper introduces analytical models for

characterizing effective throughput and energy

efficiency of uncompressed and compressed data

transfers between mobile devices and the cloud. We

have demonstrated the validity of the models

through the series of tests conducted on two state-of-

the-art smartphones.

Using the proposed analytical models, we can

initiate the development of frameworks for

optimizing data transfers between mobile devices

and the cloud. The framework can be designed to be

conscientious of the mobile device’s energy status

and network conditions, the user’s history of data

transfers (type and size of files transfers, frequency

of transfers), and the file characteristics, available

compression utilities and their performance.

ACKNOWLEDGEMENTS

This work has been supported in part by National

Science Foundation grants CNS-1205439 and CNS-

1217470.

REFERENCES

Agababov, V., Buettner, M., Chudnovsky, V., Cogan, M.,

Greenstein, B., McDaniel, S., Piatek, M., Scott, C.,

Welsh, M., Yin, B., 2015. Flywheel: Google’s Data

Compression Proxy for the Mobile Web, in:

Proceedings of the 12th USENIX Conference on

Networked Systems Design and Implementation,

NSDI’15. USENIX Association, Berkeley, CA, USA,

pp. 367–380.

Amazon, 2015. What Is Amazon Silk? - Amazon Silk

[WWW Document]. URL http://docs.aws.amazon.

com/silk/latest/developerguide/ (accessed 12.6.15).

Barr, K., Asanović, K., 2003. Energy aware lossless data

compression, in: Proceedings of the 1st International

Conference on Mobile Systems, Applications and

PEC 2016 - International Conference on Pervasive and Embedded Computing

Services (MobiSys’03). ACM Press, pp. 231–244.

doi:10.1145/1066116.1066123.

Barr, K.C., Asanović, K., 2006. Energy-aware lossless

data compression. ACM Trans. Comput. Syst. 24, 250–

291. doi:10.1145/1151690.1151692.

CISCO, 2015. Cisco Visual Networking Index: Global

Mobile Data Traffic Forecast Update 2014–2019

White Paper.

Dzhagaryan, A., Milenkovic, A., 2015. On Effectiveness

of Lossless Compression in Transferring mHealth

Data Files, in: 2015 IEEE 17th International

Conference on E-Health Networking, Applications and

Services (Healthcom). Presented at the 2015 IEEE

17th International Conference on e-Health

Networking, Applications and Services (Healthcom),

Boston, MA.

Dzhagaryan, A., Milenković, A., Burtscher, M., 2015.

Quantifying Benefits of Lossless Compression

Utilities on Modern Smartphones, in: 2015 24th

International Conference on Computer

Communication and Networks (ICCCN). Presented at

the 2015 24th International Conference on Computer

Communication and Networks (ICCCN), Las Vegas,

NV.

Dzhagaryan, A., Milenkovic, A., Burtscher, M., 2013.

Energy efficiency of lossless data compression on a

mobile device: An experimental evaluation, in:

Performance Analysis of Systems and Software

(ISPASS), 2013 IEEE International Symposium on.

Austin, TX, pp. 126–127. doi:10.1109/ISPASS.2013.

6557156.

Dzhagaryan, A., Milenkovic, A., Milosevic, M., Jovanov,

E., 2016. An Environment for Automated Measuring

of Energy Consumed by Android Mobile Devices, in:

6st International Conference on Pervasive and

Embedded Computing and Communication Systems

(PECCS). Lisbon, Portugal.

Google, 2014a. Data Server - Google Chrome [WWW

Document]. URL https://developer.chrome.com/

multidevice/data-compression (accessed 10.30.15).

Google, 2014b. About Attachment Manager [WWW

Document]. URL http://www.google.com/support/

enterprise/static/postini/docs/admin/en/admin_msd/att

ach_overview.html (accessed 10.31.15).

Google, 2014c. Nexus - Google [WWW Document]. URL

http://www.google.com/intl/all/nexus (accessed

6.15.14).

Milenkovic, A., Dzhagaryan, A., Burtscher, M., 2013b.

Performance and Energy Consumption of Lossless

Compression/Decompression Utilities on Mobile

Computing Platforms, in: 2013 IEEE 21st

International Symposium on Modeling, Analysis

Simulation of Computer and Telecommunication

Systems (MASCOTS). Presented at the 2013 IEEE

21st International Symposium on Modeling, Analysis

Simulation of Computer and Telecommunication

Systems (MASCOTS), San Francisco, CA, pp. 254–

263. doi:10.1109/MASCOTS.2013.33.

Onavo, 2015. Onavo [WWW Document]. Onavo. URL

http://www.onavo.com (accessed 12.1.15).

OnePlus, 2015. OnePlus One [WWW Document]. URL

https://oneplus.net/one (accessed 7.12.15).

Snappli, 2014. Snappli [WWW Document]. URL

http://snappli.com/ (accessed 12.1.15).

zlib, 2015. zlib Home Site [WWW Document]. URL

http://www.zlib.net/ (accessed 12.16.15).

Analytical Models for Evaluating Effectiveness of Compressed File Transfers in Mobile Computing