
Subdomain and Access Pattern Privacy
Trading off Confidentiality and Performance
Johannes Schneider
1
, Bin Lu
2
, Thomas Locher
1
, Yvonne-Anne Pignolet
1
,
Matus Harvan
1
and Sebastian Obermeier
1
1
ABB Corporate Research, Baden-Daettwil, Switzerland
2
Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland
Keywords:
Secure Computing, Remote Data Processing, Privacy-preserving Cloud Computing, Security Engineering,
Industrial Systems.
Abstract:
Homomorphic encryption and secure multi-party computation enable computations on encrypted data. How-
ever, both techniques suffer from a large performance overhead. While advances in algorithms might reduce
the overhead, we show that achieving perfect (or even computational) confidentiality is not possible without
increasing the running time compared to computations on plaintext more than exponentially in some cases. In
practice, however, perfect confidentiality is not always required. The paper discusses mechanisms to trade off
confidentiality and performance for computing on ciphertexts. It introduces a fine-grained approach to define
security levels for variables called (statistical) subdomain privacy. This concept differs substantially from
prior work because it treats a variable as confidential or non-confidential depending on the actual value. We
further propose privacy-preserving methods for memory access patterns. We apply our techniques to improve
performance of control flow logic (loops, if-then-else logic) and arithmetic operations such as multiplications.
The evaluation shows that the resulting speedup can be in the order of several magnitudes depending on the
privacy needs.
1 INTRODUCTION
Trusting a third party to handle confidential data can
be an issue, especially if the third party cannot be well
audited. Modern cryptography makes it possible to
encrypt data in a manner such that meaningful com-
putations can be carried out directly on the ciphertext,
i.e., without revealing confidential information to a
third party. In principle, this enables cloud computing
services that work on private data without violating
confidentiality. In the industrial sector, for example,
customers do not have to reveal their private data but
could still leverage analytical services carried out in
an (untrusted) cloud. The key obstacle that has hin-
dered the widespread availability of such services is
the inherent performance bottleneck of current tech-
niques enabling computations on ciphertexts such as
fully homomorphicencryption (FHE) or secure multi-
party computation (SMC). Although a lot of algorith-
mic improvements have been made in the last years,
there are inherent limitations in terms of performance
of complex programs running on encrypted data that
cannot be resolved without lowering the requirements
on data confidentiality. This fundamental issue has
not been addressed yet as prior work either consid-
ers restricted programs or tolerates large performance
penalties, rendering secure computation impractical
in many cases. For example, executing both branches
of nested “if” statements to hide the value of the cor-
responding condition can lead to a drastic increase in
running time to avoid leakage of the value of the con-
dition and, in turn, of the confidential data on which
the condition depends.
In this paper, we introduce the concept of sub-
domain privacy—a new approach to defining privacy
depending on the value of a variable. Thus, the value
of a variable is not necessarily kept secret for the
whole execution of the program, but might be re-
vealed depending on the concrete value it holds at run-
time. One could also speak of static and dynamic pri-
vacy. We show how this mechanism facilitates trading
off security and performance depending on the sce-
nario. For “if” statements, our approach can imply ex-
ecuting (with some probability) either both branches
or just one branch, leading to significant performance
gains. In particular, we leverage the observation that
Schneider, J., Lu, B., Locher, T., Pignolet, Y-A., Harvan, M. and Obermeier, S.
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance.
DOI: 10.5220/0005954100490060
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 49-60
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
49

for a variable holding a value of some (large) domain
of values, the (needed) confidentiality often depends
on the actual value of the variable. Rather than declar-
ing the variable to be confidential for its entire do-
main of values, only a certain set of values is treated
as confidential. As a result, we can even disclose the
value of the variable if it is not part of the confiden-
tial set of values. Subdomain privacy enables the sys-
tem to select algorithms at run-time that work on non-
confidential data and thus are significantly faster than
their counterparts operating on encrypted data only.
For example, an industrial plant hosts control de-
vices that operate on sensor data. Optimization algo-
rithms analyze control actions based on sensor values
for immediate control but also for long-term improve-
ment. In a typical scenario, sensor values in a nor-
mal range often do not need to be kept confidential
since this information and the corresponding control
operations might be considered common knowledge.
However, the control actions and sensor data dealing
with abnormal cases is often based on long-term ex-
perience of the control system vendor that is hard to
obtain, and thus should be kept confidential.
Another example are medical records for rare dis-
eases. The privacyof patients suffering from a disease
should be protected and their medical records should
be kept confidential. Examination data of healthy pa-
tients should in principle be kept confidential as well
but it is generally much less sensitive. Thus, rather
than not ensuring any confidentiality at all, one might
selectively encrypt or decrypt variables depending on
the actual content of a variable. For example, we
might process all data of sick persons in an encrypted
manner and all others as plaintexts. However, it might
also be valuable to operate only on some healthy pa-
tients in a non-encrypted manner. For example, as-
sume that we investigate upon 100 health records of
people from a mid-sized company. If there is one sick
person then just one record would be kept encrypted
and all other 99 records are unencrypted. Thus, given
the complete list of 100 people and those 99 that are
treated as plaintexts, one will easily identify the one
sick person, although her health record is encrypted.
In this work, we formalize these ideas and
concerns and provide a multitude of examples for
which the developed concepts are applicable and also
demonstrate how these concepts can be used. We also
give an evaluation using a recent multi-party scheme
showing that, depending on the scenario, performance
improvements of several orders of magnitude are pos-
sible.
1.1 Contributions
In short, the contributions of this work are the follow-
ing. We introduce the notion of sub-domain privacy,
a new concept for trading off confidentiality and per-
formance. Moreover, we discuss practically relevant
applications of this concept. In addition, we propose
methods to prevent an attacker from exploiting mem-
ory access patterns to derive insights about the data
and computation. Finally, we experimentally evaluate
our concepts on selected applications.
1.2 Outline
In Section 2, we describe the overall setup includ-
ing a threat model. Impossibility results showing that
achieving perfect (or computational) security might
prove infeasible due to a theoretically unbounded in-
crease in running time are presented in Section 3. Sec-
tion 4 introduces the concept of subdomain privacy
and Section 5 dicusses applications thereof. Our ap-
proach to achieve access pattern privacy is presented
in Section 6. Section 7 provides an evaluation of these
concepts. Related work is discussed in Section 8 and
Section 9 concludes the paper.
2 THREAT AND
COMPUTATIONAL MODEL
We consider a client-server setting. The client en-
crypts data and transmits encrypted data to a server
in case of homomorphic encryption. In case of secure
multi-party computation (SMC), the client transmits
keys and encrypted values to a set of servers, such
that no server on its own can decrypt any ciphertext.
Although the client might be involved in the compu-
tation, the client should perform as few operations as
possible on the data aside from the initial encryption.
We consider passive attackers that cannot alter any
values but they can monitor computations, memory
(values of memory cells and access patterns), and data
stored (at the third party). Furthermore, the attackers
can measure the execution time of the computations.
We assume that the cryptographic schemes used, are
strong enough so that an attacker cannot break the en-
cryption (for reasonable key lengths) without access
to the decryption key. For SMC we assume that the
system is secure as long as no two parties collude.
We also assume that an attacker has knowledge about
input distributions to pograms, ie. for a function f(x)
that should be evaluated on encrypted inputs x the at-
tacker knows the distribution of the plaintexts used to
call function f.
SECRYPT 2016 - International Conference on Security and Cryptography
50

3 IMPOSSIBILITY RESULTS
In this section, we provide general statements with
respect to the overhead that comes with keeping input
and output confidential.
Computation on encrypted data (performed by
some program) achieves perfect security (confiden-
tiality) if an attacker with capabilities as described
in Section 2 cannot guess the plaintext value of the
encrypted input and output values of the program
with a probability higher than someone could guess
by observing just the encrypted input and output val-
ues. Thus, the attacker gains no additional knowledge
about the encrypted data through the execution of the
program. The following theorem states that guaran-
teeing perfect secrecy can be costly.
Theorem 1. For some deterministic programs, any
possible trace (branch) of the program must be exe-
cuted in order to achieve perfect security.
Proof. Consider a program for which every “if” con-
dition depends on a secret input value. Assume that
an “if” condition is evaluated and only one of the two
possible branches is executed. An attacker observing
that a branch is not executedgets to knowthe outcome
of the condition, which in turn leaks information upon
the input.
A trace for a specific input manifests itself also
in its memory access pattern. Thus, Theorem 1 also
applies to memory locations.
Corollary 1. For some programs, all memory loca-
tions that could be accessed by one of the feasible in-
puts must be accessed for any given input in order to
achieve perfect security.
If there is an n-fold nested “if” statement, Theo-
rem 1 says that potentially all 2
n
branches may have
to be executed. Naturally, executing all branches can
lead to an exponential increase of the running time.
However, the running time may even increase much
more in the worst case.
Theorem 2. There are deterministic programs that
must run at least as long as it takes to execute the in-
put that maximizes its running time in order to achieve
perfect security.
Proof. Let the maximal time of the program be t
max
and assume that it occurs for input values I. If the ex-
ecution time is less than t
max
, the attacker can deduce
that the input was distinct from I.
Since the running time for some inputs may be
arbitrarily larger than for the actual input(s), the run-
ning time of a program guaranteeing perfect security
can be arbitrarily larger than the running time of the
unsecured version.
4 SUBDOMAIN PRIVACY
A variable is typically seen as either confidential or
non-confidential, independent of the actual value it
stores. A variable v might store a value val(v) ∈ D
of a large domain D. For instance, a 32-bit integer
variable v has val(v) ∈ [−(2
31
),2
31
− 1]. In many ap-
plication scenarios revealing the value of a variable
or parts of it might be tolerable for some values of
the domain, but not for all. For temperature measure-
ments, it might be tolerable to disclose a measured
value if the temperature is within a certain “normal”
range say [0,100] degrees but not if it is outside of this
range. To capture such characteristics, we introduce
the general notion of subdomain privacy. It enables
the refinement of a variable’s confidentiality require-
ments. Refining security constraints makes it possible
to employ fast algorithms operating on non-encrypted
data for certain values (or parts of a value).
The examples above lead to a conditional confi-
dentiality definition, where confidentiality is only en-
sured if a value is in a certain set of values. More
formally:
Definition 1 (Subdomain Privacy (with respect toC)).
A variable v with val(v) ∈ D is subdomain private
with respect to a set of values C ⊆ D if given that
val(v) ∈ C an attacker cannot do better than guessing
val(v) with probability 1/|C|. We write DOM(v,C).
The definition implies that val(v) is perfectly se-
cure forC = D. One might also say that the variable v
is perfectly secure with respect to C, meaning that we
reveal whether val(v) is in C or not but nothing else
about val(v) if the value lies in C. In practical terms
this means that given an encrypted variable v ∈ D, e.g.
as input, we can (often) check at the beginning of the
program if val(v) ∈ C. If so, we must keep the value
of v encrypted, otherwise computations can be done
using its plaintext. The set C can itself be kept se-
cret. Under the assumption that over time a variable
v takes all values in D, keeping C encrypted adds no
value, since C can be inferred as being all values that
have not been observed in plaintext.
The concept of subdomain privacy must be
applied with great care, since it might lead to in-
formation leakage of confidential variables. The
first problem arises if in the beginning it seems
that we can reveal v because val(v) /∈ C, but
later v is assigned a value in C. More precisely,
say in the beginning v := x
0
/∈ C. At some later
point in time, v is assigned the value x
1
∈ C. If
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance
51

there is any dependency between x
0
and x
1
, i.e.,
prob(v = x
1
| v = x
0
before) 6= prob(v = x
1
), then
we must keep v encrypted throughout the compu-
tation. A concrete example where we have this
dependency would be if(v = x
0
) v := x
1
. This
principle of dependency (or confidentiality propaga-
tion) also extends to any other variables w and their
values on which the assignment to v might depend.
If a variable v is read only, this problem does not arise.
It may often not be possible to disclose whether
v /∈ D (with certainty). For instance, assume a sys-
tem reveals data of all healthy patients of a hospital as
plaintext for research purposes, ie. these could be pa-
tients coming for routine checkups. It keeps all other
patient information confidential. Then, knowing that
someone is a patient and whether or not its data is
encrypted, makes it possible to determine whether or
not this person is healthy. In order to at least ensure
statistical security, we can disclose whether a person
is healthy, i.e. val(v) /∈ D, only with some probabil-
ity. In our example, we could reveal the data of a
healthy patient with a 90% rather than a 100% prob-
ability. Therefore, the information of all sick patients
as well as 10% of all healthy patients are treated con-
fidentially. Assume that 0.1% of patients have a rare
disease. Then, knowing that the information of a per-
son is treated confidentially, still ensures some degree
of statistical security. As we shall see later in detail,
if a person is treated confidentially there is only about
1% chance that this person is actually having the rare
disease. An attacker cannot gain more certainty about
the health status given all underlying primitives are
perfectly secure.
Therefore, as before we want to conceal what
value a variable stores given that this value is from
some set of values. In addition, we also do not want
to reveal with certainty whether the variable has any
of the values of this set or not. We provide statistical
security for the information whether a value v is in C.
Statistical subdomain privacy is formally defined as
follows.
Definition 2 (Statistical Subdomain Privacy (with re-
spect to membership in C)). A variable v with as-
signed fixed value val(v) ∈ D is statistically subdo-
main private with respect to membership in C if v is
subdomain private with respect to C and we reveal a
val(v) /∈ C with probability at most p
S
∈ [0,1]. We
write STATDOM(v,C, p
S
).
Note by definition, we have that subdomain pri-
vacy equals subdomain privacy, if we reveal the result
v /∈ C with probability one, i.e. STATDOM(v,C,1) =
DOM(v,C). If we never reveal whether v /∈ C, i.e.
we use STATDOM(v,C,0) then v must always be
treated confidentially, even for a value that is not in
C. The probability that an attacker can guess whether
v ∈ C given that it observed that a value v is treated
confidentially, depends on the probability distribu-
tion of values val(v) ∈ D, in particular, prob(val(v) ∈
C). In the simplest case, if all values have to be
treated confidentially, i.e. prob(val(v) ∈ C), an at-
tacker can trivially guess whether val(v) ∈ C. Using
statistical subdomain privacy in addition to the frac-
tion the probability that a value is encrypted is given
by prob(val(v) ∈ C) + prob(val(v) /∈ C)) · (1 − p
S
).
Thus, an attacker can guess prob(val(v) ∈ C) for
STATDOM(v,C, p
S
) with at most the following prob-
ability:
p(Guess val(v) ∈ C)
≤
prob(val(v) ∈ C)
prob(val(v) ∈ C) + prob(val(v) /∈ C) · (1− p
S
)
For illustration, let us look at the previous exam-
ple. Assume that 0.1% of all persons have a rare dis-
ease, ie. probability prob(val(v) ∈ C) = 0.001 and
we disclose whether a person is healthy with 90%,
ie. probability p
S
= 0.9. In this case, an attacker can
guess whether a variable that remains encrypted holds
data of a person with a rare disease with only about
1%, ie. p(Guess val(v) ∈ C) = 0.0099. From a prac-
tical perspective the question arises what happens, if
a variable v is assigned different values throughout
the execution of a program. For instance, for v := x
and later v := y, should we ensure that one cannot
guess whether x ∈ C or y ∈ C with probability p, i.e.
prob(Guess x ∈ C ∨ y ∈ C) ≤ p or is it sufficient to
ensure that no individual assignment can be guessed
with probability p, i.e. prob(Guess x ∈ C) ≤ p and
prob(Guess y ∈ C) ≤ p? Clearly, the first condition
provides better security. However, it might also limit
the usefulness of statistical subdomain privacy,i.e. as-
sume we have prob(Guess x ∈ C) = p then we have
essentially reached the maximum amount of informa-
tion to be disclosed for the variable, thus starting from
the second assignment we must always hide the fact
whether the value is in the confidential set. The above
definition of subdomain privacy, only focuses on the
case, when the variable is assigned once. We advo-
cate the scenario that after every assignment to v we
might leak its value with probability p .
Next, we discuss how to check for membership
val(v) ∈ C and present an efficient way to define sets
C based on ranges. Subsequently, we show in more
detail what computations are necessary to ensure sta-
tistical security.
SECRYPT 2016 - International Conference on Security and Cryptography
52

4.1 Range Partitioning
In principle, the set of values C ⊆ D for which confi-
dentiality has to be ensured can be defined arbitrarily.
However, computing whether val(v) ∈ C can intro-
duce significant overhead depending on the structure
of C. Therefore, we focus on defining C based on
continuous ranges that allow for efficient membership
computation val(v) ∈ C. We assume that an ordering
is defined on the domain D, i.e., for a,b ∈ D we can
compute a ≤ b. Two ways to define partitionings are:
• Domain range partitioning: Let a subdomain
range C
r
be a (continuous) range of values C
r
=
[c
0
,c
1
] with c
0
,c
1
∈ D.
• Value range partitioning: Consider a value a ∈ D.
Let a = (a
n−1
|a
n−2
|...|a
0
) be the splitting of a into
n parts. A value range partitioning C
v
= [c
0
,c
1
]
based on a part j is given by all values a ∈ D such
that for part j holds a
j
∈ C
v
.
If a and b are available in encrypted form, decid-
ing whether a value is in the given range requires the
ability to carry out comparison operations. This can
be achieved with MPC protocols or by involving the
client. For domain range decisions typically two com-
parisons with ciphertexts are necessary, i.e., one with
the lower and one with the upper bound of the range.
It requires only one comparison if the lower (or up-
per bound) is the minimum (or maximum) element
of the domain. Checking whether a value is part of
a value range C
v
is more involved, since it requires
more operations in addition to the two comparisons
to extract the part of a value that is relevant for mem-
bership computation. Depending on the encryption
scheme, one shift and one modulo operation can be
sufficient. Note that value range partitioning is a gen-
eralization of domain range partitioning. The mem-
bership computationval(v) ∈C either yields the result
in an non-encrypted manner, i.e., a boolean res that
stores whether val(v) ∈ C or an encrypted boolean
ENC
K
(res). Some multi-party protocols are inher-
ently designed for the scenario where the result of
a secure computation should be disclosed to the par-
ticipants of the computations. Generally, having the
requirement that a server should obtain the result of
some computation in plaintext puts confidentiality at
risk. For example, if a server has some (limited) ca-
pability to gain information on potentially confiden-
tial variables, it might abuse this capability by issu-
ing non-legitimate, additional or modified queries. In
the semi-honest model this does not pose any security
risk because computations are performed faithfully.
For stronger adversarial models, one way to deal with
this using FHE is to involve the client, which verifies
whether a request for revealing a value is legitimate.
One can also add more parties to split responsibilities,
i.e., mixing FHE with SMC. For example, one party
might perform homomorphic computations and an-
other party might only decrypt some values. For SMC
it must be ensured that no single party can violate
subdomain security. More precisely, no single party
should be able to trick the other parties into believ-
ing that they should reveal a value val(v) even though
it should be kept confidential, i.e., it actually holds
that val(v) ∈ C. One (general) method is that parties
must share their (partial) outcomes synchronously to
be able to decrypt the result, e.g., using commitments.
For illustration, consider two parties A,B, A having a
key K and B having an encrypted value res+ K. The
parties want to share res ∈ {0,1}. If party A sends K
to B, then B can obtain res. B can make A believe that
res is an arbitrary value by transmitting res + K + x
with x ∈ {−1,0,1}. One solution involves two com-
munication rounds: In the first round, both parties ex-
change their encrypted results together with hashes of
the keys. Once both parties have receivedthe message
from the other party they exchange the keys. A party
commits to its key in the first round, i.e., it cannot
change its choice after having received an encrypted
value (and key) from any other party.
4.2 Statistical Security
We ensure statistical security by revealing val(v) only
for a fraction of all values val(v) ∈ (D \ C) that do
not have to be confidential. More precisely, we re-
veal val(v) with probability p, ie. we use a random
Bernoulli variable b ∈ {0,1}, that is one with proba-
bility p and zero with probability 1− p. Computing a
ciphertext of such a variable b without client involve-
ment can be done in a multi-party setting: In order for
b to be one with probability p, we first compute a ran-
dom number r ∈ [1,n] (for some large value n). Then
b is one if r ≤ n· p. More precisely, each party P
i
picks
two large random numbers r
i
,k
i
∈ [1, n]. They ex-
change r
i
+ k
i
mod n. Once each party has received
these values from all other parties, they compute the
encrypted value of u =
∑
i
r
i
mod n, i.e., ENC(u) =
∑
i
(r
i
+ k
i
). The encrypted bit b is then obtained using
a secure comparison, ie. ENC(b) = ENC(u ≤ p· n),
encoded as 1 if the inequality holds and 0 otherwise.
1
For statistical security, b is multiplied with the en-
crypted result res ∈ {0,1} of val(v) /∈ C, to get b· res,
which is then decrypted. This scheme causes val(v)
to be revealed whenever b is 0. If b is 1 then the value
is revealed only if the value is not among the set of
1
Instead of this procedure, precomputed randomness could
be used.
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance
53

values for which val(v) has to be kept confidential.
Without statistical security a value is always revealed
when the result res from checking whether val(v) ∈ C
is true. Thus, we reveal fewer values in expectation
with statistical security than without statistical secu-
rity.
For FHE it is possible that a server runs a pseudo-
random number generator where the seed and all gen-
erated random numbers are encrypted. However, this
is not sufficient, since a decision must be made based
on the chosen random number. If the server can de-
crypt the random number and thereby trigger a de-
cryption of a potentially confidential value, we have
the same problem as discussed for domain range par-
titioning, i.e., a server that is not acting according to
the honest-but-curiousmodel might abuse its power to
gain confidential information. As mentioned above,
additional servers or communication with the client
can be used to prevent this.
5 APPLICATIONS
Next, we discuss a variety of applications of subdo-
main security and statistical subdomain privacy.
5.1 Secure Operations
The definition of subdomain privacy can be applied
in a straightforward manner to speed up many oper-
ations. Consider a domain range partitioning C
r
=
[c
0
,c
1
]. Assuming that a value val(v) /∈ C
R
is avail-
able in plaintext makes many operations significantly
faster. This may be obvious if all operands of an op-
eration are in plaintext, but it also holds for a variety
of operations even if only one operand is in plaintext
and the other remains encrypted.
The multiplication of a ciphertext and a plaintext
can be carried out efficiently with additive encryp-
tion schemes. E.g., in a multi-party setting (such as
(Schneider, 2016)) computing ENC(a · b) given a in
plaintext and ENC
K
(b) encrypted with key K, where
one party holds ENC(b) = b+ K, another party K, the
parties can both multiply their values by a, i.e. one
party gets a · ENC(b) = ab + aK and the other aK.
Decryption of a · ENC(b) with aK indeed yields the
product, i.e. a· ENC(b)−aK = a· b. This multiplica-
tion can be done without communication between the
two parties. In contrast, the same operation requires
several message exchanges if both a and b are en-
crypted. Similarly, the additively homomorphic Pail-
lier cryptosystem (Paillier, 1999) supports the multi-
plication of a ciphertext and a plaintext, while it is not
possible to multiply two ciphertexts. Therefore, sub-
domain privacy can in some cases enable the use of
the Paillier cryptosystem rather than resorting to fully
or somewhat homomorphic encryption mechanisms,
which are typically much slower.
Value range partitioning is generally less effec-
tive than domain range partitioning and it often re-
quires more care. For each value val(v) a plaintext
part and an encrypted part needs to be maintained.
Associative operations can then be carried out us-
ing different algorithms for each part. As an exam-
ple, assume that the last k bits of a variable are not
confidential. Thus, we have for a value val(v) an
encrypted part enc
v
for the higher order bits and a
plaintext part plain
v
for the last k bits. Multiplying
two variables u,v requires computing val(u) · val(v)
in the following way. We compute the part of the
product u·v that must remain encrypted, i.e., enc
u·v
=
enc
u
·enc
v
·2
2k
+(enc
u
· plain
v
+enc
v
· plain
u
)· 2
k
and
the part of the product that is kept as plaintext, i.e.,
plain
u·v
= plain
u
· plain
v
. Even though this increases
the number of operations, the duration of the multipli-
cation where both operands are ciphertexts typically
exceeds the others considerably. The running time of
ciphertext operations typically increases at least lin-
early with the (bit) size of a value. Thus, reducing
the number of bits of an operand might yield compu-
tational savings for an overall performance improve-
ment. Note, that plain
u·v
might be larger than 2
k
and therefore an attacker might gain some informa-
tion about bits other than the last k bits. Depending on
the application this might be acceptable or not. If this
is not allowed, one can use only k/2 bits per plain-
text part, which ensures that nothing is leaked for an
individual operation. For multiple operations, it can
be necessary to further reduce the size of the plaintext
parts.
Another operation that benefits from value range
partitioning is finding an encrypted value in a sorted
array. Comparisons are generally expensive opera-
tions when performed on encrypted data. In case, we
do not have to keep the last k bits for numbers con-
sisting of n bits confidential, we can organize the data
structure such that we first search for prefixes of the
first n − k bits. For a value a to be searched we find
the largest value that is smaller than the prefix of a
and then the smallest value that is larger than the pre-
fix of a. The exact value can then be found by look-
ing only at those values in the range for which the last
k bits match. For binary search this can reduce the
number of comparison on encrypted data from logn
to log(n/k). Binary search might leak access patterns
(for non-oblivious data access), which not be accept-
able. Resorting to linear search for hiding access pat-
SECRYPT 2016 - International Conference on Security and Cryptography
54

terns could solve this problem. Subdomain privacy
reduces the comparisons on secure data from n to n/k.
5.2 Secure Conditions
Securing conditions requires executing both branches
of a condition. This can lead to a prohibitive in-
crease in running time according to Theorem 2. Us-
ing (statistical) subdomain privacy, the evaluation of
some conditions can be disclosed without violating
confidentiality constraints and thus only one branch
needs to be executed. In other words, confidentiality
can be maintained by revealing the evaluated condi-
tion in some cases, depending upon the variables and
their values involved in the evaluation of the condi-
tion. This enables the system to only execute one of
the two branches in these cases.
Our notions of (statistical) subdomain privacy
covers the scenario where we want to secure a state-
ment of the form:
if(cond) then CodeBlock
A
; else CodeBlock
B
;
One straightforward way is to disclose the evalua-
tion of the “if” condition with some probability p
irrespective of the values involved, e.g., by defining
a variable STATDOM(v,{true, false} , p) with v :=
cond. A slightly more advanced option is to re-
veal the result of the condition only in case it is
true (or false) with some probability, i.e., by defin-
ing STATCOM(v,true, p). The second option is of
particular interest if one branch is rarely executed but
is very costly to execute. In some cases, with sub-
domain privacy, conditions can be evaluated on non-
encrypted data. In the example from the previous sec-
tion, where the last k digits are not kept confidential
for a variable v, a condition
if(a mod 2
k
= 0)
can be evaluated using plaintext operations.
When using a multitude of nested “if” statements,
several strategies can be employed to balance secu-
rity and performance, e.g., following all traces un-
til the number of traces has reached a certain limit,
selectively revealing the result of “if” conditions de-
pending on their information leakage, or branching
factor or making the choice dependent on the runtime
overhead of a branch. These strategies can be imple-
mented using the concept of subdomain privacy.
5.3 Secure Loops
In order to perfectly secure a loop we must execute
the maximal number of possible iterations for any in-
put according to Theorem 1. This can cause an ex-
tremely high overhead compared to executing only
the operations necessary to fulfill an algorithm’s pur-
pose. Therefore, we often have to balance security
and performance. A simple approach is to limit the
maximal number of iterations to a fixed value. If any
more iterations are needed, then the leakage of infor-
mation must be either implicitly accepted or variants
of the loops that are performed on non-confidential
data have to be carried out. Another approach is
to use statistical subdomain privacy and reveal the
evaluation of a condition only with a certain prob-
ability p after each iteration. Thus, in the example
(see Algorithm 1) we can define a condition vari-
able cond := F
0
(X) ∈ {0,1} and define subCond :=
STATDOM(cond, {}, p). This means that we can re-
veal any value of cond (i.e., {0,1}), but only do so
with probability p. In Algorithm 1 we use the func-
tion Revealed(subCond) to indicate whether subCond
can actually be revealed in this iteration or not. One
might also choose a deterministic function depending
on the current iteration number to decide when to re-
veal a value.
Algorithm 1: Securing a while loop.
1: {Original Loop with Variables X and Functions F
0
,F
1
}
2: WHILE(F
0
(X) = 1) X = F
1
(X)
3:
4: {Transformed, Perfectly Secure Loop}
5: maxIter := Maximum iterations for any input X
6: n
i
:= 0
7: repeat
8: ENC(cond) := ENC(F
0
(X))
9: ENC(X) := ENC(cond) · ENC(X) + (1 −
ENC(cond)) · ENC(F
1
(ENC(X)))
10: n
i
:= n
i
+ 1
11: until n
i
= maxIter
12:
13: {Secure Loop With Subdomain Private Condition}
14: repeat
15: ENC(cond) := ENC(F
0
(X))
16: ENC(X) := ENC(cond) · ENC(X) + (1 −
ENC(cond))ENC(F
1
(ENC(X)))
17: subCond := STATDOM(F
0
(X),{}, p) {Evaluate
Loop-Condition and reveal it with probability p}
18: until Revealed(subCond) AND subCond = 1
19:
20: n
i
:= 0 {Secure Loop With Fixed Intervals}
21: nextReveal := c
0
{we perform c
0
iterations until first
check}
22: repeat
23: repeat
24: ENC(cond) := ENC(F
0
(X))
25: ENC(X) := ENC(cond) · ENC(X) + (1 −
ENC(cond)) · ENC(F
1
(ENC(X)))
26: n
i
:= n
i
+ 1
27: until n
i
= nextReveal
28: nextReveal := nextReveal · c
1
{c
1
is increment fac-
tor}
29: until F
0
(X) = 1
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance
55

So far we have used subdomain privacy to reveal
the evaluation of a condition with a certain probabil-
ity p. This means that the evaluation of the condition
is revealed on average every 1/p iterations. Here, we
present an alternative that is deterministic and reveals
a condition depending on the number of current itera-
tions. This makes it easy to ensure certain degrees of
privacy as well as runtime guarantees. For example,
by always doubling the number of iterations until the
evaluation of a condition is revealed we can ensure
that the number of iterations is at most twice as much
as the actual (minimum) number of needed iterations.
In Algorithm 1, a minimum number of iterations c
0
is always executed without disclosing the evaluation
of any condition. Then, the total number of iterations
that are performed until the next condition is evalu-
ated and disclosed grows by a factor of c
1
each time
the condition is evaluated. This enables a fine-grained
tuning of performance and security.
6 ACCESS PATTERN PRIVACY
Memory access patterns might reveal information
about the underlying plaintext. For instance, the
number of input and output values of a data structure
can potentially be revealed through memory access
patterns. If the input is the name of a person and
the output is her list of medical consultations then,
typically, the length of the output should be hidden.
Another example is a sorted array of encrypted
values that is searched using binary search. Though
it might be impossible to disclose what (precise)
value is searched, the fact that the binary search
algorithm stops at a specific element, e.g., the first
element in the array, might prove valuable for an
attacker. Hiding memory access patterns might cause
significant performance penalties, eg. Corollary 1
states that it could be that a program needs to access
just one memory location for a given input, but
to hide patterns we must access many many more
locations since other inputs require to access them.
Therefore one might decide to hide access patterns
only for a certain section of code or conditionally
based upon values of a set of variables.
Let us discuss the case of searching a value in a
data structure, which covers a variety of important ap-
plications such as database queries. For a search on
an arbitrary data structure denote by PAT the set of
all possible access patterns for a fixed set of memory
locations and any input that one might search for. A
single access pattern for a value val(v) is a sequence
L(val(v)) := (l
0
,l
1
,...l
n−1
) of memory locations that
are needed to solve the problem by a specific algo-
rithm, for example, for binary search l
0
on an array
of length n could be the center element n/2, l
1
could
be the n/4th element and so on. Note that access pat-
terns might differ in length. They might not be unique
for each value in general, however, for simplicity we
assume for our scenario that they are. Access subdo-
main privacy concerns the scenario where an access
pattern should be hidden if the value of the variable
v to be searched belongs to a set C. Otherwise, the
confidentiality of v must still be protected, but access
patterns can be revealed.
Definition 3 (Access Subdomain Privacy). A variable
v with value val(v) ∈ D is access subdomain private
for a set of values C ⊆ D with respect to a set of mem-
ory locations L, denoted by ACC(v,C,L) if for any
value val(v) ∈ C an attacker cannot disclose the ac-
cess pattern L(val(v)) with probability of more than
1/|PAT|.
The above definition implies that for a private
value, we must access all memory locations that occur
potentially in any of the access sequences. Moreover
the length of the access patterns must not be disclosed
by the number of memory locations accessed, e.g., by
letting an algorithm access the same number of mem-
ory locations for all values in C. This can imply a sig-
nificant increase in the running time. E.g. an access
subdomain private algorithm can keep the number of
comparisons carried out always the same, irrespective
of the value to be found. A simple implementation of
such an algorithm may perform a binary search for
all values v /∈ C, for which the access patterns do not
need to be hidden. For the values in C, all elements
are inspected, i.e., to find a value v in a sorted array A,
v is compared with each value a
i
∈ A, returning an en-
crypted bit b
i
being 1 if v = a
i
and 0 otherwise. Thus
the access pattern is always the same for any v ∈ C.
In this implementation searching for values in C takes
linear time instead of logarithmic time.
Additionally, subdomain privacy can be extended
to relax the requirement of not revealing anything
about the access pattern. E.g., there are scenarios with
confidentiality constraints where the approximate po-
sitions within an array that is being accessed can be
revealed but not which index exactly corresponds to
the item to be found. In this case, a subdomain pri-
vate binary search only needs to hide the last steps.
Such a scheme can exploit value range partitioning.
Compared to traditional access privacy where all
values of a variable require the use of pattern hid-
ing techniques, subdomain privacy imposes the cor-
responding performance penalty only on a subset of
values.
SECRYPT 2016 - International Conference on Security and Cryptography
56

7 EVALUATION
We have evaluated our method for a selected set of
operations and the JOS scheme (Schneider, 2016). It
should be clear from prior descriptions that the useful-
ness of all concepts allowing for a more fine grained
description of privacy for variables depends heavily
upon the privacy requirements of the data at hand.
Thus, it is not possible to make precise general state-
ments with respect to performance gains. However,
our selected applications should give some guidelines
stating well-founded examples from health-care and
industry. What is evident from prior descriptions is
that (statistical) subdomain and access subdomain pri-
vacy introduces some overhead, i.e., for a value we
must determine whether it is to be kept confidential or
not. This always requires at least one comparison us-
ing an encrypted value. Additionally, the compilation
and execution of the programbecomes more involved,
since we must change code at runtime, i.e., a multipli-
cation of two variables a,b might be performed using
a protocol for encrypted values, a protocol for non-
encrypted values or a protocol using one encrypted
value and one non-encrypted value. The later source
of overhead reflects only in local computation. In our
evaluation we therefore compared against a system
that does not support our presented privacy notions
at all.
7.1 Subdomain Privacy
In Section 4 we described a scenario where common
(“normal”) values can be public, but exceptional val-
ues should be kept private and require special treat-
ment. Algorithm 2 below shows a control algorithm
with this behavior. It contains a simple branch for
normal data (v ≤ 50) and a more complex branch for
abnormal data (v ∈ [50,1000]).
Figure 1 shows the speedup for 10000 executions
depending on the probability that a value v is nor-
mal for three scenarios: i) without subdomain privacy,
ie. treating all values confidentially; ii) with domain
privacy DOM(v, [50,1000]) and iii) statistical subdo-
main privacy STATDOM(v,[50,1000],95%). Note,
that even when all data is normal, we receive the data
in encrypted form and must first check, if it is nor-
mal or not. This requires secure operations, ie. two
comparisons of the value v with the lower and up-
per bound, i.e. 50 and 1000, yielding two encrypted
bits. Since Algorithm 2 requires about seven com-
parisons (plus some computations) the speedup fac-
tor is inherently limited to roughly 10-20 – even if
all data is normal. Using subdomain privacy yields
a factor of about 800% speedup in this case. If all
Algorithm 2: Control Algorithm for Benchmarking.
1: if v > 50 then
2: {Abnormal data, handle with x,v confidential}
3: if v > 700 then
4: x = a
9
· sin(v)
5: else if v > 600 then
6: x = a
7
· sin(v)
7: else if v > 500 then
8: ...
9: else if v > 100 then
10: x = a
2
· sin(v)
11: else
12: x = a
1
· sin(v)
13: end if
14: else
15: {Normal operation, v non-confidential}
16: x = a
0
· sin(v)
17: end if
Figure 1: Speed up for Control Algorithm.
data is abnormal then subdomain privacy has a slight
negative impact, ie. a slow down of about 10%, since
all data is treated confidentially and the two compar-
isons to determine whether a value is normal or not
comprise overhead. Statistical subdomain privacy be-
haves worse, since in addition to the two comparisons
for determining whether a value is normal, it also re-
quires a generation of a (secret) random number and
comparison of the number with the percentage given
in the definition of statistical subdomain privacy.
The second benchmark assumes 1 % of val-
ues are abnormal and focuses on the behavior
of statistical subdomain privacy depending on its
security parameter p
s
. Figure 2 shows the speed
up when using statistical subdomain privacy, i.e.
STATDOM(v, [50,1000], p
S
), for varying revelation
probability p
S
for disclosing whether val(v) given
that val(v) /∈ C in Algorithm 2. If we do not reveal
any values, statistical subdomain privacy comes with
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance
57
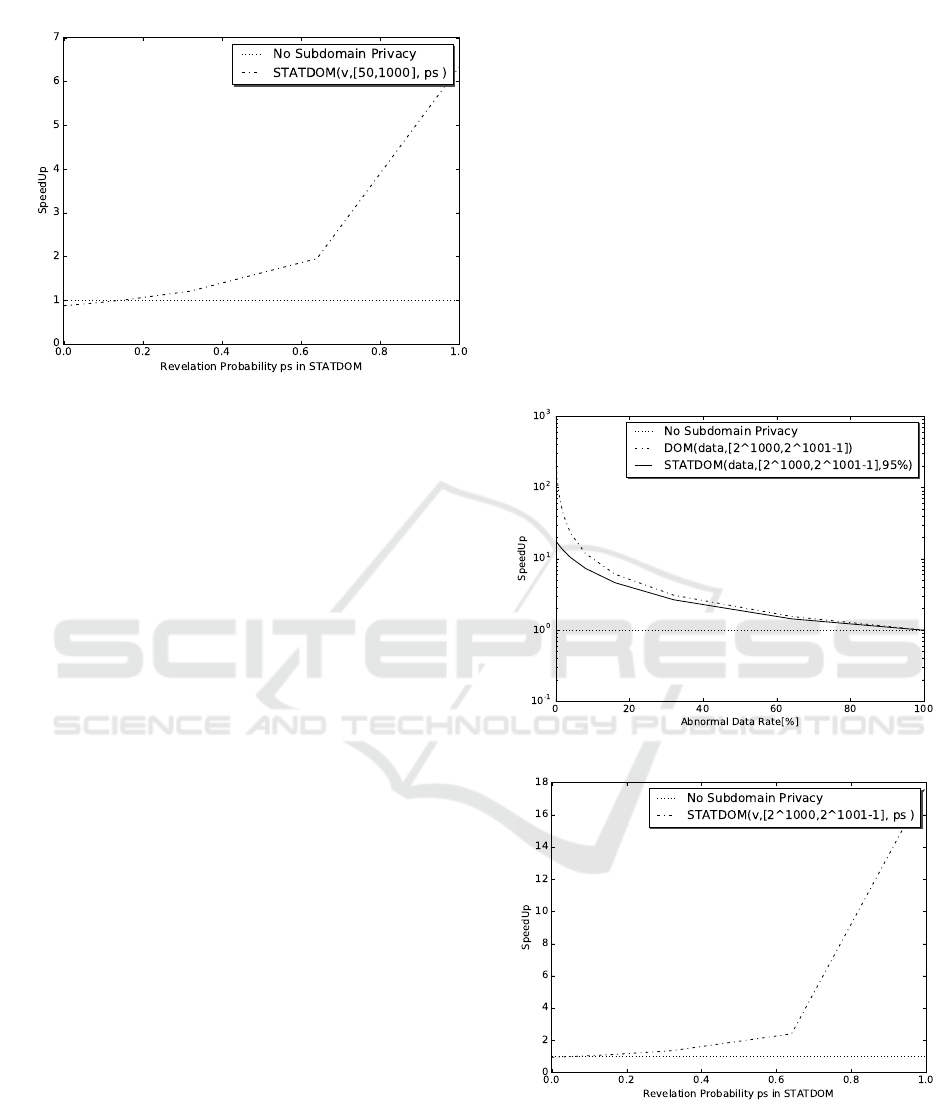
Figure 2: Speed-up for Control Algorithm for varying pa-
rameter for statistical subdomain privacy.
a slight run-time increase of about 10%. Good speed-
ups are achieved for large values of p
S
exceeding a
factor of 6.
Next, we use synthetic clinical data of patients
having some disease and healthy persons. We look
for patterns, eg. we want to determine whether spe-
cific patterns like genes in the DNA correlate with a
disease, or whether a specific pattern in body temper-
ature over time is characteristic for a disease. We
model the data by a binary sequence of 1000 bits
and try to find 10 bit sequences of 10 bits each. For
healthy patients we are allowed to decrypt the data
and compute on plaintexts. For a specific pattern our
algorithm simply checks from each position i whether
the next 10 bits match the pattern. A minor con-
cern is that in this case we have two variables, one
being the health state bit h(A) ∈ {0,1} of a person
A and a second variable being the DNA DNA(A) of
person A represented by 1000 bits. So far, we have
only discussed the notion of subdomain privacy for
a variable v depending on the value val(v) of vari-
able v itself but not dependent on the value val(w)
of another variable w. The extension is rather sim-
ple: All we need is that a variable v should be kept
confidential if a variable w is kept confidential. An
alternative but generally less efficient approach is to
concatenate variables, ie. data(A) = h(A)|DNA(A)
and to define subdomain privacy by only considering
the value of the first bit, ie. the 1001
st
bit, yielding
DOM(data,[2
1000
,2
1001
− 1]). We went for the lat-
ter option, since it is supported out of the box by our
implementation.
Figure 3 shows the speedup for 10000 persons de-
pending on the probability that a person is healthy. Up
to somewhat less than one per cent of sick people the
speed up is more than two orders of magnitude. The
maximum possible improvementis a factor of 100 for
one per cent of sick people. Getting close to this ra-
tio is only possible, since the duration of the secure
comparisons to check if a variable can be revealed are
insignificant compared to the costs of the computa-
tions that are done with the data afterwards. Given
that there are only sick persons there is essentially no
overhead.
In Figure 4 we assumed that 95% of persons are
healthy and focused on the behavior of statistical sub-
domain privacy parameter. The maximum possible
gain is a factor of 20 for a revelation probability of
100%, which we closely achieve. The decrease in
speedup is exponential given a decrease in revelation
probability.
Figure 3: Speed-up for pattern matching.
Figure 4: Speed-up for pattern matching for statistical pri-
vacy.
8 RELATED WORK
There is a rich literature on (automatically) transla-
SECRYPT 2016 - International Conference on Security and Cryptography
58

ting code into equivalent code that can be executed in
a SMC environment. Multiple existing SMC schemes
have been combined into a framework that comes
with its own programming language allowing the user
to declare different kinds of so-called protection do-
mains (Bogdanov et al., 2014). A protection do-
main serves as an abstraction of a set of SMC proto-
cols. Another SMC compiler is providedin the Share-
mind SMC framework (Laud and Randmets, 2015).
The underlying motivation is maintainability which is
achieved by introducing a domain specific language.
A variety of two-party protocols, i.e., garbled
circuits, homomorphic encryption and hybrids, have
been compared in (Ziegeldorf et al., 2015). The
authors found significant differences in the running
time. Building upon this finding, a mechanism has
been proposed to automatically select the best proto-
col in order to maximize performance for two-party
protocols using a cost model formulated as an integer
program (Kerschbaum et al., 2014). Furthermore, a
compiler has been introduced that allows the user to
state whether a data item is public or private (Zhang
et al., 2013). It also explicitly has a command for
revealing a private value, i.e., making it public. In
addition, it features explicit commands for executing
commands in parallel, using threads of a thread pool.
A formalized programming language for SMC based
on Boolean circuits evaluated with the GMW proto-
col (Goldreich et al., 1987) has also been described
and analyzed (Rastogi et al., 2014). Recently, several
schemes have been combined, including Yao’s gar-
bled circuits, circuit randomization (Beaver, 1992),
and boolean sharing (Goldreich et al., 1987), with
conversion among them to adjust for different opera-
tions (Demmler et al., 2015). Both approaches also
support mixed protocols, i.e., computations on en-
crypted and non-encrypted data.
There is a compiler for translating ANSI-C into
secure two party computation based on garbled cir-
cuits (Holzer et al., 2012). It has a few (inherent)
limitations, e.g., it can only handle bounded loops be-
cause the circuit grows with the number of iterations
of a loop. Web-server operations can be made secure
by translating (a subset of) C to secure code using par-
tially homomorphicschemes as well as a small trusted
computing base (Tople et al., 2013).
The database CryptDB enables the protection of
data stored in a relational database while preserving
the capability to run database queries (Popa et al.,
2011). In this system, security also depends on the
performed operations, i.e., certain operations such
as comparisons require revealing more information
about the confidential data. Searching on encrypted
data has been treated by means of privacy-aware
bucketization (Hacıg¨um¨us¸ et al., 2007). The idea is
that in a client-server setting in which the server hosts
a database, a client retrieves all values of a bucket and
decrypts them and searches within the decrypted data.
Thus, the server performs a preselection of values.
The paper also discusses the level of information dis-
closure due to bucketization and algorithms to mini-
mize information disclosure (depending on the data).
Parts of this work also discuss search but in the con-
text of memory access patterns. However, we do not
send the entire content of a bucket to a client. Fur-
thermore, our definition of value range partitioning
explicitly reveals parts of a value. This is also not
done in privacy-aware bucketization. Memory access
patterns can also be hidden using ORAM, eg. (Ste-
fanov et al., 2013; Bindschaedler et al., 2015). How-
ever, it comes at least with logn overhead, where n is
the memory size (Goldreich and Ostrovsky, 1996).
Non-interference (Goguen and Meseguer, 1982) is
the property of a system that its behavior and non-
confidential output, observed by an unprivileged user
(attacker), do not allow to infer confidential inputs.
There has been a lot of work on determining whether
programs achievethis property as well as constructing
such programs, see (Sabelfeld and Myers, 2003) for a
survey. In this context, our encrypted inputs and out-
puts can be seen as the confidential (high) variables.
In contrast to our work, all possible input values are
considered equally sensitive. Most closely related to
our work is quantifying information flow (Clark et al.,
2005; Clarkson et al., 2009) which quantifies, in terms
of entropy and probability, how one can learn more
about the value of confidential input variables by ob-
serving a program’s behavior or its non-confidential
outputs.
9 CONCLUSIONS
Perfect security – though highly desirable – remains
often a distant dream in reality. Aside from errors
in implementation, e.g. Heartbleed Bug, unproven
assumptions, e.g. hardness of prime factorization,
overhead related to security is often a key limita-
tion. Whereas securing communication is a standard
(and rather efficient) procedure using symmetric key
cryptography such as AES supported in hardware, for
computation on encrypted data it is impossible for
many kinds of programs to achieve a ‘reasonable’
performance overhead compared to computations on
plaintext. Therefore, the only way out is to trade off
security and performance. Our paper addresses this
need by introducing the concept of subdomain pri-
vacy, which formalizes the idea of decrypting a vari-
Subdomain and Access Pattern Privacy - Trading off Confidentiality and Performance
59

able at run-time depending on the value it contains.
Using subdomain privacy confidentiality of data can
be defined on a more fine-grained level, which we be-
lieve is an important step to making computation on
encrypted data feasible for a large range of applica-
tions.
REFERENCES
Beaver, D. (1992). Efficient multiparty protocols using
circuit randomization. In Advances in Cryptology
(CRYPTO), pages 420–432.
Bindschaedler, V., Naveed, M., Pan, X., Wang, X., and
Huang, Y. (2015). Practicing oblivious access on
cloud storage: the gap, the fallacy, and the new way
forward. In Proc. of the 22nd ACM SIGSAC Conf. on
Computer and Communications Security, pages 837–
849.
Bogdanov, D., Laud, P., and Randmets, J. (2014). Domain-
Polymorphic Programming of Privacy-Preserving Ap-
plications. In Proc. 9th ACM SIGPLAN Workshop
on Programming Languages and Analysis for Security
(PLAS), pages 53–65.
Clark, D., Hunt, S., and Malacaria, P. (2005). Quantitative
Information Flow, Relations and Polymorphic Types.
Journal of Logic and Computation, 18(2):181–199.
Clarkson, M. R., Myers, A. C., and Schneider, F. B.
(2009). Quantifying Information Flow with Beliefs.
17(5):655–701.
Demmler, D., Schneider, T., and Zohner, M. (2015). ABY
– A Framework for Efficient Mixed-Protocol Secure
Two-Party Computation. In Proc. Network and Dis-
tributed System Security (NDSS).
Goguen, J. and Meseguer, J. (1982). Security policies and
security models. In Security and Privacy, 1982 IEEE
Symposium on, pages 11–11.
Goldreich, O., Micali, S., and Wigderson, A. (1987). How
to play any mental game. In Proc. of 19th Symp. on
Theory of computing, pages 218–229.
Goldreich, O. and Ostrovsky, R. (1996). Software protec-
tion and simulation on oblivious rams. Journal of the
ACM (JACM), 43(3):431–473.
Hacıg¨um¨us¸, H., Hore, B., Iyer, B., and Mehrotra, S. (2007).
Search on Encrypted Data. In Secure Data Manage-
ment in Decentralized Systems, pages 383–425.
Holzer, A., Franz, M., Katzenbeisser, S., and Veith, H.
(2012). Secure two-party computations in ansi c. In
Proceedings of the 2012 ACM conference on Com-
puter and communications security, pages 772–783.
ACM.
Kerschbaum, F., Schneider, T., and Schr¨opfer, A. (2014).
Automatic Protocol Selection in Secure Two-Party
Computations. In Applied Cryptography and Network
Security, pages 566–584. Springer.
Laud, P. and Randmets, J. (2015). A domain-specific lan-
guage for low-level secure multiparty computation
protocols. In Proc. of the 22Nd ACM SIGSAC Con-
ference on Computer and Communications Security,
pages 1492–1503.
Paillier, P. (1999). Public-Key Cryptosystems Based on
Composite Degree Residuosity Classes. In Advances
in Cryptology–EUROCRYPT’99, pages 223–238.
Popa, R. A., Redfield, C., Zeldovich, N., and Balakrish-
nan, H. (2011). CryptDB Protecting Confidentiality
with Encrypted Query Processing. In Proc. 23rd ACM
Symposium on Operating Systems Principles (SOSP),
pages 85–100.
Rastogi, A., Hammer, M. A., and Hicks, M. (2014). Wys-
teria: A programming language for generic, mixed-
mode multiparty computations. In Security and Pri-
vacy (SP), 2014 IEEE Symposium on, pages 655–670.
IEEE.
Sabelfeld, A. and Myers, A. C. (2003). Language-based
information-flow security. IEEE Journal on Selected
Areas in Communications, 21(1):5–19.
Schneider, J. (2016). Lean and fast secure multi-party com-
putation: Minimizing communication and local com-
putation using a helper. 13th Int. Conf. on Security
and Cryptography(SECRYPT).
Stefanov, E., Van Dijk, M., Shi, E., Fletcher, C., Ren, L., Yu,
X., and Devadas, S. (2013). Path oram: An extremely
simple oblivious ram protocol. In Proc. of the SIGSAC
conference on Computer & communications security,
pages 299–310.
Tople, S., Shinde, S., Chen, Z., and Saxena, P. (2013). AU-
TOCRYPT: Enabling Homomorphic Computation on
Servers to Protect Sensitive Web Content. In Proc.
20th SIGSAC Conf. on Computer and Communica-
tions Security (CCS), pages 1297–1310.
Zhang, Y., Steele, A., and Blanton, M. (2013). PICCO:
A General-Purpose Compiler for Private Distributed
Computation. In Proc. 20th SIGSAC Conf. on Com-
puter and Communications Security (CCS), pages
813–826.
Ziegeldorf, J. H., Metzke, J., Henze, M., and Wehrle,
K. (2015). Choose Wisely: A Comparison of Se-
cure Two-Party Computation Frameworks. In Proc.
IEEE Symposium on Security and Privacy Workshops
(SPW), pages 198–205.
SECRYPT 2016 - International Conference on Security and Cryptography
60
