Study on the Use and Adaptation of Bottleneck Features for Robust

Speech Recognition of Nonlinearly Distorted Speech

Jiri Malek, Petr Cerva, Ladislav Seps and Jan Nouza

Faculty of Mechatronics, Informatics, and Interdisciplinary Studies,

Technical University of Liberec, Studentsk

a 2, 461 17 Liberec, Czech Republic

Keywords:

Deep Neural Networks, Bottleneck Features, Real-world Nonlinear Distortion, Robust Speech Recognition.

Abstract:

This paper focuses on the robust recognition of nonlinearly distorted speech. We have reported (Seps et al.,

2014) that hybrid acoustic models based on a combination of Hidden Markov Models and Deep Neural Net-

works (HMM-DNNs) are better suited to this task than conventional HMMs utilizing Gaussian Mixture Mod-

els (HMM-GMMs). To further improve recognition accuracy, this paper investigates the possibility of com-

bining the modeling power of deep neural networks with the adaptation to given acoustic conditions. For this

purpose, the deep neural networks are utilized to produce bottleneck coefﬁcients / features (BNC). The BNCs

are subsequently used for training of HMM-GMM based acoustic models and then adapted using Constrained

Maximum Likelihood Linear Regression (CMLLR). Our results obtained for three types of nonlinear distor-

tions and three types of input features show that the adapted BNC-based system (a) outperforms HMM-DNN

acoustic models in the case of strong compression and (b) yields comparable performance for speech affected

by nonlinear ampliﬁcation in the analog domain.

1 INTRODUCTION

In recent years, it has been shown that hybrid

HMM-DNN acoustic models (we further abbrevi-

ate HMM-DNN to DNN) yield signiﬁcant Word Er-

ror Rate (WER) reduction over conventional HMM-

GMM based systems for various speech recogni-

tion tasks, e.g., large-vocabulary recognition of clean

speech (Dahl et al., 2012; Dahl et al., 2013) or multi-

lingual acoustic modeling (Heigold et al., 2013).

This success motivates the utilization of DNNs for

recognition of speech distorted by environmental con-

ditions, such as additive noise or convolutive channel

distortion. The work (Seltzer et al., 2013) demon-

strates robustness of DNNs in a medium vocabulary

task from the Aurora 4 noise database (Parihar and

Picone, 2002). This paper shows that the feature-

extraction strategy employed in DNNs automatically

derives noise-robust features from input data when

multi-style training is available. However, the noise-

robustness technologies can still be of value to DNN

architecture (Delcroix et al., 2013), especially when

the network is trained on clean data and tested on

noisy data.

The utilization of many of the traditional robust

speech recognition techniques is complicated in con-

nection with DNNs. Some of the methods need an

underlying assumption that HMM-GMMs (we fur-

ther abbreviate HMM-GMM to GMM) are used for

the state likelihood evaluation. The potential solution

to this problem is proposed in (Li et al., 2014). It

consists of computing DNN-derived bottleneck coef-

ﬁcients ( BNC, see for example (Deng et al., 2010))

and subsequently utilizing them in training of GMMs.

The GMM based model can then be endowed with

conventional robust speech recognition techniques,

such as CMLLR (Gales, 1998).

In this paper, we investigate the usefulness and

possibility of adaptation of BNC features to robust

recognition of speech affected by real-world nonlin-

ear distortions. Our goal is to take advantage of the

modeling power of neural networks in combination

with a channel adaptation method. As already men-

tioned, our work is motivated by ﬁndings in (Seps

et al., 2014). It was shown there that DNNs are

more robust with respect to nonlinear distortions than

GMMs. However, GMMs endowed with adaptation

to environmental conditions via CMLLR are able to

match the performance of the former and even yield

lower WER in some cases. We focus on:

1. Utterances distorted by nonlinear ampliﬁcation

(and potential clipping) in the analog domain and

Malek, J., Cerva, P., Seps, L. and Nouza, J.

Study on the Use and Adaptation of Bottleneck Features for Robust Speech Recognition of Nonlinearly Distorted Speech.

DOI: 10.5220/0005955500650071

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 5: SIGMAP, pages 65-71

ISBN: 978-989-758-196-0

coded via a lossy codec optimized for speech per-

ceptual quality.

2. Speech compressed via lossy compression to very

low bit-rate quality.

3. Recordings denoised via spectral subtraction al-

gorithms, which exhibit an unnaturally sparse

spectrum.

In all these cases, we investigate mismatched

training conditions, i.e., we train the models on clean

data and test them on distorted datasets. This stems

from the fact that the considered distorted data (with

exception of the low bit-rate compression) are dif-

ﬁcult to simulate or collect for multi-style training.

Due to this fact, we do not consider any adaptation

techniques, which need training and training data,

such as i-vector computation proposed in (Saon et al.,

2013) or training of the DNN on features adapted

to considered distortions. We derive BNC features

from three different types of input features includ-

ing classical Mel Frequency Cepstral Coefﬁcients

(MFCCs) (Davis and Mermelstein, 1980), Filter Bank

Coefﬁcients (FBCs) (Deng et al., 2013) and Tempo-

RAl Patterns (TRAPs) (Gr

ezl and Fousek, 2008).

The paper is structured as follows. In Section 2 we

describe the considered datasets of distorted speech.

Section 3 presents our implementation of the bottle-

neck features. Section 4 speciﬁes the details of our

experimental setup. Section 5 summarizes the results

of our investigation and conclusions are drawn.

2 CONSIDERED DISTORTIONS

In our study, we consider the types of real-world non-

linear distortions mentioned below. More information

on the datasets and distortions can be found in (Seps

et al., 2014).

2.1 Nonlinear Ampliﬁcation in the

Analog Domain

This distortion is caused by an erroneous excessive

setting of the analog preampliﬁer. Then the preampli-

ﬁer becomes saturated and ampliﬁes the input signal

in a nonlinear way. In extreme, the signal becomes

clipped prior to sampling. Subsequently, the signal

is sampled and coded by a lossy codec. After cod-

ing, the potential clipping becomes difﬁcult to detect,

as the characteristic ﬂat amplitude level disappears in

the signal domain. Both the nonlinear ampliﬁcation

and the potential clipping may affect perceptual qual-

ity of the speech (Licklider and Pollack, 1948).

Our distorted dataset consists of eight lectures

given in Czech (11 hours and 45 minutes of speech,

85396 words), recorded for streaming purposes at our

university. The signal is captured by a close-talk mi-

crophone. The common background noise of a lecture

hall is present in the recording. The recordings were

originally sampled at 44.1 kHz and then compressed

by wma2 lossy codec (bit-rate 266 kbps), optimized

for perceptual quality suitable for human listeners.

Prior to recognition, the signals were downsampled

to 16 kHz. The dataset is denoted as ”Lectures” in the

experiments.

2.2 Lossy mp3 Compression to Low

Bit-rate

Low-bit-rate mp3 compression neglects frequency

components which are considered inaudible based on

a psychoacoustic model. The decompressed signal

exhibits many zeros in the time-frequency domain.

The compression to low bit-rates (<24 kbit/s) causes

suppression of phonemes at word boundaries, which

deteriorates the ASR accuracy (Pollak and Behunek,

2011; Seps et al., 2014).

Our dataset of compressed utterances consists of

22 recordings (1 hour and 12 minutes of speech, 8096

words) of radio broadcasts. Spontaneous speech by

various speakers was recorded at a sample rate of

16kHz. Subsequently, an mp3 compression was ap-

plied at a bit-rate of 16 kbit/s in order to present the

recordings on the web page of a radio station. The

dataset is denoted as ”MP3” in the experiments.

2.3 Spectral Subtraction Denoising

The denoising based on spectral subtraction estimates

the magnitude/power spectrum of the noise. This es-

timate is subsequently subtracted from the spectrum

of speech. Excessive denoising may lead to unnatu-

rally sparse speech spectrum and/or various artifacts,

such as musical noise. These artifacts deteriorate the

performance of ASR (Vaseghi, 2008).

The dataset affected by excessive denoising con-

sists of 1161 short Czech utterances read by various

speakers, recorded with a close-talk microphone. The

total duration of the dataset is 1 hour and 45 minutes,

and it contains 12780 words. The original sampling

frequency of 44.1 kHz was downsampled to 16 kHz.

During the recording, a denoising method provided

by software drivers of the sound device was turned on.

No additional compression was applied to the data.

The dataset is denoted as ”Denoised” in the experi-

ments.

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

Figure 1: The process of generation of bottleneck coefﬁ-

cients.

3 EXTRACTION OF

BOTTLENECK COEFFICIENTS

Bottleneck coefﬁcients are generated via a deep neu-

ral network containing one hidden layer with a small

number of neurons compared to other layers. This

small layer forces the network to concentrate the

crucial information for the classiﬁcation into a low-

dimensional representation. The output of the small

layer forms the BNC features. The original method

of extraction is based on auto-encoders, i.e., the net-

work is trained to predict the input features (Deng

et al., 2010). Other implementations include pre-

diction of (a) states of context-independent mono-

phones (Gr

ezl et al., 2007) or (b) physical states (so-

called ”senones”) of context-dependent tied-state tri-

phones (Yu and Seltzer, 2011). The input features

can be classical MFCCs or short/long-term energy of

speech in critical bands (Gr

ezl and Fousek, 2008).

In this paper, we adopted the process of generating

BNCs and their utilization in a GMM acoustic model

as depicted in Fig. 1. It can be described as follows:

1. A type of input features is computed. We con-

sider three different types as described in the next

Section 4.1.

2. A deep neural network is trained using state

alignments generated by the baseline tied-state

context-dependent GMM system which utilizes

conventional MFCC features. The network has

ﬁve hidden layers, all but one having 1024 units.

The middle (third) layer forms the bottleneck with

only 128 units and its output gives the raw bottle-

neck features. Details on the training conﬁgura-

tion can be found in Section 4.2.

3. An optional third step consists in a concatenation

of the raw bottleneck feature vector with the con-

ventional MFCC features. This stems from the

fact that MFCCs are considered to be highly ef-

fective features. When alternative long-term fea-

tures are used as the input for the neural network,

the resulting bottleneck coefﬁcients have the po-

tential to capture information complementary to

MFCCs (derived from the short-time spectra).

4. The raw/concatenated BNCs are analyzed using

the Principal Component Analysis (PCA, (Jol-

liffe, 2002)), in order to decorrelate the features

and lower the dimension of the resulting feature

vectors. After the application of PCA, 39 decor-

related features are always kept, which form the

ﬁnal bottleneck features. The number of 39 fea-

tures is the common length of a traditional MFCC

feature vector. The reduction performed in this

manner always keeps more than 97% of the en-

ergy of the analyzed features.

4 EXPERIMENTAL SETUP

4.1 Types of Features Used

We consider the following three types of input fea-

tures. All are computed from recordings sampled at

16 kHz. We use frames of a 25 ms length and a frame-

shift of 10 ms as is standard in speech processing.

MFCC - We utilize 13 static coefﬁcients, with

delta and delta delta parameters. The input feature

vector consists of coefﬁcients from 11 concatenated

frames, ﬁve preceding and ﬁve following the current

frame. It thus contains 11 × 39 = 429 features.

FBC - Filter Bank Coefﬁcients (described for ex-

ample in (Deng et al., 2013)) are given as short-term

mel-scaled log energy given in 29 critical frequency

bands, supplemented by the total log energy of the

current frame. We add the delta and delta-delta pa-

rameters to the static coefﬁcients. The input feature

vector consists of coefﬁcients from 11 concatenated

frames, ﬁve preceding and ﬁve following the current

frame. It thus contains 11 × 90 = 990 features.

TRAP - TempoRAl Patterns (Gr

ezl and Fousek,

2008) are deﬁned as short-term mel-scaled log energy

given in 23 critical frequency bands, supplemented by

the total log energy of the current frame. Next, 300 ms

(31 frames) long energy trajectories are transformed

by Discrete Cosine Transform and the ﬁrst 16 coefﬁ-

cients are retained. The input feature vector consists

of 24 × 31 = 384 elements.

Potentially, various combinations of the above in-

put features can be considered and submitted to the

Study on the Use and Adaptation of Bottleneck Features for Robust Speech Recognition of Nonlinearly Distorted Speech

network for selection of the most representative bot-

tleneck features. This is however beyond the scope of

the current paper.

4.2 Training of Deep Neural Networks

The DNN-based acoustic models as well as networks

for generating the bottleneck features are trained

to provide scaled likelihood estimates for physical

states of the baseline GMM model using MFCC in-

put features. The Theano library (Bergstra et al.,

2010) is used for training, which has a ﬁxed dura-

tion of 50 epochs and is carried out using settings

from (Gr

ezl and Fousek, 2008): The activation func-

tion is sigmoid. Each hidden layer consists of 1024

units. The potential bottleneck layer has 128 units.

The mini-batch size is 1000 and the learning rate is

0.08.

4.3 GMM Acoustic Models and

CMLLR Adaptation

Regardless of the input features, speaker-independent

and context-dependent tied-state HMMs of Czech

phonemes and several types of non-speech events

(e.g., breathing, various hesitation sounds, cough, lip-

smack, etc.) are utilized.

In all these cases, the training parameter which

controls the tying of states is set to the same value

so that the resulting model contains 4k physical states

with up to 32 Gaussian components per state (i.e.,

120k components in total).

The models are adapted to given acoustic condi-

tions using an unsupervised procedure, which runs in

two recognition passes as follows:

In the ﬁrst pass, we utilize the default model to

obtain phonetic transcript of the given recording. The

recording is then split into 5-minute-long segments.

For each such segment, CMLLR is employed to es-

timate a global linear transformation matrix using

the created phonetic transcript and the given acous-

tic model. Then, the second speech recognition pass

is performed, where the estimated transforms are ap-

plied on all feature vectors belonging to the corre-

sponding segments. We estimate the CMLLR trans-

form using the frames containing speech only; the

frames corresponding to noises are left out.

4.4 Recognition System Employed

The investigation is performed using our own ASR

system for Czech language. Its core is formed

by a one-pass speech decoder performing a time-

synchronous Viterbi search.

The lexicon of the system contains 550k entries

(word forms and multi-word collocations) that were

observed most frequently in a 10 GB large corpus

covering newspaper texts and broadcast program tran-

scripts. Some of the lexical entries have multiple pro-

nunciation variants. Their total number is 580k.

The employed Language Model (LM) is based on

N-grams. For practical reasons (mainly with respect

to the very large vocabulary size), the system uses

bigrams. In the training word corpus, 159 million

unique word-pairs (1062 million in total) belonging

to the items in the 550k lexicon were observed. How-

ever, 20 percent of all ”word-pairs” actually include

sequences containing three or more words, as the lex-

icon contains 4k multi-word collocations. The unseen

bigrams are backed-off by the Kneser-Ney smoothing

technique (Kneser and Ney, 1995).

5 EXPERIMENTAL EVALUATION

We present a comparison of WER achieved by the in-

vestigated acoustic models. The results are summa-

rized in Table 1. All discussed WER improvements

are meant as absolute. We use the notation ”Acoustic

Model: Features” (for example GMM:MFCC) to de-

scribe the considered conﬁgurations of our systems.

By ”aGMM” we denote the adapted GMM acoustic

models.

Along with the three distorted datasets described

in Section 2, we also present baseline accuracy

achieved on recordings without any nonlinear distor-

tion. The dataset, denoted as ”News”, consists of ra-

dio broadcasts of Czech news (2 hours and 59 minutes

of speech, 25991 words). The recordings contain read

utterances as well as the spontaneous speech of sev-

eral speakers. The recordings are sampled at 16 kHz.

5.1 Comparison of BNC and MFCC

Features within the GMM System

The baseline GMM:MFCC system exhibits perfor-

mance comparable to all GMM:BNC systems on the

undistorted dataset ”News”. On distorted data sets

”MP3” and ”Denoised”, almost all of the GMM:BNC

systems achieve signiﬁcantly lower WER (by 9.8-

17.5% or 16.2-21.3%, respectively). We explain it

partly by the fact that the neural network is able to use

the temporal context of the input features to comple-

ment the information that is missing within short-term

MFCCs computed from distorted utterances.

This holds for neural network used for feature ex-

traction as well as for DNN acoustic model. It is no-

ticeable especially for the ”MP3” dataset, which we

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

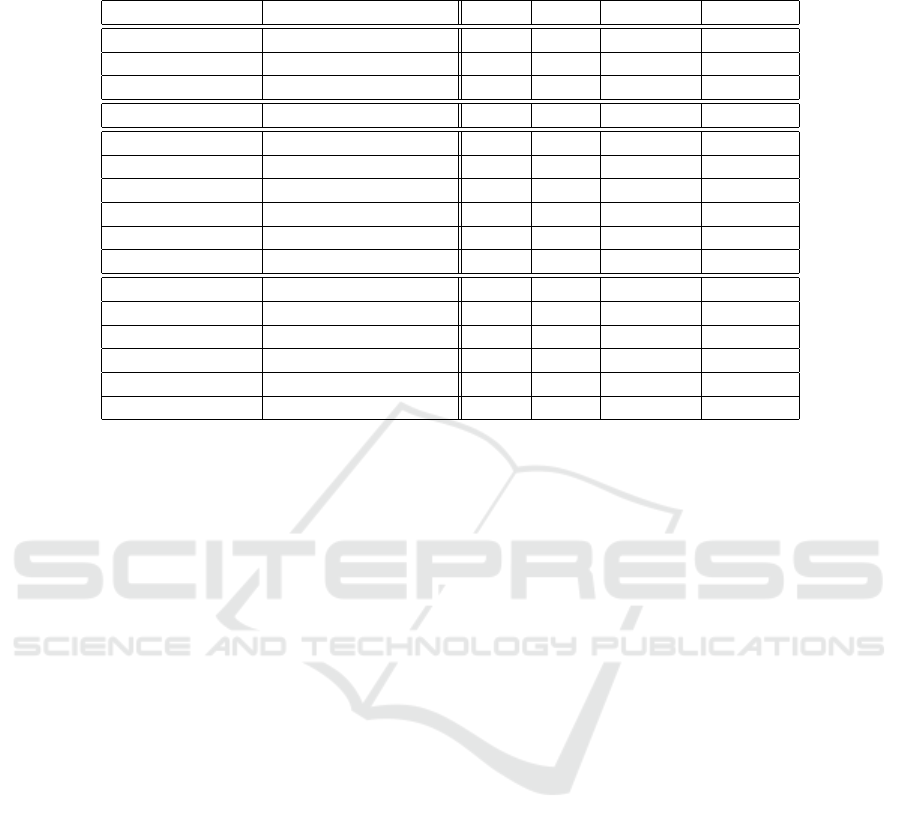
Table 1: Word Error Rates (WER) achieved on the considered datasets. Bold numbers indicate the best results among

competing systems. Abbreviation ”aGMM” denotes the adapted GMM acoustic models.

Model Features News Mp3 Denoised Lectures

DNN MFCC 10.08 19.45 15.29 47.85

DNN TRAP 9.72 22.84 13.69 46.65

DNN FBC 9.38 26.10 12.94 44.80

DNN FBC (No context) 10.35 43.00 15.73 50.56

GMM (Baseline) MFCC 13.48 43.42 45.22 56.11

GMM BNC(MFCC) 16.20 25.89 29.05 58.88

GMM BNC(FBC) 13.99 33.67 23.90 54.86

GMM BNC(TRAP) 14.13 26.45 24.19 55.20

GMM BNC(FBC)+MFCC 12.61 28.50 19.85 52.59

GMM BNC(TRAP)+MFCC 12.87 23.79 21.21 53.93

aGMM MFCC 11.32 21.44 37.94 48.22

aGMM BNC(MFCC) 14.95 21.32 28.35 53.87

aGMM BNC(FBC) 13.09 22.49 23.10 48.00

aGMM BNC(TRAP) 13.08 20.41 23.35 48.53

aGMM BNC(FBC)+MFCC 11.78 19.05 18.73 45.65

aGMM BNC(TRAP)+MFCC 11.90 18.61 20.10 47.04

demonstrate in Table 1 in row ”DNN:FBC(no con-

text)”. Here, the performance drops signiﬁcantly,

when the input features consist of only the current

frame, not the 11 consecutive frames.

The GMM:BNC systems achieve only slightly

better WER on the ”Lecture” dataset (by 1.3% at

most), which suggests that neural networks are not in-

herently robust with respect to this type of distortion,

as discussed in more detail in Section 5.3.

The concatenation of MFCC and BNC features

is beneﬁcial for the GMM:BNC systems (as was re-

ported for undistorted data in (Gr

ezl and Fousek,

2008)). It reduces the WER values by 1.3-5.2% com-

pared to non-concatenated BNCs, depending on the

dataset and input features.

The CMLLR enhances the performance of

GMM:BNC systems on all distorted datasets. The

adaptation leads to the highest WER reduction for

compressed utterances (11.2%) and the ”Lecture”

dataset (6.9%).

5.2 Comparison of DNN and

aGMM:BNC Acoustic Models

The aGMM:BNC systems, based on either TRAP or

FBC, outperform the DNN systems on the ”MP3”

dataset and yield comparable results on the ”Lec-

tures” dataset. For the other datasets, the DNN sys-

tems achieve lower values of WER.

The best input features, for both DNN acoustic

models and bottleneck feature extraction, consists of

the FBC. This observation conﬁrms that the less pro-

cessed short-term features form a more suitable input

for DNN models than conventional MFCC parame-

ters, as suggested, for example, in (Deng et al., 2013).

The computational demands of the aGMM:BNC

systems are high compared to DNN acoustic models.

Two models need to be trained (neural network and

the subsequent GMM acoustic model) and two recog-

nition passes are required to adapt the bottleneck fea-

tures.

5.3 Robustness of Investigated Systems

with Respect to Considered

Distortions

For the ”MP3” dataset, the performance of the best

DNN:FBC system deteriorated and was surpassed by

both other DNN systems and aGMM:BNC. We argue

(based on a complementary experiment) that this is

caused by a sensitivity of the DNN:FBC system to

the normalization of the input features. In all of our

experiments, we perform a robust normalization by

subtraction of the mean value estimated on the train-

ing dataset as a whole. Due to the compression of

the test set, the true mean value of the test set signif-

icantly differs from the mean estimated in this man-

ner, which deteriorates the results of DNN:FBC. On

other datasets, this deteriorating effect is not signiﬁ-

cant. The DNN:MFCC is more robust in this context,

because the conventional computation of MFCCs in-

cludes Cepstral Mean Subtraction (CMS), i.e. a mean

normalization within each training and test utterance.

The performance of GMM:BNC systems seems to be

Study on the Use and Adaptation of Bottleneck Features for Robust Speech Recognition of Nonlinearly Distorted Speech

uninﬂuenced by the effects of the normalization.

The DNN models appear insensitive to the spec-

tral subtraction artifacts contained in the ”Denoised”

dataset. The performance of the DNN system is near

to the level achieved on undistorted data. The best

GMM:BNC system is outperformed by 5.7% due to

the low efﬁciency of the CMLLR adaptation. The rea-

son is that the test data consists of very short sentences

(3 − 10 s long), which provide an amount of data too

small for estimating CMLLR.

The nonlinear analog ampliﬁcation (and potential

clipping) within the ”Lecture” dataset is very harm-

ful to both types of models and all feature conﬁgura-

tions. Additional robust recognition techniques need

to be utilized for this type of distorted data (a partial

solution can be offered, e.g., by clipping removal pro-

posed in (Eaton and Naylor, 2013)).

6 CONCLUSIONS

We investigated the robustness of bottleneck-based

systems endowed with feature adaptation with re-

spect to nonlinear distortions in speech. We showed

that the bottleneck features are more robust than the

conventional MFCCs. On most considered datasets,

the bottleneck-based GMM models, adapted to given

distortions, achieve performance comparable to the

DNN models. However, the BNC-based systems are

much more demanding computationally, which hin-

ders their utilization.

The most robust acoustic model in our experi-

ments was the DNN model using FBC input features.

This is in accord with the results presented for clean

speech in literature; low-level frequency features rep-

resent an input more suitable for DNN systems than

conventional MFCCs.

ACKNOWLEDGEMENTS

This work was supported by the Technology Agency

of the Czech Republic (Project No. TA04010199) and

partly by the Student Grant Scheme 2016 of the Tech-

nical University in Liberec.

REFERENCES

Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pas-

canu, R., Desjardins, G., Turian, J., Warde-Farley, D.,

and Bengio, Y. (2010). Theano: a cpu and gpu math

expression compiler. In Proceedings of the Python

for scientiﬁc computing conference (SciPy), volume 4,

page 3. Austin, TX.

Dahl, G. E., Sainath, T. N., and Hinton, G. E. (2013). Im-

proving deep neural networks for lvcsr using rectiﬁed

linear units and dropout. In Acoustics, Speech and

Signal Processing (ICASSP), 2013 IEEE International

Conference on, pages 8609–8613. IEEE.

Dahl, G. E., Yu, D., Deng, L., and Acero, A. (2012).

Context-dependent pre-trained deep neural networks

for large-vocabulary speech recognition. Audio,

Speech, and Language Processing, IEEE Transactions

on, 20(1):30–42.

Davis, S. B. and Mermelstein, P. (1980). Comparison

of parametric representations for monosyllabic word

recognition in continuously spoken sentences. Acous-

tics, Speech and Signal Processing, IEEE Transac-

tions on, 28(4):357–366.

Delcroix, M., Kubo, Y., Nakatani, T., and Nakamura, A.

(2013). Is speech enhancement pre-processing still

relevant when using deep neural networks for acoustic

modeling? In INTERSPEECH, pages 2992–2996.

Deng, L., Li, J., Huang, J.-T., Yao, K., Yu, D., Seide, F.,

Seltzer, M., Zweig, G., He, X., Williams, J., et al.

(2013). Recent advances in deep learning for speech

research at microsoft. In Acoustics, Speech and Signal

Processing (ICASSP), 2013 IEEE International Con-

ference on, pages 8604–8608. IEEE.

Deng, L., Seltzer, M. L., Yu, D., Acero, A., Mohamed,

A.-R., and Hinton, G. E. (2010). Binary coding of

speech spectrograms using a deep auto-encoder. In

Interspeech, pages 1692–1695. Citeseer.

Eaton, J. and Naylor, P. A. (2013). Detection of clipping

in coded speech signals. In Signal Processing Confer-

ence (EUSIPCO), 2013 Proceedings of the 21st Euro-

pean, pages 1–5. IEEE.

Gales, M. J. (1998). Maximum likelihood linear transfor-

mations for hmm-based speech recognition. Com-

puter speech & language, 12(2):75–98.

ezl, F. and Fousek, P. (2008). Optimizing bottle-neck

features for lvcsr. In Acoustics, Speech and Signal

Processing, 2008. ICASSP 2008. IEEE International

Conference on, pages 4729–4732. IEEE.

ezl, F., Karaﬁ

at, M., Kont

ar, S., and Cernocky, J. (2007).

Probabilistic and bottle-neck features for lvcsr of

meetings. In Acoustics, Speech and Signal Process-

ing, 2007. ICASSP 2007. IEEE International Confer-

ence on, volume 4, pages IV–757. IEEE.

Heigold, G., Vanhoucke, V., Senior, A., Nguyen, P., Ran-

zato, M., Devin, M., and Dean, J. (2013). Multi-

lingual acoustic models using distributed deep neural

networks. In Acoustics, Speech and Signal Process-

ing (ICASSP), 2013 IEEE International Conference

on, pages 8619–8623. IEEE.

Jolliffe, I. (2002). Principal component analysis. Wiley

Online Library.

Kneser, R. and Ney, H. (1995). Improved backing-off for

m-gram language modeling. In Acoustics, Speech,

and Signal Processing, 1995. ICASSP-95., 1995 In-

ternational Conference on, volume 1, pages 181–184.

IEEE.

SIGMAP 2016 - International Conference on Signal Processing and Multimedia Applications

Li, J., Deng, L., Gong, Y., and Haeb-Umbach, R. (2014).

An overview of noise-robust automatic speech recog-

nition. Audio, Speech, and Language Processing,

IEEE/ACM Transactions on, 22(4):745–777.

Licklider, J. C. R. and Pollack, I. (1948). Effects of differ-

entiation, integration, and inﬁnite peak clipping upon

the intelligibility of speech. The Journal of the Acous-

tical Society of America, 20(1):42–51.

Parihar, N. and Picone, J. (2002). Aurora working group:

Dsr front end lvcsr evaluation au/384/02. Inst. for Sig-

nal and Information Process, Mississippi State Uni-

versity, Tech. Rep, 40:94.

Pollak, P. and Behunek, M. (2011). Accuracy of mp3

speech recognition under real-word conditions: Ex-

perimental study. In Signal Processing and Multime-

dia Applications (SIGMAP), 2011 Proceedings of the

International Conference on, pages 1–6. IEEE.

Saon, G., Soltau, H., Nahamoo, D., and Picheny, M. (2013).

Speaker adaptation of neural network acoustic models

using i-vectors. In ASRU, pages 55–59.

Seltzer, M. L., Yu, D., and Wang, Y. (2013). An investiga-

tion of deep neural networks for noise robust speech

recognition. In Acoustics, Speech and Signal Process-

ing (ICASSP), 2013 IEEE International Conference

on, pages 7398–7402. IEEE.

Seps, L., Malek, J., Cerva, P., and Nouza, J. (2014). Investi-

gation of deep neural networks for robust recognition

of nonlinearly distorted speech. In INTERSPEECH,

pages 363–367.

Vaseghi, S. V. (2008). Advanced digital signal processing

and noise reduction. John Wiley & Sons.

Yu, D. and Seltzer, M. L. (2011). Improved bottleneck fea-

tures using pretrained deep neural networks. In IN-

TERSPEECH, volume 237, page 240.

Study on the Use and Adaptation of Bottleneck Features for Robust Speech Recognition of Nonlinearly Distorted Speech