
Temperature Correction and Reflection Removal in Thermal Images
using 3D Temperature Mapping
Björn Zeise and Bernardo Wagner
Institute of Systems Engineering, Real Time Systems Group, Leibniz Universität Hannover,
Appelstr. 9A, D-30167, Hannover, Germany
Keywords:
Infrared Thermography, 3D Temperature Mapping, Emissivity Estimation, Temperature Correction, Thermal
Reflection Removal, Mobile Service Robotics.
Abstract:
Many mobile robots nowadays use thermal imaging cameras (TICs) in order to enhance the environment
model that is created during exploration tasks. In conventional thermography, thermal images always have
to be carefully revised by human operators, which is not practicable in autonomous applications. Unknown
surface emissivities are the main source of misinterpretations in thermal images. In this work, we present
two methods dealing with these misinterpretations by exploiting the TIC’s changing point of view. While the
first approach classifies the regarded material in order to estimate improved surface temperature values, the
second one is capable of detecting and removing thermal reflections. The spatial relationship between the
thermal images and the regarded surface is made by using a rigidly mounted sensor stack consisting of a TIC
and a 3D laser range finder, whose extrinsic calibration is described. During evaluation, we demonstrate the
functionality of both approaches.
1 INTRODUCTION
In the domain of mobile service robotics, there are
plenty of possible use cases for thermal imaging cam-
eras (TICs) – not only in the context of search and
rescue (Aziz and Mertsching, 2010), but also for in-
spection tasks (Vidas et al., 2013) or traffic surveil-
lance (Iwasaki et al., 2013). Connecting 2D thermal
images with 3D structural information brings bene-
fits to robotic applications, e.g. when robot opera-
tors have to make quick decisions in demanding situ-
ations or in the context of self preservation regarding
an autonomously acting robot. The projection of ther-
mal images onto 3D structures is called temperature
mapping and depicts one of the topics covered in this
work.
While the general procedure of temperature map-
ping is similar to RGB mapping, there are possible
sources of misinterpretations in thermal images influ-
encing the temperature mapping results. This work
focuses on two of them, namely the temperature mis-
interpretations arising from unknown emissivity val-
ues as well as from thermal reflections (see Figure 1).
While a human operator would probably have no
problems figuring out that the thermal image shows
reflections or incorrectly interpreted temperature val-
ues on metal surfaces, this is a rather hard task for
a robot. Misinterpreted environment information can
lead to false assessment of the current situation which
in turn can endanger the accomplishment of the whole
mission.
This work brings the following contributions to
the domain of thermography in mobile robotics: First,
we describe how to calibrate a TIC and a 3D laser
range finder (LRF) using a heated calibration trihe-
dron. We estimate the extrinsic calibration parame-
ters in order to provide 3D points measured by the
LRF with temperature information. The second con-
tribution is an extension of our previous work (Zeise
et al., 2015) aiming at improving temperature mea-
surements of dielectric and metal surfaces. Using the
robot’s capability of changing its point of view, we
exploit the emissivity’s viewing angle dependency in
order to classify the surface material and correct the
measured temperatures accordingly. In contrast to our
previous work, this is performed not only for individ-
ual surface points and lines, but also for 2D images
of a mixed-material surface. The third contribution
is an algorithm that identifies and eliminates moving
thermal reflections.
The remainder of the paper is organized as fol-
lows: In Section 2, we give an overview on related
158
Zeise, B. and Wagner, B.
Temperature Correction and Reflection Removal in Thermal Images using 3D Temperature Mapping.
DOI: 10.5220/0005955801580165
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 158-165
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) Thermal image (b) RGB image
Figure 1: Exemplary thermal reflection: (a) False-colored
thermal image of a person containing a highly reflective
metal surface which reflects the person’s thermal radiation
and (b) a RGB image of the same scene.
work. In Section 3, we describe how to find the ex-
trinsic calibration parameters needed to perform tem-
perature mapping. Section 4 explains our approaches
to correcting temperatures and removing reflections
from thermal images. We close with an evaluation
of the proposed methods in Section 5, concluding the
presented work in Section 6.
2 RELATED WORK
Finding the extrinsic calibration parameters of a LRF
and a camera has been investigated in several works.
In (Zhang and Pless, 2004), the extrinsic calibration
of a camera and a 2D LRF is described. After finding
initial guesses for intrinsic and extrinsic parameters
with the help of a planar checkerboard pattern, the
calibration result is further refined using non-linear
minimization. Regarding the calibration between a
3D LRF and a camera, a similar procedure was used
in works such as (Pandey et al., 2010) and (Gong
et al., 2013). In these approaches, planes are detected
in both the laser and camera observations to determine
the transformation between the sensor frames.
Temperature mapping is a well-known problem
not only in the robotics domain. The most common
method is to use a ray tracing algorithm, that calcu-
lates the intersections of the laser rays and the cam-
era image plane. This principle has been applied by
e.g. (Alba et al., 2011), (Borrmann et al., 2013) and
(Vidas et al., 2013) with different kinds of range sen-
sors.
The effect of a TIC’s varying viewing angle has
been investigated in (Litwa, 2010) and (Muniz et al.,
2014) for dielectrics, and in (Iuchi and Furukawa,
2004) for metals. In (Zeise et al., 2015), we recently
showed an approach to reducing misinterpretations
in thermal images resulting from unknown emissiv-
ity values. For this purpose, we exploited the differ-
ent emissivity characteristics of dielectrics and met-
als. Using the TIC’s viewing angle we were able to
improve the interpretation of temperature values of
low-emissivity surface points and lines.
The removal of thermal reflections can be
achieved either hardware or software-based. A
hardware-based solution suppressing thermal reflec-
tions with the help of an infrared polarizing filter was
presented in (Vollmer et al., 2004). This approach
showed partially good result, but also many limita-
tions (expensive infrared polarizing filter; compliance
to strict spatial measurement setup). The general prin-
ciple of most software-based methods is to extract
background and foreground layers from the image.
This relies on the assumption that the input image
is a linear superposition of an object layer and one
or more reflection layers. In (Planas-Cuchi et al.,
2003), a user-assisted, single-image approach is pre-
sented. Several authors make use of multiple images
of the same scene taken with different camera con-
figurations. Varying the polarizer setting (Farid and
Adelson, 1999), changing the focus (Schechner et al.,
2000) or applying flashlight (Agrawal et al., 2005)
allows to separate the layers. In order to use these
methods, two still images of the same scene have
to be taken, which is not always possible on a mo-
bile robot. The reflection handling method most rele-
vant to our work is the use of the camera’s changing
point of view. Approaches to this have been presented
in (Criminisi et al., 2005), (Li and Brown, 2013) and
(Szeliski et al., 2000).
3 EXTRINSIC LASER-CAMERA
CALIBRATION
The main challenge of temperature mapping lies in
proper geometric calibration of the sensors. The
LRF
1
and the TIC are mounted in a rigid setup, that
can be seen in Figure 2(a). Pointing the sensor stack
at a calibration target of known dimensions, we first
find the transformations between the individual sen-
sors and the calibration target. After that, the trans-
formations between the sensor coordinate frames (i.e.
the TIC’s and the LRF’s coordinate frames) can be
calculated. Since we focus on finding the extrinsic
calibration parameters of the sensors, we assume the
intrinsic calibration parameters for both sensors to be
known.
Since the calibration procedure is mainly based
on the approach of (Gong et al., 2013), we only give
1
By using the term LRF, we mean a 3D LRF unless other-
wise indicated.
Temperature Correction and Reflection Removal in Thermal Images using 3D Temperature Mapping
159

(a) Sensor stack (b) Calibration setup
Figure 2: Sensors used during calibration: (a) sensor setup
consisting of LRF (bottom), TIC (center) and Kinect v2
(top, not used in this work), and (b) calibration setup be-
tween the sensor stack and the calibration target.
a short explanation at this place. The general cali-
bration setup is depicted in Figure 2(b). Let us de-
fine different coordinate frames (X, Y, Z) by using the
indices c, l and t in order to express quantities with
respect to the camera, laser and trihedron coordinate
systems (see also Figure 3). The extrinsic calibration
between the LRF and the TIC is defined by a (3 × 3)
rotation matrix R
lc
and a (3 × 1) translation vec-
tor t
lc
. This transformation can also be expressed as
a transformation from the laser coordinate frame to
the trihedron coordinate frame (R
lt
, t
lt
) = (R
−1
tl
, t
−1
tl
),
followed by a transformation to the camera coordi-
nate frame (R
tc
, t
tc
). A 3D point p
l
with respect to
the laser coordinate frame can be projected onto the
TIC’s image plane using the pinhole camera model:
s
u
v
1
= K(R
lc
p
l
+ t
lc
), (1)
where [u v]
T
is a 2D point in the image plane scaled
by the factor s and K is the camera matrix containing
intrinsic calibration parameters.
In order to find the individual geometric transfor-
mations, a common calibration target is needed. We
use a heated trihedron whose planes made of PVC
are orthogonally oriented. On each of these planes, a
pattern of small circles was created using aluminum-
containing spray. Observing these three planes with
the LRF allows to find the transformation from the tri-
hedron coordinate frame to the laser coordinate frame
(R
tl
, t
tl
). In the thermal image, the circles of the
patterns let us find the corresponding transformation
from the trihedron coordinate frame to the camera co-
ordinate frame (R
tc
, t
tc
).
In the following subsections, we show how to find
the initial transformations for the optimization proce-
dure and how to refine the calibration parameters.
Figure 3: Model of the calibration setup: Coordinate frames
of the TIC (X
c
, Y
c
, Z
c
), of the LRF (X
l
, Y
l
, Z
l
) as well as of
the calibration trihedron (X
t
, Y
t
, Z
t
). On each plane of the
trihedron, there is a pattern consisting of small circles.
3.1 Finding Initial Transformations
Finding the rotation matrix R
tl
and translation vec-
tor t
tl
that transform 3D points with respect to the
trihedron coordinate frame to 3D points with respect
to the laser coordinate frame is accomplished using
the plane equations for each of the trihedron’s planes.
In the following explanations, we utilize a superscript
notation using i, j and k (or variations) to refer to in-
dividual laser-camera data pairs (i ∈ 1, 2, ..., I), indi-
vidual planes ( j ∈ 1, 2, 3) and individual 3D points
(k ∈ 1, 2, ..., K) lying in a plane. The plane equa-
tions are acquired with the help of a RANSAC-based
plane extraction method. Each of the planes detected
by the LRF is defined by a unit normal vector
ˆ
n
( j)
l
and
a distance d
( j)
l
from the laser coordinate frame’s ori-
gin to the plane. The corresponding plane equation
is p
( j)
l
ˆ
n
( j)
l
− d
( j)
l
= 0, where p
( j)
l
is an arbitrary point
lying in the jth plane.
The individual columns of R
tl
depict the planes’
unit normal vectors
ˆ
n
( j)
l
with the result that:
R
tl
=
ˆn
(1)
l,x
ˆn
(2)
l,x
ˆn
(3)
l,x
ˆn
(1)
l,y
ˆn
(2)
l,y
ˆn
(3)
l,y
ˆn
(1)
l,z
ˆn
(2)
l,z
ˆn
(3)
l,z
. (2)
The translation vector t
tl
can be calculated multiply-
ing R
tl
with the vector of plane distances:
t
tl
= R
tl
d
(1)
l
d
(2)
l
d
(3)
l
. (3)
This vector points from the laser coordinate frame’s
origin to the trihedron’s corner, which is also the ori-
gin of the trihedron coordinate frame.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
160

The determination of rotation matrix R
tc
and
translation vector t
tc
that transform 3D points with re-
spect to the trihedron coordinate frame to 3D points
with respect to the camera coordinate frame is quite
similar to the procedure described above. Using the
circle grid patterns, we find the rotation matrices
and translation vectors for transforming the individ-
ual pattern coordinate frames to the camera coordi-
nate frame. These matrices and vectors can then be re-
lated to the trihedron coordinate frame. The columns
of R
tc
, just like for the laser transformation, are the
planes’ unit normal vectors, i.e. the third column r
( j)
3
of the rotation matrix found for each pattern/plane
j ∈ {1, 2, 3}:
R
tc
=
h
r
(1)
3
r
(2)
3
r
(3)
3
i
. (4)
The translation vector t
tc
that points from the cam-
era coordinate frame’s origin to the trihedron’s origin
can be calculated with the help of one of the pattern-
camera transformations by shifting the pattern’s ori-
gin to the trihedron’s origin.
3.2 Refining Calibration Parameters
A refinement of the calibration parameters can be ac-
complished by matching the laser points lying in the
trihedron’s planes into the plane equations estimated
based on the thermal image data. Hence, we try to
find R
lc
and t
lc
that satisfy the Hesse normal form of
each trihedron’s plane. This can be expressed as an
optimization problem of the following form:
argmin
R
lc
,t
lc
I
∑
i=1
3
∑
j=1
K
∑
k=1
ˆ
n
(i, j)
c
(R
lc
p
(i, j,k)
l
+ t
lc
) − d
(i, j)
c
2
,
(5)
where K is the total number of points detected by the
LRF in one specific plane j and data pair i, and I is
the total number of laser-camera data pairs taken. A
solution for this non-linear least squares problem can
be found using the Levenberg-Marquardt algorithm.
4 HANDLING OF
MISINTERPRETATIONS
Most misinterpretations in thermal images originate
from an unknown emissivity ε, which is a surface-
specific property dependent especially on the type of
surface material and the TIC’s viewing angle. The
viewing angle is the angle between the camera’s opti-
cal axis and the surface normal of the regarded point.
According to (Martiny et al., 1996), the signal mea-
sured by the TIC can be expressed as:
S
sum
= εS
ob j
+ (1 − ε)S
amb
(6)
with
S
ob j
=
R
exp
B
T
ob j
− F
(7)
and
S
amb
=
R
exp
B
T
amb
− F
, (8)
if the the atmospheric amount of radiation power is
neglected. In Equation 6, S
sum
, S
ob j
and S
amb
repre-
sent output signals measured per image pixel. Ac-
cording to the subscripts, they depict the total out-
put signal, the output signal corresponding to the re-
garded object’s radiation power and the output signal
corresponding to the reflected ambience’s radiation
power. In Equations 7 and 8, T
ob j
and T
amb
are the
true object/ambient temperatures, while R, B and F
are camera-specific parameters provided by the TIC’s
manufacturer. From Equation 6, it can be seen that the
higher the emissivity value, the smaller the influence
of ambient reflections on the thermal image.
Since in mobile robot exploration a preparation of
the environment before measurement (e.g. using high
emissivity coatings) is not applicable, we developed
two methods for improving the interpretation of ther-
mal images regarding unknown surface emissivities
and thermal reflections.
4.1 Estimation of Unknown Emissivities
This section refers to our previous work in (Zeise
et al., 2015), where we showed the feasibility of
temperature correction for surfaces regarded from a
known viewing angle. In our approach, we estimated
improved surface temperature values of metal and di-
electric surface points exploiting the different emis-
sivity characteristics of metals and dielectrics at a
varying viewing angle.
In general, the approach divides into two subrou-
tines. The first step is to determine the regarded sur-
face point’s material class, i.e. metal or dielectric.
This can be done by observing one individual point’s
output signal at different viewing angles. As we de-
rived from Equation 6, the total output signal depends
linearly on the emissivity. Due to the fact that the
emissivity in general shows a qualitative behavior as
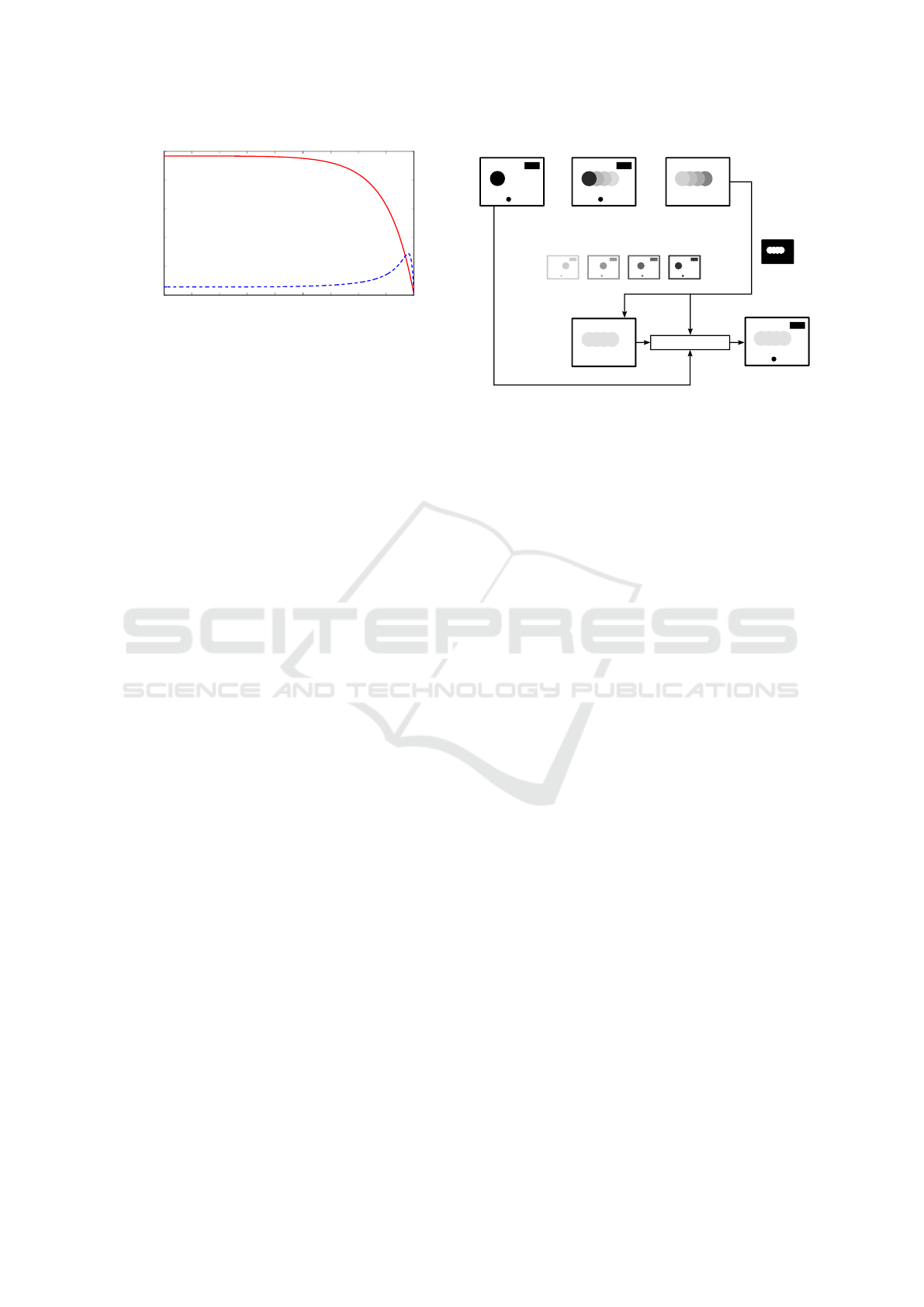
depicted in Figure 4, it is sufficient to investigate the
individual pixel’s output signal in order to assign one
of the properties metal or dielectric to the point.
Temperature Correction and Reflection Removal in Thermal Images using 3D Temperature Mapping
161
0 10 20 30 40 50 60 70 80 90
0
0.2
0.4
0.6
0.8
1
Viewing angle in °
Directional emissivity
Figure 4: Qualitative comparison of metal (blue, dashed
line) and dielectric (red, solid line) emissivity characteris-
tics depending on the viewing angle.
The second step is to estimate improved temper-
ature values for each individual point on the surface.
This can be done using non-linear least squares opti-
mization minimizing the error between the measured
output signals at different viewing angles and theoret-
ically calculated output signals that depend mostly on
emissivity. Equations describing emissivity as a func-
tion of the viewing angle can be found in the litera-
ture, e.g. in (Howell et al., 2011). The minimization
is performed as:
argmin
p
Z
∑
z=1
S
m
z
− S
c
z
(p)
2
, (9)
where p = {n, k, T
ob j
, T
amb
} is the set of parameters to
be found. In this set of parameters, the refractive in-
dex n and the extinction coefficient k, together with
the corresponding viewing angle, describe the graph
of emissivity ε. The signals S
m
z
and S
c
z
represent mea-
sured/calculated values at Z different viewing angles.
In order to use our approach, some assumptions
have to be made. On the one hand, both the surface
temperature T
ob j
and the ambient temperature T
amb
are assumed to be unknown but constant. On the
other hand, T
ob j
must be higher than T
amb
. Since the
assumption that T
amb
= const. is in conflict with the
occurrence of thermal reflections, it is necessary to
identify and remove them before correcting the sur-
face temperatures.
4.2 Thermal Reflection Removal
Handling of thermal reflections can be accomplished
by using background subtraction. The relation of
temperature values and 3D information can be used
to investigate temperature changes of specific surface
points. For our investigations, we assume a static en-
vironment, which implies that the temperatures of the
regarded surfaces do not change over time. Hence,
if an individual surface point’s measured temperature
does not change when the camera moves, it means
– =
+ + +
=
I(t) I
avg1
(t) I
diff
(t)
I(t-3)I(t-4) I(t-2) I(t-1)
+
...
I
avg2
(t)
=
Inverted
Reflection
Area Mask
w
1
= 0.30
w
2
= 0.15
I
res
(t)
Image generation
Figure 5: Illustration of the reflection removal procedure:
Weighted moving averages of thermal images are used to
handle reflections (see the text for a detailed description).
that the temperature is mostly the temperature of the
surface itself. In contrast, a changing temperature of
one specific surface point implies a superposition of
the actual surface temperature and a thermal reflec-
tion.
In Figure 5, our approach to thermal reflection re-
moval is illustrated. Let I(t), I(t − 1), ..., I(t − n) be a
set of registered thermal images of a static scene taken
from different points of view. The weighted moving
average I
avg
(t) at time t can be calculated using the
following equation:
I
avg
(t) = wI(t) + (1 − w)I
avg
(t − 1), (10)
where w is a weighting factor influencing the impor-
tance of the latest image I(t). A high value of w means
more influence of the current image on the moving
average. We use this factor to create two individual
moving averages: In the first, I
avg1
(t), the latest ther-
mal image has a major influence on the average im-
age. Subtracting this average image from the current
thermal image gives us I
di f f
(t) that can be regarded
as a reflection mask. Every pixel in I
di f f
(t) that is not
zero/white represents a potential reflection. The sec-
ond moving average image, I
avg2
(t), is created using
a smaller weighting factor in combination with the re-
flection mask. Masking out the non-reflective pixels
allows to generate an image that contains only reflec-
tive pixels. In contrast to the mask itself and the first
average image, the reflective areas in I
avg2
(t) are very
smooth. This smooth image is then used to fill the re-
flective areas during image generation. Depending on
whether the regarded pixel was marked as reflective
or not in the reflection mask, the image generation ei-
ther uses data from I
avg2
(t) or from I(t) to generate
the resulting image I
res
(t).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
162

Figure 6: Mapping results: False-colored point cloud show-
ing a person standing in front of a cupboard.
5 EVALUATION
The evaluation was performed using the Velodyne
Puck LRF and the Flir A655sc TIC. The LRF pro-
vides dense, horizontal scans with a field of view of
360
◦
, while the vertical field of view is only 30
◦
con-
sisting of 16 scan lines. The TIC has a spatial resolu-
tion of 640 x 480 pixels, working in a spectral range
between 7.5 µm and 14 µm. The camera’s field of
view is 45
◦
x 34
◦
.
5.1 Laser-Camera Calibration and
Temperature Mapping
As stated in Section 3, the intrinsic calibration param-
eters for the LRF were taken as provided by the man-
ufacturer. The intrinsics of the TIC were estimated
using a heated aluminum plate covered with squares
made of aluminum and PVC. The parameter estima-
tion was performed using standard computer vision
algorithms (Zhang, 2000).
The laser-camera calibration can be assessed look-
ing at the temperature mapping results (Figure 6).
Since the vertically sparse point cloud complicates an
objective temperature mapping evaluation, we do not
provide information on the reprojection error.
5.2 Temperature Correction
The temperature correction algorithm was evalu-
ated using the heated, low-emissive aluminum plate
(56 cm x 70 cm) depicted in Figure 7(a). On the plate,
there are several stripes of high-emissive duct tape
forming shapes of a triangle, a square and a circle.
The aim of this evaluation is to first identify the re-
garded material class for every individual pixel in the
thermal image. After that, we use this information to
(a) Reflective plate (b) Material classifi-
cation result
Figure 7: Reflective plate: (a) RGB image of the low-
emissive aluminum plate and (b) the result of the mate-
rial classification procedure (white areas = metal, black ar-
eas = dielectric, gray areas = not specified).
estimate improved values of the surface points’ tem-
peratures.
We took more than 50 laser-camera data pairs of
the heated plate while continuously increasing the
sensors’ viewing angle. Using the four elliptic tags
near the corners of the plate, we were able to reg-
ister consecutive images. In addition, we used the
LRF’s 3D point cloud data to calculate every individ-
ual pixel’s viewing angle.
The results of the material classification are de-
picted in Figure 7(b). The algorithm distinguishes be-
tween metal and dielectric points by adding up the
differences between consecutive measurements taken
from increasing viewing angles. If the resulting value
is greater than zero, the algorithm tags the surface
point as metal, otherwise as dielectric.
The temperature correction is performed for ev-
ery individual surface point. Depending on the ma-
terial class, parameters n, k, T
ob j
and T
amb
are es-
timated using non-linear optimization. To solve the
least squares minimization problem, we make use of
the Levenberg-Marquardt algorithm.
The plate’s true surface temperature was deter-
mined using an additional surface thermometer. On
the metal areas, we measured a temperature of about
317 K. The dielectric shapes had a slightly lower tem-
perature of about 316 K. The direction of reflection
was covered with a wall having a temperature of about
295 K, ensuring a constant ambient temperature T
amb
.
The optimization results are depicted in Figure 8.
The aluminum temperatures in the original thermal
image are obviously misinterpreted. While in the
original image (i.e. without taking emissivity into
account) the metal surface had an average tempera-
ture of about 297 K, our method was able to correct
this value to about 305 K for most of the metal sur-
Temperature Correction and Reflection Removal in Thermal Images using 3D Temperature Mapping
163

Temperature in K
295
300
305
310
315
320
325
330
(a) Original thermal im-
age
Temperature in K
295
300
305
310
315
320
325
330
(b) Processed thermal
image
Figure 8: Temperature correction results (false-colored): (a)
Original thermal image with metal areas interpreted as too
cold (dark) and (b) the corrected image with improved tem-
perature interpretations.
face points. Due to a high emissivity of the dielectric
points, there are almost no misinterpretations in these
areas. Hence, the corrected dielectric temperatures
are nearly the same as the ones originally measured.
While in the border areas between dielectric and
metal points we expected wrong estimations, the re-
sults regarding the metal areas are in need of improve-
ment. This can mostly be traced back to the wave-
length dependency of the optical constants n and k (as
introduced in Section 4.1). Since all measurements
taken by the TIC take into account the whole wave-
length spectrum between 7.5 µm and 14 µm, n and
k, which can vary at different wavelengths, cannot
be unambiguously determined. This is also the rea-
son for erroneously estimated high temperature val-
ues represented by the bright areas in Figure 8(b).
5.3 Reflection Detection and Removal
To evaluate the capabilities of our reflection removal
approach, we used the same aluminum plate as for the
temperature correction experiment. As stated before,
the bare aluminum surface is highly reflective to ther-
mal radiation. We placed a can filled with hot water
(approx. 350 K) in the direction of reflection. We cre-
ated a dataset, taking thermal images while simulta-
neously changing the camera’s point of view. Apply-
ing our algorithm to this dataset leads to the results
depicted in Figure 9.
The resulting image shows that the thermal reflec-
tion could be most widely removed. During our ex-
periments, we noticed a thin, black borderline in the
corrected image at the edge of the aluminum plate.
We trace this back to the fact that our algorithm cuts
out the plate in order to ensure an accurate image
registration. Assuming a complete 3D environment
model in our future research, these borderlines will
not be present anymore.
(a) Original image (b) Resulting image
Figure 9: Reflection removal result for an exemplary dataset
(false-colored): (a) shows the original image containing a
reflection of a can (marked by the ellipse), while (b) depicts
the processed image without reflection.
A possible shortcoming of our approach is that
only moving reflections can be detected at the mo-
ment. For later stages of our work, one solution for
this could be to keep track of reflections as soon as
they were detected.
6 CONCLUSION AND FUTURE
WORK
In this work, we faced the problem of handling misin-
terpretations in thermal images making use of spatial
knowledge of the regarded scene. We acquired in-
formation of the camera’s viewing angle by using a
rigidly mounted sensor setup consisting of a TIC and
a LRF, which we extrinsically calibrated with the help
of a heated calibration trihedron.
We first presented an approach that – using the
emissivity’s viewing angle dependency – is able to
improve temperature measurements of surfaces with
unknown emissivity values. Our method showed
good results in determining the material class (dielec-
tric/metal) of regarded surface points. While the gen-
eral functionality of the temperature correction was
demonstrated, the results are yet limited due to several
unsolved dependencies (e.g. wavelength-dependent
optical constants).
The second method presented deals with thermal
reflections. Exploiting the TIC’s varying viewing an-
gle, our algorithm based on background subtraction
was able to detect and remove reflections from the
images. Experiments showed that moving thermal re-
flections could successfully be removed.
Future work will focus on integrating the pre-
sented approaches into a 3D simultaneous localiza-
tion and mapping (SLAM) algorithm. By doing this,
our algorithms will benefit from the spatial knowl-
edge of the scene on the one hand, while enhancing
the generated environment model with improved tem-
perature mapping on the other hand. Additional effort
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
164

can be spent on tuning the performance of the tem-
perature correction algorithm, e.g. by using a GPU
implementation.
ACKNOWLEDGEMENTS
This work has partly been supported within H2020-
ICT by the European Commission under grant agree-
ment number 645101 (SmokeBot).
REFERENCES
Agrawal, A., Raskar, R., Nayar, S. K., and Li, Y. (2005).
Removing photography artifacts using gradient pro-
jection and flash-exposure sampling. ACM Trans.
Graph., 24(3):828–835.
Alba, M. I., Barazzetti, L., Scaioni, M., Rosina, E., and Pre-
vitali, M. (2011). Mapping infrared data on terrestrial
laser scanning 3D models of buildings. Remote Sens-
ing, 3(9):1847–1870.
Aziz, M. Z. and Mertsching, B. (2010). Survivor search
with autonomous UGVs using multimodal overt at-
tention. In IEEE Safety Security and Rescue Robotics,
pages 1–6, Bremen, Germany.
Borrmann, D., Elseberg, J., and Nüchter, A. (2013). Ther-
mal 3D mapping of building façades. In Lee, S., Cho,
H., Yoon, K.-J., and Lee, J., editors, Intelligent Au-
tonomous Systems 12, number 193 in Advances in
Intelligent Systems and Computing, pages 173–182.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Criminisi, A., Kang, S. B., Swaminathan, R., Szeliski, R.,
and Anandan, P. (2005). Extracting layers and ana-
lyzing their specular properties using epipolar-plane-
image analysis. Computer Vision and Image Under-
standing, 97(1):51–85.
Farid, H. and Adelson, E. H. (1999). Separating reflections
and lighting using independent components analysis.
In IEEE Computer Society Conference on Computer
Vision and Pattern Recognition, volume 1, pages 262–
267, Fort Collins, CO, USA.
Gong, X., Lin, Y., and Liu, J. (2013). 3D LIDAR-camera
extrinsic calibration using an arbitrary trihedron. Sen-
sors, 13(2):1902–1918.
Howell, J. R., Siegel, R., and Mengüç, M. P. (2011). Ther-
mal radiation heat transfer. CRC Press, Boca Raton,
FL, USA, 5th edition.
Iuchi, T. and Furukawa, T. (2004). Some considerations
for a method that simultaneously measures the tem-
perature and emissivity of a metal in a high tem-
perature furnace. Review of Scientific Instruments,
75(12):5326–5332.
Iwasaki, Y., Kawata, S., and Nakamiya, T. (2013). Ve-
hicle detection even in poor visibility conditions us-
ing infrared thermal images and its application to road
traffic flow monitoring. In Sobh, T. and Elleithy, K.,
editors, Emerging Trends in Computing, Informatics,
Systems Sciences, and Engineering, number 151 in
Lecture Notes in Electrical Engineering, pages 997–
1009. Springer New York, New York, NY, USA.
Li, Y. and Brown, M. S. (2013). Exploiting reflection
change for automatic reflection removal. In IEEE
International Conference on Computer Vision, pages
2432–2439, Sydney, Australia.
Litwa, M. (2010). Influence of angle of view on tempera-
ture measurements using thermovision camera. IEEE
Sensors Journal, 10(10):1552–1554.
Martiny, M., Schiele, R., Gritsch, M., Schulz, A., and Wit-
tig, S. (1996). In situ calibration for quantitative
infrared thermography. In International Conference
on Quantitative InfraRed Thermography, pages 3–8,
Stuttgart, Germany.
Muniz, P. R., Cani, S. P. N., and Magalhães, R. d. S. (2014).
Influence of field of view of thermal imagers and an-
gle of view on temperature measurements by infrared
thermovision. IEEE Sensors Journal, 14(3):729–733.
Pandey, G., McBride, J., Savarese, S., and Eustice, R.
(2010). Extrinsic calibration of a 3D laser scanner and
an omnidirectional camera. IFAC Proceedings Vol-
umes, 43(16):336 – 341.
Planas-Cuchi, E., Chatris, J. M., López, C., and Arnaldos, J.
(2003). Determination of flame emissivity in hydro-
carbon pool fires using infrared thermography. Fire
Technology, 39(3):261–273.
Schechner, Y. Y., Kiryati, N., and Basri, R. (2000). Sepa-
ration of transparent layers using focus. International
Journal of Computer Vision, 39(1):25–39.
Szeliski, R., Avidan, S., and Anandan, P. (2000). Layer
extraction from multiple images containing reflections
and transparency. In IEEE Conference on Computer
Vision and Pattern Recognition, volume 1, pages 246–
253, Hilton Head Island, SC, USA.
Vidas, S., Moghadam, P., and Bosse, M. (2013). 3D ther-
mal mapping of building interiors using an RGB-D
and thermal camera. In IEEE International Confer-
ence on Robotics and Automation, pages 2311–2318,
Karlsruhe, Germany.
Vollmer, M., Henke, S., Karstädt, D., Möllmann, K. P.,
and Pinno, F. (2004). Identification and suppression
of thermal reflections in infrared thermal imaging. In
InfraMation Proceedings, volume 5, pages 287–298,
Las Vegas, NV, USA.
Zeise, B., Kleinschmidt, S. P., and Wagner, B. (2015). Im-
proving the interpretation of thermal images with the
aid of emissivity’s angular dependency. In IEEE Inter-
national Symposium on Safety, Security, and Rescue
Robotics, pages 1–8, West Lafayette, IN, USA.
Zhang, Q. and Pless, R. (2004). Extrinsic calibration of a
camera and laser range finder (improves camera cali-
bration). In IEEE/RSJ International Conference on In-
telligent Robots and Systems, volume 3, pages 2301–
2306, Sendai, Japan.
Zhang, Z. (2000). A flexible new technique for camera cal-
ibration. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 22(11):1330–1334.
Temperature Correction and Reflection Removal in Thermal Images using 3D Temperature Mapping
165
