
A Practical Encrypted Microprocessor
Peter T. Breuer
1
, Jonathan P. Bowen
2
, Esther Palomar
3
and Zhiming Liu
4∗
1
Hecusys LLC, Atlanta, GA, U.S.A.
2
Faculty of Engineering, London South Bank University, London, U.K.
3
Faculty of Computing, Engineering & The Built Environment, Birmingham City University, Birmingham, U.K.
4
Centre for Research and Innovation in Software Engineering, Southwest University, Chongqing, China
Keywords:
Computer Security, Encrypted Computing, Computer Architecture, Applied Cryptography.
Abstract:
This paper explores a new approach to encrypted microprocessing, potentiating new trade-offs in security
versus performance engineering. The coprocessor prototype described runs standard machine code (32-bit
OpenRISC v1.1) with encrypted data in registers, on buses, and in memory. The architecture is ‘superscalar’,
executing multiple instructions simultaneously, and is sophisticated enough that it achieves speeds approaching
that of contemporary off-the-shelf processor cores.
The aim of the design is to protect user data against the operator or owner of the processor, and so-called
‘Iago’ attacks in general, for those paradigms that require trust in data-heavy computations in remote locations
and/or overseen by untrusted operators. A single idea underlies the architecture, its performance and security
properties: it is that a modified arithmetic is enough to cause all program execution to be encrypted. The
privileged operator, running unencrypted with the standard arithmetic, can see and try their luck at modifying
encrypted data, but has no special access to the information in it, as proven here. We test the issues, reporting
performance in particular for 64-bit Rijndael and 72-bit Paillier encryptions, the latter running keylessly.
1 INTRODUCTION
If the arithmetic in a conventional processor is mod-
ified appropriately, then, given three provisos (sum-
marised in Section 3), the processor operates cor-
rectly, but all the states obtained in registers and mem-
ory and on buses are one-to-many encryptions of the
states obtained in an unmodified processor running
the same program (Breuer and Bowen, 2013). That
opens a path to a new kind of processor that, operat-
ing encrypted, is a priori more secure from prying and
interference than current processors are, yet it should
in principle be as fast, because only one piece of state-
less internal logic – the arithmetic unit – has changed.
This paper reports on prototyping that tests the
idea to a pre-production level, just before the point
of gate synthesis and layout. The object is
(a) to protect user data (not code) from the operating
system and operator;
(b) to run fast enough for users wanting offline work
∗
Correspondence to: Z. Liu, RISE, Southwest Univer-
sity, 2 Tiansheng Rd, Beibei, Chongqing 400715, China.
to be performed remotely and securely.
A typical use case would be image-processing.
The prototype is sophisticated enough to bear
comparison with off-the-shelf processors: it is su-
perscalar (it executes multiple instructions at a time),
with a pipeline in which full ‘forwarding’ has been
embedded (pipeline stalls in which an instruction be-
hind waits for data from an instruction ahead have
been eliminated as far as is logically possible), along
with branch prediction, instruction and data caching,
speculative execution, etc.
The prototype in its present form is intended to
run as a coprocessor, executing ‘somewhat’ encrypted
machine code (data fields are encrypted, not opcodes).
That is set up in practice with interrupt handlers and
a few system calls in memory, never a full multiuser
multitasking operating system, and libraries and other
support would be compiled-in to encrypted code.
An encrypted processor provides the lowest level
kind of security possible and we recognise that not
many security engineers are familiar with this level
of working. To answer some basic questions imme-
diately: while encrypted and unencrypted code run in
the same core, they remain apart because they do not
Breuer, P., Bowen, J., Palomar, E. and Liu, Z.
A Practical Encrypted Microprocessor.
DOI: 10.5220/0005955902390250
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 239-250
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
239

run at the same time. The problem is they might see
remnants of the other’s data, but from both points of
view the other’s data is encrypted. Yes, a user’s pro-
gram code is visible to the system operator, and that is
as designed. The program’s control flow would in any
case become visible to an operator single-stepping the
machine or running a debugger, but the operator can-
not tell if that is an encrypted image of a mountain or
a lake being processed.
Note that if a user is determined to hide control
flow, at the expense of slower running they may sup-
ply a virtual machine to run encrypted on the plat-
form. Then both code and control flow constitute a
block of encrypted data that is repeatedly transformed
in the same way every cycle by a virtual machine’s
state transition function.
But between theory and an encrypted processor
that people might want to use lies much practical
work. Here are three questions that a sceptical tech-
nologist could ask:
1. Can an architecture based on a changed arithmetic
really approach the performance of modern pro-
cessors? Demonstrate it!
That means ‘superscalar’ (multiple instructions exe-
cuted piecewise simultaneously) and multicore tech-
nologies – we are way past the days when the In-
tel 8088 would first execute one instruction, then the
next. Modern processors break instructions up into
small operations and execute the parts simultaneously
along one or more pipelines. Some of the execution
is speculative – liable to be discarded and/or reversed
– and instructions and their component parts may be
accelerated or delayed according to a complex sys-
tem of dependencies and constraints. A processor is
not purely numerical – it is supposed to react to arith-
metic overflows and a host of exception conditions
and flags that might not be compatible with a mod-
ified arithmetic and encrypted execution. It is not a
priori clear that any of that will be sustainable.
The prototype is a platform on which to test these
issues. Broadly speaking, we do have the perfor-
mance required, reaching 70% of the speed of unen-
crypted running as of the date of this paper submis-
sion
2
(Section 6), and we do have the correct instruc-
tion semantics in all aspects with respect to a recog-
nised standard, as discussed.
2. Will the production machine be compatible with
existing soft- and hardware technologies?
After all, in terms of software, nobody today is gen-
erating encrypted machine code and nobody has an
operating system for it, and it is not clear if we know
2
80% has been reached at camera-ready copy date.
how to make user code run under an operating sys-
tem that effectively runs blind to it. How would the
two communicate? Should they? Do they? There
is no future in a hardware technology, no matter how
good it is in security terms, that requires us to discard
our software and start again. Hopefully that will not
be the case, but perhaps the machine will require too
much memory, or too wide buses, or impossibly fast
logic. A technologist needs convincing that these are
not issues. Against that, we can say that we do have
an assembler and compiler and a minimal operating
system, and we are able to run standard test codes.
3. Will a working product adapted to the realities be
as secure as the idea promises?
Here the answers are harder to specify and we
will supply data in this paper. Both encrypted
and unencrypted bits pass through common elements
in the processor in close proximity in time and
space, which is inherently dangerous. Perhaps side-
channels and attack vectors will side-step the en-
crypted/unencrypted security barrier: the system op-
erator can measure power drain and see when mem-
ory areas are used repeatedly via cache statistics, for
example. Perhaps the operator can set the machine’s
control registers to break the barrier.
One answer that does not need a paper to discuss
it is that a manufacturer may apply existing protec-
tion technology on top of this design. Technologies
make no issue about whether 1 mod 0 = 1 or not,
merely on there being details to be masked. Mask-
ing power drain is known ‘moat’ electronic technol-
ogy (e.g., (Kissell, 2006)). Randomising memory
addressing has a long history too (‘oblivious RAM’
(Ostrovsky, 1990) and its recent developments (Maas
et al., 2013; Liu et al., 2015)). Moreover, a natu-
ral masking is already present, because many differ-
ent encrypted numbers will be passed to the mem-
ory bus for what was meant by the programmer to be
the same address under the (one-to-many) encryption
(Section 3 describes how software may be compiled
to deal with this). At any rate, the situation is not
worse than for conventional processors, and the pro-
tections developed for them are admissible.
A criterion for success is that an operator, despite
their privileges, cannot access unencrypted user data,
or interfere meaningfully with it. What can a hostile
operator do then? Still everything, but not undetected,
if some simple finesses are built in: a computation
trace hash under the encryption flags up interference;
encrypted data in memory containing a hash of its ad-
dress makes copying for replay use difficult, etc.
In this paper, we report on what the pre-production
prototype tells us, running in simulation, explaining
the design’s solutions for the questions raised above.
SECRYPT 2016 - International Conference on Security and Cryptography
240

After discussing related work and other context in
Section 2, we lay out in Section 3 hardware and soft-
ware provisos, as mentioned in the first paragraph of
this section, required for the design to work. A defini-
tive account of the processor architecture is given in
Section 4. Section 5 gives answers to security ques-
tions, and Section 6 discusses performance, setting
out the numerical evidence.
2 OVERVIEW & RELATED WORK
Firstly, here are some statements to set the ground for
the reader and summarise the situation before entering
into technical details:
Standards. Our processor covers the Open-
RISC version 1.1 rev. 0 instruction set and register-
level specification (opencores.org/or1k/Architecture\
Specification). There is an answer in that to the scep-
tical technologist’s point #2, because the expertise of
existing manufacturers may be leveraged for produc-
tion and there is no doubt as to the suitability as a plat-
form for general purpose computing. We are not start-
ing from nothing. The OpenRISC specification de-
tails hundreds of conditions for the 220 machine code
instructions, and our prototype passes the Or1ksim
test suite (opencores.org/or1k/Or1ksim) in encrypted
and unencrypted running.
Sizes. Data words are 32 bits long under the en-
cryption, but they physically occupy an encryption
block, 64 or 128 bits, etc., depending on the encryp-
tion. The register size and memory word size is the
encryption block size, not 32 bits. Buses are also cor-
respondingly wider.
Instructions. Instructions are 32 bits in length,
conforming to OpenRISC. Data embedded as part of
an instruction is encrypted (see Section 4), but the rest
of the instruction is ‘in the clear’ and can be read or
rewritten by anyone. The kind of instruction is not
secret – data, not code, is protected here.
Memory. Storage in RAM is not different from
normal, and ordinary RAM sticks are to be used with
this processor. Memory access occurs at the same
points and slightly greater spacings (because of ex-
tra instructions needed to carry encrypted immedi-
ate data) in an encrypted program, but the access is
always 64 bits, or 128 bits, matching the encrypted
word size, not 32 bits. A program’s memory foot-
print is ×2 or ×4 the unencrypted size, depending on
the encryption, which has no real impact nowadays.
Cache similarly needs to be double or quadruple size
and caching is less effective than usual, overall, but
the focus of memory and cache stress lies elsewhere,
in remapping at the fine granularity required for en-
crypted addressing (see Section 4).
There is no particular stress on the widened mem-
ory bus otherwise. Fast load/store cycling stresses the
bus as much as it does in a standard processor, for
example, no more and no less. There is no extra en-
cryption/decryption on the way to memory from the
encrypted processor in our design, so no extra delays
occur there.
Software. An existing OpenRISC toolchain port
has been modified for use, the GNU ‘gcc’ version
4.9.1 compiler and ‘gas’ version 2.24.51 assembler
(the modified source is at sf.net/p/or1k64kpu-gcc and
sf.net/p/or1k64kpu-binutils respectively). Encryption
is confined to the instruction assembler, which moves
machine code around to make room for embedded
encrypted data, while compilation focuses on higher
level strategies. A standard executable file (‘ELF’ for-
mat) encapsulates the encrypted machine code in its
‘.text’ section and read-only encrypted constants are
put in subsections containing an encrypted word each,
specifying the (encrypted) address.
Encryptions. We have run the same experiments
with two different encryptions in the processor. The
first is a symmetric 64-bit encryption, Rijndael-64
(Daemen and Rijmen, 2002). Registers and words are
physically 64 bits wide (note that 64, 72, 128, etc., are
in no way design limits).
We have also tried a Paillier encryption (Paillier,
1999). That is an additively homomorphic encryp-
tion, in which addition under the encryption corre-
sponds to multiplication (modulo some m) on the en-
crypted data. The experiment embedded only 72-bit
Paillier where 512–1024 bits would be comparable to
64-bit Rijndael, but it is sufficient to draw conclu-
sions. The encrypted word takes the left 72 bits of
128, encrypting 32-bit data, and registers and words
are 128 bits wide.
Independence. It is to be emphasised that the ap-
proach here is not dependent on Rijndael or Paillier,
or 64 or 72 bits etc. Any symmetric encryption works,
Rijndael or not, provided it fits in the registers and on
buses (and their size may be designed to match the
requirement), but a key is always needed. More bits
(e.g. 128) is reasonable today, but there is a penalty
in that machine code instructions that contain embed-
ded data become correspondingly larger, such that it is
hard to contemplate from the point of view of perfor-
mance. Programs would have to be compiled to avoid
embedded data, choosing memory load and store in-
stead, or the memory and cache pathway would have
to be made wider (e.g., 8 consecutive instructions read
at a time, instead of 4). Further architectural proto-
typing than that reported here is needed to map the
trade-offs comprehensively.
A Practical Encrypted Microprocessor
241

Any additively homomorphic encryption works,
Paillier or not, provided it fits, etc., and no key is re-
quired. But Paillier needs a ‘table of signs’, discussed
below, that effectively limits its applicability to 32-
bit computing at present, no matter what block or key
size is used. An additive homomorphic encryption in
which the sign were also obtained homomorphically
would remove that limit, and we hope for one in the
near future. However, known homomorphic encryp-
tions are very ‘wide’ for the same level of security
as symmetric encryptions and that will always give a
performance hit in comparison.
Vulnerabilities. If an attacker has a scanning
electron microscope or similar advanced physical
probes, then a Rijndael encryption is vulnerable to it
because there is a codec (encryption/decryption de-
vice) forming part of the processor pipeline, as de-
scribed in Section 4. However, vulnerable areas will
normally be buried deep inside the chip in a produc-
tion model, as in the ubiquitous modern smartcard
technology (K
¨
ommerling and Kuhn, 1999). The ar-
rangement here is not less secure. Keys for the codec
may be built in at manufacture, as in a smartcard, or
managed via an established key management technol-
ogy. But key management for symmetric encryptions
is emphatically not relevant for this paper’s aims.
That is partly an issue for a business model and partly
for future research directions and we do not want to
gainsay the eventual answer here. The CIA (US Cen-
tral Intelligence Agency) is not going to want to share
their computers, for example, so one key per proces-
sor might be fine for them. If a key is to be lodged
in the codec just before use, that may be handled by
a Diffie-Hellman circuit, such as (Buer, 2006), that
can secretly transfer the key while never exposing it
in registers or memory or on buses. It does not matter
in principle if the wrong user runs when that key is
installed, as the user cannot read the results or enter
data that makes sense, nor compile a nontrivial pro-
gram that will run. Whether that user can somehow
devise programmed experiments that reveal the key is
the same question as whether the operator can, so key
management is in that sense an orthogonal issue.
Notably, there are no codecs or keys involved with
the Paillier encryption in the processor. In principle
our simulations might be run in full public view. The
parts of the processor taken up by the codec for Ri-
jndael are occupied instead by the Paillier ‘addition’
on encrypted data. That is 72-bit multiplication mod-
ulo m, with no encryption or decryption. That can
be done in hardware in one or two stages, but we en-
visage a production machine using 512- to 1024-bit
Paillier, which would require many more stages, so
our simulation pretends 10 of 15 pipeline stages are
required even for lowly 72-bit Paillier addition.
Exceptional Stresses with Paillier. In using
the Paillier encryption we follow (Tsoutsos and Ma-
niatakos, 2013; Tsoutsos and Maniatakos, 2015),
where a ‘one instruction’ stack machine architec-
ture (‘HEROIC’) for encrypted computing embed-
ding a 16-bit Paillier encryption is prototyped. In
conjunction with a lookup table for the signs (posi-
tive/negative) of encrypted data, the Paillier addition
is computationally complete (any computable func-
tion can be implemented using addition, the table, an
encrypted 1, and recursion), and addition, subtrac-
tion, and comparison machine code instructions suf-
fice to write software routines for the rest. The 72
bits is the most that is convenient without alterations
to our compile strategy to place encrypted constants
in memory rather than inline in the machine code,
and is not a hard limit. The problem is that 72 bits
does not fit in 32-bit instructions, and the sequence
is already ‘prefix; prefix; instruction’ for each inline
constant used, so increasing the number of bits would
further reduce the proportion of ‘real’ instructions in
code, affecting performance.
However, we believe the table of signs is a vul-
nerability in practice (see Section 5). It is also
very large, consisting of 2
31
× x rows of 72 bits,
where x is the number of different encryptions of
each (negative) number. That is hundreds of GBytes,
perhaps TBytes, and it is a concern with present
technology. Still, motherboards are available now
with TBytes of RAM (see for example the Super-
micro Xeon 7000 range at supermicro.com/products/
motherboard/Xeon7000/), so we expect that concern
to diminish in the future. We have ‘cheated’ in our
simulation by computing rows of the table externally
on demand and caching them locally to the processor.
Software Engineering. OpenRISC’s ‘or1ksim’
simulator project has been modified to run the pro-
cessor prototype. It is now a cycle-accurate simu-
lator, 800,000 lines of finished C code having been
added through a sequence of seven successive mod-
els. The code archive and history is available at
sf.net/p/or1ksim64kpu.
Historical use of Encryption in Computing. At-
tempts at creating a processor that works with greater
security against observation and tampering have reg-
ularly been made in the past. One of the earliest land-
marks is a US Patent “Tamper Resistant Microproces-
sor” (Hashimoto et al., 2001) which states “it should
be apparent to those skilled in the art that it is possi-
ble to add [a] data encryption function to the micro-
processor . . . ”, meaning that codecs could be placed
between processor and encrypted content in memory.
However, a codec on the memory path, adding la-
SECRYPT 2016 - International Conference on Security and Cryptography
242

tency, forms no part of our design. Data is already
encrypted by the time it leaves the processor pipeline,
so there is nothing more to do. Extra overhead is in-
curred instead by remapping for encrypted addresses,
as discussed in Section 4, which entails an extra cache
retrieval (for the mapping) for each load/store and a
minor fault handler call on a cache miss.
Keyed Access to Memory. Hashimoto et al. also
aimed to segregate memory via access keys, and that
aspect of their proposal has echoes in recent ap-
proaches such as Schuster et al.’s implementation of
MapReduce for cloud-based query processing (Schus-
ter et al., 2015) on Intel
R
SGX
TM
machines, which
employs the machine’s built-in hardware (Anati et al.,
2013) to isolate the memory regions involved to well-
defined ‘enclaves’, and encryption may also feature.
Encrypted Memory. In Hashimoto et al. and oth-
ers’ proposals the basis is that encrypted content is
kept in memory and decrypted en route. That means
that in case of a process crash and a dump of the
memory region, the file will record encrypted mem-
ory content. Thus a malicious user cannot obtain the
decryption of an encrypted CD by inducing through
some ingenious means the reading process to crash
and dump. Nor can ‘cold boot’ techniques (Halder-
man et al., 2009) recover information, as memory
contents are encrypted. But memory is only one pe-
ripheral device of many (disk, keyboard, USB, etc).
Intel SGX is competition here, but we can-
not compete with Intel’s design and implementation
teams. All we can show is that our approach is an al-
ternative, and if Intel were to apply their resources to
it they may do better yet. In principle, our approach
of embedding a codec in the processor pipeline is far
faster than encryption on the way to/from memory
can ever be, even in burst mode, because pipelining
achieves an average throughput of one encryption per
cycle though each encryption takes 20× that time.
Security Basics. The working of the encrypted
processor described in this paper is intended to be
simple enough that its security is analysable by se-
curity not hardware experts:
(I) in user mode, data circulates encrypted in the
processor, and
(II) in supervisor mode it circulates unencrypted.
If that claim is true, then a system operator may give
up on snooping an unencrypted form of user data,
and can only meaningfully move encrypted data from
place to place. Altering it is possible, but not mean-
ingful unless the operator already knows something
about the encryption.
That puts the focus on whether a system opera-
tor can determine information from the patterns of
encrypted data observed, or achieved by experiment
(submitting a known ciphertext for encrypted process-
ing, for example), essentially the position of an un-
privileged adversary who may obtain the same ends
by social engineering, e.g., by tricking debug syscalls
into submitted code.
3 THREE CONDITIONS
To make a conventional processor architecture work
encrypted by virtue of a modified arithmetic, certain
conditions must be met.
(A) The arithmetic must be ‘homomorphic’ with re-
spect to ordinary computer arithmetic.
That does not imply merely a one-to-one rearrange-
ment of the conventional (2s complement) encoding
of numbers in 32-bit binary. The constraint is
E (x+y)= f (E (x),E (y)), specifying the encrypted
output f (a, b) from the modified ALU in the proces-
sor when encrypted inputs a=E (x) and b=E (y) are
presented to it, so a designer chooses an encryption
E that achieves a trade-off between security and the
feasibility of an appropriate function f in hardware.
The encryption E is one-to-many, when random
padding or blinding is taken into account.
The requirement is formally weaker than classical
homomorphism in encryption, which has E (x+y) =
E (x)+E (y). That is not a question of ‘what is in a
name’ as to whether the function is called ‘ f ’ or ‘+’;
the designer is not obliged to co-opt the familiar ‘+’
for f . For the Paillier encryption, the ALU operation
f (a,b) is multiplication ab mod m, where m is the
Paillier modulus (m = n
2
, n = pq, p, q 36-bit primes
such that lcm{p−1,q−1} has at least one small fac-
tor, in order to allow a blinding factor of low multi-
plicative order to exist). For the Rijndael encryption
f (a,b) is E (D (a) + D(b)), invoking a codec three
times, where D is the decryption function. Clever
hardware improves that ‘dumb’ solution to work fast
and securely in the prototype (Section 4).
The detailed conditions on the changed ALU
functionality ALU
0
for every operation may be de-
rived from the rendering in Fig. 1 (Breuer and Bowen,
2013). There are three equations, corresponding to
the three kinds of arithmetic operations in the ALU:
unary operations u such as bit-flipping x → ˆx; binary
operations b such as addition (x,y) → x+y; compar-
isons r such as less than, (x,y) → (x<y). In terms of
the relation between encrypted data e and decrypted
data d, such that d = D (e), the equations are
ALU
u
(d) = D (ALU
0
u
(e)) (1)
A Practical Encrypted Microprocessor
243

ALU
D
D
32
32
32
ALU’
E
1(compare)
Figure 1: Idealised modified arithmetic logic unit (ALU)
for encrypted operation (ALU
0
), with decryption units (D)
and encryption unit (E).
ALU
b
(d
1
,d
2
) = D (ALU
0
b
(e
1
,e
2
)) (2)
ALU
r
(d
1
,d
2
) = ALU
0
r
(e
1
,e
2
) (3)
The first two constrain the encrypted data output of
the modified ALU, and the third constrains the 1-bit
comparator output. For the addition operator, the as-
sertion (2) is
d
1
+ d
2
mod 2
32
= D ( f (e
1
,e
2
))
where f is the modified ALU’s operation. If f is mul-
tiplication on the encrypted values, as in the Paillier
encryption, then (2) is
d
1
+ d
2
mod 2
32
= D (e
1
e
2
mod m)
but more solutions are possible in general.
Because they look no different and are produced
dynamically in the course of a program, for example
by adding an offset to a base address, data addresses
must be encrypted just like other data. However, pro-
gram addresses (the addresses of machine code in-
structions in memory) are not encrypted, the rationale
being that the program counter is usually advanced by
a constant at each tick of the clock, and that potenti-
ates an attack against the encryption. The solution
adopted is not to encrypt program addresses at all. So:
(B) Encrypted programs must never arithmetically
mix program addresses and ordinary data.
A conforming program may not jump to an ad-
dress given by the square root of Elvis’s birthdate.
That is easy to arrange via compilation from
source, and can be checked automatically at the ma-
chine code level (Breuer and Bowen, 2012). Dynamic
loaders and linkers are not restricted by this condition
because they run in supervisor mode, although late
linking is not recommended for a program intended
to run securely.
The third condition on correct running on the en-
crypted platform is due to the fact that many differ-
ent runtime encodings may be generated for what the
Table 1: OpenRISC instruction set coverage in the proto-
type, per User and Supervisor mode.
kind\mode
32-bit 64-bit
Encrypted Unencrypted Encrypted Unencrypted
Integer U S - S
Float U S - S
Vector - - - -
programmer intended to be the same memory address,
as a consequence of the one-to-many nature of good
encryption. That gives rise to hardware aliasing, in
that the same address (as seen by a program running
under the encryption) sporadically accesses different
data. To avoid it:
(C) Programs must be compiled to save data ad-
dresses for reuse, or recalculate them exactly the
same way the next time.
Stepping up then down a string is affected, for ex-
ample. In truth, (C) only need hold over the reads fol-
lowing a write, which is an opportunity to change the
address mapping at each write, achieving what clas-
sical ‘oblivious RAM’ does. The second option de-
pends on the processor being deterministic at bottom,
including generation of padding under the encryption.
4 ARCHITECTURE
The processor runs in two modes, user mode (32-bit
data encrypted in 64 or more bits, OpenRISC 32-
bit instructions) and supervisor mode (64-bit unen-
crypted data, 32/64-bit instructions). User mode in-
structions access 32 general purpose registers (GPRs)
and a few permitted special purpose registers (SPRs,
2
16
available in supervisor mode). Attempts to write
‘out of bounds’ SPRs are silently ignored in user
mode and a random value is read. The instruction set
coverage across modes is summarised in Table 1.
In accord with the OpenRISC specification, there
is no grand separation of memory into ‘supervisor’
and ‘user’ parts except that user mode is restricted
to 32-bit addresses in a fundamentally 64-bit archi-
tecture. A supervisor mode process can always read
user data in memory, but the data will be in encrypted
form. The other way round, (user) access is guided by
the memory mapping, which can only be programmed
in supervisor mode, via the memory management unit
(MMU). That is all quite conventional.
Unconventionally, however, in user mode, a spe-
cial ‘translation lookaside buffer’ (TLB) in the MMU
is active. It remaps encrypted addresses, which are
scattered all over the cipherspace, to a contiguous lin-
ear sequence of unencrypted addresses in a designated
region on a first-come, first-served basis. The map-
SECRYPT 2016 - International Conference on Security and Cryptography
244

5678 021 20 16 15252631
code
func
2−bit
021 20 16 15252631 11 10
fill
2−bit
31 26 25 024 23
opcode 24−bit fragment of 64−bit encrypted word
opcode
opcode
8−bit fill
021 20 16 15252631
opcode
dest.
register
source
register
source
register
dest.
register
shift
move to
spr
immediate
load/store
source
register
16−bit fragment of 64−bit encrypted word
6−bit shift
16−bit offset (ignored)
prefix
(new)
fill (ignored)
5−bit zero
5 bits of
SPR index
11 bits of SPR index
Figure 2: Modifications to OpenRISC instructions. An ex-
tra ‘prefix’ instruction carries part of an encrypted immedi-
ate, and the shift immediate instruction has been respecified
to contain 16 bits of a 64-bit encrypted (6-bit) shift value,
including the subfunction specifier. The displacement field
in a load/store instruction is ignored, as is the alternative
designator register in a move to/from SPR instruction.
ping database is stored in memory and cached and
the TLB hardware does the lookup and assignment.
The upshot is that every encrypted memory address
is blindly remapped to a contiguous region in user
mode. Temporal locality of mappings gives rise to
spatial locality in the cache, which is effective. Ev-
ery word in memory is addressed via this TLB map-
ping database but the mapping is cached so the effect
is usually not two memory accesses but one and one
TLB cache access. On the other hand, a TLB cache
miss is costly, invoking the minor TLB fault handler.
Every encrypted word in memory (64 or 128 bits) also
costs one new TLB entry (128 bits) in memory. Mem-
ory access is slower on average on that account, and
more is used. There are already separate paths for
data and program memory (‘Harvard’ layout), and we
are considering introducing a path for TLB too.
Looking beyond the relatively mundane address
engineering discussed above, the major modifications
in the processor are associated with the Rijndael im-
plementation of changed arithmetic, as illustrated in
Fig. 1. In order to reduce the frequency with which
a codec is brought into action for user mode instruc-
tions, ALU operation is extended in the time dimen-
sion, so it covers consecutive (encrypted) arithmetic
operations in user mode. Only the beginning of the
series is associated with a decryption event, when en-
crypted data from memory or registers is converted,
and only the end of the series is associated with an en-
cryption event. In between, arithmetic is carried out
unencrypted in user mode, in a set of ‘shadow regis-
ters’, unavailable in supervisor mode. An instruction
in user mode sees the shadow registers and an instruc-
tion in supervisor mode sees the ‘real’ registers. The
aliases are flipped per instruction mode per stage of
the processor pipeline, so there is no possibility of an
instruction seeing the wrong set (see Section 5).
The Rijndael codec is embedded across multiple
stages of the processor instruction pipeline. Hav-
ing it there is hugely effective, because it lets en-
cryption/decryption benefit from the ‘pipeline speed-
up’ effect largely responsible for modern processor
speeds. A 15-stage pipeline can work on 15 in-
structions at a time in parallel, completing up to 15
times as many instructions per cycle as it would other-
wise, making the processor 15 times as fast as a non-
pipelined processor. One encryption/decryption can
complete per cycle, even if each takes 10 cycles. The
upshot should be that encryption/decryption is largely
inconsequential, slowing nothing down during pro-
cessing of linear code, and contributing significantly
only on pipeline refills at jumps and branches.
That is the theory, but putting it into practice re-
quires some minor adjustments to the instruction set.
The instruction pipeline in (unencrypted) supervisor
mode is the standard short 5-stage fetch, decode, read,
execute, write pipeline of a RISC processor (Patter-
son, 1985), and it is embedded in the codec-extended
pipeline traversed by the (encrypted) user mode in-
structions. To keep the pipeline short, there should
be only one codec, yet Fig. 1 shows three around the
ALU. To solve that we slightly modify OpenRISC in-
structions so they need at most one use of the codec
in user mode (see Fig. 2). That creates two kinds of
instruction: type ‘A’ need codec use after ALU use,
and type ‘B’ need the codec before. The pipeline is
configured differently for the two as shown in Fig. 4
(hardware for those stages that adopt two different
configurations is duplicated).
The ‘A’ configuration triggers when a store in-
struction encrypts a register for memory, or a load
instruction decrypts data from memory for registers.
The ‘B’ configuration is used when encrypted imme-
diate data in an ‘add immediate’ instruction is read in
and decrypted prior to use. Instructions that do not
use the codec go through as type ‘A’, because the ear-
lier execution stage makes results available earlier for
‘forwarding’ to instructions behind.
The assembler emits, in place of what might have
been a single ‘load at offset 8’ instruction in standard
OpenRISC, the sequence shown in Fig. 3. The modi-
fied machine code does not allow nonzero load offset,
and that sequence is the result. Register 31 is treated
specially as target: no arithmetic overflow is set or ex-
ception raised. The problem is that OpenRISC does
not contain an unsigned addition and one is needed
there, else overflow might accidentally be signalled.
The codec covers 10 stages in the Rijndael imple-
A Practical Encrypted Microprocessor
245

lws r1 8(r2) −
prefix [E (8)]
63−40
prefix [E (8)]
39−16
addi r31 r2 [E(8)]
15−0
lws r1 0(r31)
Figure 3: Assembling a load signed word instruction for
encrypted execution.
ALU
ALU
A
B
Fetch Decode Read Write
codec
Fetch Decode
codec
Read WriteExecute
Execute
Figure 4: The Rijndael pipeline is configured in two differ-
ent ways, ‘A’ and ‘B’, for two different kinds of user mode
instructions during encrypted working.
mentation, corresponding to 10 clock cycles per en-
cryption/decryption, but that may be varied to suit the
encryption, and the effect is detailed in Section 6.
To further reduce codec use, a small user-mode-
only instruction cache retains instructions with their
immediate data replaced by the decrypted value
((Hampson, 1989) works the same trick). The cached
copy of the prefix instructions carrying the encrypted
constant is converted to a no-op to ensure this is done
once only. Replacement is not done if the sequence
spans cache-lines, to avoid later only half-flushing the
altered copy.
The caches lie within the security boundary of the
processor package. Fig. 5 shows the arrangement of
functional units.
It has turned out to be possible with Rijndael to
pass the unencrypted data address to the memory unit
during the processing of load and store instructions.
We do not suggest that! But the address could be
hashed or encrypted in a different way. The hardware
aliasing effect discussed in Section 3 then does not
occur (it still occurs for Paillier, as there the address
is never decrypted).
The implementation for Paillier has the same ar-
chitecture (Fig. 5) but all the instructions are of ‘A’
type and the codec stages are devoted to the Paillier
addition/subtraction operation on encrypted data. All
the data passes through in encrypted form in what are
the ‘shadow’ registers in user mode (‘real’ registers
to supervisor mode). Instructions other than addi-
tion/subtraction and comparison are implemented as
software routines.
Context switches (such as when an interrupt han-
dler is triggered) are in principle an opportunity for
system code to see unencrypted data being worked on
by the user in shadow registers in the Rijndael imple-
mentation, but the swap of ‘shadow’ for ‘real’ regis-
ters on change of mode foils that. Instructions that
copy from one register to another copy both real and
shadow values, which means that handler code can
save the user’s GPR data in the shadow registers, un-
seen, by copying GPRs to SPRs on entry and copying
them back on exit. The protocol is explained further
in Section 5, where its security is proved.
The Rijndael implementation of the processor is
not suitable for multiuser operation in its current
form, as shadow registers hold previous data in the
clear through context switches. Paillier has no such
problem as its data is never in the clear.
5 SECURITY
As discussed in Section 1, our aim is to protect
user information (keys, cookies, passwords, lists of
weapon parts, etc.) being processed in encrypted
mode on our processor against the privileged opera-
tor or operating system as adversary.
The Paillier Implementation. This appears suit-
able, because no decryption ever takes place, so unen-
crypted information ought never to be revealed. But
the ‘table of signs’ required for general computation
may give away too much. It shows the 31st bit (the
most significant) of a 32-bit 2s complement number
under the additively homomorphic encryption. Read
sign(x) for the 31st bit, then sign(x+x) for the 30th,
and so on, giving the decryption in 32 steps.
Concretely, the operator can embed a ‘sub r1 r1 r1’
(subtract in place in register r1) instruction in the
user’s program to generate an encrypted zero in gen-
eral register r1, from any encrypted datum originally
there. For any encrypted value in register r2, the oper-
ator can run ‘sflt r2 r1’ (set flag if the value in r2 is less
than the zero in r1) to get the sign bit (#31) flagged.
The operator can run ‘add r2 r2 r2’ to double the con-
tent of r2 in place, and work the same trick again to
get its next bit. That decodes r2.
(Tsoutsos and Maniatakos, 2015) avoids the prob-
lem by providing only the x+k operation, for con-
stants k, not x+y (hence not x+x or x−x), so we might
declare all two-operand OpenRISC instructions off-
limits, leaving only the one-operand ones: x+k and
x<k are formally safe because x→x+K is an automor-
phism that turns y=x+k into y+K=(x+K)+k, and
x<k into x+K<k
0
where k
0
=k+K, so there will be
2
32
self-consistent readings x+K, y+K, etc. for any
SECRYPT 2016 - International Conference on Security and Cryptography
246

User
Mode
Insn.
Cache
User
Mode
Data
Cache
4
User
Mode
TLB
Hash
PC
Data Memory
Registers
Shadow
Registers
Instruction
Memory
Instruction
Cache
Fetch Decode Read Write
TLB
Execute
Data Cache
FeALU
ALU
Rijndael codec/Paillier add
Figure 5: Pipeline integration with other functional units.
choice of K, for any guess by the operator at a con-
sistent assignment of decrypted values x, y, etc. to
encrypted values x
0
, y
0
, etc. that makes sense of the
user’s (or operator’s) program.
However, it is easy to identify the encrypted con-
stant 1 in the software routines for division and mul-
tiplication. With it, an adversary can calculate 2 =
1+1, etc., producing any message. Addition and sub-
traction give 0 when both inputs are 0, so any combi-
nation of them has that property. That is a limited set
of functions (1−x is not among them). So a Paillier-
based implementation for general computation must
secrete some encrypted nonzero constant for use, 1 or
some other (the same reasoning holds of fully homo-
morphic encryptions such as (Gentry, 2009)). That is
as vulnerable as a key for Rijndael is.
A remedy for both 1+1=2 and sign(x) vulnerabil-
ities is suggested in Section 7, but we have not yet tri-
alled it in prototyping. That ‘ABC’ solution (Breuer
and Bowen, 2014) does not restrict instructions, but
relies on a further arrangement of the arithmetic of the
processor’s arithmetic logic unit according to a typing
system, so that it produces nonsense from x+x, but
compiled code can easily produce intended results.
The Rijndael Implementation. This does de-
cryption internally, but only in user mode, and secu-
rity relies on never revealing the decrypted informa-
tion to supervisor mode code. That can be expressed
formally. There are five data types:
i 32-bit unencrypted data that originated as en-
crypted user data;
ê encrypted user data occupying 64+ bits;
$ 32-bit data in the clear that originated in supervi-
sor mode;
% notionally ‘decrypted’ data that originated in su-
pervisor mode as 32-bit data and has been marked
by a 0x7fff in the top 16 bits of 64;
* a ‘placeholder’, used to indicate a pending de-
cryption (i) or encryption (ê) that looks like the
‘decrypted’ zero datum (%).
In supervisor mode, real/shadow registers will con-
tain types ê/i or ê/* or */i or $/%. None of those
expose type i unencrypted user data.
In user mode, real/shadow registers will contain
types i/ê, or */ê or i/* or %/$. Swapping
real/shadow registers on mode change maintains the
invariant. Memory contains ê or $or *.
To maintain those invariants, every instruction
must preserve them and they must hold at start-up.
The prototype does that. User mode addition, for ex-
ample, does i/?+i/?=i/*, requiring type i in both
addend registers, otherwise it raises a ‘range’ excep-
tion (if enabled) and leaves registers as they are (we
may allow user mode arithmetic on %/$ in future).
Load from memory in user mode produces either
i/ê, decrypting encrypted data of type ê in mem-
ory via the codec, or %/$, reading plain unencrypted
supervisor mode data of type $ from memory and
marking it to type %, or it produces %/$ reading the
* value in memory as a ‘decrypted’ zero and storing
it as the */0 pair.
Store to memory in user mode takes type i/ê or
i/* or */ê and either stores the ê value or encrypts
the i value for memory via the codec. Type %/$ if
seen causes the $ value to be stored in memory.
Store in supervisor mode cannot use the codec,
and the register types ê/i, ê/*, */i, $/% result in
types ê, * and $ in memory respectively. Load from
memory in supervisor mode also cannot use the codec
and ê, $ in memory produce register content ê/*,
$/% respectively. The * value in memory is read as
zero and stored as the 0/* pair, of type $/%.
That establishes that the operator can never see the
unencrypted value, so the question of whether the Ri-
jndael implementation is secure reduces to the ques-
tion for Paillier, and the same arguments apply.
Overall, given the size of the Paillier ‘table of
A Practical Encrypted Microprocessor
247
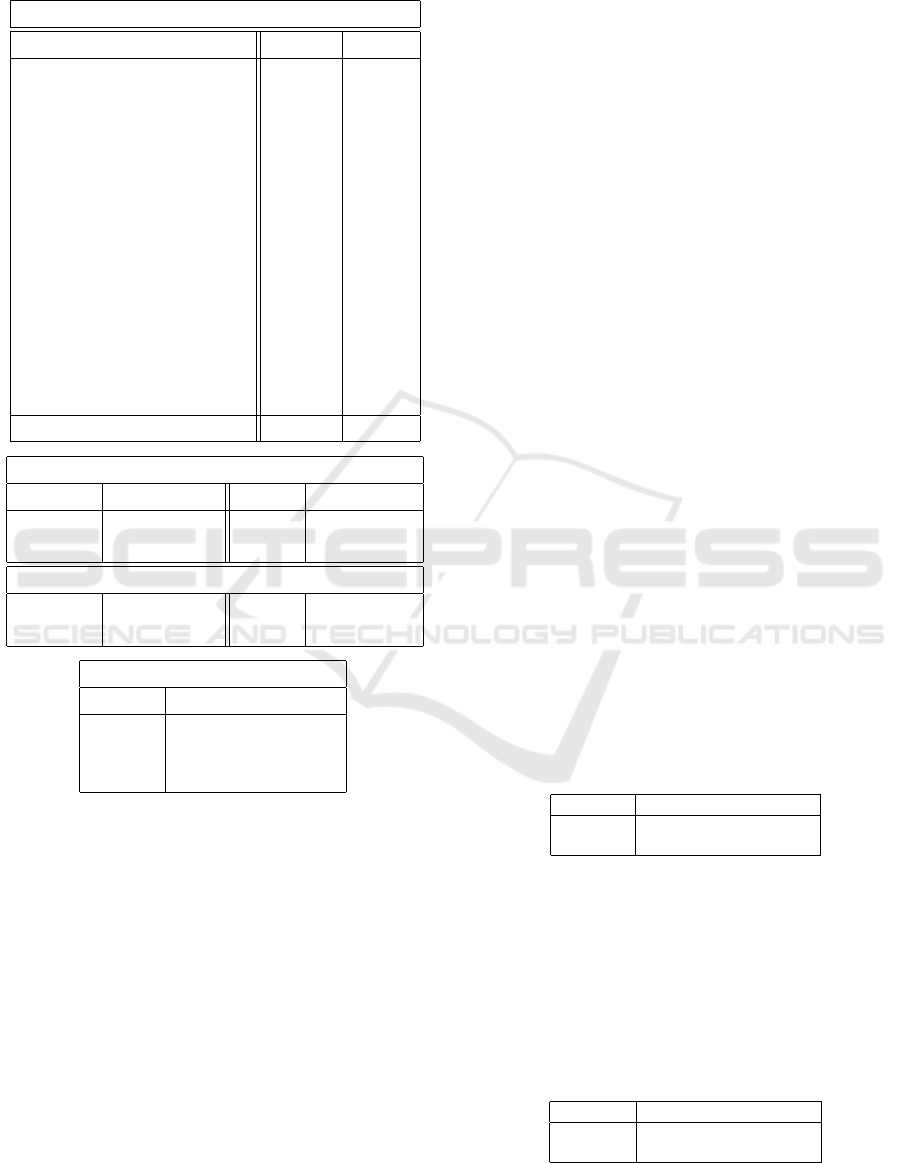
Table 2: Rijndael performance data, or1ksim test suite in-
struction set add test.
@exit : cycles 315640, instructions 222006
mode user super
register instructions 0.2% 0.2%
immediate instructions 7.3% 9.2%
load instructions 0.9% 2.8%
(cached) ( 0.9%)
store instructions 0.9% 0.0%
(cached) ( 0.9%)
branch instructions 1.0% 4.9%
jump instructions 1.1% 4.8%
no-op instructions 6.4% 15.8%
prefix instructions 11.5% 0.0%
move from/to SPR instructions 0.1% 2.7%
sys/trap instructions 0.5% 0.0%
wait states 24.7% 4.9%
(stalls) (22.1%) ( 3.8%)
(refills) ( 2.7%) ( 1.1%)
total 54.8% 45.2%
Branch Prediction Buffer
hits 10328 ( 55%) misses 8219 ( 44%)
right 8335 ( 44%) right 6495 ( 35%)
wrong 1993 ( 10%) wrong 1724 ( 9%)
User Data Cache
read hits 2942 (99%) misses 0 ( 0%)
write hits 2933 (99%) misses 9 ( 0%)
Pipeline Hazards (22.1%+3.8%)
to\ from lwz lws lbz
andi 3.3% - -
sfeqi - - 16.9%
sw - - -
signs’, as well as performance considerations (Sec-
tion 6), the Rijndael or similar symmetric encryptions
seem the better option.
6 PERFORMANCE
The Or1ksim OpenRISC test suite codes have been
modified to run encrypted in the prototype. For the
measurements, cache latency is 3 cycles and memory
latency 15 cycles, realistic for a nominal 1GHz clock.
Table 2 shows the performance summary from the
suite’s instruction set add test (‘is-add-test’). The stat-
ically compiled executable contains 185628 machine
code instructions, occupying 742512 bytes. Table 2
shows that when the test was run (successfully) to
completion in the Rijndael implementation, 222006
instructions were executed, so there are few loops and
subroutines (the code is largely built using assem-
bler macros) in 315640 cycles. If one reckons with
a 1GHz clock, then the speed was just over 700Kips
(instructions per second) overall.
In supervisor mode, pipeline occupation is just un-
der 90%, at 892Kips for a 1GHz clock (wait states,
cycles in which the pipeline fails to complete an in-
struction, comprise 4.9% of the 45.2% total), which
one may take as a baseline for a single pipeline su-
perscalar design. In user mode, pipeline occupation
is only 54.9%, as measured by numbers of non-wait
states, for 549Kips with a 1GHz clock. Measured
against supervisor mode, that is 61.6% of the unen-
crypted speed.
The wait states are caused by real pipeline data
hazards, as enumerated at bottom in Table 2. Most
are due to a load from memory instruction (lwz, lws,
lbz) feeding directly to an arithmetic instruction (andi,
sfeqi). The matrix is 64 × 64, only entries over 0.1%
being shown.
Over the whole test suite, the Rijndael imple-
mentation’s performance in encrypted mode varies
between 61.4% and 67.2% of unencrypted running
speed
2
, over many different tests running for be-
tween 12329 and 811871 cycles (respectively, 9495
and 562200 instructions) each.
The majority (13425; 82.0%) of codec uses in the
add test were decryptions of immediate data in in-
structions. Load from memory always encountered
the data already decrypted in the user-mode only data
cache, rather than having to decrypt it from memory.
Memory was not stressed at all, cache being perfectly
effective in the test.
Running the same addition test in the Paillier im-
plementation shows worse performance:
add test cycles instructions
Rijndael 315640 222006
Paillier 445099 222489
The difference is because Paillier arithmetic needs the
full length of the pipeline to complete in, stalling fol-
lowing instructions that need the result in read stage,
as far as 11 stages behind. The Rijndael implementa-
tion’s arithmetic is performed on unencrypted values
in shadow registers and completes in just one stage,
resulting in no stalls.
The disparity is more marked on other tests as
the Paillier implementation does arithmetic other than
add, subtract and compare in software:
mul. test cycles instructions
Rijndael 235037 141854
Paillier 457825 193887
To improve Paillier, several threads would have to run
SECRYPT 2016 - International Conference on Security and Cryptography
248

0
50000
100000
150000
200000
250000
300000
350000
400000
0 5 10 15 20
Cycles
Codec stages
Figure 6: Number of cycles taken to execute the 222006
instructions of the test program of Table 2 against number of
stages (cycles) taken up by the codec. Table 2 is constructed
with a 10-stage codec.
in the same pipeline. The lack of dependencies be-
tween instructions from different threads would allow
them to pass each other when the other was blocked
waiting for an instruction ahead to pass back data.
Results may be extrapolated for encryptions that
take a different number of cycles/pipeline stages than
the prototype’s default (10, for the Rijndael). Fig. 6
shows how long the test of Table 2 takes when the
Rijndael implementation does encryption in from 1 to
20 cycles/stages. It is 2.5% slower per extra stage.
7 FUTURE WORK
We plan to model memory bus interactions more
closely in order to optimise cache positioning. An
‘administrator’ mode will be added between supervi-
sor and user mode to run encrypted with privileges for
an encrypted operating system.
We are concerned by the weaknesses of homo-
morphic encryption in this setting and will investi-
gate a scheme described in (Breuer and Bowen, 2014)
in which the x, y, z in x+y=z (i.e., in two operand
instructions) are required to be in slightly different
encryptions, respectively A, B and C. The A+B=C
arrangement is allowed, as is B+C=A and C+A=B,
but anything else silently produces nonsense from the
arithmetic unit in the processor. Thus the operator
commanding x+x or x−x or x/x using an encrypted x
observed in a user process as argument for one of the
two-operand machine code instructions (which con-
tain no encrypted fields and hence can be assembled
without knowing any secret), receives a nonsense re-
sult. But the legitimate user’s compiler can perfectly
well generate code that satisfies the ABC constraints.
For Paillier, powers of different blinding multipliers
might be used for A, B, C.
8 CONCLUSION
The organisation of a sophisticated standards-
compliant superscalar processor that ‘works en-
crypted’ for remote use has been described. It is
based on the principle that a modified arithmetic au-
tomatically produces encrypted states and I/O. Data
in memory, data in registers, and data and addresses
on buses always exist in encrypted form, protecting
against the privileges of the local administrator and
operating system, who run unencrypted. The advance
reported here is in how to turn the principle into a
full-speed machine. Rijndael encryption (one codec
embedded in the processor pipeline, not on the mem-
ory pathway) and Paillier partially homomorphic en-
cryption (no codecs, no keys) have been tested. The
Rijndael implementation is 60–70% as fast as unen-
crypted running
2
and is secured by guarantees in the
hardware protocols that the administrator cannot see
unencrypted user data, which renders it exactly as safe
(or unsafe) as Paillier.
Conventional protections such as moat electron-
ics, oblivious RAM, encrypting the memory address
together with data, hashed program trace under the
encryption, etc., may be added.
ACKNOWLEDGMENTS
Zhiming Liu’s work has been funded by research
grant SWU116007 from Southwest University. Pe-
ter Breuer’s work is supported by Hecusys LLC
(www.hecusys.com), and by a visiting fellowship at
Birmingham City University in 2015.
REFERENCES
Anati, I., Gueron, S., Johnson, S. P., and Scarlata, V. R.
(2013). Innovative technology for CPU based attes-
tation and sealing. In Proc. 2nd Intl. Workshop on
Hardware and Architectural Support for Security &
Privacy (HASP ’13). ACM.
Breuer, P. and Bowen, J. (2012). Typed assembler for
a RISC crypto-processor. In Barthe, G., Livshits,
B., and Scandariato, R., editors, Proc. 4th Intl.
Symp. on Engineering Secure Software & Systems
(ESSoS ’12), number 7159 in LNCS, pages 22–29,
Berlin/Heidelberg. Springer.
Breuer, P. and Bowen, J. (2013). A fully homomorphic
crypto-processor design: Correctness of a secret com-
puter. In J
¨
urjens, J., Livshits, B., and Scandariato,
R., editors, Proc. 5th Intl. Symp. on Engineering Se-
cure Software & Systems (ESSoS ’13), number 7781 in
LNCS, pages 123–138, Berlin/Heidelberg. Springer.
Breuer, P. and Bowen, J. (2014). Towards a working fully
A Practical Encrypted Microprocessor
249

homomorphic crypto-processor: Practice and the se-
cret computer. In J
¨
orjens, J., Pressens, F., and Bielova,
N., editors, Proc. Intl. Symp. on Engineering Secure
Software & Systems (ESSoS ’14), volume 8364 of
LNCS, pages 131–140, Berlin/Heidelberg. Springer.
Buer, M. (2006). CMOS-based stateless hardware security
module. US Pat. App. 11/159,669.
Daemen, J. and Rijmen, V. (2002). The Design of Rijndael:
AES – The Advanced Encryption Standard. Springer,
Berlin/Heidelberg.
Gentry, C. (2009). Fully homomorphic encryption using
ideal lattices. In Proc. 41st Ann. ACM Symp. on The-
ory of Computing (STOC ’09), pages 169–178, New
York, NY.
Halderman, J., Schoen, S., Heninger, N., Clarkson, W.,
Paul, W., Calandrino, J., Feldman, A., Appelbaum, J.,
and Felten, E. (2009). Lest we remember: cold-boot
attacks on encryption keys. Commun. ACM, 52(5):91–
98.
Hampson, B. (1989). Digital computer system for executing
encrypted programs. US Pat. 4,847,902.
Hashimoto, M., Teramoto, K., Saito, T., Shirakawa, K., and
Fujimoto, K. (2001). Tamper resistant microproces-
sor. US Pat. 2001/0018736.
Kissell, K. (2006). Method and apparatus for disassociat-
ing power consumed within a processing system with
instructions it is executing. US Pat. App. 11/257,381.
K
¨
ommerling, O. and Kuhn, M. (1999). Design principles
for tamper-resistant smartcard processors. In Proc.
USENIX Workshop on Smartcard Technology (Smart-
card ’99), pages 9–20.
Liu, C., Harris, A., Maas, M., Hicks, M., Tiwari, M., and
Shi, E. (2015). Ghostrider: A hardware-software sys-
tem for memory trace oblivious computation. In Proc.
Intl. Conf. on Architectural Support for Programming
Languages and Operating Systems (ASPLOS’15).
Maas, M., Love, E., Stefanov, E., Tiwari, M., Shi, E.,
Asanovic, K., Kubiatowicz, J., and Song, D. (2013).
Phantom: Practical oblivious computation in a secure
processor. In Proc. ACM Conf. on Computer & Com-
munications Security (SIGSAC’13), pages 311–324.
Ostrovsky, R. (1990). Efficient computation on oblivious
RAMs. In Proc. 22nd Ann. ACM Symp. on Theory of
Computing, pages 514–523.
Paillier, P. (1999). Public-key cryptosystems based on com-
posite degree residuosity classes. In Advances in cryp-
tology – EUROCRYPT’99, pages 223–238. Springer.
Patterson, D. (1985). Reduced instruction set computers.
Commun. ACM, 28(1):8–21.
Schuster, F., Costa, M., Fournet, C., Gkantsidis, C.,
Peinado, M., Mainar-Ruiz, G., and Russinovich, M.
(2015). VC3: Trustworthy data analytics in the cloud
using SGX. In IEEE Symp. on Security & Privacy,
pages 38–54.
Tsoutsos, N. and Maniatakos, M. (2013). Investigating the
application of one instruction set computing for en-
crypted data computation. In Gierlichs, B., Guilley, S.,
and Mukhopadhyay, D., editors, Proc. Security, Pri-
vacy and Applied Cryptography Engineering (SPACE
’13), pages 21–37. Springer, Berlin/Heidelberg.
Tsoutsos, N. and Maniatakos, M. (2015). The HEROIC
framework: Encrypted computation without shared
keys. IEEE Trans. on CAD of Integrated Circuits and
Systems, 34(6):875–888.
SECRYPT 2016 - International Conference on Security and Cryptography
250
