The Growth of Oligarchy in a Yard-Sale Model of Asset Exchange

A Logistic Equation for Wealth Condensation

Bruce M. Boghosian, Adrian Devitt-Lee and Hongyan Wang

Department of Mathematics, Tufts University, Medford, Massachusetts, U.S.A.

Keywords:

Fokker-Planck Equation, Asset Exchange Model, Yard-Sale Model, Pareto Distribution, Gibrat’s Law,

Lorenz Curve, Gini Coefﬁcient, Lorenz-Pareto Exponent, Phase Transitions, Phase Coexistence, Wealth

Condensation.

Abstract:

The addition of wealth-attained advantage (WAA) to the Yard-Sale Model (YSM) of asset exchange has been

demonstrated to induce wealth condensation. In models of WAA for which the bias is a continuous function

of the wealth difference of the transacting agents, the condensation arises from a second-order phase transition

to a coexistence regime. In this paper, we present the ﬁrst analytic time-dependent results for this model, by

showing that the condensed wealth obeys a simple logistic equation in time.

1 INTRODUCTION

The scientiﬁc study of wealth inequality is motivated

by a desire to understand not only the drastic uneven-

ness in the distribution of wealth today, but also its dy-

namism. Virtually every metric of wealth inequality

is changing in the direction of increased concentration

of wealth. For example, in 2010 Oxfam International

noted that 388 individuals in the world had as much

wealth as half the human population. They have been

publishing this ﬁgure annually, and by early 2016 it

had reduced to 62 individuals (Hardoon and Ayele,

2016).

An important class of wealth distribution models

that have been analyzed using mathematical methods

of statistical physics are called Asset Exchange Mod-

els (AEMs) (Angle, 1986; Hayes, 2002). These have

been used to describe the collective behavior of large

economic systems based on simple, idealized micro-

scopic rules. In a simple AEM, there exists a col-

lection of N agents, each of whom possesses some

wealth. The agents exchange that wealth in pairwise

transactions. There are a variety of models describing

these transactions. Most conserve the total number

of agents, N, and the total wealth in the system, W,

though extended versions of these models are capa-

ble of accounting for wealth redistribution, changes

in agent population, the production and consumption

of wealth, and multi-agent transactions.

The AEM examined in this paper is a modiﬁca-

tion of the basic Yard Sale Model (YSM) of asset ex-

change (Chakraborti, 2002; Hayes, 2002), in which

agents exchange wealth solely by means of pairwise

transactions. When two agents enter such a transac-

tion, each has the same probability of winning some

amount of wealth from the other, and the amount won

is equal to a fraction of the poorer agent’s wealth.

Following the work of Ispolatov et al. (Ispolatov

et al., 1998), Boghosian derived a Boltzmann equa-

tion for the basic YSM (Boghosian, 2014b). In the

limit of small transactions, he showed that the Boltz-

mann equation reduces to a particular Fokker-Planck

(FP) equation, and later demonstrated that this FP

equation could be derived much more simply from

a stochastic process (Boghosian, 2014a). In the ab-

sence of any kind of wealth redistribution, Boghosian

et al. (Boghosian et al., 2015) proved that all of the

wealth in the system is eventually held by a single

agent. This is due to a subtle but inexorable bias in

favor of the wealthy in the rules of the YSM: Be-

cause a fraction of the poorer agent’s wealth is traded,

the wealthy do not stake as large a fraction of their

wealth in any given transaction, and therefore can

lose more frequently without risking their status. This

is ultimately due to the multiplicative nature of the

transactions on the agents’ wealth, as pointed out by

Moukarzel (Moukarzel et al., 2007).

In the above-mentioned works, Boghosian et

al. (Boghosian, 2014b; Boghosian, 2014a; Boghosian

et al., 2015) also investigated the addition of a sim-

ple Ornstein-Uhlenbeck-like model of redistribution

to the YSM (Uhlenbeck and Ornstein, 1930). They

Boghosian, B., Devitt-Lee, A. and Wang, H.

The Growth of Oligarchy in a Yard-Sale Model of Asset Exchange - A Logistic Equation for Wealth Condensation.

In Proceedings of the 1st International Conference on Complex Information Systems (COMPLEXIS 2016), pages 187-193

ISBN: 978-989-758-181-6

187

demonstrated that it suppressed the tendency of all

the wealth to go to a single agent, resulting in a

classical distribution, and exhibiting some similar-

ity with empirical forms for wealth distributions due

to Pareto (Pareto, 1965) and Gibrat (Gibrat, 1931).

In later work, however, they demonstrated that the

extreme tail of this distribution decays as a gaus-

sian (Boghosian et al., 2016).

The phenomenon of wealth condensation was

ﬁrst described by Bouchard and M´ezard in 2000,

who noted the accumulation of macroscopic levels of

weath by a single agent in a simple model of trading

and redistribution (Bouchaud and M´ezard, 2000). In

2007, Moukarzel et al. investigated wealth-attained

advantage (WAA) in the YSM by adding a ﬁxed bias

to the probability of winning in any transaction, de-

pendent only on the sign of the wealth differential.

He observed a ﬁrst-order phase transition to a wealth-

condensed state of absolute oligarchy, in which a sin-

gle agent held all the wealth (Moukarzel et al., 2007).

More recently, Boghosian et al. (Boghosian et al.,

2016) introduced a new model for WAA in the YSM,

with bias favoring the wealthier agent proportional to

the wealth differential between the two agents, thus

approaching zero continuously for transactions be-

tween agents of equal wealth. This model exhibits a

second-order phase transition to a state of coexistence

between an oligarch and a classical distribution of

non-oligarchs. In that work it was also demonstrated

that the above-mentioned gaussian tail was present

both below and above criticality, but degenerated to

exponential decay precisely at criticality.

While it is perhaps unsurprising that WAA pro-

motes the condensation of wealth, the above obser-

vation demonstrates that the way it is introduced

can have macroscopic consequences. In a ﬁrst-order

phase transition, order parameters, such as the Gini

coefﬁcient or the fraction of wealth held by the

wealthiest agent in this case, are discontinuous func-

tions of the control parameters. In a second-order

phase transition, they exhibit only slope discontinu-

ities. It seems, therefore, that the continuity or dis-

continuity of the bias in the microscopic model is di-

rectly reﬂected in the continuity or discontinuity of

the macroscopic order parameter.

To be speciﬁc, if the coefﬁcient τ

∞

measures the

level of redistribution for the wealthiest agents, and ζ

measures the level of WAA (in a fashion made pre-

cise in (Boghosian et al., 2016)), then criticality was

shown to occur at ζ = τ

∞

, and coexistence for ζ > τ

∞

The fraction of wealth held by the oligarch in the con-

tinuum limit was shown to be

∞



0 if ζ ≤ τ

∞

1−

∞

if ζ > τ

∞

(1)

Note that this is a continuous function, with a discon-

tinuous ﬁrst derivative at the critical point ζ = τ

∞

, re-

ﬂective of a second-order phase transition.

Note that all of the above-described observations

were made for the steady state situation. In this pa-

per we quantify the time dependence of the formation

of partial oligarchy in the model (Boghosian et al.,

2016). We derive a PDE, valid in the coexistence

regime ζ > τ

∞

, governing the distribution of wealth

p(w,t) amongst the non-oligarchs, coupled with an

ODE for the fraction of wealth held by the oligarch,

c(t). The latter is the logistic equation

′

(t) = c(t)[−τ

∞

+ ζ(1−c(t))], (2)

whose long-time limit c

∞

:= lim

t→∞

c(t) is consistent

with Eq. (1) for ζ > τ

∞

In Section 2 we describe the YSM, and the deriva-

tion of the FP equation describing its behavior. In

particular, we review the assumptions and methodol-

ogy of the Kramers-Moyal derivation of the FP equa-

tion from a stochastic process, because these assump-

tions are violated by the singular distributional solu-

tions that we shall be studying.

In Section 3 we provide a mathematical descrip-

tion for oligarchy as the presence of a singular dis-

tribution Ξ, correct the Kramers-Moyal derivation of

the FP equation, and present the logistic ODE that de-

scribes the wealth of the oligarch. For reasons dis-

cussed in the conclusions, this decouples from the

PDE governing the distribution of non-oligarchs.

2 THE YARD SALE MODEL

In this section we will introduce notation, discuss

the interaction between agents in the modiﬁed YSM,

and review the assumptions and methodology of the

Kramers-Moyal derivation of the FP equation from a

stochastic process. While this section follows that of

(Boghosian et al., 2016) closely, this review is neces-

sary because we shall require a weak form of the FP

equation in order to accommodate distributional solu-

tions in what follows.

A continuous distribution of wealth can be de-

scribed by the agent density function (ADF), P(w,t),

deﬁned such that the number of agents with wealth

w ∈ [a,b] at time t is given by

P(w,t)dw. The ze-

roth and ﬁrst moments of the ADF correspond to the

total number of agents and wealth,

∞

dw P(w,t),

∞

dw P(w,t)w.

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

188

We will often need the three following partial mo-

ments:

(w,t) :=

∞

P(x,t)

(w,t) :=

P(x,t)

(w,t) :=

P(x,t)

Here A

(w) denotes the Pareto potential, which is the

fraction of agents with wealth at least w. Also, L

(w)

is the Lorenz potential, which denotes the fraction of

wealth held by agents with wealth up to w. In the fol-

lowing sections, the expectation of functions over the

ADF will be denoted as E

[ f (x)] :=

∞

P(x,t)

f(x).

To describe the dynamics of wealth distributions,

we use a random walk based on the YSM, in which

two agents are randomly chosen to transact, and the

magnitude of wealth exchanged is a fraction of the

minimum wealth of the two agents. The winner is

determined by a random variable η ∈ {−1, +1}. If

we focus on a single agent whose wealth transitions

from z to w as a result of the transaction, this gives

rise to the random walk

w−z = η

√

∆tmin(z,x),

where

√

∆t is a measure of the transactional timescale

and x is the wealth of the “other agent” with whom the

agent in question interacts.

We now introduce redistribution: After each trans-

action, a wealth tax is imposed on each agent, and

the total amount collected is redistributed amongst all

the agents in the system. The fraction collected from

an agent with wealth z per unit time is denoted by

τ(z), so the total tax collected per unit time is T

(t) =

∞

dz P(z,t)τ(z)z. The average amount returned to

each agent per unit time is T

, and the fractional

deviation from this average amount for an agent of

wealth z will be denoted by σ(z), so the amount re-

turned to that agent is T

+ σ(z)z. Hence the net

taxation experienced by an agent with wealth z is

τ(z)z−



+ σ(z)z



= ρ(z)z−

where we have deﬁned ρ(z) := τ(z) −σ(z). Note

that lim

z→∞

σ(z) = 0, so τ

∞

:= lim

z→∞

τ(z) =

lim

z→∞

ρ(z) =: ρ

∞

. Because the total amount col-

lected must be equal to the total amount redistributed,

the expectation value of the deviation from average

redistribution must vanish, whence 0 = E

[σ(z)z] and

(t) =

∞

dz P(z,t)ρ(z)z. (3)

For example, if we assume that τ(z) is a constant,

independent of z, we ﬁnd that

(t) =

∞

dz P(z)τz = τW

is also constant. If we further take σ(z) = 0, so that

the redistribution is uniform, we see that the total ef-

fective taxation rate is

τz−

= τz−

τW

= τ



z−



This redistribution model is reminiscent of the

Ornstein-Uhlenbeck process (Uhlenbeck and Orn-

stein, 1930), and has been used in recent studies of

the redistributive YSM (Boghosian et al., 2016).

The addition of redistribution determines a new

random walk for an individual agent, deﬁned by

w−z = −



ρ(z)z−



∆t + η

√

∆tmin(z,x). (4)

We see that only the difference ρ(z) := τ(z) −σ(z)

matters, in terms of which T

(t) is given by Eq. (3). In

what follows, we shall allow for ρ to be negative, but

we will require that it be bounded by a polynomial.

The random variable η can be distributed fairly

(with mean E[η] = 0), or it can be biased. The bias

assumed in this paper is that for a model of WAA de-

scribed in an earlier paper (Boghosian et al., 2016),

speciﬁcally

E [η] = ζ

√

∆t(z−x), (5)

where ζ is a positive parameter that skews the proba-

bility of winning in favor of the wealthier agent. Thus,

in this model, the bias is determined by the difference

between the wealth of the two agents.

We will work from Eq. (4) from the start, and

simpler systems can be obtained by letting ζ = 0 or

τ(w) = 0. We shall ﬁrst formally derive a PDE which

is implied by the random walk in the limit as the frac-

tion of wealth traded becomes inﬁnitesimal.

We suppose that the probability of the transition

(z,t) → (w,t + ∆t) is p

∆t

(z → w;z,t), and that this

probability distribution is normalized. The Chapman-

Kolmogorov equation for this random walk is then

P(w,t + ∆t) =

∞

dz P(z,t)p

∆t

(z → w;z,t)

To derive the corresponding FP equation satisﬁed by

P, we must cast the above in weak form. To this end,

we let ψ be an analytic Schwartz function on the do-

main [0,∞), and compute its L

inner product with

The Growth of Oligarchy in a Yard-Sale Model of Asset Exchange - A Logistic Equation for Wealth Condensation

189

∂P/∂t as follows,



ψ,

∂P

∂t



ψ(w)

∂P(w,t)

∂t

= lim

∆t→0

∆t



dwψ(w)P(w,t + ∆t) −

dwψ(w)P(w,t)



= lim

∆t→0

∆t

dzP(z,t)

dw p

∆t

(z →w;z,t)[ψ(w) −ψ(z)]

= lim

∆t→0

∆t

dzP(z,t)

dw p

∆t

(z →w;z,t)

∞

∑

n=1

(w−z)

∂

ψ(z)

∂z

∞

∑

n=1

dzM

(z,t)P(z,t)

∂

ψ(z)

∂z

(6)

where we have deﬁned

(z,t) := lim

∆t→0

∆t

dw p

∆t

(z → w;z,t)(w−z)

= E

x,η



(w−z)

∆t



The above result may be written



ψ,

∂P

∂t



∞

∑

n=1



(z,t)P(z,t),

∂

ψ(z)

∂z



. (7)

whence, using integration by parts to revert to the

strong form, we obtain

∂P

∂t

∞

∑

n=1

(−1)

∂

(z,t)P(z,t)] , (8)

and thus the agent density function satisﬁes a PDE

that is determined by the moments of the random walk

on an inﬁnitesimal timescale.

2.1 Fokker-Planck equation

Recalling Eqs. (4) and (5), we can compute M

(z,t)

= lim

t→0

η,x



(w−z)

∆t



= E



(t)

−zρ(z) + ζ

(z−x)min(w,x)



(t)

−zρ(z) −ζ



(z,t) −2zL

(z,t) −z

(z,t) + z



(9)

Next, because η ∈ {−1, +1}, we have E

[η

] = 1,

which allows us to compute M

(z,t)

= lim

t→0

η,x



(w−z)

∆t



= lim

t→0

η,x



∆t(

(t)

−zρ(z))

(t)

−zρ(z))ηmin(z,x)(∆t)

1/2

+ η

min(z,x)



= E

η,x



min(z, x)



∞

P(x,t)

min(z, x)

= 2B

(z,t) + z

(z,t). (10)

Finally, we note that higher powers of η have expec-

tations E

[η

] ≤ 1 for k ≥ 3. It follows that, because

each term in the expansion of the above equation in-

cludes some positive power of

√

∆t, all of the mo-

ments approach zero for k ≥ 3,

(z,t) = lim

t→0

∆t

η,x



∆t[

(t)

−zρ(z)] + η

√

∆tmin(w,x)



= 0.

(11)

Substituting Eqs. (9), (10) and (11) into Eq. (8),

we ﬁnd that our wealth distribution obeys the fol-

lowing quadratically nonlinear, integrodifferential FP

equation,

∂P

∂t

∂

∂w



(t)

−wρ(w)





∂

∂w







∂

∂w





−2wL

−w

+ w





(12)

This system conserves wealth and agents, as was

shown in the appendix of the paper where it was ﬁrst

derived (Boghosian et al., 2016). In the case where

there is no redistribution and no WAA, we have τ =

ζ = 0, so the agent density function satisﬁes

∂P

∂t

∂

∂w



(w,t) +

(w,t)





. (13)

2.2 Oligarchy as a Distributional

Solution

The steady-state solution to Eq. (12) may involve

the condensation of a ﬁnite fraction of the system’s

wealth into the hands of a vanishingly small number

of agents. Indeed, in the absence of redistribution, as

in Eq. (13), all the wealth will condense in this man-

ner. To describe this, we must extend our function

space to include certain singular distributions.

If our system were discrete, then complete con-

centration of wealth would be described by P(w) =

−1)δ(w)+δ(w−W

), where N

−1 agents have

no wealth, and a single agent holds all of the wealth.

In the continuum limit, however, the number of agents

need not be an integer. Thus wealth condensation

could continue indeﬁnitely, with a “half an agent”

holding twice the wealth of the system, described

by the distribution P(w) = (N

−

/2)δ(w) +

/2δ(w−

). More generally, we can take the distribution to

be P(w) = (N

−ε)δ(w) + εδ(w−W

/ε), where ε is

an arbitrarily small positive number. Replacing ε by

ε and passing to the limit as ε → 0 yields

P(w) = N

δ(w) +W

Ξ(w), (14)

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

190

where we have deﬁned Ξ(w) = lim

ε→0

εδ(w −1/ε).

To be more precise, Ξ should be deﬁned as the singu-

lar distribution whose action on a test function φ is

hΞ,φi= lim

ε→0





w−



,φ



= lim

ε→0

ε φ





= lim

s→∞

φ(s)

. (15)

Here the space of test functions to which φ belongs is

∂

−2

= {φ(w) = ψ(w) + γ+ µw : ψ(w) ∈ S ([0,∞)),γ,µ ∈R},

where S([0,∞) denotes Schwartz functions on [0,∞).

3 WAA ABOVE CRITICALITY

In this section, we use the deﬁnition of Ξ provided

by Eq. (15). In earlier work (Boghosian et al., 2016),

the FP equation, Eq. (12), and its steady-state asymp-

totic behavior were discussed in detail. A second-

order phase transition was observed at the critical

point ζ = τ

∞

, and coexistence was observed between

the singular distribution Ξ and a classical distribution

for ζ > τ

∞

. This may be thought of as an oligarch in

coexistence with a population of non-oligarchs. The

presence of the singular distribution Ξ, however, vio-

lates the assumptions in the derivation of the FP equa-

tion, as our presentation leading to Eq. (8) assumed an

analytic Schwartz function in the weak form.

Recall that the mathematical phenomenon that we

describe here as “oligarch” may be modeled as the

wealth held by the wealthiest fraction ε of agents,

as ε → 0. Assume that there exists a wealth dis-

tribution which is a steady state of the random pro-

cess, Eq. (4), in the small-transaction limit. More-

over, suppose that this distribution may be written as

P(w) = p(w)+ c(t)W

Ξ(w), where p(w) is the classi-

cal agent density function for the non-oligarchs. This

is a system in which the wealthiest inﬁnitesimal of

agents hold a fraction c(t) of the total wealth of the

system at time t. We consider two sets of agents in

the random walk: There are the “normal” agents, cor-

responding to the classical distribution p(w). Then

there is what we have been calling the “oligarch,” con-

sidered to be the wealthiest fraction ε of the distribu-

tion P(w), considered as a single unit.

Now suppose that we have an oligarch, and φ =

ψ+ γ+ µw, where ψ is an analytic Schwartz function.

Then the development that led to Eq. (6) becomes:



∂P

∂t

,φ



∞

∑

n=1

(z,t)P(z,t)

∂

φ(z)

∂z

∞

∑

n=1

(z,t)P(z,t)]∂

ψ+ µM

(z,t)P(z,t)dz

∞

∑

n=1

∂

(z,t)P(z,t)]ψdz

+ µN

(z,t)]. (16)

In strong form we therefore have

∂P

∂t

∞

∑

n=1

(−1)

∂

(z,t)P(z,t)]

+ E

(z,t)]N

Ξ,

where the Ξ term arises from hM

(z,t)P(z,t),µi =

µhP(z,t),M

(z,t)i = hΞ,φi·N

(z,t)]. This im-

plies two things: the strong form of the FP equation

may not make sense in the coexistence regime, and Ξ

is likely to depend only on the M

term, which corre-

sponds to drift in the FP equation.

To carry out the full analysis, we must recalcu-

late the coefﬁcients M

(z,t) for three cases: (i) a nor-

mal agent interacting with another normal agent, (ii)

a normal agent interacting with the oligarch, and (iii)

the oligarch interacting with a normal agent. The

ﬁrst two factors would describe p(w,t), and the last

would determine c(t), the fraction of wealth held by

the oligarch. In this paper, we restrict our attention to

the wealth of the oligarch only, and we relegate the

derivation of the PDE governing the non-oligarchical

portion of the distribution to future work.

Denote the ﬁrst coefﬁcient M

of the wealthiest ε

of agents by M

. Instead of using the full machinery

of the FP derivation, we note

(z,t) = lim

t→0

η,x



c(t + ∆t)W

/ε−c(t)W

/ε

∆t



= c

′

(t)

= T

(t) −c(t)



c(t)W



+ E





c(t)W

−x





= T

(t) −(c(t)W

/ε)τ(c(t)W

/ε)

+ ζ

[c(t)W

(1−c(t))/ε −2N

(c(t)W

/ε)],

where the integrals for the expectation are between

x = 0 and x = cW

/ε, so that they do not include

the oligarch. We will assume that p decays like an

exponential or a gaussian, as was shown in earlier

work (Boghosian et al., 2016). Under this assump-

tion, the second moment of p is ﬁnite, so when we

take the limit as ε → 0, we have

′

(t) = c(t)[−τ

∞

+ ζ(1−c(t))], (17)

where we have written τ

∞

:= lim

ε→0

τ(1/ε). This is a

logistic equation for c(t) with solution

c(t) = (1−τ

∞

/ζ)

(ζ−τ

∞

(ζ−τ

∞

−1) + 1−τ

∞

/ζ

. (18)

Eq. (17) is the principal result of this paper. It indi-

cates that the wealth of the oligarch obeys a logistic

The Growth of Oligarchy in a Yard-Sale Model of Asset Exchange - A Logistic Equation for Wealth Condensation

191

equation, independent of the evolution of the classical

portion of the wealth distribution.

Equation (17) indicates that there are two asymp-

totic solutions in time, one at c= 0, and another at c=

1−τ

∞

/ζ. Since

[c((1−c)ζ−τ

∞

)]

c=0

= (ζ −τ

∞

the absence of an oligarch is stable if ζ < τ

∞

, and

is unstable otherwise. Similarly, the presence of an

oligarch is stable if ζ > τ

∞

, and is unstable other-

wise

Furthermore, since the presence of an oligarch

implies that there is ﬁnite taxation on the wealthi-

est agent, τ

∞

must exist. Monte Carlo simulations

conﬁrm the stable steady state of the oligarch both

above and below criticality: The wealth held by the

wealthiest agent, plotted in Fig. 1, is of the same or-

der as that of all the other agents, and is approximately

c = 1−τ

∞

/ζ above criticality.

Figure 1: Monte Carlo simulation of the wealth held by the

wealthiest agent in simulations of different sizes, with var-

ious values of constant τ and σ. As the number of agents

grows, this approaches the theoretical result c = 1−τ

∞

/ζ.

3.1 Gini coefﬁcients above criticality

Finally, we wish to deﬁne the notion of Gini coefﬁ-

cient in the coexistence region above criticality. In

particular, we wish to describe the Gini coefﬁcient of

the entire system in terms of that of the classical sys-

tem p, excluding the oligarch. The phenomenon of

oligarchy is evidenced by a Lorenz curve that does

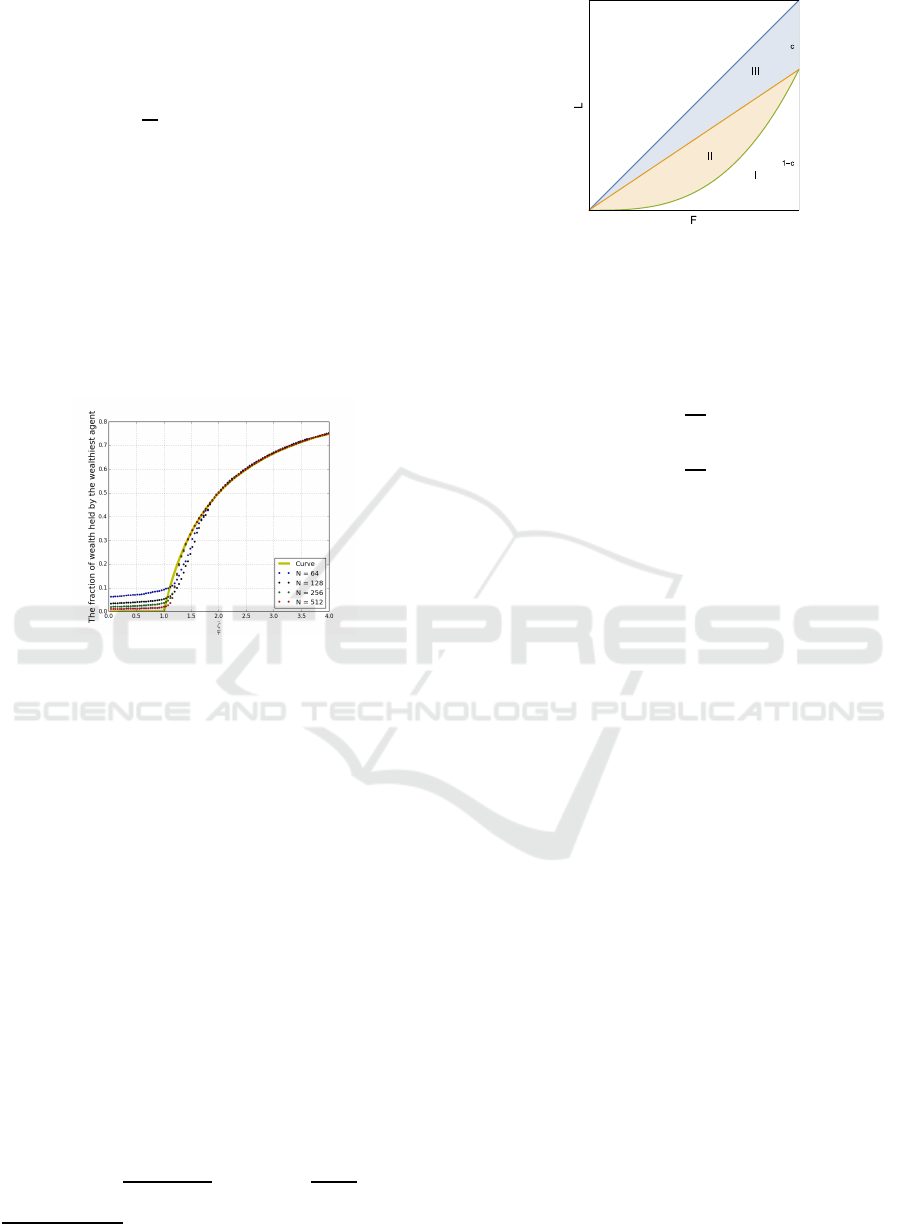
not reach the point (1,1), as illustrated in Fig. 2, where

we have labelled three distinct regions below the di-

agonal. We shall use the labels “I”, “II” and “III” to

denote the areas of these regions. Since the fraction

c of the wealth of the system is held by the inﬁnitesi-

mal agent described by the oligarch, the Lorenz curve

will reach the point (1,1-c). So if we consider the Gini

coefﬁcient of the system p, then we know that:

II + III

I + II + III

, G

I + II

(19)

Note that we never have a stable oligarch with negative

wealth; if c = 1−τ

∞

/ζ < 0, then ζ < τ

∞

Figure 2: Lorenz plot with partial wealth condensation. A

fraction c of the wealth has condensed, and 1 − c is dis-

tributed classically.

Clearly I + II + III = 1/2, I + II = (1 −c)/2, and

III = c/2. Using the supercritical value of c, this im-

mediately implies that

= +1+

∞

(1−G

) (20)

= −1+

∞

(1−G

). (21)

These equations are straightforward relations between

the versions of the Gini coefﬁcient deﬁned with and

without the presence of the oligarch.

4 DISCUSSION AND

CONCLUSIONS

Coexistence between wealth-condensed and normal

distributions in steady-state solutions of the YSM was

ﬁrst noted in earlier work (Boghosian et al., 2016).

This paper provides the ﬁrst exact analytic result for

the time-dependent behavior of that model. In partic-

ular, it demonstrates that the fraction of wealth held

by the oligarch above criticality obeys a logistic equa-

tion, Eq. (17). This equation is remarkable in that it

is completely decoupled from the classical part of the

distribution, p(w), and may be solved exactly.

The reason that the equation for c(t) decouples

from that for the classical part of the distribution can

be understood by noting that the oligarch always wins

in transactional exchanges with non-oligarchs. From

the point of view of the oligarch, the remainder of the

distribution might as well be aggregated into a sin-

gle agent with wealth W

= (1 −c)W

who, oblig-

ingly, always loses in any transaction with the oli-

garch. The oligarch’s ability to gain wealth from the

non-oligarchical portion of the distribution is there-

fore limited only by the rate at which he/she transacts

with non-oligarchs, as compared to the rate at which

he/she is taxed. This is why the steady-state fraction

of wealth held by the oligarch depends only on the

ratio of tax rate to WAA rate, τ

∞

/ζ.

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

192

From a macroeconomic perspective, it is well

known that most real-world oligarchs worry much

less than the rest of the population about individual

transactions; beyond a certain point, many do not even

know where their own money is invested. By con-

trast, they worry deeply about how taxation and re-

distribution affect their fortunes, and they expend sig-

niﬁcant effort to lobby against progressive taxation,

capital gains taxes and inheritance taxes. We believe

that the asymptotic analysis of the YSM may provide

a way to understand these priorities.

REFERENCES

Angle, J. (1986). The surplus theory of social stratiﬁcation

and the size distribution of personal wealth. Social

Forces, 65:293–326.

Boghosian, B. (2014a). Fokker-planck description of

wealth dynamics and the origin of pareto’s law. Inter-

national Journal of Modern Physics C, 25:1441008–

1441015.

Boghosian, B. (2014b). Kinetics of wealth and the pareto

law. Physical Review E, 89:042804–042825.

Boghosian, B., Devitt-Lee, A., Johnson, M., Marcq, J., and

Wang, H. (2016). Oligarchy as a phase transition:

The effect of wealth-attained advantage in a fokker-

planck description of asset exchange. arXiv preprint

arXiv:1511.00770v2 [physics.soc-ph]

Boghosian, B., Johnson, M., and Marcq, J. (2015). An

h theorem for boltzmann’s equation for the yard-

sale model of asset exchange. Journal of Statistical

Physics, 161:1339–1350.

Bouchaud, J.-P. and M´ezard, M. (2000). Wealth conden-

sation in a simple model of the economy. Physica A,

282:536–545.

Chakraborti, A. (2002). Distributions of money in model

markets of economy. Int. J. Mod. Phys. C, 13:1315–

1321.

Gibrat, R. (1931). Les In´egalit´es ´economiques. Paris: Sirey.

Hardoon, D. and Ayele, S. (2016). An economy for the

1%. Technical report, Oxfam International. 210 Ox-

fam Brieﬁng Paper (Oxfam Davos Report).

Hayes, B. (2002). Follow the money. American Scientist,

90:400–405.

Ispolatov, S., Krapivsky, P., and Redner, S. (1998). Wealth

distributions in asset exchange models. The European

Physical Journal B – Condensed Matter, 2:267–276.

Moukarzel, C., Gonc¸alves, S., Iglesias, J., and Huerta-

Quintanilla, R. (2007). Wealth condensation in a mul-

tiplicative random asset exchange model. Europhys.

J. Spec. Topics, 143:75–79.

Pareto, V. (1965). La courbe de la repartition de la richesse.

In Busino, G., editor, Oevres Completes de Vilfredo

Pareto, page 15. Geneva: Librairie Droz.

Uhlenbeck, G. and Ornstein, L. (1930). On the theory of

brownian motion. Phys. Rev., 36:823–841.

The Growth of Oligarchy in a Yard-Sale Model of Asset Exchange - A Logistic Equation for Wealth Condensation

193