Weighted Voting of Different Term Weighting Methods for Natural
Language Call Routing
Roman Sergienko
1
, Iuliia Kamshilova
2
, Eugene Semenkin
2
, and Alexander Schmitt
1
1
Institute of Communications Engineering, Ulm University, Albert-Einstein-Allee 43, Ulm, Germany
2
Department of System Analysis and Operation Research, Siberian State Aerospace University, Krasnoyarskiy Rabochiy
Avenue 31, Krasnoyarsk, Russian Federation
Keywords:
Text Classification, Term Weighting, Weighted Voting, Self-adjusting Genetic Algorithm.
Abstract:
The text classification problem for natural language call routing was considered in the paper. Seven different
term weighting methods were applied. As dimensionality reduction methods, the combination of stop-word
filtering and stemming and the feature transformation based on term belonging to classes were considered. k-
NN and SVM-FML were used as classification algorithms. In the paper the idea of voting with different term
weighting methods was proposed. The majority vote of seven considered term weighting methods provides
significant improvement of classification effectiveness. After that the weighted voting based on optimization
with self-adjusting genetic algorithm was investigated. The numerical results showed that weighted voting
provides additional improvement of classification effectiveness. Especially significant improvement of the
classification effectiveness is observed with the feature transformation based on term belonging to classes that
reduces the dimensionality radically; the dimensionality equals number of classes. Therefore, it can be useful
for real-time systems as natural language call routing.
1 INTRODUCTION
Natural language call routing is an important problem
in the design of modern automatic call services and
the solving of this problem could lead to improvement
of the call service (Suhm et al., 2002). Generally nat-
ural language call routing can be considered as two
different problems. The first one is speech recognition
of calls and the second one is topic categorization of
users utterances for further routing. Topic categoriza-
tion of users utterances can be also useful for multi-
domain spoken dialogue system design (Lee et al.,
2009). In this work we treat call routing as an ex-
ample of a text classification application.
In the vector space model (Sebastiani, 2002) text
classification is considered as a machine learning
problem. The complexity of text categorization with
a vector space model is compounded by the need to
extract the numerical data from text information be-
fore applying machine learning algorithms. There-
fore, text classification consists of two parts: text
preprocessing and classification algorithm application
using the obtained numerical data.
Text preprocessing comprises three stages:
- Textual feature extraction.
- Term weighting
- Dimensionality reduction.
The first one is the textual feature extraction based
on raw preprocessing of the documents. This pro-
cess includes deleting punctuation, transforming cap-
ital letters to lowercase, and additional procedures
such as stop-words filtering (Fox, 1989) and stem-
ming (Porter, 2001). Stop-words list contains pro-
nouns, prepositions, articles and other words that usu-
ally have no importance for the classification. Using
stemming it is possible to join different forms of the
same word into one textual feature.
The second stage is the numerical feature extrac-
tion based on term weighting. For term weighting
we use ”bag-of-words” model, in which the word or-
der is ignored. There exist different unsupervised
and supervised term weighting methods. The most
well-known unsupervised term weighting method is
TF-IDF (Salton and Buckley, 1988). The following
supervised term weighting methods are also consid-
ered in the paper: Gain Ratio (GR) (Debole and Se-
bastiani, 2004), Confident Weights (CW) (Soucy and
Mineau, 2005), Term Second Moment (TM2) (Xu
and Li, 2007), Relevance Frequency (RF) (Lan et al.,
2009), Term Relevance Ratio (TRR) (Ko, 2012),
38
Sergienko, R., Kamshilova, I., Semenkin, E. and Schmitt, A.
Weighted Voting of Different Term Weighting Methods for Natural Language Call Routing.
DOI: 10.5220/0005956600380046
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 38-46
ISBN: 978-989-758-198-4
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and Novel Term Weighting (NTW) (Gasanova et al.,
2014); these methods involve information about the
classes of the documents.
As a rule, the dimensionality for text classification
problems is high even after stop-words filtering and
stemming. Due to the high dimensionality, the classi-
fication may be inappropriate time-consuming, espe-
cially for real-time systems such as natural language
call routing. Therefore, the next stage of preprocess-
ing is the dimensionality reduction based on numeri-
cal features; it is possible with feature selection or fea-
ture transformation. In our research we use a feature
transformation method for text classification based on
term belonging to classes that reduces dimensionality
radically; number of features will be equal to number
of classes.
As classification algorithms we use the k-NN al-
gorithm and the SVM-based algorithm Fast Large
Margin (Fan et al., 2008). Some comparative stud-
ies of machine learning algorithms in the field of text
classification showed high classification effectiveness
of k-NN, SVM-based algorithms (Han et al., 2001;
Kwon and Lee, 2003; Joachims, 2002; Baharudin
et al., 2010; Morariu et al., 2005).
There exist a lot of approaches based on collec-
tives of different classification algorithms, such as
majority vote, bagging (Breiman, 1996), and boosting
(Schapire and Singer, 2000). The collectives of clas-
sification algorithms can demonstrate better classifi-
cation effectiveness than the best algorithm in the col-
lective; it was also demonstrated for text classification
(Morariu et al., 2005). Therefore, meta-classification
is very popular in the field of machine learning. In our
paper we propose an idea that collectives of different
term weighting methods can also provide text classifi-
cation effectiveness improvement even with the same
classification algorithm. For the handling of the col-
lectives, we consider a majority vote procedure. The
vote procedure may be improved with weight voting;
it means that different methods in the collective have
different weights in different situations. Optimiza-
tion of weights for voting is a complicated task due
to large training data and procedural definition of fit-
ness function. For this task solving it is appropriate
to apply genetic algorithms that are effective for such
complicated optimization problems.
One of the most complicated problem with GA ap-
plications is setting algorithm parameters. A conven-
tional genetic algorithm has at least three methods of
selection (proportional, tournament, and rank), three
methods of recombination (one-point, two-point, and
uniform). Mutation probability requires tuning as
well. The amount of various combinations can be es-
timated at tens. Exhaustive search of combinations
requires a lot of time and computational power, es-
pecially for such time-consuming problems as GA
applications for machine learning. Parameters com-
bination selection at random can be also insufficient
as algorithm efficiency on same problem can differ
very much for various parameters setting. This prob-
lem can be solved with self-adjusting GA (Semenkin
and Semenkina, 2012) or self-adapted GA (Sergienko
and Semenkin, 2010). Therefore, we propose a use of
self-adjusting GA for the weight optimization of the
voting procedure.
The tasks of our research are the following:
- Perform research of text classification for natu-
ral language call routing with different term weight-
ing methods, dimensionality reduction methods, and
classification algorithms.
- Investigate majority vote for collectives of term
weighting methods.
- Perform research of self-adjusting GA for op-
timization of weights for voting with collectives of
term weighting methods.
The paper is organized as follows: In Section 2,
we describe the considered corpus for natural lan-
guage call routing. Section 3 describes the considered
term weighting methods. The dimensionality reduc-
tion methods are explained in Section 4. Section 5
contains short description of classification algorithms.
The self-adjusting GA is described in Section 6. The
results of numerical experiments are presented in Sec-
tion 7. Finally, we provide concluding remarks in
Section 8.
2 CORPUS DESCRIPTION
The data for testing and evaluation consists of
292,156 user utterances recorded in English language
from caller interactions with commercial automated
agents. Utterances are short and contain only one
phrase for further routing. The database contains
calls in textual format after speech recognition. The
database is provided by the company Speech Cy-
cle (New York, USA). Utterances from this database
are manually labelled by experts and divided into 20
classes (such as appointments, operator, bill, internet,
phone and technical support). One of them is a spe-
cial class TE-NOMATCH which includes utterances
that cannot be put into another class or can be put into
more than one class.
The database contains 45 unclassified calls and
they were removed. The database contains also
23,561 empty calls without any words. These calls
were placed in the class TE-NOMATCH automati-
cally and they were also removed from the database.
Weighted Voting of Different Term Weighting Methods for Natural Language Call Routing
39

As a rule, the calls are short in the database; many
of them contain only one or two words. The aver-
age length of an utterance is 4.66 words, the maximal
length is 19 words. There are a lot of identical utter-
ances in the database; the corpus contains only 24,458
unique non-empty classified calls. The corpus is un-
balanced. The largest class contains 27.05% and the
smallest one contains 0.04% of the unique calls.
Due to the very high frequency of a small number
of utterances in the corpus, we formulate two different
data configurations.
Data configuration 1. The whole database with
268,550 classified non-empty calls is used for training
and test sets forming. Numbers of repetitions of the
utterances in training and test sets are used as weights
for classification. This data configuration is the clos-
est to the real situation but frequently repeated utter-
ances decrease difference between preprocessing and
classification methods. Additionally, there are some
identical utterances in training and test sets simulta-
neously. In this case the over-fitting problem of clas-
sification may be hidden. Therefore, this data con-
figuration is not very appropriate for the comparative
study.
Data configuration 2. Before training and test
samples forming, all utterance duplicates were re-
moved from the database. It means that there is no
intersection between training and test sets and fre-
quency of utterances is ignored.
Therefore, data configuration 1 is suitable for the
quality estimation of the real natural language call
routing system; data configuration 2 is the most ap-
propriate for the comparative study of different pre-
processing and classification methods.
For statistical analysis we performed 20 different
divisions of the database into training and test sam-
ples randomly. This procedure was performed for
two data configurations separately. The train samples
contain 90% of the calls and the test samples contain
10% of the calls. For each training sample we have
designed a dictionary of unique words which appear
in the training sample after deleting punctuation and
transforming capital letters to lowercase. The size of
the dictionary varies from 3,275 to 3,329 words for
data configuration 1 and from 3,277 to 3,311 for data
configuration 2.
3 TERM WEIGHTING METHODS
As a rule, term weighting is a multiplication of two
parts: the part based on the term frequency in a doc-
ument (TF) and the part based on the term frequency
in the whole training database. The TF-part is fixed
for all considered term weighting methods and is cal-
culated as following:
T F
i j
= log

t f
i j
+ 1

;t f
i j
=
n
i j
N
j
, (1)
where n
i j
is the number of times the i
th
word occurs
in the j
th
document, N
j
is the document size (number
of words in the document).
The second part of the term weighting is calcu-
lated once for each word from the dictionary and does
not depend on an utterance for classification. We con-
sider seven different methods for the calculation of
the second part of term weighting.
3.1 Inverse Document Frequency (IDF)
IDF is a well-known unsupervised term weighting
method which was proposed in (Salton and Buckley,
1988). There are some modifications of IDF and we
use the most popular one:
id f
i
= log
|
D
|
n
i
, (2)
where
|
D
|
is the number of documents in the training
set and n
i
is the number of documents that have the i
th
word.
3.2 Gain Ratio (GR)
Gain Ratio (GR) is mainly used in term selection
(Yang and Pedersen, 1997), but in (Debole and Se-
bastiani, 2004) it was shown that it could also be used
for weighting terms. The definition of GR is as fol-
lows:
GR(t
i
,c
j
) =
∑
c∈{c
j
, ¯c
j
}
∑
t∈{t
j
,
¯
t
j
}
M (t, c)
−
∑
c∈{c
j
, ¯c
j
}
P(c) · log P (c)
, (3)
M (t, c) = P (t,c) · log
P(t,c)
P(t) · P(c)
, (4)
where P(t,c) is the relative frequency that a document
contains the term t and belongs to the category c; P(t)
is the relative frequency that a document contains the
term t and P(c) is the relative frequency that a docu-
ment belongs to category c. Then, the weight of the
term t
i
is the max value between all categories as fol-
lows:
GR(t
i
) = max
c
j
∈C
GR(t
i
,c
j
), (5)
where C is a set of all classes.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
40

3.3 Confident Weights (CW)
This supervised term weighting approach has been
proposed in (Soucy and Mineau, 2005). Firstly, the
proportion of documents containing term t is defined
as the Wilson proportion estimate p(x, n) by the fol-
lowing equation:
p(x,n) =
x + 0.5z
2
α/2
n + z
2
α/2
, (6)
where x is the number of documents containing the
term t in the given corpus, n is the number of docu-
ments in the corpus and Φ

z
α/2

= α/2, where Φ is
the t-distribution (Students law) when n < 30 and the
normal distribution when n ≥ 30.
In this work α = 0.95 and 0.5z
2
α/2
= 1.96 (as rec-
ommended by the authors of the method). For each
term t and each class c two functions p
pos
(x,n) and
p
neg
(x,n) are calculated. For p
pos
(x,n) x is the num-
ber of documents which belong to the class c and have
term t; n is the number of documents which belong to
the class c. For p
neg
(x,n) x is the number of docu-
ments which have the term t but do not belong to the
class c; n is the number of documents which do not
belong to the class c.
The confidence interval (p
−
, p
+
) at 0.95 is calcu-
lated using the following equation:
M = 0,5z
2
α/2
s
p(1 − p)
n + z
2
α/2
, (7)
p
−
= p − M; p
+
= p + M. (8)
The strength of the term t in the category c is defined
as the follows:
str(t,c) =





log
2
2p
−
pos
p
−
pos
+ p
+
neg
, if p
−
pos
> p
+
neg
,
0, otherwise.
(9)
The maximum strength (Maxstr) of the term t
i
is
calculated as follows:
Maxstr(t
i
) = max
c
j
∈C
str (t
i
,c
j
)
2
. (10)
3.4 Term Second Moment (TM2)
This supervised term weighting method was proposed
in (Xu and Li, 2007). Let P(c
j
|t) be the empirical es-
timation of the probability that a document belongs to
the category c
j
with the condition that the document
contains the term t; P(c
j
) is the empirical estimation
of the probability that a document belongs to the cat-
egory c
j
without any conditions. The idea is the fol-
lowing: the more P(c
j
|t) is different from P(c
j
), the
more important the term t
i
is. Therefore, we can cal-
culate the term weight as the following:
T M2(t
i
) =
|
C
|
∑
j=1
(P(c
j
|t) − P(c
j
))
2
, (11)
where C is a set of all classes.
3.5 Relevance Frequency (RF)
The RF term weighting method was proposed in (Lan
et al., 2009) and is calculated as the following:
r f (t
i
) = max
c
j
∈C
r f (t
i
,c
j
), (12)
r f (t
i
,c
j
) = log
2

2 +
a
j
max{1, ¯a
j
}

, (13)
where a
j
is the number of documents of the category
c
j
which contain the term t
i
and ¯a
j
is the number of
documents of all the other categories which also con-
tain this term.
3.6 Term Relevance Ratio (TRR)
The TRR method (Ko, 2012) uses tf weights and it is
calculated as the following:
T RR(t
i
,c
j
) = log
2

2 +
P(t
i
|c
j
)
P(t
i
| ¯c
j
)

, (14)
P(t
i
|c) =
∑
|
T
c
|
k=1
t f
ik
∑
|
V
|
l=1
∑
|
T
c
|
k=1
t f
lk
, (15)
T RR(t
i
) = max
c
j
∈C
T RR (t
i
,c
j
), (16)
where c
j
is a class of the document, ¯c
j
is all of the
other classes of c
j
, V is the vocabulary of the training
data and T
c
is the document set of the class c.
3.7 Novel Term Weighting (NTW)
This method was proposed in (Sergienko et al., 2014;
Akhmedova et al., 2014). The details of the procedure
are the following. Let L be the number of classes; n
i
is the number of documents which belong to the i
th
class; N
i j
is the number of occurrences of the j
th
word
in all documents from the i
th
class. T
i j
= N
i j
/n
i
is the
relative frequency of occurrences of the j
th
word in
the i
th
class; R
j
= max
i
T
i j
; S
j
= argmax
i
T
i j
is the
class which we assign to the j
th
word. The term rele-
vance C
j
is calculated by the following:
C
j
=
1
∑
L
i=1
T
i j
· R
j
−
1
L − 1
·
L
∑
i=1,i6=S
j
T
i j
!
. (17)
Weighted Voting of Different Term Weighting Methods for Natural Language Call Routing
41

4 DIMENSIONALITY
REDUCTION METHODS
4.1 Stop-word Filtering with Stemming
We consider stop-word filtering with stemming as
a language-based dimensionality reduction method
which is performed before numerical feature extrac-
tion. We used special libraries (”tm”, ”SnowballC”)
in the programming language R for stop-word filter-
ing and stemming for English. Stop-word filtering
and stemming are standard techniques for text clas-
sification of large documents with the large dictio-
nary. But it is not obvious that such techniques can be
helpful in case of speech-based text classification with
short user utterances. Therefore, we also consider a
case without stop-word filtering and stemming.
4.2 Feature Transformation based on
Term Belonging to Classes
This feature transformation technique was proposed
in (Sergienko et al., 2016). It is possible to assign
each term form the dictionary to the most appropriate
class. Some novel supervised term weighting meth-
ods (GR, CW, RF, TRR, and NTW) include the de-
termination of the most appropriate classes for terms
automatically (Section 3). For IDF and TM2 we can
use relative frequencies of terms in classes for such an
assignment. The details of the method are the follow-
ing:
1. Assign each term from the dictionary of the text
classification problem to the most appropriate class:
1.1. If term weighting method includes the deter-
mination of the most appropriate class for terms itself,
this assignment is used. Go to step 2.
1.2. Otherwise assign one class for each term us-
ing the relative frequency of the term in classes:
S
j
= argmax
c∈C
n
jc
N
c
, (18)
where S
j
is the most appropriate class for the j
th
term,
c is an index of a class, C is a set of all classes, n
jc
is
number of documents of the c
th
class which contain
the j
th
term, N
c
is the number of all documents of the
c
th
class.
2. Give the document D for classification.
3. Put S
i
= 0, i=1..C, where C is the number of
classes (categories).
4. For each term t in the document D do:
4.1. S
i
= S
i
+w
t
, where i is the class of the t
th
term
in correspondence with the assignment on the step 1,
w
t
is the weight of the t
th
term.
5. Put S
i
= 0, i=1..C as transformed features of the
text classification problem.
5 CLASSIFICATION
ALGORITHMS
As classification algorithms we use the k-NN algo-
rithm with weight distance and the SVM-based al-
gorithm Fast Large Margin (SVM-FLM) (Fan et al.,
2008). RapidMiner with standard setting (Shafait
et al., 2010) was used as software for classification
algorithm application. The classification criterion is
the macro F-score (Goutte and Gaussier, 2005) which
is appropriate for classification problems with unbal-
anced classes. For k-NN we performed validation of k
from 1 to 15 on the validation sample. We used 80%
of the train sample for the first level of learning and
20% for the validation.
6 SELF-ADJUSTING GA
For solving the problem of GA setting parameters we
use the self-adjusting algorithm that was proposed in
(Semenkin and Semenkina, 2012). The scheme of the
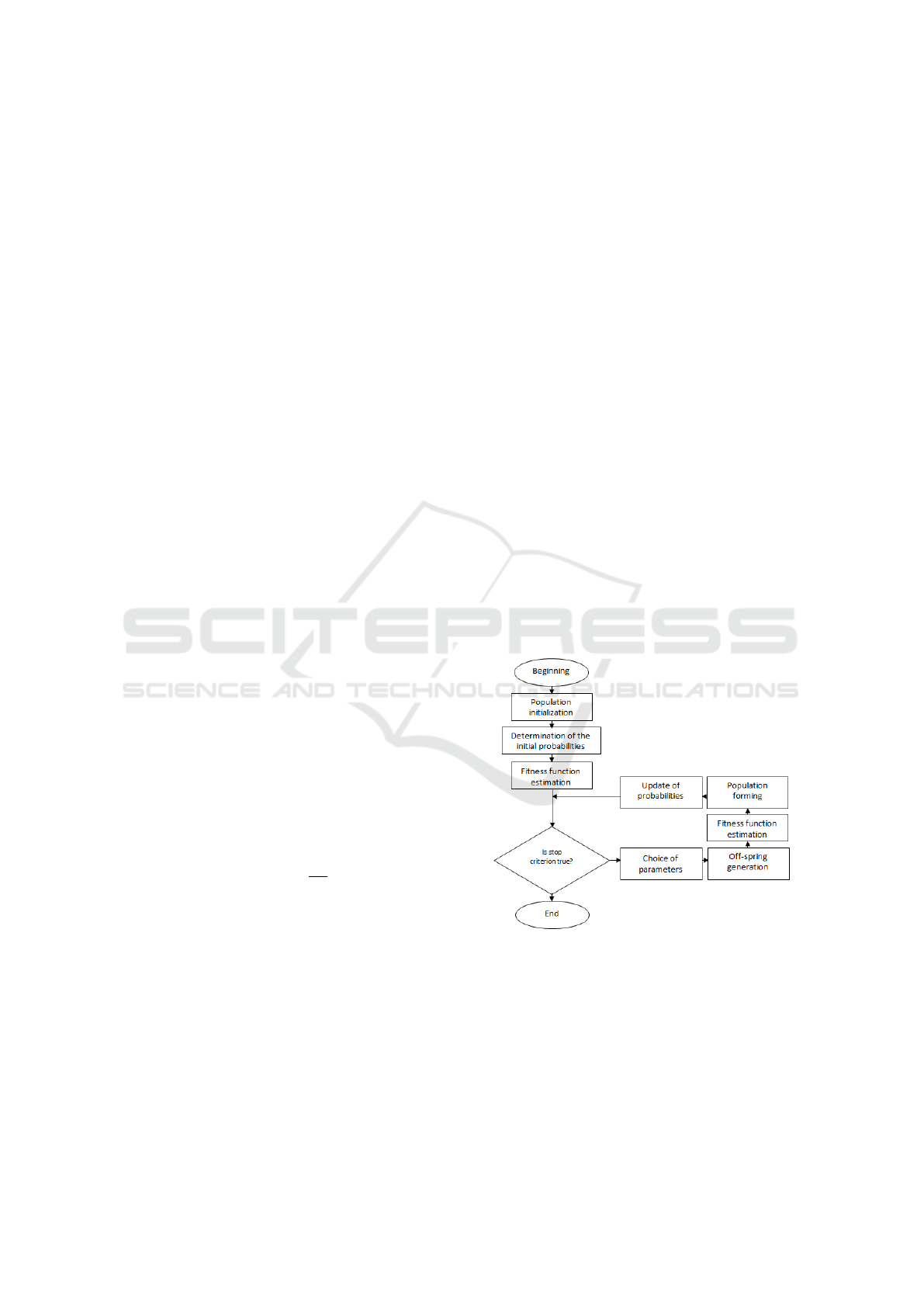
self-adjusting GA is presented in Figure 1.
Figure 1: Self-adjusting GA.
In the self-adjusting GA, different types of selec-
tion, recombination, and different levels of mutation
are performed simultaneously. In the beginning of the
algorithm, all types of GA operators have the same
probability to be use for a new off-spring generation.
After that, the dynamic adaptation of probabilities
are performed according ”usefulness” of GA opera-
tor types in terms of fitness function. The details of
the self-adjusting GA are the following:
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
42

1. Put the probabilities of all used types of GA op-
erators: p
i j
= 1/N
i
, where j = 1..N
i
, N
i
is the number
of types of the i
th
operator, i = 1..N, N is the num-
ber of GA operators. In our case N = 3: selection,
recombination, and mutation.
2. Set threshold probabilities for all used types of
GA operators: ˆp
i j
= 3/(10 · N
i
).
3. Generate new population. For each off-spring
we randomly choose types of selection, recombina-
tion, and mutation according probabilities p
i j
.
4. Recalculate the probabilities with the follow-
ing:
4.1. For each i
th
operator do:
4.1.1. Set S
i
= 0.
4.1.2. For each j
th
type of the i
th
operator do:
4.1.2.1. If p
i j
< ˆp
i j
+ 1/(T · N
i
) AND p
i j
> ˆp
i j
,
where T is the number of generations, then:
S
i
= S
i
+ (p
i j
− ˆp
i j
); p
i j
= ˆp
i j
.
4.1.2.2. If p
i j
> ˆp
i j
+ 1/(T · N
i
) then:
S
i
= S
i
+ 1/(T · N
i
); p
i j
= p
i j
− 1/(T · N
i
).
4.1.2.3. Calculate average fitness function F
i j
of
all off-springs of the current generation that were gen-
erated with the j
t
h type of the i
t
h operator.
4.1.3. Find the best type d of the i
th
operator with
the maximal fitness function on the current generation
and recalculate its probability: p
id
= p
id
+ S
i
5. Check stop criterion. If TRUE then: END; else:
go to the step 3.
For our problem, we used the following types of
GA operators:
- Selection: proportional, rank, and tournament
with tournament size equals 2, 5, and 7.
- Recombination: one-point, two-point, uniform
or cloning of one parent.
- Mutation: average mutation with the probability
equals to 1 / (l*n), where l is the length of the chro-
mosome and n is the index of the current generation;
strong mutation that is twice more than the average
one; weak mutation that is twice less than the average
one.
7 RESULTS OF NUMERICAL
EXPERIMENTS
Tables 1-4 show the results of the numerical experi-
ments for data configurations 1 and 2 with three situa-
tions: without dimensionality reduction (all terms are
used), with stop-words filtering + stemming, and with
the feature transformation method based term belong-
ing to classes (novel FT). Tables 1-4 contain results
with different term weighting methods and also re-
sults of term weighting method collectives based on
majority vote with all seven considered methods. For
all situations the ranking of term weighting methods
was performed with t-test (the confidence probabil-
ity equals 0.95). The ranks are illustrated in brackets.
Other comparisons were also performed with t-test.
The best results in tables are bold (for each case inde-
pendently).
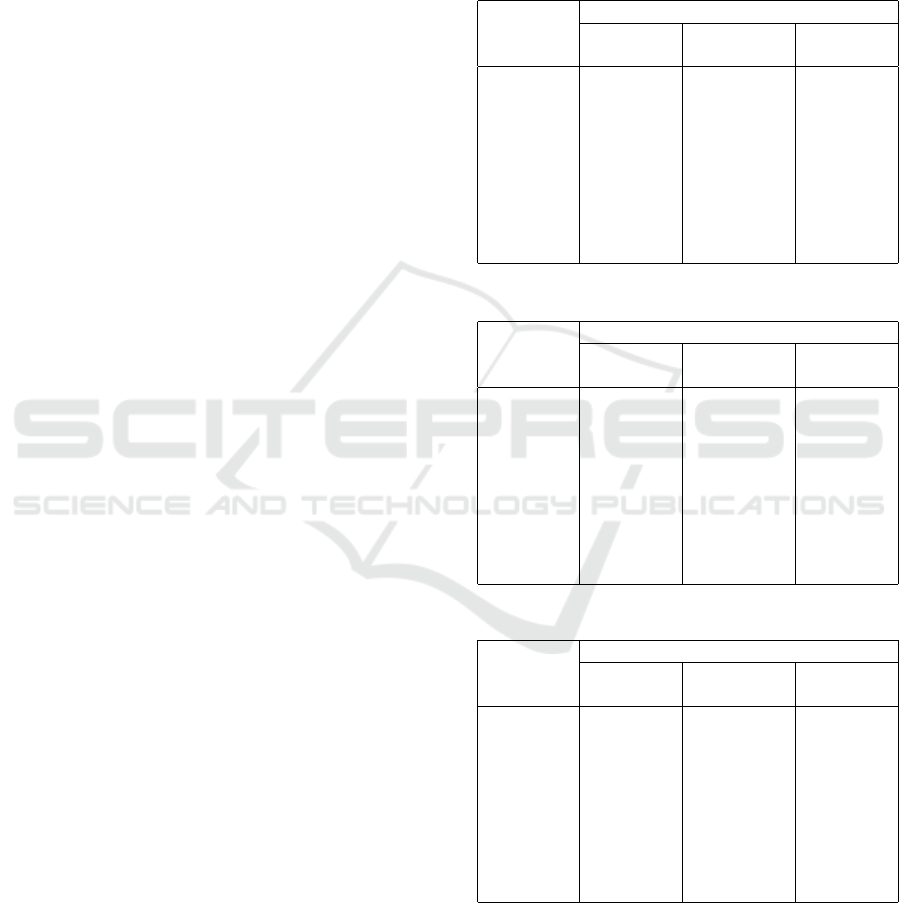
Table 1: Results for data configuration 1 with k-NN.
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
IDF 0.855(6-8) 0.777(7) 0.819(7)
GR 0.851(6-8) 0.766(8) 0.841(6)
CW 0.870(2-4) 0.784(4-6) 0.851(3-4)
RF 0.855(6-8) 0.783(4-6) 0.849(5)
TM2 0.865(5) 0.784(4-6) 0.853(3-4)
TRR 0.873(2-4) 0.793(1-2) 0.862(2)
NTW 0.871(2-4) 0.789(3) 0.844(5)
Majority
0.883(1) 0.799(1-2) 0.877(1)
vote
Table 2: Results for data configuration 2 with k-NN.
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
IDF 0.631(8) 0.636(8) 0.477(8)
GR 0.646(7) 0.667(7) 0.596(6)
CW 0.704(4-5) 0.695(5-6) 0.653(2-3)
RF 0.692(6) 0.688(5-6) 0.636(4)
TM2 0.713(2-3) 0.701(2-4) 0.621(5)
TRR 0.715(2-3) 0.704(2-4) 0.657(2-3)
NTW 0.709(4-5) 0.702(2-4) 0.584(7)
Majority
0.730(1) 0.715(1) 0.689(1)
vote
Table 3: Results for data configuration 1 with SVM-FML.
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
IDF 0.873(1) 0.836(1) 0.544(8)
GR 0.670(8) 0.680(8) 0.621(5-7)
CW 0.835(5) 0.801(5) 0.747(2-3)
RF 0.864(2-3) 0.819(3) 0.744(2-3)
TM2 0.734(7) 0.720(7) 0.618(5-7)
TRR 0.865(2-3) 0.823(2) 0.792(1)
NTW 0.825(6) 0.797(6) 0.621(5-7)
Majority
0.846(4) 0.806(4) 0.718(4)
vote
The combination of stop-words filtering and stem-
ming reduces the average dimensionality from 3,304
to 2,482 (75.1% of the original dictionary). The fea-
ture transformation based on term belonging to terms
reduces the dimensionality from 3,304 to 20 (to num-
ber of the classes). Both dimensionality reduction
Weighted Voting of Different Term Weighting Methods for Natural Language Call Routing
43

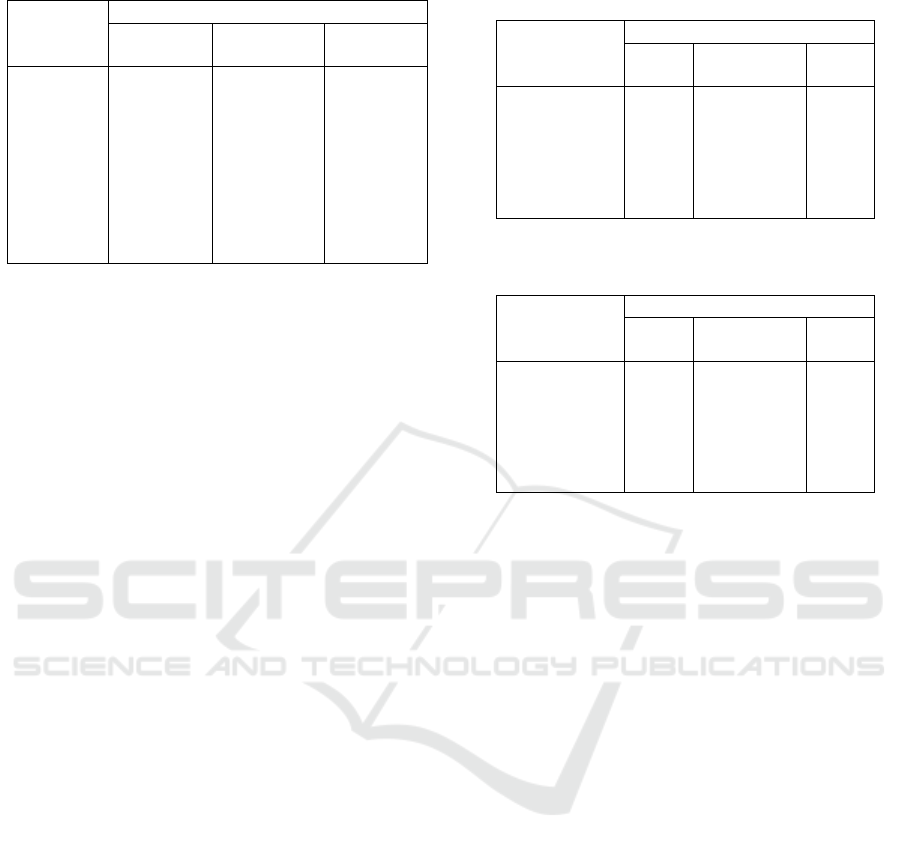
Table 4: Results for data configuration 2 with SVM-FML.
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
IDF 0.721(1-2) 0.704(1-3) 0.370(8)
GR 0.478(8) 0.521(8) 0.512(6-7)
CW 0.674(5) 0.675(5) 0.605(1-2)
RF 0.715(3) 0.700(1-3) 0.561(4)
TM2 0.563(7) 0.586(7) 0.510(6-7)
TRR 0.721(1-2) 0.701(1-3) 0.611(1-2)
NTW 0.650(6) 0.660(6) 0.528(5)
Majority
0.686(4) 0.681(4) 0.567(3)
vote
methods provide statistically significant decreament
of classification effectiveness in comparison with the
case of using all terms.
From Tables 1-4 we can conclude that collectives
of term weighting methods are effective with k-NN
but not effective with SVM-FML. The best results of
the collectives with k-NN significantly outperform the
best results of the collectives with SVM-FML (see Ta-
bles 1-4, the last rows). Therefore, we investigated the
weighted voting of different term weighting methods
only with the k-NN algorithm.
The next stage of investigation is weighting vote
based on weight optimization. As an optimization
algorithm we used self-adjusting genetic algorithm.
Optimization was performed with the validating sam-
ples (20% of the training sets). We proposed two def-
initions of the considered optimization problem:
- 7 variables: each variable means a weight for
one term weighting method. Variables are varied in
the interval [0;1].
- 7*20 variables: each variable means a weight for
one term weighting method with the specified class
(the predicted by the method class). Variables are var-
ied in the interval [0;1].
An individual for GA represents of a vector of all
considered weights in the binary form. The results
of optimization are presented in Tables 5-6. The opti-
mization algorithm was applied 20 times for each data
configuration without dimensionality reduction, with
stop-word filtering + stemming, and with the feature
transformation based on term belonging to classes
(”Novel FT”) (population size for GA equals 250).
The row ”7, best” means the results with 7 variables
and with choice the best F-score on the validating set
by 20 algorithm runs. The string ”7, average” means
the results with 7 variables and with the average F-
score by 20 algorithm runs. There is the same ex-
planation in the case with 7*20 variables. The val-
ues that were significant improved with optimization
(based on t-test) are in bold.
Table 5: Optimization of weights for data configuration 1
with k-NN.
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
Without
0.883 0.799 0.877
optimization
7, best 0.885 0.771 0.878
7, average 0.885 0.770 0.878
7*20, best 0.887 0.776 0.878
7*20, average 0.886 0.774 0.878
Table 6: Optimization of weights for data configuration 2
with k-NN
Term F-score
weighting All Stop-word Novel
method terms +stemming FT
Without
0.730 0.715 0.689
optimization
7, best 0.731 0.715 0.690
7, average 0.731 0.715 0.691
7*20, best 0.730 0.716 0.698
7*20, average 0.731 0.714 0.697
The results in Tables 5-6 showed that optimization
provides significant improvement of F-score for both
data configurations in cases without dimensionality
reduction and with the novel feature transformation.
The final results with the novel feature transformation
are very close to results without dimensionality reduc-
tion. In the same time, the novel feature transforma-
tion method reduces the dimensionality radically and
can be useful for real-time classification systems such
as natural language call routing.
Totally, the collectives of term weighting meth-
ods provide the following improvements of F-score
in comparison with the best individual term weight-
ing methods:
- For data configuration 1 with all terms: from
0.873 to 0.887 (+0.014).
- For data configuration 1 with the novel FT: from
0.862 to 0.878 (+0.016).
- For data configuration 2 with all terms: from
0.721 to 0.731 (+0.010).
- For data configuration 2 with the novel FT: from
0.657 to 0.698 (+0.041).
8 CONCLUSIONS
The text classification problem for natural language
call routing was considered in the paper. Seven differ-
ent term weighting methods were applied. As dimen-
sionality reduction methods, the combination of stop-
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
44

word filtering and stemming and the feature transfor-
mation based on term belonging to classes were con-
sidered. k-NN and SVM-FML were used as classifi-
cation algorithms.
In the paper the idea of voting with different
term weighting methods was proposed. The major-
ity vote of seven considered term weighting meth-
ods provides significant improvement of classification
effectiveness. After that the weighted voting based
on optimization with self-adjusting genetic algorithm
was investigated. The numerical results showed that
weighted voting provides additional improvement of
classification effectiveness. Especially significant im-
provement of the classification effectiveness is ob-
served with the feature transformation based on term
belonging to classes that reduces the dimensional-
ity radically; the dimensionality equals number of
classes.
REFERENCES
Akhmedova, S., Semenkin, E., and Sergienko, R. (2014).
Automatically generated classifiers for opinion min-
ing with different term weighting schemes. In
Informatics in Control, Automation and Robotics
(ICINCO), 2014 11th International Conference on,
volume 2, pages 845–850. IEEE.
Baharudin, B., Lee, L. H., and Khan, K. (2010). A review of
machine learning algorithms for text-documents clas-
sification. Journal of advances in information tech-
nology, 1(1):4–20.
Breiman, L. (1996). Bagging predictors. Machine learning,
24(2):123–140.
Debole, F. and Sebastiani, F. (2004). Supervised term
weighting for automated text categorization. In Text
mining and its applications, pages 81–97. Springer.
Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R., and
Lin, C.-J. (2008). Liblinear: A library for large lin-
ear classification. The Journal of Machine Learning
Research, 9:1871–1874.
Fox, C. (1989). A stop list for general text. In ACM SIGIR
Forum, volume 24, pages 19–21. ACM.
Gasanova, T., Sergienko, R., Akhmedova, S., Semenkin, E.,
and Minker, W. (2014). Opinion mining and topic
categorization with novel term weighting. In Pro-
ceedings of the 5th Workshop on Computational Ap-
proaches to Subjectivity, Sentiment and Social Media
Analysis, ACL 2014, pages 84–89.
Goutte, C. and Gaussier, E. (2005). A probabilistic interpre-
tation of precision, recall and f-score, with implication
for evaluation. In Advances in information retrieval,
pages 345–359. Springer.
Han, E.-H. S., Karypis, G., and Kumar, V. (2001). Text Cat-
egorization Using Weight Adjusted k-Nearest Neigh-
bor Classification. Springer.
Joachims, T. (2002). Learning to Classify Text Using Sup-
port Vector Machines: Methods, Theory and Algo-
rithms. Kluwer Academic Publishers.
Ko, Y. (2012). A study of term weighting schemes us-
ing class information for text classification. In Pro-
ceedings of the 35th international ACM SIGIR con-
ference on Research and development in information
retrieval, pages 1029–1030. ACM.
Kwon, O.-W. and Lee, J.-H. (2003). Text categorization
based on k-nearest neighbor approach for web site
classification. Information Processing & Manage-
ment, 39(1):25–44.
Lan, M., Tan, C. L., Su, J., and Lu, Y. (2009). Supervised
and traditional term weighting methods for automatic
text categorization. Pattern Analysis and Machine In-
telligence, IEEE Transactions on, 31(4):721–735.
Lee, C., Jung, S., Kim, S., and Lee, G. G. (2009). Example-
based dialog modeling for practical multi-domain di-
alog system. Speech Communication, 51(5):466–484.
Morariu, D. I., Vintan, L. N., and Tresp, V. (2005). Meta-
classification using svm classifiers for text documents.
Intl. Jrnl. of Applied Mathematics and Computer Sci-
ences, 1(1).
Porter, M. F. (2001). Snowball: A language for stemming
algorithms.
Salton, G. and Buckley, C. (1988). Term-weighting ap-
proaches in automatic text retrieval. Information pro-
cessing & management, 24(5):513–523.
Schapire, R. E. and Singer, Y. (2000). Boostexter: A
boosting-based system for text categorization. Ma-
chine learning, 39(2):135–168.
Sebastiani, F. (2002). Machine learning in automated
text categorization. ACM computing surveys (CSUR),
34(1):1–47.
Semenkin, E. and Semenkina, M. (2012). Self-configuring
genetic programming algorithm with modified uni-
form crossover. In 2012 IEEE Congress on Evolu-
tionary Computation.
Sergienko, R., Gasanova, T., Semenkin, E., and Minker, W.
(2014). Text categorization methods application for
natural language call routing. In Informatics in Con-
trol, Automation and Robotics (ICINCO), 2014 11th
International Conference on, volume 2, pages 827–
831. IEEE.
Sergienko, R., Muhammad, S., and Minker, W. (2016). A
comparative study of text preprocessing approaches
for topic detection of user utterances. In Proceed-
ings of the 10th edition of the Language Resources and
Evaluation Conference (LREC 2016).
Sergienko, R. and Semenkin, E. (2010). Competitive coop-
eration for strategy adaptation in coevolutionary ge-
netic algorithm for constrained optimization. In 2010
IEEE Congress on Evolutionary Computation.
Shafait, F., Reif, M., Kofler, C., and Breuel, T. M. (2010).
Pattern recognition engineering. In RapidMiner Com-
munity Meeting and Conference, volume 9. Citeseer.
Soucy, P. and Mineau, G. W. (2005). Beyond tfidf weighting
for text categorization in the vector space model. In
IJCAI, volume 5, pages 1130–1135.
Weighted Voting of Different Term Weighting Methods for Natural Language Call Routing
45

Suhm, B., Bers, J., McCarthy, D., Freeman, B., Getty, D.,
Godfrey, K., and Peterson, P. (2002). A comparative
study of speech in the call center: Natural language
call routing vs. touch-tone menus. In Proceedings of
the SIGCHI conference on Human Factors in Comput-
ing Systems, pages 283–290. ACM.
Xu, H. and Li, C. (2007). A novel term weighting scheme
for automated text categorization. In Intelligent Sys-
tems Design and Applications, 2007. ISDA 2007. Sev-
enth International Conference on, pages 759–764.
IEEE.
Yang, Y. and Pedersen, J. O. (1997). A comparative study
on feature selection in text categorization. In ICML,
volume 97, pages 412–420.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
46