
Modelling Radar Signal Error Performance under Atmospheric
Refraction and Clutter Attenuation
Chiemela Onunka
1
and Glen Bright
2
1
Discipline of Mechanical Engineering, University of KwaZulu-Natal, King George V Ave., Durban, South Africa
2
Discipline of Mechanical Engineering, University of KwaZulu-Natal, Durban, South Africa
Keywords: Error Performance, Radar Signal, Clutter Attenuation, Atmospheric Refraction.
Abstract: Radar signal error performance was modelled in the presence of atmospheric refraction and clutter
attenuation. The models presented in the paper exploited prior information on atmospheric refraction
properties and conditions such as partial pressure, water vapour, atmospheric temperature and the associated
clutter. The atmospheric properties and characteristics were used to model random and bias errors experienced
in radar systems. Errors which were associated with azimuth, elevation and target velocity were considered
in the performance analysis. Range resolution and Doppler resolution were key mechanisms which were
implemented in the analysis of the radar signal error performance. The radar error performance was analysed
using residual error, signal-to-clutter + noise ratio and thermal noise error. Errors from azimuth, elevation and
target velocity were combined in investigating the total effect of errors in determining the desired signal-to-
clutter + noise ratio. The results discussed in the paper enhances target detection and tracking towards
optimising the navigation system of autonomous and semi-autonomous robotic systems using radars.
1 INTRODUCTION
Radar signals are used in high-gain command-able
and agile systems such as autonomous system for
target detection and tracking (Chen et al., 2014).
Radar systems use scanned arrays and multiple-input
multiple-outputs models to increase the flexibility in
the modes of operation and application (Frankford et
al., 2014). Illumination of the environment with radar
signals provides critical information on the energy
scattered by detectable targets (Dilum Bandara et al.,
2012). Scattered energy from targets and radial
velocity of targets provide differentiable modes of
target position and motion. Modulation of radar
signals ensures accurate range determination
(Hayvaci et al., 2013). Radar range and antenna
characteristics provide critical information in the
determination of azimuth and elevation angles of the
radar system.
Resolving ambiguities associated with Doppler
frequency determination ensures that targets are
detected across various frequencies. The influence of
detection densities allows for diversification in the
detection strategies used in radar systems (Sharma et
al., 2014) (Radmard et al., 2014). Timings in radar
signal are influenced by the coherent and incoherent
characteristics of oscillators in the radar systems. The
phase reference of radar signals are hence dependent
on the characteristics of the oscillators (Eustice et al.,
2015) (Fellows et al., 2013).
The performance of radar system is subject to
external factors such as atmospheric refraction
(Panchenko et al., 2012) (Renkwitz et al., 2014) and
clutter attenuation (Agarwal, et al., 2014) (Marquis,
2010). Scattering models are used to comprehend the
nature and behaviour of the radar signal frequency
energy distribution. Radar signals experience
refraction in the elevation to and from the radar.
Splaying of radar signals in the elevation plane is also
another factor that occurs when radar signals are
refracted. Energy absorbed by the atmosphere from
the signals also affect the performance of the radar
system.
The navigational systems for autonomous and
semi-autonomous systems use radars for target
detection and tracking. Mobile robot obstacle
detection and avoidance are critical in fulfilling their
navigational objectives.
The paper discusses the performance error of
radar systems under atmospheric refraction and
clutter attenuation. Error detection mechanisms were
used in the error analysis of radar signals. The results
404
Onunka, C. and Bright, G.
Modelling Radar Signal Error Performance under Atmospheric Refraction and Clutter Attenuation.
DOI: 10.5220/0005957004040412
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 404-412
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

discussed in the paper are applicable in optimising the
navigation systems of autonomous and semi-
autonomous robotic systems
2 TARGET DETECTION,
UNCERTAINTY AND
PERFORMANCE
The technical performance of a radar system is
measured in terms of distance. More specifically, the
performance of radar systems are evaluated using the
scatter cross-sectional area and radar range. The
range scatters can be defined using different sizes.
Larger range scatters are used in evaluating the
performance of radar systems designed for long range
detection of targets. The long range of the radar
system defines the maximum range detectable by the
radar system (Jang et al., 2013). The reciprocal of the
time required by the radar signal to reach the
maximum range and echo back is used in determining
the maximum signal repetition frequency. The signal
repetition frequency provides critical information in
the determination of staggering for moving target. It
is also used in processing moving target detector
signal associated with frequency diversity. Radar
range ambiguities in medium and high signal
repetition frequencies can also be resolved using the
repeated radar signal.
Lower range boundaries in the radar range can be
created using transmit-receive switches. The mixture
of long pulses and short pulses in radar systems
increases uncertainty in detecting targets. Separate
signals for long range mode and short range ensures
that uncertainty is minimised. The amount of azimuth
in the radar design influences the choice of using
continuous target scanning or sector scanning in the
search mode (Chen and Furumoto, 2011). Elevation
properties can be introduced in the search mode or
incorporated when using broad beam in the elevation
plane. Broad beams in the elevation plane provide
coverage to a certain height above the ground.
Detecting targets using radar signals uses definite
time intervals which can be described statistically.
The number of false alarms can be set at a constant
value in order to ensure that false alarms are at an
acceptable level and hence the probability of false
alarm. Fixed number of false alarm ensures that the
thresholds set for probability of false alarm is
adequately optimised. Optimisation of probability of
false alarm sets a threshold above the thermal noise
in the radar system. A combination of radar signal and
noise exceeding the set threshold yields the
probability of detecting targets. The signal-to-noise
ratio in the scatter provide valuable information in
integrating the echoes from targets towards
performance improvement of the radar system (Su et
al., 2010). Distinguishing between targets and echoed
signals are evaluated using the radar system angular
resolution. The angular resolution is determined by
reducing the azimuth and beam elevation widths. The
radial velocity of the search scatter provides
information on the echo Doppler frequency. The
radial velocity is useful in the separation and removal
of clutter in the performance analysis of the radar
system.
3 ATMOSPHERIC CLUTTER
MODELLING
The atmosphere refracts and absorbs energy from
radar signals. The refraction sub-processes were
modelled using an exponential atmospheric algorithm
in determining the refractivity of radar signals in the
atmosphere (Meikle, 2008). The subroutine algorithm
was supplied with different input and output
parameters. The exponential atmospheric model for
refractivity of radar signals was expressed as:
(1)
Where
represented refractivity at the earth’s
surface, represented the height of the radar system
above the earth’s surface and
was a constant. Given
that the refractivity of air was approximately unity, it
was fitting to use the refractivity of air in the signal
analysis. The refractive index of air was expressed as:
110
(2)
The radar signal was analysed based on the point
of interest (Meikle, 2008). The points of interest
considered in the models were as follows:
Radar signal analysis toward determination
of target height
Determination of classical target range
Determination of classical target range with
respect to earth’s surface.
Determination of attenuation along the radar
signal
Considering radar signal as a ray, the target height
was modelled as:
(3)
∆
2
∆
(4)
Where
represented the position of the radar
system above the earth’s surface,
represented the
Modelling Radar Signal Error Performance under Atmospheric Refraction and Clutter Attenuation
405

position of the target above the earth’s surface,
represented the radius of the earth and
represented
the elevation angle. Considering the effects of partial
pressure caused by water vapour, atmospheric
temperature and signal scatter at the target position
with an elevation; the atmospheric refractive index
was expressed as (Meikle, 2008):
1
10
77.6
3.7310
(5)
The height of the radar system was determined using:
2
(6)
Refraction and reflection within the atmospheric
layer influenced the performance of radar system.
Anomalous propagation and super-refraction
occurred when there was sudden variation between
the layers of the atmosphere. It introduced extra
clutter and blind search volume in the radar coverage
area. In certain atmospheric condition, total reflection
of radar signal may cause the signal to be trapped
between the atmospheric layer and the earth’s
surface. Temperature inversions in the atmosphere
can cause radar signals to be trapped or ducted. Local
temperature inversion at higher altitudes are
consequences of atmospheric subsidence.
Temperature inversions are associated with the radar
search areas experiencing high atmospheric pressures
(Meikle, 2008).
Radar signals are sensitive to water vapour
content in the atmosphere. Attenuation and
absorption losses influenced the performance of the
radar system. The model used in determining fog
attenuation as a function water content and
frequency was expressed as:
4.8710
/
(7)
Scattering and atmospheric attenuation were
proportional to rain rates and drop sizes. Given that
atmospheric attenuation can also be found in wet
snow as result of the water content; the attenuation in
wet snow was expressed as:
0.00349
.
0.0022
/
(8)
Where represented the wave length of the radar
signal and represented the water content in the
snow. The radar cross section influenced the shape of
scatter produced within the search area of the radar
system. Scatters produced by the radar signals were
usually smaller than the radar signal emitted by the
transmitter. The radar cross section also determined
the amplitude of the echo produced by the scatter.
Weak echo signals were identified by their narrow
beams and strong echoes were identified by their
wide beams. The influence of these parameters were
suppressed by using side-lobes with sensitive time
controls. The echoes emitted by a target can be
interfered with giving rise to signal fading. Scattering
without fading in radar system can be optimised if
targets have symmetrical shapes with determinable
radar cross sections.
Polarisation of radar signals influenced the
performance evaluation of the radar system.
Considering the radar signals as polarised circular
waves with incident radar signal rotating on reflected
radar signal. The condition created a reaction radar
signal which was propagated in the opposite
direction. The problem was resolved by using flat and
smoothly curved spherical reflectors in radar signal
transmission. The spherical reflectors reversed the
effects or sense of polarisation in radar signals. The
echo returned from a spherical reflector having a
radius and normalised along its projected area
was expressed as (Meikle, 2008):
1
1
21
,
,
(9)
,
(10)
,
(11)
Where
represented the spherical Bessel
function of the first kind order within the
argument,
represented the spherical Bessel
function of the second kind order within the
argument.
Radar systems operating at higher frequencies
function adequately within an optical region.
Operating the radar at lower frequencies required the
incorporation of sphere sizes whose radius was four
times the signal wavelength. Three regions
provided variation parameters for radar signal
performance. They were the optical region, Rayleigh
and resonant region. Verifying radar signals using
large spheres of radius in the optical region was
modelled as:
;4 (12)
Analysing the radar signal under atmospheric
condition such as rain within the Raleigh region was
modelled as:
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
406

9
(13)
In considering scatter from targets within the
radar search area interfering with each other, the
signal reflections were estimated. Irregular cluster of
target echoes were only constant on short radar
signals. If the frequency at which the radar was
operated changed, the probability distribution of the
scatter was considered to be dynamic. Dynamic echo
and scatter were observed using digital signal fading
models in evaluating the degrees of dispersion in the
probability distribution of the scatter and echo
signals. Log-normal and gamma distribution were
used to express the characteristics and behaviours of
echoed signals and scatter. Describing clutter as a log-
normal distribution, the mean-to-median ratio
of
the clutter embedded in echoed signal and scatter was
expressed as a log-normal distribution:
√
(14)
Where represented the standard deviation of the
signal distribution. The gamma model as function of
the signal shape parameter and signal scale
parameter was expressed as:
(15)
The mean for the gamma distribution was given as:
(10)
And the standard deviation for the gamma
distribution was expressed as:
(17)
Clutter power spectrum was used as a measure in
quantifying the effects of clutter in the performance
of the radar systems. The power spectrum of clutter
was the sum of fixed target and moving or random
targets. Random targets were assumed to have
Gaussian characteristics. The power spectrum of
clutter was expressed as a function of the fixed-to-
random target power ratio
, clutter spectrum was
expressed as:
1
1
2
(18)
Where
represented the operating frequency of the
radar system,
represented the root mean square
frequency spread component of the clutter model and
represented the Weibull parameter. Given that
most of the clutter can be measured with minimal
operating frequency spread and zero Doppler
frequency, a simper Gaussian-shaped clutter power
spectrum was used and expressed as:
(19)
Where
represented the total clutter power.
4 RADAR ERROR CLASSES
The two major errors experienced by radar systems
are random error and bias error. In normal operation,
radar signal can be sent over Fraunhofer regions and
the analysis of the echoes returned are done in the
Fraunhofer regions. Optical calibration of radar
antennas in parallel to radar beam may be in azimuth
with the tilt angle. Azimuth corrections were required
in order to minimise bias errors. For a surface with
refractivity
, the atmospheric refraction model at an
elevation in radian was expressed as:
∆
10
(20)
The atmospheric refraction was considered and
included in the radar model after the radar elevation
was corrected. The correction on azimuth was made
directly on the radar system.
Random errors were present in the radar signal
analysis as a result errors from radar signal
measurements. Random errors were subject to radar
signal distortion and quantisation errors. Range errors
also occurred in the radar measurements. Range
errors were consequences of system jitter, signal
modulation timings, transmitter pulse timings,
receiver delays, signal amplification variation in
range estimator gates and variation in atmospheric
index.
Discussing further the errors which are
experienced in radar systems, the azimuth, elevation,
range and target velocity each generated certain
amount errors which influenced the performance of
radar system. There were errors in continuous
measurement of these parameters. The error signal
was generated by making an angular deviation from
the main axis of the radar system. The resultant error
signal described the target deviation from the main
axis of the radar beam. In order to perform error
evaluation check, the error signal was modelled as a
Modelling Radar Signal Error Performance under Atmospheric Refraction and Clutter Attenuation
407

linear function of the deviation angle. Azimuth
and
elevation
errors were expressed as:
(21)
(22)
The azimuth and elevation errors were used in
aligning the radar tracking axis on the target.
Expressing amplitude modulation signal as a function
of the azimuth and elevation errors:
sin
(23)
Where
represented the error slope,
represented
the scan frequency and represented the defined
angle.
5 PERFORMANCE ANALYSIS
The radar performance was evaluated in terms of the
ability of the radar system to accurately identify the
position of target, the resolution at which the targets
were differentiated and the clutter elimination
optimisation. These performance evaluations
parameters were grouped into radar range, accuracy,
resolution and stability. Each of these of these radar
performance characteristics were influenced by
atmospheric conditions and clutter attenuation.
The performance of the radar system was required
to exceed the critical radar signal to background ratio
in order to exceed the target detection threshold. In
clear atmospheric condition, thermal noise formed the
larger portion of the critical background parameter
influencing performance. In addition to thermal noise
was weather clutter and ground or environment
clutter. Signal interference and jamming at the
receiver terminal also affected the performance of
radar system. Radar range in clear and stable
atmospheric condition was modelled as (Mahafza and
Elsherbeni, 2004):
4
(24)
Where
represents the transmitter pulse,
represents the signal wavelength, represents the
target cross section, represents Boltzman’s constant
is the chaff echo,
represents the transmitter
gain,
represents the receiver gain,
represents the
radar power, represents losses,
represents
effective temperature, represents the system’s
noise. The effective temperature at the receiver as
influenced by atmospheric conditions was modelled
as:
(25)
Where
represented the temperature at the
antenna connector,
represented the standard
temperature in Kelvin,
represented the loss
between the radar antenna and receiver and
represented the receiver noise factor.
5.1 Error Detection Mechanism
Range resolution and Doppler resolution were used in
the radar system error detection process. The
associated accuracy and ambiguity between these two
mechanisms provided valuable information in the
radar system error performance evaluation. In order
to determine the performance of the radar system
using error analysis, integral square error was
employed in the evaluation. The integral square
included errors generated from range gate trigger,
master signal trigger, transmitter trigger, receiver
antenna, atmospheric scintillator as indicated in
figure 1.
5.1.1 Range Resolution
Considering targets with zero Doppler resolution
within the range∆. The minimum value of ∆ was
used in establishing the difference between the
targets. Considering the radar signal having a carrier
frequency
, modulation amplitude
and phase
modulation modelled as (Mahafza and
Elsherbeni, 2004):
cos
2
(26)
was expressed as the real part of a complex radar
signal where
(27)
It followed that
(28)
If echoes from two targets for instance with time
delay are represented as:
(29)
and
(30)
It followed that targets within the search area or range
resolution were distinguished by the amount of
measurable delay between the echoes returned by
the targets. The Integral square error
was used to
determine the variability of range between
the measured target ranges. The integral square
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
408

Figure 1: Integral System Components of Range Error.
between target and was expressed as
(Mahafza and Elsherbeni, 2004):
|
|
(31)
And was expressed further as:
|
|
|
|
∗
∗
(32)
Solving equation (27) and (32) yielded:
2
|
|
2
∗
(33)
Where
(34)
The energy carried by the radar signal was
expressed by the term:
2
|
|
(35)
And the range ambiguity function
was expressed
by the term:
2
∗
(36)
When expressed as a function of the radar carrier
frequency, the radar ambiguity function was
modelled as:
∗
(37)
The radar ambiguity function had a maximum value
at = 0. Resolving targets in range was performed
by computing the squared magnitude
|
|
of
the range ambiguity function. The implication of the
behaviour of the range ambiguity function was that
targets within the radar search area were
differentiated if
|
|
0
for non-zero
value of the delay in the received target echoes.
The converse behaviour of the range ambiguity
function implied that targets were indistinguishable
if
|
|
0
for none zero value of delay.
The resolution for the delay was expressed as
(Mahafza and Elsherbeni, 2004):
Δ
|
|
0
(38)
Application of Parseval’s theorem to the delay
resolution yielded:
Δ2
|
|
|
|
(39)
The minimum resolution for the radar range
∆
∆
2
(40)
The radar effective bandwidth was expressed as:
|
|
2
|
|
(41)
Hence the range as a function of signal waveform
Master Signal
Trigger Generator
Transmitter
Trigger
Generator
Range Gate
Trigger
Generator
Range Gate
Trigger Servo
Transmitte
r
Atmosphere
Scintillation
Glint
Radar Range
Total System
Error
Receiver
Antenna
Modelling Radar Signal Error Performance under Atmospheric Refraction and Clutter Attenuation
409

bandwidth was expressed as (Mahafza and
Elsherbeni, 2004):
∆
2
(42)
5.1.2 Doppler Resolution
Doppler resolution is associated with the targets
radial velocity. The target radar spectrum was
defined as:
Ψ
(43)
Considering a target with radial velocity as a
fraction of speed of light, frequency
and
wavelength, the Doppler shift was expressed as:
2
(44)
The received spectrum shifted by
was used to
differentiate targets having different velocities and
the same range values. The integral square error for
the Doppler resolution was expressed as (Mahafza
and Elsherbeni, 2004):
|
Ψ
Ψ
|
(45)
Similarly, the real part of the model was modelled
as:
2Ψ
∗
Ψ
(46)
Applying the model expressed in equation (27)
yielded:
Ψ
22
(47)
Transforming the real part the model yielded the
complex correlation function:
∗
2
22
(48)
The Doppler resolution constant was expressed as:
Δ
0
1
(49)
The target velocity resolution as function of the
target signal pulse width
was expressed as:
Δ
2
(50)
Combining the range and Doppler resolutions, the
complex envelope of the transmitted waveform was
expressed as:
(51)
The delayed target signal and the Doppler shifted
target signal was expressed as:
(52)
The integral square error for the target signal was
expressed as:
2
|
|
2
∗
(53)
The integral squared error for the target signal was
maximised by minimising the last term in equation
(54). The combined Doppler and range correlation
function was expressed
,
∗
(54)
The Doppler and range resolution were maximised
by minimising the modulus square of the Doppler-
range correlation function.
6 SIMULATION RESULTS AND
DISCUSSION
The effect of atmospheric temperature on the radar
error performance results was considered in the
form of thermal noise error
which was described
by:
1
1.81
√
2
(55)
represented the radar signal pulse width, SNR
represented the signal-to-noise ratio of target in
range. The model was used for optimum processing
of thermal noise error and its effect on the radar
signal error performance analysis. Targets within
the atmospheric clutter were detected by using the
chaff-to-signal noise ratio instead of the SNR in the
thermal noise error model. The result is shown in
Figure 2. The results shows that the lower chaff-to-
noise ratio in dB, the higher the root mean square
error of atmospheric clutter. The implication of this
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
410
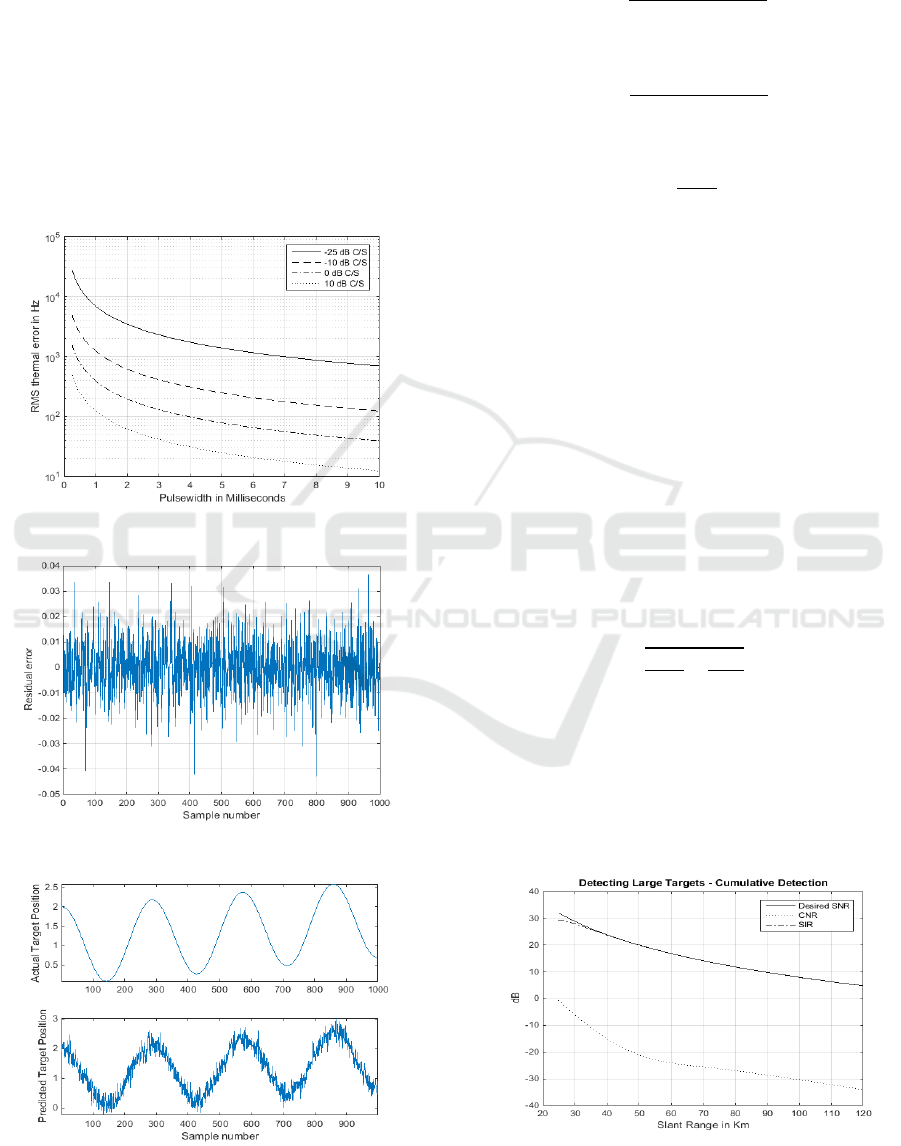
result was that the performance of the radar system
was optimum at higher chaff-to-noise ratio. Under
this condition there were fewer probability of false
alarm in target detection.
Residual error was used in determining the
position array of the targets. The result is shown in
figure 3. The variations on the result shown was due
to noise present in the position array signal. At high
gain, the error settles down quickly. The average
error with small gain coefficients in the error model
was approximately zero. Residual error was a
measure of target tracking error as shown in figure
4.
Figure 2: Error performance in clutter attenuation.
Figure 3: Residual error attenuation.
Figure 4: Target tracking attenuation.
The signal-to-noise ratio (SNR) for a target at range
was expressed as:
4
(56)
The clutter-to-noise ratio was expressed as:
4
(57)
And
(58)
Where
represented the peak power transmitted by
the radar, represented the radar antenna gain,
represented the radar signal wavelength,
represented the target radar cross section (RCS),
represented the anticipated clutter RCS,
represented Boltzman’s constant,
represented the
effective noise temperature, represented the
operating bandwidth of the radar, represented the
noise from receiver antenna and represented the
integral losses in the radar system.
In evaluating the effect of clutter in the radar
signal error performance analysis, clutter
characteristics were considered to be Gaussian. The
radar performance accuracy was measured using a
combination of returned clutter signal and noise
signal referred to as Signal-to-Clutter + Noise Ratio
(SIR). The SIR was computed as:
1
1
1
(59)
The results shown in figure 5 indicate that there was
minimal signal degradation in the required SIR for
large targets for range90. Figure 6 shows
that there was significant signal degradation in the
required SIR for small targets for range
90. Clutter mitigation and reduction ensured
that small targets were effectively detected.
Figure 5: Clutter attenuation in large target detection.
Modelling Radar Signal Error Performance under Atmospheric Refraction and Clutter Attenuation
411

Figure 6: Clutter attenuation in small target detection.
7 CONCLUSIONS
The error performance of radar system was
modelled using clutter attenuation and atmospheric
refraction. The results from the simulations revealed
that clutter and atmospheric refraction influenced by
water vapour and temperature affected the
performance of radar systems in detecting targets of
various sizes. The radar signal error performance
analysis was evaluated using residual error, thermal
noise error and signal-to-clutter + noise ratio.
Clutter mitigation ensured that small targets can
be detected at long ranges. The models presented in
the paper can be applied to the control and
navigation of autonomous systems using radar
signals. The navigation systems of mobile robots,
autonomous and semi-autonomous systems using
radar for obstacle detection and avoidance can be
optimised through minimisation of clutter and
atmospheric refraction.
REFERENCES
Agarwal, P., Jaysaval, V. K. & Rajagopal, S., 2014. A
generalized Model for Performance Analysis of
Airborne Radar in Clutter Scenario. Noida.
Chen, J.-S. & Furumoto, J., 2011. A Novel Approach to
Mitigation of Radar Beam Weighing Effect on
Coherent Radar Imaging Using VHF Atmospheric
Radar. IEEE Transactions on Geoscience and Remote
Sensing, 49(8), pp. 3059-3070.
Chen, J. et al., 2014. Surface Movement Radar Target
Detection. HangZhou, China, s.n.
Dilum Bandara, H. M. N., Jayasuman, A. P. & Zink, M.,
2012. Radar Networking in Collaborative Adaptive
Sensing of Atmosphere: State of the Art and Research
Challenges. Anaheim, CA.
Eustice, D., Baylis, C., Cohen, L. & Marks, R. L., 2015.
Effects of Power Amplifier Nonlinearities on the
Radar Ambiguity Function. Arlington, VA.
Fellows, M., C, B., Cohen, L. & J, M. R., 2013.
Calculation of the Radar Ambiguity Function from
Time-Domain Measurement Data for Real-Time,
Amplifier-in-the-Loop Waveform Optimization.
Columbus, OH.
Frankford, M. T., Stewart, K. B., Majurec, N. & Johnson,
J. T., 2014. Numerical and Experimental Studies of
Target Detection with MIMO Radar. IEEE
Transactions on Aerospace and Electronic Systems,
50(2), pp. 1569-1577.
Hayvaci, H. T., De Maio, A. & Erricolo, 2013. Improved
Detection Probability of a Radar Target in the
Presence of Multipath with Prior Knowledge of the
Environment. IET Radar, Sonar & Navigation, 7(1),
pp. 36-46.
Jang, Y., Lim, H., Oh, B. & Yoon, D., 2013. Clutter
Mapping and Performance Analysis for Vehicular
Radar Systems. Belgrade.
Mahafza, B. R. & Elsherbeni, A. Z., 2004. Simulations for
Radar Systems Design. Boca Raton: Chapman &
Hall/ CRC Press LLC.
Marquis, E., 2010. Antenna Size Versus Sea Clutter
Rejection: A new Analysis of Coastal Radar
performances and Optimization. Paris.
Meikle, H., 2008. Modern Radar Systems. 2nd ed.
Boston: Artech House Inc..
Panchenko, A. Y., Slipchenko, N. I. & Liu, C., 2012.
Comparison of Radar and Acoustic Methods for
Atmopshere Sounding. Sevastopol, Crimea, s.n.
Radmard, M., Chitgarha, M. M., Nazari Majd, M. &
Nayebi, M. M., 2014. Ambiguity Function of MIMO
radar with Widely Separated Antennas. Gdansk.
Renkwitz, T., Stober, G., Chau, J. L. & Latteck, R., 2014.
Estimation and Validation of the Radiation Pattern of
the Middle Atmosphere Alomar Radar System
(MAARSY). Beijing.
Sharma, G. V. K., Srihari, P. & Rajeswari, K. R., 2014.
MIMO Radar Ambiguity Analysis of Frequency
Hopping Pulse Waveforms. Cincinnati, OH, .
Su, X., Wu, Z. & Zhang, Y., 2010. Detection
Performance of C-Band Radar in Sea Clutter.
Guangzhou.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
412
