A Globally Convergent Method for Generalized Resistive Systems
and its Application to Stationary Problems in Gas Transport Networks
Tanja Clees, Nils Hornung, Igor Nikitin and Lialia Nikitina
Fraunhofer Institute for Algorithms and Scientific Computing, Schloss Birlinghoven, 53754, Sankt Augustin, Germany
Keywords:
Non-linear Systems, Globally Convergent Methods, Gas Transport Networks.
Abstract:
We consider generalized resistive systems, comprising linear Kirchhoff equations and non-linear element
equations, depending on the flow through the element and on two adjacent nodal variables. The derivatives of
the element equation should possess a special signature. For such systems we prove the global non-degeneracy
of the Jacobi matrix and the applicability of globally convergent solution tracing algorithms. We show that the
stationary problems in gas transport networks belong to this generalized resistive type. We apply the tracing
algorithm to several realistic networks and compare its performance with a generic Newton solver.
1 INTRODUCTION
Applied engineering problems often require to solve
large systems of non-linear equations. While solving
these systems, one cannot generally rely on the exis-
tence and the uniqueness of their solutions. Also, for
the purpose of convergence one has to choose a start-
ing point sufficiently close to the solution, to get into
a basin of attraction of the iterative method used.
A surprising feature of some network problems is
the existence of a unique solution and the availabil-
ity of a globally convergent method, able to find the
solution from an arbitrary starting point. This applies
to systems of resistive type, comprising Kirchhoff’s
flow conservation conditions and element equations
similar to Ohm’s law in electrotechnics. For systems
of this kind, written in a form f (x) = 0, one can prove
the non-degeneracy of the Jacobi matrix J = ∂ f /∂x
in the whole space of x. In other words, the map-
ping y = f (x) is a diffeomorphism and every y has a
single pre-image x. In particular, y = 0 has a single
pre-image x
∗
, in this way providing a unique solution
of the system above. The solution can be found with
the following algorithm:
Algorithm 1: Solution tracing.
start from an arbitrary point x
0
;
take its image y
0
= f (x
0
);
connect y
0
with the origin y = 0
by a straight line;
reconstruct pre-image of this line
in x-space.
The reconstruction of the pre-image of the line can be
done, using, e.g., a homotopically stabilized Newton
method (Allgower and Georg, 2003). The obtained
line in x-space goes from the starting point x
0
to the
solution x
∗
we are looking for.
In paper (Katzenelson, 1965) this idea has been
used for the solution of continuous piecewise linear
resistive systems. The system is composed of lin-
ear Kirchhoff equations and piecewise linear element
equations of the form f (P
in
− P
out
,Q) = 0, relating a
difference of nodal variables P
in
− P
out
to the flow Q
through the element. Continuity means that the map-
ping y = f (x) as a whole is C
0
-continuous, since the
purpose is to approximate continuous element equa-
tions of general non-linear form. Resistiveness means
that the element equation in every piece can be writ-
ten as P
in
− P
out
= RQ +Const, where R > 0 is the
resistance, or, in more general way, that the deriva-
tives of the element equation in every piece possess
the following signature: ∇ f = (+−). It is easy to
show that under these conditions the Jacobian deter-
minant det J of the system has the same sign in all
pieces. Although this mapping is not a diffeomor-
phism anymore, it is a homeomorphism, every point y
still has a single pre-image x. The linear system in ev-
ery piece essentially coincides with the one appearing
in Newton’s step. The only necessary modification is
that, whenever the step attempts to leave the piece, the
algorithm should stop at the border:
Algorithm 2: Piecewise linear tracing.
do Newton’s step using the current
Jacobi matrix;
64
Clees, T., Hornung, N., Nikitin, I. and Nikitina, L.
A Globally Convergent Method for Generalized Resistive Systems and its Application to Stationary Problems in Gas Transport Networks.
DOI: 10.5220/0005958700640070
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 64-70
ISBN: 978-989-758-199-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

if the solution leaves the piece:
stop at the border;
update the Jacobi matrix to
the other side;
proceed to the next piece;
else:
return the solution.
The algorithm is globally convergent and comes to the
solution in a finite number of steps.
In paper (Chien and Kuh, 1976) the condition that
detJ has to be of the same sign in all pieces has been
relaxed. This condition has been imposed only on
unbounded pieces, while in bounded ones det J can
change sign and even vanish, producing a locally de-
generate system. The tracing algorithm has been ex-
tended to process such cases, still providing conver-
gence in a finite number of steps.
In paper (Griewank et al., 2015) the continuous
piecewise linear mappings were represented in a so
called max-min form. Further, using for max-min
functions their definition in terms of absolute values:
f (x) = max
i
min
j
a
T
i j
x + b
i j
,
max(x,y) = (x + y + |x − y|)/2, (1)
min(x,y) = (x + y − |x − y|)/2,
continuous piecewise linear systems have been trans-
formed to systems combining globally linear func-
tions and absolute value functions. The paper dis-
cusses the relation of such systems with linear com-
plementarity problems (LCPs) and Karush-Kuhn-
Tucker (KKT) conditions and presents a number of
algorithms for their solution, converging in a finite
number of steps.
The general relationship between physical laws
and underlying topological structure of the systems is
well discussed in works (Kron, 1945; Bulgakov et al.,
2005; Tonti, 2013; Shai, 2001). In the present pa-
per we will concentrate on particular aspects of non-
linear transport networks and extend the solution trac-
ing algorithm from (Katzenelson, 1965; Chien and
Kuh, 1976) to a wider class of problems, which we
will call generalized resistive systems. The systems
contain linear Kirchhoff equations and non-linear ele-
ment equations of the form f (P
in
,P
out
,Q) = 0. The el-
ement equations depend separately on the nodal vari-
ables P
in
, P
out
and the flow Q. The derivatives should
possess a signature ∇ f = (+ − −). In Section 2
we will show that systems of this kind have a non-
degenerate Jacobi matrix and the solution tracing al-
gorithm can be used for them, preserving its global
convergence property. In Section 3 we will apply this
algorithm to the solution of stationary problems in gas
transport networks. These networks include so called
control elements, possessing piecewise linear element
equations of generalized resistive type. We use a max-
min form of these equations and their regularized ab-
solute value representation. We perform tests on a
number of realistic networks and show the stability of
the algorithm.
2 GENERALIZED RESISTIVE
SYSTEMS
We will consider systems of the form:
∑
e
I
ne
Q
e
= Q
(s)
n
, f
e
(P
in
,P
out
,Q
e
) = 0, (2)
where indices n = 1...N denote the nodes and e =
1...E the edges of the network graph, I
ne
is an inci-
dence matrix of the graph, Q
e
are flows through the
edges, Q
(s)
n
are source/sink contributions, localized in
supply/exit nodes, P
n
are nodal variables (pressure,
voltage, etc. – dependent on the context). The ele-
ment equations possess derivatives of the signature:
∂ f
e
/∂P
in
> 0, ∂ f
e
/∂P
out
< 0, (3)
∂ f
e
/∂Q
e
< 0.
The Jacobi matrix of the system has the form:
J =

0 I
˜
I
T
−R

, (4)
where
˜
I contains derivatives ∂ f
e
/∂P
n
of the element
equations and R is a diagonal matrix containing posi-
tive entries −∂ f
e
/∂Q
e
. Note that
˜
I has the same pat-
tern and the signs of entries as I. After elementary
transformations we have
detJ =
∏
e
(−R
e
) detIR
−1
˜
I
T
. (5)
The matrix
˜
L = IR
−1
˜
I
T
has sizes N × N and pos-
sesses a pattern and signs of entries identical with the
Laplacian matrix L = I I
T
. For the graphs contain-
ing several connected components both matrices have
a block-diagonal structure, where we can select one
block and further consider L,
˜
L corresponding to one
connected component. Both matrices have one zero
eigenvalue, corresponding to an obvious eigenvector
v = (1...1). The difference between L and
˜
L is that
L is symmetric and v is its left and right eigenvector,
while
˜
L is not symmetric and v is its left eigenvector.
This degeneracy is related to the structure of the in-
cidence matrix, i.e., every column of I contains only
two entries +1 and −1, so that the sum of entries in
every column vanishes.
A Globally Convergent Method for Generalized Resistive Systems and its Application to Stationary Problems in Gas Transport Networks
65

Are there any other vectors annulating
˜
L from the
left?
(v
˜
L)
n
0
=
∑
n,e
v
n
I
ne
R
−1
e
˜
I
n
0
e
= v
n
0
d
n
0
−
∑
n6=n
0
v
n
u
nn
0
= 0, (6)
d
n
0
=
∑
e
I
n
0
e
R
−1
e
˜
I
n
0
e
, u
nn
0
= −
∑
e
I
ne
R
−1
e
˜
I
n
0
e
.
Here we separate diagonal and non-diagonal contri-
butions and see from the sign patterns of I and
˜
I that
d
n
0
> 0, while u
nn
0
> 0 if n 6= n
0
are connected by an
edge and u
nn
0
= 0 otherwise. Also, from the annula-
tion of the matrix by v = (1...1) we have
d
n
0
=
∑
n6=n
0
u
nn
0
. (7)
Thus we have
∑
n6=n
0
(v
n
0
− v
n
)u
nn
0
= 0. (8)
Let us consider a maximal entry v
n
0
≥ v
n
for all n 6= n
0
.
The above condition gets LCP form, satisfied only if
(v
n
0
− v
n
)u
nn
0
= 0, (9)
i.e., for connected nodes v
n
0
= v
n
must be satisfied.
In this way the maximal value propagates to all con-
nected nodes in the graph, leading to the conclusion
that v
n
= Const is the only solution. Therefore, only
the vectors proportional to v = (1...1) are the left an-
nulators of
˜
L.
To eliminate the degeneracy, one has to remove (at
least) one Kirchhoff equation in the connected com-
ponent and fix the corresponding nodal variable to
a constant value. Physically this corresponds to the
creation of an entry point for the flow and setting a
pressure (voltage, etc.) value there: P
n
= Const for
n ∈ Pset. On matrix level it corresponds to the re-
moval of (at least) one row from the matrices I,
˜
I and
the corresponding row and column from L,
˜
L. Search-
ing the left annulators of
˜
L, we obtain a similar sys-
tem but with v
n
= 0 for n ∈ Pset and the equations
with n
0
6∈ Pset. We come to the conclusion that the
maximal value v
n
0
propagates to all connected nodes
6∈ Pset and to their neighbours ∈ Pset, where v
n
= 0
is set. Thus, the maximal value v
n
0
= 0. Similarly,
considering the propagation of the minimal value, we
also have v
n
0
= 0. Therefore, v = 0 is the only solu-
tion, the matrix
˜
L does not have non-zero annulators
and det
˜
L 6= 0.
Further, it is easy to show that det
˜
L > 0. The
standard Laplacian matrix L is symmetric and posi-
tive semi-definite. Removing the Pset nodes makes it
strictly positive definite, so that det L > 0. Consider-
ing a linear homotopy
ˆ
I(λ) = I(1 − λ) +
˜
Iλ,
ˆ
R(λ) = 1 · (1 − λ) + Rλ,
ˆ
L(λ) = I
ˆ
R
−1
(λ)
ˆ
I
T
(λ), (10)
ˆ
L(0) = L,
ˆ
L(1) =
˜
L,
during the transition λ ∈ [0,1] all matrices have the
same sign pattern as at the beginning and at the end
of the path. We know that det L > 0. If det
˜
L < 0,
we can find a point in between where det
ˆ
L(λ) = 0,
i.e., find a degenerate matrix in the considered class
of matrices, which, as we have just proven, does not
exist. Thus, det
˜
L > 0.
Finally, we conclude that detJ does not vanish
and has a sign (−1)
E
defined only by the number
of edges in the connected component. In particular,
when piecewise linear element equations are consid-
ered, detJ has the same sign in all pieces.
We note that “purely” resistive systems, with ele-
ment equations dependent on the difference of nodal
variables, form a special subclass of generalized resis-
tive systems, whose element equations can depend on
nodal variables separately. This special subclass cor-
responds to
˜
I = I and a symmetric Jacobi matrix. Our
main conclusion is that the generalized resistive sys-
tems can be treated in pretty the same way as resistive
ones, although their Jacobi matrix is not symmetric
anymore. Particularly, for piecewise linear systems
one can apply tracing algorithms from (Katzenelson,
1965; Chien and Kuh, 1976), providing convergence
in a finite number of steps. For non-linear systems one
can use a homotopic version of the algorithm (Allgo-
wer and Georg, 2003) together with other stabiliza-
tion strategies, such as backtracking line search (Press
et al., 1992) and its high-order versions (W
¨
achter and
Biegler, 2006). For piecewise smooth systems one
can use a combination of those:
Algorithm 3: Piecewise smooth tracing.
start from an arbitrary point x
0
;
take its image y
0
= f (x
0
);
connect y
0
with the origin y = 0
by a straight line;
select its homotopic subdivision {y
i
},
i = 0...k;
loop over i: solve the system f (x) = y
i
repeat until convergence:
update the Jacobi matrix;
perform Newton’s step;
if the solution leaves the piece:
stop at the border;
apply backtracking line search;
if still at the border:
proceed to the next piece;
end;
end.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
66

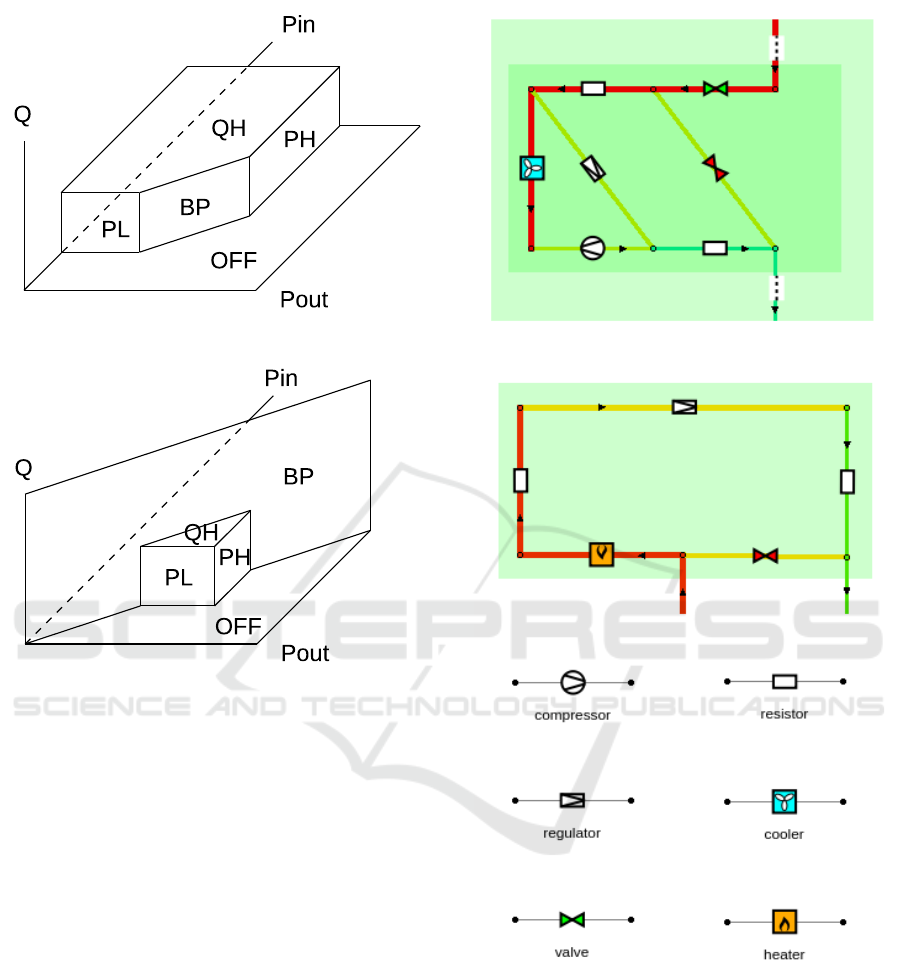
Figure 1: Control element diagrams. On the top: regulator,
on the bottom: compressor.
3 APPLICATION TO GAS
TRANSPORT NETWORKS
The simulation of the gas transport networks is per-
formed by the software Mynts (Multi-phYsics NeT-
work Simulator, www.scai.fraunhofer.de) developed
in our group. A small training network used here for
experiments is shown in Fig. 3. It contains 100 nodes,
111 pipes and other connecting elements, two Pset
sources, three Qset sinks. Detailed structure of com-
pressor and regulator stations is shown on Fig. 2. We
note that real life problems are much larger. In co-
operation with our partners we solve stationary and
transient problems for gas networks with thousands
of elements.
Stationary problems in gas transport networks are
described by a system (2) with element equations sat-
isfying the resistivity conditions ∇ f = (+ − −). Typ-
ical elements used in gas transport networks are listed
below.
Figure 2: Gas transport network simulation in Mynts. On
the top – closeup to a compressor station, on the middle
– closeup to a regulator station, on the bottom – elements
used.
Pipes: in the simplest case can be represented by a
quadratic resistive model (Mischner et al., 2011)
P
in
|P
in
| − P
out
|P
out
| = RQ|Q|, (11)
where P is a pressure, Q is a flow, R is a resistance
coefficient, depending on diameter, length and fric-
tion characteristics of the pipe. For realistic mod-
eling more complicated element equations can be
used, based on friction models by Nikuradze, Hofer
A Globally Convergent Method for Generalized Resistive Systems and its Application to Stationary Problems in Gas Transport Networks
67

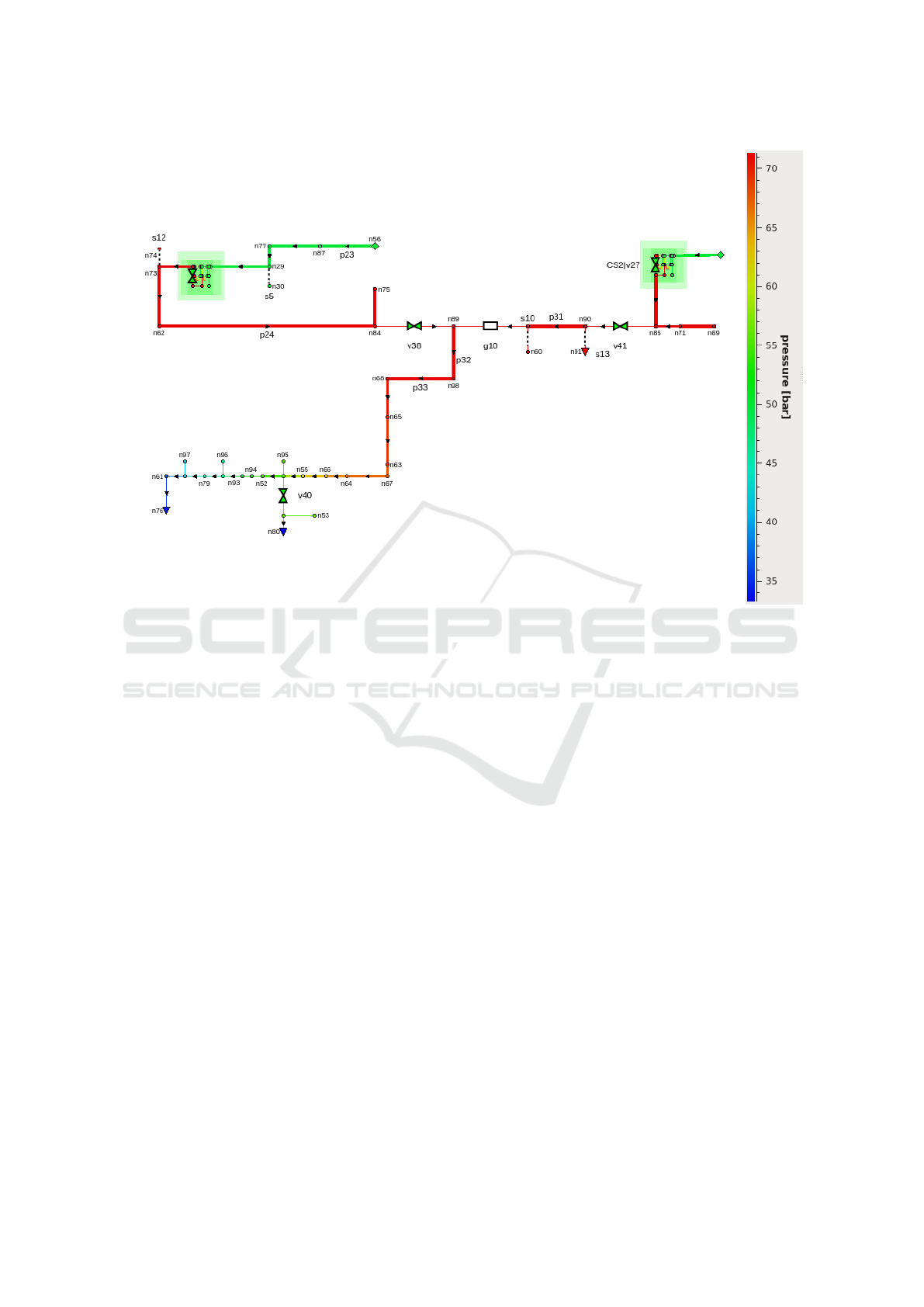
Figure 3: Gas transport network simulation in Mynts (cont’d). The network topology with the resulting pressure distribution,
shown by color.
or Prandtl-Colebrook (Mischner et al., 2011; Schmidt
et al., 2015).
Resistors: physically correspond to short pipe seg-
ments, described by the same quadratic formula, with
R specified explicitly.
Valves: simple switching elements
P
in
= P
out
(open); (12)
Q = 0 (closed).
Regulators: control elements dropping pressure,
physically correspond to a variable resistor, whose
value is automatically adjusted to satisfy one of
the following control goals: a fixed output pressure
(SPO), a fixed input pressure (SPI) or a fixed flow
value (SM). Being combined with the given upper
and lower bounds: PH = min(SPO, POMAX), PL =
max(SPI,PIMIN), QH = min(SM,MMAX), the el-
ement equation defines a polyhedral surface shown
in Fig. 1, top. Here every face corresponds to the
best possible satisfaction of the control goal, e.g.,
P
out
= PH (typical for SPO-mode), Q = QH (typi-
cal for SM-mode), P
in
= P
out
(bypass BP, equivalent
to an open valve), Q = 0 (OFF, equivalent to a closed
valve), etc. Like any piecewise linear equation, it can
be represented in max-min form:
max(min(min(min(P
in
− PL,−P
out
+ PH),
−Q + QH), P
in
− P
out
),−Q) = 0. (13)
Compressors: control elements increasing pressure,
they also have a resistive equation, similar to a bat-
tery with internal resistance in electrotechnics. They
also can be configured to satisfy the control goals of
SPO, SPI and SM type. The element equation defines
a polyhedral surface shown in Fig. 1, bottom. The
corresponding max-min form is:
max(max(min(min(P
in
− PL,−P
out
+ PH),
−Q + QH), P
in
− P
out
),−Q) = 0. (14)
Nodal equations: relate additional nodal variables,
such as density ρ, temperature T etc., have the form
of a gas law
P = f (ρ,T, ...) or ρ = f
−1
(P,T, ...), (15)
using an approximation formula, such as AGA, Pa-
pay, ISO standard AGA8-DC92, etc. (Schmidt et al.,
2015; CES, 2010). The physical stability of the
medium requires that the functions f , f
−1
increase
monotonously w.r.t. the first argument, in this way
supporting the existence and uniqueness of a solution.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
68

In real scenarios further variables and equations
are added, describing temperature distribution, gas
composition, more detailed modeling of control ele-
ments, etc.
To provide a resistive property for all elements,
their equations should be properly regularized. In
pipe/resistor equations one needs to add a laminar
term εQ to the right hand side, where ε is a small pos-
itive constant. This term provides non-degeneracy of
the system and correct signature of the equation for
Q = 0. Also the ε(P
in
− P
out
) term should be added
to the left hand side to protect the system from sim-
ilar problems at P = 0. Note that the absolute value
function in the Q|Q| and P|P| terms has a different
meaning: Q|Q| provides the correct symmetry of the
equation in reversal of the flow direction, while P|P|
removes a fold in the mapping and provides the exis-
tence and uniqueness of a solution everywhere in the
space of variables, including the non-physical domain
P < 0. Although the physical solution cannot be lo-
cated in this domain, the tracing algorithm can wander
there on intermediate iterations. Also, as we see be-
low, this domain plays an important indicator role for
the solution of feasibility problems.
For valves and control elements one should also
introduce regularization terms to provide the resis-
tive signature for every face of the element equation.
Properly regularized equations have the form:
Valves:
P
in
− P
out
= εQ (open); (16)
Q = ε(P
in
− P
out
) (closed).
Regulators:
max(min(min(min(P
in
− εP
out
− εQ − PL, (17)
εP
in
− P
out
− εQ + PH),ε(P
in
− P
out
) − Q + QH),
P
in
− P
out
− εQ),ε(P
in
− P
out
) − Q) = 0.
Compressors:
max(max(min(min(P
in
− εP
out
− εQ − PL, (18)
εP
in
− P
out
− εQ + PH),ε(P
in
− P
out
) − Q + QH),
P
in
− P
out
− εQ),ε(P
in
− P
out
) − Q) = 0.
Here the max-min functions can be transformed to
an absolute value representation
max(x,y) = (x + y + |x − y|)/2, (19)
min(x,y) = (x + y − |x − y|)/2,
one can also use, for the absolute value function, its
smooth regularization:
|x|
ε
=
p
x
2
+ ε
2
. (20)
The obtained system belongs to the generalized
resistive type and, therefore, it always has a unique
solution. On the other hand, it can happen in real
scenarios that they do not have a solution. The de-
termination whether a solution for given conditions
exists represents a so-called feasibility problem. Usu-
ally solutions disappear when one requires too much
from the network, e.g., to transport a large amount of
gas through a long pipe system with only one supply
where Pset=10 bar and all compressors are switched
off. There is no physical solution for such a scenario,
while a solution of our generalized resistive system
will exist. This solution, however, will be located
in the non-physical domain, where some nodes have
negative pressure. This can be used as an indicator of
feasibility for the tested scenario.
Practically, observing the work of the algorithm,
we often see that a solution goes to the non-physical
domain, wandering there along complex trajectories.
Finally it either returns to the physical domain if the
problem is feasible or remains in the non-physical do-
main otherwise. Considering the solution as the func-
tion of a regularization parameter x
∗
(ε) and removing
the regularization ε → +0, we observe that the so-
lution for feasible problems will have a limit in the
physical domain, while for infeasible ones it either
has a limit in the non-physical domain or tends to in-
finity.
We note that ε-regularization is one possibility to
provide global convergence of the tracing algorithm.
The other possibility is a modification of the algo-
rithm described in (Chien and Kuh, 1976), making
it applicable also for degenerate Jacobi matrices en-
countered in bounded pieces. An investigation of this
possibility is part of our further plans.
We have implemented the tracing algorithm in a
test mode in our network simulator Mynts under the
option solver strategy=stable. Using a number of re-
alistic scenarios from our partners, we have com-
pared the performance of the algorithm vs. the op-
tion solver strategy=standard, representing a generic
Newton’s solver. The results of our comparison are
presented in Table 1. We see that the generic solver
provides worse convergence and diverges in certain
scenarios, while the tracing algorithm always con-
verges, in agreement with its theoretical property. In
these experiments we use the simplest version of the
tracing algorithm with a trivial homotopic subdivision
(k = 1) and the backtracking line search switched off.
We see that already this version provides convergence
in all considered scenarios. A study of the relation-
ship between the performance of the algorithm and
its homotopic and line search settings is planned.
A Globally Convergent Method for Generalized Resistive Systems and its Application to Stationary Problems in Gas Transport Networks
69

Table 1: Gas transport network simulation, comparison of the two algorithms. For every network two scenarios are considered,
different by numerical values of Pset, Qset and compressor/regulator SM, SPO settings. Divergent cases are marked as ’div’.
Timings are given for a 3 GHz Intel i7 CPU.
solver strategy
network nodes edges scenario standard stable feasible?
iterations time, sec iterations time, sec
N1 100 111 S1 3 0.01 2 0.01 Y
S2 57 0.17 4 0.02 Y
N2 931 1047 S1 11 0.27 8 0.25 Y
S2 div – 58 1.7 N
N3 4466 5362 S1 div – 13 2.0 Y
S2 47 6.5 14 1.9 Y
4 CONCLUSIONS
We have considered generalized resistive systems,
comprising linear Kirchhoff equations and non-linear
element equations of the form f (P
in
,P
out
,Q) = 0, pos-
sessing a signature ∇ f = (+ − −). For such systems
we have proven the global non-degeneracy of the Ja-
cobi matrix and the applicability of globally conver-
gent tracing algorithms. Considering stationary prob-
lems in gas transport networks, we have shown that
the underlying equations can be rewritten in general-
ized resistive form. The piecewise smooth tracing al-
gorithm has been applied to several realistic networks
and its performance has been compared with a generic
Newton solver. The generic solver provides slower
convergence and fails in certain scenarios. The trac-
ing algorithm has better performance and converges
for all scenarios.
REFERENCES
Allgower, E. L. and Georg, K. (2003). Introduction to Nu-
merical Continuation Methods. SIAM, Philadelphia.
Bulgakov, E. N. et al. (2005). Electric circuit networks
equivalent to chaotic quantum billiards. Physical Re-
view E, 71(4):046205.
CES (2010). DIN EN ISO 12213-2: Natural Gas – Calcula-
tion of compression factor. European Committee for
Standartization.
Chien, M. J. and Kuh, E. S. (1976). Solving piecewise-
linear equations for resistive networks. International
Journal of Circuit Theory and Applications, 4(1):1–
24.
Griewank, A. et al. (2015). Solving piecewise linear sys-
tems in abs-normal form. Linear Algebra and its Ap-
plications, (471):500–530.
Katzenelson, J. (1965). An algorithm for solving nonlin-
ear resistor networks. Bell System Technical Journal,
44(8):1605 – 1620.
Kron, G. (1945). Electric Circuit Models of the Schr
¨
odinger
Equation. Phys. Rev, 67(1-2):39–43.
Mischner, J. et al. (2011). Systemplanerische Grundla-
gen der Gasversorgung. Oldenbourg Industrieverlag
GmbH.
Press, W. H. et al. (1992). Numerical Recipes in C. Cam-
bridge University Press, 2nd edition.
Schmidt, M. et al. (2015). High detail stationary optimiza-
tion models for gas networks. Optimization and Engi-
neering, 16(1):131–164.
Shai, O. (2001). The duality relation between mecha-
nisms and trusses. Mechanism and Machine Theory,
36(3):343–369.
Tonti, E. (2013). The Mathematical Structure of Classical
and Relativistic Physics. Birkh
¨
auser Springer.
W
¨
achter, A. and Biegler, L. T. (2006). On the implemen-
tation of an interior-point filter line-search algorithm
for large-scale nonlinear programming. Mathematical
Programming, 106(1):25–57.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
70