A WSN-based, RSS-driven, Real-time Location Tracking System

for Independent Living Facilities

Pawel Gburzynski

1,2,4

, Wlodek Olesinski

and Jasmien Van Vooren

Vistula University, Computer Science, Warsaw, Poland

Olsonet Communications Corporation, Ottawa, Ontario, Canada

Alphatronics, Lokeren, Belgium

Sendronet, Wierzchowo, Poland

Keywords:

Wireless Sensor Networks, Real-time Location Tracking, Ad-hoc Networking.

Abstract:

We present an indoor location tracking system (RTLS) based on a wireless sensor network (WSN) where

the received signal strength (RSS) readings collected by immobile nodes (Pegs) from mobile (tracked) nodes

(Tags) are translated into location estimates for the Tags. The process employs a database of samples pre-

viously collected from known locations; thus, the scheme falls into the category of proﬁle-based solutions,

with RSS readings being the only kind of input to the estimator. Compared to other schemes hinged on the

same general idea, the novelty of our approach consists in systematically taking advantage of multiple transmit

power levels at the Tags. This allows us to effectively emulate RFID-type of operation, when a nearby Peg

can authoritatively identify the location by perceiving a weak signal from the Tag (indicative of the Tag’s im-

mediate proximity), while otherwise falling back to elaborate ﬁtting of multiple readings (collected by several

Pegs) to produce a (possibly approximate) location estimate. The location service of our network is an add

on to its other duties which consist in providing connectivity within an independent living (IL) facility for the

purpose of inconspicuously monitoring the patients, detecting anomalies, signaling alarms, and so on.

1 INTRODUCTION

The work reported in this paper is the offspring of

our earlier study (Haque et al., 2009) evolved into a

collaborative effort undertaken by Olsonet

and Al-

phatronics

aimed at creating a comprehensive WSN

to outﬁt a number of IL facilities in Belgium. The

primary goal of the WSN is to provide an an open-

ended, low-bandwidth, self-contained, ﬂexible com-

munication platform for detecting and signaling vari-

ous events, usually related to the well being of the IL

patients, e.g., see (Boers et al., 2010).

1.1 Previous Work

Early attempts to transform RSS readings into loca-

tions (Christ et al., 1993) were based on interpreting

RSS as a function of distance between the transmit-

ter and the receiver. While some generic models of

this kind have been claimed to well capture the statis-

http://www.olsonet.com

http://www.alphatronics.be

tics of “typical” indoor environments, e.g., for simu-

lation (Mart´ınez-Sala et al., 2005), their blanket ap-

plication in RTLS has not met with success. Thus, if

used at all, they were augmented with some heuristics

or tweaks, accounting at least for some standard ob-

stacles of a permanent nature, e.g., walls (Christ et al.,

1993).

The whimsical nature of RSS indications inspired

approaches based on other features of RF signals.

The most popular among them can be categorized

as: Time of Flight (TOF), Time of Arrival (TOA),

Time Difference of Arrival (TDOA), Angle of Ar-

rival (AOA), and Near-Field Electromagnetic Rang-

ing (NFER). The ﬁrst three among them (Deak et al.,

2012) require a precise measurement of the propaga-

tion time between the sender and the receiver. With

AOA, the measured entity is the angle from the re-

ceiver towards the sender; the scheme is often com-

bined with TOA (Venkatraman and Caffery Jr, 2004)

to mitigate the impact of obstacles. The NFER tech-

nique (Schantz, 2007) relies on measuring the differ-

ence in phase between the electric and magnetic com-

ponents of the electromagnetic ﬁeld (at the receiver)

Gburzynski, P., Olesinski, W. and Vooren, J.

A WSN-based, RSS-driven, Real-time Location Tracking System for Independent Living Facilities.

DOI: 10.5220/0005959000640071

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 1: DCNET, pages 64-71

ISBN: 978-989-758-196-0

which tends to depend on the distance.

All the above techniquesrequire speciﬁc hardware

features which are not needed for “normal” RF com-

munication and often get in the way. This basically

means that an RTLS must be devised and deployed

as a separate system using its own dedicated hard-

ware. For example, NFER devices operate within the

AM band (530-1710 kHz) which is exotic from the

viewpoint of contemporary communication network-

ing. The most successful time/angle-based devices

operate in Ultra Wide Band (UWB) (Kempke et al.,

2015), to mitigate the effect of reﬂections, and, at

least in our experiments, exhibit signiﬁcantly lower

communication range (combined with a much higher

power consumption) compared to popular ISM-based

modules. All of them work reliably within LOS en-

vironments, where they are truly unbeatable in terms

of accuracy, but any obstacles (especially those caus-

ing unbypassable reﬂectons) tend to signiﬁcantly af-

fect the readings.

1.2 The Prerequisites and the Problem

The WSN constituting the basis for our system con-

sists of two types of nodes which will be referred to

as Tags and Pegs (Gburzy´nski and Olesi´nski, 2008).

Pegs are the anchors, i.e., their locations are ba-

sically ﬁxed, while Tags are mobile. Both node

types are built around the same RF module which

is CC430F6137 by Texas Instruments (Texas Instru-

ments, 2014). The device operates within the ISM

band (which is 816 MHz for the system at hand).

The Pegs jointly form the actual ad-hoc net-

work whereby (relevant) packets are forwarded, us-

ing TARP (Gburzy´nski et al., 2007), to a central sink

dubbed the master. The nominal baud rate for RF-

communication is 38,400 bps. The maximum (pay-

load) packet length is 54 bytes. The master interacts

with the OSS over a USB connection to a workstation

computer. A Tag communicates with the system via

Pegs.

Unlike (Haque et al., 2009), by location we do not

understand a point, say in 3-d, to be pinpointed with

some desirable accuracy, but a named area (or space)

whose size and shape generally depend on the con-

text. For example, its granularity may correspond to a

room, or even an apartment or a corridor, if it happens

to be satisfactory from the viewpoint of the operator.

Generally, the system is not expected to be 100% re-

liable. In particular, it may offer a number of alter-

native (suspect) locations ranking them according to

some measure of likelihood.

Note that the above assumptions shed a new light

on the comparison of the RSS-based approach to lo-

cation tracking with the other techniques mentioned

in Sec. 1.1. For example, if we switched to a TOA-

capable RF-module, we would not be able to take the

full advantage of its capability, because the applica-

tion where such a device truly excels, i.e., locating the

Tag precisely within a (potentially large) room outﬁt-

ted with several (at least three, and preferably four)

anchors-Pegs deployed within the Tag’s LOS (say, in

the corners at the ceiling), is of no interest to us. In-

stead, we want to be able to tell apart the different

rooms (or blocks of rooms) for which the TOA ap-

proach doesn’t work too well, because of the impos-

sibility of LOS communication.

2 THE TRACKING SYSTEM

A tracked Tag emits at its discretion so-called location

bursts which are series of short packets sent back-to-

back at different power levels. In the present system,

a location burst consists of 32 packets, 4 packets per

each of eight discrete transmit power levels numbered

0 through 7. Any Peg receiving any packets of a burst

prepares a location report and expedites it to the mas-

ter.

The transmit power levels have been calibrated ex-

perimentally, such that the perceived difference be-

tween two adjacent levels is about 5 dB. The value of

RSS directly translates into the received power level

in dBm quantized into steps of 0.5 dBm (plus some

ﬁxed offset). We do not assume that the location

bursts are issued at any speciﬁc intervals. Generally,

those intervals can be long, so we do not incorpo-

rate history (previous estimates) into the tracking al-

gorithm. It is obvious that making the bursts periodic

(and frequent) and accounting for the history of recent

estimates will tend to improve the accuracy of estima-

tion. For example, (Ni et al., 2004) discuss a remark-

ably accurate scheme achieved with just one anchor

node (a WiFi access point) plus some proﬁling, some

modeling, and a rather heavy reliance on the history

of previous estimates. Another possibility is to apply

prediction models for trafﬁc (Cho and Kwon, 2016)

which, considering the speciﬁcs of the target environ-

ment, is likely to further reduce the uncertainty in po-

sition. This work has been left as a natural goal for

the future.

The only relevant kind of data arriving at the loca-

tion server is a sequence of burst reports from Pegs.

Formally, a report is a 4-tuple R = (P,T,r,V) where

P is the Peg Id, T is the Tag Id, r is a by-Tag serial

number identifying the burst, and V = (v

,. .. ,v

) is

the RSS vector consisting of eight single-byte values

representing the averaged RSS readings for the eight

A WSN-based, RSS-driven, Real-time Location Tracking System for Independent Living Facilities

power levels (note that a Peg may receive up to four

packets per level). A value of zero (which can never

be a legitimate RSS reading) means that no packets

corresponding to the given power level have made it

to the Peg.

2.1 Proﬁling

The tracking is driven by a database of samples col-

lected from known locations. For this, the area is pro-

ﬁled and the reports collected during this process are

stored in the database along with their locations. Dur-

ing the actual tracking, the location reports are com-

pared against the proﬁle samples. Roughly speaking,

the Tag’s location is estimated as the one attributed

to those proﬁle samples from the database that best

match the tracking reports.

Formally, locations are identiﬁed by numbers re-

ferred to as internal location identiﬁers. The OSS is

responsible for mapping those internal identiﬁers to

external locations, i.e., descriptors presented to the

human operator. A single external location may cor-

respond to a number of internal locations acting as

their union. For example, partitioning a geometri-

cally compound location into smaller (regular) frag-

ments may lead to a simpler, less complex computa-

tionally, and more representative (reliable) coverage

of the smaller subareas with their individual sets of

samples. Also, overlapping internal locations may

represent the same area sampled in different ways,

e.g., as to capture some modal feature of the Tag: its

particular elevation above the ﬂoor, orientation, etc.

The aim of the proﬁling procedure is to collect

samples from known (internal) locations. The way

the server guesses at the location of a tracked Tag

(Sec. 2.2) suggests these recommendations for sam-

ple collection.

1. The (internal) locations should be reasonably sim-

ple, preferably rectangular and close to squares.

2. The number of samples per (internal) location

need not be large, but the samples should be com-

plete and reliable; consequently, it makes sense to

combine/average multiple samples taken from the

same point of a given location.

The server offers hooks to facilitate proﬁling. Having

moved to the point from where a sample is to be col-

lected, the user anchors the Tag. This operation tells

the server to assume that any burst reports referring

to the Tag should now be attributed to a sample. The

sample is identiﬁed by the location Id and the collec-

tion point Id, the latter being a location-relative mark

whose purpose is to tell apart different samples col-

lected from the same location. A button press on the

Tag will trigger a location burst. A report from that

burst arriving at the server will be added to the sam-

ple. Multiple reports from the same Peg are merged,

i.e., the RSS vector entries of the sample are averaged

using this formula:

i( j)

= v

× α+ v

i( j−1)

× (1− α) (1)

where v

i( j)

is the updated value of entry i in the av-

eraged RSS vector, v

i( j−1)

is the previous value of

that entry, v

is the new reading (from the newly re-

ceived report), and α is a parameter (with the default

value of 0.3). The update does not occur when v

= 0,

i.e., the report has no RSS value for the given power

level. This exponential moving average ensures that

new samples tend to override old ones, so previously

proﬁled locations can be easily (and selectively) re-

proﬁled later.

Formally, a sample is a triplet S =

(L,s,{P

}

k−1

i=0

) where L is the (internal) loca-

tion identiﬁer, s is the sample identiﬁer (relating

to the collection point within the location), and the

third element is the set of pairs: Peg Id (P

) and

the corresponding RSS vector (V

), representing the

burst reports that have contributed to the sample (k is

the number of different Pegs that have received the

bursts).

2.2 The Estimation Algorithm

The server stashes the arriving burst reports on a per-

Tag basis, aggregating them into a tracking set, i.e.,

sufﬁciently many reports (for the given Tag) to use

them for location estimation. A stashed report is time-

stamped with its arrival time.

Let us focus on some Tag T. Suppose that a new

report R = (P,T,r,V) arrives at the server at time t.

The server examines the current set of stashed reports

for T and, for each report R

= (P

,T,r

) performs

these actions:

1. Let t

be the time stamp of R

. If r

6= r andt

+δ

t, then R

is deemed obsolete and discarded from

the stash. The default value of δ

is 4 seconds.

2. If P

= P, then the new report augments the

stashed one. The elements of V

are updated in

according to formula 1, the time stamp of R

refreshed to t, the new report R is discarded. Then

the next report from the stash is taken until all the

reports have been examined.

3. If all stashed reports have been processed, and P

hasn’t matched any P

in step 2, the new reading

is added to the stash with time stamp t.

After completing the above loop, the server is ready to

attempt a location estimation, provided that the stash

DCNET 2016 - International Conference on Data Communication Networking

contains at least K = 3 reports. As the server never

knows when the last report for a burst is going to ar-

rive, it delays the attempt for δ

= 3 seconds. The

estimation procedure is described below.

We start with the tracking set, i.e., the current col-

lection of stashed reports {R

}

M− 1

i=0

, where M is the set

size (M ≥ K) and R

= (P

,T,r

). Let v

i,l

denote

the l-th element of vector V

. For each power level

l, 0 ≤ l < 8, we construct U

as the set of 4-tuples

) such that v

are the three largest elements



i,l



, over all i, 0 ≤ i < M. Then we discard all

elements from U

where v

= 0. Note that U

con-

sists of at most three elements and it can be empty. In

plain words, for each of the eight power levels, we se-

lect from all the stashed reports three with the largest

RSS readings, along with their associated Pegs.

Subsequently, the estimator executes a loop in-

dexed by the power level l starting at l = 0 (the lowest

level) and going up to 7. At any iteration, the estima-

tor maintains the current set of candidate locations C

consisting of pairs (L,r), where L is a location and r

is its inverse rank (or badness). The set is initialized

to “all locations” with the identical ranks of 0. Then

we proceed as follows.

1. Consider iteration l. Its objective is to calculate

a set of candidate locations C

with ranks based

solely on U

. Then the two sets, C and C

, are in-

tersected and their ranks combined. The intersec-

tion will possibly trim down the set in size, while

the new ranks will diversify the likelihoods of the

locations still remaining in the set.

If U

is empty, then the iteration is skipped, i.e., C

is unaffected and carried over to the next iteration.

2. If U

is nonempty, then C

is determined as con-

sisting of those locations that have at least one

sample in the database that includes all the Pegs

from U

and a nonzero RSSI entry at level l for

each of those Pegs. The procedure for calculating

the ranks for C

is discussed below.

3. An attempt is made to intersect C

with the run-

ning set C. If the intersection is empty (which will

also happen when C

is empty), the loop is exited

with the last nonempty C. Otherwise, C is set to

the intersection. The new ranks (for those loca-

tions that remain in C) are calculated as the sum

of the old ones and the new ones (from C

When the loop is terminated, the locations in C are

sorted in the inverse order of their ranks and returned

as the location estimate.

A close match to some samples on low power lev-

els is indicative of proximity to the corresponding

Pegs, so it can be used a reliable shortcut for esti-

mating the Tag’s location. In the most advantageous

case, there will be just one location selected this way,

approaching (passive) RFID-type operation. Should

the identiﬁcation by low power levels turn out to be

imperfect, then: 1) the higher levels may help the es-

timator trim out some locations, 2) a subtler compar-

ison of the reports to database samples will rank the

candidates, thus offering grounds for selection.

The number of elements in nonempty U

can 1, 2,

or 3. In the last case,U

can be interpreted as a point in

3-space. Thus we deal with one point q obtained from

and a set of points Q obtained from the database

samples (one point per sample) selected in step 2 of

the above loop. Those samples are grouped by their

locations. Let Q

∈ Q be the subset of Q containing

all those samples selected in step 2 of the algorithm

that are attributed to location L. The rank of location

L is calculated as the Euclidean distance from q to the

minimum convexhull encompassing the points in Q

With the above approach, a sample, including the

tracking set, is interpreted as a point in some simple

metric space, so it makes sense to talk about the dis-

tance between a pair of samples. One can expect that

when we take two samples, from two different spots

of some location, the RSS readings of the Pegs ap-

pearing in both samples will differ, but as one moves

between the two spots, the transition between the vec-

tors (points) is likely to be smooth. Locally, in the best

of the possible worlds, the transition can be approx-

imated by a straight line connecting the two points,

especially if no better model is available. Given mul-

tiple samples referring to the same location, the lin-

ear approach to interpreting transitions among them

boils down to drawing a polyhedron connecting their

points. As, generally, there is more than one way to

draw such a polyhedron, the most natural representa-

tive of them all is the minimum convex hull encom-

passing all the points. Then, it makes sense to assume

that the interior of that hull represents in a certain way

the location covered by the samples.

The algorithm can be tuned through a number of

parameters. First, the original RSS values can be

rescaled via an interpolation table, e.g., to amplify dif-

ferences in large values (which are more indicative of

proximity to the Peg and, generally, more reliable).

Also, when combining the location ranks (step 3), the

ranks from different power levels can be multiplied by

different factors, e.g., to assign a higher importance to

higher levels.

Although Tags are built as fairly homogeneousde-

vices, some discrepancies in the RF properties of dif-

ferent specimens of Tags are unavoidable. This means

that RSS readings from different Tags obtained under

identical conditions may differ slightly. To compen-

sate for this, when calculating the distance between

A WSN-based, RSS-driven, Real-time Location Tracking System for Independent Living Facilities

the tracking point q and the convex hull of Q

, the

ranking algorithm may turn q into a segment and cal-

culate the distance from the segment to the hull. Sup-

pose that q = (x,y,z) The segment is obtained as the

set of points Q

= {(x+ t,y+ t, z+t)}, −ρ ≤ t ≤ ρ,

where ρ is the tolerance parameter settable on a per-

power-level basis. This simple trick assumes that any

ﬂuctuations in the RF characteristics translate into a

linear shift in the transmit power level. Note that

nonzero ρ will tend to blur the quality of location sep-

aration by hulls, so it has to be selected with care.

3 EXPERIMENTS

3.1 The Test System

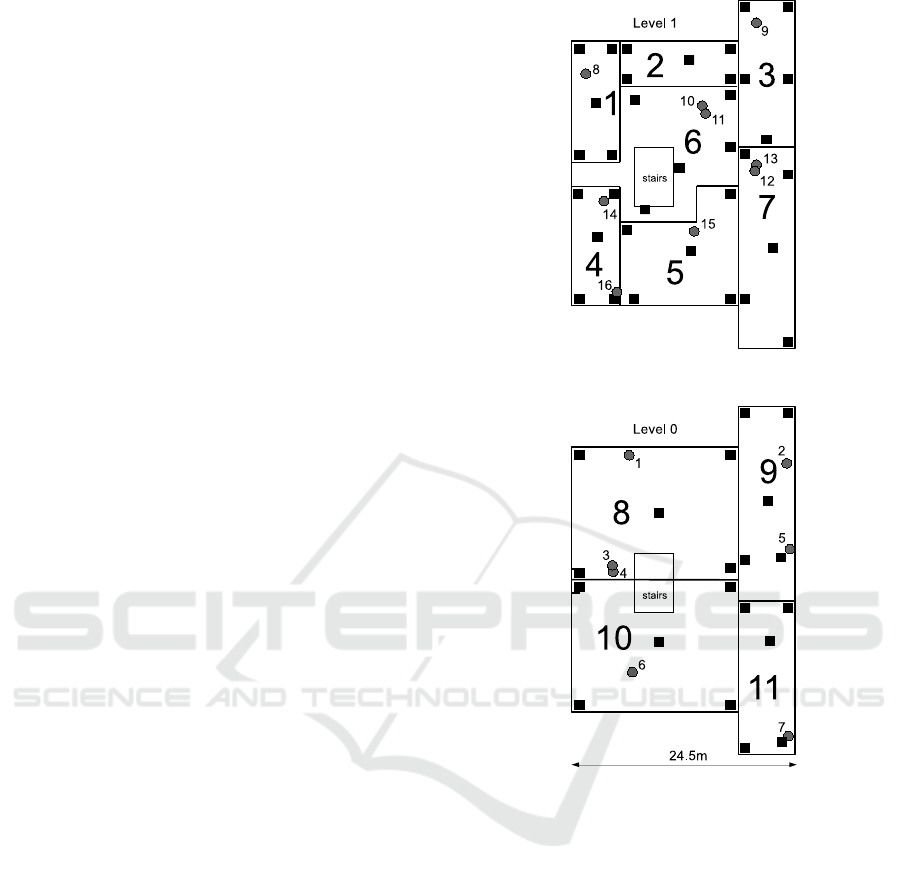
Fig. 1 illustrates a test deployment of our system. The

area consists of two ﬂoors: Level 1 comprising of-

ﬁce space with irregular rooms separated by walls,

and Level 0 including a large (exhibition) hall with

some (relatively small) meeting rooms on the south

side. The separation of the two levels into locations

does not strictly follow the division of the area by

walls. In particular, only some walls are drawn at

Level 1 (practically every location encompasses sev-

eral rooms), and the meeting rooms at Level 0 (for-

mally falling into location 10) are not drawn at all.

Also, the separation of the exhibition hall at Level 0

into locations 8 and 10 is purely imaginary. That was

intentional: we wanted to capture (also) the malicious

and fuzzy scenarios where the boundaries between lo-

cation are not clearly demarcated.

The gray circles in Fig. 1 denote the Pegs of our

WSN, 16 of them altogether. Their deployment, while

not completely accidental, is far from perfect. Note

that, e.g., in locations 6 and 8 there are pairs of Pegs

located very close together (Pegs 10, 11 and 3, 4). In

the test network, their deployment has been dictated

by the logistics of other tests carried out in parallel

with the preliminary tests of the location tracking ser-

vice (the co-located Pegs are devices of slightly dif-

ferent types). Consequently, some locations are better

covered than others. For example, the rather difﬁcult

(by its shape) location 11 has only one Peg (7) which,

to make the matters worse, is situated in a corner.

Thus, e.g., one cannot hope that location 11 will be al-

ways perfectly identiﬁed. All these problems should

be OK for tests, as long as we understand the limita-

tions.

Figure 1: The test deployment.

3.2 Proﬁling

The black squares in Fig. 1 mark the collection points

for samples. Within the conﬁnes of physical accessi-

bility, we have tried to collect samples from the four

corners of each location as well as from its center. We

shall refer to those points as NW, NE, SW, SE, and C.

Every such a point translates into one sample (being

an average of multiple takes (Sec. 2.1), yielding the

total of 55 samples. For illustration, here is the NW

sample for location 3:

12 0 0 0 0 0 67 75 83

11 0 0 0 0 67 75 78 80

8 0 0 0 0 0 0 82 82

9 82 93 103 112 124 135 148 157

10 0 0 0 0 71 72 87 95

5 0 0 0 0 72 75 80 90

13 0 0 0 0 0 64 74 83

2 0 0 0 69 78 84 92 99

DCNET 2016 - International Conference on Data Communication Networking

Each row consists of 9 values: the Peg Id followed by

eight RSS readings for the power levels from 0 to 7

(recall that 0 means “no reading”).

Owing to the inherent lack of reliability in wire-

less communication, and because the packets in loca-

tion bursts are neither acknowledged nor retransmit-

ted, any single report from a location burst can be in-

complete. We have to be prepared for this while track-

ing locations; however, the quality of proﬁled samples

is important, because a missing reading (or an entire

vector) may affect the interpretation of all tracking

sets. Consequently, a sample is only accepted if it

cannot be improved any more by subsequent bursts

issued from the given collection point, where by im-

provement we mean ﬁlling in an entry that was absent

after a previous take.

3.3 Tracking

A low-level RSS entry in a burst report can only be

nonzero when the Tag is relatively close to the Peg.

Thus, some areas are easier to recognize than others.

For example, here is a tracking set collected from the

SW quadrant of location 10:

3 72 77 95 103 113 124 137 145

5 0 0 0 0 0 70 86 96

6 91 95 106 117 128 136 149 157

7 0 0 0 0 80 92 104 109

8 0 0 0 0 0 80 97 103

10 0 0 0 71 78 92 103 109

12 0 0 0 0 0 67 84 93

13 0 0 65 76 90 96 110 115

16 82 94 101 112 124 133 147 154

For power level 0, the only three nonzero entries are

those for Pegs 3, 6, and 16. As it happens, there are

only two samples where 0-level RSS readings for all

those Pegs are present: SW and C for location 10.

Thus, a single location is found in the very ﬁrst itera-

tion, and the algorithm stops immediately. In fact, the

single report for Peg 6 would sufﬁce, because the two

samples are the only ones that include 0-level read-

ings for that Peg. If the report didn’t make it, then the

two remaining Pegs, 3 and 16, would do. For Peg 16,

there are matching samples in locations 4 (SE, SW,

C), 5 (SW, C), and 10 (SW, C), and for Peg 3, the

samples are in locations 8 (SW) and 10, the only lo-

cation shared by them being 10.

The answer produced by the algorithm is the last

set C (see Sec. 2.2) presented as a list sorted by the

location ranks. Recall that, as calculated by the algo-

rithm (after the last iteration), those ranks are reverse,

so they represent “badness” rather than “goodness” of

a location. Before presentation, they are transformed

into a positive measure of goodness as follows. Let

, i = 0,... ,n − 1 be the badness of the i-th location

from the list. Let a = (

∑

n−1

i=0

)/n be the average of

those values. Let g

= 1/(r

+ a) and S =

∑

n−1

i=0

. Set

= (g

/S) × 100 and return h

as the goodness mea-

sure of location i. Note that all h

values add to 100

(so they can be viewed as percentages) and lower val-

ues of r

translate into higher values of h

. For the

above (easy) estimation case, the server returns a triv-

ial list consisting of the pair (10, 100), i.e., location

10 has been identiﬁed as a single candidate with the

goodness rank of 100.

For a more challenging case, here is a tracking

set obtained from a Tag within the NE annex of lo-

cation 5:

5 0 0 0 0 0 70 88 94

7 0 0 0 0 0 83 97 103

9 0 0 0 0 0 0 68 76

10 0 0 0 0 0 0 63 75

12 0 0 0 0 73 85 97 106

13 0 0 62 71 83 96 105 109

16 0 0 0 0 0 75 80 96

The ﬁrst non-zero power level is 2 with a single report

(Peg 13). In the ﬁrst stage of the iteration for this

power level, all the samples with a reading for Peg 13

and power level 2 are identiﬁed. This brings in the

following list:

1 < 59> < 68> < 68>

2 < 65>

3 < 60> < 81>

4 < 69> < 69> < 58>

5 < 65> < 91> < 67> < 75> < 72>

6 < 61> < 78> < 72> < 72>

7 <109> <103> < 60> < 83> < 60>

8 < 65>

9 < 59> < 73>

10 < 69>

11 < 77> < 69> < 74> < 65>

The ﬁrst number in each line is the location identiﬁer;

following it, we see the list of points, each point en-

capsulated in <...>, corresponding to the RSS read-

ings for Peg 13 extracted from all those samples

where there was a reading for Peg 13 at level 2. As

there is a single Peg for power level 2 in the tracking

set, the points are one-dimensional, i.e., there is a sin-

gle value-coordinate for every point. We can see that

the discrimination of locations is far from perfect at

this stage: the set includes all locations, because each

of them has at least one sample with a reading for Peg

13 at power level 2. In particular, for locations 5 and

7, all ﬁve samples include such a reading, while loca-

tions 2, 8, and 10 offer just one sample each.

The iteration ranks the locations based on the min-

imum distance between the tracking point (the value

of its single coordinate is 62) to the convex hull en-

compassing the matched points from all the samples

for a given location. In this one-dimensional, degen-

erate case, the distance boils down to absolute differ-

ence, and the hull is simply the range of the respective

A WSN-based, RSS-driven, Real-time Location Tracking System for Independent Living Facilities

values. For power level 2, the algorithm assumes the

tolerance ρ (Sec. 2.2) of 8 units on either side which

means that the tracking point is turned into a segment

(range) from 54 to 70. This ranking gets us nowhere,

because all the ranks become zero in this metric.

For power level 3, we again see a single RSS entry

for the same Peg 13. The case is similar to the previ-

ous level (not surprisingly, all locations have samples

with entries for Peg 13 and power level 3) and, fol-

lowing the iteration, the ranks still remain at all ze-

ros. For iteration 4, there are two entries: 73 and 83,

for Pegs 12 and 13, respectively. The coordinates are

listed in the increasing order of Peg numbers, so their

interpretation as dimensions is unambiguous.

Still, all locations include entries for the two Pegs

(so they all still remain in the game) with the list of

points:

1 < 70 67> < 69 67> <81 65> <77 66> <77 88>

2 < 68 72> < 70 79>

3 < 68 74> < 98 101>

4 < 70 81> < 78 91>

5 < 78 80> < 98 109> <70 84> <69 76> <70 89>

6 < 70 81> < 76 70> <91 98> <78 85> <80 91>

7 <119 130> <108 120> <70 76> <84 103> <75 78>

8 < 76 81>

9 < 68 59> < 73 92>

10 < 73 69> < 81 81>

11 < 86 93> < 77 90> <81 85> <67 81>

This time the points are two-dimensional, so the hulls

amount to polygons. The tolerance ρ for power level

4 is 7, so we are looking at distances between the seg-

ment (73 + t,83+ t), −7 ≤ t ≤ 7 and the polygons

built of the above sets of points. This brings in the

non-trivial ranks: 5→1.0, 6→1.0, 11→1.0, 7→1.01,

4→1.6, 1→1.7, 9→2.4, 3→3.5, 8→3.74, 2→6.48,

10→7.48.

Power level 5 is the ﬁrst non-degenerate case with

all three coordinates present. The Pegs with the three

largest RSS readings are 7, 12, 13 and the tracking

point is (83, 85, 96). This time, the list of locations

with samples matching all three Pegs at power level

5 consists of 5, 6, 7, 8, 9, 10, 11, so these are the

locations carried over to the next iteration, their new

ranks being: 7→1.11, 11→1.71, 5→1.73, 8→4.72,

10→8.48, 6→10.27, 9→14.28. This set remains un-

changed through the remaining two iterations, how-

ever, their ranks change with the ﬁnal values (af-

ter iteration 7) being: 5→5.81, 11→8.0, 7→10.1,

10→10.02, 8→12.97, 6→33.04, 9→33.06. These

(badness) values are transformed into the follow-

ing (goodness) percentages: 5→19, 11→17, 10→16,

7→15, 8→14, 6→8, 9→8. The estimation does not

look extremely reliable, but the top candidate has

been guessed correctly.

A meaningful, quantiﬁed expression of the results

from our experiments is difﬁcult, mostly because the

location tracking problem has been deﬁned in qual-

itative terms: to have a satisfactory solution sepa-

rating named locations (potentially of various sizes

and shapes), with honest acceptance of failures in

those cases where the environment is predictably un-

friendly. This is in some contrast to our previous

work (Haque et al., 2009) where the problem was de-

ﬁned as estimating Cartesian coordinates of points in

2-space (so one could say by how far one missed the

target). In the present case, the success rate depends

on where the Tag is positioned within a givenlocation,

and it isn’t easy to express numerically how much

more important (or relevant) some of those spots are

than the others. For example, location 7 in our test

setup is poorly covered by Pegs, so estimates taken

from the bottom half of that location tend to be mostly

useless, being confused with locations 11, 5, and 10.

This is hardly unexpected. On the other hand, 95% of

attempts from location 6 succeed perfectly, with the

rate approaching 100% in the NE section, with only

slight deterioration as one gets closer to the bound-

aries. Notably, even location 2, which has no speciﬁc

Peg, is correctly identiﬁed (87% success rate in the

central area), although the results tend to be worse as

we move closer to the neighboring locations. This

is because the distribution of nearby Pegs provides

enough diversity and balance in their RSS readings to

transform those readings into meaningful (and mostly

correct) location ranks. As the success rates depend

on the position within the monitored locations, they

have to be weighted by the distribution of Tags in a

practical deployment (how likely the tracked person

or object is to be positioned close to the central area,

as opposed to its boundary) to be meaningful. Such

weights can be arrived at by inspecting room (apart-

ment) layouts, i.e., the arrangement of furniture, or

even suggesting layouts that will increase the likeli-

hood of successful positioning. Owing to the some-

what accidental distribution of Pegs in our test net-

work (not quite inspired by the location tracking prob-

lem) one can be sure that a better crafted design will

result in more reliable estimates.

4 CONCLUSIONS

We have presented a practical location tracking algo-

rithm to accompany a WSN deployable in an institu-

tion where people or objects need to be tracked with

the accuracy of rooms or apartments. The known

problem of poor representation of locations by RSS

readings is addressed in our solution in two ways.

First, by diversifying the transmit power levels of

packets in location bursts we attempt to emulate pas-

DCNET 2016 - International Conference on Data Communication Networking

sive RFIDs, thus providing for easy and reliable an-

swers in those situations where the Tag happens to

be located truly close to a nearby Peg. This is be-

cause an RSS reading obtained at the lowest trans-

mit power level is practically always indicative of im-

mediate proximity to the Tag, regardless of any ac-

cidental differences in the actual value. When the

low-power response appears ambiguous, we apply

an iterative ranking scheme whose role is to elimi-

nate some of the candidate locations and rank any re-

maining ones in the order of their assessed goodness.

Second, we admit simultaneous, multiple “planes”

of sampling whereby the same (logical) location can

be represented by its (not necessary disjoint) compo-

nents or aliases. By sampling such aliases under dif-

ferent RF propagation conditions we can incorporate

into the scheme potential plethora of dynamic distur-

bances that the monitored area can be exposed to in a

way affecting its representation by RSS samples.

The algorithm is parameterized and can be ex-

tended in several ways. The dimensionality of points

used for ranking locations can be increased, say to 4

or 5. We stopped at 3 in an attempt to strike a bal-

ance between the useful information and noise avail-

able within a tracking set consisting of many reports.

In its present version, the algorithm keeps no his-

tory of previous location estimates for a Tag. One can

easily think of affecting the location weights, espe-

cially in truly dubious cases, by higher ranks given

to the locations being close neighbors of those vis-

ited recently. This kind of enhancement may be easy

(and probablywill be incorporated into the production

version of the algorithm), but note that it redeﬁnes

the problem a bit. At present, the algorithm doesn’t

care about the geometry of locations, including their

spatial relationship. A sensible incorporation of his-

tory (or mobility prediction models) will require ad-

ditional input to the algorithm.

REFERENCES

Boers, N. M., Chodos, D., Gburzy´nski, P., Guirguis, L.,

Huang, J., Lederer, R., Liu, L., Nikolaidis, I., Sad-

owski, C., and Stroulia, E. (2010). The smart condo

project: services for independent living. E-Health, as-

sistive technologies and applications for assisted liv-

ing: challenges and solutions. IGI Global.

Cho, H. and Kwon, Y. (2016). RSS-based indoor localiza-

tion with PDR location tracking for wireless sensor

networks. AEU—International Journal of Electronics

and Communications, 70(3):250 – 256.

Christ, T. W., Godwin, P. A., and Lavigne, R. E. (1993). A

prison guard duress alarm location system. In Security

Technology, 1993. Security Technology, Proceedings.

Institute of Electrical and Electronics Engineers 1993

International Carnahan Conference on, pages 106–

116. IEEE.

Deak, G., Curran, K., and Condell, J. (2012). A survey of

active and passive indoor localisation systems. Com-

puter Communications, 35(16):1939–1954.

Gburzy´nski, P., Kaminska, B., and Olesi´nski, W. (2007). A

tiny and efﬁcient wireless ad-hoc protocol for low-cost

sensor networks. In Proceedings of DATE’07, pages

1562–1567, Nice, France.

Gburzy´nski, P. and Olesi´nski, W. (2008). On a practical ap-

proach to low-cost ad hoc wireless networking. Jour-

nal of Telecommunications and Information Technol-

ogy, 2008(1):29–42.

Haque, I., Nikolaidis, I., and Gburzy´nski, P. (2009). A

scheme for indoor localization through RF proﬁling.

In ICC’09, Dresden, Germany.

Kempke, B., Pannuto, P., and Dutta, P. (2015). Polypoint:

Guiding indoor quadrotors with ultra-wideband local-

ization. In Proceedings of the 2nd International Work-

shop on Hot Topics in Wireless, pages 16–20. ACM.

Mart´ınez-Sala, A., Molina-Garcia-Pardo, J.-M., Egea-

Ldpez, E., Vales-Alonso, J., Juan-Llacer, L., and

Garc´ıa-Haro, J. (2005). An accurate radio channel

model for wireless sensor networks simulation. Com-

munications and Networks, Journal of, 7(4):401–407.

Ni, L. M., Liu, Y., Lau, Y. C., and Patil, A. P. (2004).

LANDMARC: indoor location sensing using active

RFID. Wireless networks, 10(6):701–710.

Schantz, H. G. (2007). A real-time location system using

near-ﬁeld electromagnetic ranging. In Antennas and

Propagation Society International Symposium, 2007

IEEE, pages 3792–3795. IEEE.

Texas Instruments (2014). CC1100 Single Chip Low Cost

Low Power RF Transceiver. Document SWRS038D.

Venkatraman, S. and Caffery Jr, J. (2004). Hybrid

TOA/AOA techniques for mobile location in non-

line-of-sight environments. In Wireless Communica-

tions and Networking Conference, 2004. WCNC. 2004

IEEE, volume 1, pages 274–278. IEEE.

A WSN-based, RSS-driven, Real-time Location Tracking System for Independent Living Facilities