A Reduced Order Steering State Observer for Automated Steering
Control Functions
Enrico Raffone
FCA - Fiat Chrysler Automobiles, E/E & Connectivity Dept.,
Safety and Advanced Driver Assistance Systems – Control Systems, Strada Torino 50, 10043, Orbassano (TO), Italy
Keywords: Model based Estimation, Model Reduction, Kalman Filter, Singular Values, Least Square Model
Identification, Observability Matrix, Singular Perturbation Balanced Model Reduction, Automotive,
Steering System, Autonomous Vehicles.
Abstract: State observer design is one of the key technologies in research for autonomous vehicles, specifically the
unmanned control of the steering wheel. Currently, estimation algorithms design is one of the most
important challenges facing researchers in the field of intelligent transportation systems (ITS). In this paper
we present: mathematical model and dynamic response identification of electric power steering column by
least square identification experiments; observability analysis of identified models; model simplification via
mechanical approach and singular perturbation model reduction; and two reduced order steering Kalman
filter syntheses for estimation of steering column states and disturbances. The simulation and experimental
results conducted on a steering test bench executed in the FCA Technical Center show that designed
Kalman observers have good adaptability for steering wheel position control and safety aims. This can be
useful in intelligent vehicle path tracking in outdoor experiments.
1 INTRODUCTION
Recent developments of automated vehicle
technology have increased automation, efficiency,
and safety in this field. The development of
intelligent transportation systems (ITS) provides an
opportunity to apply advanced technologies to
systems and methods of transport for efficient,
comfortable, and safer modes of transportation (i.e.
highways, railways, inland waterways, airports,
ports, etc.). The actual implementation of full
automatic-steering control is one of most
challenging disciplines in the intelligent-vehicles
field. Perhaps this is the reason that it has a long way
to go before it comes on the market. Currently,
vehicle manufacturers focus on more mature
systems, especially for speed control, some of which
are already available on the market. There is,
however, a short-term focus to steering control, not
for unmanned lateral guidance, but as part of a
driving assistance system, i.e. Lane Departure
Warning system (also known as the Haptic Lane
Feedback system) in use on Fiat Chrysler
Automobiles. Automatic parking systems are other
steering-control applications that are already on the
market. All these systems exploit the preinstalled
vehicle electric power-steering system to
automatically manage the steering wheel for
different purposes.
Figure 1: Electric Power Steering simplified mechanical
model.
Automated steering control design is comprised
of two main ways to design controllers: imitating
human drivers or using dynamic models of cars and
methods based on linear control theory. The first
approach does not need detailed knowledge of car
dynamics, much in the way the driver of a car does
not. In this case, the algorithm key is the human
426
Raffone, E.
A Reduced Order Steering State Observer for Automated Steering Control Functions.
DOI: 10.5220/0005959704260432
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 426-432
ISBN: 978-989-758-198-4
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

driving behaviour. In the second approach, the
control-system approach, it requires detailed
knowledge of the dynamics of the car and in
particular of the steering column. This paper focuses
on the second approach, presenting solutions for
steering control of autonomous vehicle developed by
FCA Technical Center in steering control
applications with an EPS steering actuator.
Figure 2: Free body diagram of electric assist rack and
pinion steering system (Mills and Wagner, 2003).
2 ELECTRIC POWER STEERING
COLUMN MODEL
2.1 EPS Mathematical Non-linear
Model
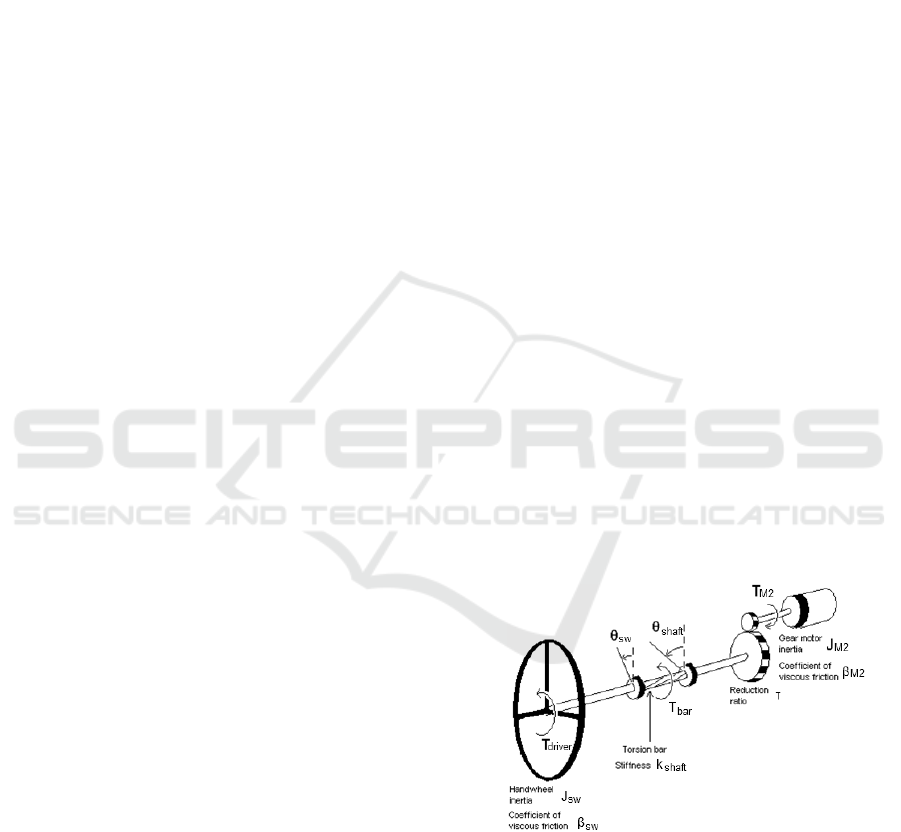
The lumped parameter mathematical model for the
high part of the steering column has been developed
to investigate the dynamic behavior of steering
column. In fig. 2 there is the free body diagram for
steering column line and in particular EPS unit
(Steering wheel, column, and assist motor
diagrams). The differential equation for the steering
wheel is:


driverswshaftshaftswshaftswsw
TkJ 


(1)
Now the shaft and gear-box rotational dynamics may
be represented as:

shaft
M
k
sw
shaftshaft
k
shaft
worm
J
shaft
J
 


2
*2
(2)
The dynamic equation for the motor angular
displacement may be expressed as:

CMshaftMMMMM
TTkJ 

22
*
2222

(3)
where 
M2
is the motor damping coefficient (see tab.
1 for other parameters).
Now, as said, the T
C
term is the only Coulombian
friction torque term in a mechanical configuration
without any link to the low part of steering column,
rack and pinion. With mechanical link, there is the
disturbance torque from wheels (e.g. M
z
) and, in
addition, inertial and friction torques of low steering
column.
The friction torque is modelled with a first order
non-linear model known as Dahl friction model
(Canudas-de-Wit et al., 2003). Dahl model was
developed for simulating control systems with
friction. The starting point of Dahl's model is the
stress-strain curve in classical solid mechanics; see
fig. 3. When subject to stress, the friction force
increases gradually until rupture occurs. Dahl
modelled the stress-strain curve by a differential
equation.
Figure 3: Identified Coulomb fiction nonlinear model.
Let  be the relative angular displacement,
dtd  

be the relative angular velocity, T the
friction torque, and T
c
the maximal friction force
(Coulombian torque). Dahl's model takes the form
(4),



















sgn1
c
T
T
d
dT
(4)
where σ is the stiffness coefficient (to be identified)
and
 is a parameter that determines the shape of the
stress-strain curve. The value
 = 1 is used in this
work and also most commonly used.
All the model parameters are known from
mechanical design of EPS unit except viscous
damping parameters (β) and Coulomb friction
nonlinear model parameters (σ e T
c
) which are
parameters identified by experimental data.
2.2 Least Square Model Identification
The identification activity used to define unknown
parameters from a described model has been
performed with an experimental test plan in
particular proving conditions, e.g. with steering
wheel locked or unlocked and without any
J
J
J





k
k
k
k
column
k
J
J
J





k
k
k
k
column
k
-80 -60 -40 -20 0 20 40 60 80
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Steering angle [deg]
Friction Torque [Nm]
Coulom b friction identified model
A Reduced Order Steering State Observer for Automated Steering Control Functions
427

mechanical link to rack and pinion steering system.
This activity phase is accomplished by minimizing
the least square error between model plant and
measurement. So given a model family:




|M
(5)
The parameters’ vector

, e.g.





mvol

, has
been estimated using least square error minimization
from real plant acquisitions

N
k
kk
uy
1
,

in the
admissible parameter set by minimizing the cost
function:




N
k
kN
N
J
1
2
1

(6)
Where
k

is the error between simulation and plant
acquisition at k
th
sampling time.
In fig. 4 there is an example of matching between
steering torque measured and simulated by identified
model with the same motor torque input, a sweep
with steering wheel locked. Then, a leave-one-out
cross-validation of presented identified model has
been performed in order to assess how the results of
identification will generalize the real behaviour of
steering unit.
Figure 4: EPS model matching.
2.3 EPS Mathematical Linear Model
Already seen non-linear model may be linearized by
eliminating Dahl frictional model. The frequency
response of linear EPS model from motor torque to
measured torque has been compared with frequency
response obtained by an FFT analysis of time history
data of the input and output (see fig. 5) in an
interesting matching between data and linear model.
The classical space state representation for EPS
linear model is:





uDxCy
dBuBxAx
d

(7)
where:


T
shaftMswshaftMsw
x 
22


;

T
measMsw
Ty
2
 
;


2M
Tu 
;

T
Csw
TTd 
and:





































000100
000010
000001
000
000
000
2
2*
22
2
*
2
*
2
2








wormshaft
shaft
wormshaft
shaft
wormshaft
shaft
MMM
M
sw
shaft
sw
shaft
sw
sw
JJ
kk
JJ
k
JJ
k
J
k
J
k
J
J
k
J
k
J
A
.0;
010000
001000
0000
;
0
0
0
0
1
0
0
0
0
0
0
1
;
0
0
0
0
1
0
22























































 D
kk
C
J
J
B
J
B
shaftshaft
M
sw
d
M
Figure 5: EPS bode diagram from linear model
(continuous line), from FFT data analysis (dotted line).
Table 1: Units for EPS mathematical model.
Symbol Description Unit
J
s
w
Steering wheel moment of inertia [Kgm
2
]
β
s
w
Steering wheel viscous damping [Nms/rad]
k
s
ha
f
t
Torsion bar spring rate [Nm/rad]
k
column
Steering column stiffness [Nm/rad]
k
*
Motor-gear coupling stiffness [Nm/rad]
β
M
2
Motor viscous damping [Nms/rad]
J
m
Motor rotor moment of inertia [Kgm
2
]
J
s
ha
f
t
Gear-box wheel moment of inertia [Kgm
2
]
J
worm
Gear-box worm moment of inertia [Kgm
2
]
Τ Gear-box ratio -
14 14.2 14.4 14.6 14.8 15 15.2 15.4 15.6 15.8 16
-10
-8
-6
-4
-2
0
2
4
6
8
10
time [s]
torque [Nm]
Sim
Acq
0 5 10 15 20 25 30 35 40 45 50 55
-10
-8
-6
-4
-2
0
2
4
6
8
10
Matching Torque measured vs simulation
time [s]
torque [Nm]
Sim
Acq
Bode Diagram
Frequency (Hz)
10
-1
10
0
10
1
10
2
-360
-270
-180
-90
0
90
Phase (deg)
-100
-50
0
50
From: Tm To: Tmeas
Magnitude (dB)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
428

3 EPS MODEL OBSERVABILITY
3.1 Observability Vs Plant Measures
Observability, in control theory, is a measure of how
well internal states of a system can be inferred by
knowledge of its external outputs. Less formally,
this means that from the system outputs it is possible
to determine the behavior of the entire system. If a
system is not observable, this means the current
values of some of its states cannot be determined
through output sensors. So, an interesting thing
about EPS mechatronic architecture is to understand
the level of observability in front of minimum
number of plant measures.
Figure 6: EPS mechanical outline.
The EPS column mechanical outline can be
modelled as in fig. 6, where according to C measures
matrix in (7) the available measures are: steering
flywheel position (φ
1
), EPS motor flywheel position
(φ
3
) and torque measure T
bar
as difference between
gear box output shaft (φ
2
) and steering wheel
position (φ
1
) multiplied for known torsion bar
stiffness (K
1
).
From the classical analysis of observability
matrix rank (see tab. 2), it’s clear that only two of
three measures are fundamental for full observability
of system modes. The presence of three different
measurements is principally due to safety reasons. A
single measure for steering or motor flywheel
position is enough to observe five of six states.
Measured torque T
bar
, seen as a relative position
difference gives a reduced level of observability,
only four states.
Table 2: EPS system observability vs plant measures.
T
bar
θ
sw
θ
M2
Observability Order
- - - 0
- -

5
-

- 5
-
 
6

- - 4

-

6
 
- 6
  
6
3.2 Spectral Decomposition for Linear
Model
The spectral decomposition of state matrix A is a
simple method to know all dynamics in the real
plant. In tab. 3, the eigenvalues for our linear model,
it’s clear that the model plant is characterized by the
presence of very low and high frequency terms.
Table 3: EPS linear model eigenvalues.
Eigenvalues Freq. [Hz]
-0.491074732452 + 706.750702094704i 112.5
-0.491074732452 - 706.750702094704i 112.5
-0.000000000001 0.000…
-8.114907494361 1.3
-3.839922431729 + 79.657898579634i 12.7
-3.839922431729 - 79.657898579634i 12.7
3.3 Observability with Disturbances
Addition
To observe disturbance inputs from driver torque
and disturbance torque from wheels, the described
model plant has been extended with two additional
states, T
driver
and T
c
, considered as Gaussian
processes with zero means.
The observability was evaluated with these two
additional states. The new state matrix A has
dimensions 8x8, and now includes also the terms in
B
d
matrix (7). New states vector is:


T
CdrivershaftMswshaftMsw
TTx 
22


(8)
But now, rank of observability matrix is only 5, this
because new state space model is ill-conditioned.
It’s due to numerical problems linked to the
presence of very different numeric parameter
entities, i.e. small gear-box inertial term in front of
steering wheel one, or torsion bar stiffness in front
of motor-gear joint coupling stiffness, etc. The only
possibility to estimate system states and disturbances
is to simplify the model structure, eliminating
unnecessary high frequency dynamics, in practice
gearbox dynamics which are over 100 Hz, out of
frequency range of interest.
4 EPS MODEL ORDER
REDUCTION
Approaches for model reduction reflect two different
points of view: a mechanical approach and a
singular values approach. The first action is to
eliminate defined dynamics considering equivalent
inertial effects and stiffness. In the second approach,
A Reduced Order Steering State Observer for Automated Steering Control Functions
429

the action is to improve observability and
controllability of the model by using an orthogonal
base change in order to reach a new linear
combination of system states (a balanced realization)
and then to eliminate the new states with weak
singular values, so less observable (singular
perturbation reduction method (Moore, 1981);
(Fernando et al., 1982); (Liu at al., 1989); (Saksena
et al., 1984)).
4.1 Mechanical Approach
The basic idea is to simplify the model plant,
starting from this equality:



2M
shaft

(9)
Then, defining an equivalent inertia for EPS motor:
2
22

shaft
wormMM
J
JJJ
new

(10)
And an equivalent stiffness for torsion bar:

*
k
kk
shaftshaft
new

(11)
The new differential equation for steering wheel is:
driversw
M
shaftswshaftswsw
TkJ
new













2
(12)
And new rotational dynamics for EPS motor:
CMsw
M
shaft
MMMM
TT
k
J
new
new









2
2
2222





(13)
So, the reduced order model is based only on (12)
and (13), in practice the same identified model with
no gear box dynamics represented.
4.2 Singular Perturbation Balanced
Model Reduction
The balanced representation technique developed in
(Saksena et al., 1984) is used as a basic tool for
deriving acceptable reduced-order model for the
dynamic analysis/synthesis on EPS system. In a
balanced representation, the controllability and
observability gramians, which represent the input-
state and output-state maps, respectively, are equal
and diagonal. The diagonal entries of these
gramians, called the singular values, measure the
degree of controllability and observability of the
states in this representation. The balanced
representation may be partitioned into the following
two interconnected systems:
1. the dominant subsystem: most controllable and
most observable part corresponding to large
singular values;
2. the non-dominant subsystem: the least
controllable and least observable part
corresponding to small singular values.
Figure 7: EPS reduced models compare.
The most controllable and most observable
states, corresponding to the singular values of the
largest magnitudes, are retained in the reduced
model.
Then singular perturbation method is an effective
method at low frequency for reducing large scale
systems. Singular perturbation approximation of
balanced systems was addressed by several
investigators (Fernando et al., 1982); (Liu at al.,
1989); (Saksena et al., 1984). The basic algorithm
can be summarized as follows:
1. Transform the system in Eq. (7) into the
balanced representation:




































2
1
21
2
1
2
1
2221
1211
2
1
~
~
~
~
~
~
x
x
CCy
u
B
B
x
x
AA
AA
x
x


(14)
Where:
xTx


~
is new balanced states vector,
1
~
x
is
system states vector strongly controllable and
10
-1
10
0
10
1
10
2
10
3
-100
-50
0
50
Bode diagram from T
M2
to T
bar
10
-1
10
0
10
1
10
2
10
3
-400
-200
0
200
10
-1
10
0
10
1
10
2
10
3
-100
-50
0
50
Bode diagram from T
M2
to Theta
M2
10
-1
10
0
10
1
10
2
10
3
-200
-100
0
Frequency [Hz]
EPS Model
Mechanical Reduced Model
Singular Perturbation Reduced Model
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
430

observable and
2
~
x
is system states vector weakly
controllable and observable.
2. Now (A
11
, B
1
, C
1
) represent the strong subsystem
and (A
22
, B
2
, C
2
) represent the weak subsystem.
3. Calculate the reduced-order model







uDxCy
uBxAx
1
1
1
1
1
11
1

(15)
as follows:
2
1
222
1
21
1
2221
1
12
1
2212
1
21
1
221211
11
BACD
AACCC
BBAAB
AAAAA








(16)
In this new reduced order model obtained above, the
steady-state error has been completely eliminated.
5 REDUCED ORDER EPS
STATES KALMAN OBSERVER
Now with either of the reduced order models, the
rank of observability matrix contains also additional
disturbances. These models have been used to
synthesize two different linear stationary Kalman
observers with estimation of EPS states in a
potential state-feedback control framework. Using a
common space-state model (17) derived from (12)
and (13) equations for mechanical approach and (15)
for singular perturbation reduced balanced model:









xCy
uBxAx
~
~
~

(17)
Where

and

are respectively assumed Gaussian
process and measurement white noises with zero
means. Now the state variables are:

T
CdriverMswMsw
TTx
22



(18)
and measures:

T
barMsw
Ty
2
 
(19)
Remember that system states vector for mechanical
approach is the same of full model excluding weak
states, so exactly the states vector (18), while the
states vector for singular perturbation method is a
linear combination of original physical states. It’s
fundamental to take into account the states
transformation from original realization to this
balanced and reduced realization in order to
reconstruct original physical states.
About observers gains synthesis (L matrix in fig.
8), all the process state variables are considered
Gaussian stochastic ones, so the assumed noise
covariance matrix has been defined in coherence
with physical characteristics of relative stochastic
variables and then tuned in order to get the best
estimation possible.
Figure 8: Linear Kalman Observer block diagram.
Figure 9: FCA Innovation Technical Center EPS test
bench.
6 OBSERVERS TEST ON EPS
TEST BENCH
A comparative test was performed on the FCA
Technical Center EPS test bench (see fig. 9) with a
first attempt linear quadratic regulator (LQR) to
realize a closed loop control of EPS output shaft
position. Developed state-feedback control uses
estimated/filtered system states: angular speeds and
positions; while steering wheel estimated torque
disturbance is used for safety reasons to understand
if a potential driver puts his hands on the steering
wheel during unmanned lateral control of a vehicle.
B
B
C
C
A
A
B
B
C
C
A
A
L
L
s
1
s
1







y
y
ˆ
x
u
x
ˆ
e


0
ˆ
x


0x




~
~
~
x
ˆ
B
B
C
C
A
A
B
B
C
C
A
A
L
L
s
1
s
1







y
y
ˆ
x
u
x
ˆ
e


0
ˆ
x


0x




~
~
~
x
ˆ
A Reduced Order Steering State Observer for Automated Steering Control Functions
431

Figure 10: Estimation test on EPS test bench.
In the graphs (see fig. 10), a comparison between
controlled steering column angular position
reference and measure (1
st
graph), then steering
wheel position (measured vs filtered) (2
nd
graph) and
steering angular speed (estimated vs offline
calculated one) (3
rd
graph), steering wheel torque
estimation signals (4
th
graph) from two synthesized
observers, steering wheel and EPS motor
filtered/measured angles (5
th
graph) and estimated
angular speeds and offline processed ones from
angular measurements (6
th
graph), so with no delay,
during a sweep of EPS output shaft position
(amplitude 30deg, frequency range [0.1, 3]Hz). Fig.
10 shows very interesting estimation results in front
of real measured signals and offline processed ones.
This test, as other tests carried out on the EPS
bench, have demonstrated the effectiveness of these
two observers as two interchangeable intelligent
algorithms developed for exploiting different
physical and numerical methods to observe optimal
EPS states.
7 CONCLUSIONS
Simple linear models/observers/controllers are
normally preferred over complex ones in control
system design for an obvious reason; they are much
easier to do analysis and synthesis with. This paper
demonstrates the utility and effectiveness of
intelligent algorithms for the steering state
estimation based on reduced order models. The
mechanical approach is an effective method to
reduce model plant when this model is well known.
The singular perturbation balanced model reduction
is a formidable tool which is more numerical and
useful to improve controllability or observability of
plant and finally to reduce model plant according to
a ‘singular values rule’. The main paper results are
two interchangeable Kalman observers useful for the
estimation of steering line states in order to control
steering wheel position. Next developments are as
follows: identification of disturbance from low part
of steering line in different conditions, and control of
electric power steering unit with optimal linear state-
feedback control approach.
REFERENCES
V. D. Mills, J. R. Wagner, 2003. “Behavioural modelling
and analysis of hybrid vehicle steering systems”, in
Proceedings of the Institution of Mechanical
Engineers Part D-Journal of Automobile Engineering.
C. Canudas-de-Wit, P. Tsiotras, E. Velenis, M. Basset, G.
Gissinger, 2003. “Dynamic Friction Models for
Road/Tire Longitudinal Interaction” in Vehicle System
Dynamics, Volume 39, Issue 3.
Moore B.C., 1981. “Principal component analysis in linear
systems: controllability, observability, and model
reduction”, in IEEE Trans Autom Contr, AC-26.
Fernando K.V., Nicholson H., 1982. “Singular
perturbation model reduction of balanced systems”. In
IEEE Trans Autom Contr, AC-27.
Liu Y., Anderson BDO, 1989. “Singular perturbation
approximation of balanced systems”. In Int J Contr.
Saksena V.R., O'Reilly J., Kokotovic P.V., 1984.
“Singular perturbations and time scale methods in
control theory: survey 1976±1983. In Automatica.
Kalman, R. E., 1960. “A New Approach to Linear
Filtering and Prediction Problems”. In Transactions of
the ASME, Journal of Basic Engineering, Pg. 35-45.
0 5 10 15 20 25 30 35 40 45 50
-40
-20
0
20
40
angle [deg]
Steering column position control - Ref. vs Meas. - Sweep 30deg [0.1-3]Hz
Reference
Measure
0 5 10 15 20 25 30 35 40 45 50
-40
-20
0
20
40
angle [deg]
Steering wheel angle
0 5 10 15 20 25 30 35 40 45 50
-1000
-500
0
500
1000
angular speed [deg/s]
time [s]
Steering wheel angular speed
0 5 10 15 20 25 30 35 40 45 50
-0.4
-0.2
0
0.2
0.4
torque [Nm]
Steering wheel torque estimation
0 5 10 15 20 25 30 35 40 45 50
-1000
-500
0
500
1000
angle [deg]
EPS Motor angle
0 5 10 15 20 25 30 35 40 45 50
-2
-1
0
1
2
x 10
4
angular speed [deg/s]
time [s]
EPS Motor angular speed
Mechanical Reduced Model Observer
Singular Perturbation Reduced Model Observer
from measures or offline processing
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
432