
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking
in Clutter
Yifan Xie
1
, Haeho Lee
2
, Myonghwan Ahn
2
, Bum Jik Lee
3
and Taek Lyul Song
1
1
Department of Electronic Systems Engineering, Hanyang University, Ansan, Republic of Korea
2
Combat System R&D Lab, LIG Nex1 Co. Ltd., Seongnam, Republic of Korea
3
Submarine Combat System Part, Daewoo Shipbuilding & Marine Engineering, Seoul, Republic of Korea
Keywords:
Multitarget, Multisensor, Target Existence, Joint Integrated Track Splitting, S-D Assignment.
Abstract:
Automatic object tracking for track initialization, confirmation and termination can be realized by using the
probability of target existence, which is a track quality measure for false track discrimination. In this paper,
we present a multi-sensor multi-target tracking application based on the probability of target existence and
multi-sensor joint integrated track splitting (MS-JITS), which is an extension of JITS framework to multi-
sensor systems. For fair comparison, incorporation of the target existence paradigm and the S-D assignment
is implemented. This work also consummates the S-D assignment based estimators for track management by
the probability of target existence.
1 INTRODUCTION
In many target tracking surveillance systems, such
as air traffic control or ground target tracking for
multiple targets, measurements can be received from
multiple sensors. Because of the limited sensing re-
gion of sensors, a single sensor can only partially
access information of the environment. Information
from multiple sensors can be combined using data
fusion algorithms to achieve cooperative observation
effects (Xiong and Svensson, 2002). However the
target tracker has no prior knowledge on the origin
of each measurement, which terms multi-dimensional
assignment (MDA) problem (Gilbertand and Hofstra,
1988) in multi-sensor systems. Pattipatti et al. pro-
posed the S-D assignment algorithm to solve this non-
deterministic polynomial-time hard (NP-hard) prob-
lem. By using the Lagrangian(dual) relaxation ap-
proach, the problem is then solved as a series of 2-D
subproblems (Pattipati et al., 1992; Deb et al., 1997).
In multi-target scenario, a mechanism is required
to decide the source (clutter or particular track) of
received measurements, and the objective is to as-
sociate measurement-to-track. This problem turns
more critical in multi-sensor multi-target situations,
where the sensor fusion problem has to be overcomed
as well. The conventional solutions for multi-target
tracking (MTT) include joint probabilistic data as-
sociation (JPDA) (Blackman and Popoli, 1999) and
multi-hypothesis tracking (MHT)(Reid, 1979; Black-
man, 2004), etc. For multi-sensor scenarios, multi-
sensor JPDA (Frei and Pao, 1998; Pao and Frei, 1995)
and multi-sensor MHT (Kirubarajan et al., 2001) are
proposed. These algorithms enumerate all possible
measurement to target allocations, and use likelihood
to evaluate each hypothesis. The number of hypothe-
ses grows exponentially in the number of tracks and
the number of measurements involved. The computa-
tional cost in generating the possibilities to data as-
sociation is usually excessive when the number of
tracks and number of measurements are large. There-
fore, suboptimal solutions with computational feasi-
bility are required.
Integrated track splitting (ITS) (Mu
ˇ
sicki et al.,
2007; Shi et al., 2015b) is a suboptimal multi-scan
single target estimator, that is capable of false track
discrimination (FTD) using the probability of target
existence as a track quality measure. The false track
discrimination identifies the true tracks and eliminates
false alarms, which is of the essential functionality
in track maintenance (Song et al., 2013; Song et al.,
2015c; Song et al., 2015a). The probability of target
existence for false track discrimination is obtained by
a simple equation which utilizes the parameters in-
volved in the associate probability calculations. ITS
has been extended for dealing with multi-target as
joint integrated track splitting (JITS) (Mu
ˇ
sicki and
Xie, Y., Lee, H., Ahn, M., Lee, B. and Song, T.
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking in Clutter.
DOI: 10.5220/0005960102990307
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 299-307
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
299

Evans, 2009; Shi et al., 2015a). Similar to MHT, each
component of JITS forms the history of measurement
hypotheses involved in the track for multiple scans.
The JITS algorithm is also able to distinguish between
the true tracks and false alarms by recursively calcu-
lating the probability of target existence.
In this paper, we present a sub-optimal multi-
sensor multi-scan multi-target tracking algorithm
based on the JITS algorithm, which we call multi-
sensor joint integrated track splitting (MS-JITS). A
comparison between the S-D assignment algorithm
and the MS-JITS algorithm is also conducted.
Problem formulation is detailed in Section II. Sec-
tion III presents the general MS-JITS algorithm. An
application of target existence paradigm to S-D as-
signment is described in Section IV. A simulation
study which demonstrates the performance of MS-
JITS is given in Section V, followed by the concluding
remarks in Section VI.
2 PROBLEM FORMULATION
2.1 Measurement Model
A number of measurements of sensors are received at
each sampling time k synchronously. Due to the un-
certainty of measurement origins, the received mea-
surements may originate from the target or clutter. Let
P
Ds
denote the target detection probability of sensor s.
Since the targets are not always detectable, P
Ds
< 1.
The gating process selects measurements from
sensor s and forms a validated measurement set y
s
(k)
with cardinality m
s
k
at time k, y
s,i
(k) indicates the ith
element of y
s
(k). P
G
is the probability that the true
measurement falls in the gate if target exists. Denote
Y
k
s
= {y
s
(k),Y
k−1
s
} as the set of validated measure-
ments up to time k. And a collection of all sensor
measurement is Y
k
= {Y
k
1
,Y
k
2
,...,Y
k
S
}.
2.2 Target Model
The target dynamics are modeled in Cartesian coor-
dinates. Under the additive noise assumption, the τth
target kinematic and measurement equations for track
τ at k scan are defined by
x
τ
k
= F
τ
k
x
τ
k−1
+ ω
τ
k
, (1)
z
τ
s,k
= H
s
x
τ
k
+ v
s,k
. (2)
where x
τ
k
is the target τ state vector, z
τ
s,k
is the tar-
get measurement. F
τ
k
and H
s
are the transition matrix
and measurement matrix of sensor s respectively. The
process noise ω
τ
k
and measurement noise v
s,k
are as-
sumed to be zero-mean, uncorrelated white Gaussian
noise sequences with known covariance Q
k
and R
s,k
.
As for track existence state, ψ
τ
k
is the event that
target τ exists. On the contrary,
¯
ψ
τ
k
suggests that target
τ does not exist at scan k.
2.3 Clutter Model
The number of clutter measurements in the surveil-
lance space follows Poisson distribution. The clut-
ter measurement density at point y
s,i
(k) is denoted
by ρ
s,i
(k) , ρ(y
s,i
(k)). Spatial distribution of clutter
measurements is assumed to be uniform in the surveil-
lance space.
3 MS-JITS ALGORITHM
3.1 Single-sensor JITS
3.1.1 Track State
The track state probability density function (pdf) con-
ditioned on the measurement set Y
k
s
at time k is given
by
p(x
τ
k
,ψ
τ
k
|Y
k
s
) = p(x
τ
k
|ψ
τ
k
,Y
k
s
)P(ψ
τ
k
|Y
k
s
), (3)
where P(ψ
τ
k
|Y
k
s
) represents the probability of target
existence of track τ. It also suggests that the track
state pdf is always calculated conditioned on the tar-
get existence event ψ
τ
k
. Specifically, the track state
pdf is approximated by a Gaussian mixture of mutu-
ally exclusive and exhaustive track components such
as
p(x
τ
k
|ψ
τ
k
,Y
k
s
) =
∑
c
τ
k
ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
)p(x
τ
k
|c
τ
k
,ψ
τ
k
,Y
k
s
). (4)
The track component c
τ
k
consists of the following
compositions:
• given measurement history;
• trajectory state pdf p(x
τ
k
|c
τ
k
,ψ
τ
k
,Y
k
s
);
• component probability ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
), which is in-
dexed by c
τ
k
, subjects to the constraint of
∑
c
τ
k
ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
) = 1. (5)
3.1.2 Track Prediction
Track state predicted pdf involved in propagating
from time k − 1 to k yields
p(x
τ
k
,ψ
τ
k
|Y
k−1
s
) = p(x
τ
k
|ψ
τ
k
,Y
k−1
s
)P(ψ
τ
k
|Y
k−1
s
). (6)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
300

Assumed that the target is always observable when-
ever it exists, then the existence and observability can
be modeled with Markov Chain 1 (Mu
ˇ
sicki et al.,
1994). The predicted target existence is given by
P(ψ
τ
k
|Y
k−1
s
) = ∆
1,1
P(ψ
τ
k−1
|Y
k−1
s
), (7)
where ∆
1,1
is the Markov transition probability.
The predicted track state pdf is denoted as
p(x
τ
k
|ψ
τ
k
,Y
k−1
s
) =
∑
c
τ
k−1
ξ
τ
k
(c
τ
k−1
|ψ
τ
k
,Y
k−1
s
) ×
p(x
τ
k
|c
τ
k−1
,ψ
τ
k
,Y
k−1
s
). (8)
Relative track component probabilities do not change
during the propagation. Each track component prop-
agates individually based on the prediction step of the
Kalman filter such that yields
p(x
τ
k
|c
τ
k−1
,ψ
τ
k
,Y
k−1
s
) = N(x
τ
k
; ˆx
τ
k|k−1
(c
τ
k−1
),
ˆ
P
τ
k|k−1
(c
τ
k−1
)). (9)
3.1.3 Measurement Selection
Each track component selects measurements from
sensor s separately, the validated measurements will
be included in the set y
s
(k). And the relevant mea-
surement likelihood becomes
p
k,i
(c
τ
k−1
) , p(y
s,i
(k)| ˆx
τ
k|k−1
(c
τ
k−1
))
=
1
P
G
N(y
s,i
(k); H ˆx
τ
k|k−1
(c
τ
k−1
),
ˆ
S
τ
k
(c
τ
k−1
)),
(10)
where
ˆ
S
τ
k
(c
τ
k−1
) is predicted measurement error co-
variance. The mixed likelihood for the common mea-
surement shared by components in track τ becomes
p
k,i
=
∑
c
τ
k−1
ξ
τ
k−1
(c
τ
k−1
)p
k,i
(c
τ
k−1
). (11)
3.1.4 Joint Multi-target Data Association
In order to reduce the computational complexity,
tracks that share common validated measurements are
termed a cluster. Joint multi-target data association is
performed simultaneously for each cluster.
A joint event ε is an assignment among possible
assignments of all measurements to all tracks in the
cluster, and it must obey the principle that each track
is assigned with zero or one measurement; each mea-
surement is assigned to zero or one track. The joint
events are mutually exclusive (Mu
ˇ
sicki and Evans,
2009).
Set T
0
(ε) is composed by tracks with no allocated
measurement; Set T
1
(ε) is the collection of tracks al-
located one measurement; i(ε, τ) indicates that mea-
surement i in ε is allocated to track τ. And the corre-
sponding joint event probability is
P(ε|Y
k
s
) = C
−1
k
∏
ε∈T
0
(ε)
[1 − P
Ds
P
G
P(ψ
τ
k
|Y
k−1
s
)] ×
∏
ε∈T
1
(ε)
[P
Ds
P
G
P(ψ
τ
k
|Y
k−1
s
)
p
k
(i(ε,τ))
ρ
s,i
(k)
], (12)
where C
k
is the normalization constant, p
k
(i(ε,τ)) is
the likelihood that measurement i originates from tar-
get τ. Since the joint events are mutually exclusive,
they form an exhaustive set
∑
ε
P(ε|Y
k
s
) = 1. (13)
A set of all joint events that measurement i is as-
signed to track τ is denoted by Ξ(i, τ). Hypothesis
θ
τ
k
(i) denotes that measurement i is the detection of
target τ at time k, and the probability of θ
τ
k
(i) satisfies
p(θ
τ
k
(0)|Y
k
s
) =
∑
ε∈Ξ(0,τ)
P(ε|Y
k
s
), (14)
p(ψ
τ
k
,θ
τ
k
(0)|Y
k
s
) =
(1 − P
Ds
P
G
)P(ψ
τ
k
|Y
k−1
s
)
1 − P
Ds
P
G
P(ψ
τ
k
|Y
k−1
s
)
×
p(θ
τ
k
(0)|Y
k
s
) (15)
p(ψ
τ
k
,θ
τ
k
(i)|Y
k
s
) =
∑
ε∈Ξ(i,τ)
P(ε|Y
k
s
). (16)
The data association probabilities based on the as-
sumption of target existence are then given by
β
τ
k,i
, p(θ
τ
k
(i)|ψ
τ
k
,Y
k
s
)
=
p(ψ
τ
k
,θ
τ
k
(i)|Y
k
s
)
P(ψ
τ
k
|Y
k
s
)
. (17)
3.1.5 Track Update
The track state pdf is updated by the measurements in
y
s
(k). The update track state can be obtained from the
Bayes rule
p(x
τ
k
,ψ
τ
k
|Y
k
s
) = p(x
τ
k
|ψ
τ
k
,Y
k
s
)P(ψ
τ
k
|Y
k
s
) (18)
where the posterior probability of target existence is
given by
P(ψ
τ
k
|Y
k
s
) =
m
s
k
∑
i=0
p(ψ
τ
k
,θ
τ
k
(i)|Y
k
s
) (19)
The track state a posterior pdf p(x
τ
k
|ψ
τ
k
,Y
k
s
) is a mix-
ture of all track components pdf such that
p(x
τ
k
|ψ
τ
k
,Y
k
s
) =
∑
c
τ
k
ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
)p(x
τ
k
|c
τ
k
,ψ
τ
k
,Y
k
s
) (20)
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking in Clutter
301

where track component posterior probability
ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
) is given by
ξ
τ
k
(c
τ
k
|ψ
τ
k
,Y
k
s
) =
(
ξ
τ
k
(c
τ
k−1
|ψ
τ
k
,Y
k−1
s
)β
τ
k,i
,i = 0
ξ
τ
k
(c
τ
k−1
|ψ
τ
k
,Y
k−1
s
)β
τ
k,i
p
k,i
(c
τ
k−1
)
p
k,i
,i 6= 0
(21)
where i = 0 represents the hypothesis that none of the
validated measurements originate from the target.
Then updated by using Kalman filter with mea-
surement y
s,i
(k),
p(x
τ
k
|c
τ
k
,ψ
τ
k
,Y
k
s
) = N(x
τ
k
; ˆx
τ
k|k
(c
τ
k
),
ˆ
P
τ
k|k
(c
τ
k
)), (22)
[ ˆx
τ
k|k
(c
τ
k
),
ˆ
P
τ
k|k
(c
τ
k
)] = KF
U
[y
s,i
(k), ˆx
τ
k|k−1
(c
τ
k−1
),
ˆ
P
τ
k|k−1
(c
τ
k−1
),H
s
,R
s,k
], (23)
where the KF
U
stands for the Kalman filter update.
3.1.6 Component Management
Without component control, the number of track com-
ponents increase exponentially in time, thus efficient
management is crucial. The component management
in JITS involves two parts: merging and pruning.
Component merging deals with track components
with similar features, for which we applied a rela-
tively short retained track component history as sim-
ilarity measure. Component pruning is to remove
those track components with low probability, so that
track is always composed by more significant compo-
nents (Challa et al., 2011).
3.2 Multi-sensor JITS
Figure 1: Sequential implementation of JITS algorithm.
Difficulties for generalizing a single sensor JITS fil-
ter to a multi-sensor case are complicated. Since the
sensors are synchronized and the measurement noises
across the sensors are uncorrelated, the two update
schemes are available: parallel processing and se-
quential update. In the parallel processing, the sen-
sor measurements are transmitted to a fusion center
and converted with respect to a reference coordinate
system. The target state is updated by applying the
JITS algorithm to the measurements in the fusion cen-
ter. However, it requires a solution for multiple de-
tection target tracking as the measurements contain
multiple detections of a target gathered from differ-
ent sensors(Habtemariam et al., 2013). To realize the
parallel processing, sensors need to be synchronized
and heavy data traffic to the fusion center is expected.
The rigorous formulas are too complicated for practi-
cal usage (Smith and Singh, 2006)(Bar-Shalom et al.,
2011).
In the sequential update, the target state is up-
dated with the data from one sensor at a time. The
essence of sequential update for multi-sensor JITS al-
gorithm is operating single sensor JITS algorithm it-
eratively, so that the computational complexity is sig-
nificantly decreased. Sensors do not have to be syn-
chronized. In (Pao and Frei, 1995), it suggests that
the sequential update gives superior tracking perfor-
mance than the parallel process when data association
is considered. This is primarily due to fact that better
filtered estimates are available after processing each
sensor’s data. Measurement selection procedure fil-
ters out many measurements that are not statistically
significant. And as a consequence, the sequential up-
date scheme, which is computationally tractable and
with better tracking performance, is applied for solv-
ing multi-sensor problem in this paper.
The way of implementing the sequential update
for the MS-JITS algorithm is to process the measure-
ments from each sensor in succession (Bar-Shalom
and Li, 1995), using single-sensor JITS algorithm as
shown in Figure 1. The outputs of the sth (s ≤ S − 1)
sensor are regarded as intermediate track stated pdf of
target τ, state vector ˆx
τ,s
k
and the covariance
ˆ
P
τ,s
k
. Us-
ing intermediate result in place of the predicted state,
then proceed to the next sensor for updating, and fi-
nally cumulates the ultimate results ˆx
τ
k
and
ˆ
P
τ
k
in the
last sensor.
[ ˆx
τ,s
k|k
,
ˆ
P
τ,s
k|k
] = JIT S[ ˆx
τ,s−1
k|k
,
ˆ
P
τ,s−1
k|k
,y
s
(k)],
s = 1, 2, ...S − 1 (24)
[ ˆx
τ
k|k
,
ˆ
P
τ
k|k
] = JIT S[ ˆx
τ,s−1
k|k
,
ˆ
P
τ,s−1
k|k
,y
s
(k)],s = S (25)
where JIT S denotes the single-sensor JITS algorithm
described in Section III-A.
The posterior probability of target existence in
multi-sensor target tracking application should give
due consideration to validated measurements in every
sensor. And it can be calculated by updating target
existence probability iteratively using the joint multi-
target data association method (19) described in Sec-
tion III.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
302
4 TARGET EXISTENCE
PROBABILITY IN S-D
ASSIGNMENT
Unlike the S-D assignment, all the tracks in MS-JITS
algorithm are automatically managed (confirmation
or termination) by probability of target existence. For
a fair result comparison, it stands to reason that this
method should be applied to S-D assignment.
Every element (including dummy measurement)
in a composite measurement contributes to the poste-
rior probability of target existence. We use the mea-
surement from the first sensor to derive an interme-
diate probability of target existence, using it in place
of the predicted probability for the next sensor. The
posterior probability of target existence is given by
P(ψ
τ
k
|Y
k
s
) =
(
∏
S
s=1
Λ
s
k
)P(ψ
τ
k
|Y
k−1
s
)
1 − (1 −
∏
S
s=1
Λ
s
k
)P(ψ
τ
k
|Y
k−1
s
)
, (26)
where Λ
s
k
is the measurement likelihood ratio in sen-
sor s, denoted by
Λ
s
k
=
(
1 − P
Ds
P
G
+ P
Ds
P
G
p
s
k,i
ρ
s,i
(k)
if κ
τ
s,i
= 1
1 − P
Ds
P
G
otherwise
. (27)
The binary variable κ
τ
s,i
= 1 indicates that y
s,i
(k) is the
measurement of target τ. The measurement likelihood
p
s
k,i
(indexed by sensor s) is given by
p
s
k,i
=
(
N(y
s,i
(k); ˆx
τ
k|k−1
,S
τ
k
),s = 1
N(y
s,i
(k); ˆx
τ,s−1
k|k
,S
τ
k
),s = 2, 3, ..., S
(28)
where S
τ
k
is the predicted measurement covariance of
the standard Kalman filter. The posterior probability
of target existence is given in (26), for the sake of
brevity, the superscript τ is omitted for Λ
s
k
, p
s
k,i
. The
derivation is described in appendix.
5 SIMULATION
This section provides a comparison between the MS-
JITS algorithm and the S-D assignment algorithm
(S = 3) by simulating the scenarios with varying clut-
ter measurement densities and target detection proba-
bilities respectively.
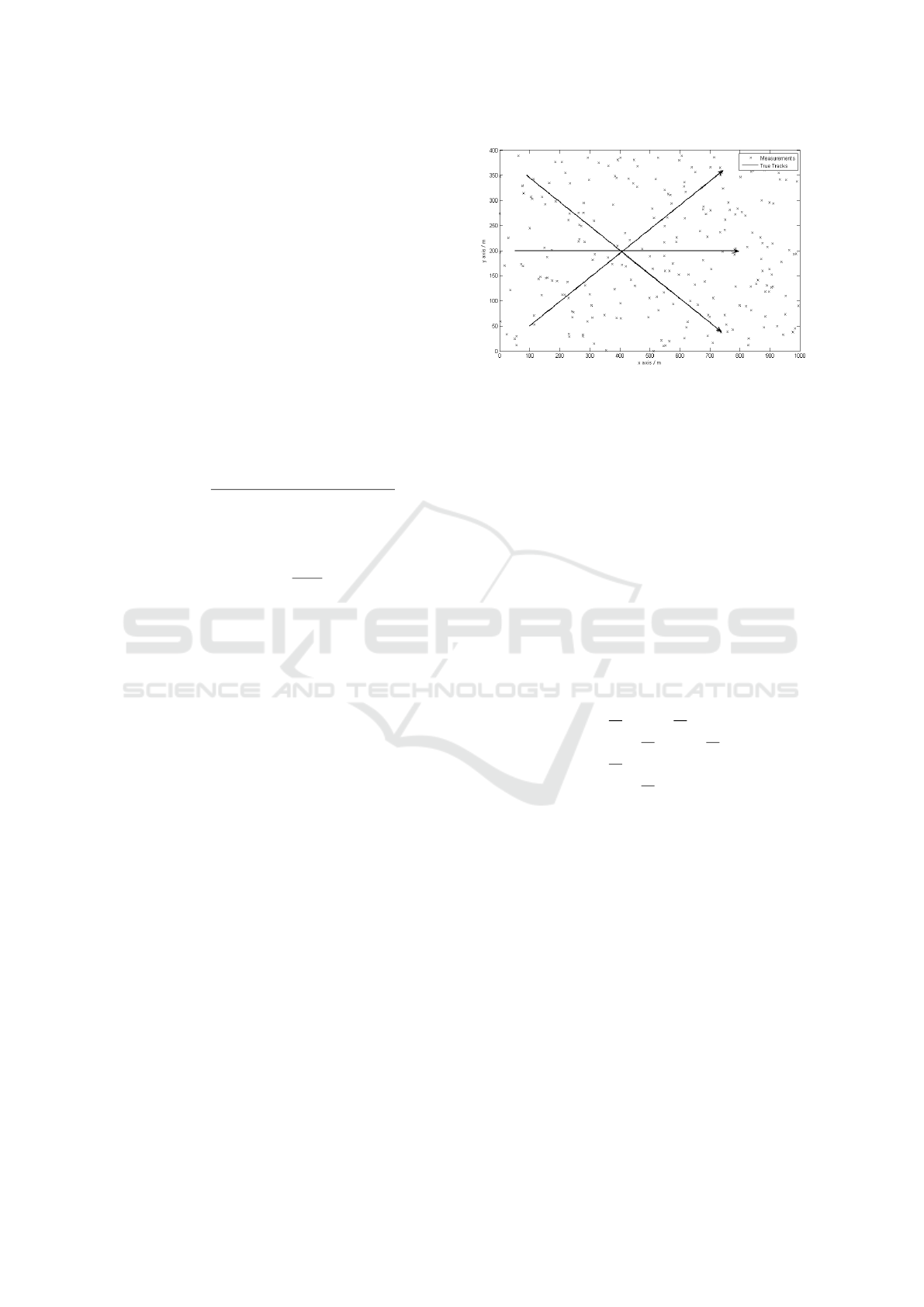
Three targets are observed in clutter on a two di-
mensional surveillance region with 1000 m in length
and 400 m in width. The clutter measurements are as-
sumed to be uniformly distributed. Figure 2 shows a
representative trial over the entire Monte Carlo trials.
The illustrated arrows and crosses are the trajectories
for each target and clutter measurements respectively.
Figure 2: Surveillance region.
The selection window size is given with gating
probability P
G
= 0.99. The measurements noise is as-
sumed to be Gaussian distributed with zero-mean and
standard deviation σ
s
= 5m. The target state vector
consists of
x
τ
k
= [x,y, ˙x, ˙y]
T
(29)
with transition matrix F
τ
k
F
τ
k
=
1 0 T 0
0 1 0 T
0 0 1 0
0 0 0 1
. (30)
The velocity vectors of the targets are
[13m/s,−6.25m/s]
T
,[15m/s,0m/s]
T
,[13m/s,6.25m/s]
T
respectively. Sampling time is T = 1s. Target maxi-
mum velocity is v
max
= 25m/s. The process noise is
zero-mean with covariance
Q
k
= q
T
4
4
0
T
3
2
0
0
T
4
4
0
T
3
2
T
3
2
0 T
2
0
0
T
3
2
0 T
2
, (31)
where q = 0.75 m
2
/s
4
.
Tracks are initialized automatically using two-
point differencing (Challa et al., 2011), and a constant
value of probability of target existence is assigned to
each newly initialized track. The probability of target
existence is recursively updated in subsequent scans.
If the probability exceeds the confirmation threshold,
the corresponding track is confirmed. And the track
will be terminated if the probability falls below the
termination threshold. The Markov transitional prob-
ability is 4
1,1
= 0.98.
Three scenarios of this experiment are consid-
ered, each with a different target detection probabil-
ity and clutter measurement density: A. clutter mea-
surement density ρ
s,i
(k) = 1 × 10
−4
and low target
detection probability P
Ds
= 0.6; B. clutter measure-
ment density ρ
s,i
(k) = 2 × 10
−4
and high target de-
tection probability P
Ds
= 0.9; C. clutter measurement
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking in Clutter
303
density ρ
s,i
(k) = 2 × 10
−4
and low target detection
probability P
Ds
= 0.6. The Monte Carlo simulations
for each scenario consist of 200 trails. MS-JITS is
updated by a Gaussian mixture of component state
pdf such that most of the measurements in the val-
idation window contributes to the update. The esti-
mator based on S-D assignment chooses the compos-
ite measurement by evaluating maximum likelihood
and the global nearest neighbor using 2-D dynamic
assignment algorithm (Popp et al., 2001).
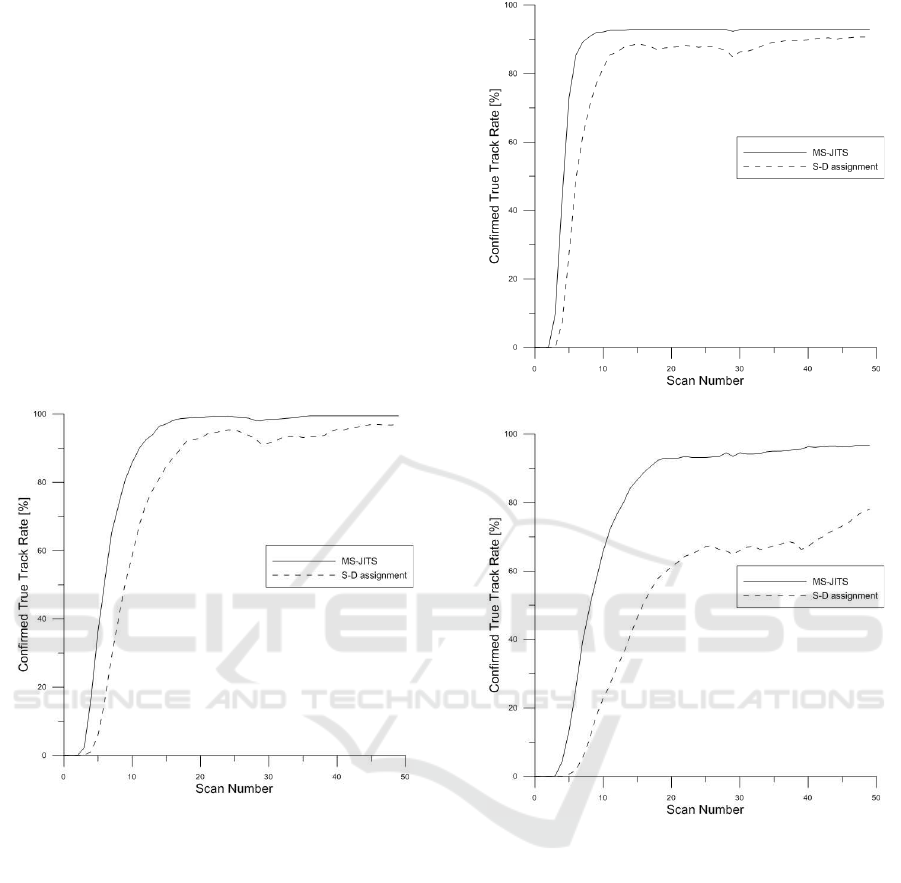
5.1 False Track Discrimination
The false track discrimination results are shown in
Figures 3, 4 and 5. The graphs show the percentage
of confirmed true tracks of MS-JITS and S-D assign-
ment over time for each scenario.
Figure 3: Confirmed true track rate-Scenario A.
MS-JITS always confirms track faster than S-D
assignment. These figures show that MS-JITS has
superior advantage of true track confirmation, which
is apparent in dense clutter density and low detection
probability environment.
In the simulation, the false alarm rates of the MS-
JITS algorithm of the 3 scenarios are 3.3%, 0.86%,
2.5% compared with the S-D assignment algorithm
of 25%, 11.67%, 32.5%. The inequality of the re-
sult is due to the fact that the essences of each algo-
rithm are distinct. In the target state update part, the
MS-JITS algorithm processes all the validated mea-
surement, whereas the S-D assignment algorithm pro-
cesses only one composite measurement that marginal
target information is utilized. If efforts were made to
minimize the gap of false alarm rates, the time dura-
tion that confirmation procedure required would de-
crease and the total confirmed true track rate would
Figure 4: Confirmed true track rate-Scenario B.
Figure 5: Confirmed true track rate-Scenario C.
increase for the MS-JITS algorithm.
5.2 Retention Test
Retention test is designed for observing the destina-
tion of every confirmed true track. Then we can eval-
uate the efficiency of an algorithm. The following in-
formation is obtained by tagging the confirmed true
tracks at scan 15 and checking them again at scan 40
(Mu
ˇ
sicki, 2006):
• nCases: Total number of tracks that following a
target at scan 15;
• nOK: Total number of tracks that still following
the original target at scan 40;
• nLost: Total number of tracks that not following
any target at scan 40;
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
304

• nSwitched: Total number of tracks that end up fol-
lowing a different target at scan 40;
• nMerged: Total number of tracks disappeared due
to merging between scan 15 and 40.
The target retention tests are listed in Table 1-3.
Table 1: Retention Statistics-Scenario A.
MS-JITS S-D
nCases 583 509
nOK 559 392
nLost 5 42
nSwitched 16 72
nMerged 3 3
Table 2: Retention Statistics-Scenario B.
MS-JITS S-D
nCases 561 541
nOK 544 377
nLost 1 85
nSwitched 16 70
nMerged 0 9
Table 3: Retention Statistics-Scenario C
MS-JITS S-D
nCases 520 279
nOK 481 137
nLost 11 99
nSwitched 23 42
nMerged 5 1
The results show that track retention capabilities
of MS-JITS, with success rates (nOK / nCases) of
96%, 97%, 93%, is better than S-D assignment, with
success rates of 77%, 70%, 49%. The percentage of
false alarms is apparently decreased. In addition, the
nLost and nSwitched number is much reduced in MS-
JITS. That displays the track trajectory maintains well
during propagation.
5.3 RMS error
Position root mean square (RMS) error is a criterion
for evaluating track trajectory accuracy, and for sim-
plicity each scenario shows the representative result
only. The results are presented in Figures 6, 7 and
8, which show the RMS errors of MS-JITS and S-
D assignment for different scenarios. The salients in
every figure are shown around scan 25, which is the
time that the close encounter between the tracks oc-
curred. Due to the incorrect measurement-to-track
association, some measurements are allocated to the
unrelated track. Therefore, the track trajectory esti-
mation accuracy degenerates. Obviously, MS-JITS
always provides better trajectory estimate than S-D
assignment.
Figure 6: RMS error in position-Scenario A.
Figure 7: RMS error in position-Scenario B.
5.4 Computation Time
The computation time of both algorithms for each
scenario are listed in Table 4.
It suggests that the MS-JITS algorithm requires
more computation time, which provides a trade off
between the computation time and tracking perfor-
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking in Clutter
305
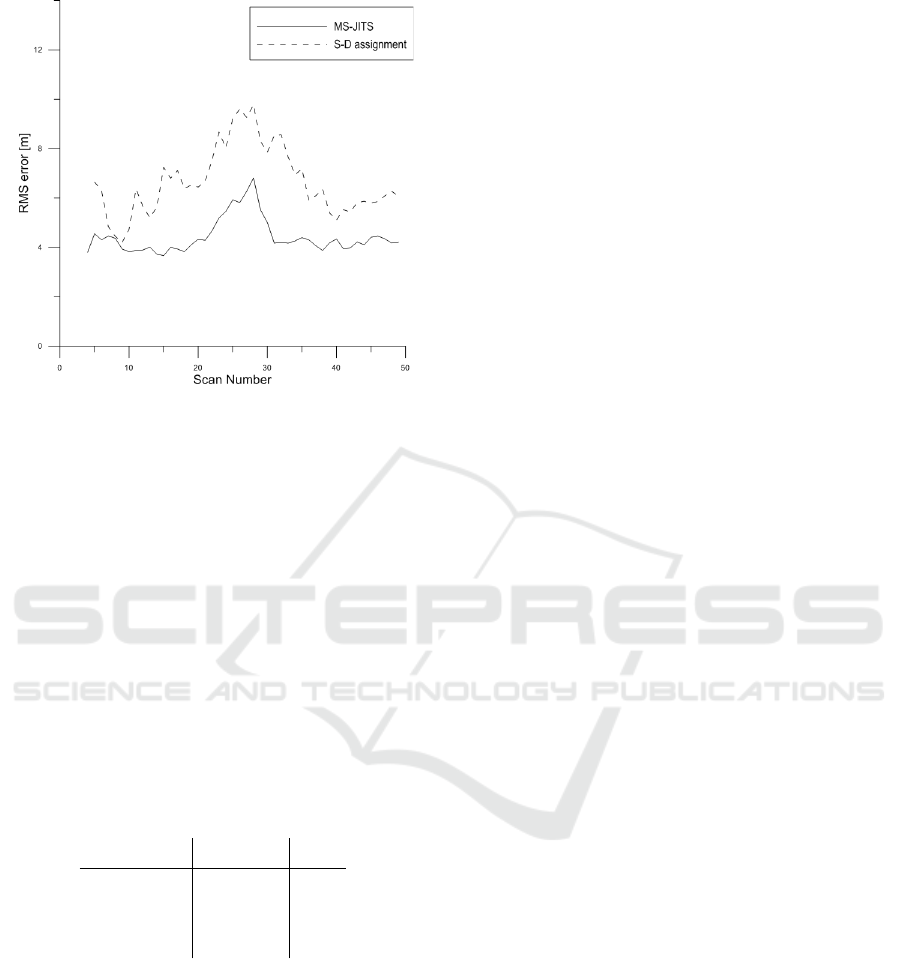
Figure 8: RMS error in position-Scenario C.
mance in practical applications. Though the com-
putational load of MS-JITS is heavier, for some sit-
uations where track trajectories are located in near
vicinity, MS-JITS is more preferable. A compro-
mise of the computation time and estimation accuracy
can be achieved by adopting an iterative implemen-
tation (Song et al., 2015b) for the JITS filter. The
computational requirements and estimation accuracy
can be classified into several levels by adjusting the
number of iterations. The iterations start with single
target tracking algorithm and each subsequent itera-
tion improves the approximation towards the optimal
multi-target solution within a finite number of itera-
tions. The application of iterative JITS filter for multi-
sensor system remains further exploration.
Table 4: Computation Time (sec.).
MS-JITS S-D
Scenario A 262 82
Scenario B 6691 415
Scenario C 4063 456
6 CONCLUSIONS
In this paper, we have presented a JITS based multi-
sensor tracking algorithm, which is capable of false
track discrimination by using the probability of target
existence as a track quality measure. And the S-D as-
signment based estimator is enhanced by incorporat-
ing the probability of target existence for false track
discrimination.
The S-D assignment algorithm may be effective in
applications where computational efficiency is more
important. But in situations where clutter measure-
ment density is dense or target detection probability
is low, the composite measurements become seriously
contaminated or mostly consisted by dummy mea-
surements. And as a consequence, the false alarm rate
rises and track trajectory accuracy decreases. In con-
trast, the MS-JITS algorithm compensates the draw-
backs at the cost of computational load. The MS-JITS
algorithm processes measurement information more
comprehensively with a more strict mechanism to dis-
tinguish the true tracks and false alarms. In addition,
the retention test proves that the MS-JITS algorithm
has stronger robustness. Thus, for applications where
track trajectory accuracy and track maintenance are
preferable, the MS-JITS algorithm offers an attractive
alternative.
ACKNOWLEDGEMENTS
This paper was supported by the LIG-Nex1 Co., Ltd.
under the contract LIGNEX1-2015-0108(00).
REFERENCES
Bar-Shalom, Y. and Li, X. (1995). Multitarget-multisensor
tracking: principles and techniques. YBS Publishing.
Bar-Shalom, Y., Willett, P. K., and Tian, X. (2011). Track-
ing and Data Fusion. YBS Publishing.
Blackman, S. (2004). Multiple hypothesis tracking for mul-
tiple target tracking. IEEE Aerospace and Electronic
Systems Magazine, 19(1):5–18.
Blackman, S. and Popoli, R. (1999). Design and Analysis
of Modern Tracking Systems. Artech House.
Challa, S., Morelande, M. R., Mu
ˇ
sicki, D., and Evans, R. J.
(2011). Fundamentals of object tracking. Cambridge
University Press.
Deb, S., Yeddanapudi, M., Pattipati, K., and Bar-Shalom,
Y. (1997). A generalized s-d assignment algorithm
for multisensor-multitarget state estimation. IEEE
Transactions on Aerospace and Electronic Systems,
33(2):523–538.
Frei, C. W. and Pao, L. Y. (1998). Alternatives to monte-
carlo simulation evaluations of two multisensor fusion
algorithms. Automatica, 34(1):103–110.
Gilbertand, K. C. and Hofstra, R. B. (1988). Multidi-
mensional assignment problems. Decision Sciences,
19(2):306–321.
Habtemariam, B., Tharmarasa, R., Thayaparan, T., Mallick,
M., and Kirubarajan, T. (2013). A multiple-detection
joint probabilistic data association filter. IEEE Jour-
nal of Selected Topics in Signal Processing, 7(3):461–
471.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
306

Kirubarajan, T., Wang, H., Bar-Shalom, Y., and Pattipati,
K. R. (2001). Efficient multisensor fusion using mul-
tidimensional data association. IEEE Transactions on
Aerospace and Electronic Systems, 37(2):386–400.
Mu
ˇ
sicki, D. (2006). Track score and target existence. In 9th
Int. Conf. on Information Fusion, pages 1–7.
Mu
ˇ
sicki, D., Evans, R., and Stankovi
´
c, S. (1994). Integrated
Probabilistic Data Association (IPDA). IEEE Trans.
Automatic Control, 39(6):1237–1241.
Mu
ˇ
sicki, D. and Evans, R. J. (2009). Multiscan multitarget
tracking in clutter with integrated track splitting filter.
IEEE Transactions on Aerospace and Electronic Sys-
tems, 45(4):1432–1447.
Mu
ˇ
sicki, D., Scala, B. F., and Evans, R. J. (2007). The in-
tegrated track splitting filter efficient multi-scan sin-
gle target tracking in clutter. IEEE Transactions on
Aerospace and Electronic Systems, 43(4):1409–1425.
Pao, L. Y. and Frei, C. W. (1995). A comparison of parallel
and sequential implementations of a multisensor mul-
titarget tracking algorithm. In American Control Con-
ference, Proceedings, volume 3, pages 1683–1687.
Pattipati, K. R., Deb, S., Bar-Shalom, Y., and Washburn,
R. B. (1992). A new relaxation algorithm and pas-
sive sensor data association. IEEE Transactions on
Aerospace and Electronic Systems, 37(2):198–213.
Popp, R. L., Pattipati, K. R., and Bar-Shalom, Y. (2001).
m-best s-d assignment algorithm with application to
multitarget tracking. IEEE Transactions on Aerospace
and Electronic Systems, 37(1):22–39.
Reid, D. (1979). An algorithm for tracking multiple targets.
IEEE Transactions Automatic Control, 24(6):843–
854.
Shi, Y. F., Song, T. L., and Lee, J. H. (2015a). Multi-
target tracking in clutter using a high pulse repetition
frequency radar. IET, Radar, Sonar and Navigation,
9(8):1047–1054.
Shi, Y. F., Song, T. L., and Mu
ˇ
scki, D. (2015b). Tar-
get tracking in clutter using a high pulse repetition
frequency radar. IET, Radar, Sonar and Navigation,
9(3):299–307.
Smith, D. and Singh, S. (2006). Approaches to multisen-
sor data fusion in target tracking: a survey. IEEE
Transactions on Knowledge and Data Engineering,
18(12):1696–1710.
Song, T. L., Kim, H., and Mu
ˇ
sicki, D. (2015a). Dis-
tributed (nonlinear) target tracking in clutter. IEEE
Transactions on Aerospace and Electronic Systems,
51(1):654–668.
Song, T. L., Kim, H. W., and Musicki, D. (2015b). Itera-
tive joint integrated probabilistic data association for
multitarget tracking. IEEE Transactions on Aerospace
and Electronic Systems, 51(1):642–653.
Song, T. L., Mu
ˇ
scki, D., and Kim, Y. (2015c). Multitarget
tracking with state dependent detection. IET, Radar,
Sonar and Navigation, 9(1):10–18.
Song, T. L., Mu
ˇ
sicki, D., Kim, H. W., and Govaers, F.
(2013). Gaussian mixture tracking: Mht and its com-
parison. In Sensor Data Fusion: Trends, Solutions,
Applications (SDF), pages 1–6.
Xiong, N. and Svensson, P. (2002). Multi-sensor manage-
ment for information fusion: issues and approaches.
In 5th Int. Conf. on Information Fusion, volume 3,
pages 163–186.
APPENDIX
Sequential Likelihood Ratio
This section is used to describe the posterior proba-
bility of target existence in MS-JITS algorithm. The
measurements from the first sensor are used to com-
pute an intermediate posterior probability of target ex-
istence P(ψ
τ,1
k
|Y
k
s
), with corresponding measurement
likelihood ratio Λ
1
k
denoted by
P(ψ
τ,1
k
|Y
k
s
) =
Λ
1
k
P(ψ
τ
k
|Y
k−1
s
)
1 − (1 − Λ
1
k
)P(ψ
τ
k
|Y
k−1
s
)
. (32)
After gating the measurements in next sensor, tar-
get existence probability is updated,
P(ψ
τ,2
k
|Y
k
s
) =
Λ
2
k
P(ψ
τ,1
k
|Y
k−1
s
)
1 − (1 − Λ
2
k
)P(ψ
τ,1
k
|Y
k−1
s
)
. (33)
Substituting the P(ψ
τ,1
k
|Y
k−1
s
) by equation (32) yields,
P(ψ
τ,2
k
|Y
k
s
) =
Λ
2
k
Λ
1
k
P(ψ
τ
k
|Y
k−1
s
)
1−(1−Λ
1
k
)P(ψ
τ
k
|Y
k−1
s
)
1 − (1 − Λ
2
k
)
Λ
1
k
P(ψ
τ
k
|Y
k−1
s
)
1−(1−Λ
1
k
)P(ψ
τ
k
|Y
k−1
s
)
=
Λ
1
k
Λ
2
k
P(ψ
τ
k
|Y
k−1
s
)
1 − (1 − Λ
1
k
Λ
2
k
)P(ψ
τ
k
|Y
k−1
s
)
. (34)
Similarly, we can obtain
P(ψ
τ,3
k
|Y
k
s
) =
Λ
1
k
Λ
2
k
Λ
3
k
P(ψ
τ
k
|Y
k−1
s
)
1 − (1 − Λ
1
k
Λ
2
k
Λ
3
k
)P(ψ
τ
k
|Y
k−1
s
)
. (35)
Finally, up to sensor S yields
P(ψ
τ
k
|Y
k
s
) =
(
∏
S
s=1
Λ
s
k
)P(ψ
τ
k
|Y
k−1
s
)
1 − (1 −
∏
S
s=1
Λ
s
k
)P(ψ
τ
k
|Y
k−1
s
)
. (36)
Joint Integrated Track Splitting for Multi-sensor Multi-target Tracking in Clutter
307
