
OpenCL-accelerated Point Feature Histogram and Its Application
in Railway Track Point Cloud Data Processing
Dongxu Lv, Peijun Wang, Wentao Li and Peng Chen
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, China
Keywords: OpenCL, PFH, Parallel Computing, Point Cloud Data.
Abstract: To meet the requirements of railway track point cloud processing, an OpenCL-accelerated Point Feature His-
togram method is proposed using heterogeneous computing to improve the low computation efficiency. Ac-
cording to the characteristics of parallel computing of OpenCL, the data structure for point cloud storage is
reconfigured. With the kernel performance analysis by CodeXL, the data reading is improved and the load of
ALU is promoted. In the test, it obtains 1.5 to 40 times speedup ratio compared with the original functions at
same precision of CPU algorithm, and achieves better real-time performance and good compatibility to PCL.
1 INTRODUCTION
Point cloud data processing is an importance issue in
computer vision, 3D reconstruction, reverse engi-
neering and other industrial fields. For the increasing
amount of point clouds, a services of function librar-
ies are developed for point cloud data processing.
Among them, PCL (Point Cloud Library) is a type of
C++ based solution with filtering, feature extraction,
model matching and surface reconstruction algo-
rithms for point cloud data processing, and has widely
applications in 3D sensing and inspection (Rusu and
Cousins, 2011). To accelerate the computing, PCL
(Point Clouds Library) has provided the support for
CUDA (Compute Unified Device Architecture). Re-
cently, the new developing project is released to in-
troduce OpenCL (Open Computing Language) mod-
ules by using heterogeneous computing acceleration
technology.
OpenCL is an open and free framework for gen-
eral-purpose parallel programming with heterogene-
ous systems, it supports a wide variety of platforms,
such as the CPU (central processing unit), AMD
GPU(graphics processing unit), NVIDIA GPU, mo-
bile platform (Gaster et al., 2012). It also has well-
portable ability that can be efficiently mapped to a ho-
mogeneous or a heterogeneous architecture. Gener-
ally. GPU contains multiple computing units
(CU),and each one CU includes various processing
elements(PE). Compared to CPU, GPU has much
more computing cores. As one of highly-well parallel
processors, GPU is particularly suitable for data par-
allel algorithms (Tompson and Schlachter, 2012).
These algorithms are implemented by OpenCL pro-
gramming and compiled into one or more kernels,
with GPU as OpenCL devices to execute these kernel.
Parallel computing technology provides more
possibility to process engineering point cloud data.
However, some PCL functions with low running effi-
ciency restrict the real-time performance of system.
The optimization of these kinds of functions is an ur-
gent task for large scale engineering cloud point data
processing. In this paper, a OpenCL-accelerated Point
Feature Histograms (PFH) method is proposed to
overcome the low computing performance of PCL
functions in railway track point cloud data pro-
cessing. According to the characteristics of hardware
model of OpenCL and PFH, the data structure of
point clouds is reconfigured and the global and local
memories of GPU are optimized by allocating
OpenCL groups properly to promote the computing
loads. With the performance test, the optimized algo-
rithm could obtain 1.5 to 40 times speedup ratio com-
pared with the original functions from PCL.
2 POINT FEATURE
HISTOGRAMS
2.1 Principle
Point feature representations is one of the most basic
Lv, D., Wang, P., Li, W. and Chen, P.
OpenCL-accelerated Point Feature Histogram and Its Application in Railway Track Point Cloud Data Processing.
DOI: 10.5220/0005960304330438
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 433-438
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
433
and crucial part in point cloud data processing (Rusu,
2010), which has great influence on the registration,
surface reconstruction and pattern recognition in fur-
ther steps. As one of the descriptions of point cloud
feature, PFH is a multi-dimensional histogram with
geometric features of query points and their nearest K
neighbors (Rusu et al., 2008).
PFH descriptor relies on the coordinates and nor-
mals of points and their nearest K neighbors. Compu-
ting of relationship between the points and their near-
est K neighbors, the point clouds variation on geomet-
ric surface is presented, which reserves the geometric
features of the point clouds. Therefore, the quality of
PFH depends on the estimated normal of each point.
The relationship between query points and their near-
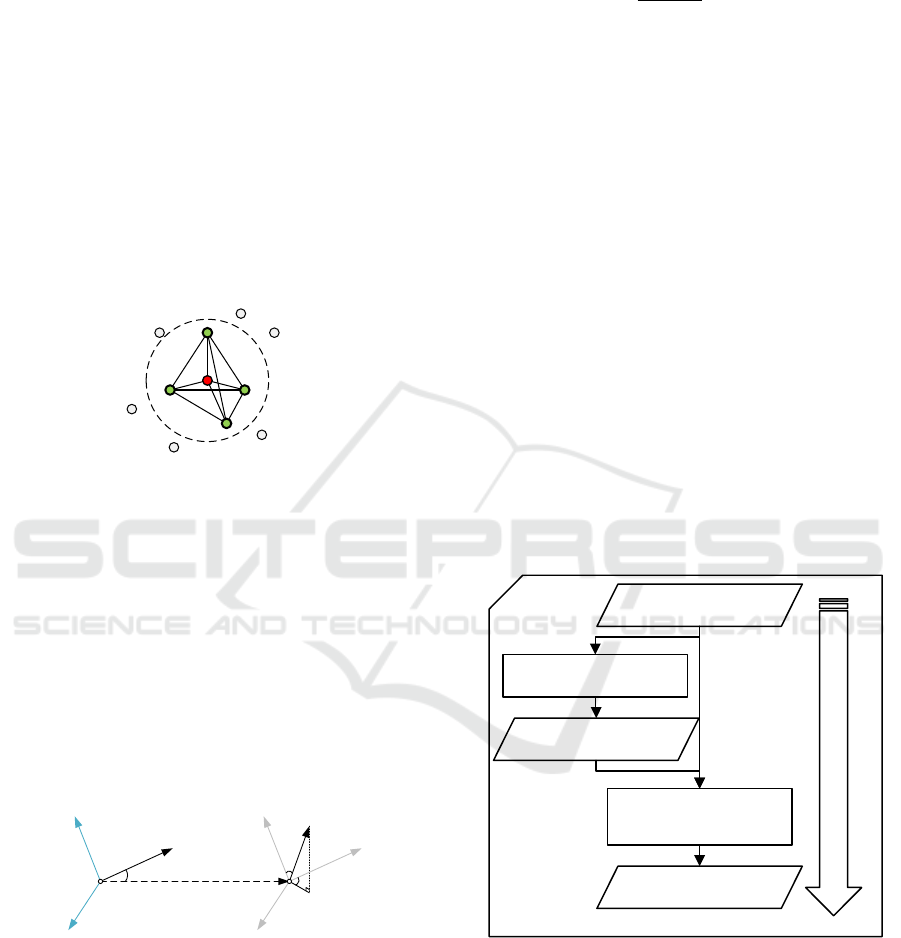
est K neighbors is shown as Figure 1.
Figure 1: Relationship between query points and their near-
est K neighbors.
P
t
is a query point of PFH, and is regarded the cir-
cle center of neighborhood with radius R for querying
K neighbors. Each pair of points in the neighborhood
are connected in the algorithm, and the final presen-
tation is a histogram, which makes it have O(k
2
)com-
plexity.
For the points P
a
and P
b
, with normals n
a
and n
b
,
the relative position and angular variation are com-
puted. One of these two points is defined as origin,
and its normal become the X axis. The local coordi-
nate frame generated is shown as Figure 2.
Figure 2: Local coordinate frame generated by the two
points.
[P
b
-P
a
]is the line between the two points, and Z s
vertical to X and this line. The angular variations be-
tween normal of P
a
and n
a
, and that of P
b
and n
b
is can
be represented as below.
arctan ,
Yn
b
PP
a
b
X
d
Z n X n
bb
(1)
In this formula, d is the distance between P
a
and
P
b
, which presents like. By computing the group of
values (α, φ, θ, d), the parameters of coordinates and
normals for the two points could be reduced from 12
to 4. Among the 4 parameters, 3 angular variations
could be easily binned into the same intervals of the
histogram. For the forth distance parameter, the local
point density of it may influence the eigen values, so
omitting d would make PFH algorithm more robust
(Rusu, 2010). Dividing the 3 angular intervals into n
equal portions, it will obtain a histogram with n
3
inter-
vals and the times for each pair of points in histogram
intervals are counted. PCL provides a data type
pcl::PFHSignature125 to store the feature histogram
with 125 floats when n=5.
2.2 PFH Algorithm in PCL
PCL provides the functions for FPH computing, and
it is implemented serially as below.
Figure 3: Serial computing of PFH.
Step1. Input the point cloud data with 3D coordi-
nates, and compute the normal of each point;
Step2. Select the searching area, and find the near-
est K neighbors of the query point;
Step3. According to the dataset of nearest K neigh-
bors, compute the angular variations of all the
points and get the normalized histogram;
P
t
P
k1
P
k2
P
k3
P
k4
a
nX
[ - ]
ba
Y P P X
Z X Y
ba
PP
a
P
b
P
Y
Z
X
b
n
Coordinates of
point cloud
Traverse all points and
compute the normals
Normals of
Point cloud
Set the searching
neighborhood, traverse all
points and compute PFH
PFH of point
cloud
CPU
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
434

Step4. Repeat Step2 and Step3, and traverse all the
points to compute their feature histogram.
The flowchart of the serial computing is as Figure 3.
3 IMPLEMENTATION OF PFH
BY OPENCL AND
CORRESPONDING
OPTIMIZATION
3.1 Parallelism Analysis of OpenCL
The points cloud of railway track from non-contact
scanner includes the coordinates of x, y, z without
normals, but the histogram needs the normals of each
point. The computing of normals would traverse all
the points in the dataset, and these normals computing
are independent each other, thus it is beneficial for
parallelism. Some tests indicate that the running time
for normals computing only take 5% of the whole
time for the railway track point cloud with 100000 to
1000000 points. OpenCL does not make any acceler-
ation but even cause performance deterioration for
some additional cost. Thus, the point cloud normals
are computed with the function from PCL directly in
serial method.
To generate PFH, the relative positions and nor-
mals should be computed for all the points in the
neighborhood dataset of each point. Suppose that the
railway track has M points, and the neighborhood has
N points for each query point, then there will be
M×(N
2
-N)loops(with repeated matching) or
M×N
2
(without repeated matching). In each loop,
there are 6 parameters including the 3D coordinate
and normal, without dependence among different
point pairs in the histogram computing, thus it runs
with good parallel performance. In the test, it cost
85% running time to compute the PHF of point pairs.
Therefore, an OpenCL-accelerated PFH is proposed
in this paper by considering the characteristics of PFH
and structure of GPU.
3.2 Optimization of GPU Memory
Access
It is costly to access the global memory (AMD Inc,
2015a), for instance, the speed is 0.14 bit per clock
cycle while it is 8 bit per clock cycle for local memory
access. It is easily costs stalling when the thread ac-
cesses global memory directly because of insufficient
bandwidth, and it will be effective to introduce local
memory to solve the problem (Munshi et al., 2011).
However, the local memory only with few tens KB
space is very small, so when PFH algorithm runs, it
requires to search neighbor point in certain neighbor-
hood. Although the index of query points is sequen-
tial, the index of neighbor points is random and
threads search neighbor points from the whole point
cloud datasets. Thus, it is not able to load all the data
into local memory.
According to this problem, the optimization is
conducted to make the data structure of railway track
point cloud suitable for parallel processing here. The
among of points in point cloud is set as M. In the k
neighborhood search, the point cloud is traversed in
default sequence, and generate a index of neighbor
points for each query points by kd-tree. Each point
has k neighbor points, so the size of neighbor points
index is M×k for the whole point cloud. By defining
two float arrays, the 3D coordinates and normals are
stored separately. Thus, a thread merely accesses lo-
cal memory without frequent global memory access
if a certain query point’s neighbor points are loaded
completely in local memory of GPU. As a result, the
delay of access is reduced greatly. The computing
steps of OpenCL-accelerated PFH is shown as below.
Figure 4: OpenCL-accelerated PFH.
It seems that the normals computing of point
cloud and the kd tree search are achieved by CPU
while the FPH computing is finished by GPU after it
receives the packed 3D coordinates and normals data
with sorting, and the computing results are transferred
back to main memory.
Coordinates of point cloud
Traverse all points and
compute the normals
Point cloud data
with normals
Traverse all points and get
neighbors as set number
Index of
neighbors
Sorted data by index
of neighbors
Coordinates arrays Normal arrays
Coordinates arrays Normal arrays
Copy to Video memory Copy to Video memory
PFH computing
PFH arrays
PFH arrays
Copy to memory
CPU
GPU
CPU
OpenCL-accelerated Point Feature Histogram and Its Application in Railway Track Point Cloud Data Processing
435

3.3 Optimization of Kernel Resource
For the GPU with AMD Graphics Core Next(GCN)
architecture, the local memory of each computing
unit can be divided into 32 banks (AMD Inc, 2015a),
which are accessed by the half-wavefront (32 threads)
unit. If certain bank is accessed by multiple threads
on the same half wavefront boundary, the bank con-
flict will occur except that the 32 threads access the
same bank. In the bank conflict, the system has to wait
for running until all the threads obtain data. There-
fore, serious bank conflict will lead the idle of large
amount computing cycles with low running effi-
ciency.
To reduce the bank conflicts, the data copy for
each thread is generated in private memory as the so-
lution, with the coordinates and the normals of the
two points stored. Additionally, the vector format
data can also reduce the bank conflicts because of its
alignment to bank (Wilt, 2013). Considering the data
structure of railway track point clouds, the 3D coor-
dinates and normals are stored in float3 vectors. For
the limited number of registers, the use of private
memory may cause the leak of registers to DRAM,
with the side effect to performance (Gaster et al.,
2012), which should be avoid. The kernel file here is
built by CodeXL so as to count the used amount of
registers(private memory) and local memory re-
sources shown as Table 1.
Table 1: Used amount of kernel resource.
Resources
Recommended amount
Factual amount
SGPRs
0-102 Registers
30 Registers
VGPRs
0-256 Registers
41 Registers
LDS size
0-32768 bytes
1280 bytes
It is shown that the resources of kernel utility dis-
tribute in the recommended range, and can be built
successfully. Thus, the performance will not be dete-
riorated for the registers leak. For different numbers
of neighbor points, the memory unit load rates are an-
alyzed by CodeXL. The comparison before and after
memory optimization is shown as Figure 5.
As is shown, the load rates after optimization is
obviously higher than that of before, but it declines
with the increasing number of neighbor points, be-
cause with the increment of neighbor points, the data
amount in local memory is increasing linearly while
the computing complexity rises exponentially. If
there is enough neighbor points, the bottleneck will
be on computing unit rather than the load of memory
unit.
Figure 5: Comparison of memory unit load rates.
3.4 The Division of Work-group
In the abstract OpenCL model, the work-group is
composed by the work-items (Scarpino, 2011) ac-
cessing the same resource, in other words, all the
work-items in the work-group share the same local
memory. In the computing of PFH, the neighbor
points for single query point is independent to these
of other query points. Therefore, it is reasonable to
map the neighbor points for single query point to a
work-group of OpenCL.
The efficiency of GPU computing relates to the
size of work-group. For the GPU with AMD GCN ar-
chitecture, a wavefront has 64 work-items, which is
the lowest level that flow control can affect (AMD
Inc, 2015b).It is better when size of work-group is in-
tegral multiple of wavefront (Scarpino, 2011). If the
number of neighbor points is k, and the size of work-
group is N, the number of loops isk
2
. All the compu-
ting goes on if each work-item loop runs for M times
with M×N≥k
2
. The value of k is set by users. With
the small k, it will get a low number of loops k
2
, and
cause excessive idle of work-items if N is set too
large. Using the analysis function of CodeXL, it can
obtain the load percentage of vector arithmetic and
logic unit(VALU) in different work-group sizes.
It demonstrates that the VALU with 64 work-
groups has comparable initialization proportion with
256 ones, but the load proportion is much higher than
the later. Thus, the VALU with 64 work-groups is
more effective corresponding to theoretical analysis.
When the number of neighbor points is large, there is
very little influence of work-group size on VALU in-
itialization proportion for the sufficient utilization of
GPU computing resources. In summary, the size of
work-group is set as a wavefront (that is 64).
0
10
20
30
40
50
60
5 10 20 50
MemUnitBusy (%)
Number of Neighbors
Before Optimization After Optimization
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
436

0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
80.00
90.00
100.00
5 10 20 50
Percent(%)
Number of Neighbors
WorkGroupSize=256 VALUUtilization(%) WorkGroupSize=256 VALUBusy(%)
WorkGroupSize=64 VALUUtilization(%) WorkGroupSize=64 VALUBusy(%)
Figure 6: Load percentage of VALU in different work-
group sizes.
4 TEST
4.1 Test Platform
The hardware and software of test platform is shown
as table 2.
Table 2: Hardware and software of test platform.
CPU
AMD A8-7600B
GPU
Radeon™ R7
Main memory
8G*2 ddr3 1600
Operating System
Windows 10 64bit
Development Environment
Visual Studio 2015
PCL Version
1.7.2 64bit
On the current test platform with the measuring
range 300×400mm, the measured data with 400117
points is obtained from TB/T2314 railway track by
structured light scanner on site.
4.2 Comparison among Tests
The PFH is computed with different numbers of
neighbor points k, and the CPU and GPU times are
recorded. The average value of 3 running times is
taken, with the CPU computing results from the orig-
inal PCL functions and GPU computing results from
the optimized PFH functions by OpenCL. The test re-
sults is shown as Figure 7.
0
100000
200000
300000
400000
500000
600000
5 10 20 50 100
Execution Time (ms)
Number of Neighbors
CPU GPU
Figure 7: Comparison between CPU and GPU PFH compu-
ting.
It indicates that the performance of CPU and GPU
platforms are similar when the number of neighbor
points is small, but the running time increases with
the neighbor points number in CPU platform. For the
GPU platform, the time has very slight increment
with speedup ratio 45 when the number of neighbor
points is 100.
4.3 Analysis of Results
There is some extra cost for using GPU platform,
such as point clouds resorting, kernel building data
copy and transferring back. Thus, the speedup effect
is not obvious because these extra cost take compara-
tively large proportion of running time, but the multi-
thread computing ability works after the number of
neighbor points increases so largely that the extra cost
of GPU become a small ratio in running time while
CPU platform running time is much more than that of
GPU.
5 CONCLUSIONS
Compared with the original algorithm in PCL, the
OpenCL-accelerated PFH proposed is more suitable
for the computing resources utilization, and it takes
advantage of GPU in data processing speed up. In the
non-contact measurement data processing of railway
track, the computing time of PFH is reduced and the
real-time performance of the program is improved. In
addition, the optimized function has excellent com-
patibility for the code reuse only by replacing the dy-
namic link library conveniently.
ACKNOWLEDGEMENTS
Supported by National Natural Science Foundation of
China (Grant No: 51305368), Science and Technol-
ogy Program of Sichuan Province(Grant No:
2013GZX0154) and Fundamental Research Funds
for the Central Universities(Grant No:
2682014BR015).
REFERENCES
Rusu, R. B., Blodow, N., Marton, Z. C. and Beetz, M.,
2008, September. Aligning point cloud views using per-
sistent feature histograms. In Intelligent Robots and
Systems, 2008. IROS 2008. IEEE/RSJ International
Conference on (pp. 3384-3391). IEEE.
OpenCL-accelerated Point Feature Histogram and Its Application in Railway Track Point Cloud Data Processing
437

Rusu, R. B., 2010. Semantic 3D object maps for everyday
manipulation in human living environments. KI-Kün-
stlicheIntelligenz, 24(4), pp.345-348.
Rusu, R. B. and Cousins, S., 2011, May. 3d is here: Point
cloud library (pcl). In Robotics and Automation (ICRA),
2011 IEEE International Conference on (pp. 1-4).
IEEE.
Munshi, A., Gaster, B., Mattson, T. G. and Ginsburg, D.,
2011. OpenCL programming guide. Pearson Education.
Scarpino, M., 2011. OpenCL in action. Westampton: Man-
ning Publications.
Tompson, J. and Schlachter, K., 2012. An introduction to
the opencl programming model. Person Education.
Gaster, B., Howes, L., Kaeli, D. R., Mistry, P. and Schaa,
D., 2012. Heterogeneous Computing with OpenCL: Re-
vised OpenCL 1. Newnes.
Wilt, N., 2013. The cuda handbook: A comprehensive guide
to gpu programming. Pearson Education.
Advanced Micro Devices Inc, 2015. OpenCL Programming
Optimization Guide. http://amd-dev.wpengine.netdna-
cdn.com/wordpress/media/2013/12/AMD_OpenCL_
Programming_Optimization_Guide2.pdf,[2016-01-22].
Advanced Micro Devices Inc, 2015 AMD OpenCL Pro-
gramming User Guide [DB/OL]. http://amd-dev.wpen-
gine.netdna-cdn.com/wordpress/me-
dia/2013/12/AMD_OpenCL_Program-
ming_User_Guide2.pdf, [2016-01-22].
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
438
