
Following a Straight Line in Visual Servoing with Elliptical Projections
Tiantian Shen
1
and Graziano Chesi
2
1
Department of Electronic Information Engineering, College of Polytechnic, Hunan Normal University, Changsha, China
2
Department of Electrical and Electronic Engineering, University of Hong Kong, Hong Kong
Keywords:
Elliptical Projection, Path Planning, Visual Servoing.
Abstract:
The problem of visual servoing to reach the desired location keeping elliptical projections in the camera field
of view (FOV) while following a straight line is considered. The proposed approach is representing the whole
path with seven polynomials of a path abscise: variables in polynomial coefficients for translational path being
zero to represent a minimum path length and for rotational part being adjustable satisfying the FOV limit. The
planned elliptical trajectories are tracked by an image-based visual servoing (IBVS) controller. The proposed
strategy is verified by a simulational case with a circle and a superposed point, where a traditional IBVS
controller directs the camera a detour to the ground, the proposed approach however keeps straight the camera
trajectory and also the circle visible. In addition, a six degrees of freedom (6-DoF) articulated arm mounted
with a pinhole camera is used to validate the proposed method by taking three Christmas balls as the target.
1 INTRODUCTION
Visual servoing is a technique which uses visual in-
formation to control the robot moving to a desired
location. Classical methods include image-based vi-
sual servoing (IBVS) (Hashimoto et al., 1991) and
position-based visual servoing (PBVS) (Taylor and
Ostrowski, 2000). They have well documented weak-
nesses and strengths (Chaumette, 1998b). In order
to better satisfy constraints that arise in visual servo-
ing, there appeared many other approaches: 2 1/2-D
visual servoing (Malis et al., 1999), partition of the
degrees of freedom (Oh and Allen, 2001), switched
controllers (Gans and Hutchinson, 2007; Chesi et al.,
2004), navigation functions (Cowan et al., 2002),
path-planning techniques (Mezouar and Chaumette,
2002; Shen and Chesi, 2012a; Shen et al., 2013), om-
nidirectional vision systems (Fomena and Chaumette,
2008), invariant visual features from spherical projec-
tion (Tahri et al., 2013) and etc. See also the survey
papers (Chaumette and Hutchinson, 2006; Chaumette
and Hutchinson, 2007) and the book (Chesi and
Hashimoto, 2010) for more details.
In addition to pixel coordinates of some repre-
sentational points as visual features used in a con-
troller, other features have also been explored includ-
ing: image moments (Chaumette, 2004; Tahri and
Chaumette, 2005; Fomena and Chaumette, 2008), lu-
minance(Collewet and Marchand, 2010) and some in-
variant features computed from spherical projection
(Tahri et al., 2013). These works allow solid ob-
jects that are more natural than a point, such as cir-
cle, sphere and cylinder to be considered as targets
in visual servoing. High-level control strategies, such
as path-planning techniques, are seldom considered
in these works to enhance the system robustness by
taking into account constraints like the camera field
of view (FOV) limits, convergence in workspace and
etc. This paper belongs to a series of works aiming
at path-planning visual servoing based on image mo-
ments of some solid objects. Our previous work in
(Shen and Chesi, 2012b) used spheres as the target to
achieve multiple constraints including FOV limit of
the sphere, occlusion avoidance among spheres and
collision avoidance in workspace. Two simulation
scenarios were considered: a sphere with two points
and three spheres.
This paper focus on steering a straight camera
path in the Cartesian space, while achieving conver-
gence and camera FOV limit in visual servoing with
elliptical projections (mainly circles). The proposed
approach is representing the whole path with seven
polynomials of a path abscise: variables in polyno-
mial coefficients for translational path being zero to
represent a minimum path length and for rotational
part being adjustable satisfying the FOV limit. The
planned elliptical trajectories are tracked by an image-
based visual servoing controller. The proposed strat-
Shen, T. and Chesi, G.
Following a Straight Line in Visual Servoing with Elliptical Projections.
DOI: 10.5220/0005960400470056
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 47-56
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
47
egy also applies to elliptical projections from spheres.
It is verified by a simulational case with a circle and
a superposed point, where a traditional IBVS con-
troller directs the camera a detour to the ground, the
proposed approach however keeps straight the camera
trajectory and also the circle visible. At last, an exper-
imental case with three Christmas balls as the target
is used to validate again the proposed method.
The paper is organized as follows. Section II in-
troduces the notation and elliptical projection of a cir-
cle. Section III presents the proposed strategy for fol-
lowing a straight line while keeping camera FOV of
circular objects. Section IV shows simulation and ex-
perimental results. Lastly, Section V concludes the
paper with some final remarks.
2 PRELIMINARIES
Let R denote the real number set, I
n
the n ×n iden-
tity matrix, e
i
the i-th column of 3 ×3 identity ma-
trix, 0
n
the n×1 null vector, u∗v the convolution of
vectors u and v, [v]
×
the skew-symmetric matrix of
v ∈ R
3
. Given two camera frames F
◦
= {R,t} and
F
∗
= {I
3
,0
3
}, the pose transformation from F
◦
to F
∗
is expressed as {R
⊤
,−R
⊤
t}. Suppose there is a 3D
point expressed as H = [x, y,z]
⊤
in the camera frame
F
∗
, then 3D coordinates of this point in the frame of
F
◦
is computed as R
⊤
(H −t). Image projection of
this point in camera frame F
◦
is denoted as
X
Y
1
= KR
⊤
(H−t),
where K ∈ R
3×3
is the camera intrinsic parameters
matrix:
K =
f
1
0 u
0 f
2
v
0 0 1
. (1)
In the above matrix, f
1
and f
2
are approximated
values of the camera focal length, image plane of
which has the boundary of ζ
x
×ζ
y
with ζ
x
= 2u and
ζ
x
= 2v. Elliptical projections are formed from either
spheres or circles. It is assumed that in the camera
frame of F
∗
= {I
3
,0
3
}, a circle is described by the in-
tersection of a sphere and a plane (Chaumette, 1998a):
(
(x−x
o
)
2
+ (y−y
o
)
2
+ (z−z
o
)
2
= r
2
,
α(x−x
o
) + β(y−y
o
) + γ(z−z
o
) = 0.
(2)
The sphere is centered at o = [x
o
,y
o
,z
o
]
⊤
with r
as its radius and the plane is determined by the point
o and a normal vector [α,β, γ]
⊤
. The corresponding
projection is in the form of an ellipse:
K
0
X
2
+ K
1
Y
2
+ 2K
2
XY + 2K
3
X + 2K
4
Y + K
5
= 0,
with
K
0
= a
2
△+ 1−2ax
0
,
K
1
= b
2
△+ 1−2by
0
,
K
2
= ab△−bx
0
−ay
0
,
K
3
= ac△−cx
0
−az
0
,
K
4
= bc△−cy
0
−bz
0
,
K
5
= c
2
△+ 1−2cz
0
.
(3)
In the above function, a, b, c and △ are given by:
a = α/δ,b = β/δ,c = γ/δ,
△ = x
2
0
+ y
2
0
+ z
2
0
−r
2
,
δ = x
0
α+ y
0
β+ z
0
γ
1/z = aX + bY + c.
(4)
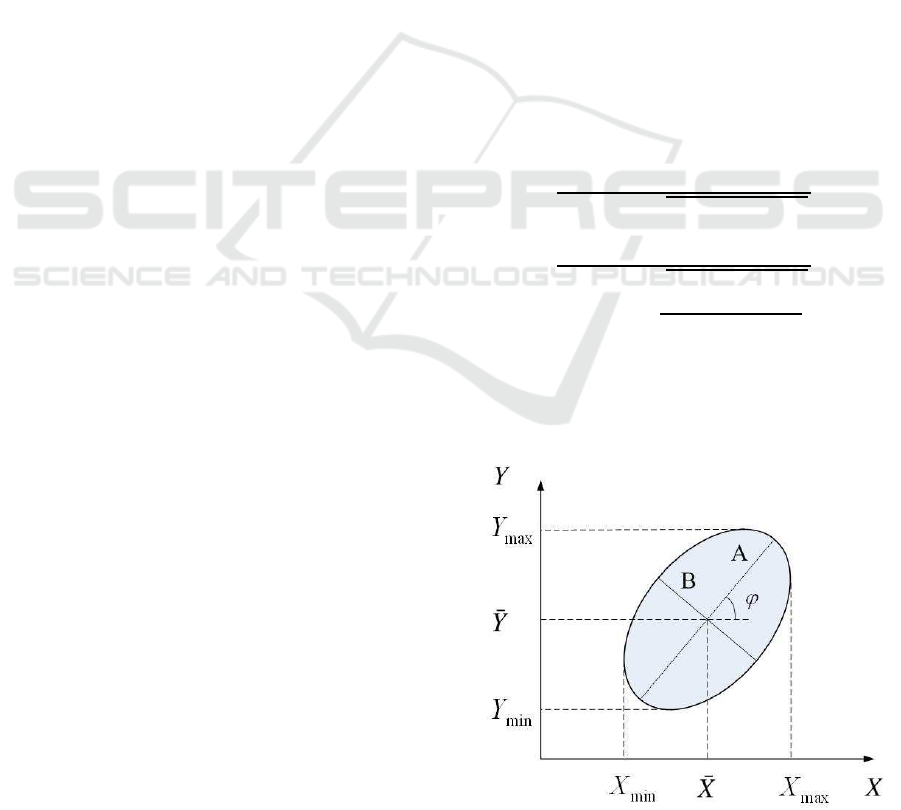
In the image plane, the ellipse is displayed in Fig.1
with its centroid, lengths of major and minor radius
and direction angle expressed in K
i
,i = 0,..., 5:
¯
X = (K
1
K
3
−K
2
K
4
)/(K
2
2
−K
0
K
1
),
¯
Y = (K
0
K
4
−K
2
K
3
)/(K
2
2
−K
0
K
1
),
A
2
=
2(K
0
¯
X
2
+ 2K
2
¯
X
¯
Y + K
1
¯
Y
2
−K
5
)
K
0
+ K
1
+
q
(K
1
−K
0
)
2
+ 4K
2
2
,
B
2
=
2(K
0
¯
X
2
+ 2K
2
¯
X
¯
Y + K
1
¯
Y
2
−K
5
)
K
0
+ K
1
−
q
(K
1
−K
0
)
2
+ 4K
2
2
,
E = (K
1
−K
0
+
q
(K
1
−K
0
)
2
+ 4K
2
2
)/2K
2
,
ϕ = arctan(E).
(5)
Degenerating case when projection boils down
into a segment will be avoided in the proposed path
Figure 1: Elliptical projection.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
48

planning algorithm, therefore not considered here.
Extreme values of elliptical projection in Fig.1 is
given by (Shen and Chesi, 2012b): X
max
=
¯
X +
√
µ
20
,
X
min
=
¯
X −
√
µ
20
,
Y
max
=
¯
Y +
√
µ
02
, Y
min
=
¯
Y −
√
µ
02
, where µ
ij
is
the central image moments of the pertinent elliptical
projection, whose centroid is calculated from raw im-
age moments m
ij
in the form of
¯
X = m
10
/m
00
and
¯
Y = m
01
/m
00
with m
00
calculates the area of the el-
lipse.
Problem. The problem consists of steering an eye-in-
hand robotic arm towards the desired location follow-
ing a straight line of the camera in the Cartesian space,
with the help of some elliptical projections. Conver-
gence and FOV limit are to be imposed when features
are mainly computed from image moments of ellipti-
cal projections.
3 PATH PLANNING
Before visual servoing, a straight path of the cam-
era in the Cartesian space will be planned in advance.
Planning of this straight path needs two end positions
of the camera, this relative camera displacement is es-
timated via a virtual VS method based on image mo-
ments. However, it is not enough by only restraining
in the Cartesian space, since corresponding image tra-
jectories may go out of the image boundaries and fail
later visual servoing applications. Polynomial mini-
mization solves for the FOV problem and generates a
satisfactory trajectory by adjusting the rotational path.
The planned elliptical trajectories are then tracked by
an IBVS controller in order to follow a straight cam-
era path in the Cartesian space, at the same time with-
out losing target features.
3.1 Two Ends of a Path
Requirement of a straight path in the Cartesian space
and also camera FOV limits motivate a path-planning
method that gives a satisfactory image trajectory to
follow. Relative camera pose between the initial and
the desired positions will serve as boundaries for sub-
sequent path optimization. The target location and
model are assumed to be known as a priori and two
camera views of the target are given. From two views
of the target and an approximated camera intrinsic pa-
rameters in (1), camera pose between F
∗
and F
o
is es-
timated by virtually moving the camera from F
∗
to F
o
with a traditional IBVS controller (Tahri et al., 2010):
T
c
(t) = −λ
1
ˆ
L
+
(s(t) −s
∗
), (6)
where T
c
(t) is a camera velocity screw at time t,
λ
1
is a positive gain, s(t) holds the current feature
values and s
∗
the desired feature values,
ˆ
L
+
is the
pseudo-inverse of the estimated interaction matrix
corresponding to the selected features. Features of a
circle is usually computed from image moments:
s = [
¯
X,
¯
Y, µ
20
,µ
11
,µ
02
]
⊤
. (7)
As specified in Section 2,
¯
X,
¯
Y are pixel coordi-
nates of the centroid of the elliptical projection. The
remaining central image moments are related to el-
lipsoid parameters in the following way (Chaumette,
1998a):
µ
20
= (A
2
+ B
2
E
2
)/(1+ E
2
),
µ
11
= E(A
2
−B
2
)/(1+ E
2
),
µ
02
= (A
2
E
2
+ B
2
)/(1+ E
2
).
(8)
The interaction matrix associated with the fea-
ture set in (7) is referred to the work in (Chaumette,
1998a). In order to reduce the chance of local min-
imum, we will add two more features, that are pixel
coordinates of a point on the circle, to the feature set
of a circle in (7). When spheres are taken as a target,
we consider at least three spheres to reduce the possi-
bility of nonsingular occurrence of the interaction ma-
trix L. Feature set for three spheres consists of nine
values based on the computation of image moments:
s =
h
¯
X
1
,
¯
Y
1
,
µ
02
1
+µ
20
1
2
,
¯
X
2
,
¯
Y
2
,
µ
02
2
+µ
20
2
2
,
¯
X
3
,
¯
Y
3
,
µ
02
3
+µ
20
3
2
i
⊤
.
(9)
The associated interaction matrix may be found
in our previous work (Shen and Chesi, 2012b). The
camera position is updated iteration by iteration by
taking steps computed from velocity screw T
c
(t) and
time interval until feature error |s(t) − s
∗
| is small
enough. If no local minima problem exists, the ul-
timate camera position will be utilized in the subse-
quent polynomial parameterization and optimization
of the camera path.
3.2 Polynomial Minimization
To describe the camera path with boundaries on both
sides, we use a path abscise w ∈ [0,1] with its value 0
implying the start of the path F
o
, and value 1 meaning
the end of the path F
∗
. Transition from F
o
to F
∗
is
developed from the results in Section 3.1 and denoted
as {R,t}. Thus we have:
{R(0),t(0)}= { I
3
,0
3
},
{R(1),t(1)}= { R,t} .
(10)
Between the above two camera poses, camera path
{R(w),t(w)} is intended to satisfy the FOV limits
Following a Straight Line in Visual Servoing with Elliptical Projections
49

when t(w) is a straight line. With path abscise w
changes from 0 to 1, camera translation t(w) linearly
changes from 0
3
to t, camera rotation R(w) changes
from I
3
to R. In between these two ends, we use
first-order polynomials in w to model translational
path and second-order polynomials in w the rotational
quaternions:
(
q(w) = U·[w
2
,w, 1]
⊤
,
t(w) = V·[w, 1]
⊤
,
(11)
with
q(w) =
sin
θ(w)
2
a(w)
cos
θ(w)
2
. (12)
In quaternion representation, θ(w) ∈ (0,π) and
a(w) ∈ R
3
are respectively rotation angle and axis of
R(w) such that R(w) = e
θ(w)[a(w)]
×
.
Boundaries defined in (10) will be satisfied by as-
signing the first and last columns in the coefficient
matrices in (11) with the other entries variable:
U = [ u
⊤
1
,u
⊤
2
,u
⊤
3
,u
⊤
4
]
⊤
= [q−b, b,0
3
],
V = [ v
⊤
1
,v
⊤
2
,v
⊤
3
]
⊤
= [t,0
3
],
(13)
where u
⊤
i
∈R
1×3
, i = 1,··· ,4 are the i-th row of ma-
trix U and v
⊤
j
∈ R
1×2
, j = 1, 2,3 the j-th row of ma-
trix V. In (13), vector b is variable and we assign it
with an initial value of 0
4
. With this initial value of
b, we can plot the parameterized path for the scenario
in Fig 2 and then we have a straight path in the Carte-
sian space as shown in Fig. 3 (a). However, Fig. 3 (b)
shows that the corresponding image trajectory goes
out of the image boundary.
Therefore, we need to find an appropriate value of
b in (13) that lets image trajectories fall within the im-
age boundaries. For a circle, depth of the circle center
is meant to be larger than the circle radius. In addi-
tion, extreme values of the elliptical projection that is
drawn in Fig. 1 are restricted to being located within
the image size:
z
o
−r > 0,
X
max
<
ζ
x
2f
,
X
min
> −
ζ
x
2f
,
Y
max
<
ζ
y
2f
,
Y
min
> −
ζ
y
2f
,
(14)
where X
max
, Y
max
, X
min
and Y
min
are computed from
image moments of the sphere. They are expressed as:
X
max
= (K
2
K
4
−K
1
K
3
+
p
G
2
)/(K
0
K
1
−K
2
2
),
X
min
= (K
2
K
4
−K
1
K
3
−
p
G
2
)/(K
0
K
1
−K
2
2
),
G
2
= (K
1
K
3
−K
2
K
4
)
2
−(K
0
K
1
−K
2
2
)(K
1
K
5
−K
2
4
),
Y
max
= (K
2
K
3
−K
0
K
4
+
p
G
3
)/(K
0
K
1
−K
2
2
),
Y
min
= (K
2
K
3
−K
0
K
4
−
p
G
3
)/(K
0
K
1
−K
2
2
),
G
3
= (K
0
K
4
−K
2
K
3
)
2
−(K
0
K
1
−K
2
2
)(K
0
K
5
−K
2
3
).
In order to realize conditions in (14), we wish to
have z
o
−r, X
max
, Y
max
, X
min
and Y
min
to be polynomi-
als in the path abscise w. After path parameterization,
in any camera frame of {R(w),t(w)}, we can assure
that the circle center and the normal vector in (2) are
polynomials in the path abscise. Let
[h
⊤
1
,h
⊤
2
,h
⊤
3
]
⊤
= [0
3
,o] −V, (15)
which indicates h
⊤
j
, j = 1, 2,3 the j-th row of matrix
[0
3
,o] −V, where o is the circle center in (2) and V is
coefficient matrix in (11). After camera displacement
caused by varying w, polynomial coefficients of the
circle center and the normal vector are computed as:
p
x
o
= r
11
∗h
1
+ r
21
∗h
2
+ r
31
∗h
3
,
p
y
o
= r
12
∗h
1
+ r
22
∗h
2
+ r
32
∗h
3
,
p
z
o
= r
13
∗h
1
+ r
23
∗h
2
+ r
33
∗h
3
,
p
α
= αr
11
+ βr
21
+ γr
31
,
p
β
= αr
12
+ βr
22
+ γr
32
,
p
γ
= αr
13
+ βr
23
+ γr
33
,
(16)
where p
x
o
,p
y
o
,p
z
o
∈ R
7
and p
α
,p
β
,p
γ
∈ R
5
, r
ij
∈
R
5
are polynomial coefficients of the entry lie in the
i-th row and the j-th column of the rotation matrix.
Specifically, we have
r
11
= u
1
∗u
1
−u
2
∗u
2
−u
3
∗u
3
+ u
4
∗u
4
,
r
12
= 2(u
1
∗u
2
−u
3
∗u
4
),
r
13
= 2(u
1
∗u
3
+ u
2
∗u
4
),
r
21
= 2(u
1
∗u
2
+ u
3
∗u
4
),
r
22
= −u
1
∗u
1
+ u
2
∗u
2
−u
3
∗u
3
+ u
4
∗u
4
,
r
23
= 2(u
2
∗u
3
−u
1
∗u
4
),
r
31
= 2(u
1
∗u
3
−u
2
∗u
4
),
r
32
= 2(u
2
∗u
3
+ u
1
∗u
4
),
r
33
= −u
1
∗u
1
−u
2
∗u
2
+ u
3
∗u
3
+ u
4
∗u
4
.
(17)
From equation (16), we can deduce that z
0
−r in
(14) is a six order polynomialin w with its coefficients
to be
p
z
o
−r
= [0
⊤
6
,r] −p
z
o
. (18)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
50

Since extreme values X
max
, Y
max
, X
min
and Y
min
are
functions of K
i
, i = 1, ··· ,5 as given in (3.2), this for-
mulation will troubles polynomial parametrization of
these values. In order to transform inequalities in (14)
concerning these extreme values into polynomials, let
k
i
= δ
2
K
i
,i = 1,. .. ,5, (19)
and we will have polynomial coefficients of all of k
i
as follows:
p
△
= p
x
o
∗p
x
o
+ p
y
o
∗p
y
o
+ p
z
o
∗p
z
o
−[0
⊤
11
,r
2
],
p
δ
= p
α
∗p
x
o
+ p
β
∗p
y
o
+ p
γ
∗p
z
o
,
p
k
0
= p
α
∗p
α
∗p
△
+ p
δ
∗p
δ
−2p
α
∗p
δ
∗p
x
o
,
p
k
1
= p
β
∗p
β
∗p
△
+ p
δ
∗p
δ
−2p
β
∗p
δ
∗p
y
o
,
p
k
2
= p
α
∗p
β
∗p
△
−p
β
∗p
δ
∗p
x
o
−p
α
∗p
δ
∗p
y
o
,
p
k
3
= p
α
∗p
γ
∗p
△
−p
γ
∗p
δ
∗p
x
o
−p
α
∗p
δ
∗p
z
o
,
p
k
4
= p
β
∗p
γ
∗p
△
−p
γ
∗p
δ
∗p
y
o
−p
β
∗p
δ
∗p
z
o
,
p
k
5
= p
γ
∗p
γ
∗p
△
+ p
δ
∗p
δ
−2p
γ
∗p
δ
∗p
z
o
.
(20)
All of the above p
k
i
∈ R
17
, i = 1, ··· ,5 are poly-
nomial coefficients of k
i
, i = 1,. .. ,5. Let
g
1
= z
o
−r,
g
8
= k
0
k
1
−k
2
2
,
(21)
we have first
g
2
= (k
1
k
3
−k
2
k
4
)
2
−g
8
(k
1
k
5
−k
2
4
),
g
3
= (k
0
k
4
−k
2
k
3
)
2
−g
8
(k
0
k
5
−k
2
3
).
(22)
Positivity of g
2
and g
3
ensures that the maxi-
mum and minimum values of elliptical projection in
the either X or Y direction are unequal. This con-
straint avoids the degenerating case: elliptical projec-
tion boils down to a segment. Image boundary limits
are developed as follows:
g
4
= g
8
ζ
x
2f
+ k
2
k
4
−k
1
k
3
2
−g
8
g
2
> 0,
g
5
= g
1
ζ
x
2f
−k
2
k
4
+ k
1
k
3
2
−g
8
g
2
> 0,
g
6
= g
8
ζ
y
2f
+ k
2
k
3
−k
0
k
4
2
−g
8
g
3
> 0,
g
7
= g
1
ζ
y
2f
−k
2
k
3
+ k
0
k
4
2
−g
8
g
3
> 0.
(23)
Since k
i
, i = 1,..., 5 are polynomials, therefore g
j
, j =
1,··· ,7 are also polynomials in w. Their coefficients
are computed from (18) and p
k
i
, i = 1, ··· ,5 in (20).
Take g
1
and g
2
for example, polynomial coefficients
of g
1
is actually: p
g
i
= p
z
o
−r
, and coefficients of g
2
is
computed as:
p
k
1
k
3
−k
2
k
4
= p
k
1
∗p
k
3
−p
k
2
∗p
k
4
,
p
k
1
k
5
−k
4
k
4
= p
k
1
∗p
k
5
−p
k
4
∗p
k
4
,
p
g
8
= p
k
0
∗p
k
1
−p
k
2
∗p
k
2
,
p
g
2
= p
k
1
k
3
−k
2
k
4
∗p
k
1
k
3
−k
2
k
4
−p
g
8
∗p
k
1
k
5
−k
4
k
4
.
(24)
Similar computation process applies to the polyno-
mial coefficients of g
j
, j = 3,··· ,7. Provided the
initial value of b in (13) is given, we derive values
of U and V and bring them sequentially into (15),
(17), (16), (18) and (20). Items in (20) are utilized
in the computation of p
g
2
in (24). In order to ensure
the value of g
2
is positive when w ∈ (0,1), we take
the derivative of p
g
2
and solve for the corresponding
w ∈ (0,1) that give zero derivatives. If such w exist,
then a local minimum of g
j
can be found at such w
values. Take all of the positivity requirements of g
j
,
j = 1,··· , 7 together, we first find local minimums for
each g
j
, j = 1, ··· ,7, and again the minimum of all of
these local minimums and denote it as g
∗
:
g
∗
= minimum
7
j=1
(minimum
w∈(0,1)
(g
j
)),
b
∗
= min
b
(−g
∗
).
(25)
No action will be taken if the value of g
∗
is pos-
itive, otherwise a minimization of −g
∗
will be con-
ducted until it converts its sign. Take a synthetic scene
of a circle as an example, Fig. 2 (a) consists of two
camera positions and a circle as a target. Fig. 2 (b)-
(c) are two views of the target. Relative camera pose
between F
∗
and F
o
is estimated using a virtual VS
method demonstrated in Section 3.1. A straight path
is then planned between F
∗
and F
o
, as shown in Fig.
3 (c). In this scenario, path planning with initial value
of b, that is 0
3
, will cause the image boundary vio-
lated though camera trajectory in the Cartesian space
is a straight line, see Fig. 3 (d). This situation indi-
cates that polynomial curve of g
7
will across below
the horizontal axis over w ∈ (0,1), and therefore g
∗
is negative. We search for appropriate value of b by
minimizing −g
∗
with MATLAB tool till g
∗
> 0. Once
the minimization result is obtained, we denote it as b
∗
and bring it into (13). Till this end, a planned path that
converges to the desired camera location following a
straight line while satisfying the camera FOV limit is
found, see Fig. 3 (e)-(f) as an example.
3.3 Tracking Image Trajectories
The robot manipulator is going to be servoed by track-
ing an well planned image trajectory. We substitute
the desired feature value s
∗
in (6) with the planned
feature value at time t, which is denoted as s
p
(w
t
)
Following a Straight Line in Visual Servoing with Elliptical Projections
51
−35
−30
−25
−20
−15
−10
−5
0
0
10
20
0
5
10
z
F
*
x
F
o
y
(a)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(b)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(c)
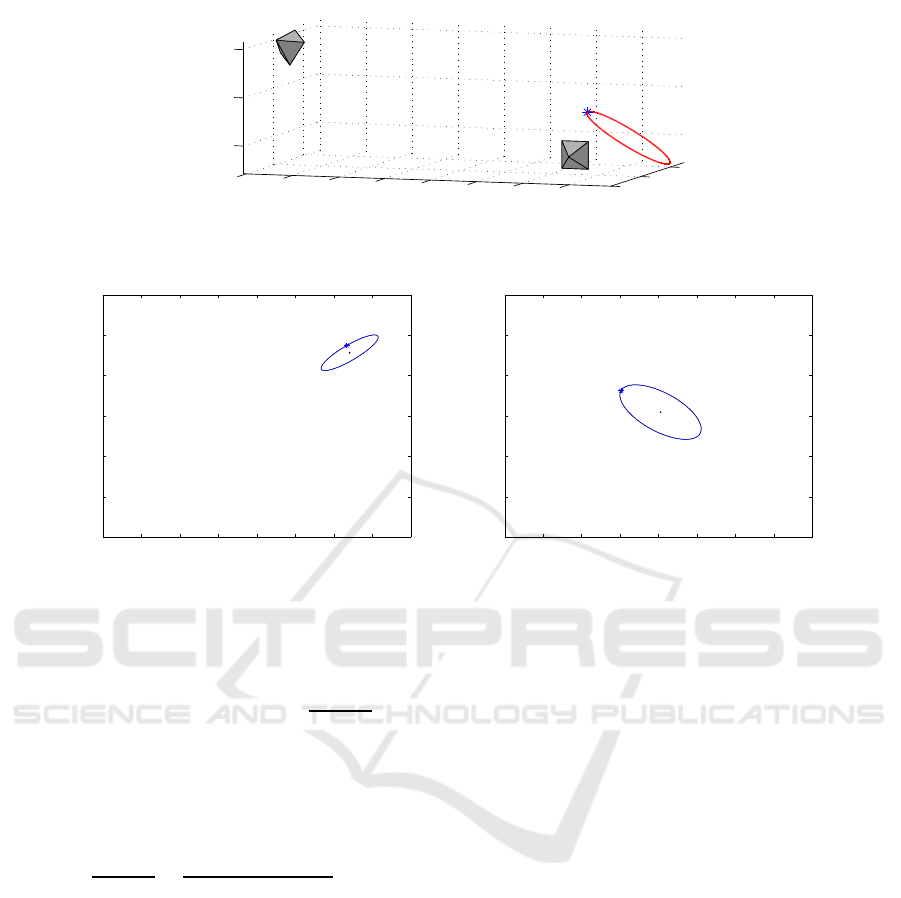
Figure 2: Scenery with a circle and a point on the circle. (a) Scenario (b) Camera view in F
o
. (c) Camera view in F
∗
.
with w
t
= 1−e
−tλ
2
:
T
c
= −λ
1
ˆ
L
+
(s(t) −s
p
(w
t
)) + λ
3
ˆ
L
+
∂s
p
(w
t
)
∂t
, (26)
The term λ
3
ˆ
L
+
∂s
p
(w
t
)/∂t allows to compensate
the tracking error (Mezouar and Chaumette, 2002).
The partial derivative of the planned feature set is
computed as:
∂s
p
(w
t
)
∂t
=
s
p
(w
t+∆t
) −s
p
(w
t
)
∆t
. (27)
4 EXAMPLES
The first example aims to follow a straight line in
the Cartesian space while keeping camera FOV of a
circle. Synthetic scene is generated using MATLAB
for the first example. The second example deals with
three Christmas balls. The algorithm keeps visibility
of all of the three balls in VS process while following
a straight line.
4.1 Simulation with a Circle
The scenario for path planning with a circle is il-
lustrated in Fig.2 (a). In the desired camera frame
of F
∗
= {I
3
,0
3
}, model parameters of the circle are
given as [x
o
,y
o
,z
o
] = [0,0,20]
⊤
, [α,β, γ] = [0,0,1]
⊤
and r = 5mm. A point on the circle is also used to
contribute features, shown as a star mark in Fig.2 (a).
The initial and the desired camera views of the tar-
get are respectively shown in Fig.2 (b-c). From these
two views, we extract features from elliptical pro-
jections of the circle and then utilize these features
to complete planning a straight path from the initial
camera frame F
o
= {e
[ρ]
×
,[−35,10,10]
⊤
mm} with
ρ = [π/12,π/4,−π/6] to the desired camera frame
F
∗
. Along this straight path, the elliptical projections
of the circle are expected to be always kept within
the camera view. Intrinsic parameters of the camera
are approximated with f
1
= 456, f
2
= 448, u = 403,
v = 301 in (1).
Relative camera pose between F
∗
and F
o
is es-
timated using a virtual VS method based on the se-
lected features. Fig. 3 (a-b) shows the camera tra-
jectory and image trajectories generated using vir-
tual VS, where the camera trajectory is extremely
close to the ground. In order to achieve the shortest
travel length, a straight path in the Cartesian space is
planned in Fig. 3 (c). With initial coefficient values in
the polynomial parametrization, elliptical projections
of the circle will go beyond the image boundary and
fail a real visual servoing application, see Fig. 3 (d).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
52

−35
−30
−25
−20
−15
−10
−5
0
0
10
20
0
5
10
z
F
*
x
y
(a)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(b)
−35
−30
−25
−20
−15
−10
−5
0
0
10
20
0
5
10
z
F
*
x
y
(c)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(d)
−35
−30
−25
−20
−15
−10
−5
0
0
10
20
0
5
10
z
F
*
x
y
(e)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(f)
−35
−30
−25
−20
−15
−10
−5
0
0
10
20
0
5
10
z
F
*
x
F
o
y
(g)
0 100 200 300 400 500 600 700 800
0
100
200
300
400
500
600
(h)
Figure 3: Path planning with a circle and a point on the circle. (a) Camera trajectory in virtual IBVS. (b) Image trajectories
in virtual IBVS. (c) Planned path in workspace and camera postures without optimization. (d) Image trajectories without
optimization. (e) Planned path and camera postures in workspace. (f) Planned image trajectories. (g) Trajectory in the
Cartesian space generated when applying an IBVS controller. (h) Image trajectories generated when applying an IBVS
controller.
Following a Straight Line in Visual Servoing with Elliptical Projections
53

Therefore, minimization of −g
∗
in (25) is performed
to make an adjustment, after which a satisfactory im-
age trajectory is generated as shown in Fig. 3 (f). The
planned image trajectory is brought into an IBVS con-
troller in (26), where positive gains λ
1
, λ
2
and λ
3
are
respectively taken as 0.015, 0.01 and 0.4. An instant
camera velocity screw T
c
is produced and used to di-
rect the camera moving towards the desired location
by iterations. Data recorded at each iteration are plot-
ted in Fig. 3 (g)-(h).
(a) (b)
(c) (d)
Figure 4: Experiment with three Christmas balls. (a) Ini-
tial robot/camera pose. (b) Desired robot/camera pose. (c)
Initial view. (d) Desired View.
4.2 Experiment with Christmas Balls
This is a very simple experimental example validating
the proposed strategy. The robot used for the exper-
iment is a Staubli RX60 6-DoF articulated arm, on
the robot end-effector mounted a video camera. The
camera is calibrated with its intrinsic parameters as
follows:
K =
851.76868 0 329.00000
0 851.76868 246.00000
0 0 1
.
(28)
The target consists of three Christmas balls with
approximately the same radius of 20 mm. Positions
of these three ball centers in the desired camera frame
F
∗
are approximately
O
1
= [25.0183,−0.0005,344.8407]
⊤
mm,
O
2
= [−48.6174, −2.4141,412.1984]
⊤
mm,
O
3
= [−128.5265, −39.0117,414.3849]
⊤
mm.
Fig. 4 shows the two configurations and correspond-
ing camera views. Displacement between the desired
and the initial camera poses is estimated by virtual vi-
sual servoing:
R =
0.9399 0.3415 −0.0000
−0.3415 0.9399 0.0001
0.0001 −0.0001 1.0000
,
t = (−44.2772, −0.0353, −0.0020)
⊤
mm.
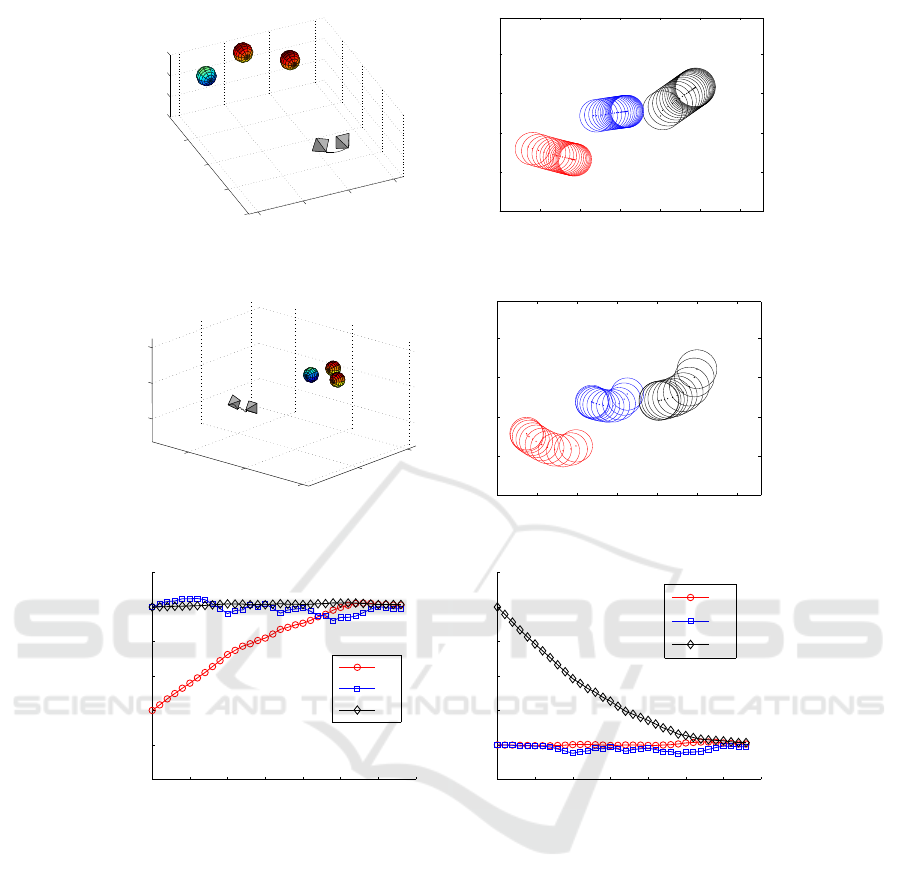
Trajectories generated in virtual VS process without
path planning are plotted in Fig. 5 (a). In virtual
VS, image trajectories of sphere centers are straight
lines, however camera trajectory is not a straight
one. After path planning and applying an IBVS con-
troller to follow the planned path, real camera tra-
jectory and image trajectories of the target are dis-
played in Fig. 5 (b)-(c), they are different from the
ones generated in virtual VS process. Iterations of
camera translation and rotation are recorded and plot-
ted in Fig. 5 (d)-(e), which show the convergence in
both camera translation and rotation. It is assumed
that iteration number in real-time step-by-step mov-
ing robotic application is denoted as t, trajectories
q
R
(t) = [q
4
(t),q
5
(t),q
6
(t)]
⊤
in Fig. 5 (e) are Cayley
representation (Craig, 2005) of the associated rotation
matrix R(t):
[q
R
(t)]
×
= (R(t) −I
3
)(R(t) + I
3
)
−1
. (29)
Fluctuations exist in the iterations mainly due to
coarse feature extraction and the value of tracking
gain used for computing the next arriving position in
VS process for the step-by-step moving robot.
5 CONCLUSIONS
This paper proposes a straight path planning approach
for visual servoing with elliptical projections. Cir-
cles and spheres may project into traditional cameras
as ellipsoids. Constrains with spheres are considered
in our previous work, this paper mainly solves for
problems with circular objects, specifically the con-
vergence and FOV limit while following a straight
line in the Cartesian space. Simulation with a cir-
cle and experiment with balls validate the proposed
path planning approach. For future work, the impact
of image noises imported from the area-based feature
extraction on the precision of pose estimation and the
subsequent path planning needs to be taken case of.
More complicated objects are going to be explored,
such as a cup to be seen as a group of two lines or two
circles.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
54
−200
−100
0
100
0
100
200
300
−100
−50
0
50
x [mm]
z [mm]
y [mm]
0 100 200 300 400 500 600
0
100
200
300
400
[pixel]
[pixel]
(a)
−200
0
200
200
400
−100
0
100
z [mm]
F
*
F
o
x [mm]
y [mm]
O
1
O
3
O
2
(b)
0 100 200 300 400 500 600
0
100
200
300
400
[pixel]
[pixel]
(c)
0 5 10 15 20 25 30 35
−10
−8
−6
−4
−2
0
2
iteration
translation [cm]
q
1
q
2
q
3
(d)
0 5 10 15 20 25 30 35
−5
0
5
10
15
20
25
iteration
rotation [deg]
q
4
q
5
q
6
(e)
Figure 5: Experiment with three Christmas balls. (a) Virtual Camera path. (b) Virtual image trajectories. (c) Real camera
path. (d) Real image trajectories. (e) Camera translation evolution. (f) Camera rotation evolution.
REFERENCES
Chaumette, F. (1998a). De la perception `a l’action:
l’asservissement visuel; de l’action `a la perception:
la vision active. Habilitation `a diriger les recherches,
Universit´e de Rennes 1.
Chaumette, F. (1998b). Potential problems of stability and
convergence in image-based and position-based visual
servoing. In Kriegman, D., Hager, G., and Morse,
A. S., editors, The Confluence of Vision and Control,
pages 66–78. LNCIS Series, No 237, Springer-Verlag.
Chaumette, F. (2004). Image moments: a general and useful
set of features for visual servoing. IEEE Transactions
on Robotics, 20(4):713–723.
Chaumette, F. and Hutchinson, S. (2006). Visual servo con-
trol, part I: Basic approaches. IEEE Robotics and Au-
tomation Magazine, 13(4):82–90.
Chaumette, F. and Hutchinson, S. (2007). Visual servo con-
trol, part II: Advanced approaches. IEEE Robotics and
Automation Magazine, 14(1):109–118.
Chesi, G. and Hashimoto, K., editors (2010). Visual Ser-
voing via Advanced Numerical Methods. Springer-
Verlag.
Chesi, G., Hashimoto, K., Prattichizzo, D., and Vicino, A.
(2004). Keeping features in the field of view in eye-
in-hand visual servoing: A switching approach. IEEE
Transactions on Robotics, 20(5):908–914.
Collewet, C. and Marchand, E. (2010). Luminance: a
new visual feature for visual servoing. In Chesi, G.
and Hashimotos, K., editors, Visual Servoing via Ad-
Following a Straight Line in Visual Servoing with Elliptical Projections
55

vanced Numerical Methods, pages 71–90. LNCIS Se-
ries, No 401, Springer-Verlag.
Cowan, N., Weingarten, J., and Koditschek, D. (2002). Vi-
sual servoing via navigation functions. IEEE Trans-
actions on Robotics and Automation, 18(4):521–533.
Craig, J. J. (2005). Introduction to Robotics: Mechanics
and Control. Pearson Education, 3rd edition.
Fomena, R. T. and Chaumette, F. (2008). Visual servoing
from two special compounds of features using a spher-
ical projection model. In IROS’08, 21st IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems, pages 3040–3045, Nice, France.
Gans, N. and Hutchinson, S. (2007). Stable visual servoing
through hybrid switched-system control. IEEE Trans-
actions on Robotics, 23(3):530–540.
Hashimoto, K., Kimoto, T., Ebine, T., and Kimura, H.
(1991). Manipulator control with image-based visual
servo. In ICRA’91, 8th IEEE International Confer-
ence on Robotics and Automation, pages 2267–2272,
San Francisco, CA.
Malis, E., Chaumette, F., and Boudet, S. (1999). 2 1/2 d
visual servoing. IEEE Transactions on Robotics and
Automation, 15(2):238–250.
Mezouar, Y. and Chaumette, F. (2002). Path planning for
robust image-based control. IEEE Transactions on
Robotics and Automation, 18(4):534–549.
Oh, P. Y. and Allen, P. K. (2001). Visual servoing by par-
titioning degrees of freedom. IEEE Transactions on
Robotics and Automation, 17(1):1–17.
Shen, T. and Chesi, G. (2012a). Visual servoing path-
planning for cameras obeying the unified model. Ad-
vanced Robotics, 26(8–9):843–860.
Shen, T. and Chesi, G. (2012b). Visual servoing path-
planning with spheres. In ICINCO’12, 9th Interna-
tional Conference on Informatics in Control, Automa-
tion and Robotics, pages 22–30, Rome, Italy.
Shen, T., Radmard, S., Chan, A., Croft, E. A., and Chesi,
G. (2013). Motion planning from demonstrations and
polynomial optimization for visual servoing applica-
tions. In IROS’13, 26th IEEE/RSJ International Con-
ference on Intelligent Robots and Systems, pages 578–
583, Tokyo Big Sight, Japan.
Tahri, O., Araujo, H., Chaumette, F., and Mezouar, Y.
(2013). Robust image-based visual servoing using in-
variant visual information. Robotics and Autonomous
Systems, 61(12):1588–1600.
Tahri, O. and Chaumette, F. (2005). Point-based and region-
based image moments for visual servoing of planar
objects. IEEE Transactions on Robotics, 21(6):1116–
1127.
Tahri, O., Mezouar, Y., Chaumette, F., and Araujo, H.
(2010). Visual servoing and pose estimation with
cameras obeying the unified model. In Chesi, G.
and Hashimotos, K., editors, Visual Servoing via Ad-
vanced Numerical Methods, pages 231–252. LNCIS
Series, No 401, Springer-Verlag.
Taylor, C. and Ostrowski, J. (2000). Robust vision-based
pose control. In ICRA’00, 17th IEEE International
Conference on Robotics and Automation, pages 2734–
2740, San Francisco, CA.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
56
