Modelling Population Growth, Shrinkage and Aging using a Hybrid

Simulation Approach: Application to Healthcare

Bożena Mielczarek and Jacek Zabawa

Department of Operations Research, Faculty of Computer Science and Management, Wrocław University of Technology,

Wybrzeże Wyspiańskiego 27, PL50-370 Wrocław, Poland

Keywords: Hybrid Simulation, System Dynamics, DES, Population, Age Pyramid.

Abstract: This paper describes a hybrid simulation model that integrates the System Dynamic approach with discrete

time control to formulate the projections of population evolution. The study relies on historical demographic

data and the officially formulated scenarios for the most likely population projections developed for the

region. The results of the simulation experiments provide valuable insights into dynamics of regional

demographic trends and offer a well-defined starting point for future research in the health policy field. The

intensity and structure of the demand for healthcare services depend heavily on age-gender profiles that

change due to ongoing extensions of the average expected length of life, the aging of population, the

continuing trend of declining number of births and the steadily growing number of deaths. The preliminary

findings show promise in using the hybrid simulation approach for more advanced exploration of

demography dependent health policy issues.

1 INTRODUCTION

Credible demographic forecasts are an essential and

imperative input for a range of economic studies.

The precise replication of population structure

affects the proper examination of long-term

implications of population dynamics on

macroeconomic performances. Quantitative

evaluations that include the effects of population

changes must consider demographic forecasts. There

is, for example, considerable interest in the impact

of population aging on economic growth and the

macro-economy in general (Lisenkova et al. 2013).

Financial sustainability of social security systems

depends on the size of the older population and the

percentage of insured employees (Tian & Zhao

2016). Population dynamics affect urban

development and land use (Lauf et al. 2016).

Population projections are utilized as inputs in health

policy models (Ansah et al. 2014).

One approach to including the population

forecast in the scientific analysis assumes that the

population projections are derived from census data

and are based on moderate demographic scenarios

developed and published by national statistical units

or world-wide organizations such as the World Bank

or the United Nations. Another approach is to utilize

the stochastic forecasting method to predict

population evolution. Time series modelling

techniques are frequently adopted to estimate the

basic input parameters such as fertility, mortality

and migration rates (Lutz et al. 2001). This well-

developed methodology allows for short-term

fluctuations in vital statistics. The original method of

stochastic forecasting with revisions of demographic

forecasts was developed by Lassila et al. (2014).

The primary concept of their approach is that each

update in the official population projection alters

people’s perception of the future.

Simulation studies are vital tools for analysing

the behaviour of many real-life systems and age

structured population models are often part of these

studies. When population projections are formulated

within simulation models, two options are available.

The stochastic population sub-models take into

account demographic uncertainty. Primary

parameters such as fertility, mortality and migration

may be considered as stochastic processes. Samples

are taken from the predictive distributions of future

population, and utilizing the Monte Carlo (MC)

stochastic simulations, the population distribution is

obtained (Tian & Zhao 2016). Certain authors

(Davis et al. 2010) prefer to use micro-simulation to

Mielczarek, B. and Zabawa, J.

Modelling Population Growth, Shrinkage and Aging using a Hybrid Simulation Approach: Application to Healthcare.

DOI: 10.5220/0005960800750083

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 75-83

ISBN: 978-989-758-199-1

model individual behaviour and the MC process to

convert probabilities into characteristics of

individuals.

Another well-known simulation methodology

utilized to capture the population evolution is

System Dynamics (SD); this methodology proved to

be useful in policy formulation and addressing

dynamic complexity of the system (Homer & Hirsch

2006). For example, Barber and Lopez-Valcarcel

(2010) used a SD submodel to simulate a

demographic pyramid to analyse the demand for

medical specialties. Masnick and McDonnel (2010)

modelled the population utilizing the SD approach to

link individuals with health conditions to the clinical

workload.

These two approaches differ significantly. MC

simulation is performed on one or more typical

individuals who are used to describe the experience

of a larger group within a population. A model

simulates hundreds or thousands of potential

scenarios and produces forecasts as outputs, usually

in the form of relevant means, probabilities and a

dispersion of results similar to an expected value.

The SD approach is particularly helpful when

attempting to formalize a mental model of a given

problem. In addition, it is useful when analysing the

relationship between a system’s structure and its

behaviour after changes have occurred. Typically,

SD models are not designed to yield exact numerical

predictions but are intended to explore multiple

policy options.

The overall goal of our project is to build a

hybrid simulation model that would allow alignment

of short-term demographic forecasts with health

policy models to predict the future demand for

healthcare services. In this paper, we present the SD

population submodel driven by the separate discrete

module that controls the frequency of near

continuous computation and shifts the members of

age cohorts. The hybrid model enables us to perform

time-step simulations that describe population

evolution according to the continuous SD paradigm.

The ongoing demographic changes directly

influence the discrete event simulation (DES)

submodel that generates the discrete demand for

healthcare services.

The values of the input parameters are calculated

based on forecasted rates of the primary

demographic parameters, retrieved from projections

published by the Polish Central Statistical Office

(CSO). The output is expressed by the total

population in every cohort; however, each individual

in our model is distinguishable. In the latter phase of

the simulation, when individuals with health

conditions first arrive at the healthcare system, the

model records their movements. In addition, the

model creates and adjusts attributes that describe

individual patients. These attributes are sampled

from empirical distributions and characterize every

individual patient.

In our research, we expect to verify the

credibility of the approach based on the System

Dynamic method developed by Forrester (1968) and

allow a modification of the time step dt inside the

population module in response to feedback from the

discrete module.

2 HEALTHCARE SIMULATION

Simulation plays a vital role in healthcare decision

making (Mustafee et al. 2010). It is widely utilized

in research studies and is also a popular educational

tool and decision support technique that allows

stakeholders to assist in long-term planning

processes. Simulation modelling provides an

opportunity to gain deeper understanding of mass

events such as the spread of infectious diseases

(Hughes et al. 2006, Alfonesca et al. 2000); to

analyse the performance of a particular healthcare

unit: hospital, operating theatre, outpatient

department and diagnostic centre (Testi et al. 2007);

or to forecast the future behaviour of a particular

system under study (Ashton et al. 2005).

Numerous applications of simulation have been

conducted in healthcare in past decades and

according to many surveys, the discrete-event

simulation approach (DES) is the most often used

technique in the field of healthcare management (Jun

et al. 1999, Mielczarek & Uziałko-Mydlikowska

2012). However, in the health policy field, when the

objective of the study is to establish long-term

predictions of the total level of demand for health

services, the SD approach is also frequently used.

Health policy studies usually begin with an analysis

of the population structure and its dynamics on a

local, regional or national level. The intensity and

structure of population needs depend on age-gender

profiles that, in turn, evolve according to changes

that occur regarding average expected length of life,

levels of birth and death rates and fluctuations in

migration parameters (Ansah et al. 2014).

Additionally, the need of services by patients with

diagnosed diseases change in relation to the amount

of time that has passed from the moment a diagnosis

was formulated (Caro et al. 2006).

According to (Lane et al. 2000), when using the

system dynamic approach, we lose the ability to

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

include uncertain factors that are prominent in

healthcare systems. In addition, patient-oriented

issues are considered on the aggregate, instead of

individual level. However, what we gain is a

systematic view of patient movements and a more

strategic perspective of system behaviour.

In this paper we used the well-established

methodology of SD modelling to capture overall

population evolution. We modified the approach to

allow for the use of age-gender cohorts simulated by

the SD submodel to generate discrete demand for

healthcare services.

3 POPULATION

The population of interest resides in the two

subregions of Lower Silesia, the fourth largest

region in Poland. These two subregions are denoted

as the Wrocław Region (WR) and encompass nine

administrative districts: the capital of Lower Silesia

(Wrocław) and eight districts that are nearby the

capital. According to the Central Statistical Office

(GUS, 2015) the total WR population increases

annually (Table 1, Figure 1) for both genders.

Table 1: Structure of the WR population according to age-

gender groups from 1995 to 2014.

1995 2000 2005 2010 2014

Total number of women (F) and men (M):

F: 604848 604226 608160 622112 633074

M 561852 557928 558057 570442 579707

Children ages 0−4 as % of total number of women:

F: 5.05% 4.19% 3.87% 5.03% 4.82%

M: 5.72% 4.79% 4.45% 5.74% 5.62%

People ages 60+ as % of total number of women/men:

F: 19.16% 20.40% 20.79% 23.38% 26.17%

M: 13.57% 14.05% 14.19% 16.84% 19.52%

4 MODEL

Our approach to chronological ageing is based on

the concept described by Eberlein et al. (2011). The

outline of the first, basic version of the model was

presented in (Mielczarek et al. 2014). To better

visualize the general concept, we present population

aging chains using System Dynamics notation

(Figure 2).

Ten state variables define the population inside

ten cohorts: five female and five male cohorts. Each

cohort represents a separate state variable described

by the stock level. In accordance with Krahl (2009),

we defined the internally generated state-change

events and linked them with state variables. The

state variables change at discrete times when their

associated flow rates also change. Input and output

flows that move to and from the particular stock are

aggregated into one dynamic object that controls the

appropriate state variable. The resultant flow

instantly increases or decreases the number of

individuals in the cohort. This eliminates rounding

errors and improves accuracy of the simulation.

Figure 1: Comparison of age pyramids of the WR

population using historical data from 1995 (dark colour)

and 2014 (light colour).

The initial population data matches historical

conditions in 2002 based on information published

by the CSO (GUS, 2015). The simulation begins in

2002 and runs through 2014 according to parameters

calculated on the basis of historical values extracted

from statistical data bases for the Wrocław Region.

Beyond 2014, the exogenous parameters are

extrapolated based on the forecasts published by the

CSO (Waligórska et al. 2014).

4.1 Computer Model

The computer model was constructed in the

ExtendSim environment. There are two submodels

that closely cooperate with each other: DES sub-

model was developed using modules from the Item

library and SD submodel was based on the Value

library. Both libraries are available in the standard

software package. The model uses over 700

elementary blocks and a number of integrated blocks

defined according to the hierarchic approach.

Modelling Population Growth, Shrinkage and Aging using a Hybrid Simulation Approach: Application to Healthcare

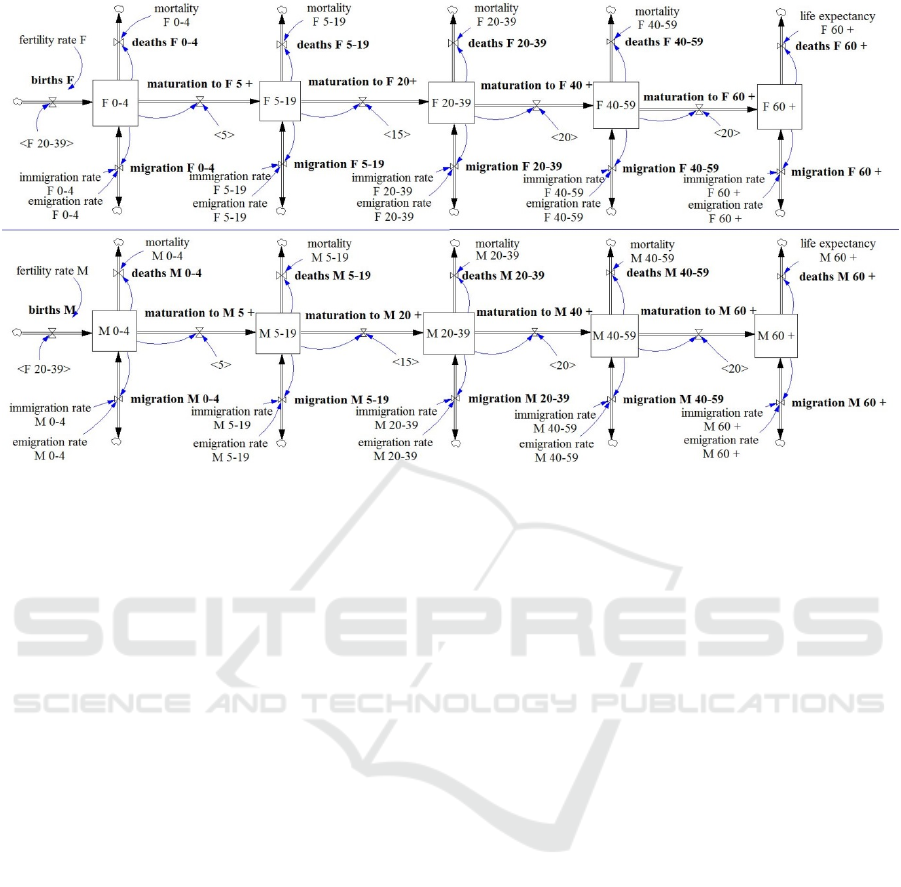
Figure 2: Population aging chains.

The SD submodel simulates the on-going

evolution of the population. It is based on ten main

integrated blocks representing ten age-gender

population cohorts (see Figure 2). The crucial role

inside the hierarchic SD blocks is played by the

Holding Tanks – the elementary blocks that

represent the stocks of the System Dynamic

approach.

The DES submodel generates patients arrivals to

the healthcare system. It consists of the integrated

block that simulates the prevalence of needs-for

service events. The additional DES module helps to

control the passage of time inside both of the

submodels. Consequently, the control of the SD

objects is overtaken by the discrete blocks.

The built-in mechanism for data base

management is applied to enable storing all the input

parameters and output simulation data in the external

data bases.

4.2 Cohorts 0 to 4

The cohorts F 0−4 and M 0−4 (Figure 2) describe

the youngest children, separately for females and

males. The youngest cohorts are affected by two

input and three output flows. There is one primary

and one additional input flow: births and

immigration and there is one primary and two

additional output flows: maturation, deaths and

emigration.

The primary input flow (births) for both females

and males depends on the current number of female

20−39 cohorts. Historical values of fertility rates

(from 2002 to 2014) are estimated based on

published data (GUS, 2015). Female fertility rates

are calculated by dividing the total number of girls

ages 0−4 by the total number of women ages 20−39

for each historical year. Accordingly, male fertility

rates are calculated by dividing the total number of

boys ages 0−4 by the total number of women ages

20−39.

The migration input and output flows depend on

migration rates (immigration and emigration) that

are calculated based on data describing the number

of young children moving to and from the Wrocław

Region and the total number in the youngest cohort.

The deaths output flow is driven by death rates

calculated based on the number of deaths among the

youngest WR citizens and the total number of

children ages 0−4 living in the Wrocław Region,

separately for females and males.

The primary output flow (maturation) is

interpreted as the average residence time that is

necessary for an individual to leave the younger

cohort and enter the older one. The values of

maturation time differ between every set of cohorts.

It is, for example, five years between F 0−4 and

F 5−10 but 20 years between M 40−59 and M 60+.

Beginning in 2015, the hypothetical values of

female and male fertility rates, migration rates and

death rates are adopted according to different

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

scenarios of population projections (Waligórska et

al. 2014)

4.3 Cohorts 5−19, 20−39 and 40−59

The series of cohorts 5−19, 20−39 and 40−59

represents the population that is between four and 60

years old, separately for females and males. Stocks

include three input and two output flows defined

similarly to those of the youngest cohort. The only

difference relates to primary input flow, where

instead of births, we use maturation from the

previous cohort.

4.4 Cohort 60 +

The final two cohorts, F 60+ and M 60+, describe

the oldest population, separately for females and

males. The cohorts are affected by two input and

two output flows: maturation from the previous

cohort, immigration, emigration and deaths. The

primary output flows (deaths) are defined using the

average life expectancy for female/male(s) at the age

of 60. Historical values of these parameters (from

2002 to 2014) are estimated based on data published

by the GUS (2015). Beginning in 2015, hypothetical

values of female and male average life expectancy

are adopted according to different scenarios of

population projections (Waligórska et al. 2014).

4.5 SD-DES Time Mechanism

The SD modelling approach is based on differential

equations and therefore enables the simulation of a

continuously changing system as well as the

continuous observation of the dynamic behaviour of

that system over time. In demography studies,

however, a more appropriate technique is to push

elements from one cohort to another at discrete

intervals to capture key events such as births and

deaths.

The time-step mechanism implemented in our

model is designed with the assumption that time

passes according to constant discrete values. At

discrete moments, the flow rates change and all

input and output flows that move to and from a

particular stock are aggregated into one dynamic

object. The resultant flow instantly increases or

decreases the number of individuals in the cohort

and the new values of stocks are registered. This

procedure is similar to sampling the values of stock

levels from the population model and then

downloading the obtained values into separate

objects (so called holding tanks). An important

feature of this approach is that not only is the

number of people belonging to a particular cohort at

any moment of simulation registered, but individual

attributes are maintained (for example age, sex or

other attributes if they were assigned to the moving

objects). This ability to memorize the attributes is an

extremely valuable quality when attempting to link

the SD and DES approaches.

The values sampled from the holding tanks are

then used to parameterize the inter-arrival time

distributions that describe the patient’s presentations

to the healthcare system and create the demand for

healthcare services. The discrete objects and their

attributes may enter the DES model without any

delay.

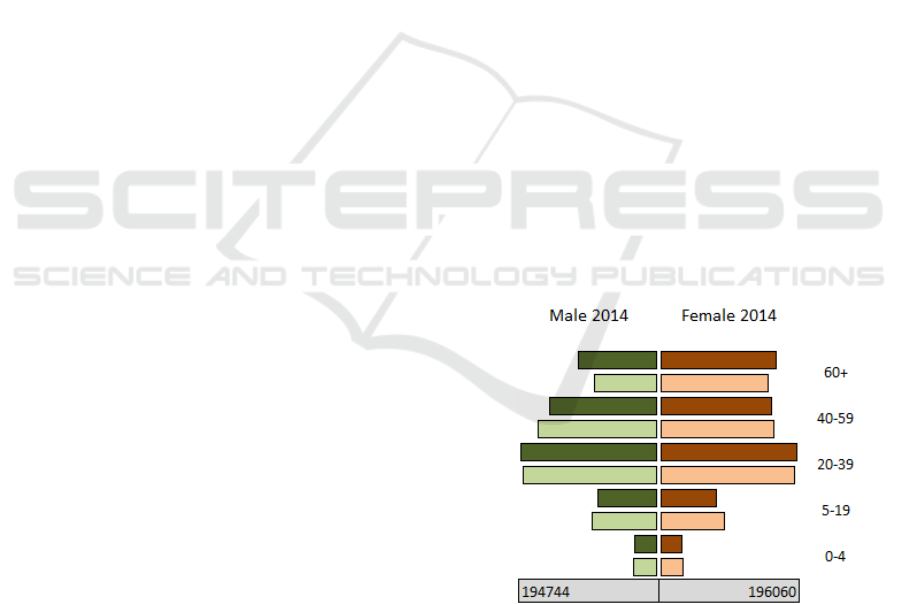
4.6 Model Testing and Calibration

The output measures of the population sub-model

are the number of individuals in every cohort as

registered during the simulation at the end of the

calendar year. The simulation begins in 2002 and

runs through 2014; it runs using parameters

estimated from historical values. Therefore, the

population module was tested for fit against 2002

–

2014. Figure 3 presents two age pyramids for 2014:

the dark-coloured pyramid represents the

distribution of the WR population based on

historical data published by the GUS (2015). The

light-coloured pyramid represents the simulation

data.

Figure 3: Comparison of the age pyramids of the WR

population built from historical (dark colour) and

simulation (light colour) data.

Relevant parameters of the model include the

values of time that are necessary for the individual to

transfer from one cohort to another. The proper

values of maturation lengths are determined

utilizing an optimization technique delivered by

Modelling Population Growth, Shrinkage and Aging using a Hybrid Simulation Approach: Application to Healthcare

ExtendSim Optimizer. This model is run several

times, and the primary function is to minimize the

total differences between the number of males and

females in particular cohorts. This infers that

although, in consecutive years, there are differences

between historical and simulation data when

comparing the particular age cohorts, the difference

that relates to the total number of population is

minimized. The maturation lengths, which are found

when the optimization process is not able to provide

more optimal solutions, are used during the

simulation experiments in forecasting the future WR

population.

Mean absolute percentage errors (MAPEs),

calculated for the entire WR population in the

particular years, indicate that the simulation model

provides on average acceptable results for the

estimation of the WR population (Table 2).

For particular age cohorts in 2014, the MAPEs

range from 5.72% to 10.93% (male population) and

from 4.87% to 9.88% (female population). These

results demonstrate the usefulness of the System

Dynamic approach to capture the population

evolution.

Table 2: Mean Absolute Percentage Errors (MAPEs)

calculated between historical and simulation data for the

total number of the WR population in particular years.

Year Male Female

2002 0.04% 0.13%

2003 0.17% 0.20%

2004 0.27% 0.31%

2005 0.54% 0.42%

2006 0.72% 0.49%

2007 1.03% 0.58%

2008 1.22% 0.71%

2009 1.28% 0.75%

2010 0.24% 0.20%

2011 0.29% 0.19%

2012 0.24% 0.39%

2013 0.06% 0.56%

2014 0.05% 0.48%

5 SIMULATION EXPERIMENTS

From among several dozens of scenarios of

projection assumptions for population dynamics

discussed by the Government Population Council in

2014 (Waligórska et al. 2014), four scenarios were

considered to be the most likely, but only one

scenario was officially recognized and published by

the CSO. Below, we present the simulation results

assuming that the development of the WR

population will be affected by demographic trends

described in the official forecasts published by the

CSO for the years 2014

–2050.

5.1 Simulation Scenario

The following assumptions were included in the

model to run the simulation beyond the year 2015:

• Fertility rates. It is assumed that fertility rates

will incur a slight decline during the next few

years and then a gradual increase will be

observed. In 2035 the increase of fertility rates

values is expected to be approximately 20.0%

(males) and 22.0% (females).

• Death rates. It is expected that death rates will

increase gradually from 2015 to 2035. However,

the number of deaths in the middle-aged cohorts

(M 40

–59 and F 40–59) will slightly decline.

• Life expectancy. The difference between Poland

and European countries will remain at the same

level during the next 20 years. This indicates that

in the year 2035, a woman age 60 will live on

average 27.75 years and a man at this same age

will live on average 24.27 more years.

• An alignment trend will be observed between

emigration and immigration and in the year

2035, the international and internal net

migrations will decrease to almost zero. The total

number of immigrating and emigrating

individuals will decrease by approximately 20%.

5.2 Simulation Results and Discussion

The forecasted number of male and female

populations within 10 distinguished age cohorts

were obtained, see Figure 4. The simulation results

are compatible with the CSO forecasts. Aging of the

population is an irreversible phenomenon. The old-

age rate, i.e., the number of the oldest cohorts

among the entire population will increase from

18.84% in 2014 to 22.17% in 2035. The median age

of population, i.e., the age that half of the population

have not yet reached and the other half has already

lived, will in 2035 be approximately 50 years. The

subpopulation of females will exceed the male

subpopulation by more than 10%. The decrease of

children 0

–18 years old in 2035 compared to 2014

will be negligible.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Figure 4: Comparison of the age pyramids of the WR

population built from the 2014 historical (light colour) and

2035 simulation (dark colour) data.

Figures 5 and 6 present selected output generated

by the SD module and directed to the DES module.

The stock level that represents the total number of

the F 60+ population (the upper line) from 2014 to

2016 is converted to the flow of patients arriving to

the healthcare system (the bottom line). The

indistinguishable mingling of individuals, often

referred to as the blending problem, was modelled

by the discrete volume of needs-for-service

expressed by women ages 60 and over, inhabiting

the WR. The results of the simulation demonstrate

the integration of two opposite perspectives: the

projection of long-term population evolution based

on the aggregated data (the upper line) and discrete

movement of individuals arriving to healthcare

system (the bottom line). The added value of this

approach is the flexibility in the modelling of the

arrival process. Figures 5 and 6 present the number

of patients F 60+ arriving to health units; however,

the graph 5 was created based on daily sampling and

graph 6 – based on weekly sampling.

Figure 5: Daily weekly trend of arrivals/day sampled from

F 60+ cohort.

Figure 6: Weekly trend of arrivals/day sampled from

F 60+ cohort.

6 CONCLUSIONS

Changes in population demography have a

significant effect on healthcare demand. The

provision of healthcare resources is a long-term

planning task and the increasingly complex nature of

problems faced by healthcare managers stimulates

growing interest in hybrid simulation approaches.

We have demonstrated the usefulness of

integrating the SD and DES approaches to better

explore the relationship between projections of

population dynamics and forecasted demand for

healthcare services. System Dynamics is a well-

known and often applied simulation technique to

model demography changes. This time-step

simulation produces, however, the indistinguishable

blending of age/gender cohorts. The discrete event

simulation is, in turn, the most often used technique

in the healthcare management field. This approach

easily captures individual choices made by patients.

Individual attributes, such as age, place of residence,

type of injury and requested services, influence

patients’ decisions and consequently determines the

utilization of healthcare resources. Our goal was to

construct the hybrid simulation model that would

allow linkage of short-term demographic forecasts

with a discrete model to predict future demand for

healthcare services.

This analysis is a first step in the direction of

more comprehensive studies and several research

topics seem to be warranted. The aging chain

population model needs more extensive refinement

and testing. Although the total population is

precisely simulated in the model, the sizes of

particular cohorts require additional calibration. We

also seek to better specify the uncertainty describing

the morbidity trends and to determine the impact of

this uncertainty on the demand for healthcare

services. It could be also interesting to parameterise

154000

154500

155000

155500

156000

156500

157000

157500

113

127

141

155

169

183

197

211

225

239

253

267

281

295

309

323

337

351

365

100

200

300

400

500

600

Yearly trend of arrivals/day F 60+ cohort

500

1000

1500

2000

2500

3000

154000

154500

155000

155500

156000

156500

157000

157500

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51

F 60+ cohort Yearly trend of arrivals/week

Modelling Population Growth, Shrinkage and Aging using a Hybrid Simulation Approach: Application to Healthcare

the model with some external/indirect incentives

such as the economic growth, the development of

education or transportation infrastructure, and the

influence of the national pro-demography

programme that has been recently started by the

Polish Government. The so called family 500+

programme supports the families having at least two

children by granting the monetary educational

benefits. The programme is intended to increase the

fertility rates.

There are still numerous technical problems that

need to be solved to better integrate two modules

driven by different simulation paradigms. For

example, the single simulation run lasts about 25

minutes. This length of time is unacceptable when

running the stochastic simulation that requires a

number of independent replications.

ACKNOWLEDGEMENTS

This project was financed by the grant Simulation

modeling of the demand for healthcare services from

the National Science Centre, Poland, and was

awarded based on the decision

2015/17/B/HS4/00306.

REFERENCES

Alfonesca, M., Martinez-Bravo, M.T., Torrea, J.L., 2000.

Mathematical models for the analysis of Hepatitis B

and AIDS epidemics. Simulation - transactions of the

society for modeling and simulation international,

74(4), pp. 219-226.

Ansah, J.P., Eberlein, R.L., Love, S.R., Bautista, M.A.,

Thompson, J.P., Malhotra, R. and Matchar, D.B.,

2014. Implications of long-term care capacity response

policies for an aging population: A simulation

analysis. Health Policy, 116(1), pp. 105-113.

Ashton, R., Hague, L., Brandreth, M., Worthington, D.

and Cropper, S., 2005. A simulation-based study of a

NHS walk-in centre. The Journal of the Operational

Research Society, 56(2), pp. 153-161.

Barber, P. and Lopez-Valcarcel, B., 2010. Forecasting the

need for medical specialists in Spain: application of a

system dynamics model. Human Resources for

Health, 8(1), pp. 24.

Caro, J.J., Guo, S., Ward, A., Shajil, C., Malik, F. and

Leyva, F., 2006. Modelling the economic and health

consequences of cardiac resynchronization therapy in

the UK. Current medical research and opinion, 22(6),

pp. 1171-9.

Davis, P., Lay-Yee, R. and Pearson, J., 2010. Using micro-

simulation to create a synthesised data set and test

policy options: The case of health service effects under

demographic ageing. Health Policy, 97(2–3), pp. 267-

274.

Eberlein, R.L., Thompson, J.P. and Matchar, D.B., 2011.

Chronological aging in continuous time, E. Husemann

and D. Lane, eds. In: Proceedings of the 30th

International Conference of the System Dynamics

Society, July 22-26, 2011 St. Gallen, Switzerland

2011.

Forrester, J.W., 1968. Industrial dynamics - after the first

decade. Management Science, 14(7), pp. 398-415.

GUS, 2015, Główny Urząd Statystyczny. Available:

www.stat.gov.pl [December, 2015].

Homer, J.B. and Hirsch, G.B., 2006. System dynamics

modeling for public health: background and

opportunities. American Journal of Public Health,

96(3), pp. 452-458.

Hughes, G.R., Currie, C.S.M. and Corbett, E.L., 2006.

Modeling tuberculosis in areas of high HIV

prevalence. Proceedings of the 38th conference on

Winter Simulation. Monterey, California, pp. 459-465.

Jun, J.B., Jacobson, S.H. and Swisher, J.R., 1999.

Application of discrete-event simulation in health care

clinics: A survey. The Journal of the Operational

Research Society, 50(2), pp. 109-123.

Krahl, D., 2009. ExtendSim advanced techology: discrete

rate simulation, M.D. Rossetti, R.R. Hill, B.

Johansson, A. Dunkin and R.G. Ingalls, eds. In:

Proceedings of the 2009 Winter Simulation

Conference 2009, pp. 333-338.

Lane, D.C., Monefeldt, C. and Rosenhead, J.V., 2000.

Looking in the wrong place for healthcare

improvements: A system dynamics study of an

accident and emergency department. The Journal of

the Operational Research Society, 51(5), pp. 518-531.

Lassila, J., Valkonen, T. and Alho, J.M., 2014.

Demographic forecasts and fiscal policy rules.

International Journal of Forecasting, 30(4), pp. 1098-

1109.

Lauf, S., Haase, D. and Kleinschmit, B., 2016. The effects

of growth, shrinkage, population aging and preference

shifts on urban development—A spatial scenario

analysis of Berlin, Germany. Land Use Policy, 52, pp.

240-254.

Lisenkova, K., Mérette, M. and Wright, R., 2013.

Population ageing and the labour market: Modelling

size and age-specific effects. Economic Modelling, 35,

pp. 981-989.

Lutz, W., Sanderson, W. and Scherbov, S., 2001. The end

of world population growth. Nature, 412(6846), pp.

543-545.

Masnick, K. and Mcdonnell, G., 2010. A model linking

clinical workforce skill mix planning to health and

health care dynamics. Human Resources for Health,

8(1), pp. 11.

Mielczarek, B., Zabawa, J. and Lubicz, M., 2014. A

system dynamics model to study the impact of an age

pyramid on emergency demand, M.S. Obaidat, J.

Kacprzyk and T. Oren, eds. In: SIMULTECH 2014 -

Proceedings of the 4th International Conference on

Simulation and Modeling Methodologies,

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Technologies and Applications 2014, SciTePress, pp.

879-888.

Mielczarek, B. and Uziałko-Mydlikowska, J., 2012.

Application of computer simulation modeling in the

health care sector: a survey. Simulation - transactions

of the society for modeling and simulation

international, 88(2), pp. 197-216.

Mustafee, N., Katsaliaki, K. and Taylor, S.J.E., 2010.

Profiling literature in healthcare simulation.

Simulation, 86(8-9), pp. 543-558.

Testi, A., Tanfani, E. and Torre, G., 2007. A three-phase

approach for operating theatre schedules. Health Care

Management Science, 10(2), pp. 163-72.

Tian, Y. and Zhao, X., 2016. Stochastic Forecast of the

Financial Sustainability of Basic Pension in China.

Sustainability, 8(1), pp. 46.

Waligórska, M., Kostrzewa, Z., Potyra, M. and

Rutkowska, L., 2014. Population projection 2014-

2050. CSO, Demographic Surveys and Labour Market

Department.

Modelling Population Growth, Shrinkage and Aging using a Hybrid Simulation Approach: Application to Healthcare