Lithium-ion Batteries Aging Motinoring Througth Open Circuit

Voltage (OCV) Curve Modelling and Adjustment

Loic Lavigne

, Jocelyn Sabatier

, Junior Mbala Francisco

Franck Guillemard

and Agneiszka Noury

IMS Laboratory, UMR 5218 CNRS, Bordeaux University, 351 Cours de la Libération, 33405 Talence, France

PSA Peugeot Citroën ,2 Route de Gisy, 78943 Vélizy-Villacoublay, France

Keywords: Lithium-ion Cell, Open Circuit Voltage (OCV) Curve Adjustment, Battery Aging Monitoring.

Abstract: This paper is a contribution to lithium-ion batteries modeling tacking into account aging effects. It first

analyses the impact of aging on electrode stoichiometry and then on lithium-ion cell Open Circuit Voltage

(OCV) curve. Through some hypotheses and an appropriate definition of the cell state of charge, it shows

that each electrode equilibrium potential, but also the whole cell equilibrium potential can be modelled by a

polynomial that requires only one adjustment parameter during aging. An adjustment algorithm, based on

the idea that for two fixed OCVs, the state of charge between these two equilibrium states is unique for a

given aging level, is then proposed. Its efficiency is evaluated on a battery pack constituted of four cells.

This adjustment parameter can thus be viewed as a State Of Health (SOH) or aging indicator.

1 INTRODUCTION

Due to their high energy and power densities

compared to other existing technologies, Li-ion

batteries are increasingly used as energy storage

system in mobile applications (Armand and

Tarascon, 2008). The onboard Li-ion battery packs

have to work together with reliable battery

management systems (BMS) to ensure their optimal

and safe use (Liaw et al, 2010). Among the tasks

ensured by the BMS, State-Of-Charge (SOC)

estimation is of an extreme importance. The energy

management strategies in hybrid vehicles, for

instance, rely on the accurate knowledge of the

SOC, the latter being an indicator of available

energy. SOC estimation methods commonly used

impose a characterization of the Open Circuit

Voltage (OCV) curve (through a polynomial, a look-

up table, …) as they use :

- either a direct OCV curve inversion methods (if

the application permits cells steady state voltage

measurement) (Lee et al, 2008),

- or cells models based methods (Plett, 2004),

(Kim, 2010), (Sabatier et al, 2014), (Francisco et

al, 2014), (Sabatier et al, 2015).

As OCV is closely related to SOC, the SOC

estimators require an accurate OCV model (Piller et

al, 2001), (Santhanagopalan and White, 2006).

However, at battery aging, the OCV curve of

each cell changes as OCV reflect battery aging and

performance degradation (Roscher et al, 2011). The

impact of aging on cell equilibrium voltage is

analyzed in (Schmidt and al, 2013). This change

distorts the estimator if nothing is done to adjust the

curve law. Aging correction can be thus

implemented as done in (Cheng et al, 2015). But this

class of methods does not take into account the

underlying physical phenomenon of lithium-ion

intercalation process. This knowledge makes

possible analytical descriptions of the OCV curve

and then permits the implementation of accurate

estimation methods for both SOC and State of

Health (SOH). Some of these methods are known in

the literature as incremental capacity analysis (ICA)

technique (Dubarry and Liaw, 2009) or the

differential voltage analysis (DVA) (Honkuraa et al,

2008).

Most of the analytical descriptions for OCV

curve available in the literature involve a large

number of parameter (Hu et al, 2011), (Weng et al,

2014) that all must be adjusted as battery aging. This

imposes to implement complex and resources

consuming on-board iterative optimization

Lavigne, L., Sabatier, J., Francisco, J., Guillemard, F. and Noury, A.

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment.

DOI: 10.5220/0005961400570067

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 57-67

ISBN: 978-989-758-198-4

algorithms.

In this paper, a new polynomial parametrization

for OCV curve is proposed. As ageing of lithium-ion

cell, only one parameter must be adjusted to ensure

an accurate fitting of the OCV curve by the

polynomial. Such a parametrization results in an

analysis of the cell using "communicating vessels”

idea introduced in (Schmidt and al, 2013). If each

electrode equilibrium voltages at the unused state is

modelled as in (Karthikeyan et al, 2008),

introduction of some simplifying hypothesis permits

to show that the OCV curve can be modelled by a

polynomial that requires only one adjustment

parameter during aging. An adjustment algorithm,

based on the idea that for two fixed OCVs, the state

of charge between these two equilibrium state is

unique for a given aging level, is then proposed. Its

efficiency is evaluated on a battery pack constituted

of four cells.

2 PARAMETRIZATION OF A

LITHIUM-ION CELL OCV

2.1 Notations and Electrode

Equilibrium Potential Definition

It is supposed in the sequel that subscript p and n are

used to denote respectively the positive and the

negative electrode of a lithium-ion cell. Electrodes

stoichiometry x

, i{p, n} (Bard et al., 2008) are

defined as the ratio of the inserted lithium quantities

over the maximal theoretical quantities that can

be inserted Q

i,max



max,



(1)

If T denotes the temperature, cell OCV can be

defined using the equilibrium potentials of the two

electrodes, by:









TxETxETE

nnpp





(2)

positive electrode equilibrium potential, denoted





TxE

, and negative electrode equilibrium

potential, denoted



TxE

, being respectively

defined by:







iINTiNernstii

xVTxVTxE  ,,



pni ,

(3)

Using standard potential

, Nernst potential





TxV

iNernst

, is defined by the relation



















iiNernst

ETxV

ln,





pni ,



(4)

In the previous relation, R denotes the universal

gas constant (R = 8.314 472 J K

−1

mol

−1

) and F is the

Faraday constant (F=96485.33°C mol

−1

). Among the

models available in the literature for





iINT

Redlich-Kister model given by the following

relation is used in the sequel (Karthikeyan, Sikha,

and White 2008) with





pni ,

  



























kiiINT

xkx

xAxV

(5)

It is the expression of V

INT

(for non-ideal

interaction), that gives the closest experimental

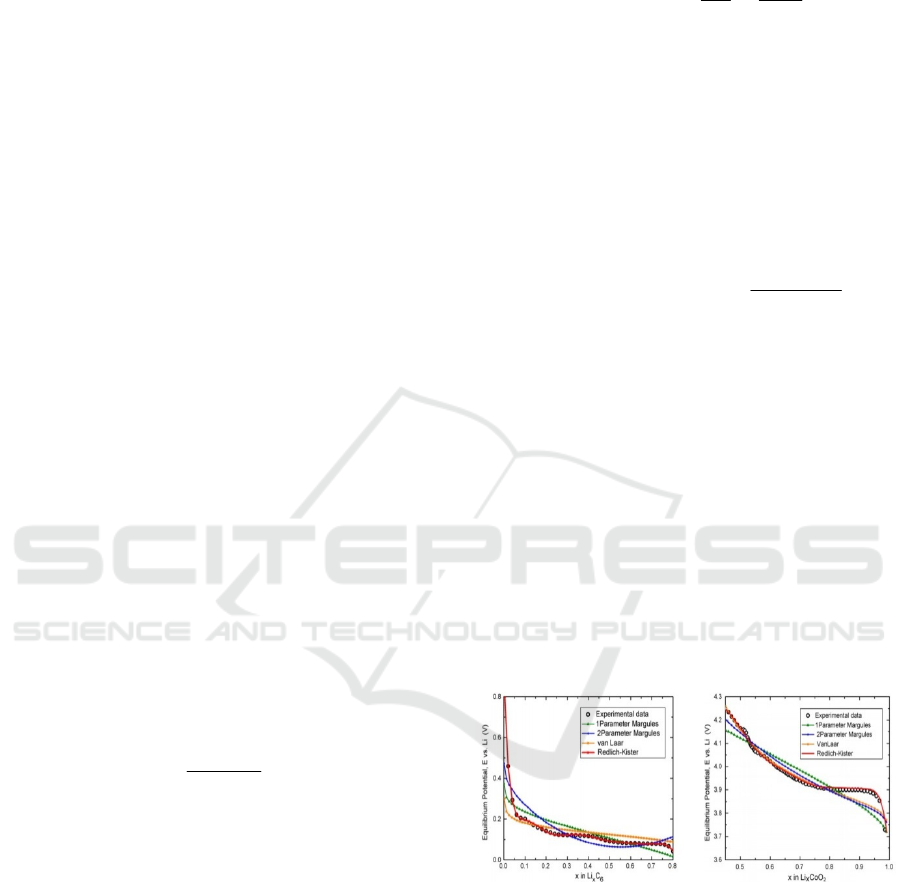
measures fitting as shown in Figure 1, comparing to

several other equilibrium potential laws

(Karthikeyan, Sikha, and White 2008).

Remark 1 - According to relation (21) and (22) in

(Karthikeyan, Sikha, and White 2008), note that a

linear dependence to temperature can be introduced

in coefficients

to take into account temperature

variations:





TaTA

kiki ,,



(

being an additional

parameter for temperature dependence such as for

0,,

TaA

kiki



for parameters

in relation (5) and

for a reference temperature T

Figure 1: Comparison of various equilibrium electrode

potentials laws for experimental data fitting (Karthikeyan,

Sikha, and White 2008).

2.2 Polynomial Approximations of

Electrode Equilibrium Potentials

The goal now is to make simplifying assumptions in

order to obtain polynomial expressions for

electrodes equilibrium potentials.

Given that

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

 

)1(1ln1ln

ln 

















pni ,

(6)

expansion of



xx1ln



1,0x

is given by:







































(7)

with



pni ,

and permits the following

approximation, denoted



TxV

iNernst

, for relation

(4):



  



111













iiNernst

ETxV

(8)

Thus, for a large enough N

, the function



FxxRT

1ln

can be reduced to a

polynomial. By way of illustration, Figure 2 shows

that the approximation error

 

TxVTxV

iNernstiNernst

, 

remains minor and

limited to a few millivolts and also shows a low

impact of temperature T.

Thus, using relation (8) and through expansion

of relation (5), electrode equilibrium potentials in

relation (2) can be written in polynomial form:







ikii

xAE



pni ,

(9)

with





LNii

NKN ;max

(10)

where coefficients

are combinations of

coefficients

of relation (5).

As shown in the application section, temperature

has a low impact on coefficients

but according

to remark 1, temperature dependence can be

introduced in coefficients

and thus relation (9)

can be rewritten as:









ikiiii

xTaTaaE



pni ,

(11)

2.3 Ageing Effects on Electrodes

Stoichiometry

From relation (9), cell OCV depends on:

Figure 2: Approximation error between









TxVTxV

iNernstiNernst

, 

for various values of N

(a) and impact of the temperature on



TxV

iNernst

with



(b).

- parameters

and more weakly on the

temperature T;

- electrodes stoichiometries x

which themselves

depends on the amount of inserted lithium

and

the maximal theoretical capacity

max,i

according

to relation (1).

In agreement with the authors of (Karthikeyan et

al. 2008), the following assumption is made on

coefficients

Hypothesis 1

For a constant temperature, coefficients

Redlich-Kister model are supposed constants as

intrinsic to the electrode electrochemistry

∎

As a consequence, coefficients

are not

affected by the cell aging. Aging is then necessarily

passed on electrodes stoichiometry

and

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

-0.06

-0.04

-0.02

0.02

0.04

0.06

Nernst

-V

Nernst

(V)

=10

=20

=30

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

Nernst

(V) for E

T=20°C

T=-10°C

T=50°C

(a)

(b)

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment

Specifically, it is then expected that the only aging

reactions impacting the cell OCV are those resulting

in at least one of the following effects:

- a change in the electrode geometry, (eg

formation of dendritic deposits (Arora et al. 1998))

this change impacting the cell theoretical maximum

capacity

max,i

and thus the stoichiometry





linked to the amount of charge



in electrode i;

- a loss



cycling ions (ion consumption in

aging reactions).

Since the cell OCV characterizes a cell at rest,

charge transfer equations can be ignored in the

following developments. For the analysis of



cycling ions concentration, the cell will be

represented by two communicating tanks as in (Po et

al. 2007).

In the previous equations, the OCV is expressed

according to electrode stoichiometries. We now

establish the link between the electrode

stoichiometries and the SOC (estimated in practice).

This last one is defined by the relation:

ref

dispo

SOC



(12)

where Q

dispo

is the possible capacity extractible of

the cell. In usual definition of SOC, Q

ref

is the cell

maximum capacity which varies with aging cells.

This is a problem if OCV adjustment during aging

requires SOC measures, as SOC definition requires

the cell real capacity knowledge which is precisely

to identify. To treat this problem, the Q

ref

uncertainty

during aging is eliminated by adopting the following

definition:

Definition 1









ref

tConsQIif

EEif

tSOC

%100

tan0

%100

(13)



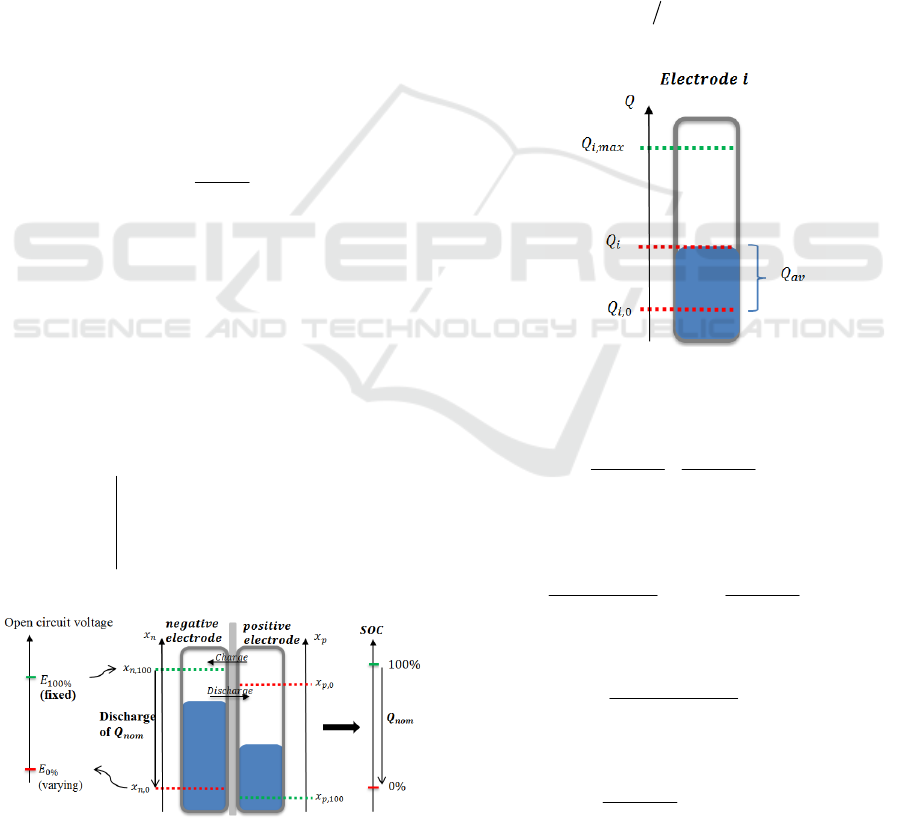
Figure 3: Link between the electrodes stoichiometry and

the SOC.

This definition imposes

- a SOC equal to 100% when OCV is maximum

and equal to E

100%

(for example 4V) for all cells

ageing.

- a SOC equal to 0% after discharge, starting to

E = E

100%

, and a fixed Q

ref

. The Q

ref

choice is not

important and is determined by the user. In practice

the reference capacity is usually fixed to the nominal

capacity (Q

ref

= Q

nom

). Definition 1 is illustrated in

Figure 3.

For an electrode i (i{n, p}), and as illustrated

by Figure 4, the available capacity can be defined

by:

0,iiav

QQQ





(14)

where Q

i,0

is the capacity in the electrode at SOC =

0, then

max,0,0, iii

QQx



is the electrode

stoichiometry for SOC = 0%.

Figure 4: Available capacity definition for an electrode.

From relation (1) and previous analysis:











max,





(15)

then













max,

dispo

tQtQ

tx 





(16)







 

max,

refi

disporef

tQtQ

tx 

(17)

and finally









max,

)(

ref

xtSOC

tx 

(18)

Then, for SOC = 100%, the following equation is

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

verified











tQtQtxtx

irefii max,0,100,



The previous analysis shows that the electrode

stoichiometries are proportional to the SOC and can

be written:









0,0,100,

nnnn

pppp

xSOCxxtx



(19)

Let us consider a given state of charge

SOC. The

corresponding OCV is varying with cell aging,

excepted for the point

SOC =100% (according to

definition 1). For the positive electrode, this change

modifies the parameter

p,0

which is then depending

of cell aging (

p,0

 x

p,0

(age)). The parameter



(age) is then introduced such as:

   

agextSOCage

init

ref

p 0,

max,









(20)

or with a more compact form :

   

agetSOCagetx

ppp





(21)

where

 

agexage

age

init

ref

max,











(22)

The same equation holds for the negative electrode

with parameters



age



and



age



   

agetSOCagetx

nnn





(23)

2.4 Open Circuit Voltage

Parametrization with Knowledges

of Each Cell Equilibrium Potential

In this section, equilibrium potentials E

and E

, and

then coefficients

and

are supposed

known. From relations (21) and (23), the equilibrium

potentials

and E

given by relation (9) can be

expressed as a function of cell ageing with the 4

parameters



age





age





age



and



age



, and thus relation (2) becomes:

 



 



EA ageSOC age

A age SOC age











(24)

The OCV adjustment problem after ageing

consists in the identification of these 4 parameters.

This adjustment can for instance, be realized with a

set of

M measures







ESOC

;



through

minimization of criteria:

 



 



jpp p

nn n

E E age SOC age

E age SOC age





























(25)

with the constraint:

 



 











nnkn

ppkp

ageageA

ageageAE

,%100



(26)

As the SOC definition given by relation (13)

imposes a fixed Q

ref

capacity, estimation of







;

supplies maximum capacities estimations

max,p

and

max,n

2.5 Open Circuit Voltage

Parametrization without

Knowledge of Each Cell

Equilibrium Potential

When equilibrium potentials E

and E

are not

known (practical case),

and

coefficients

become unknowns. The only OCV curve available is

an experimental measure of this one obtained from

the interpolation of a set of OCV measures with

large SOC variations. This OCV curve will be noted

OCVC

init

. A study of different OCV measure

technics is given in (Petzl and Danzer, 2013).

Measures in charge and discharge are used to

determine the OCV curve. An average curve

obtained with a charge curve and a discharge curve

seems to be the best compromise because of

hysteresis effects (Roscher et al. 2011). OCV curves

(OCVC

init

) used in the following are determined for

discharge measures (see Figure 5).

Figure 5: OCVCinit identification with OCV measures.

The curve OCVC

init

obtained with polynomial

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment

interpolation at start time, has the following

structure:





kinit

SOCDE

(27)

To prove that aging impact on OCV can be

expressed like in relation (24), the link between the

two electrodes stoichiometries x

and x

is now

established.

In (Pop et al. 2007), a cell is represented for two

communicating tanks according to figure 6.

Figure 6: Cell Li-ion simplified scheme.

Figure 6 permits to write the following equation:

CstQQ





(28)

where by dividing by

max,p

max,max,

Cst



(29)

and thus

max,

Cstx



(30)

Relation (30) shows that a linear equation can

connect the electrode stoichiometries x

and x

as:

pnpp

dxcx





(31)

npnn

dxcx





(32)

Then relation (2) becomes:

 







npnkn

pkp

dxcAxAE

(33)

Expansion of terms in the second sum permits a

new relation:













xDxDE

,max

(34)

Coefficients

are combinations of coefficients

and

. The ageing impact on the

OCV, can then be introduced by relation (21), thus

leading to:

  









ppk

agetSOCageDE



(35)

Remark 2 - According to relation (11) in relation

(33), temperature dependence can be introduced in

relation (35), leading to

  











ppk

agetSOCageTd

TddE



(36)

From relation (35), the OCV adjustment problem

after ageing consists in the identification of only the

two parameters



and



. This identification can,

for instance, be realized with a set of

M measures







ESOC

;



through minimization of

criterion:

 











ppj

ageSOCageEE



(37)

with constraint:

 









ppk

ageageDE

%100



(38)

2.6 Experimental Validation

To experimentally validate the relation (35), several

OCV curves stemming from accelerated aging

process (described in section 3.1) are now identified

by assuming that the OCV after aging is given by:

 







ageSOCageDE



(39)

Search for



and



parameters is performed

manually. A wide range of values for



and  are

used. For each pair (





), the following criterion is

evaluated:

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics



,, ,

mesures j

test

k mesures j

EDSOC























(40)

The three couples of measures





jmesuresjmesures

ESOC

;

are derived from a charge

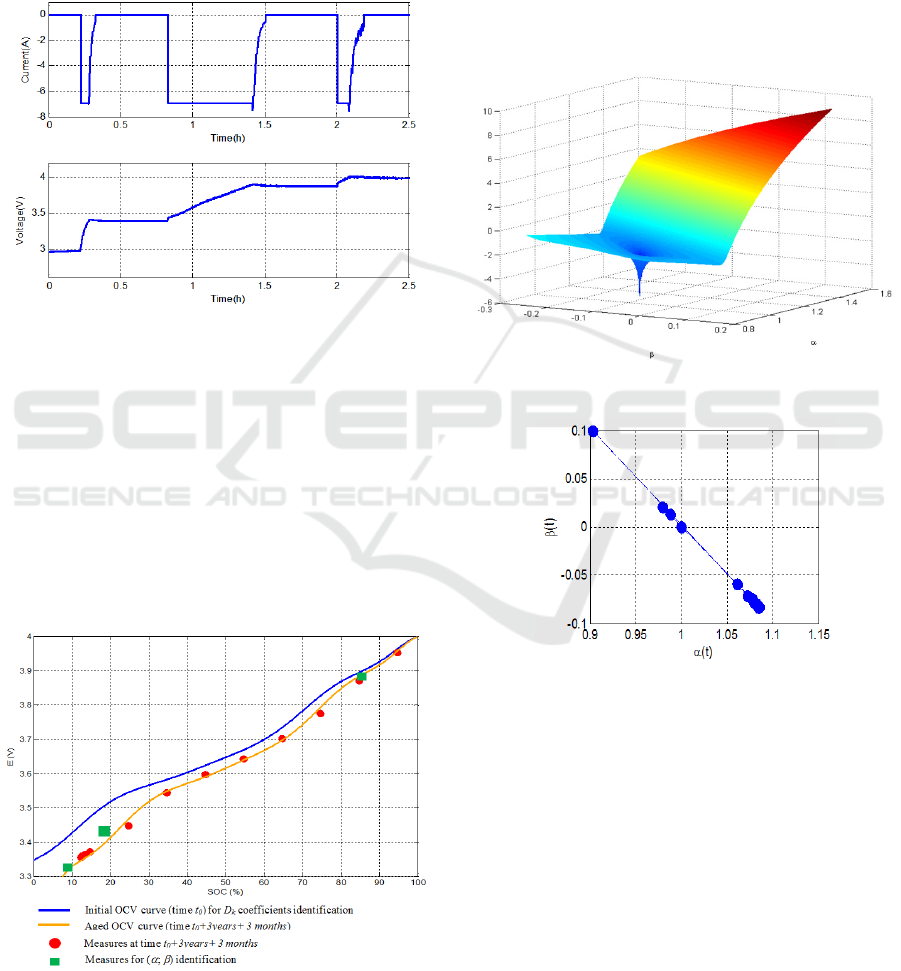
profile such as that shown in Figure 7. The pair (





) selected minimizes J

test

Figure 7: Charge profile example used to get the necessary

measures for the OCV curve adjustment.

To validate the pair (





) selected, the identified

OCV curve is compared with the measured OCV

curve in Figure 8. This figure shows the feasibility

of the parametrization given by relation (39) and

also shows that the proposed optimization leads to a

reliable reconstruction of the OCV curve over a wide

range of SOC and with a reduced number of voltage

measurements (namely three during on a charge

profile). Figure 9 shows the shape of the logarithm

of J

test

criterion that exhibits a global minimum.

Figure 8: Identification of the OCV curve using charge

profile measures and manual search of parameters



and



of a cell after two years calendar ageing.

The previous adjustment was performed for

several cell aging. From optimal identified pairs (





), figure 10 shows the variations of



as a function



. This figure shows that parameters



and



are

linked by the equation



= -



+ 1 which makes it

possible to write the relation:





11 



SOCSOC

init



(41)

This remark permits to transform the OCV curve

adjustment problem after aging to the research for a

single parameter: parameter



Figure 9: Criterion J

test

as a function of the pair (



;



Figure 10: Variation of



as a function of



2.7 Unicity of Coefficient  for Each

OCV Curve

Coefficient α characterizes the cell capacity loss and

is unique for each OCV curve. It is therefore an

aging indicator. The uniqueness of α is due to three

reasons:

1 - Polynomials defined by coefficients

init

(relation (27)) is strictly increasing.

2 -





11: SOCSOCT



is an application

strictly increasing and that defines a straight line

whose slope is α.

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment

3 - Equation

 

SOCESOCE



has an unique

solution

 SOCSOC

Thus



= 1 corresponds to the initial ageing state;



> 1 indicates a cell capacity loss. The cell

may be considered to be aged.

3 OCV MODEL ADJUSTMENT AS

AGING

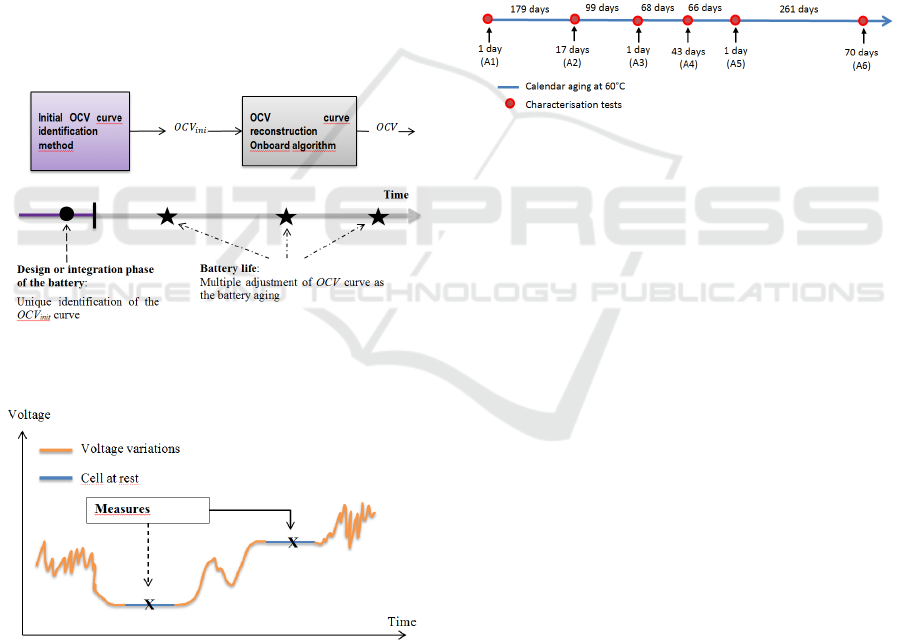
The proposed method has two steps illustrated in

figure 11. The first step is the identification of the

OCV curve at initial state (using relation (26) thus

leading to coefficients

init

). In the second step,



parameter characterizing the aging of the cell is

identified from at least two OCV measures in

normal operation or in specific operation (charge

phase for instance).

Figure 11: Block diagram of the OCV curve

reconstruction method during cell aging.

Figure 12: Description of measures and rest periods

required for the step two adjustments method

implementation.

To implement step 2 of figure 11 method, it is

require as shown in figure 12 to have two

consecutive rest periods that permits to measure the

cell OCV without the cell age has changed

significantly between the two measures.

3.1 Aging Characterization and Bench

Description

The strategy previously described is now applied to

a battery pack constituted of four 7 A.h VL6P type

lithium-ion cells from JCS-SAFT (LiNiCoAl

Oxide). The cells, numbered form 1 to 4, have

undergone an accelerated calendar aging at 60°C.

The aging phases are punctuated by characterization

tests. Characterization tests on Digatron bench

include measures of capacity, internal resistance and

OCV for each cell and for various temperatures. The

chronology of the aging and characterization tests is

given in Figure 13.

Figure 13: Chronology of calendar aging and

characterization tests.

3.2 Initial OCV Identification

Each battery cell initial OCV curve OCVC

init

must

be fitted by relation (27) before battery usage. This

necessary initial fitting can be time and resource

consuming but can be done off-line and is only once

realized.

However this relative complexity can be

reduced. Hypothesis 1 supposes that coefficients A

i,k

depend only on electrode electrochemistry and are

constant. Then, if the battery is made of the same

cells, the same initial OCV curve fitting should be

used for all the battery cells. If OCV curves are

different, these differences can be associated to

electrode stoichiometry dispersion in manufacturing.

These dispersions can be assimilated to aging

consequences and can be taken into account through

an appropriated parameter



This result is verified with the 4 cells battery

pack. Table 1 shows that each OCVC

init

can be

obtained by the mapping of each other cell. This

table shows that a unique OCVC

init

can be used for

the 4 cells (with a maximal error less than the

measurement noise magnitude recorded when

implemented in a car). The cell2 OCVC

init

is defined

by (see relation (27)):

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics





kinit

SOCDE

(42)

with the following coefficients

will be used in the following.

Table 1: OCVC

init

fitting of 4 cells using a unique

polynomial and computation of parameter . The grey

boxes highlight the considered cell for polynomials fitting

for each experience. The fitting maximal absolute errors

are also gathered in the table for each experience.

3.3 OCV Curve Adjustment as Aging

The algorithm is based on the idea that for two OCV

voltages E

and E

such that E

< E

, the state of

charge variation



EESOC ,

differs for each

aging state, especially if voltage E

and E

are very

different. This statement is demonstrated by

expressing the state of charge variation



EESOC ,

at the initial state and for two other

aging states characterized by parameters 

and 

At initial state, state of charges leading to OCV E

and E

are denoted

init

SOC

and

init

SOC

and are

such that:



nom

init

EEQ

SOCSOCEESOC













;

(43)

Let then SOC denotes the state of charge of an

aged cell and SOC

init

the state of charge of the same

unused battery for the same OCV. According to

relation (41), the two states of charge are linked by

the relation:





init

SOCSOC



(44)

At ageing state characterized by 

, state of

charge variation between the two OCV E

and E

given by:

 

init

EESOCEESOC

;

; 



(45)

Similarly, at ageing state characterized by 

:

 

init

EESOCEESOC

;

; 



(46)

Aging difference characterized by

III





implies a difference in state of charge variations:

III

SOCSOC





(47)

Thus, a measure



EESOC ;;

corresponds to

an unique OCV curve. With a set of

2M

measures of state of charge variations



;





EESOC

with

EE  ...

, there will be

1M

associated parameters



If the measures are perfects, all parameters



are

equals. If however measures are for instance marred

by noise, an optimal parameter α allowing to

accurately representing the experimental data must

be deduced. To solve this problem, a least square

problem can be formulated leading to the

minimization of the following criterion:



























EESOC

;;

;



(48)

3.4 Validation

The implementation of the OCV curve adjustment

algorithm previously described requires at least two

OCV measures. These measures are obtained here

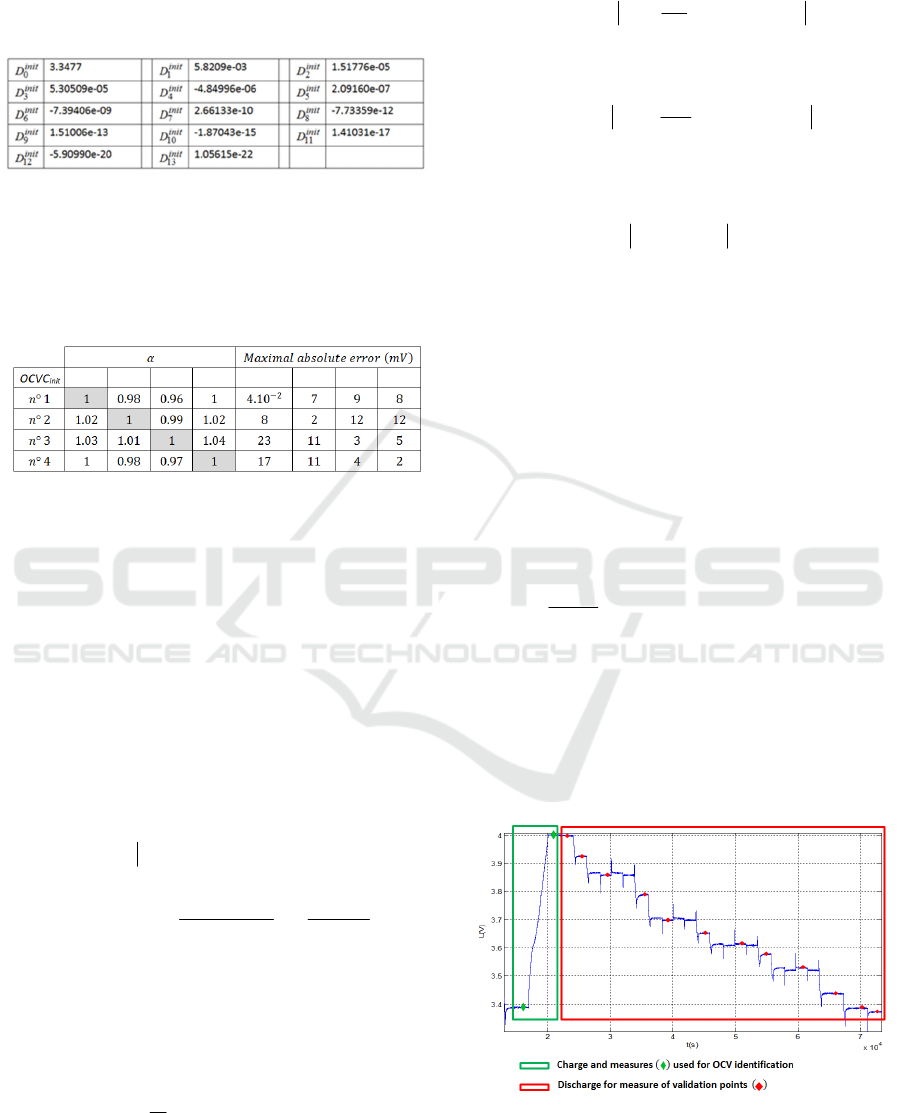
on voltage profiles presented in Figure 14.

Figure 14: Example of charge profile providing two

measures for OCV curve reconstruction (second measure

at 4V) and OCV measure (during a discharge) for

validation.

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment

The charge part is used to get the two OCV

measures required for the curve adjustment. The

discharge part is used to get OCV measures required

to validate the method. During discharge, the

relaxation time after each step is about 30 minutes.

On the discharge part the SOC information required

for each validation points is calculated by current

integration from the reference point for SOC =

100% defined by E= E

100%

namely 4V.

Table 2 gives in column max(



) the 4 more

important errors (on all measures of the discharge)

and for 4 different temperatures. The column

Δ

gives voltages variations due to aging. These errors

are determined for the 6 aging denoted {A1, A2, A3,

A4, A5, A6} that appears in figure 13.

Table 2: Maximum identification errors for different

ageing and temperatures.

Figure 15: variation according to aging for different

temperatures.

Figure 15 shows parameter variations



according to temperature and cells aging. On this

figure,

 parameter value grows according to

ageing. For cells 1, 3 and 4 the

 values are more or

less equals. For cell2 case, the ageing is more

important and

 is higher than 1.5 for measures at

A6.

Figure 15 shows that OCV curves are very little

affected by temperature, indeed no particular

variations are noted on the parameter



when

temperature is varying. The standard deviation, on



values, is higher for cell2 and on A4 measures (



variations are mainly attributed to identification

errors.

4 CONCLUSIONS

The paper proposes a lithium-ion Open Circuit

Voltage (OCV) curve model that requires only one

parameter adjustment as batteries aging. Such a

result has been obtained through an analysis of

electrodes stoichiometries variations as ageing. A

two steps algorithm is then proposed for model

adjustment as aging. The first step is the

identification of the OCV curve at initial state. In the

second step, a parameter characterizing the aging of

the cell is identified from at least two OCV measures

in normal operation or in specific operation (charge

phase for instance). The efficiency of this algorithm

has been shown with a battery pack constituted of

four Lithium-ion cells. The modelling error remains

small in spite of cells aging and temperature

variations. Moreover, the OCV curve adjustment as

cell aging requires the optimization of only one

parameter and this parameter variations can be

correlated to battery aging. This parameter can thus

be viewed as a State Of Health (SOH) indicator.

The authors have recently proposed lithium-ion

cells models based on fractional differentiation

(Sabatier et al, 2014). They now intend to include

the OCV curve adjustment method proposed in this

paper into the cell model and also to propose

adjustment methods for the other model parameter in

order to get a cell model that is robust versus aging.

ACKNOWLEDGEMENTS

This work took place in the framework of the Open

Lab Electronics and Systems for Automotive

combining IMS laboratory and PSA Peugeot Citroën

company.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

REFERENCES

Armand M., Tarascon J. M., Building better batteries,

Nature 451, pp 652-657, 2008.

Arora, P, White R. E., Doyle M. Capacity Fade

Mechanisms and Side Reactions in Lithium-Ion

Batteries, Journal of the Electrochemical Society, Vol.

145, N° 10, pp. 3647–67.

Bard A. J., Inzelt G., Scholz F., Electrochemical

Dictionary Springer-Verlag Berlin Heidelberg. 2008.

Cheng M. W., Lee Y. S., Liu M., Sun C. C., State-of-

charge estimation with aging effect and correction for

lithium-ion battery, Electrical Systems in

Transportation, IET, Vol. 5, N° 2, 2015.

Dubarry M., Liaw B.Y., Identify capacity fading

mechanism in a commercial LiFePO4 cell, J. Power

Sources 194, pp 541-549, 2009.

Francisco J. M., Sabatier J., Lavigne L., Guillemard F.,

Moze M., Tari M., Merveillaut M., Noury A.,

Lithium-ion battery state of charge estimation using a

fractional battery model, IEEE International

Conference on Fractional Differentiation and its

Applications, 23-25 June 2014, Catania, Italy.

Honkuraa K., Honboa H., Koishikawab Y., Horibab T.,

State Analysis of Lithium-Ion Batteries Using

Discharge Curves, ECS Transaction, Vol. 13, pp 61-

73, 2008.

Hu Y., Yurkovich S., Guezennec Y., Yurkovich B.,

Electro-thermal battery model identification for

automotive applications, J. Power Sources 196, pp

449-457, 2011.

Karthikeyan D. K, Sikha G, White R. E., Thermodynamic

Model Development for Lithium Intercalation

Electrodes, J. Power Sources, 185: pp1398–1407.

2008.

Kim I. S., A Technique for Estimating the State of Health

of Lithium Batteries Through a Dual-Sliding-Mode

Observer, IEEE Transactions on power electronics,

Vol. 25, No. 4, April 2010.

Liaw B. Y., Dubarry M., in: G. Pistoia (Ed.), Electric and

Hybrid Vehicles: Power Sources, Models,

Sustainability, Infrastructure and the Market, Elsevier,

pp. 375-403, 2010.

Lee S., Kim J., Lee J., Cho B. H., State-of-charge and

capacity estimation of lithium-ion battery using a new

open-circuit voltage versus state-of-charge, Journal of

Power Sources, vol. 185, no. 2, pp. 1367–1373, 2008.

Petzl M., Danzer, M. A., Advancements in OCV

Measurement and Analysis for Lithium-Ion Batteries.

IEEE Transactions on Energy Conversion, 28(3),

pp.675–681., 2013.

Piller S., Perrin M., Jossen A., Methods for state-of-charge

determination and their applications, Journal of Power

Sources 96 (2001) 113-120, 2001.

Plett G. L., Extended Kalman ﬁltering for battery

management systems of LiPB-based HEV battery

packs Part 3. State and parameter estimation, Journal

of Power Sources, 134, 277–292, 2004.

Pop V., Bergveldb H. J., Regtiena P. P. L., Op het Veldc J.

H. G., Danilovd D., Notten P. H. L., Battery Aging

and Its Influence on the Electromotive Force. Journal

of The Electrochemical Society, 154(8), p.A744-A750,

2007.

Roscher M.A., Assfalg J., Bohlen O.S., Detection of

Utilizable Capacity Deterioration in Battery Systems,

IEEE Trans. Veh. Technol. 60 pp. 98-103, 2011.

Roscher, M.A., Bohlen, O., Vetter, J., OCV Hysteresis in

Li-Ion Batteries including Two-Phase Transition

Materials, International Journal of Electrochemistry,

pp.1–6,2011.

Sabatier J., Merveillaut M., Francisco J., Guillemard F.,

Lithium-ion batteries modelling involving fractional

differentiation, Journal of power sources, 262C, pp.

36-43, 2014.

Sabatier J., Francisco J., Guillemard F., Lavigne L., Moze

M., Merveillaut M., Lithium-ion batteries modelling: a

simple fractional differentiation based model and its

associated parameters estimation method, Signal

Processing, Vol 207, pp. 290-301, 2015.

Santhanagopalan S., White R. E., Online estimation of the

state of charge of a lithium ion cell, Journal of Power

Sources 161, pp 1346-1355, 2006.

Schmidt, J.P., Tran H. Y., Richtera J., Ivers-Tifféea E.,

Wohlfahrt-Mehrensb M., Analysis and prediction of

the open circuit potential of lithium-ion cells. Journal

of Power Sources, 239, pp.696–704, 2013.

Weng C, Sun J., Peng H., A unified open-circuit-voltage

model of lithium-ion batteries for state-of-charge

estimation and state-of-health monitoring, Journal of

Power Sources, vol. 258, pp. 228-237, 2014.

Lithium-ion Batteries Aging Motinoring Througth Open Circuit Voltage (OCV) Curve Modelling and Adjustment