Future Prediction of Regional City based on Causal Inference using

Time-series Data

Katsuhito Nakazawa, Tetsuyoshi Shiota and Tsutomu Tanaka

R&D Strategy and Planning Unit, Fujitsu Laboratories Ltd., 10-1 Morinosato-Wakamiya, Atsugi, Japan

Keywords: Causal Inference, Future Prediction, Time-series Data, Regional City, Social Issue.

Abstract: Regional cities in Japan have a lot of social issues. Various measures are being considered to solve these

social issues, but it is difficult to ascertain and implement practical and effective measures to address them.

In this study, we proposed a method for selecting indicators that have a causal relation to solve the social

issues based on a causal inference. If there was a causal relation between two sets of time-series data, the

slope of the approximation line of the time-shifted correlation coefficients at the base time returned a

negative value. The causal inference was verified by using samples of time-series data and we constructed a

network of the causal indicators based on the causal inference. In addition, we achieved future predictions

via the vector autoregressive model using the network of causal indicators. The model was verified using

the actual time-series data of the 87 regional cities. As a result, it was possible to simulate future predictions

by introducing practical and effective measure that originated from the social issue.

1 INTRODUCTION

Regional cities in Japan have a lot of social issues

such as depopulation, a decreasing birth rate and

aging populations, and decline of regional industries.

Various measures are being considered to solve

these social issues, but it is difficult to ascertain and

implement practical and effective measures to

address them. If indicators related to the measures

that have a causal relation with these issues can be

determined through data-based analyses, more

practical and effective measures can be employed.

Though several causal inferences using statistical

analysis have been proposed so far, they prove the

causal relations of already-known incidents based on

hypothesis (Rubin, 1974; Pearl, 1985; Shimizu,

2005).

In this study, our objectives are to propose a

method for selecting indicators that have a causal

relation to solve social issues and to achieve future

predictions for regional cities using the causal

indicators and quantifying the effects of the

measures introduced. As a result, it is possible to

plan the practical and effective measures that

originate in the causal indicators obtained using this

method. In addition, we are able to make predictions

regarding regional cities in the future according to a

model using the indicators that have a causal relation

with various social issues.

2 CAUSAL INFERENCE USING

TIME-SERIES DATA

We considered that time-series data were useful to

determine causal relations because the causal

indicators and the effect indicators were

distinguished easily by shifting the time of two time-

series data sets. The Granger causality concept is

already well-known for determining causality using

time-series data (Granger, 1969). However, it is

difficult to explain the causal relation between two

time-series data sets for a short term.

“e-Stat”, a portal site in Japan, releases various

time-series data for 1,742 Japanese regional cities

(Ministry of Internal Affairs and Communications,

2016). The term of the time-series data investigated

every year is mainly from 2000 to 2013, and we

need a new causal inference using the time-series

data for the short time period to discover various

indicators that have a causal relation with social

issues.

In this work, we propose a causal inference using

time-series data to plan practical and efficient

Nakazawa, K., Shiota, T. and Tanaka, T.

Future Prediction of Regional City based on Causal Inference using Time-series Data.

DOI: 10.5220/0005961902030210

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 203-210

ISBN: 978-989-758-199-1

203

measures for regional cities and to carry out future

prediction via models using indicators that have a

causal relation. The following hypothesis of the

causal inference was conceived in this study.

2.1 Hypothesis of Causal Inference

using Time-series Data

We proposed a method to find out the causal

relations from the variation of correlation

coefficients between two indicators by shifting the

time of two sets of time-series data.

According to the Pearson product-moment

correlation coefficient (Rodgers and Nicewander,

1988), the correlation coefficient R of Indicator X

and Indicator Y is calculated from the following

equation (1):

R

∑











x











∑











x







∑

















(1)

where x indicates the time-series data of Indicator X

and y indicates the time-series data of Indicator Y.

Expressing this with the average equation (2) of

the time-series data of indicator X and the average

equation (3) of the time-series data of indicator Y

gives us following equation (4).











(2)











(3)

R

∑











∑









∑











∑











–

∑















∑













∑











(4)

Then, expressing equation (4) with equation (5),

(6), (7), (8) and (9) respectively, gives us equation

(10).















(5)













(6)













(7)













(8)













(9)

R





























(10)

Simple time-series data of Indicator X shown in

Table 1 were prepared to prove the hypothesis.

These time-series data A, B and C change in three

patterns from Time T1-2 to Time T1+1.

Table 1: Time-series data of Indicator X.

t T1-2 T1-1 T1 T1+1

A x-1 x x+1 x+2

B x x x x

C x+3 x+2 x+1 x

If Indicator Y has a causal relation with Indicator

X completely (R=1.0), the time-series data of

Indicator Y are shown as per Table 2 according to

the regression line: Y(t)

= aX(t-1) + b (a>0). We

assumed simply that Indicator X influences Indicator

Y at the next unit time.

Table 2: Time-series data of Indicator Y.

t T1-1 T1 T1+1

A a(x-1)+b ax+b a(x+1)+b

B ax+b ax+b ax+b

C a(x+3)+b a(x+2)+b a(x+1)+b

From Table 1 and Table 2, when Indicator Y is

fixed at Time T1 and Indicator X is shifted at each

Time T1-1, T1 and T1+1, equations (5), (6), (7), (8)

and (9) are shown in Table 3.

Table 3: Expressions of Indicator X and Indicator Y when

Indicator Y is at Time T1 and Indicator X is at each Time

T1-1, T1 and T1+1.

t for X T1-1 T1 T1+1

(3x+2)/3 (3x+2)/3 (3x+2)/3

(3y+2a)/3 (3y+2a)/3 (3y+2a)/3

(3x

+4x+4)

(3x

+4x+2

) /3

(3x

+4x+4)

(3y

+4ay+4a

)/3

(3y

+4ay+4

) /3

(3y

+4ay+4a

)/3

(3xy+2y+2ax

+4a)/3

(3xy+2y+2a

x +2a)/3

(3xy+2y+2ax)

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

204

Equation (10) provides the correlation coefficient

by substituting the equations of Table 3. Figure 1

shows the correlation coefficient of Indicator X to

Indicator Y at Time T1. This is the representative

result as it is not dependent on the values of a and b.

From this result, we can build the following

hypothesis: if Indicator Y has a causal relation with

Indicator X and Indicator X is the causal indicator of

Indicator Y, R t-1＞R t＞R t+1 is completed.

Figure 1: Correlation coefficient of Indicator X at each

time to Indicator Y at Time t.

In other words, the correlation coefficients of

Indicator X to Indicator Y at a base time: T1 become

lower as shown in Figure 2 (a), and the slope of the

approximation line has a negative value. Similarly,

the correlation coefficients of Indicator Y to

Indicator X at a base time: T2 rise, as shown in

Figure 2 (b) if Indicator X is the causal indicator of

Indicator Y, and the slope of the approximation line

has a positive value.

Figure 2: Correlation coefficient of Indicator X to

Indicator Y at base time (a) and correlation coefficient of

Indicator Y to Indicator X at base time (b) when Indicator

X is a causal indicator of Indicator Y.

2.2 Verification of Causal Inference

using Samples of Time-Series Data

The causal inference was applied to samples of time-

series data with an already-known causal relation to

confirm the above-mentioned hypothesis. The

samples of time-series data in this verification are

shown in Figure 3.

Figure 3: Causal samples of time-series data for 10 cities

between 1990 and 2010.

We assumed and prepared the samples of time-

series data for 10 cities from City A to City J

between 1990 and 2010. The data of each city

increased 10% per year for 10 years and decreased

10% per year for 10 years, and the changing years

and the initial values of the 10 cities were different

respectively. Next, we assumed that the causal

samples of time-series data affected effect samples

of time-series data in the next year by 30%. And the

T1-1

T1+1

Future Prediction of Regional City based on Causal Inference using Time-series Data

205

influence of the causal samples of time-series data

gradually decreased by 3% every year, which lasted

for 10 years. The effect samples of time-series data

for 10 cities from City A to City J between 2000 and

2010 in this verification are shown in Figure 4.

Figure 4: Effect samples of time-series data for 10 cities

between 2000 and 2010.

We calculated the correlation coefficients using

the effect sample data based on 2005 and the causal

samples of time-series data between 2000 and 2010,

and Figure 5 shows the result. From this result, if

there is a causal relation between two sets of time-

series data, the slope of the approximation line of the

correlation coefficients at the base time returns a

negative value, and our hypothesis could be proved

by using samples of time-series data.

Figure 5: Correlation coefficients using the effect sample

data based on 2005 and the causal samples of time-series

data between 2000 and 2010.

3 SIMULATION MODEL FOR

FUTURE PREDICTION

We considered that future predictions of regional

cities could be conducted by selecting an appropriate

model using the causal indicators. As mentioned

below, a number of simulation models for the future

predictions were verified, and the most suitable

model was selected.

3.1 Selecting Simulation Models using

Causal Indicators

The model selection was considered using the

following simulation models, time-series data, and a

verification method.

3.1.1 Simulation Model

As models in which plural causal indicators as

explanatory variables were available, the following 3

types of regression model - the multivariate

regression model (MR model), the stepwise

regression model (SW model), and the vector

autoregressive model (VAR model) - were verified

in this study (Sims, 1980).

3.1.2 Time-series Data

First, we constructed a network of causal indicators

based on the above-mentioned causal inference. 238

kinds of time-series data between 2000 and 2013 for

1,742 regional cities in Japan were included in this

network and the causal relations were mutually

calculated using the causal inference. Causal

indicators can be easily selected using this network.

Population issue is a common significant target

for a lot of regional cities in Japan. The following 6

kinds of time-series data - live births (person), in-

migrants from other prefectures (person),

kindergarten pupils (person), marriages, taxable

income (thousand yen), and tax debtors per income

levy (person) - were selected as the causal indicators

of total population from the network of causal

indicators. We also conducted the verification using

time-series data that directly influenced total

population such as deaths (person) and out-migrants

to other prefectures (person) in addition to live births

and in-migrants. The time-series data in this

verification are shown in Table 4.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

206

Table 4: Time-series data of causal and direct indicators from 1985 to 1999 for verification of each simulation model.

Year

Population Live births In-migrants Marriages Taxable income Tax debtors Kindergarten Deaths Out-migrants

(person) (person) (person) (couple) (thousand yen) (person) pupils (person) (person) (person)

1985 1,088,624 14,003 83,718 8,697 1,317,664,207 443,164 21,452 4,477 78,451

1986 1,106,148 13,773 87,562 8,522 1,410,421,764 455,918 21,317 4,523 78,085

1987 1,126,485 13,999 90,742 8,885 1,521,779,615 471,283 21,790 4,753 80,193

1988 1,142,953 13,920 88,421 9,166 1,696,876,283 487,709 22,004 5,060 81,131

1989 1,157,005 13,090 91,848 9,484 1,793,159,486 496,645 21,918 5,038 85,576

1990 1,173,603 13,279 93,797 9,696 2,030,951,252 505,254 21,515 5,346 86,633

1991 1,187,034 13,494 91,537 10,049 2,243,247,257 528,811 21,582 5,487 87,751

1992 1,195,464 13,356 91,587 10,226 2,407,042,715 545,002 21,254 5,736 91,665

1993 1,199,707 12,855 90,167 10,718 2,341,293,380 557,276 20,895 6,032 93,102

1994 1,202,069 13,476 89,639 10,857 2,378,227,721 561,607 19,952 6,153 94,026

1995 1,202,820 13,146 87,846 10,897 2,398,720,169 561,574 19,476 6,399 91,268

1996 1,209,212 13,309 88,284 11,147 2,381,925,353 564,303 19,673 6,265 88,317

1997 1,217,359 13,423 87,209 10,465 2,443,414,810 567,349 19,799 6,461 85,304

1998 1,229,789 13,756 88,702 10,759 2,459,854,574 572,562 20,565 6,783 83,223

1999 1,240,172 13,590 87,196 10,211 2,417,084,645 572,331 21,071 7,186 83,975

3.1.3 Verification Method

We predicted the total population from 2000 to 2013

by 3 types of simulation models and the 8 kinds of

time-series data from 1985 to 1999, compared with

actual data from 2000 to 2013. In this verification,

an actual city (City K) of 1.2 million population

scale was targeted.

3.2 Verification of Future Prediction

using Simulation Models

The verification result using 3 types of simulation

models and using the 8 kinds of time-series data is

shown in Figure 6. In this verification, we tried out 5

types of simulation: 1 VAR model using 6 kinds of

causal indicators, 2 VAR model using 4 kinds of

direct indicators, 3 MR model using 6 kinds of

causal indicators, 4 MR model using 4 kinds of

direct indicators, and 5 SW model using in-migrants,

deaths, tax debtors, and kindergarten pupils that

were chosen as effective explanatory variables. As a

result, we observed that the simulations using a

VAR model showed good coincidence with the

actual data, especially in terms of selecting the

causal indicators. The average rate of relative error

for the actual data with the VAR model using the

causal indicators was the lowest by 1.1 %/year. The

next lowest simulation was the VAR model using

the direct indicators, and the average relative error

was 3.7%/year. The average relative errors in the

other simulations were 5.6%/year at the same level.

The future population investigated by the cohort-

component method is used as a bench mark in Japan

(National Institute of Population and Social Security

Research, 2013). We calculated the average rate of

relative error for the actual data with the VAR model

using the causal indicators, compared with the

cohort-component method. In this comparison, 87

cities that were 5% cities divided into 10 categories

on Japanese population scale were selected. The

total population from 2007 to 2013 was predicted by

the VAR model using time-series data from 2000 to

2006 of the 6 kinds of causal indicators. Figure 7

showed the number of cities in each relative error of

the population prediction by both methods. It was

confirmed that the population prediction via VAR

model using the causal indicators was predictable in

a smaller relative error.

We concluded that it was possible to predict

regional cities in the future via the vector

autoregressive model using the causal indicators that

have a causal relation with social issues.

Future Prediction of Regional City based on Causal Inference using Time-series Data

207

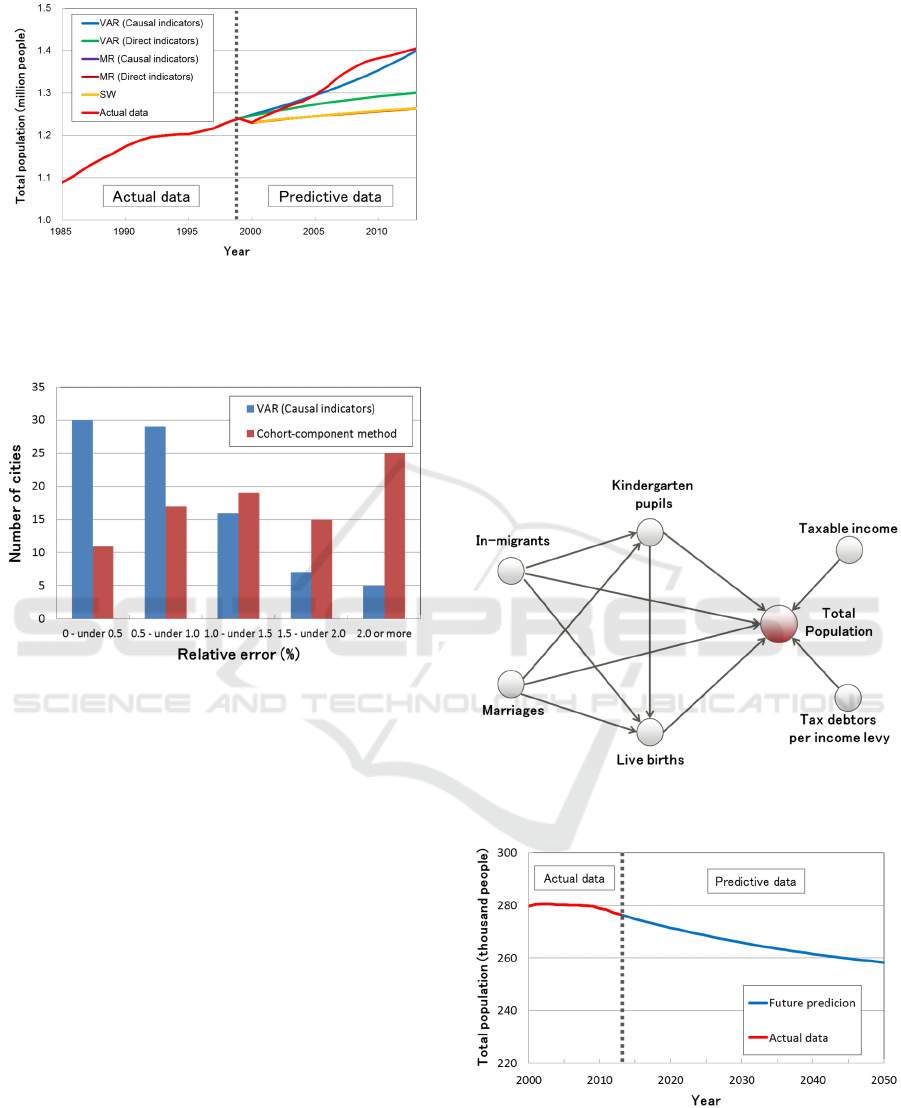
Figure 6: Verification of total population based on 5 types

of simulations using different kinds of time-series data.

The results using MR models are almost the same as the

result using SW model.

Figure 7: The number of cities in each relative error of the

population prediction by VAR model and cohort-

component method.

4 FUTURE PREDICTION OF

REGIONAL CITY USING

CAUSAL INDICATORS

We predicted a regional city in the future using the

network of causal indicators. A lot of regional cities

in Japan are experiencing depopulation issues as

described above, and the future population of the

regional city was simulated using the causal

indicators.

4.1 Future Prediction for Regional City

in the Future

We selected the causal indicators of live births, in-

migrants, kindergarten pupils, marriages, taxable

income, and tax debtors per income levy that have a

causal relation with total population. Figure 8 shows

the causal relation diagram of total population and

the causal indicators. These causal indicators that

have correlation coefficients of 0.9 or more based on

the total population data in 2006 were selected from

the network of causal indicators. We predicted the

total population from 2014 to 2050 via the VAR

model using actual time-series data for the causal

indicators from 2000 to 2013. In this future

prediction, City L with a population of 275,000 was

targeted.

The future prediction of total population in City

L is shown in Figure 9. As a result, we predicted that

the population of City L would decrease from

276,000 people to 258,000 people between 2014 and

2050 (the population decrease rate being 6.3%). It

was suggested that population decrease was the

social issue for City L as well as a lot of regional

cities in Japan.

Figure 8: Causal relation diagram of total population

selected from network of causal indicators.

Figure 9: Future prediction of total population in City L

from 2014 to 2050.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

208

Figure 10: Verification of total population in 4 regional cities by introducing measure for in-migrants.

4.2 Future Prediction of Total

Population by Introducing Measure

As shown in Figure 8, in-migrants were one of

important causal indicators of total population from

the viewpoint of population growth in the future.

Then, we verified future predictions by actual case

studies introducing a measure of in-migrants

increase. 4 regional cities from City M to City P that

introduced a measure to increase in-migrants were

selected in this verification. In these cities, the

measure that the residential area was increased by

the land development was introduced in 2006 or

2007, and in-migrants consequently increased by

68%, 25%, 66% and 38% in 2013, respectively. The

total populations from 2007 or 2008 to 2013 were

verified via the VAR model using actual time-series

data of in-migrants from 2007 or 2008 to 2013,

compared with actual data. Figure 10 showed the

verification results of 4 regional cities introducing

the measure to increase in-migrants. Each average

rate of relative error for the actual data was 1.2, 3.0,

3.6 and 2.6 %/year, and we confirmed the total

population introducing the measure via VAR model

was predictable in a smaller relative error.

Next, we assumed a measure for increasing in-

migrants in City L, and set 5 types of scenario that

increase in-migrants gradually from 2017 to 2025,

and increase from 2026 to 2050 by 10% (Scenario 1),

20% (Scenario 2), 30% (Scenario 3), 40% (Scenario

4) and 50% (Scenario 5), compared with the BAU

scenario. Figure 11 shows the simulation result for

total population in each scenario. From this result,

we confirmed that total population in City L

increased by increasing in-migrants between 2017

and 2050. In the case of Scenario A4 (increasing by

40% from 2026 to 2050), the current population in

City L (275,000 people) could be maintained in

2050.

Figure 12 shows the relationship between the

increase rate of total population and the increase rate

of in-migrants. We obtained the result that total

population increased by 1.8% by increasing in-

migrants by 10%.

It was suggested that in-migrants were important

causal indicators from the viewpoint of population

growth in the future, and the measure for in-migrants

could be effective in increasing total population.

Future Prediction of Regional City based on Causal Inference using Time-series Data

209

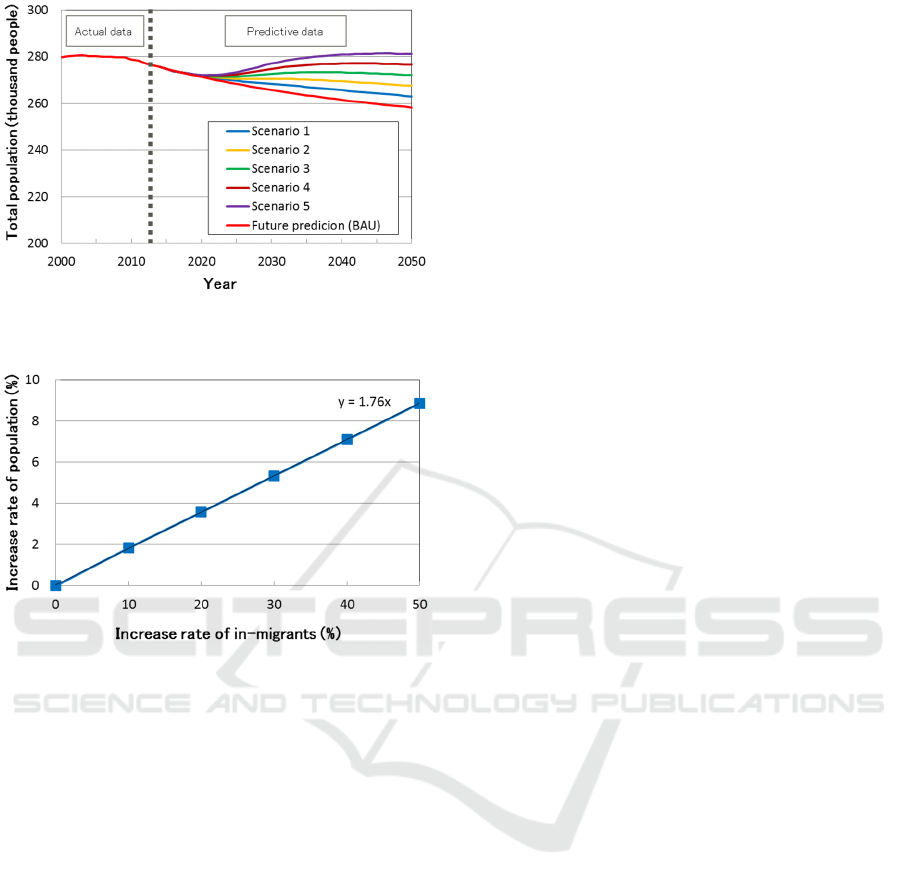
Figure 11: Simulation result for total population in 5

scenarios by introducing measure for in-migrants in City L.

Figure 12: Relationship between increase rate of total

population and increase rate of in-migrants in City L.

5 CONCLUSIONS

We proposed a method for selecting indicators that

have a causal relation with social issues based on a

causal inference. If there was a causal relation

between two sets of time-series data, the slope of the

approximation line of the time-shifted correlation

coefficients at the base time returned a negative

value. The causal inference was verified by using the

samples of time-series data and we constructed a

network of the causal indicators. In addition, we also

achieved future predictions via the vector

autoregressive model using the causal indicators.

The model was verified using the actual time-series

data of the 87 regional cities. As a result, it was

possible to simulate future predictions by

introducing the practical and effective measures (for

in-migrants) that originated from the social issue

(with a total population decrease).

It was easily possible to determine the causal

indicators and to quantify the effect of introducing

the measures via the model using the causal

indicators in this study. For future work, we will be

able to apply this method to a number of issues by

including more indicators related to economic

factors and the environment in the network, and

expanding it to various fields. Moreover, it is

necessary to verify the effects of introducing

measures considering regional characteristics based

on actual case studies.

In terms of establishing a sustainable society, we

consider that regional cities can decide on

appropriate measures related to indicators that have

a causal relation with the social issues, and execute

future predictions easily if these measures are

introduced.

REFERENCES

Rubin, Donald, 1974. Estimating Causal Effects of

Treatments in Randomized and Nonrandomized

Studies. Journal of Educational Psychology, 66 (5),

688–701.

Pearl, Judea, 1985. Bayesian Networks: a Model of Self-

Activated Memory for Evidential Reasoning.

Proceedings, Cognitive Science Society, 329-334.

S. Shimizu, A. Hyvärinen, Y. Kano, P. O. Hoyer, 2005.

Discovery of non-gaussian linear causal models using

ICA. In Proceedings of the 21st Conference on

Uncertainty in Artificial Intelligence, UAI2005, 526-

533.

Granger, C. W. J., 1969. Investigating Causal Relations by

Econometric Models and Cross-spectral Methods.

Econometrica, 37 (3), 424–438.

Ministry of Internal Affairs and Communications, 2016. e-

Stat: Portal site of official statistics of Japan.

http://www.e-sat.go.jp/SG1/estat/eStatTopPortalE.do.

Rodgers, J. L., Nicewander, W. A., 1988. Thirteen ways to

look at the correlation coefficient. The American

Statistician, 42 (1), 59–66.

Sims, Christopher A., 1980. Macroeconomics and Reality.

Econometrica, 48, 1-48.

National Institute of Population and Social Security

Research, 2013. Regional population projections for

Japan: 2010-2040, Population Research Series, 330.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

210