
Two Secure Anonymous Proxy-based Data Storages
∗
Olivier Blazy
1
, Xavier Bultel
2
and Pascal Lafourcade
2
1
Universit
´
e de Limoges, Xlim, Limoges, France
2
Universit
´
e Clermont Auvergne, LIMOS, BP 10448, 63000 Clermont-Ferrand, France
Keywords:
Anonymous Storage, Public Key Cryptography, Proxy, Standard Model.
Abstract:
Unidirectional proxy re-encryption (PRE) can be used to realize an efficient and secure shared storage. How-
ever, this type of storage does not yet protect its users’ privacy: to retrieve some data a user must give his
identity and his query to the proxy. We propose two secure data storage systems that allow authorized users to
anonymously get access to the content of encrypted data on a storage. Each scheme corresponds to a certain
economic model. In the first one, a user has to pay for each downloaded file, whereas in the second one, users
pay each month a subscription to get an unlimited access to all their files.
1 INTRODUCTION
Users’ anonymity is a property often required in mod-
ern security protocols especially in the post-Snowden
era, not only towards outsiders but also towards in-
termediaries in a protocol. To motivate our work,
we consider the following scenario where a video
provider, called the owner, stores some videos on a
database. To control access to the videos, he stores
all of them encrypted on a remote server, and allows
access to accredited users modulo some fees. Users
wish to retrieve videos easily, and to disclose no in-
formation about their interest. According to some
marketing issues the owner can enroll the users in
different groups, like premium or privilege accord-
ing to the prices of the services. The owner wants
to meet the requirement of each group of users, and to
bill them accordingly. He also wants an easy update
procedure so that he can revoke access to users who
misbehave and/or are late in the payment. Using a
proxy, who helps the user to open encrypted videos in
an anonymous way, we provide two solutions walking
the fine line between these two seemingly opposite re-
quirements (anonymity of the users and billing of the
owner).
A na
¨
ıve solution is to use a public key cryptosys-
tem and an anonymous storage. The owner constructs
a pair of public/private key for a group of users and
gives the private key to each group member. Any-
∗
This research was conducted with the support of the “Dig-
ital Trust” Chair from the University of Auvergne Founda-
tion.
body can encrypt data with the public key and store it
in the database. Thus, each group member can anony-
mously recover this encrypted data and retrieve the
plaintext with the help of the group secret key. Un-
fortunately, this method does not allow the owner to
revoke a group user, except by resetting all keys for
groups and re-encrypting all the database where the
revoked user belonged. This solution is not realistic.
Our goal is to design anonymous storage where
each stored data is encrypted for a group of users
and where the owner can easily revoke some users.
Moreover, each authorized user can anonymously re-
cover and decrypt data, i.e. without revealing neither
his identity, nor his group, nor the recovered cipher-
text. We also allow the owner of the storage, de-
noted O, to manage authorized users using two us-
age models: pay-per-download or monthly-fee. In
the pay-per-download model, the owner only knows
how many data are downloaded by a user and does not
know which data have been asked by each user. The
monthly-fee model is similar to Netflix
2
, the user pays
a subscription each month for an unlimited access to
the data anonymously. The owner also manages the
group of users: he can add new users or can revoke
users that did not pay for this anonymous service. The
revoked users cannot get access to any data anymore.
To analyze the security of both systems, we consider
an honest but curious proxy, also called semi-trusted
proxy, who does not learn any information about the
user and the requested files.
2
A provider of on-demand Internet streaming media
Blazy, O., Bultel, X. and Lafourcade, P.
Two Secure Anonymous Proxy-based Data Storages.
DOI: 10.5220/0005962402510258
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 251-258
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
251

Contributions: We propose two schemes to
anonymously manage a secure data storage. Like
proxy re-encryption (PRE) based storage, the owner
lets the access right management responsibility to the
proxy and can be always offline during storage ac-
cess. Both schemes use a semi-trusted proxy that
gives only to authorized users the material to open en-
crypted data anonymously collected. The proxy does
not know enough information to learn the identity of
the users, this guarantees their anonymity. Further-
more, updating public parameters and proxy material,
the owner can revoke any user. Both instantiations use
public key encryption functions and a proxy. Both
schemes are round optimal since user and proxy ex-
change in one round only. Our schemes differ on how
the owner manages the users’ rights.
• The first scheme, called Direct Revocation
Anonymous Storage (DRAS), offers a pay-per-
download model. The owner O manages users
such that: i) he knows how many files have been
downloaded anonymously by each user ii) he re-
vokes a user with a direct mechanism based on a
black list BL sent by O to the proxy P and con-
taining identities of users.
• The second one, called Indirect Revocation
Anonymous Storage (IRAS) offers a monthly-fee
model. The owner gives each month a key to each
user who has paid his subscription to get an unlim-
ited access to all files. The revocation mechanism
is indirect, meaning that the owner only has to
change his own public key when he updates each
month and distributes cryptographic material for
all remaining users.
We use an anonymous access to the information
stored in a database D. This can be done using a Pri-
vate Information Retrieval (Chor et al., 1995) that al-
lows to retrieve a line in the database. This is more
efficient than an Oblivious Transfer (Rabin, 1981)
based solution, with a slight compromise on the obliv-
iousness. In both cases, solutions exist to communi-
cate with the proxy in only one round. We use such
a mechanism to collect anonymously encrypted data
in the database D. We will not focus on the kind
of instantiation chosen as this is out of the scope of
our contribution. However notice that pairing based
solutions exist in the Standard Model with various
level of security depending on the global security ex-
pected (Peikert et al., 2008,Abdalla et al., 2013,Blazy
and Chevalier, 2015).
Moreover, for each scheme, we define the secu-
rity models for anonymity and revocability. Then we
prove that our two solutions are secure in the Stan-
dard Model, with respect to the model of semi-trusted
proxy and under usual cryptographic assumptions.
The models and the proofs are given in the full ver-
sion of this paper. Our schemes have the following
security properties:
• All data are IND-CPA encrypted for any unautho-
rized user, any revoked user and the proxy.
• DRAS scheme is partially anonymous, since the
proxy P can link a user to a group, only if the
user uses several times one of his group’s mem-
ber key. Thanks to the information stored by the
proxy the owner knows only the identity of user
and the number of files that he has downloaded.
Then a user has to pay twice when he downloads
twice a file in order to preserve his privacy.
• The IRAS scheme is fully anonymous, it means
that the proxy does not learn any information on
the ciphertext, the user and his membership group.
The owner can only recover the group who has
requested the files. This scheme uses a Smooth
Projective Hash Function (SPHF (Cramer and
Shoup, 2002)) to be fully anonymous.
The required storage for our solutions is linear in the
number of stored data times the number of groups for
each data. Our protocols are also optimal in terms of
communication costs.
Related Work: Shared storage based on proxy
re-encryption (PRE) are very attractive for many rea-
sons: after initialization of the proxy, the data owner
is not required to manage the rights policy of the stor-
age. Thus, the proxy can remain offline. To revoke
a user’s right, the owner simply updates informations
given to the proxy. The owner can also give access
to a set of data to several users without duplication
of ciphertexts in the storage. However several dis-
advantages remain in PRE: partial trust in the proxy
is mandatory, and there is no privacy protection. In-
deed, the proxy learns several information about the
user: his identity, his access rights and all ciphertexts
that he wants to decrypt.
In (Blaze et al., 1998), Blaze et al. define “proxy
cryptography”. To delegate decryption rights they
use a semi-trusted proxy, meaning that the proxy fol-
lows the protocol but tries to learn some informa-
tion. The proxy receives the decryption rights, from
a user A to a user B, even when user A is offline.
The first bidirectional proxy re-encryption scheme
has been described in (Ivan and Dodis, 2003): a user
A gives delegation rights to the proxy by forging a
re-encryption key from both secret keys of A and B.
In (Ateniese et al., 2006), they describe the first uni-
directional proxy re-encryption that allows to dele-
gate decryption rights with delegator secret key and
only delegate’s public key. This paper introduces
PRE schemes to manage an encrypted shared stor-
age. Authors give an analysis of their PRE based stor-
SECRYPT 2016 - International Conference on Security and Cryptography
252
age implementation. In (Canetti and Hohenberger,
2007), they give a chosen ciphertext security defini-
tion of proxy re-encryption and provide a secure bidi-
rectional scheme. In (Libert and Vergnaud, 2008),
Libert et al. present the first chosen ciphertext se-
cure unidirectional proxy re-encryption. Some other
results deal with anonymity and privacy protection in
PRE based storage: in (Ateniese et al., 2009), authors
present the notion of key-private (or anonymous re-
encryption key) in PRE. This property does not allow
the proxy to find the user public key corresponding to
a re-encryption key. In (Zheng et al., 2014), authors
propose a scheme that is both CCA secure and anony-
mous (in the anonymity model given by the previous
article). On the other hand, the notion of Anonymous
proxy re-encryption, from (Shao et al., 2012), protects
the identity of the ciphertext (or re-encrypted cipher-
text) recipient for anybody who does not know the
re-encryption keys.
However, all these cryptographic primitives
only partially resolve the privacy protection prob-
lem of PRE: the proxy can link all transactions of
the same user, since the proxy uses the same re-
encryption keys for each user. Moreover, ciphertexts
that the proxy decrypts are not protected, and he can
deduce the identity of the user. Our aim is to solve this
problem by proposing two secure proxy based data
storages that have strong privacy properties while try-
ing to keep the benefits of PRE based storage (mini-
mizing data duplication).
To control the access to the data, a classical solu-
tion would be to use an anonymous credential system
(Chaum, 1985) where users are given credential cor-
responding to their access rights. In the following,
the granularity of those credentials are set at group
level. This allows us to define anonymity on two
levels: first anonymity inside a group, even knowing
which group can access a data, the user interacting
with the protocol keeps his identity secret from an ad-
versary. Such notion directly echoes to group signa-
tures (Chaum and van Heyst, 1991), where anonymity
is only defined for user belonging to the group. Sec-
ond a weaker version of group anonymity: it should
be difficult to learn which group a user belongs to.
2 SCHEMES DESCRIPTION
Our idea is to achieve anonymity of users and efficient
user revocation mechanism by using proxy cryptogra-
phy to manage users. To preserve the benefits of the
anonymous storage, the proxy should not be able to
learn any private information about the user (identity,
access rights and data that he needs to decrypt).
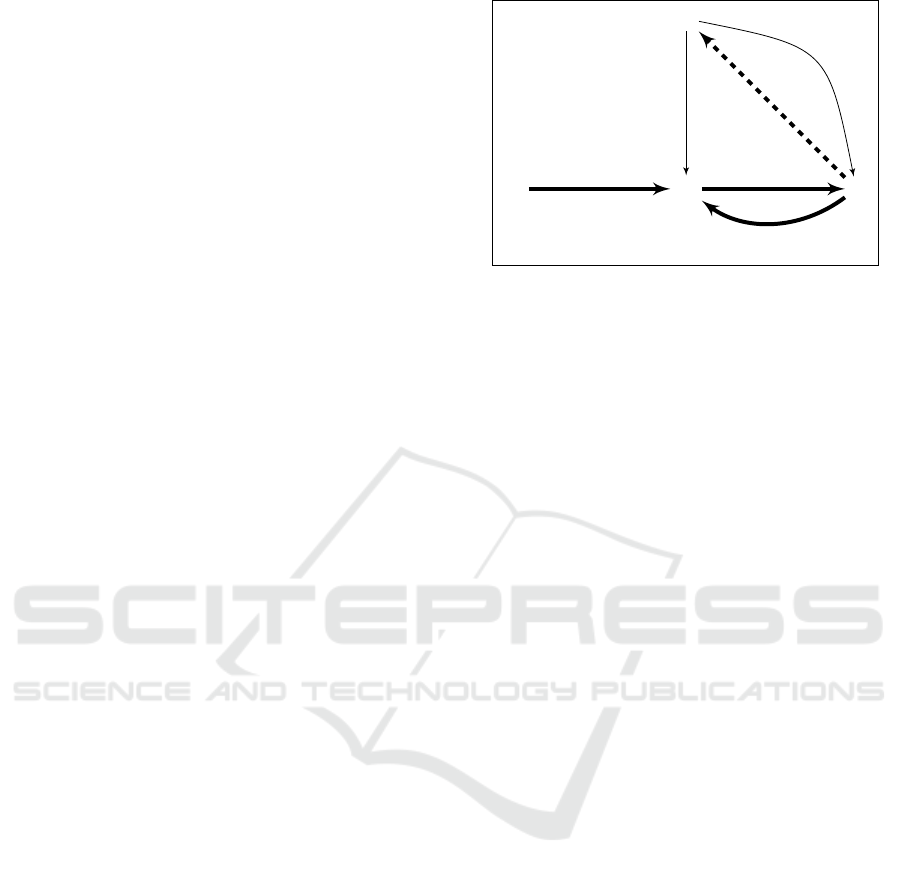
O
U
i
PD
MSK
j
i
C
VIEW
SKP
(1)
(2)
(3)
(4)
Figure 1: Schemes overview, where dashed line is only for
DRAS, bold arrows represent decryption interactions and
thin arrows correspond to the key’s distribution (where SKP
is the proxy secret key and MSK
j
i
is the group member key
for the user U
i
in the group G
j
).
From a high level point of view, our two schemes
have a similar workflow: Firstly, the owner O of the
storage builds and distributes required keys for groups
G
j
of users that have same access rights. Secondly, he
generates a secret group member key SKG
j
for each
group and publishes the associated public key PKG
j
.
Everybody can, using groups public key, store in the
database D an encrypted data C for one of the groups.
Lastly, the owner generates and distributes the secret
key SKP to the proxy and a secret key MSK
j
i
to each
user U
i
belonging to the group G
j
. Using these keys
a user and the proxy interact, allowing user to decrypt
the encrypted data C. Moreover the owner, who has
all private keys, can decrypt all ciphertexts. In Fig. 1,
we give the workflows of our two schemes that work
as follows after the keys distribution in a setup phase:
• Step (1): a user U
i
privately downloads a cipher-
text C from the anonymous storage D, using for
instance a PIR. However, his member key MSK
j
i
is not sufficient to open C.
• Step (2) and (3): the user U
i
interacts with the
proxy in order to obtain the required material to
open C. The proxy verifies the authorization of
U
i
and only helps authorized users to open C.
• Step (4): in DRAS scheme, the proxy P sends
some information for the billing phase in the mes-
sage denoted by VIEW to the owner O.
We describe our two schemes starting with the
DRAS scheme as a stepping stone for our IRAS
scheme. On one hand, DRAS scheme has the follow-
ing revocation property: the owner can easily revoke
any user at any time. However this scheme does not
perfectly preserve the privacy of users: if a user re-
quests the proxy twice with two data encrypted with
the same group key, then the proxy can link the two
requests. On the other hand, IRAS scheme is more
Two Secure Anonymous Proxy-based Data Storages
253

complex and offers a different revocation mechanism
since we cannot revoke the users at any time, but this
scheme allows us to perfectly preserve all private in-
formation of the users.
2.1 Description of DRAS Scheme
We use an IND-CCA2 public key cryptosystem
PKE = (Gen, Enc, Dec). Anybody can encrypt a
data with the public key of the group PKG
j
and store
it in an anonymous database D. This encryption is
done with ElGamal based (ElGamal, 1985) encryp-
tion denoted by Encrypt(PKG
j
, m), where m is the
data and PKG
j
the group public key. The main idea
behind DRAS is to allow the owner to revoke a user
using a blacklist BL transferred by O to the proxy P
and to use a white list WL to bill the authorized users.
The white list is composed of couples of identities and
re-encryption keys. With the blacklist, P is able to
help users that are not on BL to open the ciphertexts.
In Fig. 2, we describe DRAS that contains:
Setup(K): take a security parameter K as input and
return the parameters P = (g, G, p, PKE).
P-Gen(P): generate the pair of keys (PKP, SKP)
for the proxy P ,
G-Gen(P): generate the pair of keys
(PKG
j
, SKG
j
) for the group of users G
j
,
Join(SKG
j
, WL, U
i
): generate the secret key MSK
j
i
that allows a user U
i
of a group G
j
to transform
a ciphertext C to the proxy. The user identity U
i
and the re-encryption key MSK
j
i
are added to the
white list WL.
Encrypt(PKG
j
, m): allow a user to encrypt the mes-
sage m for the group G
j
in C and to store it in the
database D.
Those algorithms allow the owner to set up prop-
erly the system. The first ones generate all the re-
quired keys, while the last one allows anyone to add
a data to the database encrypted for a specific group.
To decrypt a message, there are two different ways:
Decrypt(SKG
j
, C): use a group secret key SKG
j
to
recover the plaintext in C.
ProxyDec(U
i
, P ): a protocol between a user U
i
and
the proxy P allowing a non revocated user to in-
teract with the proxy, in order to decrypt the ci-
phertext C. The proxy outputs to the owner O the
value VIEW that contains data needed for billing.
Those algorithms allow a user to recover an en-
crypted data stored in the database D. The first one
allows the owner to decrypt any data of D, while the
second one allows a user U
i
to access an encrypted
message, and decrypts it through an exchange proto-
col with the proxy that is described in Fig. 3. First,
user encrypts, with the public key PKP, a randomiza-
tion of C
1
(the first part of the ciphertext C) and RK
(the first part of MSK
j
i
). Once the message B is re-
ceived by the proxy. After verification that the key RK
is not blacklisted (
˜
B
2
6∈ BL), the proxy, using RK and
SKP (a key unknown by the user), transforms the part
˜
B
1
into another ciphertext
ˆ
C. The user U
i
then recov-
ers the message m using his secrets. On the same
time the proxy provides a VIEW of the interaction to
the owner. Finally, DRAS contains:
Revoke(MSK
j
i
, BL): add the user U
i
using MSK
j
i
to
the blacklist BL of revocated users.
Open(VIEW, WL): output the user identity corre-
sponding to the VIEW message.
Those algorithms are for administrative purposes.
The first one, simply allows to revoke a user, without
having to update the whole database, while the second
one allows the owner to exploit the VIEW in order to
bill according the number of data downloaded.
2.2 Description of IRAS Scheme
Under the monthly-fee model, a revocation system
at any time is not usefull anymore. Then the black-
list and the white list used for billing and for revo-
cation are not required anymore. We propose IRAS
scheme, that has a different revocation process: the
owner revokes a user by updating his own signing
key. Once an owner’s key is updated, all group mem-
ber keys are unusable as long as the owner updates
them. Morover, this scheme is perfectly anonymous
for any users, and all decryptions are not traceable
by O. Comparing to the previous scheme, IRAS is
more complex: it requires an EUF-CMA signature
scheme S = (Gen
S
, Sign
S
, Verif
S
), a bilinear pair-
ing of type 3, an IND-CPA public key cryptosystem
PKE = (Gen, Enc, Dec) and a Smooth Projective
Hash Function (SPHF). We start by recalling how an
SPHF works before presenting IRAS.
Smooth projective hash functions (SPHF) were in-
troduced by Cramer et al. to construct encryption
schemes in (Cramer and Shoup, 2002). A projective
hashing family is a family of hash functions that can
be evaluated in two ways: either using the (secret)
hashing key, one can compute the function on every
point in its domain, or using the (public) projected key
one can only compute the function on a special sub-
set of its domain. Such a family is deemed smooth
if the value of the hash function on any point out-
side the special subset is independent of the projected
key. The notion of SPHF has already found numer-
ous applications in various contexts in cryptography
(e.g. (Gennaro and Lindell, 2003,Kalai, 2005,Abdalla
et al., 2009, Blazy et al., 2012)).
Definition 1 (Smooth Projective Hashing System). A
SECRYPT 2016 - International Conference on Security and Cryptography
254

Setup(K): pick a group G of prime order p generated
by g, returns P = (g, G, p, PKE).
P-Gen(P): use Gen to generate (PKP, SKP).
G-Gen(P): pick γ
$
← Z
∗
p
, set PKG
j
= g
γ
and
SKG
j
= γ, and then return (PKG
j
, SKG
j
).
Join(SKG
j
, WL, U
i
): For SKG
j
= γ, pick t
$
← Z
∗
p
,
set MSK
j
i
= (t, RK) where RK = Enc
PKP
(
t
γ
), add
(MSK
j
i
, U
i
) in WL and return MSK
j
i
.
Encrypt(PKG
j
, m): For PKG
j
= g
γ
, user U picks
r
$
← Z
∗
p
, computes C = (C
1
, C
2
) = (g
γr
, g
r
· m),
and then stores C in the database D.
Revoke(MSK
j
i
, BL): add RK to the blacklist BL where
MSK
j
i
= (t, RK).
Open(VIEW, WL): The owner finds U
i
and t such that
((t, VIEW), U
i
) ∈ WL to get the iU
i
user.
Decrypt(SKG
j
i
, C): For SKG
j
i
= γ, return m =
C
2
C
1/γ
1
, where C = (C
1
, C
2
).
ProxyDec(U
i
, P ): protocol described in Figure 3.
Figure 2: DRAS scheme.
User U
i
Proxy P
PKP; MSK
j
i
= (t, RK); C = (C
1
, C
2
) SKP; BL
s
$
← Z
∗
p
; B = Enc
PKP
((C
1
)
s
, RK)
B
−−−−−−−−−−−−−−→
e
B = (
e
B
1
,
e
B
2
) = Dec
SKP
(B)
If
e
B
2
∈ BL then abort; else w = Dec
SKP
(
e
B
2
)
m =
C
2
b
C
(1/st)
b
C
←−−−−−−−−−−−−−−
b
C = (
e
B
1
)
w
Output m Output VIEW =
e
B
2
.
Figure 3: ProxyDec(U
i
, P ) protocol for DRAS.
Smooth Projective Hash Function over a language
L ⊂ X and W ∈ L, with hashes v, v
0
∈ V is de-
fined by the following algorithms:
• Setup(1
K
) generates the global parameters P of
the scheme, and the description of an N P lan-
guage L;
• HashKG(L, P), outputs a hashing key hk for the
language L;
• ProjKG(hk, (L, P), W ), derives the projection
key hp, thanks to the key hk,
• Hash(hk, (L, P), W ), outputs the hash value v ∈
V, thanks to the key hk, and W ,
• ProjHash(hp, (L, P), W, w), outputs the hash
value v
0
∈ V, thanks to hp,W and the witness
w.
In the following, we consider L as a hard-
partitioned subset of X, i.e. it is computationally hard
to distinguish a random element in L from a random
element in X \ L. An SPHF should satisfy the fol-
lowing properties:
• Correctness: Let W ∈ L and w a wit-
ness of this membership. Then, for all
hashing keys hk and associated projection
keys hp we have: Hash(hk, (L, P), W ) =
ProjHash(hp, (L, P), W, w)
• Smoothness: For all W ∈ X \ L the distributions
∆
0
and ∆
1
are statistically indistinguishable:
∆
0
= {(L, P, W, hp, v)| P = Setup(1
K
), hk =
HashKG(L, P), hp = ProjKG(hk, (L, P), W ), v =
Hash(hk, (L, P), W )} and ∆
1
= {(L, P, W, hp, v)|
P = Setup(1
K
), hk = HashKG(L, P), hp =
ProjKG(hk, (L, P), W ), v
$
← V }
• Pseudo-Randomness: If W ∈ L, then without a
witness of membership the two previous distri-
butions should remain computationally indistin-
guishable.
Our IRAS scheme is given in Fig. 4 and is composed
of the following algorithms:
Setup(K): takes a security parameter K in
input and return the parameters P =
(G
1
, G
2
, G
T
, g
1
, g
2
, e, p, PKE, S).
O-Gen(P): create the owner keys (PKO, SKO).
P-Gen(P): create the proxy keys (PKP, SKP).
G-Gen(P): generate the group keys
(PKG
j
, SKG
j
).
Join(SKG
j
, ssk
o
, PKP): compute a group member
secret key MSK
j
i
for the user U
i
.
O-Update(SKO, PKO): update the owner keys.
U-Update(MSK
j
i
, SKG
j
, SKO): update a user
group member secret key MSK
j
i
.
Encrypt(PKG
j
, m): encrypt a message m for a
group into the ciphertext C.
Decrypt(SKG
j
, C): decrypt a ciphertext C into m
using a group secret key SKG
j
.
ProxyDec(U
i
, P ): a protocol between a user U and
the proxy P , that allows an authorized user to re-
cover the plaintext in C.
To revoke a user U
i
in a group j, the owner only
updates his signature keys (PKO, SKO) used to sign
the users member group key MSK
j
i
and he does not
re-sign it with his new signing key.
Moreover, each user has a secret key MSK
j
i
for each of their groups. This key contains a re-
encryption key RK encrypted with the public key of
Two Secure Anonymous Proxy-based Data Storages
255

Setup(K): pick a bilinear group (G
1
, G
2
, G
T
) of prime
order p and generators g
1
, g
2
respectively with a
pairing e : G
1
× G
2
→ G
T
, and return P =
(G
1
, G
2
, G
T
, g
1
, g
2
, e, p, PKE, S).
O-Gen(P): generate a pair of signature keys
(ssk
o
, svk
o
) ← Gen
S
, a pair of encryption keys
(pk
o
, sk
o
) ← Gen and return PKO = (pk
o
, svk
o
)
and SKO = (sk
o
, ssk
o
).
P-Gen(P): generate (pk
p
, sk
p
) ← Gen, pick x
$
←
Z
∗
p
, set PKP = (pk
p
, g
x
2
) and SKP = (sk
p
, x) and
return (PKP, SKP).
G-Gen(P): pick γ
0
, γ
1
$
← Z
∗
p
, set PKG
j
= (g
γ
0
1
, g
γ
1
1
)
and SKG
j
= (γ
0
, γ
1
), and return (PKG
j
, SKG
j
).
Join(SKG
j
, ssk
o
, PKP): pick r
0
, r
1
$
← Z
∗
p
, know-
ing that SKG = (γ
0
, γ
1
), set RK =
(RK
1
, RK
2
, RK
3
, RK
4
) where γ
0
=
γ
1
γ
0
, RK
1
=
g
r
0
2
, RK
2
= g
xr
0
2
· g
(1/γ
0
)
2
, RK
3
= g
r
1
2
, RK
4
=
g
xr
1
2
· g
γ
0
2
and σ = Sign
S
(ssk
o
, RK) and then re-
turn MSK
j
i
= (RK, σ).
O-Update(SKO, PKO): generate a fresh (ssk
0
o
, svk
0
o
)
← Gen
S
and update svk
o
:= svk
0
o
and ssk
o
:=
ssk
0
o
in SKO = (sk
o
, ssk
o
) and PKO =
(pk
o
, svk
o
).
U-Update(MSK
j
i
, SKO): compute MSK
j
0
i
=
(RK, Sign
S
(ssk
o
, RK)) from MSK
j
i
= (RK, σ)
and SKO = (sk
o
, ssk
o
). Update MSK
j
i
:= MSK
j
0
i
.
Encrypt(PKG, m): pick s
$
← Z
∗
p
, compute C =
(g
γ
0
s
1
, g
γ
1
s
1
, e(g
1
, g
2
)
s
· m), where PKG =
(g
γ
0
1
, g
γ
1
1
) and after storing C in the database D re-
turn it.
Decrypt(SKG
j
, C): return m =
C
3
e(C
1
,g
2
)
1/γ
0
using
SKG
j
= (γ
0
, γ
1
) and C = (C
1
, C
2
, C
3
).
ProxyDec(U
i
, P ): protocol described in Figure 5. Fol-
lowing our SPHF: the proxy computes the hash keys
hk = HashKG(
f
RK, E) for the language stating that
f
RK is a valid randomization of the value encrypted
in E, signed by the authority in the committed σ us-
ing PKO. If the user U
i
is revoked, this value will be
indistinguishable from a random noise. This gives
him hp = ProjKG(
f
RK, E, hk) and a hash value
H = Hash(
f
RK, E, hk).
Figure 4: IRAS Scheme.
the proxy PKP by an ElGamal cryptosystem. Thus,
a user can raise the re-encryption key RK to a ran-
dom power µ in this ElGamal ciphertext thanks to the
malleability property of this encryption scheme. This
allows the user to send to the proxy a re-encryption
key RK
0
which is RK hidden by a secret value µ. The
proxy, using the ElGamal secret key SKP, finds the
masked re-encryption key RK
0
to compute the infor-
mation
b
C which is also hidden by the same secret
values µ that hides the re-encryption key RK. This
masked value
b
C gives no information to the proxy
who sends it to U
i
. The user can remove the mask
µ on
b
C and obtain the information that he needs to
compute the plaintext m. This decryption protocol is
called ProxyDec(U
i
, P ) and is detailed in Figure 5.
It is a 3-step protocol:
• First the user, sends two ciphertexts B and E
to the proxy. B is an encryption for the proxy,
which contains a randomization of the ciphertext
C and a randomization of the re-encryption key
RK. Moreover, E is an encryption of the user
group member secret key MSK
j
i
for the owner.
• Then the proxy decrypts the values in B, checks
the consistency of the various randomizations,
and if this holds, the proxy computes
ˆ
C
0
a de-
cryption of the randomized ciphertext chosen
by the user. Now, since the full decryption
should only be done for truthful user, the proxy
hides the outcome of the decryption. He does
it with the hash value associated with the fol-
lowing language of the SPHF: E is an en-
cryption of an MSK
j
i
signed by the owner, and
is consistent with the randomized values given
in B (namely there exists a µ linking the en-
crypted RK
1
, RK
2
with RK
µ
1
, RK
µ
2
, and a µ
0
link-
ing the encrypted RK
3
, RK
4
with RK
µ
0
3
, RK
µ
0
4
).
To do so, the proxy computes a hash key hk =
HashKG(
e
B
MSK
, E), its associated projected key
hp = ProjKG(
e
B
MSK
, E, hk), and computes the
associated hash H = Hash(
e
B
MSK
, E, hk). Those
algorithms are derived from those on the sublan-
guages as described afterwards.
The proxy then simply uses H to do a one time
pad of
ˆ
C
0
and sends the resulting value together
with the projected key hp to the user. The
Smoothness of the SPHF ensures that if the user
misbehaved, this will be indistinguishable from a
random noise. (This step allows the user to do an
implicit proof of knowledge of his secret key en-
crypted under PKO)
• Now the user, knowing the randoms he used to
generate E and to do the initial randomization
(µ, µ
0
), is able to compute the Projected Hash
H
0
= ProjHash(hp, µ, µ
0
). If he is honest then
H = H
0
, so he can recover
ˆ
C
0
, from which he
recovers the message m.
Constructing the Required Smooth Projective
Hash Function: Conjunction techniques were de-
tailed in (Abdalla et al., 2009), to show how to com-
bine Smooth Projective Hash Functions on various
SECRYPT 2016 - International Conference on Security and Cryptography
256

User U
i
Proxy P
pk
p
; MSK
j
i
= (RK, σ); C = (C
1
, C
2
, C
3
) SKP = (sk
p
, x)
where RK = (RK
1
, RK
2
, RK
3
, RK
4
)
ω, µ, µ
0
$
← Z
∗
p
e
C = (C
ω
1
, C
ω
2
, e(
e
C
2
, g
2
)
µ
0
)
f
RK = (RK
µ
1
, RK
µ
2
, RK
µ
0
3
, RK
µ
0
4
)
B = Enc
pk
p
(
e
C
1
,
e
C
2
,
e
C
3
,
f
RK)
E = Enc
pk
o
(RK)
B,E
−−−−−−−−−−−−−−→ (
e
C
1
,
e
C
2
,
e
C
3
,
f
RK) = Dec
sk
p
(B),
where
f
RK = (
f
RK
1
,
f
RK
2
,
f
RK
3
,
f
RK
4
)
U =
f
RK
2
/
f
RK
x
1
; V =
f
RK
4
/
f
RK
x
3
If
e
C
3
= e(
e
C
1
, V )
then
b
C
0
= e(
e
C
1
, U)
else
b
C
0
$
← G
T
hk = HashKG(
f
RK, E); hp = ProjKG(
f
RK, E, hk)
H
0
= ProjHash(hp, µ, µ
0
)
b
C
H
,hp
←−−−−−−−−−−−−−−
b
C
H
= Hash(
f
RK, E, hk) ⊕
b
C
0
Output m =
C
3
(
b
C
H
⊕H
0
)
1/ωµ
Figure 5: ProxyDec(U
i
, P ) protocol for IRAS.
languages. In the following, we consider the vari-
ous building blocks required by the language above.
One side, we need to consider the language of valid
randomization of encrypted values, on the other we
consider the language of the encryption of a valid sig-
nature under a given public key.
• The first language requires to show (twice), that
a pair of values are a proper randomization of an
encrypted value. We then suppose that there ex-
ists an ElGamal encryption scheme described by
the generators h and g. A user possesses non triv-
ial values X, Y i.e. X = g
x
, Y = g
y
for x 6=
0, y 6= 0, and wants to send (h
r
X, g
r
, h
s
Y, g
s
)
the ElGamal encryption of X, Y (with h
r
X 6=
1
G
), together with a randomization of X
a
, Y
a
.
The proxy wants to build a smooth projective
hash function for the language L of follow-
ing tuple: W = (h
r
X, g
r
, h
s
Y, g
s
, X
a
, Y
a
) =
(W
1
, W
2
, W
3
, W
4
, W
5
, W
6
).
– HashKG(L, P), picks random scalars
λ, η, θ, µ
$
← Z
∗
p
to define hk
1
,
– ProjKG(hk
1
, (L, P), W ), derives hp
1
=
W
λ
1
W
µ
3
W
η
2
W
θ
4
, h
λ
g
η
, h
µ
g
θ
,
– Hash(hk
1
, (L, P), W ), outputs a hash value
v = W
λ
5
W
µ
6
, thanks to hk
1
, and W ,
– ProjHash(hp
1
, (L, P), W, w), thanks to hp
1
and the witness w that W ∈ L, outputs the hash
value v
0
=
hp
1,1
hp
−r
1,2
hp
−s
1,3
a
.
• The second language requires to show that we
have an encryption of a valid signature, as
in (Blazy et al., 2012) by combining a ElGamal
Encryption and an asymmetric Waters signature,
denoted ek = g
y
1
and vk = g
z
2
.
– HashKG(L), picks x
1
, x
2
∈ Z
∗
p
to define hk
2
;
– Hash(hk
2
; L, C), outputs a hash value
H = e(c
1
, g
2
)
x
1
· (e(c
2
, g
2
)/(e(h
1
, vk) ·e(F (M ),
σ
3
)))
x
2
;
– ProjKG(hk
2
; L, C) derives hp
2
= g
x
1
1
ek
x
2
;
– ProjHash(hp
2
; L, r
1
) computes the projected
hash value e(hp
r
1
2
, g
2
).
One can further extend the language to prove that
one possesses a valid signature under a public verifi-
cation key vk on an element in this language.
IRAS requires to prove that two pairs are valid
randomization, hence using conjunction techniques
from (Abdalla et al., 2009) one obtains a projection
key hp involving six elements for the pairs (two iter-
ations of hp
1
, one for the randomization of the pair
(RK
1
, RK
2
) with µ, and one for the randomization of
(RK
3
, RK
4
) with µ
0
) and an additional five elements
for the projected keys to handle the signature on an
encrypted message (one hp
2
for the language of valid
encrypted signature σ, and four to combine with the
encrypted message RK).
3 CONCLUSION
We have presented two secure anonymous storages
based on proxy cryptography. The aim of the proxy
is to allow only authorized users to open ciphertexts
collected anonymously. We proposed two schemes
answering to different use cases. The first one, called
DRAS, allows the owner to revoke a user by giving
a black list to the proxy, while the second one, called
IRAS, provides an indirect way for the owner to re-
voke a user, by not renewing his key. Then only the
users who have paid their subscriptions receive the
Two Secure Anonymous Proxy-based Data Storages
257

new keys and can open the encrypted files. Those con-
structions are proved secure in the Standard Model
while considering a semi-trusted proxy.
The next step will be to propose a concrete im-
plementation of our two schemes in order to com-
pare their efficiency. Moreover, one can see that in
some of our proofs, the proxy can even be a little
more malicious than just curious without impacting
the user privacy, and it would be a major development
to construct a resilient scheme in the covert adversary
model. In (Fiat and Naor, 1994) Broadcast Encryp-
tion (BE) was introduced, current BE schemes allow
to send messages to a given set of users depending
on their current subscription/privileges and the revo-
cation is done in a similar way to our second scheme,
by updating the decryption keys at certain time pe-
riod. However this requires a user to be online all
the time and prevents on the fly access to stored mes-
sages. We would like to find a nice combination of
these two techniques.
REFERENCES
Abdalla, M., Benhamouda, F., Blazy, O., Chevalier, C.,
and Pointcheval, D. (2013). SPHF-friendly non-
interactive commitments. In Sako, K. and Sarkar,
P., editors, ASIACRYPT 2013, Part I, volume 8269 of
LNCS, pages 214–234. Springer.
Abdalla, M., Chevalier, C., and Pointcheval, D. (2009).
Smooth projective hashing for conditionally ex-
tractable commitments. In Halevi, S., editor,
CRYPTO 2009, volume 5677 of LNCS, pages 671–
689. Springer.
Ateniese, G., Benson, K., and Hohenberger, S. (2009). Key-
private proxy re-encryption. In Fischlin, M., editor,
CT-RSA 2009, volume 5473 of LNCS, pages 279–294.
Springer.
Ateniese, G., Fu, K., Green, M., and Hohenberger, S.
(2006). Improved proxy re-encryption schemes with
applications to secure distributed storage. ACM Trans.
Inf. Syst. Secur., 9(1):1–30.
Blaze, M., Bleumer, G., and Strauss, M. (1998). Divertible
protocols and atomic proxy cryptography. In Nyberg,
K., editor, EUROCRYPT’98, volume 1403 of LNCS,
pages 127–144. Springer.
Blazy, O. and Chevalier, C. (2015). Generic construction
of UC-secure oblivious transfer. In ACNS 15, LNCS,
pages 65–86. Springer.
Blazy, O., Pointcheval, D., and Vergnaud, D. (2012).
Round-optimal privacy-preserving protocols with
smooth projective hash functions. In Cramer, R., edi-
tor, TCC 2012, volume 7194 of LNCS, pages 94–111.
Springer.
Canetti, R. and Hohenberger, S. (2007). Chosen-ciphertext
secure proxy re-encryption. In Ning, P., di Vimercati,
S. D. C., and Syverson, P. F., editors, ACM CCS 07,
pages 185–194. ACM Press.
Chaum, D. (1985). Security without identification: Trans-
action systems to make big brother obsolete. Com-
mun. ACM, 28(10):1030–1044.
Chaum, D. and van Heyst, E. (1991). Group signatures. In
Davies, D. W., editor, EUROCRYPT’91, volume 547
of LNCS, pages 257–265. Springer.
Chor, B., Goldreich, O., Kushilevitz, E., and Sudan, M.
(1995). Private information retrieval. In 36th FOCS,
pages 41–50. IEEE Computer Society Press.
Cramer, R. and Shoup, V. (2002). Universal hash proofs
and a paradigm for adaptive chosen ciphertext secure
public-key encryption. In Knudsen, L. R., editor, EU-
ROCRYPT 2002, volume 2332 of LNCS, pages 45–64.
Springer.
ElGamal, T. (1985). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. IEEE
Transactions on Information Theory, 31(4):469–472.
Fiat, A. and Naor, M. (1994). Broadcast encryption. In Stin-
son, D. R., editor, CRYPTO’93, volume 773 of LNCS,
pages 480–491. Springer.
Gennaro, R. and Lindell, Y. (2003). A framework for
password-based authenticated key exchange. In Bi-
ham, E., editor, EUROCRYPT 2003, volume 2656 of
LNCS, pages 524–543. Springer.
Ivan, A. and Dodis, Y. (2003). Proxy cryptography revis-
ited. In NDSS 2003. The Internet Society.
Kalai, Y. T. (2005). Smooth projective hashing and two-
message oblivious transfer. In Cramer, R., editor, EU-
ROCRYPT 2005, volume 3494 of LNCS, pages 78–95.
Springer.
Libert, B. and Vergnaud, D. (2008). Unidirectional chosen-
ciphertext secure proxy re-encryption. In Cramer, R.,
editor, PKC 2008, volume 4939 of LNCS, pages 360–
379. Springer.
Peikert, C., Vaikuntanathan, V., and Waters, B. (2008).
A framework for efficient and composable oblivious
transfer. In Wagner, D., editor, CRYPTO 2008, vol-
ume 5157 of LNCS, pages 554–571. Springer.
Rabin, M. O. (1981). How to exchange secrets with oblivi-
ous transfer. Technical Report TR81, Harvard Univer-
sity.
Shao, J., Liu, P., Wei, G., and Ling, Y. (2012). Anonymous
proxy re-encryption. In Security Comm. Networks, 5:
439–449. doi: 10.1002/sec.326.
Zheng, Q., Zhu, W., Zhu, J., and Zhang, X. (2014). Im-
proved anonymous proxy re-encryption with CCA se-
curity. In Moriai, S., Jaeger, T., and Sakurai, K., edi-
tors, ASIACCS 14, pages 249–258. ACM Press.
SECRYPT 2016 - International Conference on Security and Cryptography
258
