Finite Element Analysis of Asymmetrical Leg-length in Closed

U-bending Process

Sutasn Thipprakmas

, Untika Boochakul

and Wiriyakorn Phanitwong

Dept. of Tool and Materials Engineering, King Mongkut’s University of Technology Thonburi,

PrachaUthit Rd., Bangkok, Thailand

Dept. of Tool and Materials Engineering, King Mongkut’s University of Technology Thonburi, PrachaUthit Rd.,

Bangkok, Thailand

Keywords: U-bending Process, Spring-back, Asymmetry, Leg-length, Finite Element Analysis.

Abstract: In almost all industrial fields such as automobile and aerospace industries, in recent years, the precisely

complicated shapes of channel and frame parts are increasingly applied. To fabricate these parts, the U-

bending process being a common sheet-metal forming process is widely employed. However, the

asymmetrical U-bending process lacks researches. Therefore, in this study, the effects of asymmetrical leg-

length on spring-back characteristics in the U-bending process were investigated by using the finite element

method (FEM) and laboratory experiments. Specifically, on the basis of stress distribution analysis, they

were clearly clarified and also compared with those in the symmetrical leg-length case. These results

revealed that, with asymmetrical leg-length in a U-shaped part, the changes in leg-length on one side did not

result in any different spring-back characteristics and the obtained bend angle on the other side compared

with the symmetrical U-shaped parts. Furthermore, the effects of leg-length on the spring-back

characteristics were confirmed that the spring-back slightly increased as the leg-length increased.

Laboratory experiments were performed to validate the accuracy of the FEM simulation results. Based on

the bend angles and bend forces, the FEM simulation showed good agreement with the experiments in terms

of both the bend angles and bending forces.

1 INTRODUCTION

In recent years, the precision requirements on sheet-

metal parts shaped channels, beams, and frames of

various sizes in almost all industrial fields such as

automobile industry, aerospace industry, electronics

industry, and housing-utensil industry are increased.

To fabricate these shapes of channel, beam, and

frame parts, the closed U-die bending process being

a common sheet-metal forming process is employed

(Lange, 1985, Schuler, 1998). With the merits of

closed U-bending process, the thickness at the

corner radius and required corner radius could be

controlled (Lange, 1985, Schuler, 1998). The

secondary operations could be cut off and result in

the increases in productivity as well as the decreases

in a time consuming and a material loss. In the past,

many researches were carried out to focus on the

improvement of quality of U-shaped parts by using

the experiments and the FEM. Those researches,

however, were carried out to investigate the

symmetrical closed U-die bending process (Zhang,

2007, Bakhsi-Jooybari, 2009, Panthi, 2010,

Thipprakmas, 2012, Phanitwong, 2013). Therefore,

the asymmetrical closed U-die bending process has

lacked research and then the basic database of its

information was insufficient to design the suitable

U-bending die (Thipprakmas, 2015). This resulted in

the processing difficulty in the control of spring-

back feature as well as this major problem also is

the main barrier faced in product quality upgrading

in the precision U-bending process. The means

being absolutely need to provide for countering them

is the understanding on process parameter effects on

bending mechanism and spring-back characteristics

in the asymmetrical closed U-die bending process.

In the present research, the FEM simulation was

used as a tool to investigate and clearly identify the

asymmetrical leg-length effects on bending

mechanism and spring-back characteristics, and

laboratory experiments were also performed to

validate the FEM simulation results. The FEM

Thipprakmas, S., Boochakul, U. and Phanitwong, W.

Finite Element Analysis of Asymmetrical Leg-length in Closed U-bending Process.

DOI: 10.5220/0005963902110216

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 211-216

ISBN: 978-989-758-199-1

211

885.153

20.0





simulation results elucidated that the bending

mechanism and spring-back characteristics were

clearly elucidated via the changes of stress

distribution on the bending allowance zone, the

bottom of bent part, and the leg of the bent part.

Based on these stress distribution analysis, the FEM

simulation clearly revealed the effects of

asymmetrical leg-length on bending mechanism and

spring-back characteristics. The laboratory

experiments confirmed the accuracy of the FEM

simulation results. The FEM simulation results

showed good agreement with the experimental

results with reference to the bend angles and

bending force.

2 THE FEM SIMULATION AND

EXPERIMENTAL

PROCEDURES

In this research, the FEM simulation was used as a

tool to investigate and clearly identify the

asymmetrical leg-length effects on bending

mechanism and spring-back characteristics, and

laboratory experiments were also performed to

validate the FEM simulation results. Therefore, the

FEM simulation and experimental procedures were

consequently explained as the followings.

2.1 FEM Simulation Procedure

In this research, to clearly identify the asymmetrical

leg-length effects in the closed U-bending process,

the models of symmetrical and asymmetrical leg-

length were investigated and shown in Fig. 1. Fig.

1(a) and (b) depicted the symmetrical and

asymmetrical leg-lengths in the closed U-pending

process, respectively. The details of these models

and the process parameter conditions investigated in

the present research were listed in Table 1.

Specifically, the U-die bending model with the die

radius (R

) of 8 mm, punch radius (R

) of 5 mm, and

U-channel width (W) of 40 mm was investigated.

The three asymmetrical leg-length levels, as listed in

Table 1, were investigated. The 90 bend angle was

used as the U-bending angle model to investigate the

leg-length effects. The FEM simulation model was

a two-dimensional plane strain 3 mm in thickness.

The commercial analytical code for the two-

dimensional implicit quasi-static finite element

method (DEFORM-2D) with the automatic

remeshing generation was used as the FEM

simulation tool. The work piece material was set as

an elasto-plastic type with the rectangular element of

approximately 3,500 elements. The punch and die

were set as a rigid type. As per the past researches

(Thipprakmas, 2012, Phanitwong, 2013), the

material used, in the present study, was aluminum

A1100-O (JIS). The power-law isotropic hardening

model was used and the constitutive equation was

determined from the SS-curve obtained by the

tensile testing experiment. Specifically, the strength

coefficient and strain hardening exponent values

were 153.5 MPa and 0.20, respectively.

(a) Symmetrical leg-length (b) Asymmetrical leg-length

Figure 1: FEM simulation models.

Table 1: FEM simulation and experimental conditions.

Simulation model Plane strain model

Object types Workpiece : Elasto-plastic

Punch/Die : Rigid

Workpiece material A1100-O,

Thickness (t): 3 mm

Friction coefficient (µ) 0.1

Flow curve equation

Leg-length (WP

-WP

)

(mm-mm)

40-50, 50-50, 70-50

U-die geometries U-channel width (W): 40

Punch radius (R

): 5 mm

Die radius (R

): 8 mm

Bend angle (θ): 90

Upper die radius (R

): 5

2.2 Experimental Procedure

The laboratory experiments were performed to

validate the FEM simulation results. As per the

experiments of past researches (Thipprakmas, 2012,

Phanitwong, 2013), Fig. 2 shows punch and die sets

used for the closed U-bending experiments. The 5-

ton universal testing machine (Lloyd instruments

Ltd) were used for the laboratory U-die bending

experiments. After unloading a profile projector

(Mitutoyo model PJ-A3000) was used for the bend

angle measurement.The bend angle was observed,

Die

Punch

Die

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

212

and the bending force was recorded and compared

with the bending force analysed by the FEM

simulation.

Figure 2: The punch and die components for experiments.

3 RESULTS AND DISCUSSIONS

3.1 Comparison of Bending

Mechanism between Symmetrical

and Asymmetrical Leg-lengths in

Closed U-bending Process

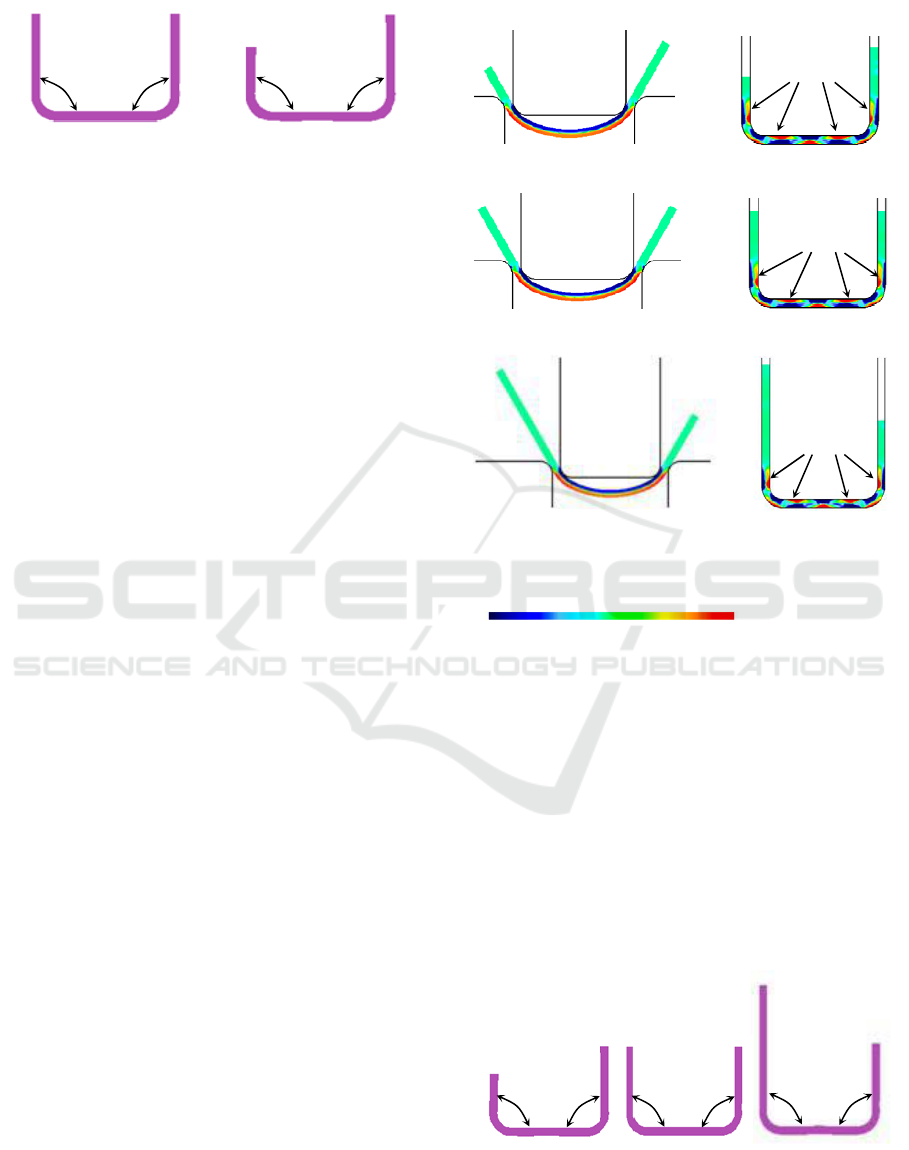
Fig. 3 shows the comparison of stress distribution

analysis during bending phase between symmetrical

and asymmetrical leg-length cases in closed U-

bending process. Fig. 3(a) and (b) show the

symmetrical and asymmetrical leg-length cases,

respectively. With the bending stroke of

approximate 9.5 mm, based on the bending theory,

the workpiece was bent underneath the punch and

the bending moment was generated. This

characteristic resulted in the compressive and tensile

stresses respectively generated on the punch and die

sides, as illustrated in Fig. 3(a-1) and (b-1). These

manners of the stress distribution analysis

corresponded well with the bending theory and the

literature (Lange, 1985, Schuler, 1998,

Thipprakmas, 2012). As the bending stroke

proceeded further, as illustrated in Fig. 3(a-2) and

(b-2), the workpiece was moved downward and

made a contact with die. After that, the reversed

bending stress was initially generated in which the

tensile and compressive stresses generated on the

punch and die sides, respectively. It was observed

that the reversed bending stresses were initially

generated in the legs as well. These manners of the

reversed bending stress distribution analysis again

corresponded well with the bending theory and the

literature (Phanitwong, 2013). Next, as the bending

stroke increased to be 50.0 mm, the workpiece was

again bent and it also made a contact with the punch

again. These manners resulted in the generated

bending and reversed bending stresses as depicted in

Fig. 3(a-3), and (b-3). It was also noted that the

reversed bending stresses were completely generated

in the legs. These manners of the stress distribution

analysis corresponded well with the bending theory

and the literature (Phanitwong, 2013).

Figure 3: Comparison of stress distribution analysis

between symmetrical and asymmetrical leg-length cases.

As per the past researches (Thipprakmas, 2012,

Phanitwong, 2013), with compensating these

bending and reversed bending stresses, the obtained

bend angle could be predicted. After removing

punch, as shown in Fig. 4(a) and (b), the predicted

bend angles were of 89.24° and 89.24°, and 89.16°

and 89.23° in the cases of symmetrical and

asymmetrical leg-lengths, respectively. As these

results, they corresponded well with the bending

theory and the literature (Phanitwong, 2013).

Specifically, the spring-back slightly increased as

the leg-length increased. These results

also confirmed the effects of leg-length on the

(1) Bending stroke 9.5 mm

Punch

Die

Workpiece

(a) Symmetrical case (b) Asymmetrical case

Reversed

bending

Reversed

bending

(2) Bending stroke 46.0 mm

Reversed

bending

Reversed

bending

(3) Bending stroke 50.0 mm

-100

Mean stress (MPa)

100

-33 33

Finite Element Analysis of Asymmetrical Leg-length in Closed U-bending Process

213

spring-back characteristic.

(a) Symmetrical case

(50-50 mm)

(b) Asymmetrical case

(40-50 mm)

Figure 4: Comparison of the predicted bend angles

between symmetrical and asymmetrical leg-length cases.

3.2 Effects of Leg-length on

Spring-back Characteristics

To clearly understand the effects of leg-length on the

spring-back characteristics, the symmetrical 90°

bend angle was set as the U-bending angle models.

Fig. 5 illustrates the stress distribution analyses in

the leg-length cases of 40-50 mm, 50-50 mm, and

70-50 mm. With the bending stroke of approximate

9.5 mm, the results showed the same manners of

stress distribution analysis in all leg-length cases, as

illustrated in Fig. 5(a-1), (a-2), and (a-3). These

manners corresponded well with the bending theory

and the literature (Thipprakmas, 2012, Phanitwong,

2013). Specifically, the compressive and tensile

stresses respectively generated on the punch and die

sides. Before unloading phase, as shown in Fig. 5(b-

1), (b-2), and (b-3), as aforementioned, the bending

and reversed bending stresses were generated in the

bottom surface as well as the reversed bending stress

was also generated in the leg. The results again

showed the same manners of stress distribution

analysis in all leg-length cases with a little different

scale. These results corresponded well with the

bending theory and the literature (Phanitwong,

2013). Specifically, for the symmetrical leg-length,

the generated stresses on the left and right sides were

equally balanced. In contrast, in the asymmetrical

leg-length, the generated stresses were not balanced.

Specifically, due to the effects of the leg-length

during the bending phase, the generated bending

stress depended upon the leg-length as previously

mentioned. Therefore, after removing punch, these

bending and reversed bending stresses generated in

bottom surface and leg were compensated. As

depicted in Fig. 6, the results revealed the slightly

difference levels of the predicted bend angle being

89.16° and 89.23°, 89.24° and 89.24°, and 89.42°

and 89.26° in the leg-length cases of 40-50 mm, 50-

50 mm, and 70-50 mm, respectively. However, in

the case of too small leg-length as depicted in Fig. 7,

it was observed that the reversed bending stress

generated in the leg was very small.

Figure 5: Illustration of stress distribution analysis with

respect to the various leg-lengths.

In addition, it was also observed that the poor U-

shape was formed. Therefore, these results revealed

that, with asymmetrical leg-length in a U-shaped

part, the changes in leg-length on one side did not

result in any different spring-back characteristics

and the obtained bend angle on the other side

compared with the symmetrical U-shaped parts. As

these results, on practical use, the effect of

asymmetrical leg-length in a U-shaped part on

spring-back characteristics could be ignored for the

design of U-bending die.

Figure 6: Comparison of the predicted bend angles with

respect to the various leg-lengths.

(

)

40-50 mm

(

)

50-50 m

89.16

89.33

89.34

89.48

89.36 

Reversed

bending

(

)

-len

th 70-50 mm

Punch

(2) Leg-length 50-50 mm

Punch

Reversed

bending

(1) Leg-length 40-50 mm

Punch

Reversed

bending

(a) Bending str. 9.5 mm (b) Before unloading

-100

Mean stress (MPa)

100

-33 33

89.34

89.16 89.33

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

214

(a) Stress distribution analysis. (b) Predicted bend angle

Figure 7: Illustration of stress distribution analysis and

predicted bend angle in too small leg-length case.

3.3 Validation of FEM Simulation

Results

In this research, the laboratory experiments were

carried out to validate the accuracy of the FEM

simulation results. Fig. 8 shows the comparison of

the bent parts in the case of symmetrical and

asymmetrical leg-length with 90° bend angle and 5

mm in tool radius obtained by the FEM simulation

analyses and the experiments. The FEM simulation

result showed good agreement with the experimental

result, in which the errors in the bend angles as

compared to the experimental results were

Figure 8: Comparison of the bend angles between the

experimental and simulation results.

5000

10000

15000

20000

25000

30000

35000

0 102030405060

Bending force / (N)

Bending Stroke / (mm)

EXP FEM

Figure 9: Comparison of the bend forces between the

simulation and the experimental results. (Leg-length 40-50

mm).

approximately 1 %. The analysed bending force was

also compared with that obtained by experiment, as

shown in Fig. 9. The FEM simulation result

illustrated a good agreement with the experimental

result, in which the error was approximately 1 %.

4 CONCLUSIONS

In the present research, the bending mechanism in

the case of asymmetrical leg-length was investigated

by using the FEM simulation to clearly understand

the spring-back characteristics in the closed U-

bending process. Based on the stress distribution

analysis, the bending mechanism was investigated

and clearly identified via the changes of stress

distribution analysis. This bending mechanism was

also compared with that in the symmetrical leg-

length case. The FEM simulation results revealed

that the bending and reversed bending stresses

generated in the corner radius, bottom surface, and

legs. With the different asymmetrical leg-length

cases, the results illustrated that, with asymmetrical

leg-length in a U-shaped part, the changes in leg-

length on one side did not result in any different

spring-back characteristics and the obtained bend

angle on the other side compared with the

symmetrical U-shaped parts. However, the effects of

leg-length on the spring-back characteristic which

corresponded well with the past research were again

confirmed that the spring-back slightly increased as

the leg-length increased. It was also noted that the

application of too small leg-length caused the poor

U-shape part. The FEM simulation results, as

validated by laboratory experiments, showed good

agreement with the experimental results, in which

the errors in both the bend angles and bending forces

compared with the laboratory experimental results

89.48 89.36

89.57

89.49

89.16 89.33 89.29

89.46

(a) Leg-length 50-50 mm

89.34 89.34

89.49

89.35

Poor

shape

(b) Leg-length 40-50 mm

Experiment FEM simulation

Finite Element Analysis of Asymmetrical Leg-length in Closed U-bending Process

215

were approximately 1% and 1%, respectively.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to

the Thailand Research Fund (TRF) (MSD56I0089),

the Diamond Dimension Co., Ltd., and the Higher

Education Research Promotion and National

Research University Project of Thailand, Office of

the Higher Education Commission, under Grant No.

57000618 for their financial assistance to this study.

The authors also thank Mr. Pakkawat Komolruji and

Mr. Arkarapon Sontamino, graduate students, for

their help in this study.

REFERENCES

Bakhsi-Jooybari, M., Rahmani, B., Daeezadeh, V., Gorji,

A., 2009, The study of spring-back of CK67 steel

sheet in V-die and U-die bending processes, Mater.

Design, 30:2410-2419.

Lange K., 1985, Handbook of metal forming. McGraw-

Hill Inc., New York.

Panthi, S.K., Ramakrishnan, N., Ahmed, M., Singh, S. S.,

Goel, M.D., 2010, Finite Element Analysis of sheet

metal bending process to predict the springback,

Mater. Design, 31:657–662.

Phanitwong, W., Sontamino, A., Thipprakmas, S., 2013,

Effects of part geometry on spring-back/spring-go

feature in U-bending process, Key Eng Mater,

549:100-107.

Schuler, 1998, Metal forming handbook. Springer, Berlin.

Thipprakmas, S. and Phanitwong, W., 2012, Finite

element analysis of bending mechanism and spring-

back/spring-go feature in various U-bending

Processes, Steel Res Int., 379-382.

Thipprakmas, S., Boochakul, U., 2015, Comparison of

spring-back characteristics in symmetrical and

asymmetrical U-bending processes, Int J Precis Eng

Manuf, 16(7):1441–1446.

Zhang D., Cui Z., Ruan X., Li Y., 2007, An analytical

model for predicting springback and side wall curl of

sheet after U-bending, Comp Mater Sci, 38:707–715.

APPENDIX

NOMENCLATURES

= Die radius

= Punch radius

= Upper die radius

t = Workpiece thickness

W = U-channel width

= Workpiece length left side

= Workpiece length right side

θ = Bend angle

µ = Friction coefficient.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

216