
Mobile Application Usage Concentration in a Multidevice World
Benjamin Finley
1
, Tapio Soikkeli
2
and Kalevi Kilkki
1
1
Department of Communications and Networking, Aalto University, Otakaari 5, Espoo, Finland
2
Verto Analytics, Innopoli 2, Tekniikantie 14, Espoo, Finland
Keywords:
Mobile Applications, Device Based Monitoring, Mobile Usage.
Abstract:
Mobile applications are a ubiquitous part of modern mobile devices. However the concentration of mobile
application usage has been primarily studied only in the smartphone context and only at an aggregate level. In
this work we examine the app usage concentration of a detailed multidevice panel of US users that includes
smartphones, tablets, and personal computers. Thus we study app usage concentration at both an aggregate
and individual device level and we compare the app usage concentration of different device types. We detail
a variety of novel results. For example we show that the level of app usage concentration is not correlated
between smartphones and tablets of the same user. Thus extrapolation between a user’s devices might be
difficult. Overall, the study results emphasize the importance of a multidevice and multilevel approach.
1 INTRODUCTION
The rise of the smartphone has led to the mobile ap-
plication (app) as a basic and ubiquitous part of mo-
bile device usage. This ubiquity implies that un-
derstanding mobile app usage in general is impor-
tant for the entire mobile ecosystem. Furthermore,
the widespread use of smartphones in daily life sug-
gests that mobile app usage is interesting to an array
of broader fields (such as media theory). In light of
this, mobile app usage has been studied by many re-
searchers (Falaki et al., 2010; B
¨
ohmer et al., 2011; Xu
et al., 2011; Soikkeli et al., 2013; Jung et al., 2014;
Hintze et al., 2014).
Mobile app studies have often examined basic us-
age statistics such as mean app session length and
transition probabilities between apps (B
¨
ohmer et al.,
2011; Soikkeli et al., 2013). However despite the
large volume of apps available from curated apps
stores, relatively few studies have examined the con-
centration of usage across apps
1
. Furthermore, stud-
ies that have examined app usage concentration have
analyzed only aggregate level smartphone usage (typ-
ically because tablet or other device type usage is not
available) (Jung et al., 2014).
1
Note that by the term concentration of usage we mean the
concentration of the distribution of total time across mo-
bile apps. Such concentration can be on an individual (time
of an individual distributed among their apps) or aggre-
gate level (total time of all individuals distributed among
all apps)
Contrastingly, in this study we aim to provide
a holistic view of mobile app usage concentration.
Specifically, we examine the app usage concentration
for a highly granular multidevice panel that includes
smartphones, tablets, and personal computers (PC).
Thus we can study and compare app usage concen-
tration levels for different device types at both the ag-
gregate (market) level and individual device level. In
addition, because the panel contains users with multi-
ple devices in the panel we can determine if measures
such as the Theil index (a concentration measure) or
the number of utilized apps are correlated between de-
vices of the same user.
In summary, we enumerate the following novel
contributions:
1. We show that, on an aggregate level, app usage
is highly concentrated on all three device types
(smartphone, tablet, and PC) but that significant
differences in app usage concentration between
the device types still exist. These differences re-
sult partly from differences in the types (cate-
gories) of apps typically utilized with each device
type.
2. We show that, on the device level, there are large
variations in app usage concentration within all
device types. In other words characterizing the
typical user’s app usage concentration is difficult.
3. We show that app usage concentration is not cor-
related in cases of smartphone and tablet, smart-
phone and PC, or tablet and PC of the same user.
40
Finley, B., Soikkeli, T. and Kilkki, K.
Mobile Application Usage Concentration in a Multidevice World.
DOI: 10.5220/0005964000400051
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 6: WINSYS, pages 40-51
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Therefore, extrapolation of app usage concentra-
tion between devices of the same user might be
difficult.
4. We show that the total number of utilized
apps is significantly negatively correlated (r =
−0.304, p ≤ 0.05) between PCs and tablets of
the same user, weakly positively correlated (r =
0.146) between tablets and smartphones of the
same user, and not correlated (r = −0.024) be-
tween smartphones and PCs of the same user.
We relate the significant negative correlation be-
tween PCs and tablets to device type substitu-
tion. Whereas a further exploration of smartphone
and tablet app usage finds that only a relatively
small fraction (~17%) of a user’s total mobile apps
(union of apps on their smartphone and tablet)
are actually utilized on both their smartphone and
tablet.
Overall the concentration of app usage has theoreti-
cal and practical implications in several fields. For
example, app usage concentration has been linked to
media repertoire theory and more general concepts of
media usage concentration (Jung et al., 2014). As an
example in terms of entertainment apps, users do not
access all of their entertainment apps randomly and
for random lengths of time but rather respond to the
problem of choice by creating a repertoire or subset
of entertainment apps to utilize frequently. Then habit
formation reinforces these choices over time leading
to concentration.
Furthermore, beyond theory, app usage and usage
concentration are important in the area of mobile ad-
vertising. For example, our research on app usage
across devices of the same user could help in devel-
oping models of multidevice in-app advertisement ex-
posure and in understanding the mobile advertising
landscape more generally.
2 BACKGROUND
2.1 Concentration Measures
The concentration or dispersion of a resource (such
as money, or in our case user time) can be character-
ized by a large number of different measures such as
the Gini coefficient. These measures have primarily
been utilized by economists to compare income and
wealth inequality. In this work we utilize two distinct
concentration measures: the Gini coefficient and the
Theil index. We utilize the Gini coefficient because
it is the most well known and widely reported mea-
sure. While we utilize the Theil index because it has
stronger theoretical underpinnings in information the-
ory. In addition the Theil index is more sensitive to
large tail values than the Gini coefficient and thus is
complementary (Cowell and Flachaire, 2007).
The Gini coefficient is based on the concept of the
Lorenz curve, an empirical curve on the plot of the cu-
mulative proportion of the population versus the cu-
mulative proportion of a variable distributed among
that population (such as income). The Gini coefficient
is then the area between the Lorenz curve and the per-
fectly equal distribution curve (of 45 degrees) divided
by the total area under the equal distribution curve.
The Gini coefficient has a range of [0, 1] indicating
minimum and maximum concentration respectively.
The standard Gini coefficient formulation we utilize
is shown in Equation 1 where n is the total number
of apps, y
i
is total usage time in seconds for app i,
i = 1, . . . , n indicates the total app usage times y
i
as or-
der statistics (in other words y
1
≤ y
2
≤ y
3
≤ · ·· ≤ y
n
),
and ¯y is the mean usage time for an app (Cowell and
Flachaire, 2014).
G =
n
∑
i=1
2i − n − 1
¯y · n(n − 1)
y
i
(1)
The Theil index is derived from information theory
and represents the maximum theoretical entropy of
data minus the actual data entropy (Theil, 1967). The
Theil index formulation we utilize (known as the
Theil-T redundancy) is detailed in Equation 2 where
where n is the total number of apps, y
i
is total us-
age time in seconds for app i, and ¯y is the mean usage
time for a single app. This formulation includes a nor-
malization of
1
lnn
so that the Theil index is a relative
rather than absolute inequality measure and compar-
isons between data with different numbers of groups
(in our case apps) are feasible (Roberto, 2015). This
normalized Theil index has a range of [0, 1] indicating
minimum and maximum concentration respectively.
T =
1
n · lnn
n
∑
i=1
y
i
¯y
· ln
y
i
¯y
(2)
2.2 Aggregate and Device Levels, and
Utilized Apps
We briefly define the aggregate level and device level
of analysis.
In the aggregate level of analysis, we aggregate
(sum) the total usage of each app over all devices of
a given platform-device type combination. As an ex-
ample, in the aggregate iOS tablet case each app value
is the total usage of that app from all iOS tablets. We
utilize platform-device type combinations instead of
simply device types because app packages are plat-
form specific and the same app typically has different
Mobile Application Usage Concentration in a Multidevice World
41

package names on iOS and Android. Thus instead of
smartphone, tablet, and PC, we have Android smart-
phone, iOS smartphone, Android tablet, iOS tablet,
and PC.
In the device level of analysis, we examine the app
usage for only that individual given device. We can
still group these individual devices based on platform-
device type combinations but importantly each device
will have, for example, a Gini coefficient based on
that device’s app usage.
Finally, we note that all of our analysis looks at us-
age concentration of utilized apps. In other words, we
do not include apps that are installed but not utilized
at all in the one month observation period.
3 PANEL DATA
The main data are several subsets of a large user panel
arranged by Verto Analytics
2
in the United States
in February 2015 (one month observation period).
Panelists were recruited online and were surveyed
through an initial recruitment survey to determine the
devices they own. Panelists were then instructed to in-
stall custom monitoring apps to all of their applicable
devices (specifically their smartphone, tablet, and/or
PC). Only panelists that installed the monitoring apps
to all their applicable devices were considered for the
panel. The monitoring apps log events such as an app
moving to the foreground or background of the dis-
play and HTTP network requests. All panelists were
paid for participation. All provided user data was
anonymized with no personally identifying informa-
tion.
In terms of extracting subsets of data we utilize
the notion of active panelists. We define a panelist
as active with a given device if the length between
their first usage of the month and last usage of the
month for that device is at least 23 days. The num-
ber of active panelists for each platform-device type
combination are detailed in Table 2. The number of
active panelists with two device types in the panel (in-
dicating that the user is active with both devices) are
detailed in Table 3. All analysis is performed on these
active panelist data.
In terms of representativeness, the large panel is
quite diverse as the intent of the panel recruitment
procedure was to acquire a nationally representative
panel. For example, the initial recruitment survey
was also utilized to screen potential panelists to im-
prove the demographic and technographic match be-
tween the accepted panelists and the population (an
2
http://vertoanalytics.com/
approach known as a quota-sampling). However all
opt-in panels by definition use non-probability sam-
pling and thus representativeness is a concern
3
. We
direct the reader to Hays et al. (2015) for a more de-
tailed discussion about Internet based opt-in panels.
For reference we provide a summary of pan-
elist demographic data for active smartphone pan-
elists along with demographic data for US smart-
phone users in general in Table 1. The clearest de-
mographic discrepancies are that the group over rep-
resents females and users with lower household in-
comes. Overall these factors should be considered in
generalization. We omit data for the other groups (i.e.
active tablet panelists) due to space limitations but
the considerations are similar. We discuss our over-
all view of generalizability in panel based studies in
Section 6.
4 APP SESSION DEFINITION
In order to study app usage we first need to define the
concept of an application session in the context of our
different device types.
In the case of smartphone and tablet, we define
an app session as a time interval starting with an app
moving to the foreground of the device and ending
with the app moving out of the foreground (either
replaced by a different app or screen off). This app
session definition has been utilized in previous litera-
ture (B
¨
ohmer et al., 2011; Falaki et al., 2010; Soikkeli
et al., 2013).
In the case of PC, we define an app session as a
time interval starting with a window of an app gaining
focus and ending with that app window losing focus.
A problem with this simplistic PC app session def-
inition is that PC apps can remain in focus for long
periods without user activity and without the screen
turning off. These long-lived sessions with significant
inactivity skew the app usage distributions.
We have found that a significant proportion of
all long-lived PC sessions are web browser sessions.
Therefore we combine the app session data with the
HTTP request data to determine when HTTP requests
occur during each browser session. Then we are able
to enforce a timeout such that we remove any peri-
ods in web browsing sessions that do not contain any
HTTP requests for 10 minutes.
However, even this timeout does not find cases
where there is no actual user activity but, for example,
3
We note though that the device based monitoring collec-
tion method, as compared to normal surveys, is robust to
false and fake answers, careless answers, or repeatedly giv-
ing the same answer.
WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems
42

Table 1: Demographic Summaries for Active Smartphone Panelists and US Smartphone Users.
Demographic Active Smartphone Panelists US Smartphone Users
a
Mean Age (Years)
b
37.08 (12.54) 41.30 (15.08)
Gender (% Male) 26.42 50.08
Education (% w/ Some College or Less) 62.18 53.04
Marital Status (% Married) 41.45 48.96
Household Income (% <50K USD) 64.08 40.72
Mean Household Size 2.96 (1.51) 3.05 (1.61)
Mean Children in Household 0.91 (1.19) 0.74 (1.27)
Race (% White) 70.98 71.53
a
US smartphone user demographic data is from Pew Research survey (June-July 2015, subpop with smartphone n=1327) (Pew Internet and
American Life Project, 2015). The survey utilizes weighting to population parameters of census data to create nationally representative results
(refer to (Pew Research Center, 2016)). We note that Verto Analytics also performs its own national surveys, we utilize the Pew Research
survey only for brevity.
b
All mean values also include standard deviations.
Table 2: Number of active panelists for different platform-
device type combinations in panel.
Device Type Active Panelists
Smartphone (Android) 435
Smartphone (iOS) 127
Tablet (Android) 78
Tablet (iOS) 47
PC (Windows) 630
Table 3: Number of active panelists with both device types
in panel.
Device Types Active Panelists
Smartphone/Tablet 77
Smartphone/PC 269
Tablet/PC 52
a browser page simply automatically refreshes at a
specific interval. In other words, sessions that consist
mostly of highly periodic HTTP requests rather than
actual browsing behavior (which is typically bursty).
We can utilize periodicity detection to identify these
cases.
For a given session, a group of related periodic
HTTP requests should all target the same domain
(for example, auto-refresh of the same page), thus we
check for periodicity for each set of requests to the
same second level domain within a session. In other
words, if a session has 10 requests to Amazon.com
and 10 requests to Google.com, we check for period-
icity on these two sets separately. If we find period-
icity we simply remove the requests from the session.
Thus the enforced timeout, which is applied after the
periodicity detection, can shorten the session.
In terms of the actual periodicity detection pro-
cedure, we first estimate the power spectral density
(PSD) of each set of requests by the squared coeffi-
cients of the discrete Fourier transform of the signal.
We then classify a signal as periodic if 50% or more of
the total signal power is contained in the top 10% (in
terms of power) of frequencies. We select this 50%
level empirically through examination of the cumu-
lative distribution function (CDF) of the fraction of
power in the top 10% of frequencies of the PSDs. This
CDF is illustrated in figure 1. Furthermore, we illus-
trate the PSDs of two example request sets (from the
data): one periodic and one non-periodic in Figures 2
and 3 respectively.
Fraction of Power in Top 10% of Frequencies of PSDs
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
P (≤ x)
0
0.2
0.4
0.6
0.8
1
Figure 1: CDF for fraction of power in top 10% of frequen-
cies from power spectral densities.
We utilize this simple heuristic to detect signals
that are primarily periodic. This detection objective
contrasts with other methods that attempt to detect the
existence of any statistically significant periodicity ir-
regardless of whether that periodicity dominates the
total power of the signal (as an example refer to (Vla-
chos et al., 2004)). In terms of the effects of both the
timeout and periodicity detection, the mean session
length of PC web browsing sessions is 15.1 min with-
out timeout or periodicity detection, 9.58 min with
only timeout, and 8.96 min with both timeout and pe-
riodicity detection.
Mobile Application Usage Concentration in a Multidevice World
43

Frequency (Hz)
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
Power
10
-10
10
-8
10
-6
10
-4
10
-2
Figure 2: Example power spectral density for set of HTTP
requests that are classified as periodic.
Frequency (Hz)
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
Power
10
-10
10
-8
10
-6
10
-4
10
-2
Figure 3: Example power spectral density for set of HTTP
requests that are classified as non-periodic.
5 RESULTS
We present the results of aggregate and individual
level app usage and concentration and then of corre-
lations of usage and concentration measures between
devices of the same user.
5.1 App Usage and Concentration
Statistics
5.1.1 Aggregate Level App Usage and
Distribution Fitting
We first examine the aggregate normalized app us-
age for different platform-device type combinations.
We illustrate these data through commonly used rank-
frequency distributions in Figure 4. Note that the
rank-frequency distribution is a transformation of the
discrete CDF that simply emphasizes a different part
of the data.
We find that most of the distributions are concave
on a log-log scale with quickly decaying tails and sim-
ilar shapes. However, the PC distribution is a clear
outlier with a distinct shape and a large discontinuity
after the first three apps. We find that these first three
apps are all web browsers and that these browsers ac-
count for about 66% of total PC app usage. Thus we
expect PC app usage to be very highly concentrated.
Interesting, the iOS distributions have much larger
values at the very first rank and less overall ranks than
Android distributions. We find that the large first rank
is not a single app but instead a group of apps that
could not be identified by the iOS monitoring app due
to technical limitations. Furthermore, we find that this
group of unidentifiable apps likely includes many in-
frequently utilized apps that would be seen at the tail
of the distribution, thus the group also accounts for the
fewer overall ranks. Hereafter, we remove this group
from the iOS data.
In terms of theoretical distribution fits, the
shape of the data suggests a heavy tail distribu-
tion. Therefore we fit several well known heavy
tail distributions (log-normal, exponential
4
, stretched-
exponential, power law, and truncated power law)
to the data through maximum likelihood estimations
(Alstott et al., 2014; Clauset et al., 2009). We utilize
a two step process for model selection: we first select
a best fit candidate via Akaike weights, we then per-
form Vuong likelihood ratio (LR) tests to ensure the
statistical significance of the best fit (Vuong, 1989)
compared to the other distributions.
We find that log-normal distributions provide the
best fits for the two smartphone and two tablet data
with both the highest Akaike weights and signifi-
cantly (p ≤ 0.001) higher likelihoods than the other
distributions. Whereas a stretched exponential distri-
bution provides the best fit for the PC data accord-
ing to the same criteria (p ≤ 0.001). The root mean
squared error (RMSE) of these best fits in terms of
predicting the CDF are all less than 2%. We detail the
estimated best fit parameters and RMSE of CDFs in
Table 4.
These log-normal and stretched exponential best
fits clearly indicate that aggregate smartphone, tablet
or PC app usage do not follow a power law over the
entire data range. However we can find the head pro-
portion (the proportion starting with the first rank) of
each distribution that might follow a power law by
finding the optimal cut-off rank in terms of power
law fitting (Alstott et al., 2014). We find that for the
five distributions the cut-offs range from the 99th to
586th app rank and that even for the distribution with
the largest cut-off (iOS smartphone), the power law
would only cover 41% of the total ranks.
4
The exponential distribution is by definition not heavy
tailed but we included it for comprehensiveness.
WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems
44

App Rank
10
0
10
1
10
2
10
3
10
4
Normalized App Usage
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Android Smartphone
Android Tablet
iOS Smartphone
iOS Tablet
PC
Figure 4: Rank-frequency distributions of normalized app usage for device type-platform combinations.
Table 4: Parameter estimates and CDF error for aggregate app usage distribution fitting.
Device Type Best Fit Distribution Parameter Estimates RMSE of CDF
a
(%)
Smartphone (Android) Log-Normal µ = 6.624 σ = 2.703 1.94
Smartphone (iOS) Log-Normal µ = 6.392 σ = 2.512 1.71
Tablet (Android) Log-Normal µ = 7.092 σ = 2.832 1.82
Tablet (iOS) Log-Normal µ = 6.381 σ = 2.481 1.41
PC (Windows) Stretched Exponential λ = 0.002 β = 0.173 1.78
a
Root mean squared error between empirical and predicted cumulative distribution functions.
5.1.2 Device Level App Usage and Distribution
Fitting
Next, we examine the device level app usage data. For
space considerations we limit our analysis and dis-
cussion to Android smartphones and PCs as we find
the other platform-device type combinations are sim-
ilar, in terms of fitting, to Android smartphones. We
perform distribution fitting on the app usage data of
each Android smartphone and PC device with a simi-
lar method to Section 5.1.1.
For Android smartphones, we find that 78% of de-
vices are best fit by log-normal and 22% are best fit by
stretched exponential according to Akaike weights.
Interestingly though not all of these best fit candidates
are statistically significant according to the LR tests.
For example, we find that only 20% of devices are sig-
nificantly (p ≤ 0.05) best fit by log-normal. However
overall, we find that 99% of devices are plausibly best
fit by log-normal (in other words either log-normal is
the significantly (p ≤ 0.05) best fit or no other distri-
bution is a significantly (p ≤ 0.05) better fit).
We find that the average RMSE of these plausible
best fits in terms of predicting the CDF is 4%. Thus
the app usage of many smartphones can be accurately
fit through a simple log-normal distribution. We illus-
trate the CDF of the app usage of an example Android
smartphone along with a log-normal best fit in Figure
5.
For PCs, we find more variation in best fits with no
single distribution covering a plurality of the devices
according to Akaike weights. This variation is likely
due to the relatively few apps and the dominance of
the web browser app on each PC.
5.1.3 Aggregate Level Concentration Statistics
We calculate the Gini coefficient and Theil index for
Mobile Application Usage Concentration in a Multidevice World
45

App Usage (seconds)
10
1
10
2
10
3
10
4
10
5
10
6
P (≤ x)
0
0.2
0.4
0.6
0.8
1
Android Smartphone
Log-Normal
Figure 5: CDF of example Android smartphone app usage
and CDF of log-normal best fit.
each aggregate platform-device type combination so
the concentrations can be studied and compared. We
also utilize a percentile-t bootstrap method (1000 iter-
ations) to calculate 95% confidence intervals (CI) for
each concentration measure (Cowell and Flachaire,
2014). Importantly in our bootstrap method we utilize
individual devices (before aggregation) as the resam-
pling unit rather than the apps of the aggregate distri-
bution. The measures and CIs are detailed in Table
5.
We make note of two important issues regarding
the comparison of concentration measures. First, in
the comparisons between two platform-device type
combinations (for example Android smartphone and
Android tablets) we do not account for users with a
device in each of the groups. In other words, the two
groups are not completely independent. However as
we will show in Section 5.2 there is almost no corre-
lation of Theil indexes between devices of the same
user. Therefore we ignore this dependence. Second,
percentile-t bootstrap CIs of inequality measures of
heavy tailed data can be suspect depending on the
heaviness of the tail (Cowell and Flachaire, 2014).
However they still provide significant improvements
over pure asymptotic CIs, therefore we proceed with
caution
5
.
In general terms, we first note that all device
types have relatively high app usage concentration as
shown by, for example, the Gini coefficients and as
illustrated in the rank-frequency distributions. Previ-
ously, Jung et al. (2014) found that aggregate Android
smartphone app usage from a panel in Korea had a
Gini coefficient of 0.74. Thus our Android smart-
phone Gini coefficient of 0.96 suggests even higher
concentration. The difference might result from dif-
ferent panel time-frames or panelist cultural differ-
ences. Specifically the panel of Jung et al. (2014) was
5
We look to utilize more robust CI methods such as finite
mixture model CIs as detailed in Cowell and Flachaire
(2014) in future work.
a panel from Korea in November 2011 compared with
our panel from the United States in February 2015.
In terms of comparison between device types, we
find that Android and iOS smartphones have sig-
nificantly higher app usage concentrations than An-
droid and iOS tablets respectively (note the non-
overlapping CIs indicate at least p ≤ 0.05). These dif-
ferences can be partly explained through differences
in the primary types (categories) of apps utilized with
each device type. To illustrate this phenomenon we
first calculate the aggregate normalized usage times
and Theil indexes for each app category for both An-
droid smartphone and tablets. We then plot these pairs
as a scatterplot for the two device types in Figure 6.
As illustrated, we find that a larger fraction of
smartphone usage is from higher Theil index cate-
gories (like Social Networking) compared to tablets.
Similarly a larger fraction of tablet usage is from
lower Theil index categories (like Games and Kids).
Interestingly some categories (such as Uncategorized)
have both substantially different Theil indexes and
normalized usage between device types. These results
potentially indicate both inter and intra-category com-
ponents to the differences between aggregate smart-
phone and tablet concentration.
In terms of theory, the higher usage concentration
of social networking (communication) apps compared
to other categories such as games has also been doc-
umented by Jung et al. (2014). They suggest that the
difference is related to network effects wherein the
value of a communication service is proportional to
the number of users utilizing the service. Our anal-
ysis supports this supposition by illustrating that the
difference also exists on tablet devices and thus is not
device type specific.
In terms of platform differences, concentration
of iOS (smartphone and tablet) usage is not signifi-
cantly different compared to concentration of Android
(smartphone and tablet) usage.
Finally, the significantly (p ≤ 0.05) higher con-
centration of PC app usage than any other device type
is, as mentioned, due to the web browser as the dom-
inant app.
5.1.4 Device Level Concentration Statistics
In terms of the device level concentration, we calcu-
late the Gini coefficient and Theil index for the app
usage data of each individual device. To illustrate de-
vice level diversity, we plot the CDFs of individual
Theil indexes for each platform-device type combina-
tion in Figure 7. The figure indicates significant di-
versity in terms of individual usage concentration for
all device types.
WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems
46

Table 5: Gini coefficients and Theil indexes (including confidence intervals
a
) for
aggregate data.
Device Type Gini Coefficient Theil Index
Smartphone (Android) 0.962 [0.961, 0.968] 0.436 [0.433, 0.457]
Smartphone (iOS) 0.939 [0.935, 0.952] 0.425 [0.405, 0.462]
Tablet (Android) 0.920 [0.908, 0.935] 0.365 [0.333, 0.385]
Tablet (iOS) 0.904 [0.883, 0.930] 0.380 [0.329, 0.436]
PC (Windows) 0.976 [0.976, 0.981] 0.601 [0.595, 0.625]
a
95% confidence intervals based on percentile-t bootstrap method.
Theil Index of Category For Device Type
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Normalized App Usage (as Fraction of Total App Usage of Device Type)
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Android Smartphone
Android Tablet
Social Networking
Social Networking
Utilities
Games and Kids
Games and Kids
Uncategorized
Uncategorized
Sports
Figure 6: Scatterplot of Normalized app usage vs. Theil indexes for app categories by device type (Android).
Theil Index
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
P (≤ x)
0
0.2
0.4
0.6
0.8
1
Android Smartphones
Android Tablets
iOS Smartphones
iOS Tablets
PC
Figure 7: CDFs for device level Theil indexes for each
platform-device type combination.
Next, we compare the typical individual concen-
tration between device types. We calculate the me-
dian (with 95% CI) Gini coefficient and Theil index
for each combination and detail these medians and
CIs in Table 6.
Interestingly, we find that the median Theil index
of Android tablets is significantly (p ≤ 0.05) larger
than that of Android smartphones. This contrasts with
our aggregate level analysis which found the opposite
phenomenon. Similarly, the platform comparison be-
tween Android and iOS smartphones also contrasts
with the aggregate level analysis. These differences
underscore the importance of analysis at both the ag-
gregate and individual level.
Though in terms of PCs we find unsurprisingly
that the median Theil index of PC is significantly
higher than all other device types. This in in line with
the aggregate level analysis.
Mobile Application Usage Concentration in a Multidevice World
47

Table 6: Median Gini coefficients and Theil indexes (including confidence intervals
a
)
for device level data.
Device Type Median Gini Coefficient Median Theil Index
Smartphone (Android) 0.856 [0.850, 0.861] 0.415 [0.405, 0.423]
Smartphone (iOS) 0.807 [0.787, 0.818] 0.363 [0.322, 0.393]
Tablet (Android) 0.888 [0.857, 0.895] 0.507 [0.450, 0.551]
Tablet (iOS) 0.813 [0.789, 0.839] 0.417 [0.348, 0.468]
PC (Windows) 0.929 [0.923, 0.935] 0.651 [0.638, 0.669]
a
95% confidence intervals based on binomial method.
5.2 Correlation of App Usage Measures
between a User’s Devices
Finally, we can also compare measures of app usage
for different devices of the same user. In this way we
can determine if app usage measures are correlated
across devices of the same user.
We examine two distinct measures: the Theil in-
dex and the total number of utilized apps. Further-
more, for each measure we compare three differ-
ent device type combinations: smartphone and tablet
(smartphone/tablet), smartphone and PC (smart-
phone/PC), and tablet and PC (tablet/PC). For each
statistic-device type combination (for example smart-
phone/PC Theil index) we calculate the Pearson cor-
relation coefficient and the significance level of the
coefficient according to the related student’s t-test.
Table 7 details these coefficients and significance lev-
els.
In terms of Theil index, we find that all combi-
nations are not significant and near zero. Thus ex-
trapolation of app usage concentration from a single
device to other devices of the same user might be dif-
ficult. The likely reason for the low correlation be-
tween the mobile devices and PC is again related to
web browsers as the dominant platform for apps on
PCs. Hence future work might try to include browser
based apps.
In terms of the total number of utilized apps, we
find that the smartphone/tablet correlation is posi-
tive but not significant, the tablet/PC correlation is
negative and significant (p ≤ 0.05), and the smart-
phone/PC correlation is not significant and near zero.
The significant negative correlation of tablet/PC
might relate to device substitution between tablets and
PCs. In other words, users might perform tasks on
their tablets that they would otherwise perform on
their PCs. Therefore the more apps utilized on the
tablet, the less apps utilized on the PC. In general,
tablets and PCs are more often seen as substitutes
rather than smartphones and PCs because both tablets
and PCs are typically larger and less mobile (Xu et al.,
2015). To further support this theory, we calculate the
correlation between the total usage times (sum of all
app sessions) of tablet/PC. We also find a significant
(p ≤ 0.05) correlation of −0.242.
Similarly, the weak and non-significant correla-
tion of smartphone/tablet might relate to device com-
plementation. In other words, users primarily perform
different types of tasks on smartphones and tablets.
Thus the number of utilized apps on smartphone and
tablet should be uncorrelated. Interestingly, we can
better understand app usage across smartphones and
tablets by examining the similarity between the smart-
phone app set and tablet app set of the same user.
Thus if smartphones and tablets are primarily compli-
mentary then the similarity should be relatively small.
For such an examination we need a measure to
define the similarity between the two app sets. We
utilize the well known Jaccard similarity coefficient
which is simply the cardinality of the intersection of
two sets divided by the cardinality of the union of
those sets as detailed for sets A and B in Equation
3.
J(A, B) =
|A ∩ B|
|A ∪ B|
(3)
We calculate the Jaccard similarity between the sets
of apps for each user with a smartphone and tablet
that share the same platform
6
.
We can then examine the distribution of the Jac-
card similarities of the 57 applicable users. We illus-
trate the distribution as a CDF plot in Figure 8. We
include the distribution of a random matching (per-
mutation) of the app sets in the plot for reference. We
find users are quite evenly dispersed with similarities
between 5% and 25% but that no user has a simi-
larity larger than 25%. In other words no user uses
more than 25% of their total (utilized) smartphone
and tablet apps on both smartphone and tablet. This
supports our hypothesis of smartphone/tablet compli-
mentarity.
Finally, we can also test if the calculated user simi-
larities would be expected simply based on the overall
6
Again we note that application package names are plat-
form specific hence we cannot analyze users with smart-
phones and tablets with different platforms.
WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems
48
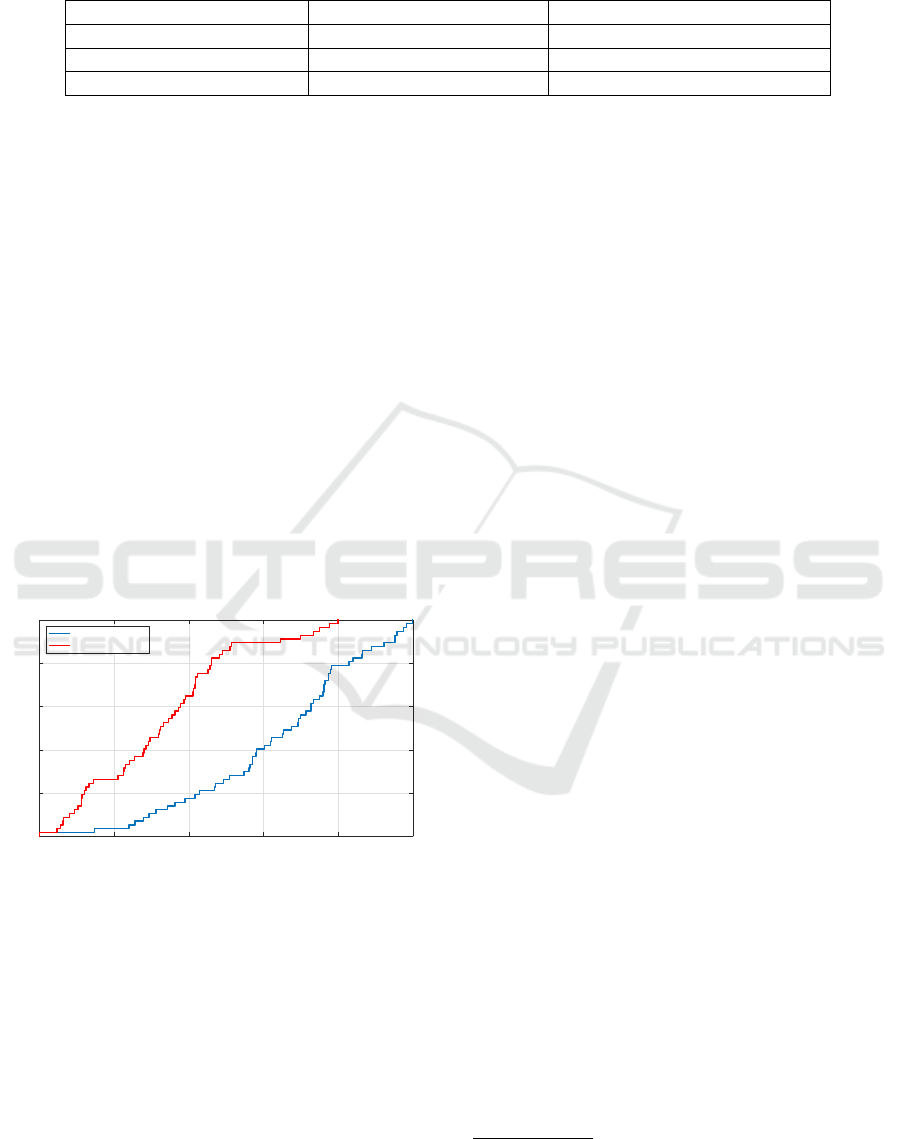
Table 7: Pearson correlation coefficients (including significance levels
a
) for Thiel indexes and total number
of utilized apps for different device type combinations.
Device Type Combination Correlation (Theil Index) Correlation (Number of Apps)
Smartphone/Tablet (n=77) 0.054 0.146
Smartphone/PC (n=269) 0.022 -0.024
Tablet/PC (n=52) 0.042 -0.305*
a
* : 5%, ** : 1%, *** : 0.1%
popularity of each app. In other words, is there any
statistically significant similarity between the user’s
smartphone and tablet app sets?
For this test we utilize the median similarity as the
test measure for a permutation test. For the 57 users
this median similarity is 0.169. Specifically we per-
mute the smartphone and tablet app sets such that the
links between app sets of the same user are broken.
We then recalculate the median similarity over the 57
random matchings of smartphone and tablet app sets.
We repeat this entire permuting and recalculation pro-
cess for 100000 iterations to get a distribution of me-
dian similarities. We then find the percentile values
corresponding to difference significance levels.
The permutation test gives a 99.99% percentile
similarity of 0.104, thus suggesting that the empirical
similarity of 0.169 is highly significant (p ≤ 0.0001).
Thus we do find a statistically significant similarity,
even though the maximum similarity of users is rela-
tively low.
Jaccard Similarity between Smartphone and Tablet App Sets
0 0.05 0.1 0.15 0.2 0.25
P (≤ x)
0
0.2
0.4
0.6
0.8
1
Users
Random Matching
Figure 8: CDF of users Jaccard similarities between their
smartphone and tablet app sets and CDF for a random
matching of smartphone and tablet app sets.
6 REPLICABILITY AND
GENERALIZABILITY
Generalizing or replicating a given panel based study
is typically difficult in areas with rapid technological
and behavioral change such as mobile device usage.
Thus concerns about the usefulness of such studies
have been raised. Overall though, we take the view
that such panel based studies are primarily studies
about the panel populations themselves and that the
value lies in allowing researchers to contrast experi-
ences with diverse user populations to construct an
overall understanding of user diversity and behavior.
Thus our study provides an point of reference for fur-
ther multidevice studies. We refer to (Church et al.,
2015) for a thorough discussion on this topic.
7 DISCUSSION
In terms of applications, as mentioned, our research
has implications for understanding and modeling the
landscape of mobile advertising. For example, from
the ad demand side, our research suggests that total
app ad inventory and the concentration of that inven-
tory between certain apps depends strongly on app
category and device type. Whereas, similarly from the
ad supply side, our research suggests that apps in cer-
tain categories and device types might have more col-
lective bargaining power (against large ad exchanges
due to this concentration) than apps in other cate-
gories and device types
7
.
Furthermore such usage concentration research
will become more important as the mobile ad mar-
ket (specifically display ads) potentially shifts from
an impression (how many views) to impression time
(how many views and how long is each view) based
business model (see Rula et al. (2015) for further ex-
planation). This shift seems like a possibility given
the impact of impression time on ad recognition and
recall (Goldstein et al., 2011).
8 RELATED WORK
The related work can divided into previous studies
that have examined smartphone application usage and
previous studies that have included multiple device
types.
7
We note that not all apps utilize ads but that mobile ads
have become the dominant mobile app monitization strat-
egy.
Mobile Application Usage Concentration in a Multidevice World
49

8.1 Mobile Application Studies
B
¨
ohmer et al. (2011) performed one of the first large
scale study on mobile app usage with a panel of An-
droid smartphone users. They utilized a similar con-
cept of app sessions defined by foregrounding and
backgrounding of apps. However they did not look
at the app usage concentration as their focus was
on sequential and temporal app patterns. Similarly
Soikkeli et al. (2013) analyzed smartphone app us-
age from a panel of Finnish smartphone users. They
detailed app usage statistics for several very popu-
lar apps but again do not look at usage concentration
among apps.
Falaki et al. (2010) analyzed smartphone app us-
age with two panels of users: one Windows Phone
and one Android based. They do illustrate and model
device-level app usage and find that exponential dis-
tributions fit most device app usage data well.
Closest to our work, Jung et al. (2014) examined
the aggregate app usage for a panel of Korean An-
droid smartphone users. They found highly concen-
trated usage though with lower Gini coefficient than
the coefficient for our smartphone data. They also
found differences in usage concentration between app
categories. However, they only examined aggregate
level app usage and did not examine device level app
usage. Furthermore, they did not examine app usage
concentration across multiple device types.
8.2 Multidevice Studies
Montanez et al. (2014) and Wang et al. (2013) exam-
ined multidevice usage but often only from the per-
spective of a single app (search) as the data was col-
lected from Microsoft’s search service (Bing).
Hintze et al. (2014) analyzed both smartphone and
tablet usage from the large Device Analyzer dataset.
Device Analyzer is a dataset based on a popular An-
droid device monitoring app from Cambridge Uni-
versity (Wagner et al., 2014). The dataset contains
both smartphone and tablet devices however corre-
lating usage of smartphone and tablet devices to a
single user is not possible thus comparing app us-
age between devices with the same user is infeasible.
Furthermore individual app names are not available
therefore app-specific insights are difficult to extract.
Finally, Google (2012) and Microsoft (2013) stud-
ied multidevice usage through combinations of sur-
veys, user diaries, and device meters but did not study
multidevice app usage concentration.
9 CONCLUSIONS
In this work we have analyzed app usage with a fo-
cus on usage concentration in a multidevice context
including smartphones, tablets, and personal comput-
ers. Furthermore, we analyze usage concentration on
both an aggregate (market) level and individual device
level. Thus we provide a thorough view of app usage
concentration.
We highlight a few key takeaways from our analy-
sis. Overall, we show that, on an aggregate level, app
usage concentration will vary significantly by device
type and thus future work, for example in modeling,
should take these differences into account to gain a
holistic view. Whereas, on an individual level, we find
significant diversity in app usage concentration even
for users with the same device type, therefore charac-
terizing a typical user is difficult. Finally, we show
that several app usage measures are not strongly cor-
related between devices of the same user, thus empha-
sizing the need to capture all of users devices rather
than simply extrapolating from a single device. In
other words, a multidevice approach is warranted.
REFERENCES
Alstott, J., Bullmore, E., and Plenz, D. (2014). powerlaw:
A python package for analysis of heavy-tailed distri-
butions. PLoS ONE, 9(1):e85777.
B
¨
ohmer, M., Hecht, B., Sch
¨
oning, J., Kr
¨
uger, A., and Bauer,
G. (2011). Falling asleep with angry birds, facebook
and kindle: A large scale study on mobile application
usage. In Proceedings of the 13th International Con-
ference on Human Computer Interaction with Mobile
Devices and Services, MobileHCI ’11, pages 47–56,
New York, NY, USA. ACM.
Church, K., Ferreira, D., Banovic, N., and Lyons, K. (2015).
Understanding the challenges of mobile phone usage
data. In Proceedings of the 17th International Con-
ference on Human-Computer Interaction with Mobile
Devices and Services, MobileHCI ’15, pages 504–
514, New York, NY, USA. ACM.
Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009).
Power-law distributions in empirical data. SIAM Re-
view, 51(4):661–703.
Cowell, F. A. and Flachaire, E. (2007). Income distribution
and inequality measurement: The problem of extreme
values. Journal of Econometrics, 141(2):1044–1072.
Cowell, F. A. and Flachaire, E. (2014). Statistical methods
for distributional analysis. In Atkinson, A. and Bour-
guignon, F., editors, Handbook of Income Distribution
SET vols. 2A-2B, Handbooks in economics. Elsevier
Science.
Falaki, H., Mahajan, R., Kandula, S., Lymberopoulos, D.,
Govindan, R., and Estrin, D. (2010). Diversity in
WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems
50

smartphone usage. In Proceedings of the 8th In-
ternational Conference on Mobile Systems, Applica-
tions, and Services, MobiSys ’10, pages 179–194,
New York, NY, USA. ACM.
Goldstein, D. G., McAfee, R. P., and Suri, S. (2011). The
effects of exposure time on memory of display adver-
tisements. In Proceedings of the 12th ACM Confer-
ence on Electronic Commerce, EC ’11, pages 49–58.
Google (2012). The new multi-screen world: Un-
derstanding cross-platform consumer behavior.
https://think.withgoogle.com/databoard/media/pdfs/the-
new-multi-screen-world-study research-studies.pdf.
Hays, R. D., Liu, H., and Kapteyn, A. (2015). Use of in-
ternet panels to conduct surveys. Behavior Research
Methods, 47(3):685–690.
Hintze, D., Findling, R. D., Scholz, S., and Mayrhofer, R.
(2014). Mobile device usage characteristics: The ef-
fect of context and form factor on locked and unlocked
usage. In Proceedings of the 12th International Con-
ference on Advances in Mobile Computing and Multi-
media, MoMM ’14, pages 105–114. ACM.
Jung, J., Kim, Y., and Chan-Olmsted, S. (2014). Measuring
usage concentration of smartphone applications: Se-
lective repertoire in a marketplace of choices. Mobile
Media & Communication, 2(3):352–368.
Microsoft (2013). Cross-screen engagement.
http://advertising.microsoft.com/es-xl/WWDocs/
User/display/cl/researchreport/1932/global/Cross
Sc
reenWhitepaper.pdf.
Montanez, G. D., White, R. W., and Huang, X. (2014).
Cross-device search. In Proceedings of the 23rd ACM
International Conference on Conference on Informa-
tion and Knowledge Management, CIKM ’14, pages
1669–1678, New York, NY, USA. ACM.
Pew Internet and American Life Project (2015). June
10-july 12, 2015 gaming, jobs and broad-
band. http://www.pewinternet.org/datasets/june-10-
july-12-2015-gaming-jobs-and-broadband/.
Pew Research Center (2016). Our survey methodology in
detail. http://www.pewresearch.org/methodology/u-s-
survey-research/our-survey-methodology-in-detail/.
Roberto, E. (2015). The Boundaries of Spatial Inequal-
ity: Three Essays on the Measurement and Analysis
of Residential Segregation. PhD thesis, Yale Univer-
sity.
Rula, J. P., Jun, B., and Bustamante, F. (2015). Mobile
ad(d): Estimating mobile app session times for better
ads. In Proceedings of the 16th International Work-
shop on Mobile Computing Systems and Applications,
HotMobile ’15, pages 123–128.
Soikkeli, T., Karikoski, J., and Hammainen, H. (2013).
Characterizing smartphone usage: Diversity and end
user context. International Journal of Handheld Com-
puting Research, 4(1):15–36.
Theil, H. (1967). Economics and information theory.
Studies in mathematical and managerial economics.
North-Holland Pub. Co.
Vlachos, M., Meek, C., Vagena, Z., and Gunopulos, D.
(2004). Identifying similarities, periodicities and
bursts for online search queries. In Proceedings of
the 2004 ACM SIGMOD International Conference on
Management of Data, SIGMOD ’04, pages 131–142.
Vuong, Q. H. (1989). Likelihood ratio tests for model se-
lection and non-nested hypotheses. Econometrica,
57(2):307–333.
Wagner, D. T., Rice, A., and Beresford, A. R. (2014). De-
vice analyzer: Understanding smartphone usage. In
Mobile and Ubiquitous Systems: Computing, Net-
working, and Services, pages 195–208. Springer.
Wang, Y., Huang, X., and White, R. W. (2013). Charac-
terizing and supporting cross-device search tasks. In
Proceedings of the Sixth ACM International Confer-
ence on Web Search and Data Mining, WSDM ’13,
pages 707–716, New York, NY, USA. ACM.
Xu, K., Chan, J., Ghose, A., and Han, S. P. (2015). Bat-
tle of the channels: The impact of tablets on digital
commerce. Management Science.
Xu, Q., Erman, J., Gerber, A., Mao, Z., Pang, J., and
Venkataraman, S. (2011). Identifying diverse usage
behaviors of smartphone apps. In Proceedings of the
2011 ACM SIGCOMM Conference on Internet Mea-
surement Conference, IMC ’11, pages 329–344.
Mobile Application Usage Concentration in a Multidevice World
51
