
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo
Voting
Dirk Achenbach
2
, Bernhard L
¨
owe
1
, J
¨
orn M
¨
uller-Quade
1
and Jochen Rill
2
1
Karlsruhe Institute of Technology, Karlsruhe, Germany
2
FZI Research Center for Information Technology, Karlsruhe, Germany
Keywords:
Electronic Voting, Ballot Secrecy, Bingo Voting.
Abstract:
When designing an electronic voting scheme it is notoriously difficult to guarantee the secrecy of the vote
as well as the correctness of the tally, even in the presence of a malicious adversary. Research in (offline)
cryptographic voting schemes has largely relied on a trusted voting machine for guaranteeing security. We
alleviate part of this trust requirement. Our scheme ensures the confidentiality of the vote even in the presence
of an honest-but-curious voting machine. We improve on Bohli et al.’s Bingo Voting scheme (Bohli et al., 2007).
Bingo Voting already guarantees the correctness and public verifiability of the election in spite of a malicious
voting machine. The voting machine learns the voter’s input however, and is trusted not to violate ballot secrecy.
Our novel construction’s output is identical to that of Bingo Voting. We devise an electro-mechanical Physical
Oblivious Transfer (pOT) device to remove that trust requirement by hiding the voter’s choice from the voting
machine. The pOT device is realised in such a way that the voter merely operates a button to express her choice.
Our construction is thus particularly user-friendly.
1 INTRODUCTION
Advances in electronic voting systems increase conve-
nience, but imperil the foundation of democracy.
There is a strong tendency to migrate formerly
“analogue” systems to digital systems to increase effec-
tiveness and reduce costs. Elections are no exception.
Indeed, counting votes by hand is error-prone and does
not scale well. By contrast, machines do not suffer
from oversights and never tire. However, as their per-
formance scales well, their damage potential does also.
For a malicious adversary bent on rigging an election,
voting machines are a prime target.
Research in cryptographic voting schemes ad-
dresses this issue. Indeed, a number of schemes have
been proposed that produce a provably-correct tally
even if the voting machine is compromised (Bohli
et al., 2007; Chaum et al., 2009). On the other hand,
they do not hide the voter’s choice from a potentially
corrupted voting machine. This neglect seems un-
reasonable as voting machines are often made from
general-purpose memory-programmable computers
and thus pose an easy target for an adversary (Feldman
et al., 2006). Such a weakness is deemed unavoidable,
as the device that receives the voter’s input naturally
is aware of it. But for a voter to resist coercion, the se-
crecy of her vote is essential. Many security notions for
coercion resistance in presence elections consequently
assume that the machine that handles the user’s input
is trusted.
Further, to achieve coercion resistance one must de-
sign electronic voting schemes such that no adversary
can discern information about any voter’s behaviour,
even in the long run. Thus, all data that is published
must have everlasting privacy, i.e. be perfectly secret.
Another concern when designing electronic voting
schemes is usability. Voting schemes that require the
voter to calculate some integer or to navigate an intri-
cate user interface may be of academic interest, but
are not well-suited for real-world elections where peo-
ple are bound to make mistakes (Chaum et al., 2010).
Only a simple point-and-push interface guarantees that
the voter actually votes as intended. We limit the scope
of this work to schemes that allow for such interfaces.
We address the above-mentioned concerns by
introducing an architecture where the trust is dis-
tributed among several components with very lim-
ited functionality—they do not have to be capable of
general-purpose computation—and where an honest-
but-curious voting machine can not glean any knowl-
edge about the voter’s choice. To cast a vote, the voter
pushes the mechanical button that is associated with
Achenbach, D., Löwe, B., Müller-Quade, J. and Rill, J.
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting.
DOI: 10.5220/0005964300850096
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 85-96
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
85

Voting Receipt P
1
1234523134
P
2
7634875451
P
3
3422335718
Figure 1: A Bingo Voting receipt. The numbers printed next
to the candidates are chosen uniformly at random. Yet, only
one of them has been drawn in the presence of the voter.
her choice. An electro-mechanical principle then en-
sures that the rest of the machine is unaware of which
data it processes. To the best of our knowledge, we are
the first to address the privacy of the voter’s choice in
light of a passively corrupted voting machine in this
setting. Our work is an improvement over the Bingo
Voting (Bohli et al., 2007) scheme.
Bingo Voting in a Nutshell.
Bingo Voting is a pro-
tocol for presence elections. Before the actual election,
for each candidate a number of dummy votes is pre-
pared. A dummy vote is a number drawn uniformly
at random. To cast a vote, the voter marks her choice
on a designated voting machine. The machine then
generates a receipt for the voter with the name of all
candidates and a random number next to it: a dummy
vote next to each candidate the voter did not vote for
and a fresh random number for the candidate of choice.
For the chosen candidate a fresh number is generated
from a trusted and observable random number gener-
ator, e.g. a bingo cage (hence the name). All receipts
generated in this manner are published after the elec-
tion. The final tally is obtained by counting the number
of dummy votes not used and thus inferring the number
of fresh votes a candidate received. The trick behind
the scheme is that during the casting process the voter
can observe that the candidate she voted for is assigned
a fresh random number. As dummy votes and fresh
randomness are indistinguishable after the fact, the
receipt is of no use to an outside adversary and hence
Bingo Voting is receipt-free (see Figure 1). The voting
machine learns the voter’s choice, however, and must
be trusted not to leak that information.
Oblivious Bingo Voting.
We propose a remedy for
this weakness by employing a second device: physical
oblivious transfer (Physical Oblivious Transfer (pOT)).
The central idea is that the voter selects between “fresh”
and “dummy” randomness using the pOT device and
thus leaves the voting machine oblivious as to which
kind of “randomness” was selected. Hence, the voting
machine cannot tell which candidate was voted for. We
believe this idea of using a mechanical device to shield
information from a potentially untrusted machine is of
independent interest for the design of cryptographic
schemes.
1.1 Our Contribution
We present a novel protocol for a “point and push” type
electronic voting machine. In addition to producing
a provably-correct tally, our scheme ensures that no
single component can learn the voter’s choice. To the
best of our knowledge, this is the first protocol with
such a guarantee.
More concretely, our construction is an extension
to Bohli et al.’s Bingo Voting (Bohli et al., 2007). In
Bingo Voting, the voting machine learns the voter’s
input and thus can easily determine the voter’s choice.
Thus, the scheme is only coercion resistant if one as-
sumes the voting machine can be trusted not to record
the voters’ inputs.
We use a physical principle to conceal the voter’s
input from the voting machine. The voter selects one
of two candidate ciphertexts using a physical oblivious
transfer (pOT). The selected ciphertext determines the
vote while keeping the voting machine oblivious as to
which vote is cast. We discuss a possible realisation of
such a pOT device. An isolated printing device finally
outputs a receipt identical to the one provided to the
voter in the Bingo Voting scheme.
Our scheme allows for a fixed ordering of the candi-
date list which will be presented to every voter, as it is
mandated by law in several countries (e.g. Germany).
To make our idea work in the concrete setting, we
need another primitive, blind commitments. We give a
definition of the primitive and propose a realisation.
This work is structured as follows. After reviewing
related work in this section, we discuss preliminaries
in Section 2. Namely, we introduce two major build-
ing blocks, blind commitments and physical oblivious
transfer. In Section 3 we give a short introduction to
Bingo Voting. We present our construction in Sec-
tion 4. Section 5 concludes.
1.2 Related Work
Related work on electronic voting can roughly be di-
vided into two categories: protocols which are exe-
cuted offline in a voting booth on dedicated machines,
and protocols which are run on general-purpose ma-
chines in a decentralised manner (e.g. over the Inter-
net). In an online setting, coercion resistance is gener-
ally much harder to achieve than offline (one reason is
that a coercer can literally look over the voter’s shoul-
der). It requires very different mechanisms to achieve
the same level of coercion resistance or correctness in
an online setting. As our scheme is offline, we only
address related work on offline voting. Also, there
are numerous voting schemes used in practice (both
online and offline) whose main design goals do not
SECRYPT 2016 - International Conference on Security and Cryptography
86

include security. These schemes are not cryptographic
and can often trivially be broken. We only address
cryptographic voting protocols.
•
In PEVS (Based et al., 2012), Based et al. ensure
coercion resistance by allowing the voter to gener-
ate an unbounded number of key pairs. They get
signed by the voting authority using a blind signa-
ture. The adversary cannot know which key pair
was actually used to vote. The scheme requires the
voting machine to be trusted however, since it can
collude with the adversary and use a specific key
to cast the vote (e.g. always the first). Also, the
scheme is not robust against a passively-corrupted
voting machine, as the voting machine can simply
observe the keys the voter used.
•
Split-ballot voting (Moran and Naor, 2010) ad-
dresses the requirement to trust one single voting
authority. The basic scheme does not involve a
voting machine, however. It requires the voter to
perform a modular addition on paper to split her
vote. It seems a strong assumption that every voter
is capable of such a feat. However, implementing
the operation on a voting machine to simplify the
voting process, again requires trust in the voting
machine, since it will know how the voter split
his vote among the ballots. Similar to our scheme,
in order to achieve everlasting security, they also
jointly compute commitments and encryptions of
their reveal information.
•
BeleniosRF (Cortier et al., 2015) is an extension
to Helios (Adida, 2008) to achieve strong receipt-
freeness (even a malicious voter cannot prove how
she voted). To achieve that, Cortier et al. use “sig-
natures on randomisable ciphertexts”, a crypto-
graphic primitive introduced by Blazy et al. (Blazy
et al., 2011). It makes possible that the voting ma-
chine can re-randomise the encrypted and signed
vote of the voter, as well as its signature, before
publishing the vote. This way, a voter cannot iden-
tify her published vote. However, a passively cor-
rupted voting machine can learn the individual
votes since it must encrypt them. Also the scheme
also does not offer everlasting security.
•
Selene (Ryan et al., 2015) aims to simplify the
interface for the voter to allow her to easily verify
that her vote was counted correctly. To achieve
that, Selene publishes the vote in the clear and as-
signs each voter a tracking number which she can
use to verify that her vote was counted correctly.
Ryan et al. argue that a voter can mitigate coercion
by lying to an adversary about her tracking number.
However, as with other voting schemes, the voting
machine learns the individual votes, since it has to
encrypt them.
•
Scantegrity II (Chaum et al., 2009; Chaum et al.,
2010) is a coercion resistant voting scheme which
has been used for a municipal election at Takoma
Park. It is based on a scanner and uses verification
codes for end-to-end verifiability. The coercion
resistance has been proven. However, the polling
station, the server which creates the verification
codes, and the printing service, have to be honest.
2 PRELIMINARIES
In this section, we give an overview of our notation
and introduce blind commitments, which are a main
building block of our construction.
2.1 Notation
In this section, we give an overview about the notation
we use in this paper. We consider an election with
n
P
parties (candidates)
p
i
and
n
E
electors (voters)
e
j
:
P := {p
i
}
n
P
i=1
and
E := {e
j
}
n
E
j=1
. To avoid confusion,
we use the index variable
i
in the context of one voter’s
choice and
j
to differentiate between different voters.
We rely on the trustworthiness of an authority with
n
A
members. As long as less than
k
members are cor-
rupted, the group is trustworthy, where
k
is a security
parameter of the threshold encryption scheme we use
in the following chapters. For the authority members
we use
l
as the index variable. Each authority mem-
ber
a
l
owns a public verification key
s
l
for verifying
signatures.
Further,
c
is a commitment,
u
and
v
are ciphertexts,
and
N
and
R
are random numbers.
g
and
h
are public
parameters of a Pedersen commitment scheme (Peder-
sen, 1992).
C
,
C
0
,
D
, and
D
0
are 3-tuples containing a
commitment c and two ciphertexts u and v.
2.2 Blind Commitments
For protecting the privacy of the votes in the presence
of a corrupted voting machine, we introduce a new
primitive blind commitments. Cryptographic commit-
ments allow a sender to commit to a value without
revealing it to the receiver of the commitment. He can
then later send unveil information to unveil the value.
Commitments are required to be hiding as well as bind-
ing—a commitment may not reveal its contents before
it is unveiled by the sender, while also only allowing
the sender to unveil to the value he committed to. We
extend this standard notion of commitments to blind
commitments whose content and unveil information
is encrypted and not known to a single person. The
unveil information is kept in encrypted form so that the
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting
87

voting machine cannot unveil on its own. This is simi-
lar to the technique used by Moran et al. (Moran and
Naor, 2010). By using perfectly-hiding commitments,
one can then achieve everlasting security for the public
data. Our intent is to create the blind commitments in
a distributed computation. We require the following
properties from a blind commitment:
Definition 1
(Homomorphic Encryption, Homomor-
phic Commitment)
.
Let
enc(m, r)
be an
IND-CPA
se-
cure homomorphic encryption scheme, encrypting mes-
sage
m
with randomness
r
. Let
enc(m)
be the same
scheme without explicit mention of the randomness.
Let
com(m, r)
be a perfectly hiding and computa-
tionally binding homomorphic commitment scheme,
committing on message
m
with randomness
r
. Let
com(m)
be the same scheme without explicit mention
of the randomness.
For messages
m
,
m
0
with randomness
r
,
r
0
, we re-
quire that there exist operations +, ·, ◦ such that
• enc(m, r) · enc(m
0
, r
0
) = enc(m +m
0
, r +r
0
).
• com(m, r) · com(m
0
, r
0
) = com(m + m
0
, r +r
0
).
• com(m, r) ◦ r
0
= com(m, r +r
0
).
Definition 2
(Blind Commitment)
.
We call
C :=
bCom(m, r
1
, r
2
, r
3
) = (c, u, v)
a blind commitment on
a message m with randomness r
1
, r
2
, r
3
, where
• c := com(m, r
1
)
is a perfectly hiding and computa-
tionally binding commitment on message
m
using
randomness r
1
,
• u := enc(m, r
2
)
is an encryption of the message
m
using randomness r
2
, and
• v := enc(r
1
, r
3
)
is an encryption of randomness
r
1
using randomness r
3
.
Let
bCom(m)
be the same scheme without explicit
mention of the randomness.
We call a pair of blind commitments
(C, C
0
) :=
(bCom(p
i
, r
1
, r
2
, r
3
), bCom(N
i, j
, r
0
1
, r
0
2
, r
0
3
))
a commit-
ment pair on a candidate p
i
and a dummy vote N
i, j
.
During the tallying, the blind commitments have
to be shuffled. To achieve that, all three parts
c
,
u
, and
v
of each commitment have to be re-randomisable. We
can achieve this, using the homomorphic properties of
both the encryption and the commitment scheme.
Definition 3
(Re-randomisation)
.
Let
C = (c, u, v) =
bCom(m, r
1
, r
2
, r
3
)
be a blind commitment to message
m
with randomness
r
1
, r
2
, r
3
. Let
r
4
, r
5
, r
6
be fresh
random values, and let
0
be the neutral element for
+
.
We define
re-rand(C, r
4
, r
5
, r
6
) := (c
0
, u
0
, v
0
)
with
c
0
:= c ◦ r
4
= com(m, r
1
+ r
4
)
u
0
:= u · enc(0, r
5
) = enc(m, r
2
+ r
5
)
v
0
:= v · enc(r
4
, r
6
) = enc(r
1
+ r
4
, r
3
+ r
6
)
Thus,
re-rand(bCom(m, r
1
, r
2
, r
3
), r
4
, r
5
, r
6
) =
bCom(m, r
1
+ r
4
, r
2
+ r
5
, r
3
+ r
6
).
Definition 4
(Indistinguishability of Re-randomisa-
tions)
.
We require that
re-rand(C, r
4
, r
5
, r
6
)
is indistin-
guishable from a blind commitment to any different
value, i.e. for any messages
m, m
0
and randomness
r
1
, r
2
, r
3
, r
4
, r
5
, r
6
there exists randomness
r
7
, r
8
, r
9
such that
re-rand(bCom(m, r
1
, r
2
, r
3
), r
4
, r
5
, r
6
)
is in-
distinguishable to bCom(m
0
, r
7
, r
8
, r
9
).
The correctness of the shuffle is proven by using
shadow mixes (Adida, 2008).
As already mentioned, we need to create the en-
cryptions and commitments in a distributed way. Us-
ing a threshold encryption scheme, we can generate
the encryptions in a distributed way easily. It is not im-
mediately clear how to create the blind commitments
in a distributed way at the same time. (In a nutshell, a
threshold encryption scheme is a public-key cryptosys-
tem with a shared secret key
sk
l
and a common public
key
pk
T
. To decrypt, a threshold number of “share
holders” (of the secret key) have to come together.)
We instantiate the commitment scheme with the
Pedersen commitment scheme (Pedersen, 1992) and
the encryption scheme with a compatible threshold
encryption (e.g. as described by Cramer et al. (Cramer
et al., 2001)). We then exploit the homomorphic prop-
erty of those schemes. Using these tools, we create the
blind commitments. During the pre-voting phase the
authorities generate
n
E
blind commitments on random
numbers N
i, j
for every candidate p
i
.
Let
g
and
h
be the generators for a Pedersen com-
mitment. Each authority member a
l
generates
c
(a
l
)
i, j
:= com(N
(a
l
)
i, j
, R
(a
l
)
i, j
) = g
N
(a
l
)
i, j
h
R
(a
l
)
i, j
,
where 1 ≤ i ≤ n
P
, 1 ≤ j ≤ n
E
, and 1 ≤ l ≤ n
A
,
as well as the ciphertexts
u
(a
l
)
i, j
:= enc(N
(a
l
)
i, j
) and v
(a
l
)
i, j
:= enc(R
(a
l
)
i, j
).
The product
c
i, j
:= com(N
i, j
, R
i, j
)
= com(
n
A
∑
l=1
N
(a
l
)
i, j
,
n
A
∑
l=1
R
(a
l
)
i, j
)
=
n
A
∏
l=1
c
(a
l
)
i, j
is the commitment on the dummy vote N
i, j
.
The two products
u
i, j
:= enc(N
i, j
) = enc(
n
A
∑
l=1
N
(a
l
)
i, j
) =
n
A
∏
l=1
u
(a
l
)
i, j
v
i, j
:= enc(R
i, j
) = enc(
n
A
∑
l=1
R
(a
l
)
i, j
) =
n
A
∏
l=1
v
(a
l
)
i, j
SECRYPT 2016 - International Conference on Security and Cryptography
88

are the corresponding encrypted unveil information. If
at least one authority member keeps her choice private,
the value of N
i, j
and R
i, j
can not predicted.
Additionally, for each commitment
c
i, j
, a sec-
ond blind commitment on the candidate to which the
dummy vote belongs is created in the same fashion.
With this construction, no subgroup with less than
k
authority members can predict information about the
dummy votes.
2.3 Physical Oblivious Transfer
In traditional elections, the trust in the integrity and
confidentiality of ballots relies on sealed ballot boxes.
Cryptographically speaking, an intact mechanical seal
serves as a trust anchor for the voting protocol. In-
deed, many cryptographic schemes also use tamper-
proof hardware as their setup assumption (Katz, 2007;
Moran and Segev, 2008). The idea is to exploit a phys-
ical property of a device that no adversary can violate.
We propose such a device—physical oblivious trans-
fer (pOT)—with two inputs and one output. The pOT
outputs exactly one of its two inputs and also obscures
which input was selected. The decision which of the
two inputs to take is made by the voter who operates a
physical button to indicate her decision.
The name for the device is inspired by the oblivious
transfer (OT) cryptographic primitive (Kilian, 1988).
Here, the receiver selects which of the inputs to receive,
without learning the other input, while the sender never
learns which of the inputs was delivered.
We imagine the pOT device to be realised in a
electromechanical fashion. On the electrical side, it is
constructed like an optocoupler, but with two sending
diodes (see Figure 2). One of the diodes is covered
by a screen. By pushing a button, the voter moves
the screen from one diode to the other. Constructed
this way, the pOT acts as a galvanic isolation between
the input and the output pins. As both diodes are
connected and consume power, the sender cannot gain
any knowledge on which input is delivered.
3 BINGO VOTING
We first describe the original Bingo Voting scheme as
it is outlined by Bohli et al. (Bohli et al., 2007). Bingo
Voting aims to provide both a secure and verifiable
voting mechanism as well as coercion resistance to
the voters. The main idea is that each voter is given a
receipt for her elected candidate as well as a receipt for
every other candidate (so called “dummy votes”). This
ensures that the voter can, on the one hand, verify that
her vote was counted correctly, and on the other hand,
Voter’s Choice
m
i
m
0
m
1
Figure 2: pOT device: The device functions similarly to
an optocoupler. On the left, two diodes (permanently) send
messages
m
0
and
m
1
. On the right, there is a phototransistor.
One of the diodes is screened. When the voter selects a vote,
she moves the screen from one diode to the other.
present a receipt for any candidate. Both the dummy
votes, as well as the real vote of the voter will be pub-
lished on a public bulletin board and are represented by
a unique number. The tallying and the separation from
the dummy votes from the real votes will be performed
by cryptographic means. This is done by choosing the
dummy votes out of a pool of numbers chosen uni-
formly at random and committing to them before the
actual voting takes place. The number to represent the
voter’s actual vote is be generated in the voting booth,
where the voter can witness its “freshness”. To get
the number of votes per candidate, the scheme will
determine the number of unused dummy votes, since
when a candidate receives a vote, a dummy vote is left
unused. In the following we describe the scheme in
more detail. We assume a poll with
n
P
candidates and
n
E
voters.
3.1 Pre-voting Phase
Before the election, the voting machine generates
n
E
random numbers
N
i, j
for every candidate
p
i
resulting
in
m := n
P
· n
E
pairs
(N
i, j
, p
i
)
of random numbers and
candidates (dummy votes). Unconditionally hiding
commitments
c
1,1
, . . . , c
n
P
,n
E
to these pairs are com-
puted with
c
i, j
= com((N
i, j
, p
i
), r
i, j
)
where
r
i, j
denotes
a fresh random coin. The commitments are shuffled
and published on a public bulletin board. Further, it is
proven that the dummy votes are equally distributed
among the candidates.
3.2 Voting Phase
In order to cast a vote, the following steps are per-
formed.
•
The voter enters her choice into the voting ma-
chine.
•
A trusted random number generator generates a
fresh random number
R
j
(it must be visible to the
voter) and transfers it to the voting machine. Note
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting
89

that these random numbers are indistinguishable
from the precalculated dummy votes.
•
The voting machine uses the fresh number for the
selected candidate and draws a random dummy
vote for all other candidates from the pool of
dummy votes for that candidate. (Each dummy
vote is only used once.)
•
The voting machine prints a receipt containing the
dummy votes as well as the fresh number.
•
The voter verifies that the fresh number is assigned
to the candidate she voted for.
Even though the voter receives a receipt for her
vote, an outside person (e.g. a coercer) can not dis-
tinguish the fresh number from the dummy votes and
thus can not tell which candidate the vote was cast
for. Since the voter knows which one of the numbers
on the receipt was generated freshly, she can check if
that number also appears on the public bulletin board
afterwards.
3.3 Post-voting Phase
After the election, the voting machine publishes the
results together with a proof of correctness on a public
bulletin board. The published data consists of
• the final outcome of the poll,
•
a lexicographically sorted list of all receipts issued
to voters,
•
a list of all unused dummy votes with the respective
reveal information, and
•
non-interactive zero-knowledge proofs that each
unopened dummy vote was indeed used on one
receipt.
The voters can verify the correctness of the election
by checking if their individual receipt is included in
the list of all receipts and by checking whether the
number of unopened commitments is as expected (that
is, for every vote cast, one dummy vote will be left
unused).
3.4 Assumptions
For correctness, Bingo Voting relies only on the trust-
worthiness of the random number generator. However,
since the voting machine learns the voters inputs, bal-
lot secrecy requires that the voting machine is fully
trusted.
4 OUR CONSTRUCTION
In this section we introduce our construction. It is
based on a modularisation of the original Bingo Voting
protocol. First we give a brief summary of the protocol
and our goal. We then describe the components of our
construction in detail. The public output of our scheme
is identical to that of the original protocol. Thus, we
inherit the correctness and security properties of the
original Bingo Voting construction.
4.1 Basic Idea
In the original Bingo Voting construction the voting
machine itself is trusted to keep the secrecy of the
ballot. It is aware of the dummy votes
N
i, j
and the
fresh random number
R
j
, and it thus learns the choice
of the voter. With this information, the voting machine
can not only reconstruct the voter’s choice, but it also
has the ability to determine interim election results.
The general idea behind our construction is to
shield the voter’s choice from the voting machine.
In particular, we deal with an untrusted voting ma-
chine by letting it only handle encrypted informa-
tion. Any public data is—like in the original scheme—
unconditionally hidden. Private data is protected by
a computationally hiding (encryption) scheme. The
voting authorities only take part in the process during
the pre- and post-voting phases. We mainly use three
techniques:
1.
During the pre-voting phase the commitments to
the pairs of candidate and dummy vote are com-
puted jointly and blindly by the authorities a
l
.
2.
The encrypted unveil information for these com-
mitments is also jointly and blindly generated us-
ing an additive homomorphic threshold encryption
scheme.
3.
The voter chooses her vote using a mechanism
that hides the actual choice from the rest of the
machine.
As the unveil information for all commitments is
encrypted and has never been revealed, the voting ma-
chine cannot unveil the precomputed commitments and
thus cannot calculate intermediate results of the elec-
tion by the commitments alone. Additionally, since
both the commitments, as well as the encrypted reveal
information are jointly and blindly computed using a
k
-out-of-
n
threshold encryption scheme,
k
members
of the authorities are required to decrypt the unveil
information. (For details see Sections 2.2 and 4.3.)
Our construction keeps the choice of the voter hid-
den from all components. We achieve this by using an
electro-mechanical pOT device to select between an
encrypted dummy vote and an encrypted fresh random
number (and also an encrypted
1
versus an encrypted
0
). The component used to “evaluate” the pOT has
no computational power itself and only makes the fi-
nal result available to the other components. Because
dummy votes and “fresh” randomness are indistin-
SECRYPT 2016 - International Conference on Security and Cryptography
90
guishable, no component has a way of determining the
voter’s choice. We describe a possible realisation of
pOT in Section 2.3.
For the receipt to be printed, we envision a print-
ing device to which each of the voting authorities can
input their keys for the threshold encryption scheme in
form of a security token. The printing device will then
use these tokens to jointly decrypt the dummy votes
and the fresh random number. At this point, the print-
ing device does not learn the choice of the voter since
the dummy votes are indistinguishable from the fresh
random numbers of the Random Number Generator.
During the tallying we publish the same information as
in the Bingo Voting scheme. When a commitment has
to be revealed (i.e. as it is the case with dummy votes),
the voting authorities will decrypt the corresponding
reveal information jointly. Note that, because we use a
threshold encryption scheme, no single voting author-
ity can unveil commitments by itself. As it is the case
with the original Bingo Voting scheme, all votes will
be shuffled and re-randomised before being published.
4.2 A Modular Voting Protocol
The original Bingo Voting protocol introduced a sepa-
ration between the random number generator and the
voting machine to ensure correctness of the result in
spite of a corrupted voting machine. We build upon
this idea and further separate the protocol (see Fig-
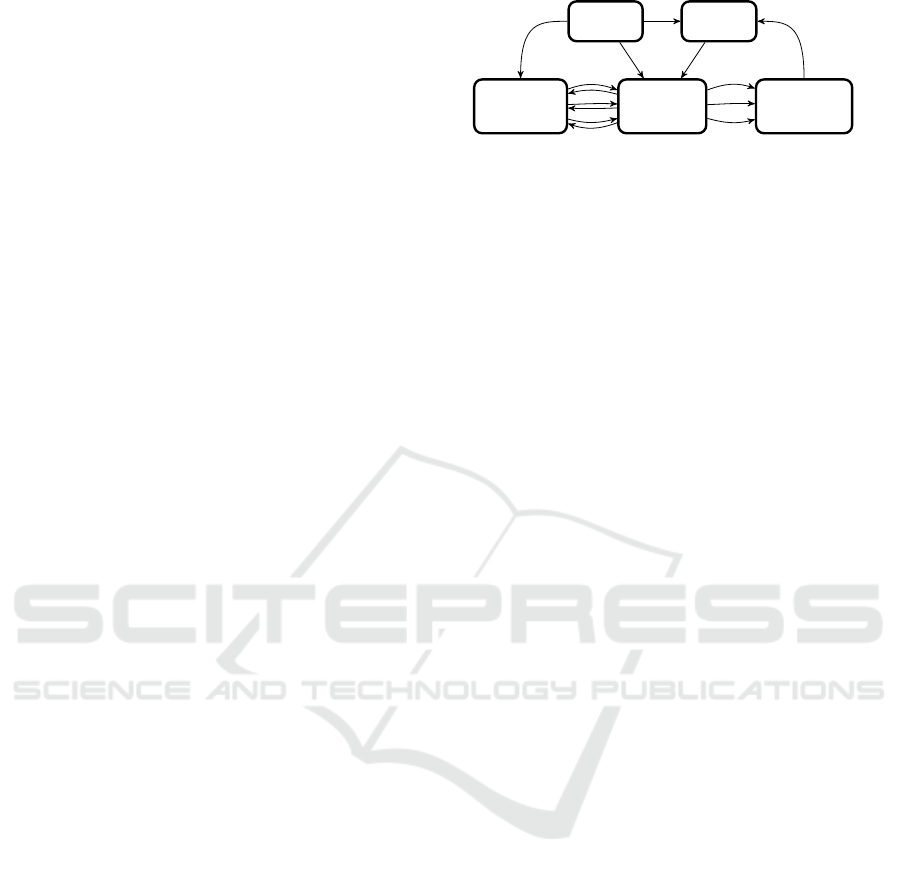
ure 3). In particular, we separate the voting machine
into an input device, a storage device, and a separate
printing device. The input device is used to select a
vote (using our novel pOT mechanism), the storage de-
vice stores the precomputed blind commitments, while
the printing device eliminates the need for the voting
machine to decrypt votes. We also use the random
number generator from the Bingo Voting scheme in
the same way. Further, we define several small com-
ponents for very specific tasks: an append box, a split
box, and a re-randomisation box. The append box
appends a fixed string to its input. The split box is
its counterpart: It receives an input and outputs the
split parts on different channels. The re-randomisation
box re-randomises a ciphertext. All these components
are assumed to be dedicated hardware devices with
a very distinct functionality. They are thus easy to
build and verify. We assume them to be trusted, thus
removing the trust assumption from the entire machine
and distributing it among the components. This is not
only a reduction in scope, but also in complexity. The
assumption is reminiscent of standard tamper-proof
hardware assumptions (Katz, 2007; Moran and Segev,
2008). We assume a dedicated channel between each
of the components.
Storage
Device
Input
Device
RNG Voter
Printing
Device
choice
receipt
R
j
Figure 3: We separate the voting protocol into four main
components: a storage device, used to store the blind com-
mitments calculated during the pre-voting phase; an input
device, used to perform the actual voting based on an oblivi-
ous transfer mechanism; a printing device, used to print the
receipts; and a random number generator to provide fresh
randomness during the vote. In this example, the voter has
three options to choose from.
The Storage Device.
The central element of our
modular voting machine is the storage device. Only
this part stores data permanently. All other parts need
not keep state. In the pre-voting phase the pairs of
blind commitments
(D
i, j
, D
0
i, j
) = (bCom(p
i
), bCom(N
i, j
))
=
(c
(D)
i, j
, u
(D)
i, j
, v
(D)
i, j
),
(c
(D
0
)
i, j
, u
(D
0
)
i, j
, v
(D
0
)
i, j
)
=
(com(p
i
, r), enc(p
i
), enc(r)),
(com(N
i, j
, r
0
), enc(N
i, j
), enc(r
0
))
are stored on the storage device. Figure 4 is a symbolic
representation of all data stored on the storage device.
For each expected voter
j
and each candidate
i
an entry
is generated. We call all entries for a voter
j
a set. For
each possible candidate, there is a dedicated channel
from the storage device to the input device, over which
the actual voting can be performed.
The Random Number Generator.
The Random
Number Generator (RNG) has similar functionality
as in the Bingo Voting scheme. During each voting
process, it creates a “fresh” random number
R
j
and
displays it to the voter. This random number will then
be used for the candidate of the voter’s choice, instead
of the precalculated dummy vote. Instead of sending
the fresh random number
R
j
as plaintext to the voting
machine, the RNG sends
R
j
in encrypted form to each
pOT in the input device and
C
i, j
and
C
0
i, j
(see Figure 4)
to the storage device. The public key
pk
T
, used for
this encryption, is the same as it has been used for
the blind commitments (see Section 2.2). We envi-
sion a dedicated channel from the RNG to each pOT
instance. In order to save the fresh random number,
the RNG also has a link to the storage device (see Fig-
ure 5). We point out that, since the RNG generated
the fresh random number (and thus can distinguish it
from dummy votes) it can break the security of the
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting
91

B
i, j
C
i, j
C
0
i, j
D
i, j
D
0
i, j
j
(Voter)
i
(Candidate)
enc(b
i, j
)
c
(C)
i, j
= com(p
i
, r
00
)
u
(C)
i, j
= enc(p
i
)
v
(C)
i, j
= enc(r
00
)
c
(C
0
)
i, j
= com(R
j
, r
000
)
u
(C
0
)
i, j
= enc(R
j
)
v
(C
0
)
i, j
= enc(r
000
)
c
(D)
i, j
= com(p
i
, r)
u
(D)
i, j
= enc(p
i
)
v
(D)
i, j
= enc(r)
c
(D
0
)
i, j
= com(N
i, j
, r
0
)
u
(D
0
)
i, j
= enc(N
i, j
)
v
(D
0
)
i, j
= enc(r
0
)
1
1
2
.
.
.
n
P
2
1
.
.
.
.
.
.
.
.
.
Figure 4: The contents of the storage device before and during the election. Before the voting phase,
n
E
· n
P
(with
1 ≤ j ≤ n
E
and
1 ≤ i ≤ n
P
) entries are stored on the storage device. These entries consist of blind commitments on the candidate (
D
)
and the corresponding dummy vote (
D
0
) (light grey). During the election, additional information is stored: the encrypted
information whether a dummy vote was used (
B
), a blind commitment on the candidate
i
(
C
), as well as a blind commitment on
the fresh random number which was used for the selected candidate (C
0
) (dark grey).
RNG
Display: 7634875451
create: R
j
:= 7634875451
create: (bCom(p
1
), bCom(R
j
))
(bCom(p
2
), bCom(R
j
))
.
.
.
(bCom(p
n
P
), bCom(R
j
))
to Input Device:
enc(R
j
)
to Storage Device:
(bCom(p
1
), bCom(R
j
))
(bCom(p
2
), bCom(R
j
))
.
.
.
(bCom(p
n
P
), bCom(R
j
))
Figure 5: The random number generator has two outputs:
first, it outputs an encryption of the fresh random number to
the input devices, second it outputs a blind commitment to
the random number to the storage device.
protocol. Thus, similar to the original Bingo Voting
scheme, we require the RNG to be trusted. However,
to improve upon this, the generation of the random
numbers can also be done in a distributed manner with
several random number generators, as it is done with
the blind commitments and multiple authorities. Then,
it would be possible to maintain security, as long as
one source of randomness is uncorrupted. We leave
this for future work.
Append-x Box, Re-Randomisation Box, and Split
Box.
In order to control the flow of information be-
tween the main components of the voting machine, we
use small, state-less devices (see Figure 7).
One device (Append Box) appends an encryption of
a
1
or an encryption of a
0
to each message it receives.
Note that the device does not necessarily need to en-
crypt these two values every time, since encryptions
can be precomputed and encoded into the device as
a fixed string (which will be re-randomized later on).
We call the two versions of this device “append-
1
box”
and “append-0 box”.
The second device (Split Box) splits an input tu-
ple into its parts and sends each part to a dedicated
component.
The third device (Re-Randomisation Box) re-
randomises ciphertexts. On input
(enc(m
1
, r
1
)
,
enc(m
2
, r
2
))
it chooses uniformly at random
¯r
1
and
¯r
2
and outputs a tuple of ciphertexts containing the
same plaintext:
(enc(m
1
, r
1
) · enc(0, ¯r
1
), enc(m
2
, r
2
) ·
enc(0, ¯r
2
)) = (enc(m
1
, r
0
1
), enc(m
2
, r
0
2
)).
Such devices have a very limited and fixed func-
tionality. Thus, we assume them to be easy to build
and to verify and therefore trustworthy.
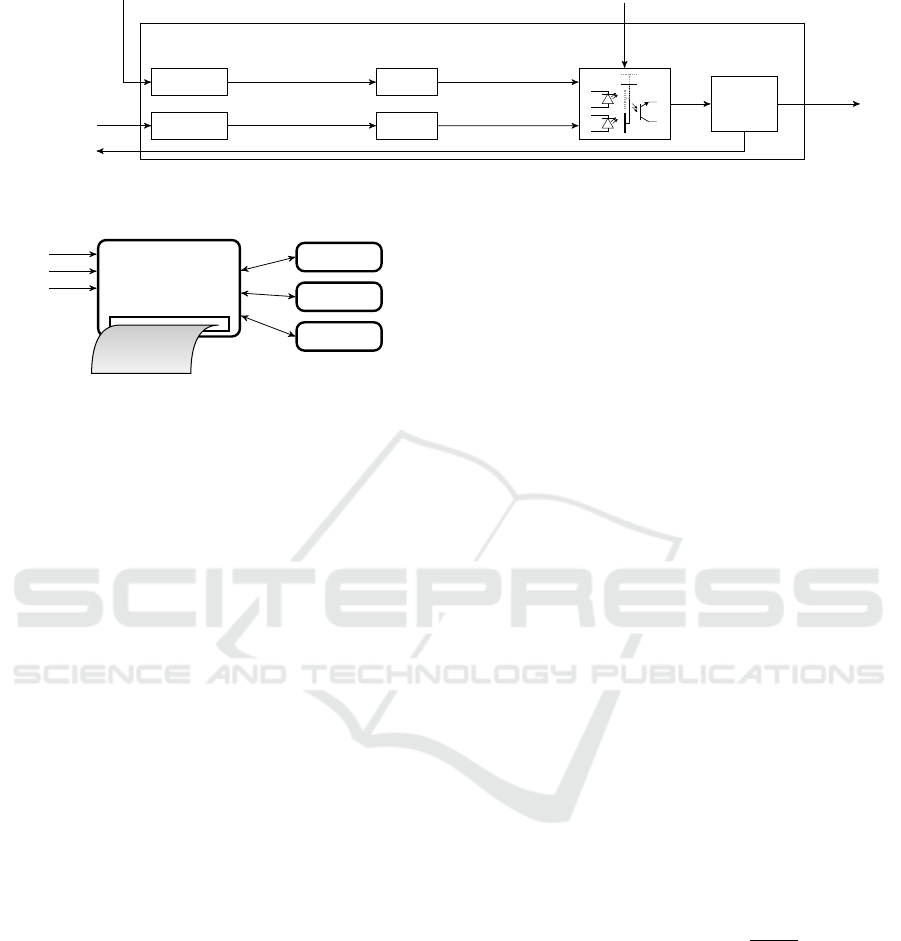
Input Device with Physical Oblivious Transfer.
The input device consists of one Physical Oblivious
Transfer (pOT) module for each candidate. We de-
scribe a possible realisation of a pOT in Section 2.3.
Each of these modules takes two inputs: the first in-
put is an encryption of the fresh random number gen-
erated by the RNG. The second input (the standard
selection) is an encryption of the dummy vote as it is
stored in the storage device (see Figure 6). Both of
these values are marked (by appending an encrypted
0
or a
1
, respectively). Afterwards, the tuples are re-
randomised. When voting for a specific candidate, the
voter advises the corresponding pOT module for that
SECRYPT 2016 - International Conference on Security and Cryptography
92

Input Device
pOT with Button
for candidate 1
pOT with Button
for candidate 2
pOT with Button
for candidate 3
from RNG:
enc(R
j
)
from / to
Input Device
enc(N
1, j
)
enc(b
1, j
)
enc(N
2, j
)
enc(b
2, j
)
enc(N
3, j
)
enc(b
3, j
)
to Printer:
enc(R
j
) or
enc(N
1, j
)
enc(R
j
) or
enc(N
2, j
)
enc(R
j
) or
enc(N
3, j
)
Figure 6: Our input device consists of one pOT module
per candidate. Each module receives two inputs: and en-
crypted dummy vote and encrypted fresh random number.
See Figure 7 for details.
candidate to select the fresh random number instead
of the encrypted dummy vote. As per the construction
of the pOT module, the storage device cannot learn
whether the dummy vote or the fresh randomness was
selected, and thus will not know for which candidate
the vote was cast. The outputs of all these pOT mod-
ules are processed by split boxes. The first part is sent
to the printing device, where it is used to print out the
receipt. The second part is sent to the storage device,
where it is used to produce the tally.
Printing Device.
The printing device’s task is to cre-
ate a receipt identical to the receipt used in the original
Bingo Voting scheme. It has the list of candidates
stored internally and receives encrypted random num-
bers from the input device. They arrive in the order of
the list of candidates, but need to be decrypted prior
to printing. To this end, the printing device is supplied
with security tokens that hold copies of the author-
ity’s decryption keys. They jointly decrypt the random
numbers without revealing their keys (see Figure 8).
We point out that the printing device is unaware of the
origin of the random numbers and thus cannot break
the confidentiality of the vote even given access to the
decryption tokens. To deter attempts at stealing the
security tokens, the printing device is to be placed in
a secure container. Further, for each voting machine,
different keys are to be used. This way, a potential
theft of the security tokens has a limited effect (similar
to that of an broken ballot box).
4.3 Pre-voting Phase
In the pre-voting phase the keys of the threshold en-
cryption scheme are created and distributed. Every
authority member publishes the public key of her sign-
ing key
s
l
with
1 ≤ l ≤ n
A
. After this step
n
P
·n
E
blind
commitment pairs to the dummy votes
(D
i, j
, D
0
i, j
)
with
1 ≤ i ≤ n
P
and
1 ≤ j ≤ n
E
are created in a distributed
manner (see Section 2.2). When all commitment pairs
are created, each authority member signs the published
data and publishes the signature as well. (Recall that
only the commitments are published—the encrypted
unveil information stays private.)
After the pre-computation the voting machine is
prepared and the commitment pairs on the dummy
votes
(D
i, j
D
0
i, j
)
are stored on the voting machine. Fur-
thermore, each authority member provides the printing
device with a secure hardware module that contains
her secret decryption key.
4.4 The Execution of the Voting
Protocol
Recall that during the pre-voting phase, we store a
set of commitment pairs
{(D
i, j
, D
0
i, j
)}
n
P
i=1
for each ex-
pected vote
1 ≤ j ≤ n
E
on the storage device (see
Figure 4). During each individual voting process by
voter
j
, for each candidate
i
two additional data com-
ponents are stored on the storage device: commitment
pairs
(C
i, j
, C
0
i, j
)
and encryptions of bits
b
i, j
. An entry
(i, j)
with
1 ≤ i ≤ n
P
consists of the blind commit-
ment pair
(D
i, j
, D
0
i, j
)
on the dummy vote
N
i, j
(and the
corresponding candidate), a blind commitment pair
(C
i, j
, C
0
i, j
)
on the fresh random number
R
j
(and the
corresponding candidate) created by the RNG during
the election, and an encrypted bit
b
i, j
which contains
the information whether the dummy vote has been
used (b = 1) or not (b = 0).
During the beginning of the voting process, the
storage device sends one element of the set of en-
crypted dummy votes (
{u
(D
0
)
i, j
}
n
P
i=1
) to each pOT in-
stance of the input device via its
n
P
dedicated chan-
nels (one dummy vote per candidate). On their way,
these encrypted values are fed through an “append-
1
box” and re-randomised. At the same time the RNG
sends the encrypted fresh random number
R
j
to each
pOT. On its way to the pOT an encrypted
0
is attached
by an “append-
0
box” and—both—re-randomised by
a “re-randomisation box”. Also, the RNG creates
{(C
i, j
, C
0
i, j
)}
n
P
i=1
and sends them to the storage device.
By appending an encrypted
0
to all fresh random
numbers and an encrypted
1
to all dummy votes, they
allow the authorities (which possess the decryption
keys) to distinguish which dummy votes were used
and which were not.
Now, the voter makes her choice and votes for one
candidate by pressing a button on the input device.
Afterwards, the voter confirms her choice by press-
ing a cast vote button. This causes all of the pOT
instances to be evaluated. For the candidate the voter
has selected, the fresh random number is requested
from the pOT module. For all other candidates, the
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting
93
Part of Input Device
m
i
m
0
m
1
re-rand
re-rand
append-0
append-1
Split
Box
(α, β)
enc(R
j
, r
0
1
), enc(0, r
0
2
)
enc(N
i, j
, r
0
3
), enc(1, r
0
4
)
enc(R
j
, r
1
), enc(0, r
2
)
enc(N
i, j
, r
3
), enc(1, r
4
)
from RNG:
enc(R
j
)
from / to
Storage Device:
enc(N
i, j
)
enc(b
i, j
)
to Printer:
enc(R
j
) or
enc(N
i, j
)
from Voter:
choice
β
α
Figure 7: Physical Oblivious Transfer (pOT) module: Both inputs are amended with an encryption of a
0
or a
1
, respectively
and re-randomised.
Printing Device
Token 0
Token 1
Token 2
from
Input Device
receipt
Figure 8: The printing device uses security tokens to decrypt
the encrypted random numbers, obtained by the input device
through the pOT mechanism. The security token store the
key securely and are able to decrypt.
dummy vote is used. The RNG displays the fresh ran-
dom number it generated, so that the voter can verify
that it matches the number which appears on the re-
ceipt later on. After selecting the candidate the output
(enc(R
j
), enc(b
i, j
))
for the chosen candidate and the
outputs
(enc(N
i, j
), enc(b
i, j
))
for all other candidates
are sent to a “split box”. There, the first part is sent to
the printing device and the second part is sent back to
the storage device to mark which dummy votes were
used and which were not.
The printing device then uses the authority mem-
bers’ security tokens to decrypt each
enc(N
i, j
)
(and
one
enc(R
j
)
) and prints the results next to the corre-
sponding candidate name
p
i
. The voter verifies that the
number displayed on the RNG is assigned to the party
she intended to vote for. If this is not the case, the voter
has to protest immediately (Bohli et al., 2007). When
the voter is satisfied with the receipt, it is published on
a public bulletin board using a commercially available
data diode hardware appliance.
4.5 Tally
To compute the tally, the authority members process
the entries of the storage device. In the following, we
do not consider the unused dummy votes. They can
be (mixed and) unveiled to show they have never been
used. During the election phase, dummy votes (
D
,
D
0
)
are completed with commitment pairs to the used fresh
random number (
C
0
) and the corresponding candidate
(
C
) and an encryption of a bit (
b
i, j
) which indicates
whether the dummy vote has been printed on the ballot.
These entries are shuffled by the authority members.
Afterwards the authority jointly decrypts the bit
b
i, j
of
each entry. Now all information required to compute
the tally and an accompanying proof of correctness is
available: First of all, empty lists
U
(“Unused”) and
B
(“Ballot”) are created.
• b
i, j
= 0
:
U := U ∪(D
i, j
, D
0
i, j
)
;
B := B∪(C
i, j
, C
0
i, j
)
• b
i, j
= 1: B := B ∪ (D
i, j
, D
0
i, j
); delete (C
i, j
, C
0
i, j
)
U
now contains the blind commitments of all unused
dummy votes. All blind commitments to dummy votes
and fresh random numbers printed on receipts are part
of
B
.
U
serves to figure out the final tally and to
prove its correctness: After shuffling
U
, the commit-
ment pairs are unveiled. Each pair contains an unused
dummy vote and the according candidate. This list
of unveiled candidate names is the tally.
B
serves to
prove the correctness of the ballots: After shuffling
B
,
the correctness of each ballot is shown as it has been
done in the original Bingo Voting protocol. To this
end the (unpublished) encrypted unveil information is
decrypted jointly by the authority members.
4.6 Verification
The verification of the tally does not differ from Bingo
Voting. In an independent step, each authority member
verifies how often her secure token—plugged into the
printing device—has been used during the election.
Assuming a
k
-out-of-
n
A
threshold encryption scheme,
n
P
candidates and
n
E
published ballots, the expected
number of decryption requests is d
k·n
E
·n
P
n
A
e.
4.7 Authority
Trust assumptions are a fundamental aspect of crypto-
graphic election schemes. It is our belief that such trust
is best placed in an independently constituted group
who form the voting authority. The size of the group
and the tasks of the group members should not depend
on the design of the voting scheme. In our case all au-
thority members have the same task: Create a share for
each dummy vote and ensure that her share is part of
the according dummy vote. During the tallying the au-
SECRYPT 2016 - International Conference on Security and Cryptography
94

thority members jointly decrypt the tally as described
above. The size of the group can be chosen as neces-
sary (e.g. one member of each pressure group). Thus,
coercion resistance can not be undermined without the
collusion of at least k authority members.
4.8 Security
We claim that a passively corrupted voting machine
does not receive any information about the voter’s
choice. We hide the voters choice from the storage
device by using our pOT mechanism. We prove that
the storage device can not learn anything from the in-
formation it observes using an adaptive game-based
indistinguishability proof. In this game, the attacker
first votes on behalf of a number of voters and observes
all communication inside the storage device. Then, he
outputs two candidates and receives the transfered data
for one of them. We prove that he can not tell which
vote he received the communication for by giving a re-
duction to
IND-CPA
. (This is sufficient, as we assume
that only a minority of authorities is corrupted in the
underlying threshold encryption system.) Concluding,
the adversary cannot learn a single bit of the voter’s
choice.
Definition 5
(View)
.
We define
view( j, x) := {∀i ≤
n
p
: (enc(b
i, j
), com(p
i
, r), enc(p
i
), enc(r),
com(R
j
, r
0
), enc(R
j
), enc(r
0
))}
(with
b
i, j
= 0
if
i = x
)
as the set of all messages the voting machine can
observe when voter e
j
has voted for candidate p
x
.
Security Game 1 (IND-CV
A
(enc,com)
(k))
1.
The experiment performs the setup for
enc
, re-
ceives
(pk, sk)
and chooses a random bit
b ←
{0, 1}.
2.
The adversary outputs
n
p
and
n
E
to the experiment.
The experiment performs the precomputation for
the voting scheme according to these parameters.
It gives the precomputed values to the adversary.
3.
The adversary chooses a voter
1 ≤ j ≤ n
E
and
a choice
1 ≤ x ≤ n
p
for the voter, and outputs
( j, x)
to the experiment. The experiment executes
the voting protocol for voter
j
choosing candidate
x
, and outputs
view( j, x)
to the adversary. (The
adversary is only allowed to choose a voter
j
that
has yet to vote.)
4.
The adversary can repeat this step as often as he
wishes (bounded by his running time). Afterwards,
he outputs “end” to the experiment.
5.
The adversary then again chooses a (yet-
undecided) voter
1 ≤ j
c
≤ n
E
and two votes
for candidates
x
0
, x
1
with
x
0
6= x
1
and submits
( j
c
, x
0
, x
1
)
to the experiment. The adversary re-
ceives view( j
c
, x
b
).
6. The adversary outputs b
0
as a guess for b.
Definition 6
(Indistinguishability under Chosen
Votes)
.
A voting process has indistinguishability under
chosen votes (IND-CV), if
∀A, c ∈ N∃k
0
∀k > k
0
: |Pr[IND-CV
A
(enc,com)
= 1]| ≤
1
2
+k
−c
We give a standard definition for
IND-CPA
secu-
rity (Katz and Lindell, 2007).
Security Game 2 (IND-CPA
A
enc
(k))
1.
The experiment performs the setup for
enc
and
receives keys (pk, sk).
2. The experiment chooses b ← {0, 1} at random.
3.
The adversary receives input
1
k
and
pk
. He can
now perform arbitrary computations.
4.
The adversary outputs two messages
m
0
and
m
1
with |m
0
| = |m
1
|.
5. The experiment outputs enc(m
b
) to the adversary.
6. The adversary submits a guess b
0
for b.
Theorem 1.
Oblivious Bingo Voting has indistin-
guishability under chosen votes if
enc
is an
IND-CPA
secure encryption scheme and
com
is a perfectly hid-
ing commitment scheme.
Proof.
We prove the claim in two steps. First, we
modify the security game: we omit the commit-
ments from the view. By assumption the commit-
ments are perfectly hiding, and thus information-
theoretically indistinguishable from randomness.
The adversary cannot gain information from them.
The remaining view is
view( j, x) := {∀i ≤ n
p
:
(enc(b
i, j
), enc(p
i
), enc(r), enc(R
j
), enc(r
0
))}.
Second, towards a contradiction assume a success-
ful adversary on
IND-CV
. We will use this adversary
to break
IND-CPA
. To this end, the reduction has
to simulate
IND-CV
to the adversary, using only the
IND-CPA experiment. The reduction is as follows:
•
When receiving
n
p
and
n
E
from the adversary, use
(pk)
(received from the
IND-CPA
experiment) to
generate all hidden commitments on dummy votes
and give them to the adversary.
•
Receive a voter
1 ≤ j ≤ n
E
and a choice
1 ≤ x ≤ n
p
from the adversary. Generate the encryptions in
the view using enc with pk as key.
•
When receiving the “
end
” message from the adver-
sary, also receive a voter
j
c
and candidates
x
0
, x
1
from the adversary.
•
Generate two views
view( j
c
, x
0
) =: m
0
and
view( j
c
, x
1
) =: m
1
and pass them as the challenge
to the IND-CPA experiment.
•
Upon receiving
m
b
from the experiment, pass it to
the adversary running in
IND-CV
and forward its
guess b
0
to the IND-CPA experiment.
Oblivious Voting—Hiding Votes from the Voting Machine in Bingo Voting
95

The reduction perfectly simulates the
IND-CV
ex-
periment to the adversary. Thus, we inherit the adver-
sary’s success probability. As we assumed that the
encryption scheme has
IND-CPA
security, this is a
contradiction, which concludes the argument.
5 CONCLUSION AND FUTURE
WORK
We present a voting scheme that, to the best of our
knowledge, is the first to achieve ballot secrecy as
well as correctness without relying on a fully trusted
voting machine. Assuming a passive adversary, no
single component of our voting machine can break the
coercion resistance on its own. To achieve this we
substitute complete trust in the voting machine with
trust in simpler components which are easier to com-
prehend and to verify. In particular, we use a physical
mechanism, pOT to hide the selection of the vote from
the voting machine which might be of independent
interest. We believe that this device is easy to build out
of commercially available parts but this requires fur-
ther validation. Also, we assume security tokens which
can securely store the authorities’ keys and decrypt in
order to print a receipt for the voter, without even the
printer being able to break coercion resistance. Such
security tokens are already available commercially, for
example in the form of USB dongles.
As with the original Bingo Voting scheme, we also
assume that the random number generator is trusted.
Our scheme does not provide coercion resistance
against an active adversary, however. An adversary
who fully controls the storage device can coerce a voter
to vote for a specific candidate by forcing the proof of
correctness to fail for specific candidates. This should
be investigated in future work.
REFERENCES
Adida, B. (2008). Helios: Web-based open-audit voting.
In USENIX Security Symposium, volume 17, pages
335–348.
Based, M. A., Tsay, J.-K., and Mjølsnes, S. F. (2012). Pevs:
A secure electronic voting scheme using polling booths.
In Data and Knowledge Engineering, pages 189–205.
Springer.
Blazy, O., Fuchsbauer, G., Pointcheval, D., and Vergnaud,
D. (2011). Signatures on randomizable ciphertexts. In
Public Key Cryptography–PKC 2011, pages 403–422.
Springer.
Bohli, J.-M., M
¨
uller-Quade, J., and R
¨
ohrich, S. (2007).
Bingo voting: Secure and coercion-free voting using
a trusted random number generator. In Alkassar, A.
and Volkamer, M., editors, E-Voting and Identity, vol-
ume 4896 of Lecture Notes in Computer Science, pages
111–124. Springer Berlin Heidelberg.
Chaum, D., Carback, R. T., Clark, J., Conway, J., Essex, A.,
S, H. P., Mayberry, T., Popoveniuc, S., Rivest, R. L.,
Shen, E., Sherman, A. T., and Vora, P. L. (2010). Scant-
egrity ii municipal election at takoma park: the first
e2e binding governmental election with ballot privacy.
In 19th USENIX Security Symposium.
Chaum, D., Carback, R. T., Clark, J., Essex, A., Popoveniuc,
S., Rivest, R. L., Ryan, P. Y., Shen, E., Sherman, A. T.,
and Vora, P. L. (2009). Scantegrity ii: End-to-end ver-
ifiability by voters of optical scan elections through
confirmation codes. Information Forensics and Secu-
rity, IEEE Transactions on, 4(4):611–627.
Cortier, V., Fuchsbauer, G., and Galindo, D. (2015). Be-
leniosrf: A strongly receipt-free electronic voting
scheme. Cryptology ePrint Archive, Report 2015/629.
http://eprint.iacr.org/2015/629.
Cramer, R., Damg
˚
ard, I., and Nielsen, J. B. (2001). Mul-
tiparty computation from threshold homomorphic en-
cryption. Springer.
Feldman, A. J., Halderman, J. A., and Felten, E. W. (2006).
Security analysis of the diebold accuvote-ts voting ma-
chine.
Katz, J. (2007). Universally composable multi-party com-
putation using tamper-proof hardware. In Advances
in Cryptology-EUROCRYPT 2007, pages 115–128.
Springer.
Katz, J. and Lindell, Y. (2007). Introduction to modern
cryptography: principles and protocols. CRC press.
Kilian, J. (1988). Founding crytpography on oblivious trans-
fer. In Proceedings of the twentieth annual ACM sym-
posium on Theory of computing, pages 20–31. ACM.
Moran, T. and Naor, M. (2010). Split-ballot voting: everlast-
ing privacy with distributed trust. ACM Transactions on
Information and System Security (TISSEC), 13(2):16.
Moran, T. and Segev, G. (2008). David and goliath commit-
ments: Uc computation for asymmetric parties using
tamper-proof hardware. In Advances in Cryptology–
EUROCRYPT 2008, pages 527–544. Springer.
Pedersen, T. P. (1992). Advances in Cryptology —
CRYPTO ’91: Proceedings, chapter Non-Interactive
and Information-Theoretic Secure Verifiable Secret
Sharing, pages 129–140. Springer Berlin Heidelberg,
Berlin, Heidelberg.
Ryan, P. Y. A., Roenne, P. B., and Iovino, V. (2015).
Selene: Voting with transparent verifiability and
coercion-mitigation. Cryptology ePrint Archive, Re-
port 2015/1105. http://eprint.iacr.org/2015/1105.
SECRYPT 2016 - International Conference on Security and Cryptography
96
