Transitioning to a Javascript Voting Client for Remote Online Voting

Jordi Cucurull

, Sandra Guasch

and David Galindo

Scytl Secure Online Voting, Pl. Gal·la Placídia, 1-3, 1st ﬂoor, 08006, Barcelona, Spain

School of Computer Science, The University of Birmingham, Edgbaston, Birmingham, B15 2TT, U.K.

Keywords:

Remote Electronic Voting, Javascript Security, Implementation, Performance, Random Number Generation.

Abstract:

Voters in remote electronic voting systems typically cast their votes from their own devices, such as PCs

and smartphones. The software executed at their devices in charge of performing the ballot presentation,

navigation and most of the cryptographic operations required to protect the integrity and privacy of the ballot,

is referred to as the voting client. The ﬁrst voting clients were developed as Java Applets. However, the use of

this technology has become relegated in front of web technologies such as Javascript, which provide a better

multi-platform user experience. This is the reason why in 2013 Scytl decided it was imperative to develop

a voting client purely based on Javascript. This industrial paper shows the implementation experiences and

lessons learned during the development and deployment of Javascript voting clients for our remote electronic

voting systems. The paper is complemented with a performance study of 1) the main cryptographic primitives

used in voting clients and 2) the voting casting process of one of the voting clients used in a real election.

1 INTRODUCTION

In remote electronic voting systems, voters are usu-

ally allowed to cast their votes from their own de-

vices, such as PCs, laptops, smartphones, etc. This

is specially suitable for voters who live abroad, who

are outside of their region during the election day, and

for impaired voters who may have mobility issues.

In general, remote electronic voting systems have

to fulﬁll a set of security requirements in order to be

used in electoral processes, which are focused on en-

suring that at least the same properties of traditional

voting scenarios are maintained, such as vote authen-

ticity and privacy, result accuracy, secrecy of interme-

diate results, veriﬁability and auditability, and unco-

ercibility and vote selling protection. In order to fulﬁll

such security requirements, remote electronic voting

systems use advanced cryptographic protocols (see

for example (Adida, 2008), (Gjosteen, 2013), (Juels

et al., 2010)). These protocols require to perform

some cryptographic operations both at the client and

server sides. The piece of software which is run in the

voter’s device, which is in charge of performing the

ballot presentation, navigation and most of the crypto-

graphic operations, is referred to as the voting client.

The ﬁrst voting clients implemented in Scytl’s

products were developed as Java Applets. The usage

of Java enabled 1) the possibility to perform complex

cryptographic operations on a multiplatform setup

and 2) code and expertise reuse of the developers that

were already working on the backend. However, the

use of Java Applets implied a high price to pay in

terms of user experience and security. Voters’ devices

required a Java Runtime Environment (JRE), that was

not always present neither updated, being a source of

security vulnerabilities, not even supported in most

of mobile devices and with support recently removed

from the most popular browsers. In recent years, the

natural evolution of the World Wide Web standards

and the introduction of HTML5 have strengthened the

use of Javascript for increasingly complex operations,

reaching a point where performing cryptographic op-

erations in Javascript at the browser has become fea-

sible. Due to this feasibility and the advantages the

Javascript technology offered in terms of user expe-

rience and multi-platform compatibility (specially for

mobile devices), in 2013 Scytl decided it was imper-

ative to develop a voting client purely based on this

technology to replace the former Java-based versions.

Thus, the main contribution of this industrial pa-

per is to show the implementation experiences and

lessons learned, along with the whole process of de-

veloping and deploying Javascript voting clients used

in several real elections. The paper is organized in

seven sections: Section 2 describes a generic vot-

ing client and the cryptographic operations it may

Cucurull, J., Guasch, S. and Galindo, D.

Transitioning to a Javascript Voting Client for Remote Online Voting.

DOI: 10.5220/0005967301210132

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 121-132

ISBN: 978-989-758-196-0

121

require; Sections 3 and 4 describe the challenges

to implement a Javascript-based voting client and

the solutions adopted; Section 5 explains the test-

ing of a pseudo-random number generator imple-

mented; Section 6 analyses the performance of cryp-

tographic primitives and a voting client implemented

in Javascript, and also explains some of the ap-

proaches followed to improve it; ﬁnally Section 7

presents the conclusions reached.

2 VOTING CLIENT

This section introduces the details of generic voting

clients used in remote electronic voting systems.

2.1 Remote Electronic Voting Systems

From a high level point of view, a remote voting sys-

tem is composed of two main components, the voting

servers and the voting client (see Figure 1). During

the election, the voting servers provide the back-end

services that allow voter authentication, ballot provi-

sion, and veriﬁcation and storage of cast ballots in

the ballot box. During the counting phase, the vot-

ing servers decrypt and tally the votes providing the

election results, while protecting the voter’s privacy.

A usual approach for this is to use a mix-net (Chaum

and Pedersen, 1992) in order to shufﬂe and transform

the encrypted votes prior to decryption.

A good practice in remote electronic voting is

to cryptographically protect the vote by encrypting

and digitally signing it at the voter’s device, before

it is sent to the remote voting server for being stored.

Hence the privacy and the integrity of the vote are pro-

tected from the very beginning, right after the vote is

generated until it is processed at the counting stage.

This is commonly known as end-to-end encryption

and it is possible thanks to the voting client applica-

tion executed at the voter’s device.

The voting client is the front-end that allows the

voters to authenticate, navigate through the ballot, se-

lect their voting options, generate an encrypted and

signed ballot and cast it.

2.2 Basic Components

The voting client comprises a graphical user interface

and some underlying logics. These last ones can be

divided in several components:

• Authentication: This component authenticates

the voter in front of the voting system. The com-

ponent can be adapted for integration with the cus-

tomer infrastructure or totally replaced by a third-

party authentication system.

• Vote Generation: This component generates the

ballot to be cast, i.e. encoding the voting op-

tions selected by the voter, encrypting and digi-

tally signing the ballot containing them, and send-

ing the ballot to the remote voting server. Addi-

tionally, it may generate mathematical proofs to

prove the correctness of the operations performed.

• Cryptographic Library: The authentication and

ballot generation components require the usage of

cryptographic primitives that are not natively pro-

vided by the Javascript language. Thus they are

included as cryptographic libraries.

• Pseudo Random Number Generator and En-

tropy Collector: A module to generate sequences

of secure random numbers, required by some

cryptographic primitives, is included for the plat-

forms that do not possess a built-in generator.

2.3 Basic Voting Flow

The ﬂow in the voting client depends on the spe-

ciﬁc voting protocol implemented each one provid-

ing different security properties under different as-

sumptions (Gharadaghy and Volkamer, 2010), (Puig-

galí et al., ). Despite this, a generic set of operations

can be deﬁned: 1) The voter authenticates to the sys-

tem; 2) upon presentation of her ballot, she selects the

voting options that represent her voting intent; 3) after

the voter conﬁrms her vote, the voting options are en-

coded and encrypted; 4) mathematical proofs of cor-

rect encryption are generated (if required by the pro-

tocol); 5) the encrypted voting options and the mathe-

matical proofs are digitally signed; 6) the vote is cast

to the remote server; 7) the server provides a conﬁr-

mation receipt which is presented to the voter.

2.4 Cryptographic Functionalities

The following generic set of cryptographic function-

alities and algorithms, depending on the voting proto-

col implemented, may be required in the voting client:

• Hash Functions: they are used for computing

certiﬁcate ﬁngerprinting and digital signatures.

Although the standard for SHA-3 has already

been published (NIST, 2015), the previous stan-

dard SHA-2 (NIST, 2012) (speciﬁcally, SHA-

256) has been considered due to compatibility is-

sues.

• Digital Signature Functions: they are used for

digitally signing the vote and for verifying the dig-

ital signatures of the information received from

SECRYPT 2016 - International Conference on Security and Cryptography

122

Figure 1: Remote electronic voting system.

the remote voting server. The RSA algorithm with

the hash variant (RSA Full Domain Hash signa-

ture scheme (RSA-FDH) (Bellare and Rogaway,

1993)) has been considered.

• Encryption Algorithms: they are used for en-

crypting the voting options. RSA and ElGa-

mal encryption algorithms (Menezes et al., 1996),

and the AES encryption algorithm (NIST, 2001),

are considered for public key and symmetric key

cryptography respectively.

• Zero-Knowledge Proofs of Knowledge

(ZKPK): they (Damgaard, 2010) are used

to prove a certain statement without revealing any

other information than the statement is true. For

example the Schnorr Signature (Schnorr, 1991)

can prove knowledge of the randomness used for

encrypting a message, providing assurance of the

originator of an encrypted vote, and preventing

vote copying (Cortier and Smyth, 2011).

• Pseudo-random Number Generators (PRNG):

these are used for generating the random values

required by the cryptographic algorithms.

• Password-based Key Derivation Functions: in

the voting client they are used to derive keys for

the authentication of the voter and to access pri-

vate data. The PBKDF2 (RSA Laboratories, b)

algorithm is the one selected.

• Functionalities for Parsing and Opening Key-

stores: these are used for providing private

signing and encrypting keys to the voters.

PKCS#12 (RSA Laboratories, a) or equivalent

key containers are used.

• Reading, Parsing and Validation of Digital

Certiﬁcates: these are used to check the valid-

ity of the cryptographic keys and X509v3 (RFC-

5280, 2008) certiﬁcates used in the application.

3 CHALLENGES

The implementation of a voting client in Javascript

implied several challenges on cryptography, security

and performance.

3.1 Cryptography

3.1.1 Availability of Cryptographic Primitives

JavaScript does not implement the cryptographic

functionalities required by the voting client. An anal-

ysis of existing third party libraries was done to deter-

mine which of the required functionalities were pro-

vided by each library. The following factors were

considered: functionality provided, in order to know

if the library provided exactly what was needed, or if

it required some modiﬁcation; conﬁdence level, the

popularity of the library and the maintenance of the

code; license, to analyse if the license terms were

compatible with the license of the voting client ap-

plication. In our particular context we preferred BSD,

MIT or LGPL licensed libraries.

The results of the analysis, updated on April 2015,

are shown on Table 1. The conclusion was the Forge

library is one of the best alternatives to implement a

voting client. It provides functions for parsing and

opening PKCS#12 containers, as well as managing

digital certiﬁcates and public key cryptography. Be-

sides this, it has a strong developer support and up-

dates are made constantly. Both SJCL

(Stark et al.,

2009) and jsbn

are also broadly used in other soft-

ware. Speciﬁcally, jsbn is used in other of the ana-

lyzed libraries to provide BigInteger support (Forge,

http://digitalbazaar.com/forge

http://crypto.stanford.edu/sjcl

http://www-cs-students.stanford.edu/˜tjw/jsbn

Transitioning to a Javascript Voting Client for Remote Online Voting

123

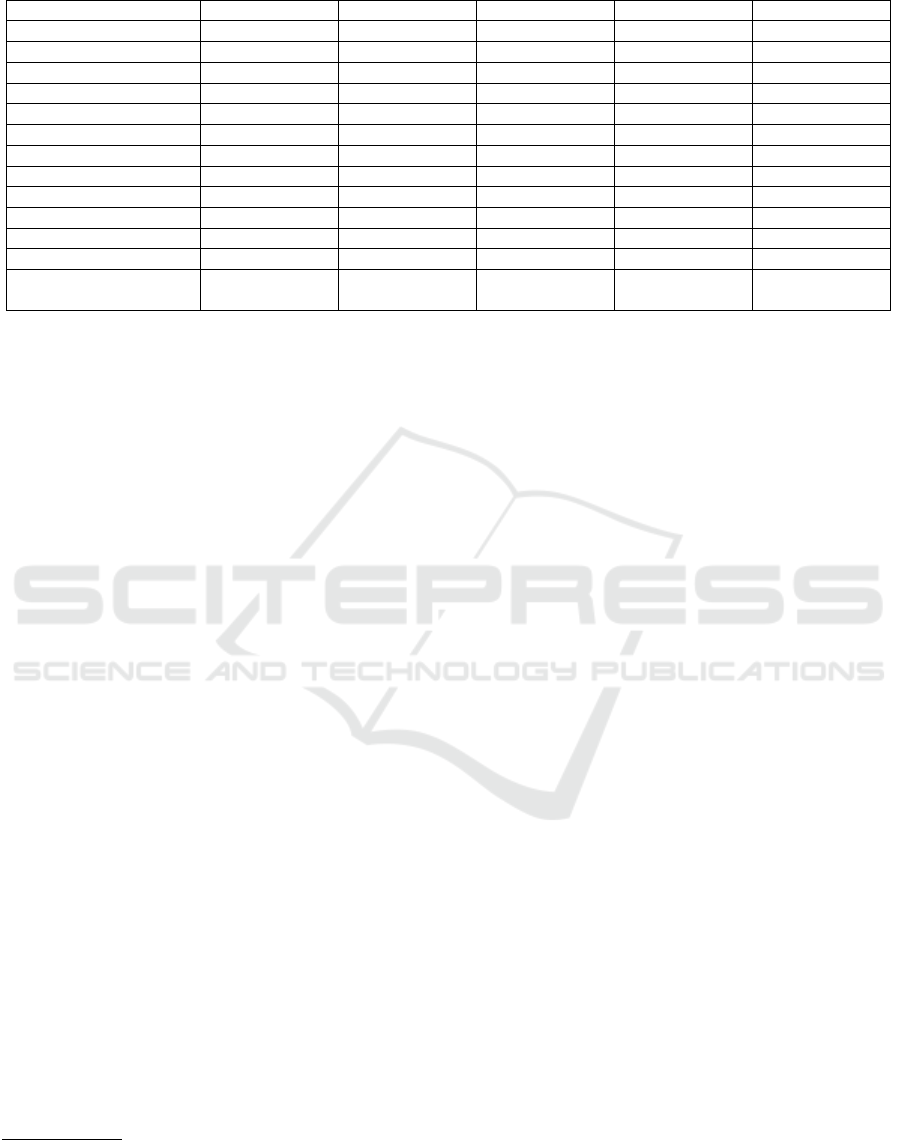
Table 1: Cryptographic functionalities provided by third party libraries.

Functionality SJCL Forge jsbn jsrsasign CryptoJS

SHA-256

√ √

RSA signature with SHA-256 X

√

RSA encryption X

√ √

X X

ElGamal encryption (over Zp) X X X X X

AES encryption

√ √

X X

√

Schnorr Signature or ZKPKs X X X X X

BigInteger support

√ √ √ √

PRNG

√ √ √

X X

Parsing PKCS#12 containers X

√

X X X

Parsing X.509 certiﬁcates X

√

PBKDF2

√ √

Conﬁdence level Maintained Maintained No updates Few updates Few updates

License BSD, GPL-2.0 BSD 3-Clause,

GPL-2.0

BSD MIT BSD

jrsasign

), and in the Helios voting system (Adida,

2008). SJCL is a library developed by highly recog-

nized cryptographers. Therefore it was worth to con-

sider it for some of the needed functionalities, such

as secure random generation or hash algorithms. jsr-

sasign and CryptoJS

did not seem to provide enough

support from the point of view of maintenance and

use, as well as functionalities. Considering the anal-

ysis performed, the Forge library was selected. The

functionalities missing in the library were imple-

mented on top of it (see Section 4.1.1).

3.1.2 Secure Random Numbers and Entropy

Several cryptographic primitives require the use of

random values. The quality of the random val-

ues (in the sense of their unpredictability) determine

the security offered by these primitives (for exam-

ple, non-random values can lead to weak encryp-

tions). Although Javascript has a native method

for random number generation, Math.random() (EC-

MAScript, 2011), its implementation is not consid-

ered cryptographically secure (Klein, 2008). Alter-

natively, there is a W3C standardization initiative for

a JavaScript API for performing basic cryptographic

operations (W3C, b). This includes a Pseudo Ran-

dom Number Generator (PRNG) suitable for cryp-

tographic uses, window.crypto.getRandomValues(),

which uses the browser’s host system entropy, but is

only implemented in recent versions of the browsers

and not for all mobile devices’ browsers

Some of the cryptographic libraries analized have

their own PRNG implementations. Speciﬁcally, SJCL

and Forge implement the Fortuna PRNG by Schneier

http://kjur.github.com/jsrsasign

http://code.google.com/p/crypto-js

https://developer.mozilla.org/en-

US/docs/DOM/window.crypto.getRandomValues

and Ferguson (Ferguson and Schneier, 2003). This

PRNG is intended to be used in long-term systems,

such as servers, and provides measures for collect-

ing randomness from the system events, and mixing

it in order to provide secure random values. How-

ever, web sessions in which Javascript cryptography

may be used can be very different from a server sys-

tem, and therefore the same approaches taken in the

design of the Fortuna algorithm may not be the best

choice. For example, web sessions have a short life

time, and the sources of entropy in a browser or in

a server are not the same. Current implementations

from SJCL and Forge of Fortuna have modiﬁcations

regarding the original scheme (Stark et al., 2009).

However, they still have some limitations regarding

the entropy sources they use to generate the random

numbers. Thus a custom PRNG, based on the Fortuna

PRNG, has been implemented (see Section 4.2).

3.2 Security

3.2.1 Code Authenticity

One of the challenges to develop a Javascript voting

client is to ensure the authenticity of the code to be

executed in the voter’s device. A modiﬁcation of this

code by an attacker could have severe implications in

the security of the solution, for example compromis-

ing the integrity and secrecy of the votes.

A classical solution to ensure the authenticity of

the code consists of signing it using public key cryp-

tography and enforcing the validation of this signature

in the browser. However, as opposed to other tech-

nologies such as Java Applets, there is no standard to

sign and verify the Javascript code delivered to the

browsers. There only exists a proprietary, and depre-

SECRYPT 2016 - International Conference on Security and Cryptography

124

cated, solution

, implemented in Mozilla and, for-

merly, Netscape Communicator 4.x, browsers. This

solution was based on packaging the Javascript and

HTML code within a signed Jar ﬁle, that was veriﬁed

by the browser when accessed. More promising is the

new Candidate Recommendation W3C Subresource

Integrity (W3C, a) that enables the HTML code to in-

clude ﬁngerprints of the Javascript code it refers. De-

spite this ensures the integrity of the included third

party code, it does not guarantee the integrity of the

HTML ﬁles that contain the hashes. Thus, it is not

a complete solution for the authenticity of the whole

code of the voting client. Finally, there exist proposals

ensuring end to end integrity, but they require the in-

stallation of browser plugins (Karapanos et al., 2016).

Given the current lack of support for guaranteeing

the JS code authenticity, the following approaches, to

detect code manipulation, have been implemented: 1)

TLS communications to guarantee the code transport

authenticity (preventing man-in-the-middle attacks);

2) Regular checks of ﬁle integrity in the server, in-

cluding the Javascript voting client code against a

baseline, e.g. using software scanning tools such as

AIDE

; 3) Running a Javascript remote integrity val-

idation service, i.e an externally executed service to

remotely download a selected set of Javascript code

from the server as a regular user and check if it

matches a previously generated baseline. This service

has been implemented and used within the context of

an election, but still not to check a voting client code.

3.2.2 Third Party Code

Javascript allows the inclusion of third party code and,

more important, the dynamic loading of scripts from

different servers. However, embedding third party

code dynamically loaded from external servers inside

the voting application’s website can pose a serious

security risk and it is totally unadvised, as this code

could access any variable or method of the voting ap-

plication. A server that does not belong to the elec-

tion realm may not fulﬁll the same security policies,

potentially becoming a weak point of attack. Any le-

gitimate external server acting as code source must be

secured as the main code server is.

An example of this is the vulnerability (Halder-

man and Teague, 2015) that a team of researchers dis-

covered in the Javascript voting client that we imple-

mented for the State General Elections 2015 of New

South Wales

. In this case a third party code owned

http://www.mozilla.org/projects/security/components/

signed-scripts.html

http://aide.sourceforge.net

http://www.vote.nsw.gov.au

by Piwik, used by monitoring purposes, was included

on behalf of NSW. A manipulation of this code, ex-

ploiting the FREAK vulnerability present in the ex-

ternal Piwik server that hosted the code, could poten-

tially allow a sophisticated attacker to alter the voting

client code running on the voter’s browser and mod-

ify the intended voting options. From the point of

view of the secrecy and integrity of the vote, the re-

ported vulnerability’s potential damage was similar to

that of having malware installed in the voter’s device.

This possibility was already considered in the design

of iVote 2015, and the defence against it (regarding

the integrity of the vote) was the inclusion of a voice

veriﬁcation mechanism using the DTMF phone input.

Thus, we do not recommend including third party

code from external servers. But, this may change if

the W3C Subresource Integrity (W3C, a) candidate

recommendation becomes an adopted standard.

3.3 Performance

The computational performance of Javascript is con-

stantly improving, but still below the one obtained by

native applications. In addition, the Javascript appli-

cations can be executed in a myriad of devices with

very different computational capabilities, e.g. smart-

phones, laptops, etc. Some existing voting client

implementations (Adida, 2008) combined Javascript

with the usage of Java for certain primitives that re-

quired higher performance using a technology called

LiveConnect. However, this alternative could not be

considered because the aim was to completely elimi-

nate the dependency with the Java Virtual Machine.

As cryptographic operations are computationally

expensive, an efﬁcient implementation was required

and several optimizations had to be performed at

the cryptographic protocol level (see Sections 4.1.1

and 4.3) to provide reasonable voting times.

4 IMPLEMENTATION

EXPERIENCE

During 2013-2015, most of the Scytl voting systems

were transitioned to use a Javascript voting client.

This section describes the most relevant aspects of the

implementation of them considering the challenges

previously described.

4.1 Cryptographic Library

Scytl provides different voting systems with different

cryptographic protocols, thus several variants of the

Transitioning to a Javascript Voting Client for Remote Online Voting

125

Javascript voting client were implemented. As a con-

sequence, a cryptographic library containing a large

amount of primitives was developed:

4.1.1 Basic Primitives

The basic cryptographic primitives are the most

widely used in standard web applications and, there-

fore, present in some of the libraries studied. For ex-

ample, SHA-256 hash functions, RSA digital signa-

ture, AES symmetric encryption, key derivation func-

tions such as PBKDF2, and support for X.509 certiﬁ-

cates and PKCS#12 containers. These primitives have

been wrapped in our library from the Forge library.

4.1.2 ElGamal and ZKPK Primitives

Other primitives such as ElGamal encryption or

ZKPKs are more speciﬁc to cryptographic protocols

such as those for e-voting. Therefore, they are not in-

cluded in the existing libraries. A custom implemen-

tation of these primitives has been built.

ElGamal encryption scheme has homomorphic

properties that are essential in electronic vot-

ing (Adida, 2008), (Gjosteen, 2013), (Galindo et al.,

2015). However, the usage of modular exponenti-

ations with large integers is computationally expen-

sive. Therefore, two modiﬁcations were performed to

the original scheme to improve its efﬁciency:

• ElGamal Encryption with Short Exponents:

This is a well-known optimization (Gennaro,

2005; van Oorschot and Wiener, 1996) consisting

of using shorter exponents (e.g. of about 256 bits)

than those deﬁned by the cyclic group used in the

scheme (which may be of about 2048 bits). This

reduces the cost of the modular exponentiations

without posing at risk the security of the scheme

in practice (Koshiba and Kurosawa, 2004).

• ElGamal Encryption with Multiple Keys:

When the number of plaintexts to be encrypted is

higher than one, an optimization consists of re-

ducing the number of exponentiations to compute

by using a different public key for computing each

ciphertext, but the same randomness for all them.

This does not affect the security of the encryption

scheme (Gjosteen, 2013; Kurosawa, 2002).

In order to maximize the code reuse and reduce

the likelihood of errors, we used the Maurer frame-

work (Maurer, 2009), which generalizes the imple-

mentation of ZKPKs for different statements. Thus

a unique base code is used for all the ZKPK vari-

ants of our voting systems. The Java-like BigInteger

functionalities required to operate with the large mag-

nitude integers used in these primitives were reused

from the existing libraries.

4.2 Pseudo-random Number Generator

A pseudo-random number generator (PRNG) is an

algorithm that generates a sequence of numbers

which is cryptographically indistinguishable from a

sequence of true random numbers. PRNGs gener-

ate the sequence of numbers in a deterministic man-

ner. The unpredictability of the values generated by

a PRNG is given by the unpredictability of the value

with which it is initialized, which is called the seed.

In order to provide high quality random values for the

cryptographic primitives, the PRNG is seeded with

entropy (random data) from the system events and in-

formation.

We have implemented a custom PRNG to be

used in the voting client. Its design has taken into

account requirements and particularities of voting

clients, speciﬁcally a short runtime life and strong

unpredictability of the random values produced. The

following principles were followed in the design and

use: 1) the collection of entropy to seed the PRNG

had to start as soon as possible, preferably as soon

as the voter started interacting with the system. The

implemented PRNG provides methods to start the

entropy collection task before the protocol-speciﬁc

functions have to be called; 2) in order to collect en-

tropy as fast as possible, user-driven events from an

extense set of sources were collected; 3) entropy es-

timation mechanisms were included in order to es-

timate how much entropy can be attributed to each

type of information collected in the browser. These

mechanisms ensure that enough entropy is collected

for seeding the PRNG and starting generating secure

random values.

The PRNG functionality implemented is com-

posed by several parts (see Figure 2) detailed in the

following sections.

Entropy Collection Mechanism. Collects infor-

mation available in the browser, as well as events gen-

erated by web navigation and user interaction:

• Sources of information available in the browser or

in the voting application.

– Random numbers from Javascript crypto-

graphic API if available in the used browser

– Browser information (e.g. User Agent string)

– Date

– Regular random numbers from the standard

Math library

SECRYPT 2016 - International Conference on Security and Cryptography

126

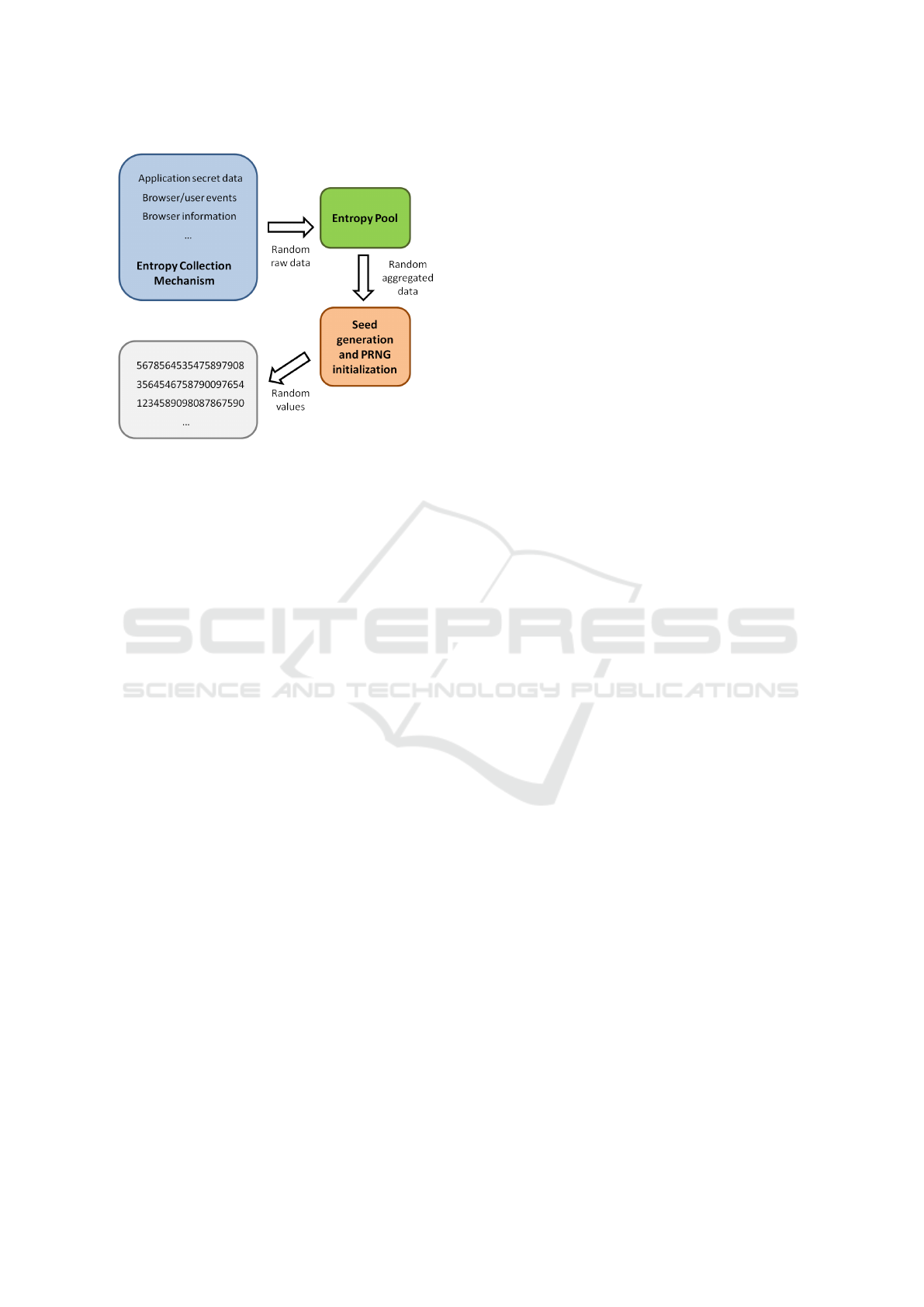
Figure 2: Diagram of the Pseudo-Random Number Gener-

ator.

• Events triggered by JavaScript or Ajax calls, as

well as user events.

– Mouse: mousemove, mousedown, mouseup,

wheel

– Keyboard: keydown, keyup

– Touch: touchstart, touchmove, touchend, ges-

turestart, gesturechange, gestureend

– Device accelerometer/compass: devicemotion,

deviceorientation

– Page loads and other AJAX calls

Since the Javascript cryptographic API is a source

of cryptographically strong random values, this col-

lector is deﬁned to be the ﬁrst one to be called. In user

events the following information is collected when

possible: relative position to the window and to the

screen, key/button, date, angle (only for compass) and

acceleration components (x,y,z) (only for accelerom-

eter in smartphones, tablets and alike). Each event

collected has been assigned with an estimated entropy

value, thus it is possible to estimate the amount of en-

tropy gathered by the entropy collector. Most of the

estimated entropy values were obtained from existing

analysis (Stark et al., 2009).

Seed Generation and Initialization. The data

gathered by the entropy collection mechanism is ac-

cumulated into an entropy pool, and at the same time

an entropy counter is increased with the estimated en-

tropy. The entropy collection starts at the very begin-

ning after downloading the voting client. Every time

new data is collected, there is the possibility to check

if a minimum amount of entropy required by the ap-

plication has been reached. After collecting enough

entropy the collector mechanism is stopped and the

PRNG is seeded. An amount of 128 bits of entropy is

enough for initializing the PRNG.

Pseudo-random Values Generation. The PRNG

generates sequences of pseudo-random values suit-

able for cryptographic purposes. Our implementa-

tion is based on the Fortuna PRNG (Ferguson and

Schneier, 2003) and the random values are obtained

from an AES cipher in counter mode. The PRNG

output has been tested against statistical analysis tools

(see Section 5) to guarantee its robustness.

4.3 Vote Generator

The Javascript implementation of the voting client has

inﬂuenced the voting protocols because the computa-

tional efﬁciency is limited and the trust of the under-

lying platform cannot be guaranteed. An overview of

the main considerations is shown below.

Pre-computations. The idea behind this is to pre-

compute some cryptographic operations’ values while

the voter selects the voting options, so that when the

voter decides to cast the vote the number of remaining

computations is small and the time the voter has to

wait for the ballot to be cast is considerably shorter.

The amount of operations that can be pre-computed

can account up to 95% in certain voting protocols.

Cast as Intended Validation. Since the voter de-

vice cannot be trusted, e.g. it may be infected by

malware, some of the voting protocols implemented

provide validation mechanisms that allow the voter

to check the integrity of the vote cast. For exam-

ple, in the Norwegian project eValg2013 (Gjosteen,

2013) secret codes received via SMS allowed voters

to check that the votes cast contained the voting op-

tions they selected. In the Neuchâtel e-voting plat-

form (Galindo et al., 2015), the same approach was

followed with the difference that the codes were re-

turned by the same voting client. This option was pos-

sible in this case because multiple voting was not al-

lowed, thus the voting client could not learn the codes

and vote again with manipulated voting options.

Defense Against User Manipulation. Develop-

ment tools provided by browsers make the manipula-

tion of the code easier for a regular user than in other

languages. A non honest voter could take advan-

tage of this by manipulating the processes that happen

on her browser to disrupt the election. As a general

rule, it is recommended to make at server-side some

pre-processing over the data received from the voting

Transitioning to a Javascript Voting Client for Remote Online Voting

127

client prior to passing it to further layers of the pro-

tocol. In addition, voting protocols must be designed

to cope with these cases, e.g. including ZKPKs to be

veriﬁed at the voting server when the vote is received.

5 TEST OF THE PRNG

Since the PRNG is required to produce values with

strong randomness, we tested its output against a sta-

tistical analysis tool. The tests proved that the im-

plemented PRNG provides random values of the exp-

tected quality.

5.1 Testing Tool

Dieharder (Brown et al., 2009) was the tool selected

to perform the statistical analysis, a random number

generator testing suite, intended to test generators. It

includes tests from the original Diehard Battery of

Tests of Randomness (Marsaglia, 1996), as well as

tests from the Statistical Test Suite (STS) (Rukhin

et al., 2010) developed by the National Institute

for Standards and Technology (NIST) and tests de-

veloped by the author of the Dieharder test suite.

Dieharder is well known and highly reputed due to

the broad characteristics of random number genera-

tors that are evaluated in its tests.

5.2 Test-bed Setup

In order to test the PRNG, most of the tests available

in the Dieharder suite have been performed, except

those which need an overwhelming quantity of data

(more than 4GB).

Most of the discarded tests overlapped with other

tests, thus it was considered not to affect the quality

of the testing. Tests which supported different con-

ﬁgurations were performed using different input pa-

rameters, thus in total an amount of 78 statistical tests

were performed.

In order to have a reference of what should be

expected from the tests on the implemented Scytl

PRNG, two other PRNGs have also been evaluated

in the same way: a Flawed PRNG which is known

to generate sequences of correlated random numbers,

and the AES_OFB generator as the Gold Standard

PRNG, which is a commonly known good PRNG.

A set of datasets were generated for each of the

PRNGs to test (11 datasets for the Scytl PRNG, 5

datasets for the Gold Standard PRNG and 3 datasets

for the Flawed PRNG). Each dataset contained 256

million random unsigned 32-bit integers, which was

composed of 400 sets of 640.000 values that were

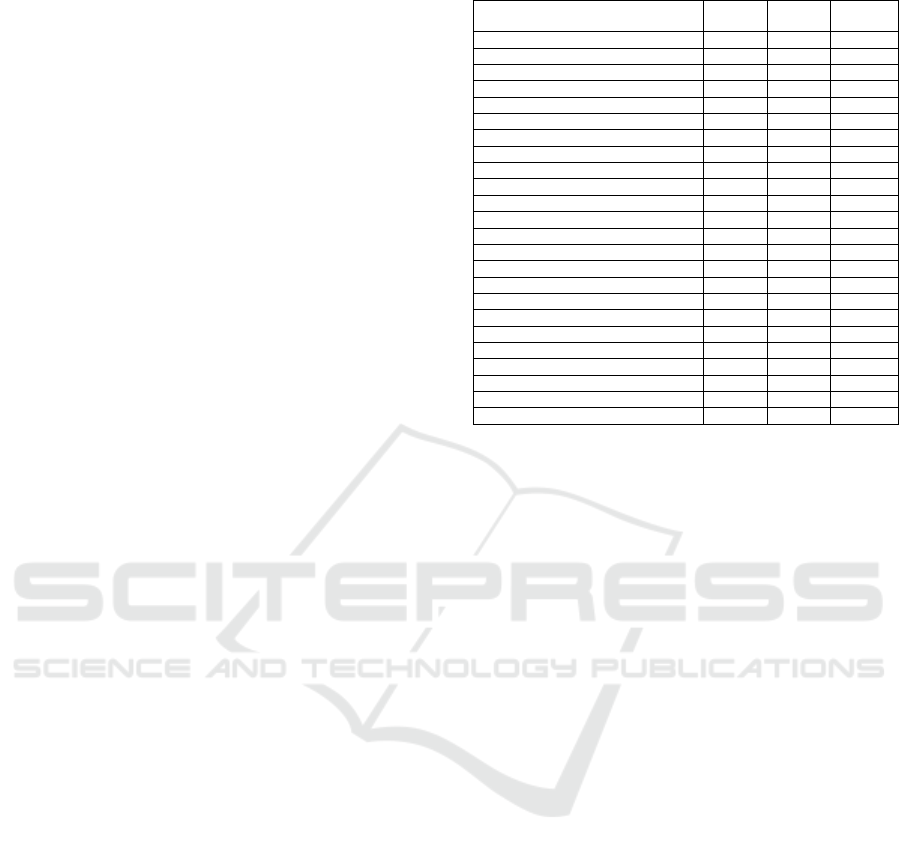
Table 2: Dieharder tests performed.

Dieharder tests performed

Gold

PRNG

Scytl

PRNG

Flawed

PRNG

Diehard Birthdays Test X X X

Diehard 32x32 Binary Rank Test X X X

Diehard 6x8 Binary Rank Test X X X

Diehard Bitstream Test X X X

Diehard OPSO X X X

Diehard OQSO Test X X X

Diehard DNA Test X X X

Diehard Count the 1s (stream) Test X X X

Diehard Count the 1s Test (byte) X X X

Diehard Parking Lot Test X X X

Diehard Min. Dist. (2d Circle) Test X X X

Diehard 3d Sphere (Min. Dist.) Test X X X

Diehard Squeeze Test X X X

Diehard Sums Test X X X

Diehard Runs Test X X X

Diehard Craps Test X X X

STS Monobit Test X X X

STS Runs Test X X X

STS Serial Test (Generalized) X X X

RGB Bit Distribution Test X X X

RGB Generalized Min. Dist. Test X X X

RGB Permutations Test X X X

RGB Lagged Sum Test X X X

RGB Kolmogorov-Smirnov Test Test X X X

generated with a different PRNG instance and seed.

These values composed the input of the Dieharder

test suite. Values generated with the PRNG initial-

ized with different seeds have been used in order to

test, not only that the values sequentially generated by

a PRNG instance have the expected properties (corre-

sponding to a sequence of random numbers), but also

to test that different instances of the PRNG (initial-

ized with different seeds) generate uncorrelated ran-

dom numbers.

5.3 Results

All the tests have been successfully passed by the im-

plemented Scytl PRNG, as well as by the Gold Stan-

dard PRNG (see Table 2). On the other hand, the

Flawed PRNG has failed most of the tests.

In order to determine the quality of a PRNG,

Dieharder tests the null hypothesis, which is that the

sequence of numbers generated by the random num-

ber generator under test is trully random. Dieharder

computes certain statistics over the random values

generated by the PRNG, which ultimately lead to the

p-value. This value denotes the probability that a true

random number generator would produce a sequence

of similar characteristics. That is, it summarizes the

evidence against the null hypothesis: if the p-value

is lower than a certain signiﬁcance level, the null hy-

pothesis is rejected and the PRNG under test is not

accepted as a good one. For other p-values, the null

hypothesis is not accepted, but it fails to be rejected

for this particular test. In fact, for good PRNGs, p-

values extracted from different rounds of each test are

SECRYPT 2016 - International Conference on Security and Cryptography

128

expected to be uniformly distributed. More informa-

tion about the null hypothesis and the p-values can be

found in (NIST, 2010) and the Dieharder manuals

More explicitly, in order to determine whether a

test succeeds or fails, Dieharder internally calculates a

set of p-values performing several executions of each

test with different data. If the p-values of a given test

are smaller than the signiﬁcance level (usually values

in the range of 0.1 to 0.001), then the test fails. In

addition, the set of p-values obtained are tested with

the Kolmogorov-Smirnov (KS) test to check the null

hypothesis is not rejected. The result of this check is

a number between 0 and 1.

Since several datasets were generated for each

PRNG, each Dieharder test was repeated a few times

for each PRNG. In order to test the different runs of

each test, we have treated the KS test values output

for each test as p-values. Then, we have set a sig-

niﬁcance level of 0.005 and we have considered the

test failed if any of the values were below this thresh-

old. Another issue to be considered is that these val-

ues are random variables and, as such, the same test

over different datasets should produce noticeably dif-

ferent values. This is why we compared the difference

between the maximum and minimum values, and con-

sidered the test failed if this difference was smaller

than 0.1. Both Scytl ’s and the Gold Standard PRNG

succeed with this test as well, in particular such differ-

ence was much bigger than 0.1 for all the tests. On the

other hand, the ﬂawed PRNG had many similar val-

ues, and as a consequence it failed most of the tests.

6 PERFORMANCE

A good performance of the voting client application is

important to guarantee a smooth user experience. The

next sections study the timing associated to the voting

client and its cryptographic operations.

6.1 Cryptographic Operations

A benchmarking application was developed to mea-

sure the speed of some cryptographic operations. The

benchmarks were performed on a PC with several op-

erating systems and browsers and on two smartphones

based on Android and iOS operating systems. The re-

sults obtained (see Table 3) are product of one exe-

cution of the benchmark application on each of the

systems detailed. The time shown for each opera-

tion is the average of 1000 executions for the SHA-

256, HMACwithSHA256 and AES-128 operations,

http://manpages.ubuntu.com/manpages/precise/man1/

dieharder.1.html

100 executions for the PBKDF2 operation, and 10 ex-

ecutions for the rest of operations respectively. Fur-

thermore, the PBKDF2 is setup with 1000 iterations

and computes a key of length 256 bits. ElGamal and

RSA algorithms are tested with 2048-bit keys.

Several conclusions can be extracted from the re-

sults. First, the performance is heavily inﬂuenced by

the type of device, i.e. regular PC or mobile device,

and browser. As expected, the regular PC performs

faster since it is more powerful than a mobile de-

vice. There is also a huge difference between different

browsers, e.g. Google Chrome and Firefox perform

certain operations more than 6 times faster than Inter-

net Explorer. The operating system does not have a

strong impact on the results, e.g. similar results are

obtained in Linux and Windows. Regarding the op-

eration types, hashing is much faster than asymmetric

encryption and decryption, as expected. The results

also show a 5-7 times speedup in the optimized El-

Gamal encryption based on short exponents (see Sec-

tion 4.1), reaching a speed closer to RSA.

6.2 Voting Client Application

The performance of the voting client may present a

high variability depending of:

• Voting Protocol: deﬁnes the cryptographic prim-

itives and communication handshakes performed

with the server.

• Election and Cryptographic Parameters: The

election parameters deﬁne the number of candi-

dates, parties and contests of an election, implying

different vote lengths and number of encryptions.

The cryptographic parameters deﬁne the length of

the keys and algorithms used, which inﬂuences

the timings of the cryptographic primitives.

• Browser: Certain browser Javascript engines are

much more efﬁcient than others executing the

cryptographic operations implemented.

• Device: Voter device’s processor and memory

considerably affect the performance.

The tests performed were focused on measuring

the user experience in different browsers and devices

for a given voting protocol and set of election param-

eters. The results reﬂect the time passed since the

voter requests the cast of the vote until the process

ﬁnishes. Pre-computed operations are not considered

since they are executed before the mentioned process.

6.2.1 Neuchâtel e-voting Protocol

The selected voting protocol is the one used in a re-

cent election in Neuchâtel e-voting platform (Galindo

Transitioning to a Javascript Voting Client for Remote Online Voting

129

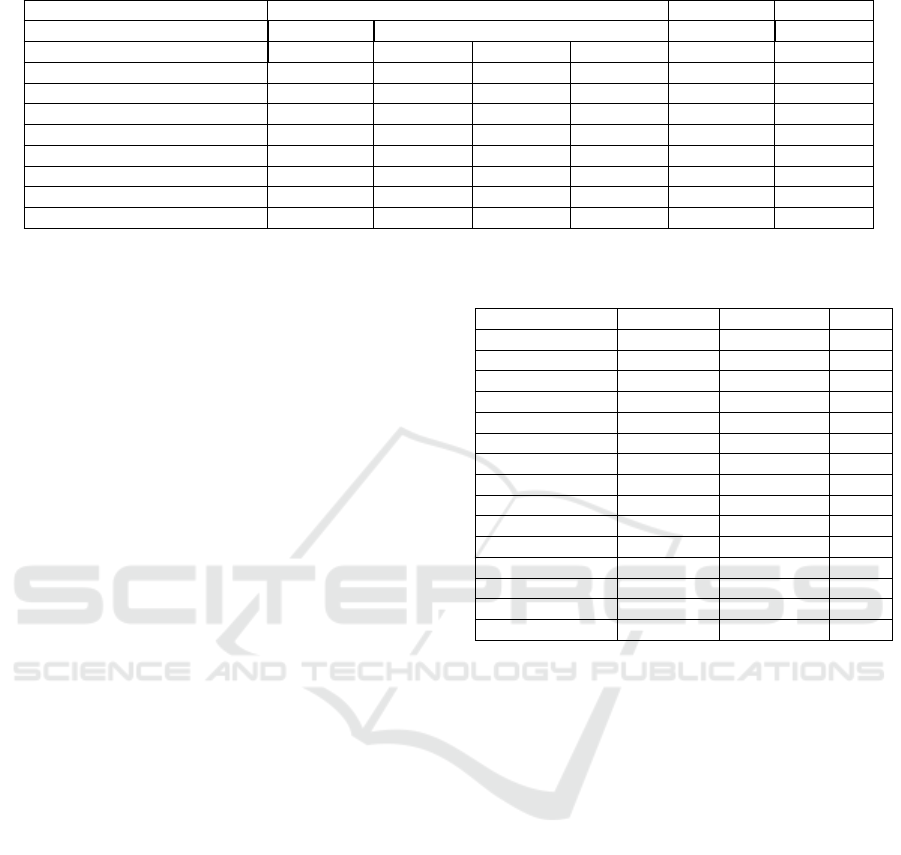
Table 3: Cryptographic operations performance (time in ms).

Device PC i5-2450M CPU 2,50GHz, 4GB RAM LG G2 iPhone 5s

OS Ubuntu 14.10 Windows 7 Android 4.4.2 iOS 8.2

Browser Chrome 42 Chrome 42 Firefox 37 IE 11 Chrome 42 Safari

SHA-256 0,053 0,042 0,051 0,040 0,114 0,127

HMACwithSHA256 0,065 0,041 0,040 0,042 0,150 0,204

Generate PBKDF2 with SHA256 9,480 9,510 12,780 23,880 31,620 4,541

AES-128 Enc / Dec 0,031 / 0,017 0,031 / 0,015 0,045 / 0,024 0,179 / 0,008 0,197 / 0,097 0,146 / 0,072

ElGamal Enc / Dec (Normal Exp) 343 / 180 354 / 183 285 / 154 1.888 / 940 1.002 / 500 1.505 / 790

ElGamal Enc / Dec (Short Exp) 48 / 29 49 / 29 47 / 23 252 / 139 160 / 105 213 / 134

Schnorr Proof Gen / Ver (Short Exp) 24 / 47 24 / 48 21 / 40 137 / 288 68 / 135 108 / 213

RSA Enc / Dec 2 / 48 2 / 48 2 / 45 8 / 259 7 / 156 8 / 213

et al., 2015) (March 2015). A test election was setup

where the voters had to vote for two contests. In the

ﬁrst contest the voter had to choose one party and 5

candidates, whereas in the second contest the voter

had to choose one party and 41 candidates. The oper-

ations computed by this voting protocol are summa-

rized here:

1. Encryption of the Selected Voting Options: the

voting options selected of both contests are mul-

tiplied together and the result is encrypted into

one ciphertext. The ciphertext is computed using

the ElGamal encryption algorithm, which requires

2 exponentiations which have been pre-computed

while the voter navigates through the application

(see Section 4.3).

2. Computation of Partial Return Codes: these

are codes used to provide cast as intended ver-

iﬁability (see Section 4.3). The computation of

partial return codes requires one exponentiation of

each voter selection to a voter-speciﬁc secret key,

which in the test election sums up to 47 exponen-

tiations. Every time the voter selects an option,

the corresponding partial return code is computed.

Therefore, these operations are already done when

the voter pulses the send button. Thus this time is

not included in the presented test results.

3. Encryption of Partial Return Codes: the par-

tial return codes are encrypted using the ElGamal

encryption algorithm, under the public key of the

server, in order to protect their privacy during their

transmission from the voting client to the server.

The variant with multiple key encryption, as de-

scribed in Section 4.1.1, is used. The required ex-

ponentiations, which sum up to 47, are also pre-

computed while the voter navigates through the

application.

4. Generation of Cryptographic Proofs (ZKPKs):

two ZKPKs are computed. The ﬁrst, based on the

Schnorr (Schnorr, 1991) identiﬁcation protocol,

proves the encrypted ballot is well-formed. The

second, based on the Chaum-Pedersen (Chaum

Table 4: Vote casting performance in a HP Intel Core i5-

3470 3.2 GHz PC, with Windows 7 Professional OS.

Device OS Browser Time

PC Windows 7 IE10 22 sec

PC Windows 7 IE11 5 sec

PC Windows 7 Firefox 35 5 sec

PC Windows 7 G. Chrome 39 5.5 sec

PC Ubuntu Firefox 35 5 sec

PC Ubuntu G. Chrome 39 6 sec

Mac Mac OS 10.8 Firefox 35 5.5 sec

Mac Mac OS 10.8 G. Chrome 39 5.5 sec

Mac Mac OS 10.8 Safari 6 sec

HTC Desire 610 Android 4.4 G. Chrome 39 43 sec

Nokia Lumia 730 W. Phone 8.1 IE Mobile 11.0 29 sec

iPhone 5C iOS 8.1.2 Safari 8.0 18 sec

S. Galaxy Tab3 Android 4.2.2 G. Chrome 39 23 sec

Enc. M. WT7-C-100 Windows 8.1 IE 11 14 sec

iPad Air iOS 8.1.2 Safari 7.0 11 sec

and Pedersen, 1992) protocol, prove to the server

that the partial return codes match the voting op-

tions of the encrypted ballot. For the ﬁrst proof

1 exponentiation, which can be pre-computed, is

required. For the second proof, 7 exponentiations

are required, of which 5 can be pre-computed.

Thus, in total 8 exponentiations are computed dur-

ing the proof generation process, from which 6

can be pre-computed.

5. Signature of the Computed Values: all the com-

puted values are digitally signed using the RSA

digital signature algorithm.

The ElGamal encryption and the RSA signature

algorithms use 2048 bit keys. The approach described

in Section 4.1.2 for using short exponents (256-bit ex-

ponents instead of 2047-bit ones) in ElGamal is used

for the encryption of the voting options, for the en-

cryption of partial return codes, and for the Schnorr

and plaintext equality proofs.

6.2.2 Results Obtained

The results (see Table 4) are aligned with the ones

obtained for the cryptographic primitives, where the

SECRYPT 2016 - International Conference on Security and Cryptography

130

platforms chosen have a strong inﬂuence on them.

But what it is more relevant is that in most of the

tested devices the time needed for casting a vote is

always below 45 seconds, and usually much less,

clearly demonstrating the Javascript technology is ap-

propriate for implementing a voting client.

6.3 Performance Challenges

During the development, one of the ﬁrst points that

arose was that, the execution of cryptographic prim-

itives could be slow on certain browsers and/or plat-

forms. This generated two effects: a) the browser pre-

sented a pop-up indicating the script was not respond-

ing and b) the time to generate the encrypted ballot

was too long. Two solutions were applied to the ﬁrst

issue. The HTML5 Web Workers

were used if avail-

able. This prevented the script from blocking the view

of the page and no pop-up was presented to the user.

For browsers no compatible with this technology, the

solution implemented consisted of dividing the costly

operations in smaller operations, thus avoiding ex-

ceeding the timeout associated to the pop-up. For

the second issue, the overall time taken to generate

a ballot, the primitive optimizations described in Sec-

tion 4.1, i.e. ElGamal encryption with short expo-

nents and multiple keys, and the pre-computation of

part of the cryptographic operations described in Sec-

tion 4.3 were applied. A second point was related to

the generation of random numbers. The amount of

entropy we initially required to seed the PRNG was

128 bits. This is recommended, in order to ensure

that the random generation is strong enough (i.e. the

random values generated are unpredictable). Never-

theless, in order to prevent usability issues due to ex-

ceptional cases where the minimum entropy cannot

be reached, a minimum amount of entropy collection

was not enforced in production. Instead, the entropy

estimation mechanism was used only during develop-

ment time to perform tests that ensured a minimum

level of entropy was reached before the ﬁrst random

values were requested.

7 CONCLUSIONS

In this paper we have described our experience and

lessons learnt on implementing a Javascript voting

client in an industrial environment, focusing on the

main challenges encountered, implementation details

and performance results obtained.

https://developer.mozilla.org/en-US/docs/Web/API/

Web_Workers_API/Using_web_workers

In comparison to Java implementations, the over-

all security of Javascript voting clients is similar,

whereas the user experience and interoperability is

largely better since these clients are much lighter and

multi-platform than the Java ones. A browser with

Javascript support is the only usage requirement. The

fact that there is no dependency with the Java Run-

time Environment (JRE) has extensively reduced the

usability and interoperability problems, as well as the

exposure to critical security bugs, associated to the

former Java implementations. Regarding the security,

the only disadvantage is the Javascript implementa-

tion lacks the support for signing the code. However,

additional security measures mitigate this issue, e.g.

remote code integrity validation services and use of

veriﬁable voting protocols allowing the voter to verify

the vote cast with independence of the voting client

logics. In addition, we also reported on the usage of

the client in real elections, with a positive outcome.

Further work is being peformed to deal with the

Javascript weaknesses, mostly the lack of code signed

support. On the one hand, an intelligent application

for remote code integrity validation service is being

implemented. This application issues requests, which

should not distinguishable from regular requests is-

sued by real voters, to retrieve and validate the code

served. On the other hand, the development of spe-

ciﬁc voting client apps for the most popular mobile

platforms is studied, since these provide code in-

tegrity mechanisms for their applications.

REFERENCES

Adida, B. (2008). Helios: Web-based open-audit voting. In

van Oorschot, P. C., editor, USENIX Security Sympo-

sium, pages 335–348. USENIX Association.

Bellare, M. and Rogaway, P. (1993). Random oracles are

practical: A paradigm for designing efﬁcient proto-

cols. In Proceedings of the 1st ACM Conference on

Computer and Communications Security, CCS ’93,

pages 62–73, New York, NY, USA. ACM.

Brown, R. G., Eddelbuettel, D., and Bauer, D. (2009).

Dieharder: A random number test suite. Duke Uni-

versity Physics Department.

Chaum, D. and Pedersen, T. P. (1992). Wallet databases

with observers. In Brickell, E. F., editor, Advances

in Cryptology - CRYPTO ’92, 12th Annual Interna-

tional Cryptology Conference, Santa Barbara, Cali-

fornia, USA, August 16-20, 1992, Proceedings, vol-

ume 740 of Lecture Notes in Computer Science, pages

89–105. Springer.

Cortier, V. and Smyth, B. (2011). Attacking and ﬁxing He-

lios: An analysis of ballot secrecy. In Proceedings of

the 24th IEEE Computer Security Foundations Sym-

posium, CSF 2011, pages 297–311. IEEE Computer

Society.

Transitioning to a Javascript Voting Client for Remote Online Voting

131

Damgaard, I. (2010). On σ-protocols. Cryptologic Protocol

Theory, CPT 2010, v.2.

ECMAScript (2011). ECMAScript



Language Speciﬁca-

tion 5.1 Edition.

Ferguson, N. and Schneier, B. (2003). Practical Cryptogra-

phy. John Wiley & Sons, Inc., New York, NY, USA,

1 edition.

Galindo, D., Guasch, S., and Puiggalí, J. (2015). 2015

Neuchâtel’s cast-as-intended veriﬁcation mechanism.

In Haenni, R., Koenig, R. E., and Wikstro

m, D., ed-

itors, E-Voting and Identity, volume 9269 of Lecture

Notes in Computer Science, pages 3–18. Springer In-

ternational Publishing.

Gennaro, R. (2005). An improved pseudo-random genera-

tor based on the discrete logarithm problem. J. Cryp-

tology, 18(2):91–110.

Gharadaghy, R. and Volkamer, M. (2010). Veriﬁability

in electronic voting - explanations for non security

experts. In Krimmer, R. and Grimm, R., editors,

Electronic Voting 2010, EVOTE 2010, 4th Interna-

tional Conference, Co-organized by Council of Eu-

rope, Gesellschaft für Informatik and E-Voting.CC,

July 21st - 24th, 2010, in Castle Hofen, Bregenz, Aus-

tria, volume 167 of LNI, pages 151–162. GI.

Gjosteen, K. (2013). The norwegian internet voting proto-

col. ePrint. eprint.iacr.org/2013/473.pdf.

Halderman, J. A. and Teague, V. (2015). The new south

wales ivote system: Security failures and veriﬁcation

ﬂaws in a live online election. In Haenni, R., Koenig,

E. R., and Wikström, D., editors, E-Voting and Iden-

tity: 5th International Conference, VoteID 2015, Bern,

Switzerland, September 2-4, 2015 Proceedings, pages

35–53. Springer International Publishing.

Juels, A., Catalano, D., and Jakobsson, M. (2010).

Coercion-resistant electronic elections. In Chaum, D.,

Jakobsson, M., Rivest, R. L., Ryan, P. Y. A., Benaloh,

J., Kutylowski, M., and Adida, B., editors, Towards

Trustworthy Elections, New Directions in Electronic

Voting, volume 6000 of Lecture Notes in Computer

Science, pages 37–63. Springer.

Karapanos, N., Filios, A., Popa, R. A., and Capkun, S.

(2016). Verena: End-to-end integrity protection for

web applications. In 2016 IEEE Symposium on Secu-

rity and Privacy (to appear), pages 895–913.

Klein, A. (2008). Temporary user tracking in major

browsers and Cross-domain information leakage and

attacks. September-November, 2008, Trusteer.

Koshiba, T. and Kurosawa, K. (2004). Short exponent

difﬁe-hellman problems. In Bao, F., Deng, R. H.,

and Zhou, J., editors, Public Key Cryptography - PKC

2004, 7th Int. Workshop on Theory and Practice in

Public Key Cryptography, volume 2947 of Lecture

Notes in Computer Science, pages 173–186. Springer.

Kurosawa, K. (2002). Multi-recipient public-key encryp-

tion with shortened ciphertext. In Naccache, D. and

Paillier, P., editors, Public Key Cryptography, 5th Int.

Workshop on Practice and Theory in Public Key Cryp-

tosystems, PKC 2002, volume 2274 of Lecture Notes

in Computer Science, pages 48–63. Springer.

Marsaglia, G. (1996). Diehard: a battery of tests of random-

ness.

Maurer, U. (2009). Unifying zero-knowledge proofs of

knowledge. In Preneel, B., editor, Progress in Cryp-

tology AFRICACRYPT 2009, volume 5580 of Lecture

Notes in Computer Science, pages 272–286. Springer

Berlin Heidelberg.

Menezes, A. J., Vanstone, S. A., and Oorschot, P. C. V.

(1996). Handbook of Applied Cryptography. CRC

Press, Inc., Boca Raton, FL, USA, 1st edition.

NIST (2001). Federal Information Processing Standard

(FIPS) 197, Advanced Encryption Standard (AES).

Technical report, U.S. Department Of Commerce.

NIST (2010). A Statistical Test Suite for the Validation

of Random Number Generators and Pseudo Random

Number Generators for Cryptographic Applications,

NIST Special Publication 800-22rev1a. Technical re-

port, U.S. Department Of Commerce.

NIST (2012). Federal Information Processing Standard

(FIPS 180-4), Secure Hash Standard. Technical re-

port, U.S. Department Of Commerce.

NIST (2015). Federal Information Processing Standard

(FIPS) 202, SHA-3 Standard: Permutation-Based

Hash and Extendable-Output Functions. Technical re-

port, U.S. Department Of Commerce.

Puiggalí, J., Chóliz, J., and Guasch, S. Best practices in in-

ternet voting. In NIST: Workshop on UOCAVA Remote

Voting Systems. Washington DC, August 2010.

RFC-5280 (2008). Internet X.509 Public Key Infrastructure

Certiﬁcate and Certiﬁcate Revocation List Proﬁle.

RSA Laboratories. PKCS #12: Personal Information Ex-

change Syntax Standard.

RSA Laboratories. PKCS #5: Password-Based Cryptogra-

phy Standard.

Rukhin, A., Soto, J., Nechvatal, J., Barker, E., Leigh, S.,

Levenson, M., Banks, D., Heckert, A., Dray, J., Vo,

S., Rukhin, A., Soto, J., Smid, M., Leigh, S., Van-

gel, M., Heckert, A., Dray, J., and Iii, L. E. B. (2010).

NIST Special Publication 800-22 Rev 1a: Statistical

test suite for random and pseudorandom number gen-

erators for cryptographic applications.

Schnorr, C. P. (1991). Efﬁcient signature generation by

smart cards. J. Cryptol., 4(3):161–174.

Stark, E., Hamburg, M., and Boneh, D. (2009). Symmetric

cryptography in JavaScript. In ACSAC, pages 373–

381. IEEE Computer Society.

van Oorschot, P. C. and Wiener, M. J. (1996). On difﬁe-

hellman key agreement with short exponents. In Mau-

rer, U. M., editor, Advances in Cryptology - EURO-

CRYPT ’96, Int.l Conf. on the Theory and Application

of Cryptographic Techniques, volume 1070 of Lecture

Notes in Computer Science, pages 332–343. Springer.

W3C. W3C Subresource Integrity. W3C Candidate Rec-

ommendation, November, 2015.

W3C. Web Cryptography API. W3C Candidate Recom-

mendation, December, 2014.

SECRYPT 2016 - International Conference on Security and Cryptography

132