
Real-time Simulation of Distributed Control Systems: The example of
Functional Electrical Stimulation
Daniel Simon
1
and David Andreu
2
1
CAMIN team, INRIA, LIRMM Bat 5 CC05 017, 860 Rue Saint Priest, Montpellier Cedex 5, France
2
CAMIN team, Univ. Montpellier, LIRMM Bat 5 CC05 017, 860 Rue Saint Priest, Montpellier Cedex 5, France
Keywords:
Hybrid Simulation, Real-time Control, Control Architecture Validation.
Abstract:
The paper presents a real-time open software simulation framework, dedicated to the analysis of control sys-
tems deployed over distributed execution resources and wireless links. It is able to consistently simulate in
parallel the numerical devices (real-time tasks and communication links) and the evolution of the controlled
continuous time plant. It is applied to foresee future enhancements of a Functional Electrical Stimulation
(FES) system used in therapy for rehabilitation or substitution for disabled people. It is a distributed control
system using electrodes to interface a digital control system with livings. Hence the whole system gathers
continuous-time (muscles and nerves) and discrete-time (controllers and wireless links) components. During
the design process, realistic simulation remains a precious tool ahead of real experiments to check without dan-
ger that the implementation matches the functional and safety requirements. The simulation tool is especially
devoted to the joint design and analysis of control loops and real-time features.
1 FROM CONTROL DESIGN TO
REAL-TIME EXPERIMENTS
The design and validation of complex systems, like
cyber-physical systems which include both physical
and computational devices, is costly, time consum-
ing and needs knowledge and cooperation of different
disciplines (Ben Khaled-El Feki, 2014). For example,
medical robotics belong to such category and require
the coordinated design of both bio-mechanical, elec-
trical, and chemical models (from a physical point of
view) and many-sided controllers (from a computa-
tional point of view).
Simulations, handling both the components and
their interaction, are needed from the early stage
to speed-up the design, development and validation
phases, especially when real experiments are costly
or dangerous for human beings.
1.1 Simulation Needs
Understanding and modeling the influence of an im-
plementation (support system) on the QoC (Qual-
ity of control) is a challenging objective in con-
trol/computing co-design process. Real-time prop-
erties (task response times) and the network Qual-
ity of Service (QoS) influence the controlled system
properties and QoC. However real-life size problems,
involving non-linear systems and uncertain compo-
nents, still escape from a purely theoretic framework.
In this design process, simulation is an indisputable
step between concept design and prototype validation.
Models are needed to describe the mechatronic
continuous system, to compute the discrete time con-
trol laws and diagnosers, and to handle the network
behavior. As usual, choosing the right model results
of a trade-off between complexity and fidelity. Indeed
several models with different granularity are used dur-
ing the design and validation process, from fast proto-
typing until real-time simulation and implementation.
1.2 Numerical Simulation of Control
Process
The main purpose of the numerical simulation is to
approximate as faithfully as possible the behavior of
the complex dynamic system. In other words, bound-
ing the simulation errors is an important goal of nu-
merical simulations so that the designers can be con-
fident with the prediction.
A distinctive feature of real-time control systems
is that they are hybrid. Indeed, they gather compo-
nents with different time nature. Digital components,
Simon, D. and Andreu, D.
Real-time Simulation of Distributed Control Systems: The example of Functional Electrical Stimulation.
DOI: 10.5220/0005967804550462
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 455-462
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
455
such as CPUs and networks, run over discrete time
scale while handling real-time tasks and communica-
tion packets. Digital components can be easily exe-
cuted on the CPUs, using the multitasking capabili-
ties of the simulation cores to simulate the concurrent
nature of the distributed control system.
On the other hand, the physical components of
the control system – such as actuators, sensors and
mechatronic parts – are continuous time components
which can be described by some kind of non-linear
differential equations. As real system are too complex
to lead to explicit solutions of their dynamic behavior,
they must be integrated on computers using a numeri-
cal solver. Numerical integration is still an active field
in numerical analysis, and provides many effective
numerical solvers and associated software suites, able
to solve the continuous models either using time dis-
cretization or state quantization (Ben Khaled-El Feki,
2014).
Finally, all the components of the simulated sys-
tem must be carefully interconnected, and their time
scales must be meshed to provide consistent simula-
tion results over the different time representations and
scales. Both modeling and numerical integration deal
with approximations, hence it is first needed to find
a satisfactory trade-off between the simulation speed
and precision.
Real-time simulation needs to consider two time
scales:
• Real-time: it is the time reference of the real physical
system that is modeled and simulated, e.g. as mea-
sured by an absolute wall clock;
• Simulated time: it is the time elapsed during the exe-
cution of the simulation that can be measured by the
numerical integrator clock (i.e., by the accumulation
of integration steps).
To be consistent, the simulated time and real-time
must be carefully meshed to meet at some precise
points (Ben Khaled-El Feki, 2014).
Several simulation steps of growing accuracy and
fidelity to the real implementation can be processed,
from basic functional investigation in continuous time
until hardware-in-the-loop setups including parts of
the final components, just prior to real tests.
Model-in-the-loop. A first step is the choice of a
control structure, based on a model of the plant and
on the control objective. The control toolbox now
contains many tools to state and solve a large vari-
ety of control problems applied to various plants. Be-
sides control theory, preliminary design and tests of-
ten rely on simulation tools such as Scilab/Scicos or
Matlab/Simulink.
Software-in-the-loop. As for MIL, the SIL phase
considers only simulated (i.e. software) elements,
but it takes into account the actual production code,
including implementation related constraints such as
fixed-point computations and memory size limits.
Hardware-in-the-loop. After validating the soft-
ware in a real-time SIL simulation, the production
hardware can be checked in a real-time Hardware-
In-the-Loop (HIL) simulation. A HIL simulation is
made of mixed simulated and real components, which
means that some real components –usually the phys-
ical control target– are replaced by their software
avatar.
The next sections are devoted to the development
of a simulation framework dedicated to the case of a
distributed electrical functional electrical system.
2 THE FES FRAMEWORK
Functional electrical stimulation (FES) is one of ex-
isting rehabilitation techniques to restore lost motor
functions for motor-impaired people. For example, in
case of spinal cord injuries, the natural pathways be-
tween the central nervous system (CNS) and periph-
eral nerves are open under the lesion level. Therefore
such lesions forbid both the activation of movements
through motor nerves and the collection of sensory
information by the CNS.
In FES systems, electrodes are connected to
nerves or muscles and generate electrical pulses to in-
duce contractions of muscles. Similar electrodes can
be used to collect activity signals from muscles (Elec-
troMyoGrams EMG) or from nerves (ElectroNeuro-
Grams ENG). FES is primarily used for rehabilitation
of functions for people with disabilities. Until now
FES is mainly used in open-loop mode, where the
therapist selects predefined currents patterns (e.g., fre-
quency, intensity) according to the desired effect on
the patient. It is argued, e.g. (Zhang et al., 2013), that
closed-loop FES is necessary to safely control and co-
ordinate the numerous electrodes and muscles needed
to generate complex movements such as walking.
Sensors 1
st
ctrl Sensors 2
nd
ctrl
Actuators Ctrl 1 Actuators Ctrl 2
Ctrl law 1
POD
EMG
POD
STIM
Set-point
Controller
Ctrl law 2
Set-point
POD
EMG
POD
EMG
POD
STIM
Shared
sensors
Mutual exclusion
between
Controllers
Figure 1: Feedback FES.
In that case (Figure 1), the stimulation controller
is fed back by various sensors, such as limbs joints
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
456

angles, IMUs providing accelerations, EMG sig-
nals. . . These signals are used by feedback controllers
to accurately control the artificially actuated limbs.
Indeed it is well known that feedback control pro-
vides adaptability w.r.t. varying operation conditions
and robustness w.r.t. the uncertainties spoiling the
control loops components.
Compared with mechanical devices, the large un-
certainties and variability of livings make them espe-
cially difficult to be accurately modeled and safely
controlled. Conversely, considering humans in the
loop, the safety of the technology must be validated,
e.g. formally assessed, to allow for its certification
and usage in everyday life on a large scale.
2.1 The Phenix Liberty FES System
The Phenix Liberty FES system has been developed
along a partnership between the Demar research team
and the Vivaltis company
1
. It is devoted to external
stimulation, i.e. the electrodes are glued on the skin,
facing the target muscle or nerve. Compared with
its competitors, a distinctive feature of the system is
its wireless implementation. Considering the multi-
ple sensors and actuators needed to control complex
motion, distributed systems over wireless links com-
ply with mobility constraints, leading to acceptance
from the human users. The marketed system executes
a preset stimulation sequence in open-loop. Although
it is fluently used to correct, e.g., foot drop, finite-
state controllers typically are not adequate to adapt
stimulation patterns for frequent changes of walking
speed. FES also fastly involves muscular fatique,
thus needed an on-line detection and adaptation of the
stimulation profiles. Current research aims to design
and implement closed-loop FES using this system.
PC
Control device
Stimulation unit
Electrode
Micro sensor
Acquisition unit
Figure 2: The Phenix FES system.
The main components are:
• A main PC is used as a end-users (i.e. a therapist)
interface, to select the stimulation pattern out of a li-
brary of pre-defined profiles, and to provide the gate-
way with the controller using an USB link;
• The control device manages the communications with
the distributed stimulation units through the wireless
1
http://www.vivaltis.com/
network running the protocol stack. For future feed-
back controlled stimulation it will also run the real-
time control loops. The controller board is equipped
with a Freescale MC1322X micro-controller and an
integrated IEEE802.15.4 2.4 GHz Radio Frequency
(RF) emitting/receiving chip.
There are several kind of distributed units (DSUs, also
named PODs) :
• The ”Stim/Bio” DSUs allows for both the stimula-
tion of muscles for movement generation and for the
acquisition of EMG signals for biofeedback purpose.
They are made of two electronic boards :
– A generic board embeds the housekeeping hardware
and software to provide the electrical supply (bat-
tery), switches and LEDs, and a physical network
transceiver. The protocol stack and the requests (stim-
ulation and acquisition) processing are handled by a
Freescale MC1322X micro-controller.
– A daughter board executes the stimulation patterns or
the acquisition requests through two input/output ana-
logue channels.
• The ”universal” DSUs use the same generic board, but
embeds in its daughter board specific sensors. For ex-
ample, IMUs or goniometers are planned to be em-
bedded in a near future.
The communication architecture uses a specifi-
cally designed 3-layer protocol stack, compliant with
the reduced OSI model. These layers are the Applica-
tion layer, the MAC layer and the Physical layer. The
physical layer manages the wireless medium. The
MAC layer ensures a deterministic medium sharing,
so that only one unit can speak at a time (no colli-
sion), to provide known and bounded response times.
It allows for either a single (unicast) or a group of tar-
get DSUs (multicast) by using an individual or group
identifier (Godary-Dejean et al., 2011).
These various tasks run on the µcontrollers under
control of a CMX real-time multi-tasking executive.
3 SIMULATION SETUP
The long term objective is the safe and efficient im-
plementation of motion control using FES feedback
loops. As the analysis of such complex hybrid system
is out of scope of pure theoretic analysis, we need a
software tool to help for the design, sizing, analysis
and tuning of the components and of their interaction,
w.r.t. specified performance and safety levels.
More precisely, we need that the system uses an
open source framework and run in real-time on stock
Real-time Simulation of Distributed Control Systems: The example of Functional Electrical Stimulation
457
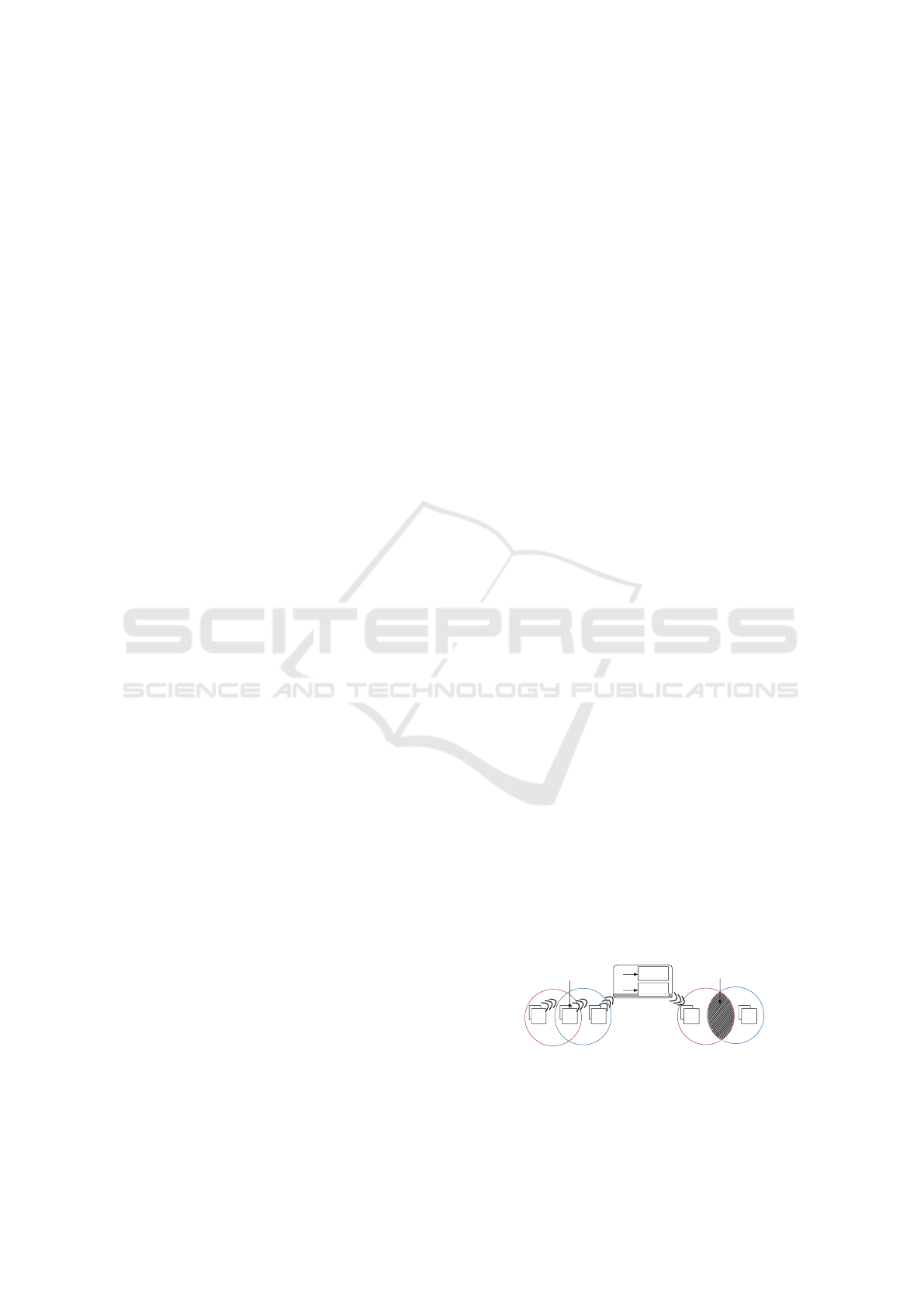
Medium Process
Controler Process
POD Process
Acquisition DSU
threads
Stimulation DSU
threads
Spy
C−>P
P−>C
Patient
model
thread
UDP sockets
Unix process
Posix thread
Sensor
processing
Comm.
manager
functions
FES
protocol stack
MAC layer
Motion
sensing
Biomechanical models
Muscles
Joints
kinematics
Comm.
manager
Stimulation
processing
FES
functions
Probes
MAC layer
protocol stack
control
FES
laws
Messages
scheduler
Task
scheduler
Scheduling
controler
Control
supervision
Disturbances
medium
medium
model
model
protocol stack
MAC layer
Communication
Communication
Numerical integrator
Stimulation
Currents
Figure 3: Simulation architecture.
PCs. It must easily evolve from functional simula-
tion to HIL to cover the different phases of software
development. Hence, according to the design cur-
rent phase, some simulated components might use
quite simple models while others should be more de-
tailed. For example, a preliminary analysis of the con-
trol loops sampling rate do not need a very detailed
physical model of the communication medium (which
could be added later on for refined tuning).
3.1 Simulation Architecture
Processes and Threads. Based on previous expe-
rience the simulation software is designed as a set
of Unix processes and Posix threads running under
Linux on stock multi-core PCs. The first version of
the simulator is a pure software which does not inte-
grate any piece of real hardware, and calculations are
performed with the usual floating point capabilities of
the PC.
However, to mimic the real distributed architec-
ture, it is split in 3 processes so that it can be run on
a multi-core PC (see Figure 3), for example one core
simulates the controller and each DSU is simulated on
another core :
• the ”Controller” process executes the FES controllers
running on the control chip under supervision of
a multitasks O.S.; it also simulates the network
transceiver through a simplified model of the commu-
nication stack;
• the ”Medium” process is used to simulate the physical
features of the wireless link;
• the ”DSU” process handles models of the Stim and
Acquisition DSU fonctions in dedicated threads. It
also handles the computation thread running the nu-
merical integrator.
Using the (non portable)
pthread attr setaffinity np CPU allocation state-
ment, each of these process can be run on a different
core. In the future these processes might be easily
allocated on different chips connected by the real
transceivers to enhance the simulation framework
towards an HIL simulation.
Communication and Synchronization. A simpli-
fied version of the communication protocol stack is
implemented in dedicated communication threads.
The data exchanged between the controller and the
DSUs are encapsulated in packets whose structure is
similar to those handled by the real network. In the
simulation, the packets are handled in two steps by
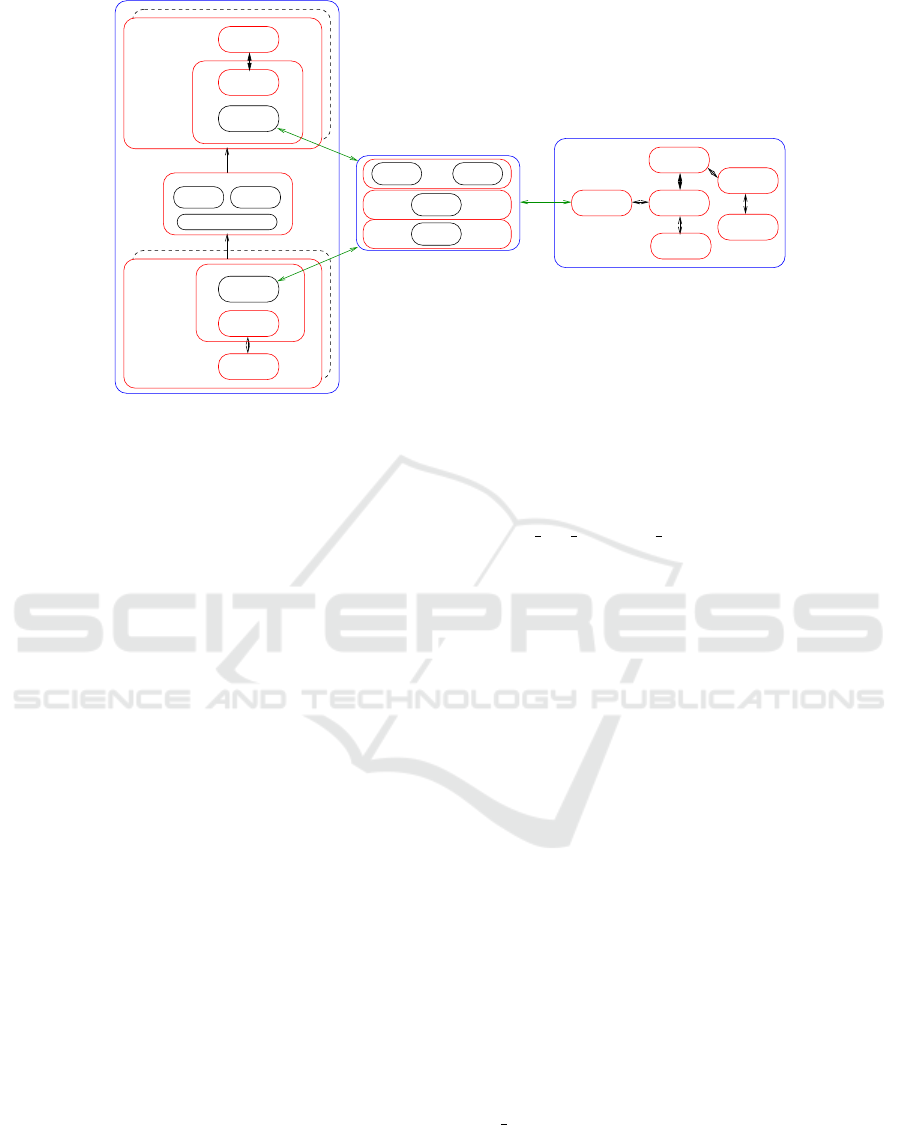
UDP Unix sockets (Figure 4):
• the packet is first transmitted using a point-to-point
UDP socket from the communication manager of the
controller (or of the Pod) to the medium process re-
ceiving thread;
• in the current version, the model of the medium just
add a constant delay to the packet transmission, and
data loss are handled by a simple random process.
• after being delayed, the packet is sent to all re-
ceivers using a diffusion UDP socket (using the
”so broadcast” parameter of UDP sockets). This fea-
ture allows for sending data with a unique time stamp
to groups of Pods.
Timing Values. All threads in the simulation can be
unlocked either by signals from clocks (e.g. for pe-
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
458
broadcast socket
point−to−point
DSU
Stimulation
DSU
Acquisition
Medium Control Device
sockets
Figure 4: Communication sockets.
riodic control tasks), by blocking waiting messages
on an incoming socket or by semaphores signaled by
communication requests sent by another thread. The
threads are scheduled by the Linux kernel, set with the
RT FIFO real-time mode, according to their priorities
and locks. However stock Linux kernels sometimes
provides inconsistent behaviors, although the simula-
tion works coherently with kernel compiled with real-
time options, i.e. with high resolution timers and low
latency preemption model under superuser privilege.
The transmission delays on the wireless links are
simulated by pure delays in the medium component.
Probes using functions of the Posix real-time library
can be inserted anywhere in the threads to measure,
e.g., communication delays between two tags or to
record missed deadlines.
Solver Triggering. The numerical integration
thread is a special case. Indeed this thread is not
the ghost of a real time task existing in the real
implementation.
In real life the state of the physical process nat-
urally evolves in parallel with the numerical execu-
tion of the control and communication systems. The
time scales of the continuous and numerical entities
are meshed at some meeting instants at the occurence
of different kind of events :
• when a control system requests an updated sensor
value;
• when a control system sends a new control value;
• when the simulation system needs a snapshot of the
controlled process and of its environment;
• when the continuous process raises an event (e.g., via
an asynchronous sensor or crossing a model disconti-
nuity).
The integration thread is triggered by any of these
events. At each triggering event the integrator is first
run from the last interruption until the current time
to update the state of the continuous process, then it
delivers the new state or accept new control inputs.
In practice, for the current set-up the simulation
runs very comfortably faster than real-time on a mod-
ern laptop (e.g., 100 times faster on a i7 CPU). Com-
putation times and overruns can be easily checked by
software probes and reported to provide information
and warnings about the timing behavior and quality
of the simulation.
Note that, if the numerical integration cost be-
comes prohibitive to run the simulation on a single
CPU w.r.t. real-time, the model can be split over
several CPUs. Slackened synchronization between
decoupled sub-models allows for significant speed-
ups while keeping the integration errors under control
(Ben Khaled-El Feki, 2014).
3.2 Continuous Plant and Numerical
Integration
Continuous Model. The model of the continuous
plant is usually given as a set of ordinary differ-
ential equations (ODEs), differential algebraic equa-
tions (DAEs) or partial derivative equations (PDEs),
where the continuous (physical) time is an indepen-
dent variable.
Building high fidelity system-level models of
complex systems, like mechatronic systems and even
more systems involving livings, is a challenging duty.
One problem is the diversity of modeling and simula-
tion environments used by the various involved multi-
disciplinary teams. Particular environments are pre-
ferred for a specific use due to distinctive strengths
(modeling language, libraries, solvers, cost, etc.), for
example the automatic derivation of the kinematic and
dynamic equations of a multi-body system can be a
distinctive feature.
Perfect modeling must be forgot. A model is al-
ways an approximation of reality, both in its structure
and in its parameters values. A problem for simula-
tion, due to both model complexity and fast system
dynamics, is the prohibitive CPU times which can be
observed when high-fidelity models are run, therefore
preventing any real-time simulation. It is needed to
find a satisfactory trade-off between the simulation
speed and precision. A good model captures the es-
sential behavior of the physical plant. Therefore, ac-
cording to its user and objectives (e.g. an control sci-
entist dealing with gains tuning, or a therapist willing
to choose the stimulation frequency), different models
of a given physical plant can be chosen.
Building a high-fidelity model needs precise
knowledge about the plant itself, here coming from
bio-mechanics and neuroscience. The simulation
setup has been tested using the model of a human knee
controlled by electrostimulation, a topic for which
the Demar team developed a strong experience over
years. The main structure and parameters of the
Real-time Simulation of Distributed Control Systems: The example of Functional Electrical Stimulation
459

model were mainly taken from (Benoussaad, 2009)
for artificially excited muscles and from (McFaull and
Lamontagne, 1998) for the joint non-linear parame-
ters.
Figure 5: Simplified knee kinematics.
It is given as a small set of non-linear ODEs. A
contractile element (CE) dynamics is given by (Be-
noussaad, 2009) :
˙
K
c
= −K
c
|u| + αK
cm
Fl
c
(ε
c
)|u|
+
− K
c
|
˙
ε
c
| (1)
˙
F
c
= −F
c
|u| + αF
cm
Fl
c
(ε
c
)|u|
+
− F
c
|
˙
ε
c
| + L
c0
K
c
˙
ε
c
where K
c
and F
c
are the stiffness and force devel-
oped by the CE, K
cm
and F
cm
their maximum values,
u and |u|
+
chemical control variables coming from an
activation model, Fl
c
(ε
c
) the force/length relation of
the CE, α the recruitment rate, and
˙
ε
c
the contraction
speed of the CE.
The numerical integration of the later variable,
given by
˙
ε
c
=
k
s
L
0
˙
ε + F
c
|u| − αF
cm
Fl
c
(ε
c
)|u|
+
k
s
L
c0
+ K
c
L
c0
− s
v
F
c
(2)
needs a special attention as it involves the sign func-
tion :
s
v
= sign(k
s
L
0
˙
ε + F
c
|u| − αF
cm
Fl
c
(ε
c
)|u|
+
) (3)
Correctly handling this non-linearity needs an inte-
grator enabled with a root-finding capability to pro-
vide a fast and stable integration (see next section).
The two muscles involved in the knee flex-
ion/extension, i.e. the quadriceps and hamstring, have
similar models with different parameters and are ac-
tuated by their own electrode. For our purpose, the
knee joint is considered to be a perfect cylindrical
d.o.f. leading the usual equation of motion (Figure
5
¨
Θ =
1
J
(F
2
r
2
− F
1
r
1
− MgL
og
sin(Θ − Θ
0
) − B
˙
Θ + T
e
)
(4)
where F
i
is the force induced by muscle i, B a non-
linear damping and T
e
a passive elasticity torque.
Finally the model is encoded for integration as a
set of 8 first order non-linear ODEs, three for each
muscle and two for the joint dynamics.
Numerical Integration. The non-linear model of
a robot (or of most mechatronic systems involv-
ing mechanical and electrical components) is usu-
ally described by a set of ordinary differential equa-
tions (ODEs) (or sometimes by a set of differential-
algebraic equations (DAEs)) (Arnold et al., 2011).
There already exist a broad family of algorithms
and corresponding software used to numerically solve
such a set of ODEs.
With most existing integration packages, the end-
user’s choices can be :
• set the value of a fixed-step integrator, leading to a
predictable number of steps and computing time, but
the precision cannot be controlled and may lead to
false results;
• specify the precision of the integration and delegate
the adaptive step management to the integrator, but in
that case the computing time cannot be predicted.
With an adaptive step integration method the con-
trolled variable is the precision (or more exactly the
estimate of the integration error). The open-source
LSODAR package we have elected (Hindmarsh and
Petzold, 1995) for this experiment uses a variable
step, variable number of steps integration algorithm.
It is suitable for both stiff and non-stiff systems,
and automatically selects between non-stiff and stiff
methods.
It is associated with a root-finding stopping cri-
teria : when it detects a sign change in a particular
function of the states (root detection), it runs a root-
finding algorithm to find the exact time point at which
the sign change occurred. The later feature is essential
to correctly integrate continuous plants with disconti-
nuities, i.e. where the values of some states or pa-
rameters, or even the model structure itself, suddenly
change where a given threshold is crossed (zero-
crossing). It is for example the case for models of
impacts, dry friction, and here for muscles contrac-
tion (due to eq. (3)).
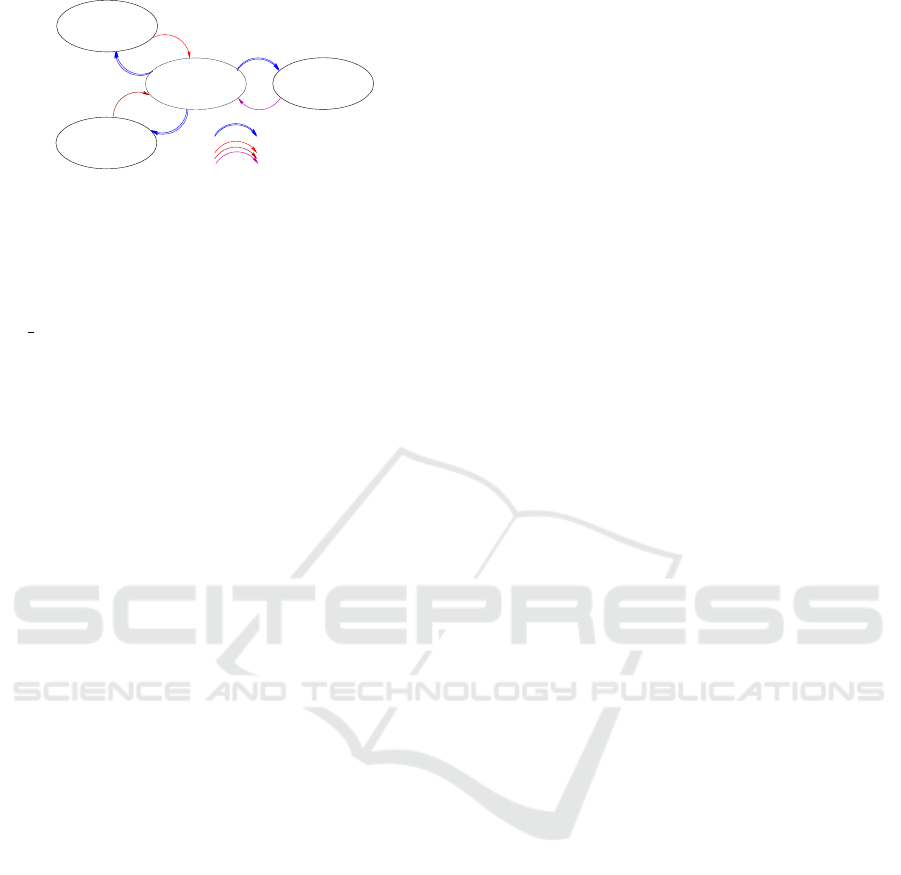
3.3 Control Design
To generate movement for a joint, two muscles (an ag-
onist and antagonist pair) must be stimulated. For the
knee these two muscles are the quadriceps on the an-
terior face (extension actuator) and the hamstring on
the posterior face (flexion actuator). In a first simple
control approach, the two muscles will be actuated in
mutual exclusion according to the flexion and exten-
sion phases of the movements, see Figure 6.
As usual, the first control algorithm to be consid-
ered is a PID, a simple controller able to control many
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
460

Angle desiré
PID
-1
Sat
Sat
Muscle agoniste
—————————
Muscle antagoniste
Capteur
Goniometre
-
+
Angle
U1
U2
Figure 6: Control scheme.
single input/single output (SISO) systems through a
very simple modeling and tuning effort.
Here it is discretized using a backward difference
method (with T
s
the sampling period), yielding
u
k
= u
k−1
+ K[e
k
− e
k−1
] +
K · T
s
T
i
e
k
+
K · T
d
T
s
[e
k
− 2e
k−1
+ e
k−2
] (5)
4 PRELIMINARY EXPERIMENTS
In this preliminary version, the simulation system is a
”Model-in-the-loop” simulation, where all the objects
are modeled, the physical plant state is evaluated by
a numerical integrator and the control functions are
encoded in plain C and executed using the floating
point features of a modern laptop. Anyway, it goes
beyond usual simulations with Scicos or Simulink as
it handles quite precisely some implementation and
scheduling related features such as tasks and events
interleaving, or computation and communication in-
duces delays. Hence it can be already used to explore
the possible performance of FES feedback loops ac-
cording to various scheduling parameters.
4.1 PID Tuning and Sampling Rate
A simple PID controller has been setup for prelimi-
nary tests of the simulation platform. Indeed a PID
with fixed gains would perform uniformly for a linear
system, which is not the case for the knee joint, where
even a simplified model shows several sources of non-
linearities. Hence the PID has been empirically tuned
to provide acceptable responses for the whole reach-
able motion amplitude.
Initially simulations were made with a 40 msec
sampling rate, i.e. the one used by the marketed
version of the Phenix system. In fact, the end-to-
end communication time (including control tasks ex-
ecution and messages transmission and acknowledg-
ment) between the controller and the DSUs is lower
than 5 msecs (Figure 7b). Lowering the sampling
rate to 5 msecs shows an improved performance of
the joint controller (Figure 7a). Note that, as the net-
work model is included in the simulation, sampling
rates smaller than 5 msec induce data loss and poor
control performance. Hence the real-time simulator
allows for a fine tuning of control gains w.r.t the exe-
cution resources at hand, far beyond the usually rec-
Knee angle (rad)
Time (sec)
sampling 40 msec
sampling 5 msec
sampling 2 msec
Time (sec)
End−to−end communication time (msec)
Figure 7: a) Knee position – b) End-to-end delay.
ommended sampling rates between 3 and 10 times the
Shannon sampling rate.
4.2 Network Protocol Enhancements
The current communication threads do not implement
the production code of the full protocol stacks, but
only its main features. The simulated transceiver en-
capsulates data in frames according to the STIMAP
protocol (Godary-Dejean et al., 2011) used to con-
nect the controller and DSUs. The frames are further
sent/received over UDP sockets. Several versions of
the communication frames were tested, and their im-
pact on the feedback control performance and on the
communication load was evaluated (see Figure 8).
Single Receiver (Production Version) (in red). A
data frame issued by the controller contains the ad-
dress of a single receiving/answering DSU, and the
payload only contains the stimulation parameters for
this particular DSU (red plot, 6 ms average delay);
Single Receiver with Optimization (in green). The
optimization uses the mutual exclusion between the
agonist/antagonist muscle and send only frames to the
active muscle in the current motion phase. However
some safety messages are sent (at a slower rate com-
pared with control messages) to keep alive the DSU
of the passive muscle, leading to irregular timing pat-
terns (green plot, 75% of samples near 3 ms and 25%
of samples near 6 ms);
Multiple Receivers (in blue). Messages are ad-
dressed to a group of DSUs, with a payload made of
the concatenation of the individual stimulation param-
eters: the frame is longer than a single receiver frame
but shorter than the concatenation of the single re-
ceiver frames, thus saving communication bandwidth
(blue plot, 4.5 ms average delay);
The observation of the simulations traces show that
using optimized versions of the protocol may signif-
icantly save bandwidth and decrease the end-to-end
communication delay between sensing and actuation,
leading to improvements in the performance and ro-
bustness of the FES control law. Such results are use-
ful to motivate (even costly) modifications of the pro-
duction hardware and software.
Real-time Simulation of Distributed Control Systems: The example of Functional Electrical Stimulation
461
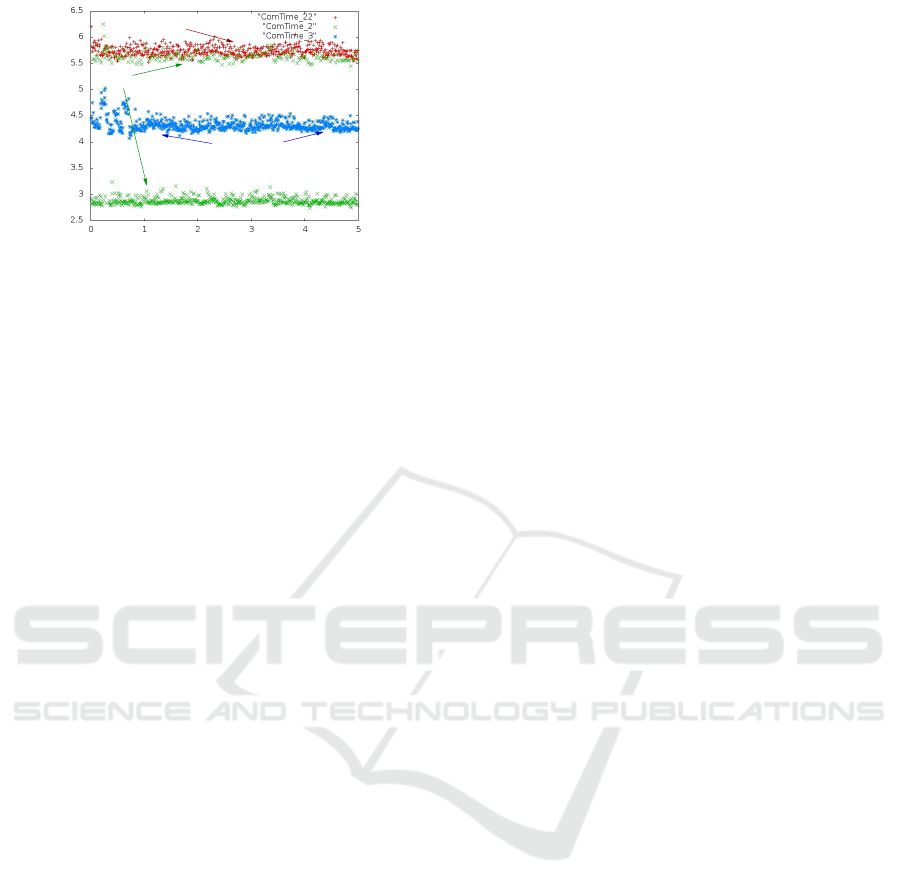
Time (sec)
End−to−end communication time {msec)
Multiple receivers
Single receiver
Single receiver, optimized
Figure 8: End-to-end communication time.
5 SUMMARY AND FUTURE
DEVELOPMENTS
Realistic simulations are effective tools to design and
tune complex systems whose analysis cannot be pro-
vided only by theory. Several simulation steps can be
explored, from simple functional analysis until HIL,
to design, test, tune and validate both the single com-
ponents of the system and their interactions in a dis-
tributed architecture. Simulations are precious, as
they allow for non-destructive trials, anticipation for
future technological development at lowered cost and
exploration of a system behavior until its limits with
no danger.
For the particular setup presented here, it is ex-
pected that such simulator will provide inputs in two
main directions. Firstly it allows for preliminary test-
ing new FES protocols prior to experiments with pa-
tients, and may help for writing the ethical protocols
needed for any experiments involving livings. Sec-
ondly it can be used for preliminary evaluation of new
technologies or implementations, without costly re-
working of existing electronic chips or certified com-
ponents.
The simulation software is open, so that enhance-
ments w.r.t. to the original release can be added upon
request of various designers and to fulfill various de-
sign objectives. For example, some future enhance-
ments may be :
• Development and test of feedback schedulers for au-
tomatic adaptation of the CPU and communication
loads in complex FES applications such as walking;
• Refinement of the physical communication medium
model, so that the wireless link fading due to of
obstacles can be evaluated, leading to the design
of a feedback control of the emission power of the
transceivers;
• Integration of others continuous plants. The dynamic
model of a human hand with 23 d.o.f. is currently
developed to provide a complex case for numerical
integration and control coordination;
• Progressive integration of the production code of
some components, e.g., the full protocol stack, and of
some real components, e.g., wireless transceivers be-
tween simulated nodes, to incrementally provide HIL
simulation setups.
As for any simulation, a crucial problem is the cal-
ibration of the models and the validation of the over-
all simulation system. This process needs, at some
points, comparisons with observations of real experi-
ments, which is costly but necessary. Anyway this is
needed to gain the confidence of the various users of
the system.
REFERENCES
Arnold, M., Burgermeister, B., F
¨
uhrer, C., Hippmann, G.,
and Rill, G. (2011). Numerical methods in vehicle
system dynamics: State of the art and current devel-
opments. Vehicle System Dynamics.
Ben Khaled-El Feki, A. (2014). Distributed real-
time simulation of numerical models: applica-
tion to powertrain. PhD thesis, EEATS, Au-
tomatique Productique, Universit
´
e de Grenoble.
http://www.theses.fr/2014GRENT033.
Benoussaad, M. (2009). Protocole d’identification sous
FES et synth
`
ese des s
´
equences de stimulation chez le
bless
´
e m
´
edullaire. PhD thesis, Univ. Montpellier II.
Godary-Dejean, K., Andreu, D., and Romain, R. (2011).
Temporal bounds verification of the STIMAP proto-
col. In RTNS 2011 : 19th International Conference
on Real-Time and Network Systems, page 10, Nantes,
France.
Hindmarsh, A. C. and Petzold, L. R. (1995). Algo-
rithms and software for Ordinary Differential Equa-
tions and Differential-Algebraic Equations, part II:
Higher-order methods and software packages. Com-
put. Phys., 9:148–155.
McFaull, S. R. and Lamontagne, M. (1998). In vivo
measurement of the passive viscoelastic properties of
the human knee joint. Human Movement Science,
17(2):139 – 165.
Zhang, Q., Hayashibe, M., and Azevedo Coste, C.
(2013). Evoked Electromyography-Based Closed-
Loop Torque Control in Functional Electrical Stimula-
tion. IEEE Transactions on Biomedical Engineering,
60(8):2299–2307.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
462
