
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators
based on Zynq MPSoC: A Chaotic Iterations Post Processing Case Study
Mohammed Bakiri
1,2
, Jean-Franc¸ois Couchot
1
and Christophe Guyeux
1
1
FEMTO-ST Institute, University of Franche-Comt
´
e, Rue du Mar
´
echal Juin, Belfort, France
2
Centre de D
´
eveloppement des Technologies Avanc
´
ees, ASM-IPLS Team, Baba Hassen, Algeria
Keywords:
Random Number Generators, System on Chip, FPGA, High Level Synthesis, RTL, Chaotic Iterations,
Statistical Tests, Security.
Abstract:
Pseudorandom number generation (PRNG) is a key element in hardware security platforms like field-
programmable gate array FPGA circuits. In this article, 18 PRNGs belonging in 4 families (xorshift, LFSR,
TGFSR, and LCG) are physically implemented in a FPGA and compared in terms of area, throughput, and
statistical tests. Two flows of conception are used for Register Transfer Level (RTL) and High-level Synthe-
sis (HLS). Additionally, the relations between linear complexity, seeds, and arithmetic operations on the one
hand, and the resources deployed in FPGA on the other hand, are deeply investigated. In order to do that, a
SoC based on Zynq EPP with ARM Cortex-A9 MPSoC is developed to accelerate the implementation and the
tests of various PRNGs on FPGA hardware. A case study is finally proposed using chaotic iterations as a post
processing for FPGA. The latter has improved the statistical profile of a combination of PRNGs that, without
it, failed in the so-called TestU01 statistical battery of tests.
1 INTRODUCTION
Producing randomness is a common need in many ap-
plications such as simulation (Gentle, 2013), numer-
ical analysis (Zepernick and Finger, 2013), computer
programing, cryptography (Luby, 1996). Such gen-
erators are usually divided in two categories: “pseu-
dorandom” (PRNGs), which use algorithms to deter-
ministically produce numbers that look like random
(they pass statistical tests with success), and “true”
random number generators (TRNGs) that use a phys-
ical source of entropy to produce randomness.
Deterministic algorithms of pseudorandom gener-
ation can be developed by targeting a specific hard-
ware system, like a Field Programmable Gate Ar-
ray (FPGA), before automatically deploying it on the
hardware architecture by using ad hoc frameworks.
Modern FPGAs allow rapid prototyping to explore
various hardware solutions and accelerate Time to
Market. The design methodology on FPGA relies on
the use of two high levels of implementation, namely
the Register Transfer Level (RTL) flow and the High
Level Synthesis (HLS) (Cong et al., 2011) one. The
HLS flow enables an automatic synthesis to FPGA
support in a high programing level. It also acceler-
ates the IP creation by enabling C, C++, and Sys-
temC specifications to generate the RTL level for FP-
GAs implementation. Conversely, traditional RTL
flow summarizes the Hardware Description Language
(HDL) using verilog/VHDL languages. In fact, many
recent papers use HLS flow to accelerate some re-
search study in many applications like in cryptogra-
phy (Homsirikamol and Gaj, 2015).
A way to solve at least partially such secu-
rity issues is to rigorously and directly implement
PRNGs on FPGAs. To do so, we studied the main
functionalities and complexity that distinguish one
PRNG for another, which are: LFSR (LFSR113,
LFSR258, and LUT-SR), LCG (PCG32, MWC256,
CMWC4096, and MRG32k3a), TGFRS (Mersenne
Twister, Well512, and TT800), xorshift (xorshift64,
xorshift128, xorshift
∗
, and xorshift+), and Cellular
Automata generators (cf., Section 2). Then, Section 3
presents a deep analysis to identify characteristics and
main proprieties that contribute to the hardware per-
formance of each PRNG. To do so, we use a Zynq
device (Rajagopalan et al., 2011) and the two flows
(HLS & RTL) as support to develop a complete Sys-
tem on Chip physical support for hardware PRNG,
which is detailed in Section 4. Due to well known
limitations of these linear generators in cryptographic
applications (e.g., linear complexity as described in
302
Mohammed, B., Couchot, J-F. and Guyeux, C.
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case Study.
DOI: 10.5220/0005967903020309
In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 302-309
ISBN: 978-989-758-196-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Section 3), chaotic iterations are finally introduced
in Section 5 as a possible post processing for hard-
ware PRNGs. The latter improves the statistical pro-
file of the generated numbers as verified by the so-
called TestU01 battery of tests (L’Ecuyer and Simard,
2007).
2 F
2
-LINEAR GENERATORS
Let F
2
be the finite field of cardinality 2. Let us
firstly recall that a common way to define a pseu-
dorandom number generator is to consider two func-
tions, namely f : F
N
2
→ F
N
2
and g : F
N
2
→ F
M
2
, where
usually N > M and g is one way, such that internally
x
n+1
= f (x
n
) is computed, while externally y
n+1
=
g(x
n+1
) is produced (x
0
being a seed provided by the
user). A linear PRNG of r bits are a special case of
linear recurrence modulo 2, which can be defined by
the following equations:
x
i
= A × x
i−1
(a) y
i
= B × x
i
(b)
r =
k
∑
`=l
y
{i,`−1}
2
−`
= y
{i,0}
y
{i,1}
y
{i,2}
...(c)
(1)
Indeed the first equation (a) defines the function f ,
where x
i
= (x
i,0
,...,x
i,k−1
) ∈ F
k
2
is the k-bit vector
at step i and A is a k × k transition matrix with k-bit
F
2
-vector. The other equations (b) and (c) define the
function g, where y
i
= (y
i,0
,...,y
i,w−1
) ∈ F
k
2
is the w-
bit output vector at step i, while B is a w × k output
transformation matrix with elements in F
2
. The latter
produces the output bits that correspond to the inter-
nal RNG state, which is rewritten as r ∈ [0,1]: the
output at step i. We focus on implementing four fam-
ilies of generators in one or both flows, which are:
Linear Feedback Shift Register. It uses a se-
quence of shift registers to generate one bit per it-
eration. In such a PRNG, the matrix A represents
the LFSR coefficients. Accordingly, if any of these
coefficients exists, it deploys a XOR operand on
some designed registers to build a feeadback input
to the first register. LFSR113, LFSR258 (L’Ecuyer,
1999b), and Taus88 (L’Ecuyer, 1996) are examples
of LFSR. Additionally, Look-up Table Shift Register
(LUT-SR) (Thomas and Luk, 2013)) is another LFSR
generator, which uses LUT as a k-bit shift-register to
allow the cascading for any required size.
Linear Congruential Generators. They
are based on linear recurrence equations having
the form: x
i+1
= (ax
i
+ c) mod 2
k
. Multiply-
With-Carry MWC256 and Complementary MWC
CMWC4096 (Couture and L’Ecuyer, 1997) are
two implementations of LCG, where in MWC
the increment c = b(ax
i−r
+ c
i−1
)/2
k
c is an initial
carry, and the CMWC takes the complement of
(2
k
− 1) − x
i
(MWC) to form a new output. Another
example is a new improvement of LCG named
PCG32 (O’Neill, 1988), which uses a permutation
function (dropping bits using fixed and random
rotations). We can also evoke the MRG32K3a
generator (L’Ecuyer, 1999a), which is a combined
Multiple Recursive Generator computed as follows:
y
i
= x
i
/2
k
.
Twisted Generalized Feedback Shift Register.
It is based on matrix linear recurrence of n sequence
words, each containing w-bits. For each recurrence
operation k, k = 0,1,...,m, the TGFSR operates with
three sequence words: the first two sequence words
x
k
and x
k+1
being computed with bitmask vectors
(S
MSB
,S
LSB
) with the middle sequence word x
k+m
,
0 6 m 6 n, as follows:
x
k+n
= x
k+m
⊕ (((x
k
& S
MSB
) | (x
k+1
& S
LSB
)) × A).
(2)
At iteration i = k + n, TGFSR uses a tamper-
ing module (bitwise/shift computation) to reduce
the dimensionality n of equidistribution. Mersenne
Twister (MT) (Matsumoto and Nishimura, 1998),
Well512 (Panneton et al., 2006), and TT800 (Mat-
sumoto and Kurita, 1994) are examples of TGFSR.
XORshift Generators. They are very fast
PRNGs, in which the internal state is repeatedly
changed by applying a series of shift and exclusive-
or (XOR ⊗) operations. XORshift
∗
generators (Vi-
gna, 2014a), XORshift64 (Marsaglia et al., 2003), and
XORshift+ (Vigna, 2014b) are instances of such gen-
erators.
Cellular Automata Generator. This is a dis-
crete generator proposed as formal models of self-
reproducing robots. It includes at least 3 cells with
an internal state machine that can be a Boolean func-
tion rule. Therefore, the CA structure can hold and
update the internal state for each cell, depending on
the local rules registered by the Wolfram code (Gleick,
1997) (2
8
possibilities) and the states of their neigh-
borhoods.
3 HARDWARE
IMPLEMENTATION
In this section, we start a deep analysis of the PRNG
implementations on FPGA using Register Trans-
fer Level (RTL) and/or High Level Synthesis (HLS)
flows. Results are studied according to: (1) the space,
timing, and computational complexity, (2) the seed
and period, and (3) the arithmetic operators and dy-
namic range FPGA resources. Table 1 and Table 2
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case
Study
303

(a) LCG Familly
(b) TGFSR Familly
(c) xorshift Familly
(d) LFSR Familly
Figure 1: Computational Complexity Analysis with
Berlekamp-Massey Algorithm.
show obtained results when implementing 18 PRNGs.
Figure 1 presents, for its part, the computation com-
plexity and its impact on performance. Each PRNG is
implemented either in just one or both (HLS & RTL)
flows. Concerning the software platform, we used Vi-
vado HLS tool for HLS flow and Vivado synthesis for
RTL flow of Xilinx.
3.1 Space, Timing, and Computational
Complexities
The space represents the allocated cost of most ob-
jects used in the algorithm (tables, indexes, loops,
etc.). Regarding FPGAs, the latter can be translated
in memories, registers, and LUT resources, etc. The
question raised in this section is thus: how much
space states are needed to provide pseudorandom
numbers with a good statistics profile? We won-
der too whether there is any relation between the
space (mean resources) used in FPGA and a suc-
cess in passing stringent statistical Linear Complexity
Test (Blackburn et al., 1994) of test. To answer this
question, we first define what is a linear complexity.
Most PRNGs mentioned in this article are linearly
recursive. If we take a finite binary sequence (x
i
) =
(x
i,0
,...,x
i,k−1
) ∈ F
k
2
, its linear complexity L
k
(x
i
) is
the length of the shortest characteristic polynomial
(see Equation (1)) of the LFSR generating the same
sequence (for a sequence equal to x
0
= x
1
= ··· =
x
k−2
= 0 and x
k−1
= 1, the linear complexity is k
and L
k+1
> L
k
). Non randomness is claimed when
the length is short. This is confirmed by the fact that
almost all generators (with the exception of PCG32,
xorshift
∗
, and MRG32k3a) presented in this article
fail in statistical Linear Complexity Test of Test.
A first way to compute this complexity is to con-
sider the NIST tests battery (Barker and Roginsky,
2010). But the improved Test battery additionally in-
corporates some “jump” aspects in this test, leading
to the fact that most generators succeeding in NIST
linear complexity test finally fail to pass the one of
Test. Indeed, the latter calculates the jumps that occur
in the linear complexity for each local subsequence,
that is, the k’s that satisfy L(k) − L(k − 1) > 0. This
number of jumps represents how much bits have to be
added to the sequence to increase its linear complex-
ity. Ideal PRNGs have to perform jumps symmetric
to the k/2-line (Rueppel, 1985), as in a perfect linear
complexity, maximum jump heights of k/4 and close
to b(k + 1)/2c for k-sequences are required.
Regarding FPGAs, these jumps determine how
much resources are required in order to have a perfect
complexity profile. For illustration purposes, some
of these PRNG jumps have been computed, see Fig-
ure 2. Concerning 32 bit sequences, the number of
perfect successive jumps (< 2) is large for all PRNGs
(XOR64, for instance, has a total of 6 jumps, 4 of
them being perfect). However, in the 64 bit case, two
kind of results have been obtained. On the one hand,
we found PCG32 and MRG that can pass Test have
low successive jumps compared to xorshift
∗
. This is
due to the multiplication space used for these gen-
erators. This is confirmed in Figure 1, that summa-
rizes the linear complexity for each family of PRNGs,
which is close to k/2 = 32.
Let us now consider xorshift
∗
generators, which
also use 64-bit multiplications. Their linear complex-
ity is closely perfect, as can be seen in Figure 1. The
key difference here is the permutation function used
for multiplication. In LCG family, this is the main
function applied to perform an uniform scrambling
operation. On the opposite, they are deployed to inject
bias in randomness in xorshift
∗
. The PCG32 deploys
SECRYPT 2016 - International Conference on Security and Cryptography
304
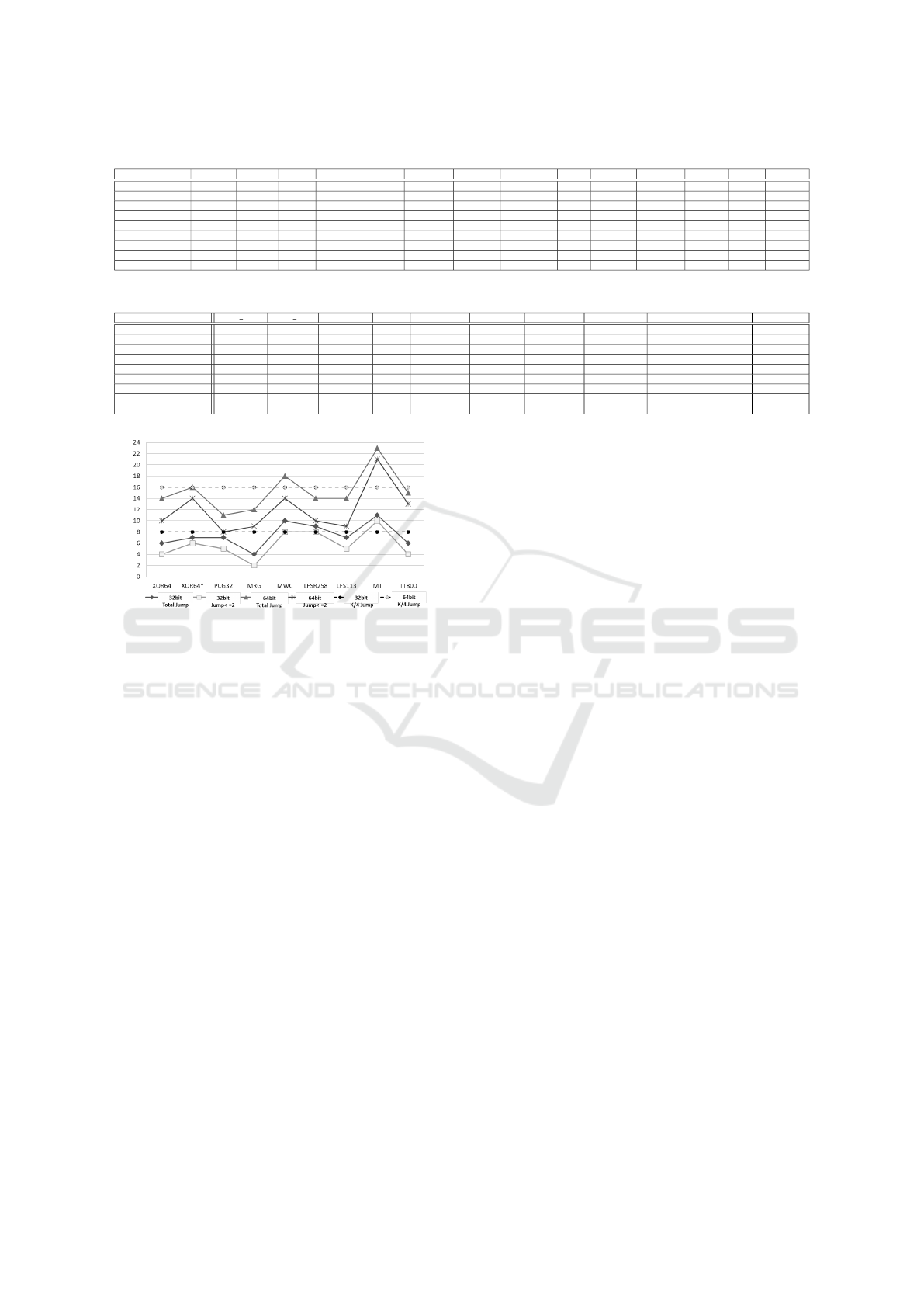
Table 1: HLS Implementation.
PRNG LFSR113 TAUS88 PCG32 MRG32k3a TT800 WELL512 MWC256 CMWC4096 XOR
∗
LFSR258 XORP128 XORP64 XOR+ KISS124
Output Range 32 32 32 32 32 32 32 32 64 64 64 64 64 64
Period 2ˆ 113 88 32 191 800 512 8222 131086 1024 258 128 64 128 124
LUT 66 56 371 214 173 90 219 285 303 132 49 64 136 271
FF 113 88 367 522 549 147 399 471 394 258 64 65 133 746
RAM 0 0 0 0 2 2 1 8 4 0 0 0 4 0
DSP 0 0 10 8 6 0 4 2 10 0 0 0 0 7
Frequences Mhz 769 555 333 160 160 214 153 148 224 617 510 894.45 225 149
Area 1432 1152 5904 5888 5776 1896 4944 6048 5576 3120 904 1032 2152 8136
Throughput Gbps 24.6 17.76 10.6 5.12 5.12 6.8 4.9 4.7 14.33 39.5 156.32 57.24 14.40 4.7
Table 2: RTL Implementation on FPGA.
PRNG MT WS MT NS LUT-SR CA LFSR113 TAUS88 LFSR258 XORP128 XORP64 XOR+ KISS124
Output Rang 32 32 32 32 32 32 64 64 64 64 64
Period 2ˆ 19937 19937 1024 32 113 88 258 128 64 128 124
LUT 523 184 64 98 95 96 207 53 65 147 742
FF 120 179 64 40 128 77 320 128 64 196 256
RAM 2 2 0 0 0 0 0 0 0 0 0
DSP 3 0 0 0 0 0 0 0 0 0 6
Frequences Mhz 118 462 609 598 595 667 556 531 588 403 78.1
Area 5144 3272 576 1104 1784 1384 4216 1448 1032 2744 7984
Throughput Gbps 3.8 13.2 19.5 19.1 19 21.3 35.5 17 37.6 25.7 5
Figure 2: Jump Computation for 32/64 bit of random.
64-bit multiplications (128-bit state), but it uses only
36-bit of state while always dropping the MSB parts
(the states space used are constant for any operation).
This fact means a loss of information that can create
a new jump in complexity, even if we use more com-
plected seeds (i.e., pcglong). In other words, it needs
some time to be perfectly linear (see Figure 1(a) start-
ing from 41-bit). In hardware level, doing the same
operation leads to unnecessary area and power con-
suming.
The second point to investigate is the size and
number of jumps in complexity profile. If we consider
multiplications for instance, each PRNGs embedding
them needs 2 ∗ n outputs of multipliers (DSP or LUT
blocs in FPGA) for each n-bit input multiplication:
for each jump, an additional input multiplier is used.
In other words and compared to stable complexity, a
fixed jump during time does not use the full capacity
of the multiplier (see Section 3.3).
3.2 Seed and Period
Most generator implementations require a seed to ini-
tiate the internal states. It is also a space determinis-
tic parameter for the PRNG. Regardless of the space
size, the consumption can be quite large if the seed is
large. This seed can be: single or multiple value(s) in
table(s), a constant or a value generated from a given
algorithm, or it can even be extracted from a physical
source (TRNG). Additionally, the seed can also con-
tribute to the period of the PRNG. A period of a power
of two is recommended to have an uniform output,
due to the following reason: if it is not the case, some
hardware resources cannot be used (e.g., MRG32k3
has an output of 2
32
− 209 and 209 values are never
used).
In our implementations (RTL and HLS), we
choose to seed TGFSR and MWC generators with
an array using one of Knuth’s generators (see (Knuth,
1997, p. 106) for multiplier). Depending on the seed
period and using MT as an example, we can store each
value of the seed in one memory at a time and for each
clock cycle. The RAM memory, configured in the
read-before-write mode, operates like a feedback shift
register. In this mode, new inputs are stored in mem-
ory at an appropriate write address, while the previ-
ous data are transferred to the output ports. The latter,
coming from RAM, are then processed following the
Equation (2). Therefore, different address controllers
are used for each process (seed and generation). For
the other PRNGs, the seed can be a constant or gen-
erated by another algorithm.
Let us illustrate the performance impact using
Mersenne Twister (MT) with (WS) and without (NS)
the seed algorithm in RTL level. When including the
seed in implementation, we need to store 624 values
in two memories for each clock cycle, which are used
later in random transformation and tempering. There-
fore, the total area and time resources is increased.
Otherwise, in the case of the absence of the seed, the
latter is generated and stored separately in memories,
before the deployment of the PRNG. During our com-
parisons of the two approaches on MT generator, we
have remarked that, with seed, frequency is reduced
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case
Study
305

to less than 200MHz compared to the case without
it. Therefore, to increase performances, most PRNGs
do not include the seed internally (software is used).
The LUT-SR PRNG is an exception, which consumes
less space but needs to wait 1,024 clock cycles for the
seed generation.
3.3 Arithmetic Operators and Dynamic
Range
The arithmetic operators area is a key issue at hard-
ware level, which can be considered as a major factor
of the quality of the final implementation. These oper-
ators can be a single basic operation (like addition or
subtraction, multiplication of variables or constants),
algebraic functions (division, modulo, etc.), or any
other elementary function. However, in hardware
level, these arithmetic operations (specially the mul-
tiplication) are hard coded by the tools (Xilinx) us-
ing optimized algorithms for that (Canonical Signed
Digit (CSD), Booth recoding, etc.).
In the binary field F
2
, most PRNGs use only pos-
itive integer values and fixed point representations
in hardware level, while if we take for instance the
computing of the partial products, the latter can use
only glue logic (i.e., AND gates or a series of ad-
ditions). These partial products are defined as Dis-
tributed Arithmetic (DA (Meyer-Baese and Meyer-
Baese, 2007)), they perform a multiply-and-add op-
eration at the same time using most basic logic ele-
ments (LUTs). Their size and performance depend on
both the word length (addressing the LUT increases
the table exponentially) and their binary representa-
tions, regarding dynamic range and precision. This
word length represents the ratio between the largest
and the smallest nonzero and positive number that can
be represented (integer), which is expressed as follow:
DR
fxpt
= r
n
− 1 where r is in binary format (Radix-2)
and n is the number of digits in fixed-point precision.
Modern FPGAs use Digital Signal Processing
(DSP48E1) slices to obtain the optimal implementa-
tion of these operators and avoid overflows and un-
derflows for complex operations. It supports many in-
dependent functions including multiply, MAC, mag-
nitude comparator, bit-wise logic functions, etc. Be-
cause multiplications are widely used in PRNGs, they
can be implemented with DSP used as a 25x18-bit
multiplier, and which can be pipe-lined. In Figure 1,
we can see the obvious impact of DR on computation
complexity, which means that larger DR are translated
to logic space, operator, and timing. Let us take for
instance the LFSR258 of DR= 2
64
, which applies ex-
act logic operators as shift, logic AND, and xorshift.
Its complexity is linear with the “DA” used when
1 < DR < 16 bits, otherwise it jumps higher with the
use of more complicated logic to operate multiplica-
tions (DSP) and store values.
4 SOC SYSTEM BASED ON ZYNQ
PLATFORM FOR PRNG
4.1 Hardware and Firmware Design
Xilinx Zynq-7000 Extensible Processing Platform
(EPP) (Rajagopalan et al., 2011) is a silicon system
on chip (SoC) for FPGAs, which has been proposed
by Xilinx. The latter is defined as Peripheral Sys-
tem (PS), which is a sub-system with ARM. The full
FPGA, for its part, is the Programmable Logic (PL)
that is connected with PS through an AXI bus inter-
face. Therefore, and for pseudorandom number gen-
eration, we have developed a complete SoC infras-
tructure divided in two parts: hardware and firmware.
The hardware architecture of our system used to
integrate and test PRNGs is illstrated in Figure 3.
It contains, respectively: the ARM Cortex-A9 dual
cores MPSoC, the high performance DDR3 512Mb,
an UART, and finally the PRNGs (RTL or HLS imple-
mentation). Additionally, to read the random output
on the CPU, we have used both an AXI-PRNG inter-
connect and an AXI Direct Memory Access controller
engine (DMA). The firmware for it parts, is used to
initialize the system, for transaction synchronization,
and for the interface with an external peripheral.
Meanwhile, the CPU initialises and reads/writes
data of an IP in PL (i.e., PRNG) over the AXI mas-
ter using general-purpose GP ports. On the other
hand, the AXI slave is used for PL master IP over
High Performance (HP) ports. Each of these inter-
faces can handle up to 16 bytes of data. The inter-
face protocol, for its part, can be configured either as
Stream for high-speed streaming data, or as Lite/Full
for high-performance memory-mapped requirements
(data transactions over an address).
This interconnect component is re-configurable
using the firmware, which deploys two GPIO IPs for
that task. GPIO-0 is used to select one PRNG at a
time, and GPIO-1 is used for the data burst size of
the PRNG. For instance, all PRNGs implemented in
HLS or RTL including the AXI-PRNG interconnect
are AXI Stream Interface, while the CPU is Memory-
Mapped Interface. Additionally to CPU, the AXI
DMA engines, which oversees the data transaction
between the slave and master IPs, deploys the receiver
channel Slave to Memory Map (S2MM) connected to
a salve port and the transmitter channel Memory-Map
SECRYPT 2016 - International Conference on Security and Cryptography
306

Figure 3: PRNG Platform Based on Zynq.
to Slave (MM2S) connected with the master.
4.2 Comparison
Table 1 and Table 2 give some performance results of
PRNG implementation in terms of area (space) and
throughput (speed). The Xilinx tool calculates all re-
sources used in FPGA as logic gates, LUT, Flip-Flop
(register), additionally to DSP and memory blocks.
Hence, for our area comparison, we only calculated
LUT and FF as (LUT + FF) × 8, since DSPs and
RAM memories are hard blocs that can mostly affect
time performances. The throughput performance is
calculated as Frequency× Output range. It depends
on two parameters, namely the logic critical path used
and the output range (32 or 64 bits).
We obtained that the lowest area resources are
for LUT-SR, Taus88, and xorshift64, while combined
PRNGs like KISS and MRG32k3a have a large area
consumption too. Additionally, the throughput of
Taus88 and LUT-SR with LFSR113 of 32 bit genera-
tors, have the highest throughput performance, while
the best are xorshift64 and LFSR258 in the 64 bit
case. On the other hand, the LCG and TGFSR fam-
ilies are expected to have the lowest throughput per-
formance, as they operate large arithmetic operations
like 64 bit multiplications using DSP (it will be worse
when using LUT). Besides that, using memories for
TGFSR will drop the PRNG frequency automatically
to the half without counting other logic. Once again,
the combined generators have the weakest throughput
performances. To conclude the FPGA resource per-
formance aspects of this comparison, LFSR and xor-
shift PRNGs are more recommended to limit space
and for better speed performances in hardware appli-
cations (mobile phone, smart cards, and so on).
Hardware PRNGs presented here must be evalu-
ated too regarding their randomness, which can be
done using statistical tests. The TestU01 battery is
currently the most complete and stringent battery of
tests for RNGs, which groups more than 516 tests in-
side 7 big sub-batteries. Among them, the Big Crush
is the most difficult one.
After applying our experiments illustrated in
Figure 4, we have obtained that only PCG32,
MRG32K3a, and xorshift
∗
generators can pass the
Big-Crush of TestU01, which is coherent with the lit-
erature. Obtained test results have shown that a par-
ticular and common test called the linearity complex-
ity test is very frequently failed. In details, TestU01
uses the Berlekamp-Massey algorithm with the jump
statistic to calculate the expected values compared to
a chi-square test (the expected value). Such a fail-
ure is related to what has been detailed in Section 3.1
about the linear complexity computation. Indeed all
PRNGs are linear, but this does not lead to the linear
complexity of a long random sequence.
Figure 4: Linear Complexity Test failing for TestU01.
To put it in a nutshell, if we take the ratio of
area/throughput as main criterion, we are balancing
between high performance (xorshift64 and LFSR113)
and the ability to pass statistical tests (PCG32 and
xorshift
∗
), which is not surprising. Another result
is that combining PRNGs leads to a performance
decrease in hardware level. Next section studies a
family of specific combinations which are based on
Chaotic Iteration.
5 CHAOTIC ITERATION POST
PROCESSING
In this section, a recent pseudorandom number post
treatment based on Chaotic Iterations (CIs (Bahi
et al., 2009; Fang et al., 2014; Bahi et al., 2013))
is recalled. It is based on Devaney (Devaney, 2003)
theory of chaos. This theory focuses on recurrent se-
quences of the form x
0
∈ R: x
i+1
= f (x
i
), and stud-
ies for which function f such sequences presents el-
ements of complexity and disorder. In particular, it
is wondered when effects of an alteration of the ini-
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case
Study
307

tial term x
0
can be predicted. Such chaotic sequences
are candidate to provide pseudorandomness, leading
to the field of chaotic pseudorandom number genera-
tors (CPRNGs).
Let us now recall the mathematical definition of
chaotic iterations CIs (Bahi et al., 2009). They are a
particular kind of vectorial discrete dynamical system
in which at i-th iteration, only a subset of components
of the iteration vector are updated.
Definition 5.1. Let f : {0; 1}
N
−→ {0;1}
N
and S ∈
P (J1, NK)
N
a sequence of subsets of the integer inter-
val J1, NK called a “chaotic strategy”, where P (X) is
the set of all subsets of X and N is the set of natural
numbers. General chaotic iterations ( f ,(x
0
,S)) are
defined for any n ∈ N
∗
and i ∈ J1; N K by:
x
0
∈ B
N
, N > 2
x
n
i
=
(
x
n−1
i
if i /∈ S
n
f (x
n−1
)
i
if i ∈ S
n
.
For our PRNG applications, CIs have been im-
plemented by the following process. The iteration
function f is the negation function ( f ((x
1
,...,x
N
)) =
(x
1
,...,x
N
)). In this case, the CI based pseudoran-
dom number generator is denoted by XOR-CIPRNG,
which can be rewritten as x
i+1
= x
i
⊗ S
i
(Bahi et al.,
2015). In the modified version we implemented, two
inputted PRNGs denoted by x
i
and y
i
are used for
defining the chaotic strategy S, as described in Algo-
rithm 1. Furthermore, we added a third inputted set
generator z
i
for more complexity. This generator will
pick randomly a subset of the inputs at each iteration.
Only the log(log(n)) least significant bits (in this case,
3 bits) are finally taken for pseudorandomness.
Algorithm 1: Xorshift based Chaotic Iteration.
Input: s (a 32-bit word)
Output: r (a 32-bit word)
X
i
← PRNG1, y
i
← PRNG2, z
i
← PRNG3
if (z
i
& 1) 6= 0 then
s ← s ⊗ (x
i
& 0x0 f f f f f f f f )
end
if (z
i
& 2) 6= 0 then
s ← s ⊗ (x
i
32)
end
if (z
i
& 4) 6= 0 then
s ← s ⊗ (y
i
& 0x0 f f f f f f f f )
end
r ← s ⊗ (y
i
32)
We tested more than 275 combinations using CI
post processing, a few of them being summarized
in Table 3. In the first row of this table, triplets
[i, j, k] represent the combination of PRNG1, PRNG2,
and PRNG3 successively, where for i and j, 0 is for
xorshift64, 1 means xorshift
+
, while the third compo-
nent k is respectively set to 1,2,3,4, and 5, correspond-
ing to LFSR113, Taus88, TT800, WELLRNG512,
and Mersenne Twister.
If we compare with the combined generators KISS
and MRG32k3a previously evaluated, we can no-
tice the same characteristic in terms of area and
throughput. Let us remark that some combinations
need huge area resources, due to internal space re-
quired for some PRNGs like the Mersenne Twister
or CMWC4096. But objective of this article is
to show that PRNGs which previously failed some
statistical tests can pass them after the CI post
treatment: indeed, all the combinations of Table 3
achieve to pass the most stringent Big-Crush bat-
tery of Testu01. Furthermore, if we consider the
combinations of [xorshift64, xorshift
+
, LFSR113]
or [xorshift
+
, xorshift
+
, Taus88], the obtained CI-
PRNGs are more performing than MRG32k3a (which
also pass the TestU01) without using any DSP&RAM
blocs. To sum up, chaotic iterations post processing
can contribute to increase the statistical performance
of PRNGs.
Table 3: Chaotic Iterations Post Processing Implementa-
tion.
PRNG 011 012 013 014 015 112
LUT 283 430 362 499 367 356
FF 540 975 557 854 607 519
DSP 0 6 0 3 2 0
RAM 0 2 2 2 8 0
Area/10
3
6.58 11.2 7.3 10.8 7.79 7.0
T(Gbps) 6.9 5.5 6.5 5 5.5 5.9
6 CONCLUSION
A novel implementation of various PRNGs in FPGA
is detailed in this paper, in which two flows of con-
ception (RTL and HLS) demonstrate the performance
level of each PRNG in terms of area throughout and
statistical tests. Our study has shown that these per-
formances are related to linear complexity, seed size,
and arithmetic operations. In order to investigate
these parameters, a SoC based on Zynq EPP platform
(hardware and firmware) has been developed to accel-
erate the implementation and tests of various PRNGs
on FPGA. On this platform, xorshift64 and LFSR113
have outperformed the other candidates when con-
sidering hardware performance, while PCG32 and
xorshift
∗
are the best when studying statistical ones
(they succeeded to pass the whole TestU01 batteries).
Finally, a hardware post processing treatment based
SECRYPT 2016 - International Conference on Security and Cryptography
308

on chaotic iterations has been proposed, which has
achieved to improve the statistical profile of flawed
generators. We plan to investigate which combina-
tions and parameters of chaotic iterations can be cho-
sen to reach an ideal PRNG (fast, small, and secure).
ACKNOWLEDGEMENTS
This work is partially funded by the Labex ACTION
program (contract ANR-11-LABX-01-01).
REFERENCES
Bahi, J., Couturier, R., Guyeux, C., and H
´
eam, P.-C. (2015).
Efficient and cryptographically secure generation of
chaotic pseudorandom numbers on gpu. The journal
of Supercomputing, 71(10):3877–3903.
Bahi, J., Guyeux, C., and Wang, Q. (2009). A novel pseudo-
random generator based on discrete chaotic iterations.
In INTERNET’09, 1-st Int. Conf. on Evolving Internet,
pages 71–76, Cannes, France.
Bahi, J. M., Fang, X., Guyeux, C., and Larger, L. (2013).
Fpga design for pseudorandom number generator
based on chaotic iteration used in information hiding
application. Appl. Math, 7(6):2175–2188.
Barker, E. and Roginsky, A. (2010). Draft NIST special
publication 800-131 recommendation for the transi-
tioning of cryptographic algorithms and key sizes.
Blackburn, S., Carter, G., Gollmann, D., Murphy, S., Pa-
terson, K., Piper, F., and Wild, P. (1994). Aspects of
linear complexity. In Communications and Cryptog-
raphy, pages 35–42. Springer.
Cong, J., Liu, B., Neuendorffer, S., Noguera, J., Vissers,
K., and Zhang, Z. (2011). High-level synthesis for
fpgas: From prototyping to deployment. Computer-
Aided Design of Integrated Circuits and Systems,
IEEE Transactions on, 30(4):473–491.
Couture, R. and L’Ecuyer, P. (1997). Distribution proper-
ties of multiply-with-c arry random number genera-
tors. Mathematics of Computation of the American
Mathematical Society, 66(218):591–607.
Devaney, R. L. (2003). An Introduction to Chaotic Dynam-
ical Systems, 2nd Edition. Westview Pr.
Fang, X., Wang, Q., Guyeux, C., and Bahi, J. M. (2014).
Fpga acceleration of a pseudorandom number genera-
tor based on chaotic iterations. Journal of Information
Security and Applications, 19(1):78–87.
Gentle, J. E. (2013). Random number generation and Monte
Carlo methods. Springer Science & Business Media.
Gleick, J. (1997). Chaos: Making a new science. Random
House.
Homsirikamol, E. and Gaj, K. (2015). Hardware bench-
marking of cryptographic algorithms using high-level
synthesis tools: The sha-3 contest case study. In
Applied Reconfigurable Computing, pages 217–228.
Springer.
Knuth, D. E. (1997). The Art of Computer Program-
ming, Volume 2 (3rd Ed.): Seminumerical Algo-
rithms. Addison-Wesley Longman Publishing Co.,
Inc., Boston, MA, USA.
L’Ecuyer, P. (1996). Maximally equidistributed combined
tausworthe generators. Mathematics of Computation
of the American Mathematical Society, 65(213):203–
213.
L’Ecuyer, P. (1999a). Good parameters and implementa-
tions for combined multiple recursive random number
generators. Operations Research, 47(1):159–164.
L’Ecuyer, P. (1999b). Tables of maximally equidis-
tributed combined lfsr generators. Mathematics of
Computation of the American Mathematical Society,
68(225):261–269.
L’Ecuyer, P. and Simard, R. (2007). Testu01: Ac li-
brary for empirical testing of random number gener-
ators. ACM Transactions on Mathematical Software
(TOMS), 33(4):22.
Luby, M. G. (1996). Pseudorandomness and cryptographic
applications. Princeton University Press.
Marsaglia, G. et al. (2003). Xorshift rngs. Journal of Sta-
tistical Software, 8(14):1–6.
Matsumoto, M. and Kurita, Y. (1994). Twisted gfsr genera-
tors ii. ACM Transactions on Modeling and Computer
Simulation (TOMACS), 4(3):254–266.
Matsumoto, M. and Nishimura, T. (1998). Mersenne
twister: a 623-dimensionally equidistributed uniform
pseudo-random number generator. ACM Transactions
on Modeling and Computer Simulation (TOMACS),
8(1):3–30.
Meyer-Baese, U. and Meyer-Baese, U. (2007). Digital sig-
nal processing with field programmable gate arrays,
volume 65. Springer.
O’Neill, M. E. (1988). PCG: A family of simple fast
space-efficient statistically good algorithms for ran-
dom number generation.
Panneton, F., L’Ecuyer, P., and Matsumoto, M. (2006). Im-
proved long-period generators based on linear recur-
rences modulo 2. ACM Transactions on Mathematical
Software (TOMS), 32(1):1–16.
Rajagopalan, V., Boppana, V., Dutta, S., Taylor, B., and
Wittig, R. (2011). Xilinx zynq-7000 epp–an exten-
sible processing platform family. In 23rd Hot Chips
Symposium, pages 1352–1357.
Rueppel, R. A. (1985). Linear complexity and random se-
quences. In Advances in CryptologyEUROCRYPT85,
pages 167–188. Springer.
Thomas, D. B. and Luk, W. (2013). The lut-sr family of
uniform random number generators for fpga architec-
tures. Very Large Scale Integration (VLSI) Systems,
IEEE Transactions on, 21(4):761–770.
Vigna, S. (2014a). An experimental exploration of
marsaglia’s xorshift generators, scrambled. arXiv
preprint arXiv:1402.6246.
Vigna, S. (2014b). Further scramblings of marsaglia’s xor-
shift generators. arXiv preprint arXiv:1404.0390.
Zepernick, H.-J. and Finger, A. (2013). Pseudo random
signal processing: theory and application. John Wiley
& Sons.
FPGA Implementation of F
2
-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case
Study
309
