Feature and Sensor Selection for Detection of Driver Stress

Simon Ollander

, Christelle Godin

, Sylvie Charbonnier

and Aur´elie Campagne

CEA, LETI, MINATEC Campus, F-38054 Grenoble, France

Univ. Grenoble Alpes, F-38000 Grenoble, France

Gipsa-Lab, Univ. Grenoble Alpes & CNRS, F-38402 Grenoble, France

LPNC, Univ. Grenoble Alpes, CNRS, F-38040 Grenoble, France

Keywords:

Stress, Features, Classiﬁcation, Feature Selection, Sensor Selection, Driver Stress, Naive Bayes.

Abstract:

This study presents a real-life application-based feature and sensor relevance analysis for detecting stress in

drivers. Using the MIT Database for Stress Recognition in Automobile Drivers, the relevance of various

physiological sensor signals and features for distinguishing the driver’s state have been analyzed. Features

related to heart rate, skin conductivity, electromuscular activity, and respiration have been compared using

ﬁlter and wrapper selection methods. For distinguishing rest from activity, relevant sensors have been found

to be heart rate, skin conductivity, and respiration (giving up to 94.6± 1.9 % accuracy). For distinguishing

low stress from high stress, relevant sensors have been found to be heart rate and respiration (giving up to

78.1±4.1 % accuracy). In both cases, a multi-user model that requires only a calibration from the user in rest,

without prior knowledge of the user’s individual stress dynamics, resulted in a different optimal sensor and

feature conﬁguration, giving 87.3±2.8 % and 72.1±4.3 % accuracy respectively.

1 INTRODUCTION

Driving a vehicle is a part of many people’s daily life,

which can generate a variety of stressful situations.

Examples are social stress from other nearby drivers

and time pressure due to the necessity of taking quick

driving decisions. Too great driver stress levels might

encourage aggressive driving, such as road rage (Hen-

nessy and Wiesenthal, 1999), exposing the driver and

other trafﬁc for risk of physical harm. A part of the

solution to this problem is to automatically detect the

mental state of the driver using non-invasive sensors.

Depending on the driver’s stress state, the car could

automatically adapt e.g. the user interface and the

music, and advice the driver differently (Hernandez

et al., 2014).

Common physiological signals for detecting

driver stress include electrodermal activity (EDA),

electrocardiogram (ECG), electromuscular activity

(EMG), and respiration (Resp) (Rigas et al., 2012),

(Healey and Picard, 2000). Other examples are video

recordings tracking facial expressions (Gao et al.,

2014), speech (Boˇril et al., 2009), the CAN bus of

the vehicle (Boˇril et al., 2009), (Rigas et al., 2012),

and GPS information (Rigas et al., 2012). A review

of several studies on driver stress, comparing systems

and signals for monitoring can be found in (Singh and

Queyam, 2013). Examples of other sensors and sig-

nals that have been tried for stress detection are skin

temperature, eye tracking and pupil diameter (Palinko

et al., 2010), and behavioural measures such as ges-

tures and accelerometer data.

In this study, the signals of the MIT Stress Recog-

nition in Automobile Drivers Database (Healey and

Picard, 2008) have been analyzed to determine which

ones best distinguish the mental state of the driver in

rest versus driving, and highway versus city driving.

(Healey and Picard, 2005), (Akbas, 2011), (Queyam,

2013), and (Yong Deng, 2013) analyzed the same

database and reached up to 94.7 % of correct clas-

siﬁcation for different conﬁgurations.

We emphasize on the design of an automatic state

detector using physiological sensors. We consider

two classiﬁcation problems: distinguishing rest from

activity, and low stress from higher stress. Calibra-

tion is a critical point when developing such a sys-

tem. Most of the previous studies consider samples

from all drivers in both the training and the valida-

tion steps. This supposes a use case where data from

a period when the subject is resting and from when

the subject is stressed is available, letting the model

adapt to individual stress dynamics by training a dif-

Ollander, S., Godin, C., Charbonnier, S. and Campagne, A.

Feature and Sensor Selection for Detection of Driver Stress.

DOI: 10.5220/0005973901150122

In Proceedings of the 3rd International Conference on Physiological Computing Systems (PhyCS 2016), pages 115-122

ISBN: 978-989-758-197-7

115

ferent model for each person (single-user). This cal-

ibration allows for high precision, however it is very

constraining, which makes it less useful for real-life

applications. In a ﬁnal application it could also re-

quire embedding the training part of a machine learn-

ing algorithm. For these reasons, we also consider a

more realistic calibration case: multi-user. This case

creates one universal model, which would only re-

quire calibration from a resting period (for removing

individual baselines). This is more feasible in a real-

life situation, but it demands a more general model

than the single-user case.

Within this scope, we focus on selecting the set of

sensors and signal features that most accurately pre-

dicts driver stress. Firstly, the data is presented in Sec-

tion 2. Secondly, the classiﬁcation problem is deﬁned

in Section 3. Thirdly, all the features and their phys-

iological meaning are explained Section 4. Subse-

quently, Section 5 gives an overview of all the feature

selection methods used in this study. Finally, Sec-

tion 6 presents and discusses the results, while Sec-

tion 7 concludes this work.

2 THE DRIVE DATABASE

The MIT Stress Recognition in Automobile Drivers

Database (Healey and Picard, 2008) consists of phys-

iological data originating from drivers in the state of

rest, highway driving, or city driving. It contains a to-

tal of 16 data sets (drives), where 7 signals have been

recorded: ECG at 496 Hz, HR at 15.5 Hz, EMG at

15.5 Hz (placed at the left shoulder), SC at 31 Hz

(placed at left foot and hand), and respiration at 31

Hz. Additionally, there is a marker signal, which indi-

cates the phase of the experiment. Due to various ac-

quisition problems being present in some of the data

sets, only 9 of the drives were analyzed in this study.

3 CLASSIFICATION PROBLEM

The marker signal was used to separate the six phases

of the experimental phase, speciﬁed in Table 1. Fig-

ure 1 gives an example of the signals, for the Drive

15 data set. The start of the six phases are identi-

ﬁed by a red vertical line. In this study, the phases

were grouped in two different ways. The ﬁrst one,

rest vs. driving (RvsD) uses the data from the initial

rest to deﬁne the class “rest” (R), and the data from

all city and highway phases to deﬁne the class “drive”

(D). This corresponds to distinguishing a person that

is resting from when the person is doing an activity.

The second way of grouping the phases is highway vs.

Table 1: The six phases of each drive, their abbreviation and

their mean durations with standard deviation.

Phase Abbr. Duration µ ± σ

Initial rest R

15 m 7 s ± 21 s

City drive 1 C

14 m 59 s ± 2 m 5 s

Highway drive 1 H

7 m 59 s ± 1 m 14 s

City drive 2 C

6 m 50 s ± 1 m 47 s

Highway drive 2 H

7 m 17 s ± 28 s

City drive 3 C

11 m 23 s ± 3 m 0 s

city (HvsC). In this case, the ﬁrst class consists of all

highway drives, and is called “highway” (H), while

the class “city” (C) consists of all city drives. The

idea of distinguishing between these states is based

upon the assumption that people ﬁnd it more stressful

to drive in a city environment than on the highway.

This was conﬁrmed by the questionnaires in (Healey

and Picard, 2005, p. 159).

4 FEATURES

The mean HR, along with HRV features measure the

variations of the inter-beat intervals (IBI) of an ECG,

and are known as relevant stress indicators (Sun et al.,

2010, p. 3). Activation of the sympathetic nervous

system ensures a more regular heart beat, which is

why features such as the root mean square (RMS) of

the difference between successive IBI are expected

to decrease in stressful situations. Similarly, HRV

power spectrum features are relevant, especially the

low frequency component, regulated by both the sym-

pathetic and parasympathetic nervous system, and the

high frequency component, regulated by the parasym-

pathetic nervous system. Their ratio is used as an in-

dex of the balance between the two nervous systems,

and is expected to decrease with increasing stress.

Another widely used measure in stress detection is

the electrodermal activity, which can be recorded us-

ing electrodes that measure the skin conductivity (SC)

or the skin resistance between so called active sites

on the inner surface of the hands or the feet. In this

work, the skin conductivity will be used. The SC is

purely regulated by the sympathetic nervous system,

and manifests itself by an increase in skin conduc-

tance level in stressful conditions, with rapidly rising

peaks that slowly return to base level (Kappeler-Setz

et al., 2010). Thus for detecting stress, features such

as the mean SC and features for distinguishing the

rising and falling parts of the signals (e.g. the mean

of the absolute derivative and proportions of positive

samples in derivative) can be used.

Furthermore EMG activity, e.g. in the trapezoid

muscle (Lundberg et al., 1994) are known to increase

PhyCS 2016 - 3rd International Conference on Physiological Computing Systems

116

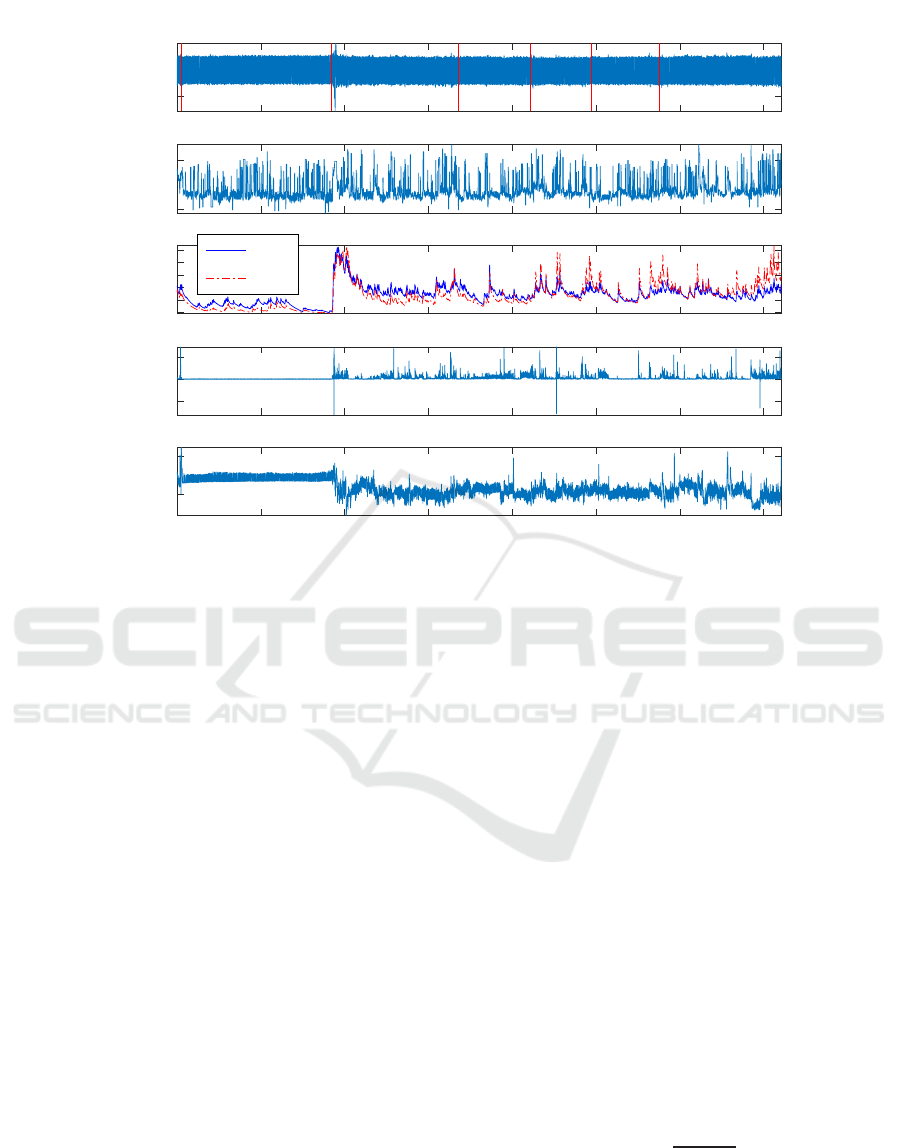
500 1000 1500 2000 2500 3000 3500

-1

ECG [mV]

Drive 15 preprocessed

R1 C1 H1 C2 H2 C3

500 1000 1500 2000 2500 3000 3500

100

HR [bpm]

500 1000 1500 2000 2500 3000 3500

SC [µ S]

foot

hand

500 1000 1500 2000 2500 3000 3500

-20

EMG [mV]

500 1000 1500 2000 2500 3000 3500

time [s]

RESP [mV]

Figure 1: All physiological signals from Drive 15, preprocessed for artifact removal and split into 6 phases according to the

marker signal.

with stress, correspondingto muscle tension. This can

be observed by an increase in the signal energy.

A ﬁnal physiological signal for detection of stress

is the respiration, usually measured by a band that

records chest expansion. This signal is highly cou-

pled with HR by respiratory sinus arrhythmia, which

decreases the HR while exhaling. The respiration

signal can thus be used to remove respiratory inﬂu-

ence on the ECG signal, allowing for more relevant

HRV analysis in stress detection (Choi and Gutierrez-

Osuna, 2010). The same applies for the SC sig-

nal, which increases while breathing out (Cacioppo

et al., 2007, p. 239), making the respiration signal

useful combined with electrodermal activity (Bouc-

sein, 2012). Examples of respiration signal features

for stress detection include ones related to breath size

and its variability (e.g. the mean and standard devia-

tion of the signal), and energy in different frequency

bands (Yong Deng, 2013). Another example is the

respiration rate (Wijsman et al., 2011).

4.1 Feature Calculation

Firstly, all signals were visually inspected for arti-

facts, e.g. unreasonably high heart rates (above 220

bpm) or sensor contact problems. Secondly, the pre-

processed signals of each class were split into non-

overlapping time-windows of 60 seconds, each with

a label Y = −1 or Y = 1 depending on the class of

the time-window. For the RvsD classes, the number

of samples n

in each drive varied between 14 and 16

for class R and 37 ≤ n

≤ 52 for class D. Similarly,

for the HvsC classes, 13 ≤ n

≤ 17 in class H and

22 ≤ n

≤ 36 in class C. This means that the classes

were imbalanced, which will be dealt with further on.

The 14 selected features are speciﬁed in Table 2. The

SC features originated from the hand electrodes; the

foot SC signal was excluded due to it representing the

same measure as the SC hand signal, which gives un-

wanted side effects on wrapper feature selection algo-

rithms.

4.2 Normalization

To compensate for inter-individual differences (e.g.

different resting heart rates), the initial rest period R

was used for normalizing each feature F to F

accord-

ing to

F − µ

, (1)

where σ

represents the standard deviation of the fea-

ture across all users and periods and µ

represents

the mean of the feature during the last two time-

windows of the initial rest period. Only the last two

Feature and Sensor Selection for Detection of Driver Stress

117

Table 2: The features and their descriptions.

Feature Description

Signal: HR [bpm]

mean heart rate

RMS

IBIdif f

root mean square of successive

differences of inter-beat inter-

vals

sum of energy in low frequency

(LF) band (0.04 – 0.15 Hz)

sum of energy in high fre-

quency (HF) band (0.15 – 0.50

Hz)

LFHF

ratio between energies in LF

and HF bands

Signal: SC [mV] (foot and hand)

mean skin conductance level

′+ mean of positive derivative

|SC

′

mean of absolute derivative

+/SC

′

proportion of positive samples

in derivative

max

number of local maxima

Signal: EMG [mV]

RMS

EMG

root mean square of EMG

Signal: Resp [mV]

(max− µ)

Resp

maximal respiration – mean of

respiration (range)

Resp

respiration rate

Resp

standard deviation of the respi-

ration

time-windows were used since R

is also a class in

the RvsD case. These two time-windows were sub-

sequently deleted from the RvsD R class, to prevent

their inﬂuence on the classiﬁer accuracy. This means

that after normalization, in the RvsD case class R

contained 12 ≤ n

≤ 14. The reason for dividing by

the standard deviation across all features is to avoid

bias of choosing features with great variance without

involving any subject-speciﬁc data that could poten-

tially lead to overlearning.

5 METHOD

Having deﬁned a set of features, it is important to

choose an optimal subset among them by different

feature selection methods. This serves two purposes:

training the most generalizable and accurate model,

and getting a better understanding of the relationship

between the physiological signals and the stress state

of the subject. This subset (the feature space), needs

to contain enough features to distinguish the classes,

but limiting its size is important to avoid overﬁtting.

This can be done by univariate (ﬁlter) methods, that

consider the features one by one, or by multivariate

(wrapper) methods, that try different combinations of

the features with the help of a classiﬁer. The chosen

methods are presented in Sections 5.2 and 5.3. For all

feature selection methods, we deﬁne X as the features

and Y as the labels.

5.1 Use Cases

By combining the two calibration methods described

in Section 1 with the two previously explained class

deﬁnitions (RvsD and HvsC), we obtain four use

cases:

1. Rest versus driving, single-user

2. Rest versus driving, multi-user

3. Highway versus city, single-user

4. Highway versus city, multi-user

These four use cases were analyzed and compared, in

order to provide a basis for an optimal feature and sen-

sor choice for each of them. All the following meth-

ods have been applied to every use case.

5.2 Filter Feature Selection

This section presents all the ﬁlter feature selection

methods used in this work. Their common element

is that they test features individually, to get an idea

of their predictive power of stress levels one by one

(although some versions exist that are capable of an-

alyzing feature combinations). For all ﬁlter methods,

the single-user case means calculating the coefﬁcients

for each drive, then averaging across all drives. The

multi-user case means putting the data from all drives

together in a large vector, then calculating the coefﬁ-

cients.

Pearson’s linear correlation coefﬁcient r (Duda

et al., 2000, p. 614) is a simple tool for studying the

relevance of features. This can give a preliminary in-

dication of the importance of a feature, but one must

keep in mind that it only analyzes linear correlations.

Spearman’s rank correlation ρ (Spearman,

1904) measures the statistical dependence between

two variables by testing how well they can be re-

lated by a monotonic function. This has the advan-

tage of being capable of detecting non-linear depen-

dencies, as opposed to Pearson’s linear correlation.

Kendall’s rank correlation coefﬁcient (Kendall and

Gibbons, 1990) was also tested, with identical results.

The Fisher score F

(Arunasakthi et al., 2014) was

PhyCS 2016 - 3rd International Conference on Physiological Computing Systems

118

calculated for each feature. It is given by

(µ

(Y=−1)

− µ

(Y=1)

)

(Y=−1)

+ σ

(Y=1)

, (2)

where µ and σ correspond to the mean and the stan-

dard deviation of the feature over each class, re-

spectively. Features having means that differ greatly

across classes with low standard deviation will have

high Fisher scores.

A widely used tool in classiﬁcation problems is

the receiver operating characteristic (ROC) (Han-

ley and Mcneil, 1982), which compares the number of

correctly predicted positive samples among all posi-

tive samples (true positive rate, TPR), versus the num-

ber of falsely predicted positive samples among all

positive samples (false positive rate, FPR). A ROC

curve can be obtained by letting a feature predict the

label when varying its threshold, followed by plotting

FPR against TPR for each threshold. A feature with

high predictive power will then maintain a high TPR

with a low FPR. The area under the ROC curve (AUC)

will thus increase, which is why it is an interesting

analysis for feature selection. The numerical integra-

tion of the area under the curve was calculated by the

trapezoid method.

5.3 Wrapper Feature Selection

Individually useless features can have a great pre-

dictive power when combined with other features in

classiﬁcation algorithms. Furthermore, a safe way of

knowing that the feature subset is good, is letting the

classiﬁer itself choose it. Wrapper feature selection

methods solve this problem by choosing feature com-

binations based upon their classiﬁcation performance.

This has of course the disadvantage of introducing

a bias from the choice of classiﬁer and its parame-

ters, as well as increasing the risk of overlearning the

model by adapting it too much to the data. For the

wrapper feature selection, in the single-user case a 5-

fold crossvalidation was performed, combined with

bootstrap aggregating (Duda et al., 2000, p. 474) re-

peated 100 times (to reduce the variance in perfor-

mance between the random crossvalidation subsets).

In the multi-user case, leave-one-drive-out cross val-

idation was used, by excluding one entire drive of

one participant, and learning with the remaining ones.

This gives the basis for a stress model that is generic

(capable of classifying the state of new drivers that

have not been used for training it). In multi-user, be-

fore the learning step, the minority class data was uni-

formly oversampled to achieve class balance, discour-

aging the model from always predicting only the ma-

jority class. Oversampling could not be done in the

single-user validation since both classes are not guar-

anteed to be represented in every bootstrap conﬁgura-

tion.

5.3.1 The Naive Bayes Classiﬁer

In this study, we use the naive Bayes (NB) classi-

ﬁer, a simple probabilistic classiﬁer (Hastie et al.,

2009, p. 210-211). Based upon the feature vector

X = X

,.. .,X

(containing n

features), it calculates

the posterior probability P(Y

|X) of X belonging to

class Y

(among a total of n

classes) using Bayes’

theorem:

P(Y

|X) =

P(Y

)P(X|Y

)

P(X)

. (3)

The prior probability P(Y

) is simply the frequency

of class Y

. The evidence P(X) is the frequency of

the feature, which is irrelevant for the classiﬁcation

problem. The NB classiﬁer assumes conditional in-

dependence of all features X in class c, i.e. that no

correlations exist between them. The likelihood P(X)

can thus be written as

P(X|Y

) =

∏

f=1

P(X

). (4)

Assuming a normal distribution of the data (Gaussian

naive Bayes), the learning step consists of calculating

the mean µ

f,c

and the standard deviation σ

f,c

of each

feature f over each class c. The likelihood of a new

observation X belonging to class Y

is then given by

P(X

) =

2πσ

f,c

−

−µ

f,c

)

2σ

f,c

. (5)

The class of X is ﬁnally predicted as the one with the

highest posterior probability:

Y = argmax

P(Y

|X). (6)

The motivebehind choosing the naive Bayes classiﬁer

is that it is parameterless (unlike e.g. support vector

machines (SVM), (Hastie et al., 2009, p. 417-419)).

An SVM requires choosing an appropriate kernel and

tuning a parameter, which will not necessarily be the

same for all our use cases.

5.3.2 Performance Measure

To measure the classiﬁer performance, we deﬁne the

balanced accuracy

TPR+ TNR

, (7)

Feature and Sensor Selection for Detection of Driver Stress

119

TNR being the true negative rate, the amount of cor-

rectly predicted negatives among all negative sam-

ples. The balanced accuracy punishes misclassiﬁca-

tion of minority class samples more heavily, compen-

sating for the fact that the classes are not represented

by the same number of samples. Upon a

, the margin

of error at 95 % is deﬁned:

m = 1.96

(1− a

)

, (8)

where n

represents the total number of samples used

in the cross-validated prediction.

5.3.3 Exhaustive Feature Selection

The absolutely safest way of choosing an optimal fea-

ture space is to test the classiﬁcation performance

of all possible subsets, i.e. exhaustive feature selec-

tion. This quickly becomes very computationally ex-

pensive. To reduce this problem, an exhaustive fea-

ture selection was performed within the features of

each sensor, giving an optimal subset of features from

every sensor signal. To decide whether adding an

additional feature gave a signiﬁcant improvement or

not, Student’s paired t-test (Kreyszig, 1970, p. 206)

was performed on all cross-validated performances,

with a signiﬁcativity threshold set at 0.05. Similarly,

Student’s paired t-test was performed to decide if

each performance was signiﬁcantly greater than pure

guessing (a

= 50 %), denoted t

, also with a signi-

ﬁcativity threshold set at 0.05.

5.3.4 Sensor Selection

When an optimal subset for each individual sensor

had been deﬁned, the respective subsets were com-

bined. This resulted in six sensor pairs, four sensor

triples and ﬁnally one combination where all four sen-

sors were represented. The combination with the best

classiﬁcation performance was then chosen for each

use case. t

was also calculated for each sensor com-

bination, to determine if its performance was superior

to random guessing.

6 RESULTS AND DISCUSSION

The results of the previously mentioned feature se-

lection methods are presented and discussed in this

section. Table 3 summarizes the best 5 features ac-

cording to the ﬁlter feature selection methods. For

each method and use case, the features have been

given a rank (descending order through the 14 tested

features), depending on their ﬁlter feature selection

score. The mean of all ranksµ

rank

has then been calcu-

lated, to give a notion of the combined score for each

feature across all the methods. Table 4 presents the

optimal combination of features extracted from each

sensor (exhaustively selected). The “Sensors” row

then speciﬁes the optimal sensor combination. Re-

sults upon validation data are presented for each op-

timal feature combination, using the balanced accu-

racy a

. Across the two tables, seven features are fre-

quently represented: max

, µ

|SC

′

, +/SC

′

(max−µ)

Resp

, and σ

Resp

. To a lesser extent, ﬁve other

features can also be found: RMS

EMG

, F

Resp

, µ

′+ ,

, and HF

. In terms of sensor choice, the HR

sensor is consistently chosen across all cases, often

with support of SC and/or respiration respiration mea-

sures. The EMG sensor is chosen only in one of the

cases. As in (Akbas, 2011) and (Queyam, 2013), the

mean heart rate and the mean SC level prove them-

selves relevant. Like in (Healey and Picard, 2005)

and (Yong Deng, 2013), µ

is among the top choices.

Resp

is not present in previous studies on the same

database, which primarily favor the respiration rate.

Concerning the classiﬁcation performances, RvsD

is a quite easy task, even in multi-user. Using only

the respiration signal, reasonable accuracy is reached.

HvsC is naturally more difﬁcult, reaching signiﬁcant

accuracy in the single-user case, while the multi-user

case is just slightly above random guessing for some

sensors. Compared to previous studies (e.g. 94.7 % in

(Healey and Picard, 2005)), the classiﬁcation perfor-

mances are quite low, at least for the HvsC. However

in terms of calibration, cross-validation method and

signal segmentation with respect to the experimental

phases, this study corresponds to a more realistic ap-

plication.

To further validate the results, the same study with

other classiﬁer algorithms should be done. No com-

plete exhaustive feature selection is performed, since

this is ﬁrstly done within each sensor. This means that

not all feature combinations are considered, and fea-

ture combinations that might improve accuracy could

be excluded. It would however be extremely time-

consuming to try all feature combinations, which is

why we perform a subselection within each sensor

ﬁrstly. Furthermore, when selecting sensors it is im-

portant to point out that an EMG sensor is compli-

cated to equip and can be quite invasive, which is also

true for the respiration sensor to a certain extent. It is

mainly the HR and SC signals that can be acquired by

simple wearable sensors with the current technology,

which is important to point out when selecting them.

PhyCS 2016 - 3rd International Conference on Physiological Computing Systems

120

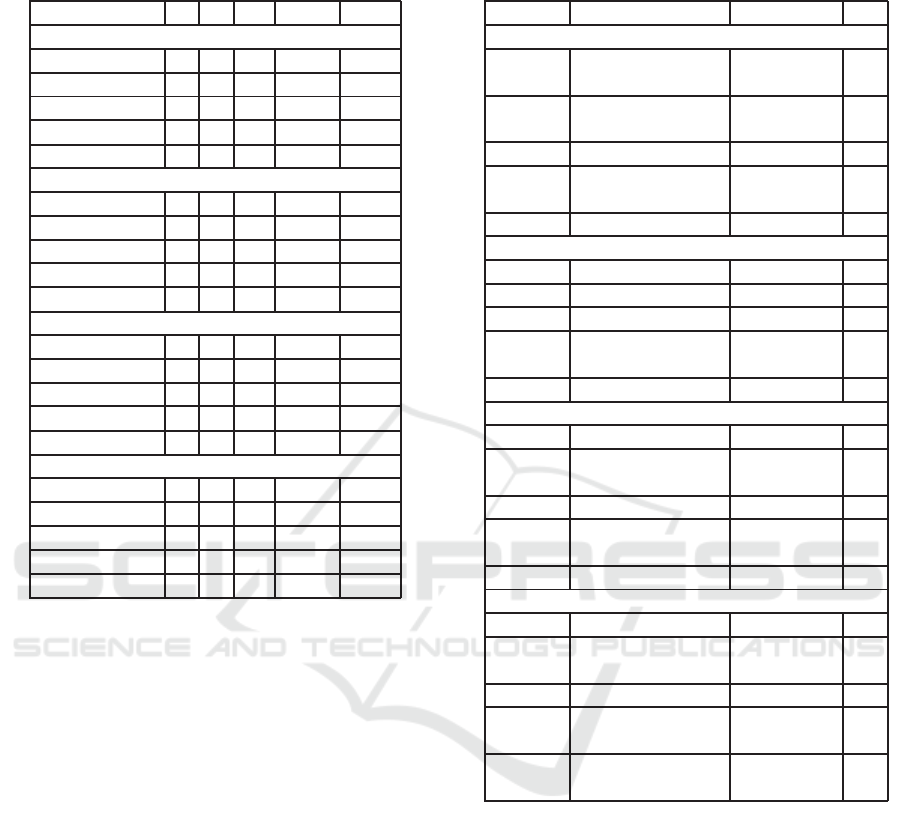
Table 3: Top 5 ranked features for each use case, according

to the ﬁlter methods.

Feature r ρ F

AUC µ

rank

Rest vs. driving, single-user

2 2 2 1 1.75

+/SC

′

3 3 3 2 2.75

max

1 1 1 11 3.5

|SC

′

5 4 6 3 4.5

4 6 4 6 5

Rest vs. driving, multi-user

max

1 1 1 1 1

3 2 3 2 2.5

+/SC

′

2 3 2 3 2.5

4 5 4 5 4.5

|SC

′

5 4 5 4 4.5

Highway vs. city, single-user

max

1 2 1 2 1.5

Resp

2 1 3 1 1.75

3 4 2 3 3

|SC

′

5 3 5 4 4.25

+/SC

′

4 6 4 6 5

Highway vs. city, multi-user

max

1 2 1 2 1.5

Resp

2 1 3 1 1.75

|SC

′

4 3 4 3 3.5

+/SC

′

3 5 2 5 3.75

(max− µ)

Resp

5 4 5 4 4.5

7 CONCLUSIONS

In terms of classiﬁcation, learning one model per user

yields better accuracy than creating a universal multi-

user model. Moreover, classifying rest from activity

is easier than classifying a less stressful task from a

more stressful one. Independentlyof the classiﬁcation

problem (rest from activity or low stress from high

stress) and independently of the calibration method,

seven features have been found to be robust across

both ﬁlter and wrapper methods: max

, µ

|SC

′

, +/SC

′

, (max−µ)

Resp

, and σ

Resp

. The ﬁlter fea-

ture selection used in this study has given a good pre-

liminary idea of the usefulness of each feature, but to

deal with feature combinations wrapper methods are

necessary.

A problem with the MIT Stress Recognition in

Automobile Drivers Database is that it consists solely

of one type of stress. For a robust real-time algorithm

to work in daily life, one needs to identify stress char-

acteristics from several different stress types. This is

the purpose of an experimental database currently in

development, where laboratory stressors correspond-

Table 4: Exhaustive feature selection and sensor selection

results.

Signal Optimal content a

± m [%] t

Rest vs. driving, single-user

HR µ

, LF

82.3 ± 3.3 1

SC µ

, µ

′+ ,

+/SC

′

93.2 ± 2.2 1

EMG RMS

EMG

87.5 ± 2.8 1

Resp (max − µ)

Resp

, σ

Resp

89.3 ± 2.7 1

Sensors HR + SC 94.6 ± 1.9 1

Rest vs. driving, multi-user

HR µ

76.0 ± 3.6 1

SC max

83.6 ± 3.2 1

EMG RMS

EMG

66.6 ± 4.0 1

Resp (max − µ)

Resp

, σ

Resp

85.3 ± 3.0 1

Sensors HR + SC + Resp 87.3 ± 2.8 1

Highway vs. city, single-user

HR µ

, LF

64.8 ± 4.7 1

SC µ

, µ

′+ , µ

|SC

′

max

74.9± 4.3 1

EMG RMS

EMG

59.4 ± 4.8 1

Resp (max − µ)

Resp

, σ

Resp

71.2 ± 4.4 1

Sensors HR + SC + Resp 78.1 ± 4.1 1

Highway vs. city, multi-user

HR µ

60.1 ± 4.7 1

SC µ

, µ

|SC

′

max

65.0 ± 4.6 1

EMG RMS

EMG

57.7 ± 4.7 1

Resp (max − µ)

Resp

, σ

Resp

71.8 ± 4.3 1

Sensors HR + EMG +

Resp

72.1 ± 4.3 1

ing to different stress types are applied to subjects

equipped with a similar sensor conﬁguration. Addi-

tionally, an experiment is planned where the subjects

are equipped with wearable sensors every day for a

week, allowing an analysis of physiological reactions

to daily events, including transport and driving. Fu-

ture work includes acquiring and analyzing this data,

for further validation of the most relevant sensors and

features in stress detection.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Horizon 2020 research and innovation pro-

gramme under grant agreement No 635867.

Feature and Sensor Selection for Detection of Driver Stress

121

REFERENCES

Akbas, A. (2011). Evaluation of the Physiological Data In-

dicating the Dynamic Stress Level of Drivers. Scien-

tiﬁc Research and Essays, 6(2):430 – 439.

Arunasakthi, K., KamatchiPriya, L., and Askerunisa, A.

(2014). Fisher Score Dimensionality Reduction

for Svm Classiﬁcation. In International Confer-

ence on Innovations in Engineering and Technology

(ICIET14), pages 1900–1904. International Journal

of Innovative Research in Science, Engineering and

Technology.

Boucsein, W. (2012). Electrodermal Activity. The Springer

series in behavioral psychophysiology and medicine.

Springer US.

Boˇril, H., Boyraz, P., and Hansen, J. H. (2009). Towards

Multi-Modal Drivers Stress Detection. In 4th Biennial

Workshop on DSP for In-Vehicle Systems and Safety,

Dallas, TX, USA.

Cacioppo, J. T., Tassinary, L. G., and Berntson, G., editors

(2007). Handbook of Psychophysiology. Cambridge

University Press, third edition. Cambridge Books On-

line.

Choi, J. and Gutierrez-Osuna, R. (2010). Estimating Mental

Stress Using a Wearable Cardio-respiratory Sensor. In

Proceedings of IEEE Sensors, pages 150–154. IEEE.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern

Classiﬁcation. Wiley-Interscience, second edition.

Gao, H., Yuce, A., and Thiran, J.-P. (2014). Detecting

Emotional Stress from Facial Expressions for Driv-

ing Safety. In Image Processing (ICIP), 2014 IEEE

International Conference on, pages 5961–5965.

Hanley, J. A. and Mcneil, B. J. (1982). The Meaning and

Use of the Area Under a Receiver Operating Charac-

teristic (ROC) Curve. Radiology, 143:29–36.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The El-

ements of Statistical Learning. Springer, second edi-

tion.

Healey, J. and Picard, R. (2000). SmartCar: Detecting

Driver Stress. In Pattern Recognition, 2000. Proceed-

ings. 15th International Conference on, volume 4,

pages 218–221.

Healey, J. and Picard, R. W. (2008). Stress Recogni-

tion in Automobile Drivers (drivedb). Available at

http://physionet.org/cgi-bin/atm/ATM.

Healey, J. A. and Picard, R. W. (2005). Detecting Stress

During Real-World Driving Tasks Using Physiologi-

cal Sensors. Intelligent Transportation Systems, IEEE

Transactions on, 6(2):156–166.

Hennessy, D. A. and Wiesenthal, D. L. (1999). Trafﬁc Con-

gestion, Driver Stress, and Driver Aggression. Ag-

gressive Behavior, 25(6):409–423.

Hernandez, J., McDuff, D., Benavides, X., Amores, J.,

Maes, P., and Picard, R. (2014). AutoEmotive: Bring-

ing Empathy to the Driving Experience to Manage

Stress. In Proceedings of the 2014 Companion Pub-

lication on Designing Interactive Systems, DIS Com-

panion ’14, pages 53–56, New York, NY, USA. ACM.

Kappeler-Setz, C., Arnrich, B., Schumm, J., La Marca, R.,

Tr¨oster, G., and Ehlert, U. (2010). Discriminating

Stress From Cognitive Load Using a Wearable EDA

Device. IEEE Transactions on Information Technol-

ogy in Biomedicine, 14(2):410–417.

Kendall, M. and Gibbons, J. (1990). Rank Correlation

Methods. A Charles Grifﬁn Book. E. Arnold.

Kreyszig, E. (1970). Introductory Mathematical Statistics:

Principles and Methods. Wiley.

Lundberg, U., Kadefors, R., Melin, B., Palmerud, G.,

Hassm´en, P., Engstr¨om, M., and Elfsberg Dohns, I.

(1994). Psychophysiological Stress and EMG Activ-

ity of the Trapezius Muscle. International Journal of

Behavioral Medicine, 1(4):354–370.

Palinko, O., Kun, A. L., Shyrokov, A., and Heeman, P.

(2010). Estimating Cognitive Load Using Remote Eye

Tracking in a Driving Simulator. In Proceedings of the

2010 Symposium on Eye-Tracking Research &

Applications, ETRA ’10, pages 141–144, New York,

NY, USA. ACM.

Queyam, A. B. (2013). A Novel Method of Stress Detec-

tion using Physiological Measurements of Automo-

bile Drivers. Master’s thesis, Thapar University.

Rigas, G., Goletsis, Y., and Fotiadis, D. (2012). Real-Time

Driver’s Stress Event Detection. Intelligent Trans-

portation Systems, IEEE Transactions on, 13(1):221–

234.

Singh, M. and Queyam, A. B. (2013). Stress Detection in

Automobile Drivers using Physiological Parameters:

A Review. International Journal of Engineering Edu-

cation, 5(2):1 –5.

Spearman, C. (1904). The Proof and Measurement of As-

sociation Between Two Things. American Journal of

Psychology, 15:88–103.

Sun, F., Kuo, C., Cheng, H., Buthpitiya, S., Collins, P., and

Griss, M. L. (2010). Activity-Aware Mental Stress

Detection Using Physiological Sensors. In Mobile

Computing, Applications, and Services - Second In-

ternational ICST Conference, MobiCASE 2010, Santa

Clara, CA, USA, October 25-28, 2010, Revised Se-

lected Papers, pages 211–230.

Wijsman, J., Grundlehner, B., Liu, H., Hermens, H., and

Penders, J. (2011). Towards Mental Stress Detec-

tion Using Wearable Physiological Sensors. In Engi-

neering in Medicine and Biology Society,EMBC, 2011

Annual International Conference of the IEEE, pages

1798–1801.

Yong Deng, Zhonghai Wu, C.-H. C. Q. Z. D. F. H. (2013).

Sensor Feature Selection and Combination for Stress

Identiﬁcation Using Combinatorial Fusion. Interna-

tional Journal of Advanced Robotic Systems, 10.

PhyCS 2016 - 3rd International Conference on Physiological Computing Systems

122