Fuzzy Rule-based Classifier Design with Co-Operative Bionic

Algorithm for Opinion Mining Problems

Shakhnaz Akhmedova, Eugene Semenkin and Vladimir Stanovov

Department of System Analysis and Operations Research, Siberian State Aerospace University,

“Krasnoyarskiy Rabochiy” Avenue, 31, Krasnoyarsk, 660037, Russia

Keywords: Fuzzy Rule-based Classifiers, Bionic Algorithms, Optimization, Opinion Mining.

Abstract: Automatically generated fuzzy rule-based classifiers for opinion mining are presented in this paper. A

collective nature-inspired self-tuning meta-heuristic for solving unconstrained real-valued optimization

problems called Co-Operation of Biology Related Algorithms and its modification with a biogeography

migration operator for binary-parameter optimization problems were used for the design of classifiers. The

basic idea consists in the representation of a fuzzy classifier rule base as a binary string and the parameters

of the membership functions of the fuzzy classifier as a string of real-valued variables. Three opinion

mining problems from the DEFT’07 competition were solved using the proposed classifiers. Experiments

showed that the fuzzy classifiers developed in this way outperform many alternative methods at the given

problems. The workability and usefulness of the proposed algorithm are confirmed.

1 INTRODUCTION

Opinion mining problems are the problems of

determining the judgement of a speaker about a

particular topic. This kind of problem is also called

sentiment analysis, and for example, can be found in

the analysis of a person’s opinion through a

document (Pang and Lee, 2008). The person’s

attitude may be described as an emotional state,

judgement or evaluation. A typical approach is to

use terms which explicitly express the person’s

opinion, for example, a “positive” or “negative”

review.

One of the applications of these opinion mining

algorithms is the monitoring of astronauts’

emotional states and hidden misunderstandings

during a long-term mission. For this aim, an opinion

mining model can be implemented on Earth using a

set of data obtained during experiments and then

included in an on-board and/or ground-based control

system for monitoring and controlling the mission.

Today, there are several machine learning

approaches developed for opinion mining problems,

including “bag of words”, semantic analysis, etc.

(Pang et al., 2002). One of the ways to address these

problems is by considering them as text

categorization problems, as the representation of the

documents influences the classification quality (Ko,

2012).

In this study the fuzzy rule-based classifiers

generated by a meta-heuristic called Co-Operation

of Biology Related Algorithms (COBRA)

(Akhmedova and Semenkin, 2013) and its

modification, which uses a biogeography migration

operator, are described. COBRA is based on the

cooperation of 5 nature-inspired algorithms: Particle

Swarm Optimization (PSO) (Kennedy and Eberhart,

1995), Wolf Pack Search (WPS) (Yang et al., 2007),

the Firefly Algorithm (FFA) (Yang, 2009), the

Cuckoo Search Algorithm (CSA) (Yang and Deb,

2009) and the Bat Algorithm (BA) (Yang, 2010).

The workability and reliability of COBRA was

shown in (Akhmedova and Semenkin, 2013) on a set

of benchmark functions.

Thus the mentioned fuzzy rule-based classifiers

were used with the text pre-processing technique

proposed in (Gasanova et al., 2013) for solving three

opinion mining problems which were taken from the

DEFT’07 competition. The rest of this paper is

organized as follows. In the second section the

proposed algorithm is described. The term weighting

scheme is shown in the third section. Next

experimental results are presented and some

conclusions are given.

Akhmedova, S., Semenkin, E. and Stanovov, V.

Fuzzy Rule-based Classiﬁer Design with Co-Operative Bionic Algorithm for Opinion Mining Problems.

DOI: 10.5220/0005974700680074

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 68-74

ISBN: 978-989-758-198-4

2 AUTOMATICALLY

GENERATED FUZZY

RULE-BASED CLASSIFIERS

2.1 Co-Operation of Biology Related

Algorithms (COBRA)

The meta-heuristic approach Co-Operation of Biology

Related Algorithms (COBRA) was originally

developed for solving real-valued optimization

problems (Akhmedova and Semenkin, 2013). The

mentioned approach is based on the collective work

of PSO, WPS, FFA, CSA and BA and consists in

generating 5 populations which are then executed in

parallel cooperating with each other.

The algorithm COBRA is a self-tuning meta-

heuristic, so there is no need to choose the population

size. The number of individuals in the population of

each algorithm can increase or decrease depending on

whether the fitness value improves: if the fitness

value does not improve over a given number of

generations, then the size of all populations increases

and vice versa. Besides, on each generation a “winner

algorithm” is determined: the algorithm with the best

population’s average fitness value. The population of

the winner algorithm “grows” by accepting

individuals removed from other populations. The

migration operator of the given approach consists in

replacement of the worst individuals of each

population by the best individuals of others.

However, frequently the applied problems are

defined in discrete valued spaces where the domain

of the variables is finite. Therefore, a modification

of COBRA called COBRA-b for solving binary-

parameter optimization problems was introduced in

(Akhmedova and Semenkin, 2014). Namely its

component-algorithms were adapted to search in

binary spaces by applying a sigmoid transformation

(Kennedy and Eberhart, 1997) to the velocity

components (PSO, BA) or coordinates (WPS, FFA,

CSA) to squash them into a range [0, 1] and force

the component values of the positions of individuals

to be 0’s or 1’s:

()

exp1

−+

(1)

So the binarization of individuals in algorithms is

conducted using the calculated value of the sigmoid

function. After that a random number rand from the

range [0, 1] is generated and the corresponding

component value of the position of the individual is

1 if rand is smaller than s(v) and 0 otherwise.

An experiment showed that the COBRA

algorithm and its modification COBRA-b work

efficiently and that they are reliable. Moreover, it

was established that the meta-heuristics COBRA and

COBRA-b outperform their component-algorithms.

Yet in some cases COBRA-b requires too many

calculations.

As a consequence COBRA-b was also modified,

specifically its migration operator (Akhmedova and

Semenkin, 2016). For this purpose a biogeography-

based optimization (BBO) (Simon, 2008) algorithm,

which translates the natural distribution of species

into a general problem solution, was used.

Habitat, in biogeography, is a particular type of

local environment occupied by an organism, where

the island is any area of suitable habitat. Each island

represents one solution, where a good problem

solution means that the island has lots of good biotic

and abiotic factors, and attracts more species than

the other islands. In BBO the number of species on

an island is based on the dynamic between new

immigrated species onto an island and the extinct

species from that island. The purpose of the

migration process is to use “good” islands as a

source of modification to share their features with

“bad” islands, so the poor solutions can be

probabilistically enhanced and may become better

than those good solutions (Simon, 2008).

Thus, in the new version of COBRA-b the

individuals of each population can be updated (but not

replaced) by the individuals of the other populations.

However a certain number of individuals with the

highest fitness value will not be changed but can be

used for updating other individuals.

Experiments show that the modification of

COBRA-b with a BBO migration operator allows

better solutions to be found with a smaller number of

calculations (Akhmedova and Semenkin, 2016). The

results obtained in (Akhmedova and Semenkin,

2016) demonstrate that the new version of the

algorithm outperforms the original COBRA-b both

by the average number of function evaluations and

by the best function value achieved during the work

of the algorithm, averaged over 100 program runs.

2.2 Fuzzy Rule-based Classifiers

The classification problem can be described as a

problem of creating a classifier C: R

→ L, where C

is the classifier, R

is the feature space with N

variables, and L is the set of labels. Each vector in

the feature space x = [x

,…,x

]

ϵ R

is an object of

the available sample.

The fuzzy logic-based classifier consists of a

number of rules R

, m = 1,…,M; where M is the

Fuzzy Rule-based Classiﬁer Design with Co-Operative Bionic Algorithm for Opinion Mining Problems

number of rules:

= IF x

is A

1,j(m,1)

and … and x

is A

N,j(m,N)

THEN Y is L

(2)

where Y is the output, L

is the label for rule m,

N,j(m,N)

is the fuzzy set for the N-th feature, and

j(m,N) is the number of fuzzy set for the m-th rule

and the N-th feature. For the current study the

maximum number of rules was set to be equal to 10

and repeating rules were removed at the end.

In this work we used 3 fuzzy sets for each

feature, plus the “Don’t Care” condition (DC). Each

fuzzy set was described by a Gaussian function:

()

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

−

−=

exp

(3)

where a is the mean value and σ is the variance. So

there are 2 parameters for each function and therefore

N real-valued parameters that have to be tuned.

The fuzzy inference method used the minimum

product calculation method to derive the

membership values for the output. The object was

classified by the winner-rule, i.e. the rule having the

largest membership value.

The rule base was encoded by numbers j(m,N)

and labels L

. For each feature in a rule, the number

of the fuzzy set was encoded by 2 bits: “00” means

DC condition (feature is not used), “01” is the first

fuzzy set, “10” and “11” are the second and third

fuzzy sets respectively. The class label was encoded

by several bits, depending on the number of classes.

The total number of binary variables, therefore, is

N+1)

Consequently the binary version of COBRA with

a biogeography migration operator is used for

finding the best rule base and the original COBRA is

used for the membership function parameter

adjustment of every rule base.

3 TERM WEIGHTING SCHEME

It is known that most machine learning algorithms

are designed for vector space models. Therefore, text

documents are usually transformed into vector

representation in so-called feature space. However

the document mapping into the feature space

remains a complex non-trivial task.

Text pre-processing techniques can be

considered as term weighting schemes: calculating

the weight of each word. At the same time the term

weighting methods can be divided into two groups:

supervised and unsupervised methods and almost all

of them use the frequency of the term occurring.

In this study we used the term relevance

estimation method which was proposed and

described in (Gasanova et al., 2013) and called “C-

values”. Its basic idea is that every word that appears

in the text has to contribute some value to a certain

class. So, the real number term relevance is assigned

for each word; and this number depends on the

frequency of the word occurrence. The term

relevance is calculated using a modified formula of

the fuzzy rule relevance estimation for the fuzzy

classifier. The membership function has been

replaced by word frequency in the current class.

Let L be the number of classes; n

is the number

of instances of the i-th class; N

is the number of the

j-th word occurrence in all instances of the i-th class;

= N

is the relative frequency of the j-th word

occurrence in the i-th class. R

= max

, S

arg(max

) is the number of class which we assign

to the j-th word. The term relevance, C

, is calculated

in the following way:

(

∑

≠

−

−=

jij

(4)

So each instance is represented by a vector of

L+1 numbers, where the first number is a class

identifier, and the other numbers are the sum of C

values of all the words that occurred in this instance

(according to their S

4 EXPERIMENTAL RESULTS

The DEFT07 or “Défi Fouille de Texte” Evaluation

Package (Actes de l'atelier DEFT'07, 2007) has been

used for the application of fuzzy rule-based

classifiers and the comparison of obtained results

with published data. For the testing of the proposed

approach three corpora were used, namely “Books”,

“Video games” (later just “Games”) and “Debates in

Parliament” (later just “Debates”). Descriptions of

the corpora are given in Table 1.

Table 1: Test corpora.

Corpus Description Marking scale

Books 3000 commentaries

about books, films

and shows

0:negative,

1:neutral,

2:positive

Games 4000 commentaries

about video games

0:negative,

1:neutral,

2:positive

Debates 28800 interventions

by Representatives in

the French Assembly

0:against the

proposed law,

1:for it

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

These corpora were divided into train (60%) and

test (40%) sets by the organizers of the DEFT’07

competition and this partition has been retained in

our study to be able to directly compare the

performance achieved using the fuzzy rule-based

classifiers described in this study with the algorithms

of participants. The train and test sets parameters of

all corpora are shown in Table 2.

Table 2: Corpora sizes.

Corpus Data set sizes Classes

(train set)

Classes

(test set)

Books Train = 2074

Test = 1386

Vocabulary =

52507

negative:

309

neutral: 615

positive:

1150

negative:

207

neutral: 411

positive:

768

Games Train = 2537

Test = 1694

Vocabulary =

63144

negative:

497

neutral:

1166

positive:

874

negative:

332 neutral:

583

positive:

779

Debates Train = 17299

Test = 11533

Vocabulary =

59615

against:

10400

for: 6899

against:

6572

for: 4961

In order to apply the classifiers, all words which

appear in the train and test sets have been extracted.

Then words have been assigned the same letter case:

dots, commas and other punctuation marks have

been removed. It should be mentioned that no other

information related to the language or domain, for

example stop or ignore word lists, has been used in

the pre-processing.

The F-score value with β = 1 (Van Rijsbergen,

1979) was used for evaluating the obtained results.

The F-score depends on the “precision” and “recall”

of each criterion.

()

recallprecision

scoreF

+×

××+

=−

(5)

The classification “precision” for each class is

calculated as the number of correctly classified

instances for a given class divided by the number of

all instances which the algorithm has assigned for this

class. “Recall” is the number of correctly classified

instances for a given class divided by the number of

instances that should have been in this class.

From the viewpoint of optimization, fuzzy rule-

based classifiers for these problems have from 50 to

70 binary variables for the rule base and from 18 to

24 real-valued variables for the membership

function parameters. For the final parameter

adjustment of membership functions (for the best

obtained rule base) the maximum number of

function evaluations was equal to 15000.

The results for all text categorization problems are

presented in Table 3 (there are also results obtained

for the best submission of other researchers for each

corpus which had been taken from (Actes de l'atelier

DEFT'07, 2007) and (Akhmedova et al., 2014)).

The results for each corpus were ranked and then

the total rank was evaluated by the following formula:

321 rankrankrank

Rank

(6)

Therefore the best results were obtained by the

method with the smallest Rank value, and vice versa,

the worst results were obtained by the method with

the largest Rank value.

Table 3: Comparison of results obtained by different

research teams.

Team or

method

Books

(rank1)

Games

(rank2)

Debates

(rank3)

Rank

J.-M. Torres-

Moreno (LIA)

0.603

(3)

0.784

(1)

0.720

(1)

G. Denhiere

(EPHE)

0.599

(5)

0.699

(7)

0.681

(6)

S. Maurel

(CELI France)

0.519

(8)

0.706

(5)

0.697

(5)

M. Vernier

(GREYC)

0.577

(6)

0.761

(3)

0.673

(9)

E. Crestan

(Yahoo ! Inc.)

0.529

(9)

0.673

(9)

0.703

(4)

M. Plantie

(LGI2P)

0.472

(11)

0.783

(2)

0.671

(10)

A.-P. Trinh

(LIP6)

0.542

(7)

0.659

(10)

0.676

(8)

M. Genereux

(NLTG)

0.464

(12)

0.626

(11)

0.569

(13)

E. Charton

(LIA)

0.504

(10)

0.619

(12)

0.616

(11)

A. Acosta

(Lattice)

0.392

(13)

0.536

(13)

0.582

(12)

SVM+COBRA

0.619

(1)

0.696

(8)

0.714

(2)

ANN+COBRA

0.613

(2)

0.727

(4)

0.709

(3)

FRBC+COBRA

(This study)

0.601

(4)

0.705

(6)

0.680

(7)

It should also be noted that in Table 3 only the

best results for the proposed technique are presented.

For the problem “Books” the best result obtained by

fuzzy rule-based classifiers was fourth, but the

difference between it and the third best result is not

significant. Generally, the new classification method

outperformed almost all alternative approaches.

Fuzzy Rule-based Classiﬁer Design with Co-Operative Bionic Algorithm for Opinion Mining Problems

Altogether the most recent results from

(Akhmedova et al., 2014) are better than the results

obtained in this study. However fuzzy rule-based

classifiers outperformed support vector machines

generated by COBRA for the problem “Games”.

On the other hand in the mentioned study

(Akhmedova et al., 2014) authors used different text

pre-processing techniques while solving these

opinion mining problems. And the following results

were presented in the same work (Akhmedova et al.,

2014) for the “C-value” term weighting scheme:

Table 4: Results presented in (Akhmedova et al., 2014) for

“C-values” term weighing scheme.

Team or method Books Games Debates

SVM+COBRA 0.619 0.696 0.700

ANN+COBRA 0.585 0.692 0.704

Thus, the classifiers proposed in this study with

the “C-values” text pre-processing technique

outperform both support vector machines and neural

networks designed by the COBRA approach with

the same term weighting scheme for the problem

“Games”; also fuzzy rule-based classifiers

outperforms neural networks for the problem

“Books”.

Besides, an advantage of the proposed

classification technique is the interpretability of the

obtained results. For example, it was established that

generally for the problem “Books” the second

attribute of instances is not important and can be

ignored if instances are negative or neutral

commentaries.

Examples of the rule base for the problems

“Books”, “Games” and “Debates” obtained during

one of the program runs are presented in Tables 5, 6

and 7 respectively. The presented rule bases are

typical for the solved problems. The following

denotations are used: DC – feature does not appear in

a given rule, 1, 2 or 3 – the first, the second or the

third membership function for a given feature is used,

and the class identifier is given in the last column.

Table 5: Example of the rule base for the problem

“Books”.

3 2 3 positive

3 1 2 neutral

3 DC 3 negative

1 DC 3 neutral

3 DC 2 negative

3 2 1 positive

DC 1 1 positive

2 3 3 neutral

DC 1 DC neutral

2 DC 3 negative

Table 6: Example of the rule base for the problem

“Games”.

2 3 2 neutral

2 2 DC negative

3 3 2 positive

2 2 2 neutral

2 3 3 negative

3 1 2 neutral

3 3 1 neutral

DC 2 2 neutral

1 1 3 positive

3 DC DC positive

Table 7: Example of the rule base for the problem

“Debates”.

2 1 against

DC 2 for

DC 3 for

2 3 for

3 2 against

1 DC against

2 2 for

Let us consider the problem “Games” as an

example to demonstrate the interpretability of the

obtained results. Instance for this problem were

described by a class identifier and 3 “C-values”

attributes, namely by the 3 sums of the C

values of

all words that occurred in this instance for the first

(“negative”), the second (“neutral”) and the third

(“positive”) classes respectively.

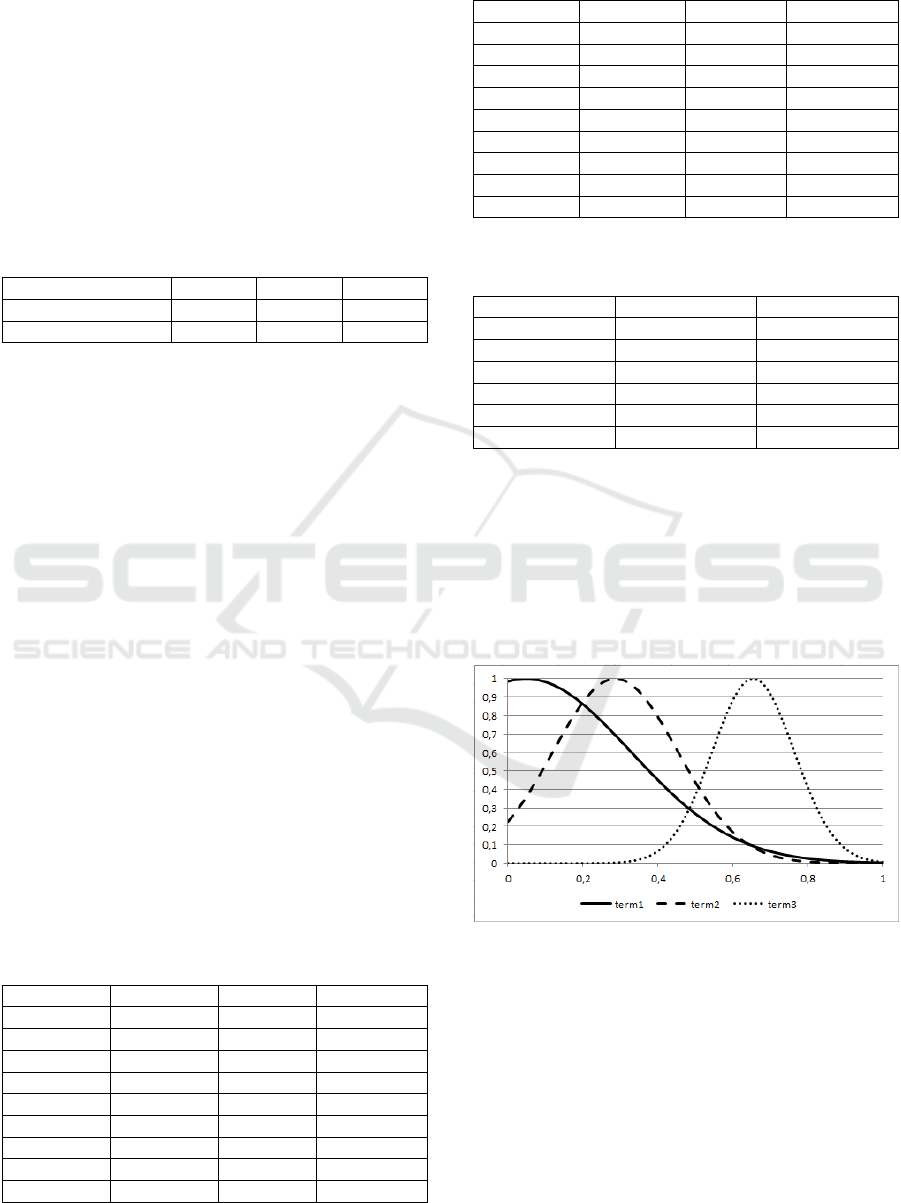
Figure 1: The membership functions of rules for the first

feature for the Games problem.

Figures 1, 2 and 3 demonstrate the membership

functions of rules presented in Table 6 for the

features of the problem “Games”.

Thus for the given rule base for the “Games”

problem the third linguistic variable of instances was

not important and could be ignored if instances were

negative commentaries. Also in general if the third

linguistic variable was about 0.3 then the instance

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

Figure 2: The membership functions of rules for the

second feature for the Games problem.

Figure 3: The membership functions of rules for the third

feature for the Games problem.

was determined by the classifier as “neutral

commentary”. And if the first linguistic variable was

about 0.7 then the instance was determined by

classifier as “positive commentary”.

In addition, figures 4 and 5 demonstrate

examples of the membership functions of rules

obtained for the first features of the problems

“Books” and “Debates” during one of the program

runs.

Figure 4: Examples of the membership functions of rules

for a feature for the Books problem (a).

Figure 5: Examples of the membership functions of rules

for a feature for the Debates problem (b).

Consequently the suggested algorithms

successfully solved all the problems of designing

classifiers with competitive performance. Thus the

study results can be considered as confirming the

reliability, workability and usefulness of the

algorithms in solving real world optimization

problems.

5 CONCLUSIONS

In this paper a modification of a self-tuning bionic

meta-heuristic called COBRA-b for solving

optimization problems with binary variables, which

consists in the implementation of a migration

operator from a BBO algorithm, is described. The

main purpose for modification was to lessen the

number of function evaluations required for solving

an optimization problem. The new technique

demonstrated better results than the original

COBRA-b, so it outperformed not only the

component algorithms but also COBRA-b.

The described optimization methods were used

for the automated design of fuzzy rule-based

classifiers. The modification of COBRA-b with a

BBO migration operator was used for the rule base

optimization of the classifier and the original

COBRA was used for the parameter adjustment of

membership functions. This approach was applied to

three opinion mining problems which were taken

from the DEFT’07 competition. A comparison with

alternative classification methods showed that fuzzy

rule-based classifiers designed by COBRA

outperformed many of them. This fact allows us to

consider the study results as confirmation of the

reliability, workability and usefulness of the

algorithms in solving real world optimization

problems.

Fuzzy Rule-based Classiﬁer Design with Co-Operative Bionic Algorithm for Opinion Mining Problems

Directions for future research are heterogeneous:

improvement of the cooperation and competition

scheme within the approach, addition of other

algorithms in cooperation, development of a

modification for mixed optimization problems, etc.

Also the application of the biogeography migration

operator to real-parameter constrained and

unconstrained versions of the meta-heuristic

COBRA may improve its workability.

ACKNOWLEDGEMENTS

This research is supported by the Russian

Foundation for Basic Research, within project № 16-

31-00349.

REFERENCES

Actes de l'atelier DEFT'07. Plate-forme AFIA 2007.

Grenoble, Juillet. http://deft07.limsi.fr/actes.php.

Akhmedova, Sh., Semenkin, E., 2013. Co-operation of

biology related algorithms. In IEEE Congress on

Evolutionary Computations. IEEE Publications.

Akhmedova, Sh., Semenkin, E., 2014. Co-operation of

biology related algorithms meta-heuristic in ANN-

based classifiers design. In IEEE World Congress on

Computational Intelligence. IEEE Publications.

Akhmedova, Sh., Semenkin, E., Sergienko, R.

automatically generated classifiers for opinion mining

with different term weighting schemes. In 11th

International Conference on Informatics in Control,

Automation and Robotics.

Akhmedova, Sh., Semenkin, E., 2016. Collective bionic

algorithm with biogeography based migration

operator for binary optimization, Journal of Siberian

Federal University, Mathematics & Physics, Vol. 9

(1).

Gasanova, T., Sergienko, R., Minker, W., Semenkin, E.,

Zhukov, E., 2013. A semi-supervised approach for

natural language call routing. In SIGDIAL 2013

Conference.

Kennedy, J., Eberhart, R., 1995. Particle swarm

optimization. In IEEE International Conference on

Neural Networks.

Kennedy, J., Eberhart, R., 1997. A discrete binary version

of the particle swarm algorithm. In World

Multiconference on Systemics, Cybernetics and

Informatics.

Ko, Y., 2012. A study of term weighting schemes using

class information for text classification. In 35th

international ACM SIGIR conference on Research and

development in information retrieval.

Pang, B., Lee, L, 2008. Opinion mining and sentiment

analysis, Now Publishers Inc. New-York.

Pang, B., Lee, L., Vaithyanathan, Sh., 2002. Thumbs up?

Sentiment classification using machine learning

techniques. In EMNLP, Conference on Empirical

Methods in Natural Language Processing.

Simon, D., 2008. Biogeography-based optimization, IEEE

Transactions on Evolutionary Computation, Vol. 12

(6).

Van Rijsbergen, C.J., 1979. Information retrieval.

Butterworth, 2nd edition.

Yang, Ch., Tu, X., Chen, J., 2007. Algorithm of marriage

in honey bees optimization based on the wolf pack

search. In International Conference on Intelligent

Pervasive Computing.

Yang, X.S., 2009 Firefly algorithms for multimodal

optimization. In The 5th Symposium on Stochastic

Algorithms, Foundations and Applications.

Yang, X.S., 2010. A new metaheuristic bat-inspired

algorithm. Nature Inspired Cooperative Strategies for

Optimization, Studies in Computational Intelligence.

Vol. 284.

Yang, X.S., Deb, S., 2009. Cuckoo Search via Levy

flights. In World Congress on Nature & Biologically

Inspired Computing. IEEE Publications.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics