
Passivity-based Control of Surge and Rotating Stall in Axial Flow
Compressors
Gholam-Reza Sari
1
, Ouassima Akhrif
2
and Lahcen Saydy
1
1
Electrical Engineering Department, Polytechnique Montreal, University of Montreal, 2900 Boul. Edouard-Montpetit,
Montreal, Canada
2
Electrical Engineering Department, Ecole de Technologie Superieure, University of Quebec, 1100 Rue Notre-Dame O,
Montreal, Canada
Keywords: Robust Passivity-based Control, Axial Compressor, Rotating Stall and Surge Control, Close-Coupled Valve,
Model Uncertainty and Disturbance Rejection.
Abstract: In this work, we address the stability of compression systems and the active control of performance limiting
phenomena: surge and rotating stall. Despite considerable efforts to stabilize axial compressors at efficient
operating points, preventing and suppressing rotating stall and surge are still challenging problems. Due to
certain passivity properties of the widely used Moore and Greitzer model for axial compressors, a robust
passivity-based control approach is applied here to tackle the problem. The main advantage of this approach
is that robust stabilization and high performance control can be achieved by simple control laws and limited
control efforts. Analytical developments and time-domain simulations demonstrate that the developed
control laws can effectively damp out rotating stall and surge limit cycles by throttle and close-coupled
valve actuations. The robust performance of the controller is validated in the presence of bounded mass flow
and pressure disturbances, as well as model uncertainties.
1 INTRODUCTION
Passivity theory, which provides an energy based
perspective in control theory, has been the subject of
much research over the last decades (Byrnes et al.,
1991; Sepulchre et al., 1997; Willems, 2007). The
essential role of energy in the stability and
performance of physical systems has resulted in the
increasing attention to passivity. Basically, passive
systems are a class of processes that dissipate a
certain type of physical or virtual energy described
by Lyapunov-like functions (Bao and Lee, 2007).
The concept of passivity especially plays an
important role in robust control. Since passive
systems are easy to control, the first step in passive
system theory is to render a process passive via
either feedback or feedforward. Sufficient
robustness to model uncertainties, parameter
variations, and external disturbances can be ensured
by passivity-based control (PBC) which guarantees
the passivity of the system for the whole range of
parameters. Achieving passivity with feedback is an
appealing issue due to its input-output concept.
However, one of the major challenges in feedback
passification designs is to make it constructive. The
key part of the design procedure is to select a proper
output satisfying the required conditions (Sepulchre,
et al., 1997). In 1991, Byrnes et al. (Byrnes et al.,
1991) derived the conditions under which a
nonlinear system can be rendered passive via smooth
state feedback and in 2009, Tsai and Wu (Tsai and
Wu, 2009) presented a constructive method for
robust PBC (RPBC) of a certain class of weakly
minimum phase nonlinear uncertain systems. They
proposed a control law that renders the system
passive and asymptotically stabilizes the closed loop
system.
In this work, we utilize RPBC to effectively
stabilize nonlinear phenomena in compression
systems. Compression systems suffer from two types
of nonlinearities with different natures: surge and
rotating stall. Rotating stall is a non-axisymmetric
perturbation that travels around the annulus of the
compressor, while surge is a violent limit-cycle in
compressor characteristic that can lead to a flow
reversal and large axial oscillations (see (Gu et al.,
1999) for more information). Despite the
considerable efforts that have been made to
Sari, G-R., Akhrif, O. and Saydy, L.
Passivity-based Control of Surge and Rotating Stall in Axial Flow Compressors.
DOI: 10.5220/0005975500750083
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 75-83
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
75

investigate these phenomena, different aspects of the
problem such as sensing, actuating and model-based
control are still challenging issues.
From a control point of view, the nonlinear 2D
model developed by Moore and Greitzer (Moore
and Greitzer, 1986) for constant speed axial
compressors (CSACs) dominates recent studies on
rotating stall and surge control (Gu et al., 1999).
The
lumped parameter Moore and Greitzer model (so-
called MG3) is based on the first harmonic
approximation of rotating stall. This model was
developed using Galerkin procedure applied to the
original PDE form. In spite of the simple form of the
model, it can capture surge and rotating stall
nonlinearities and qualitative behavior of the system
including bifurcations (see (Hős et al., 2002) for
more information).
Remarkable efforts channeled into augmenting
MG3 in different ways; among them obtaining
higher order accurate model and including the force
of actuators (Krstic and Wang, 1997; Leonessa et al.,
1997; Mansoux et al., 1994). One of the most
promising actuators is the close-coupled valve
(CCV). The early work of Dussourd in 1977
(Dussourd et al., 1977) and the work of Simon and
Valavani in 1991 (Simon and Valavani, 1991)
addressed CCV in compression system control. In
1998, Gravdahl introduced an augmented MG3
model including CCV in error coordinates
(Gravdahl, 1998). Recently, once again, this actuator
attracted close attention of researchers in surge
control ((Bartolini et al., 2008; Liaw et al., 2008;
Shehata et al., 2009)).
Gravdahl demonstrated that the two-state
simplified form of MG3 including CCV shows
certain passivity properties and then applied PBC to
develop a surge controller (Gravdahl and Egeland,
1998). This simple proportional PBC law effectively
stabilized surge limit cycles. Although the controller
was not able to damp out rotating stall, it showed
promise for suppressing this hard-to-control
nonlinearity. This interesting open problem was
suggested as future work by Gravdahl.
Here, we address this problem and design a
RPBC to suppress rotating stall in CSACs. The
simple proportional and low order form of the
developed controller is the first advantage of the
applied method. It is not based on full-state feedback
(the square amplitude of rotating stall as the third
state of MG3 is practically hard to measure) and
does not require the detailed knowledge of model
parameters, which cannot be accurately estimated.
The controller actuates the system with feedback
from mass flow and pressure rise by using both the
throttle valve and CCV. Simulation results
corroborating the analytical developments
demonstrate that the applied RPBC effectively
damps out the developed rotating stall and stabilizes
efficient operating points (OPs) in the presence of
bounded external disturbances and model
uncertainties. The utilized approach eliminates surge
limit cycles as well.
The rest of the paper is organized as follows. In
Section 2, we start by reviewing the Gravdahl model
representing CSACs comprising CCV. Section 3
presents the control design and Section 4 reports
time-domain simulations. Finally, some conclusions
about this work are drawn in Section 5.
2 AXIAL COMPRESSORS
MODELS
Here, we briefly review Gravdahl model for CSACs
including CCV and throttle actuators. The
compressor comprising CCV is shown in Figure 1
where the pressure rise over the equivalent
compressor is the sum of the pressure rise of the
compressor and the pressure drop over CCV:
Ψ
(
Φ
)
=Ψ
(
Φ
)
−Ψ
(
Φ
)
where Φ is the
circumferentially averaged flow coefficient and Ψ is
the total-to-static pressure rise coefficient. Ψ
(
Φ
)
is
known as the compressor characteristic (map) which
describes a nonlinear relationship (assumed cubic in
(Gravdahl, 1998)) between Φ and Ψ:
Ψ
(
Φ
)
=
+1+1.5
−1−0.5
−1
(1)
Here, is the compressor characteristic height
factor, is the compressor characteristic width
factor, and
is shut-off head. The CCV
characteristic that describes the pressure drop over
CCV as a function of flow is given by Ψ
(
Φ
)
=
Φ
where
is the gain of CCV. The throttle
characteristic Ψ
(
Φ
)
=
Φ
gives the pressure
over the throttle as a function of flow, where
is
the throttle gain. The throttle can be thought as a
simplified model of a power turbine.
For a given operating point (OP) (
,
), the
dynamic model is developed in the form of state-
space equations =
(
,
)
z=f
(
z,Γ
)
(Eqs. (2-4)),
where ∈ℝ
,∈ℝ
. =(,,)
represents
the state vector of the system and =
(
,
)
is the
control vector. It is defined in error coordinates with
respect to the coordinates of the operating point
(
,
). In this model, =Φ −
, and =Ψ−
. is the squared amplitude of the first harmonic
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
76

of rotating stall. Control variables
=
and
=
() include the effect of throttle and the pressure
drop over CCV (in error coordinates) respectively.
A partially closed CCV during normal operation of
the compressor leads to a bidirectional control law
.
=
+ϕ
−
+Ψ
−Δ
(2)
=
−−
+Δ
−
−1−
(3)
=
1−
(
)
−1
−
−
(
)
(4)
The compressor characteristic given in Eq. (1) in
global coordinates can be expressed in error
coordinates as:
(
)
=−
−
−
(5)
where
=
(
−2) ,
=
−1 ,
and
=
>0 .
Figure 1: Compression system comprising CCV.
All derivatives are calculated with respect to a
normalized time :=
where
is the actual
time, is the mean compressor radius, and
. is the
constant compressor tangential speed. Here,
=
,
=
, and
is the effective flow-passage
nondimensional length of the compressor and ducts.
B is a positive parameter (so-called Greitzer’s B-
parameter). The type of the developed nonlinear
behavior to a great extent depends on the value of
this parameter (small B can lead to rotating stall, and
large B can cause surge).
In the model,
=Φ
+
and
=
+
include model uncertainties and external
disturbances. Mass flow disturbance Φ
() and
pressure disturbance Ψ
() are both considered as
defined by Simon and Valavani (Simon and
Valavani, 1991). The disturbances are time varying
and bounded (
‖
Φ
‖
and
‖
Ψ
‖
exist). In addition
to time varying disturbances, constant or slow
varying offsets
and
are also introduced. These
can be respectively thought of as an uncertainty in
the compressor and throttle characteristics.
Setting
=
=
=0 leads to two equilibria:
=0 where the compressor is in its active
operating point
(
,
)
or
=4(1−
Φ
−1
−
Φ
) when the system is in fully
developed rotating stall. By using
in Eq. (3), one
can obtain the equivalent stall characteristic Ψ
(
Φ
)
,
which is affected by pressure drop over CCV as can
be seen in Eq. (6) (see (Gravdahl, 1998) for more
information).
Ψ
(
Φ
)
=
+1−
Φ
−1+
Φ
−1
+
Ψ
(
Φ
)
−
1−
Φ
(6)
Figure 2a plots these characteristics: Ψ
(
Φ
)
(compressor map without CCV), Ψ
(
Φ
)
(equivalent
compressor map with CCV), Ψ
(
Φ
)
(pressure drop
over CCV), Ψ
(
Φ
)
(pressure drop over throttle),
Ψ
(
Φ
)
(stall characteristic without CCV), and
Ψ
(
Φ
)
(equivalent stall characteristic with CCV) in
(Φ,Ψ) plane. The OP of the compression system
(
,
) is the intersection of the throttle
characteristic and the equivalent compressor map.
An efficient and stable OP is normally located near
the peak of the equivalent compressor map
(corresponding to a high pressure rise). Moreover, it
can be shown that this OP corresponds to fully
damped stall (Hős et al., 2002).
Figure 2a shows how the pressure drop over
CCV can modify the equivalent compressor map and
equivalent stall characteristic as well (see (Gravdahl,
1998) for more details). This actuator can therefore
be used to stabilize an unstable OP. Roughly
speaking, when an OP is located in the negative
slope area of the equivalent compressor map, it is
stable (Willems, 1997). Figure 2b shows that due to
the pressure drop over CCV an unstable initial OP in
the positive slope area of the compressor map is
changed to a stable OP in the negative slope area of
the equivalent compressor map. Furthermore,
throttle control can also be applied to move the OP.
In this work, these two actuators are used to stabilize
the system and eliminate rotating stall and surge.
Passivity-based Control of Surge and Rotating Stall in Axial Flow Compressors
77
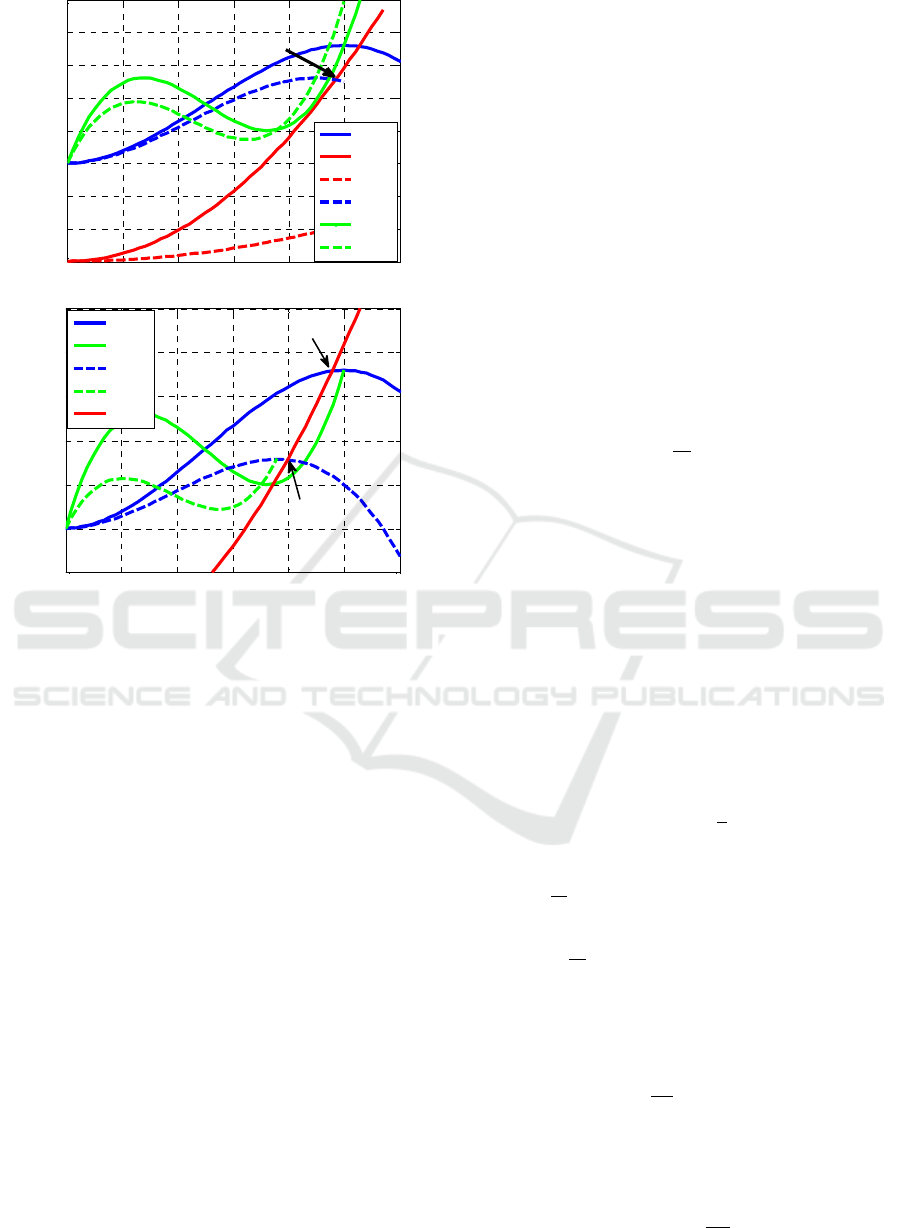
Figure 2: a) Plot of pressure drop over throttle and CCV
and compressor and stall characteristics with and without
CCV b) Effect of pressure drop over CCV on the
equivalent compressor characteristic and the stability of
the OP.
3 PASSIVITY-BASED CONTROL
The main objectives of this section are, firstly, to
passificate the axial compression system model and,
secondly, to achieve both input-to-state stability
(ISS, see (Krstic et al., 1995) for definition) and
disturbance rejection. In (Byrnes et al., 1991),
conditions under which a nonlinear system can be
rendered passive via smooth state feedback are
driven. Based on this work, several authors have
proposed to include uncertain terms (model
uncertainties and external disturbances) in order to
develop a RPBC (Lin and Shen, 1999; Tsai and Wu,
2009; Jiang and Hill, 1998). These works based on
assumptions on uncertainties (vanishing
perturbation) or measurable states (full-state
feedback with stall as a state-variable), which are not
applicable here. Consequently, we remove certain
restrictions that are imposed on the uncertainties
(e.g. output dependency) and propose a new
Lyapunov function stability analysis. We
demonstrate that the control law developed in
Theorem 3.1 below ensures robust asymptotic
stabilization of the compression system model.
Furthermore, this easy-to-implement RPBC does not
require a full-state feedback.
Theorem 3.1:
Consider the following disturbed system:
Σ1:
=
(
,0
)
+
(
,
)
=
(
,
)
+
(
,
)
+
(
,
)
+Δ
(
,
)
(7)
where
(,),
(,),
(,), and
(,) are
smooth functions and
(,) is invertible for all
,. Δ(,) is the system uncertainty and (,) is
the external disturbance.
If Δ(,) and (,) are bounded and if the
zero dynamics of the system are stable (i.e. there
exists a positive storage function () such
that:
(
0
)
=0 and
(,0)≤0) then the
following feedback control law
=−
(
,
)
(
,
)
+
(
)
(8)
where
(
)
satisfies
(
)
>0, renders the
closed-loop system input-to-state stable with respect
to disturbances and model uncertainties, guarantees
global uniform boundedness of
(
)
, and ensures the
convergence to a residual set. The size of the
residual set can be arbitrarily made small by the
choice of design parameters.
Proof:
Given a positive storage function for the system
Σ1 as:
(
,
)
=
(
)
+
1
2
(9)
Differentiating (,) gives:
(
,
)
=
(
(
,0
)
+
(
,
)
)
+
(
,
)
+
(
,
)
+
(
+Δ
)
(10)
Since
(
,0
)
≤0, the substitution of the
control law Eq. (8) into Eq. (10) gives that:
(
,
)
≤−
(
)
+
(11)
where
=
[
…
]
=[
(
,
)
]
+
(
+Δ
)
(12)
Now, we use the simplified form of Young’s
inequality which states that for all >0 and all
(
,
)∈ℝ
:
≤
+
1
4
(13)
0 0.1 0.2 0.3 0.4 0.5 0.6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Mass Flow
Φ
Pressure Rise
Ψ
Ψ
c
(
Φ
)
Ψ
T
(
Φ
)
Ψ
v
(
Φ
)
Ψ
ec
(
Φ
)
Ψ
s
(
Φ
)
Ψ
es
(
Φ
)
a)
(
φ
0
,
ψ
0
)
0 0.1 0.2 0.3 0.4 0.5 0.6
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Mass Flow
Φ
Pressure Rise
Ψ
Ψ
C
(
Φ
)
Ψ
s
(
Φ
)
Ψ
ec
(
Φ
)
Ψ
es
(
Φ
)
Ψ
T
(
Φ
)
Initial
unstable OP
Modified
stable OP
b)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
78

By applying Eq. (13) to each term of
, we
have:
≤
+
1
4
∀>0,=1,…,
(14)
Following the boundedness of uncertainties and
assuming that
(
,
)
exists, we have:
≤
+
4
‖
‖
(15)
therefore:
(
,
)
≤−
(
)
+
4
‖
‖
(16)
where
(
)
=
(
)
−
(17)
Appropriate choice of
(
)
can satisfy the
condition
(
)
>0 (e.g.
(
)
= with −
positive definite). Since
() and (,) are
radially unbounded and positive definite, according
to the work of Krstic et al. (Lemma 2.26) (Krstic et
al., 1995), we can demonstrate that the control law
of Eq. (8) renders the closed loop system ISS with
respect to the uncertain terms and hence guarantees
the global uniform boundedness of () and
convergence to residual set
, outside which
(
,
)
0.
=:
|
|
≤
.
.
4
‖
‖
(18)
where
,
, and
are −
functions such
that:
(
|
|
)≤(,)≤
(
|
|
)
(19)
(
|
|
)≤
()
(20)
The size of this set depends on
‖
‖
and design
parameter. A smaller size of
requires a large
parameter, which implies higher controller gain.
4 PBC DESIGN FOR MG3
Here, it is supposed that mass flow and pressure
rise in the error coordinates can both be measured.
Then =
[
]
and the model (Eqs. 2-4) can be
rewritten in the form of system Σ1 including
matched uncertainties. Since cannot be practically
measured, the idea in this paper is to consider all the
term containing as part of the disturbances. This
simplifies the control design and allows us to have
an output feedback strategy. Here,
and
do not
depend on and the assumptions of perturbation
boundedness of Theorem 3.1 are satisfied.
=
(
,0
)
+
(
,
)
=
(
)
+
(
)
+
(
,
)
+Δ
(
)
(21)
where
=
0−
−
+
0
(22)
=
(−+
)
(+
)
(23)
=
−
−
(
−1+
−Ψ
)
(24)
Δ=
−
(25)
is nonsingular in the operating range of the
compressor where +
>0. Furthermore,
Gravdahl showed that the squared amplitude of
rotating stall and mass flow have upper bounds
(Gravdahl, 1998):
∃
∞such that
(
)
≤
∀>0, and
≤Φ≤
, where
is the choking
value of the mass flow and
is the negative flow
during deep surge. The CCV gain is practically
limited as well, in other words
∈[
,
].
Consequently, and Δ are both bounded. Similarly,
(
,
)
existssince:
(
,
)
=(−
+
−
)
(26)
where , , and
are nonzero.
To investigate the stability of zero dynamics,
suppose that a nominal OP is initially located at the
peak of the compressor map (which is ideally the
case). It can be seen that the peak of the compressor
map in Eq. (1) is located at
(
Φ,Ψ
)
=(2,2+
). Therefore,
=2 at this OP:
(
,0
)
=−
−
(27)
Considering=
, one can show that:
(
,0
)
=
−
−
(28)
In Eq. (28) the parameters (, ),
, and are
all positive. Hence
(
,0
)
≤0
This satisfies the first condition of Theorem 3.1.
By choosing
(
)
=, Theorem 3.1 states that the
following control law Eq. (29) can stabilize the OP
in the presence of the external disturbances and the
model uncertainties.
Passivity-based Control of Surge and Rotating Stall in Axial Flow Compressors
79
=
[
,
]
=
−+
+
(29)
In the developed control law, =[
0
0
]
consists of two high enough positive design
parameters (
and
) that guarantee the
convergence to
and limit the size of this residual
convergence set.
Note that the control law Eq. (29) cancels all the
nonlinearities in the model. Since the term
is
always positive in Eq. (5), we propose the following
modification to avoid canceling the stabilizing
nonlinearities (−
):
=
[
,
]
=
−−
−
+
(30)
It is worth noting that all uncertainties in the
model parameters are considered in the terms of Δ,
therefore the parameter set used in Eq. (30) is only a
reasonable estimation.
Remark:
In the case of deep surge, the system does not
include the zero dynamics and the simplified form of
control system can be derived by putting =0 in
Eq. (21). It can be seen that =0 considerably
relaxes the boundedness conditions; however, the
developed control laws Eq. (30) remains effective.
5 RESULTS AND DISCUSSION
All of the numerical constants and model
parameters, which are used in this section, are
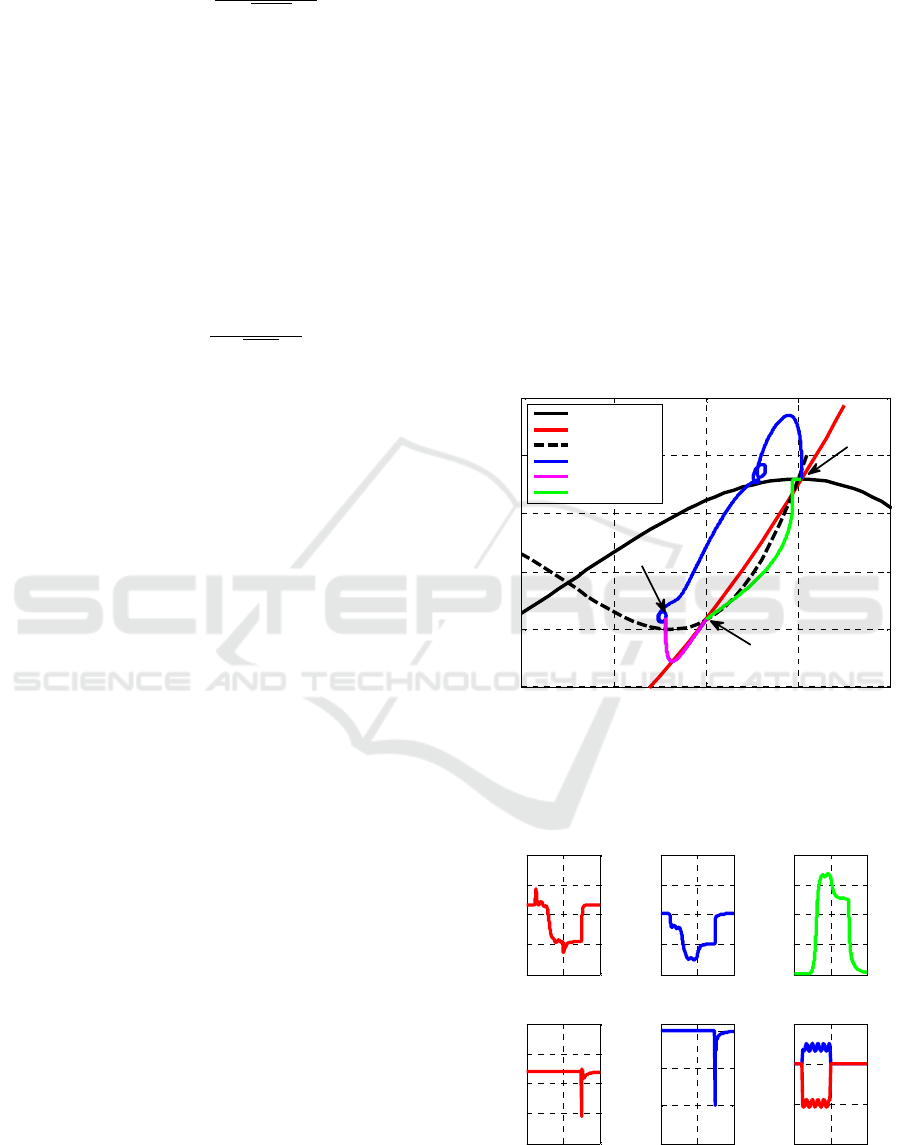
mentioned in Table 1. At first, we demonstrate that
external disturbances and model uncertainties can
lead to rotating stall when the controller is
deactivated (B-parameter in this case is 0.1.). The
system initially starts from OP1 (the intersection of
throttle characteristic
=0.62 and compressor
map at (
,
)=(0.51,0.66) (see Figure 3)). This
OP is located in the negative slope area and the
system is initially stable. As seen in Figure 4f,
disturbances including time varying sinusoidal and
constant offsets are applied at =50.
Consequently, the system develops rotating stall
(Figure 4c) and output pressure drops (Figure 4a).
This spells trouble for normal operation of the axial
compressor. In Figure 3, the disturbed trajectory
(blue line) settles down at OP2 consisting of the
effect of rotating stall and disturbances. The
disturbances last until =200, but due to the
hysteresis in the qualitative behavior of the system,
rotating stall cannot be automatically removed (see
Figure 4c). When disturbances disappear,
uncontrolled trajectory (magenta line) ends up in
OP3 which is located on the stall characteristic
where pressure is considerably reduced.
At =300, the controller starts and rapidly
damps out rotating stall and imposes the controlled
trajectory (green line) toward the initial efficient
OP1 where output pressure is high. In this
simulation,
=10 and
=0.2. Figure 4d and 4e
respectively report the control laws
and
.
trajectory (green line) toward the initial efficient
OP1 where output pressure is high. In this
simulation,
=10 and
=0.2. Figure 4d and 4e
respectively report the control laws
and
.
Figure 3: Perturbations lead to rotating stall, but RPBC
effectively damps it out. OP1: efficient OP, OP2:
developed rotating stall and disturbances, OP3: rotating
stall OP.
Figure 4: RPBC returns the system to its initial efficient
OP and removes rotating stall.
0.2 0.3 0.4 0.5
0.3
0.4
0.5
0.6
0.7
0.8
Mass Flow
Pressure Rise
Compressor Map
Throttle Ch.
Stall Ch.
Disturbed Traj.
Uncontrolled Traj.
Controlled Traj.
OP1
OP2
OP3
0 200 400
0.2
0.4
0.6
0.8
1
a) time
ξ
Pressure Rise
0 200 400
0.4
0.5
0.6
0.7
b) time
ξ
Flow
0 200 400
0
1
2
3
4
c) time
ξ
1t Harmonic of Stall
0 200 400
0.5
0.55
0.6
0.65
0.7
d) time
ξ
Control Law: U1
0 200 400
-1.5
-1
-0.5
0
e) time
ξ
Control Law: U2
0 200 400
-0.1
-0.05
0
0.05
f) time
ξ
Press. (red) & Flow (blue) Dist.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
80
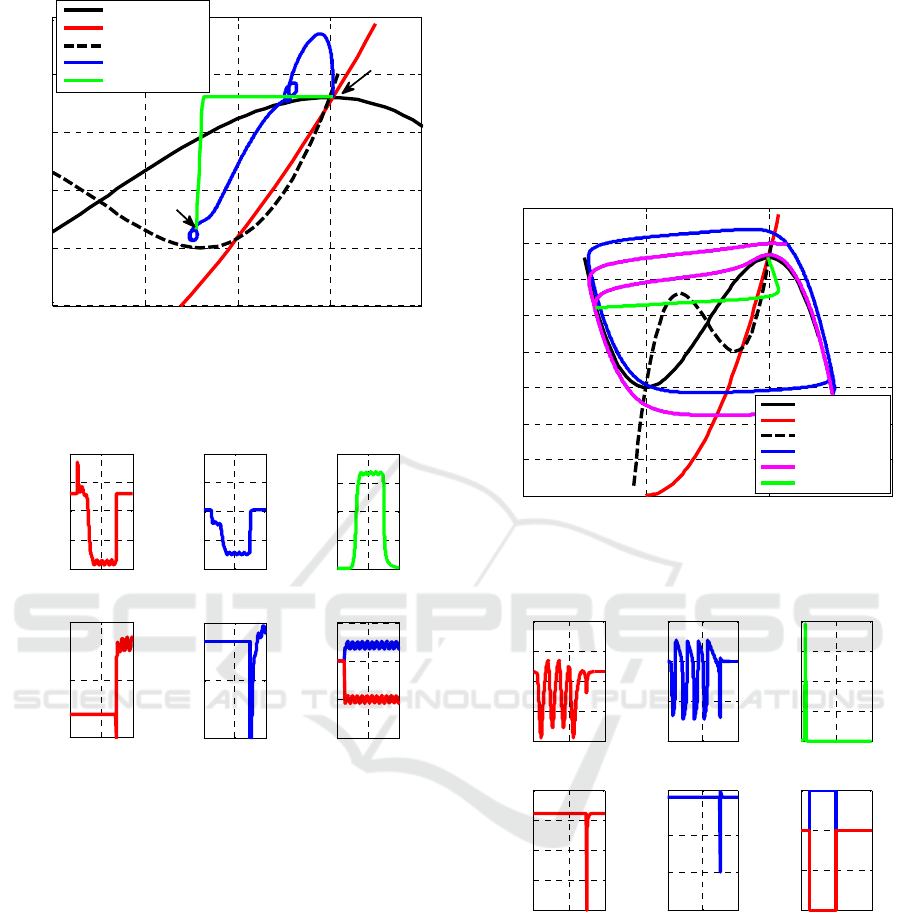
Figure 5: RPBC removes rotating stall and returns the
system to its desired initial OP1. OP1: initial efficient OP,
OP2: OP including rotating stall and disturbances.
Figure 6: RPBC increases the output pressure and
eliminates rotating stall.
To investigate the effectiveness of the controller
in the presence of perturbations, long lasting
disturbances are applied to the system for >50
(Figure 6f). Again, Figure 5 and 6 show that the
controller, which is activated at =300, stabilizes
the system at the desired OP1. In Figure 5, the
controlled system trajectory finally reaches to the
initial desired OP1. Figure 6c shows that rotating
stall is rapidly damped out and Figure 6a reports the
corresponding pressure increase after the activation
of the controller at =300. In this case,
=
=
20. These two design parameters also modify the
transient response of the system (e.g. the fall time of
rotating stall). The scale of Figure 6d and 6e are
adjusted to show the variation of control laws due to
the time varying sinusoidal disturbances.
Compressors suffer from deep surge as well. For
surge simulations, the system initially starts at an
efficient OP at the peak of compressor map. In this
case, at =50, we apply only the offset
disturbances (thought of as model uncertainties) that
move the system toward surge condition. Deep surge
can be simulated by choosing a high enough value of
B-parameter (e.g. =2 leads to surge).
Figure 7: RPBC stabilizes the compression system and
eliminates deep surge.
Figure 8: Deep surge including flow reversal and pressure
oscillation is damped out due to RPBC activation.
During deep surge, flow reversal occurs (see
Figure 8b with negative flow values). Although
perturbations are removed at =2000, the system
remains in surge condition (see Figure 8f and 8b).
Then at =3000, the controller starts and quickly
stabilizes deep surge as shown in Figure 8a and 8b.
Control efforts are shown in Figure 5d and 5e.
Figure 7 reports disturbed and uncontrolled
trajectories showing a limit cycle. Finally, when the
0.2 0.3 0.4 0.5
0.3
0.4
0.5
0.6
0.7
0.8
Mass Flow
Pressure Rise
Compressor Map
Throt t le Ch.
Stall Ch.
Disturbed Traj.
Controlled Traj.
OP1
OP2
0 200 400
0.4
0.5
0.6
0.7
0.8
a) time
ξ
Pressure Rise
0 200 400
0.4
0.5
0.6
0.7
b) time
ξ
Flow
0 200 400
0
1
2
3
4
c) time
ξ
1t Harmonic of Stall
0 200 400
0.6
0.65
0.7
d) time
ξ
Control Law: U1
0 200 400
-0.1
-0.04
0.02
e) time
ξ
Control Law: U2
0 200 400
-0.1
-0.05
0
0.05
f) time
ξ
Press. (red) & Flow (blue) Dist.
-0.5 0 0.5 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Mass Flow
Pressure Rise
Compressor Map
Throt t le Ch.
Stall Ch.
Disturbed Traj.
Uncontrolled Traj.
Controlled Traj.
0 2000 4000
0.2
0.4
0.6
0.8
1
a) time
ξ
Pressure Rise
0 2000 4000
-0.5
0
0.5
1
b) time
ξ
Flow
0 2000 4000
0
1
2
3
4
c) time
ξ
1t Harmonic of Stall
0 2000 4000
-1
-0.5
0
0.5
1
d) time
ξ
Control Law: U1
0 2000 4000
-1.5
-1
-0.5
0
e) time
ξ
Control Law: U2
0 2000 4000
-0.1
-0.05
0
0.05
f) time
ξ
PR(r) & FL(b) Dist.
Passivity-based Control of Surge and Rotating Stall in Axial Flow Compressors
81

control is applied at =3000, the controlled system
trajectory settles down at the initial efficient OP1
(green trajectory). This time-domain simulation
shows that the developed control law Eq. (30) can
robustly stabilize deep surge as well.
6 CONCLUSIONS
In this paper, the effectiveness of RPBC in
stabilizing compression systems is demonstrated.
Here, surge and rotating stall being potentially able
to cause mechanical damages and performance
reduction are robustly controlled in the presence of
external disturbances and model uncertainties. The
controller derives the control signal from pressure
and flow measurements and applies it to the system
by CCV and throttle actuations. The main
contribution of this paper is to propose a simple and
easy-to-implement RPBC algorithm that only relies
on a small number of design parameters and does
not require accurate knowledge of the model
parameters.
Analytical developments demonstrate that RPBC
accomplishes theISSpropertyoftheclosed-loop
disturbed system. The size of the residual
convergencesetandthe transient response can be
adjusted by control parameters. Time-domain
simulation evaluates the performance of the control
system and widely supports analytical outcomes.
This brings us to the conclusion that by taking
advantage of control methods based on the passivity
of compression systems, a wide range of machines
using compressors can obtain higher performance
and greater operational reliability. Among these
machines, gas turbines play an essential role both in
aerospace and energy industries.
REFERENCES
Bao J., Lee P. L., 2007. Process control, Springer, 1st
edition.
Bartolini, G., Muntoni, A., Pisano, A., Usai, E., 2008.
Compressor surge active control via throttle and CCV
actuators. A second-order sliding-mode approach. In
IEEE 10th International Workshop on Variable
Structure Systems, VSS'08, June 2008, (pp. 274-279).
Antalya, Turkey.
Byrnes, C. I., Isidori, A., Willems, J. C., 1991. Passivity,
feedback equivalence, and the global stabilization of
minimum phase nonlinear systems. IEEE Transactions
on Automatic Control, 36, 1228-1240.
Dussourd J.L., Pfannebecker G.W. , Singhania, S.K.,
1977. An experimental investigation of the control of
surge in radial compressors using close coupled
resistances. Journal of Fuids Engineering : Trans.
ASME, 99, 64-76.
Gravdahl J. T., 1998. Modeling and control of surge and
rotating stall in compressors. Norwegian University of
Science and Technology, Trondheim.
Gravdahl J. T., Egeland O., 1998. Two results on
compressor surge control with disturbance rejection.
In Proceedings of the 37th IEEE Conference on
Decision and Control, 1998. (Vol. 3, pp. 2563-2568).
Gu, G., Sparks, A., Banda, S. S., 1999. An overview of
rotating stall and surge control for axial flow
compressors. IEEE Transactions on Control Systems
Technology, 7, 639-647.
Hős C., Champneys A., Kullmann L., 2003. Bifurcation
analysis of surge and rotating stall in the Moore-
Greitzer compression system. IMA J. Applied Math,
68(2): 205-228.
Krstic, M., Ioannis, K., Petar, K., 1995. Nonlinear and
adaptive control design. John Wiley and Sons, Inc.
Krstic M., Wang H., 1997. Control of deep-hysteresis
aeroengine compressors - Part II: design of control
laws. In Proceedings of the 1997 American Control
Conference, June 1997, Vol. 2, pp. 1003-1007,
Albuquerque, USA.
Leonessa A., Chellaboina V., Haddad W., 1997. Globally
stabilizing controllers for multi-mode axial flow
compressor models via equilibria-dependent Lyapunov
functions. In Proceedings of the 1997 IEEE
International Conference on Control Applications,
October 1997 (pp. 63-68). Hartford, USA.
Liaw, D., Ren, S. M., Chang, S., 2008. A feedback
linearization design for compressor's surge control. In
Industrial Technology, ICIT 2008 (pp. 1-6).
Lin W., Shen, T., 1999. Robust passivity and feedback
design for minimum-phase nonlinear systems with
structural uncertainty. Automatica, 35, 35-47.
Mansoux C. A., Gysling D. L., Setiawan J. D., Paduano J.
D., 1994. Distributed nonlinear modeling and stability
analysis of axial compressor stall and surge. American
Control Conference, Volume: 2, 2305- 2316.
Moore, F. K., Greitzer, E. M., 1986. Theory of post-stall
transients in axial compression systems: part I -
development of equations. Journal of Engineering for
Gas Turbines and Power, 108, 68-76.
Sepulchre R., Jankovic M., Kokotovic P. V., 1997.
Constructive nonlinear control. Springer-Verlag, New
York.
Shehata, R. S., Abdullah, H. A., Areed, F., 2009. Variable
structure surge control for constant speed centrifugal
compressors. Control Engineering Practice, 17, 815-
833.
Simon J. S., Valavani L., 1991. A Lyapunov based
nonlinear control scheme for stabilizing a basic
compression system using a close-coupled control
valve. In Proceedings of the 1991 American Control
Conference, June 1991 (Vol. 3, pp. 2398-2406).
Boston, USA.
Tsai C., Wu H., 2009. Robust passivity-based control of
weakly minimum phase nonlinear uncertain systems:
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
82

An application to manipulator. In 2009 7th Asian
Control Conference, ASCC 2009 (pp. 919-924).
Willems F., 1997. Modeling and control of compressor
flow instabilities. Eindhoven University of
Technology.
Willems J. C., 2007. Dissipative dynamical systems.
European Journal of Control, 13:134- 151.
Jiang, Z. P., Hill D. J., 1998. Passivity and disturbance
attenuation via output feedback for uncertain nonlinear
systems. IEEE Transactions on Automatic Control,
43, 992-997.
APPENDIX
Table 1: Numerical values used in simulations.
3
0.25
0.18
for rotating stall
0.1
for deep surge
2
0.425
−0.05
0.02
Ψ
() 0.01(0.2)
Φ
() 0.01(0.2)
Passivity-based Control of Surge and Rotating Stall in Axial Flow Compressors
83
