
Autoencoder Networks for Water Demand Predictive Modelling
Ishmael S. Msiza and Tshilidzi Marwala
Faculty of Engineering & The Built Environment, University of Johannesburg, Auckland Park, Johannesburg, South Africa
Keywords:
Neural Network, Autoencoder Network, Multi-layer Perceptron, Water Demand, Time Series, Regression
Approximation, Predictive Modelling, Hidden Units, Network Dimensionality, Arbitrary Complexity.
Abstract:
Following a number of studies that have interrogated the usability of an autoencoder neural network in various
classification and regression approximation problems, this manuscript focuses on its usability in water demand
predictive modelling, with the Gauteng Province of the Republic of South Africa being chosen as a case study.
Water demand predictive modelling is a regression approximation problem. This autoencoder network is
constructed from a simple multi-layer network, with a total of 6 parameters in both the input and output
units, and 5 nodes in the hidden unit. These 6 parameters include a figure that represents population size
and water demand values of 5 consecutive days. The water demand value of the fifth day is the variable of
interest, that is, the variable that is being predicted. The optimum number of nodes in the hidden unit is
determined through the use of a simple, less computationally expensive technique. The performance of this
network is measured against prediction accuracy, average prediction error, and the time it takes the network
to generate a single output. The dimensionality of the network is also taken into consideration. In order to
benchmark the performance of this autoencoder network, a conventional neural network is also implemented
and evaluated using the same measures of performance. The conventional network is slightly outperformed
by the autoencoder network.
1 INTRODUCTION
Artificial neural networks – simply known as neural
networks – occur in many different forms and types,
and one of these types is known as an autoencoder
network. This is a network trained to recall its in-
put, and the purpose of the work presented in this
manuscript is to interrogate the usability of this net-
work in a predictive modelling application. This ap-
plication involves the analysis and prediction of a wa-
ter demand time series. This interrogation is informed
by the constantly eminent need that neural network
practitioners have to, whenever possible, reduce the
dimensionality or size of any neural network. An au-
toencoder network is known for its ability to compress
data (Marivate et al., 2008), hence it is chosen for the
dimensionality reduction component of this study.
The importance of having a neural network with
reduced dimensionality is presented as part of the the-
ory of autoencoder networks in section 2. The state
of the current literature – regarding autoencoder net-
work applications – is presented in section 3, and the
implementation of this network in water demand pre-
dictive modelling – together with the evaluation of its
performance – is discussed in section 4. In order to
endorse the performance of this autoencoder network,
it is necessary or useful to compare it against that of
a conventional neural network. The implementation
of this conventional network is presented in section 5,
and the comparison between the two models is car-
ried out in section 6, just before the conclusions and
proposed future work in section 7.
2 NEURAL NETWORKS
This section of the manuscript serves to introduce the
theory of conventional neural networks, in general,
and autoencoder neural networks, in particular.
2.1 Conventional Neural Networks
A neural network could be defined as a computer-
based machine that is designed to model the way in
which the human brain executes a particular task or
function of interest (Marwala, 2016). What this im-
plies is that, a neural network is a computer model
that is taught to duplicate the manner in which the
human brain performs a given task. Because the op-
Msiza, I. and Marwala, T.
Autoencoder Networks for Water Demand Predictive Modelling.
DOI: 10.5220/0005977202310238
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 231-238
ISBN: 978-989-758-199-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
231

Figure 1: An example of a simple MLP neural network that
has 2 layers of weighted connections and 3 layers of pro-
cessing units.
erations of the brain are primarily facilitated by struc-
tures known as biological neural networks (van De-
venter and Mojapelo-Batka, 2013), a computer-based
neural network is specifically referred to as an artifi-
cial neural network.
When sketched on a piece of paper, a neural net-
work looks like a physical linkage of processing units
through weighted connections. It can occur in the
form of various architectures, including a multi-layer
perceptron (MLP) and a radial basis function (RBF).
The MLP is, however, the most common neural net-
work architecture in terms of use. It is important to
note that an MLP network can be configured in the
form of any number of weighted connections, but
many practitioners have demonstrated that a neural
network configured to have two weighted connections
is capable of modelling just about any functional map-
ping, however complex it may be. This is a network
with three processing units: the input unit, the hidden
unit, and the output unit. Figure 1 depicts an example
of a simple MLP network that has five inputs, three
hidden nodes, and two outputs.
2.2 Autoencoder Neural Networks
An autoencoder network is a type of the conventional
neural network. For the conventional neural network
to be regarded as an autoencoder neural network, it
has to conform to the following two rules.
• Autoencoder Rule 1: the neural network has to
be auto-associative.
• Autoencoder Rule 2: the hidden unit of the net-
work has to be narrow, that is, the network must
have what is often referred to as a bottleneck.
Its auto-associative nature implies that the autoen-
coder network tries to associate the input unit with
the output unit, so as to minimize the error between
the two. In practical terms, this implies that – when
Figure 2: An example of an autoencoder neural network. It
has 5 inputs, 3 nodes in the hidden unit, and 5 outputs.
presented with a set of inputs – the autoencoder net-
work attempts to produce the same set of inputs in the
output unit. The immediate advantage of this behav-
ior is that this network can map both the linear and the
non-linear relations between all the inputs (Thompson
et al., 2002).
The bottleneck implies that the number of nodes
in the hidden unit should be less than the number of
nodes in both the input and output units. This results
in a network that has a narrow hidden unit, with the in-
put and output units having the same size, hence hav-
ing a butterfly-like structure, as depicted in figure 2.
This bottleneck compresses the input space data into a
smaller dimension, then decompresses it into the out-
put space. The key advantage of having a narrow hid-
den unit is that the network becomes less complex,
and its dimensionality (size) is reduced. This is be-
cause of the fact that the complexity of a neural net-
work has a directly proportional relationship with the
number of nodes in the hidden unit.
The number of nodes in the hidden unit is also pro-
portional to the dimensionality of the network. A net-
work with large dimensionality tends to have a small
error between the input and output data during the
training process, but this error increases when the net-
work is presented with previously unseen data. A net-
work that behaves in this manner is said to have poor
generalization ability. This, therefore, implies that the
idea behind using an autoencoder network is to have
a system that: has low dimensionality, is less com-
plex, is accurate, and has good generalization abil-
ity. These factors play an important role in the per-
formance evaluation of a predictive modelling system
that is based on neural computing.
2.3 Optimum Dimensionality Selection
When using neural networks (conventional or other-
wise), one of the most important exercises is the pro-
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
232

cess of selecting the optimum number of nodes in the
hidden unit, that is, the optimum dimensionality of
the network at hand. This exercise is a form of model
tuning and optimisation. Just to demonstrate how im-
portant this exercise is, some pratitioners dedicate an
entire document writing about model tuning and opti-
misation (Hessel et al., 2014). When dealing with an
autoencoder network, this exercise becomes less un-
certain because – when taking Autoencoder Rule 2,
mentioned above, into consideration – the following
condition will always be true:
1 ≤ N
hidden
≤ (M −1), f or M = N
input
= N
out put
(1)
where N
hidden
is the number of nodes in the hidden
unit, M is a value that is equal to the number of nodes
in both the input and output units, N
input
and N
out put
.
Equation 1 implies that the optimum number of nodes
in the hidden unit will be a value that is between 1 and
(M − 1).
In order to select this optimum number of nodes
in the hidden unit, this work takes advantage of cross-
validation and introduces a variable called ∆E. Cross-
validation is a technique used to monitor and evalu-
ate the network’s performance, where the dataset in-
volved is split into three partitions: the training set,
the validation set, and the testing set. For the com-
plexity of this study, a single round of cross-validation
is sufficient. For more complex studies, it is often
necessary to perform multiple rounds, while rotating
these partitions of data. ∆E is a measure of the change
in average error between the training and validation
data sets. It is an indication of the trained model’s
generalization ability. It is mathematically defined
as the arithmetic difference between the average er-
ror obtained from the training data set – the average
training error, E
training
– and the one from the valida-
tion data set – the average validation error, E
validation
– as indicated in equation 2.
∆E = E
training
− E
validation
(2)
Because this measure only uses the training and the
validation data sets, it could be said that it uses the
hold-out (train and test) method, which is the sim-
plest form of the cross-validation technique. Using
this measure to select the optimum number of nodes
in the hidden unit, it is essential to heed these three
important notes:
• Note A: this change in error can have a positive
or a negative value.
• Note B: a negative value indicates that the number
of nodes in the hidden unit leads to poor general-
ization ability on the part of the network.
• Note C: the optimum number of nodes in the
hidden unit is indicated by the smallest positive
value.
Note A is immediately obvious from the mathemati-
cal relationship in equation 2. Note B talks to an in-
stance where the average validation error is greater
than the average training error. This would be an in-
dication of the fact that the trained network has poor
generalization ability, hence the number of hidden
nodes is not optimum. Note C talks to an instance
where the average validation error is less than the av-
erage training error. This would be an indication of
the fact that the trained network does have an ability
to generalize.
3 STATE OF THE ART
Literature has, by far, not revealed any work that in-
terrogates the use of autoencoder networks in wa-
ter demand predictive modelling – a reality that be-
gins to suggest that this manuscript is the first doc-
ument to report on such works. Practitioners such
as Jain (and his co-workers) and Msiza (and his co-
workers) have used conventional neural networks in
their water demand predictive modelling studies (Jain
et al., 2001), (Msiza et al., 2007), (Msiza et al., 2008).
Bougadis (and his co-workers) also used a conven-
tional neural network model in municipal water de-
mand forecasting, where the model inputs included
rainfall and maximum air temperature, in addition to
previous water demand data (Bougadis et al., 2005).
The need to consider the use of an autoencoder net-
work in water demand predictive modelling is in-
spired by its reported usability in various regression
approximation problems. Predictive modelling is a
regression approximation exercise.
Marivate used an autoencoder network, with prin-
cipal component analysis (PCA) and the genetic al-
gorithm (GA) in a missing data estimation prob-
lem (Marivate et al., 2008). They reported an accu-
racy of up to 97.4% obtained from an HIV survey data
set. Nelwamondo used a dynamic programming prin-
ciple in the imputation of missing data with an autoen-
coder network (Nelwamondo et al., 2013). One of the
lessons reported to have been learnt from that work is
that an autoencoder network is relevant in regression
problems.
In the field of water resources management, au-
toencoder networks have been used – in a stacked
configuration – to extract water bodies from remote
sensing images (Zhiyin et al., 2015). In addition, a
sparse autoencoder network – in combination with
a softmax classifier – has been used to assess water
quality, based on the China Surface Water Environ-
mental Quality Standard (GB3838-2002) (Yuan and
Jia, 2015). Solanki (and his co-workers) used an ap-
Autoencoder Networks for Water Demand Predictive Modelling
233
proach that included autoencoder networks when pre-
dicting parameters that affect water quality (Solanki
et al., 2015).
The relevance of an autoencoder network is
demonstrated by the fact that, in addition to being
used in regression problems, it has also been used in
classification problems. Leke-Betechuoh used an au-
toencoder network in the classification of a person’s
HIV status from demographic data (Leke-Betechuoh
et al., 2006). They obtained a classification accuracy
of 92%, which was much better than the 84% ob-
tained using a conventional neural network.
In terms of choosing the optimum number
of nodes in the hidden unit of a neural net-
work, practitioners like Marivate, Nelwamondo, and
Leke-Betechuoh used GA as an optimization tech-
nique (Marivate et al., 2008), (Nelwamondo et al.,
2013), (Leke-Betechuoh et al., 2006). That was, per-
haps, not necessary for an autoencoder network – es-
pecially if the number of nodes in the input and output
units is relatively small. The use of optimizers such as
GA is an unnecessary overhead on the computational
resources.
4 AUTOENCODER NETWORK
IMPLEMENTATION
This section of the manuscript reports on the details
and the process followed in the implementation of the
autoencoder network, from the manipulation of the
initial data, all the way to the evaluation of its per-
formance.
4.1 Place Setting
For the reasons presented by Msiza, the Gauteng
Province (GP) of the Republic of South Africa
(RSA) is chosen as the geographic location of this
study (Msiza et al., 2007). Two features are identi-
fied as being the main drivers of the water demand
trajectory in the GP. These two features are; the daily
water sales figures, and the annual population figures.
It is easy to make sense of the fact that there is a
causal link between water sales, the population dy-
namics, and water demand. The simplest explanation
of this causal link is that a water supplier sells what a
population demands, at a particular point in time. It
is even more relevant to say that a water sales figure
translates to a water demand figure. The daily water
sales figures were obtained from a bulk water supplier
known as Rand Water (Cooks, 2004), located in the
GP. The annual population estimates of any province
in South Africa – including the GP – is public infor-
mation, readily available through various national in-
formation systems.
4.2 Model Inputs and Outputs Selection
The two features mentioned above, are used to serve
as input to the proposed water demand predictive
model. Because of the non-linearity and arbitrary
complexity of the water demand time series used
in this study, Msiza and co-workers previously had
to determine the optimum number of previous wa-
ter demand figures to be used as part of the model’s
input vector in an empirical fashion (Msiza et al.,
2007), (Msiza et al., 2008). They established that a
water demand figure of the current day is influenced
by the water demand figures of the past four days,
coupled with the population size during those days.
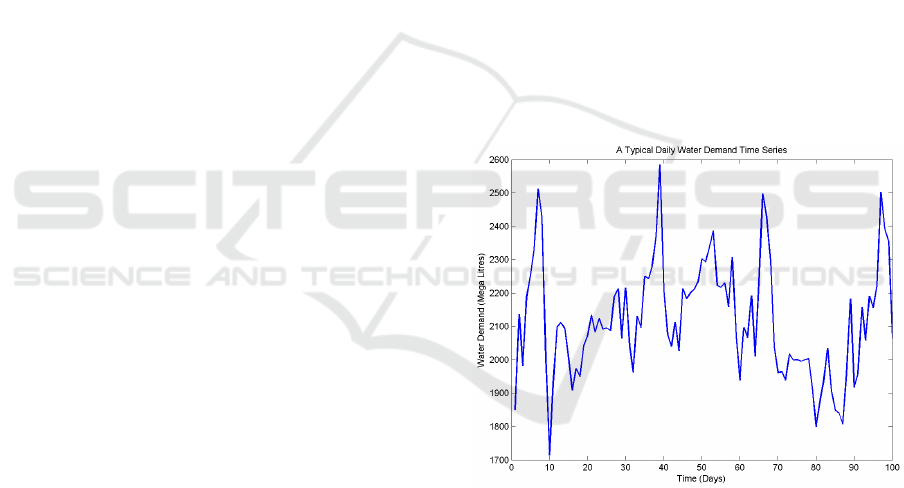
Figure 3 depicts a snapshot of this water demand time
series. The water demand time series used in this
study has a total of 3 470 instances of data with daily
frequency, but the snapshot in figure 3 shows only 100
data instances – with daily fequency – in the interest
of clearer visualization.
Figure 3: A snapshot of the water demand time series (with
daily frequency) used in this study. It is characterised by
non-linearity and arbitrary complexity.
A conventional neural network model would,
therefore, end up with a total of five inputs (four wa-
ter demand figures and one population figure) and one
output (water demand figure of the fifth day). An au-
toencoder network, as mentioned before, is trained to
recall its inputs and, thereafter, expected to present
the same inputs in the output space. This implies that
the variable of interest (water demand figure of every
fifth day), has to form part of the input space. The au-
toencoder network used in this study, therefore, ends
up with a total of six inputs and six outputs.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
234

4.3 Data Treatment
The data used in this study is treated in two ways;
data division and data normalization. The data is di-
vided in accordance with the cross-validation tech-
nique, where there is a total of three data sets: the
training set, the validation set, and the testing set.
Table 1: The Division of Data into Three Separate Sets.
Data Set Distribution Total
Training 294 × 6 1 764
Validation 201 × 6 1 206
Testing 199 × 6 1 194
The training set is used to optimize the model,
with close monitoring achieved through the valida-
tion set. The testing set is used to evaluate the per-
formance of the trained network, and determine if it
has generalization ability. The resulting data distribu-
tion is summarized in table 1. This distribution of data
is exactly the same is the one reported in Msiza’s lat-
est work on water demand predictive modelling using
neural computing (Msiza et al., 2008).
Data normalization is done so as to ensure that all
the instances of data are of the same order of magni-
tude and hence simplify the network training process.
The largest value in the dataset is scaled to one, and
the smallest value is scaled to zero. This normaliza-
tion is achieved by making use of the following rela-
tionship:
x
norm
=
x − x
min
x
max
− x
min
(3)
where x
norm
is the normalized version of x, x
min
is the
smallest instance in the dataset, and x
max
is the largest
instance in the dataset.
4.4 Hidden Nodes Experiment
Now that both the input and the output space have
been determined, there is a need to determine the op-
timum number of nodes in the hidden unit, in order
to complete the architecture of the network. This is
done by making use of ∆E between the training set
and the validation set. Because this is an autoencoder
network with six nodes in both the input and output
units, the number of nodes in the hidden unit has to
be any figure between one and five. The training set
is used to – under supervision – optimize the network,
while the validation set is used to ensure that the av-
erage validation error,
E
validation
, is less than or equal
to the training error, E
training
.
The average training error is the error between the
target output and the output produced by the autoen-
coder network, when presented with training data.
Similarly, the average validation error is the error be-
tween the target output and the output estimated by
the autoencoder network, when presented with val-
idation data. A validation error that is less than or
equal to the training error implies that the network
does have the ability to generalize, that is, it can make
reliable estimates when presented with previously un-
seen data.
To the contrary, a validation error that is greater
than the training error means that the network has
poor generalization ability. The error is computed as
the absolute value of the Residual divided by the tar-
get value, expressed as a percentage. The Residual
is a statistical term used for the arithmetic difference
between a predicted value and its targeted value (Utts
and Heckard, 2015). The mathematical definition of
this error (E) is as follows:
E =
|y
t
− y
p
|
y
t
× 100% (4)
where y
p
is the output predicted by the trained net-
work, and y
t
is the targeted output. The average of
this error is defined as:
E =
1
M
M
∑
k=1
(y
t
)
k
− (y
p
)
k
(y
t
)
k
× 100% (5)
where (y
t
)
k
and (y
p
)
k
are – in the given order – the
target and the predicted output for the k
th
instance of
data, and M is the total number of instances in a given
data set.
Nabney’s Netlab Toolbox (Nabney, 2004) is used
to create the autoencoder network using the MLP ar-
chitecture. It is trained using the scaled conjugate gra-
dient (SCG) algorithm with a linear activation func-
tion, for 5 000 cycles. The average validation error
is computed for each value of N
hidden
. Recall that the
validation error is just the error defined in equation 4,
for the validation set. The word “average” is used to
indicate the validation errors of all the data instances
have been added up, and divided by the total number
of instances in the dataset, expressed as a percentage,
as defined in equation 5. The results obtained from
this experiment are summarized in table 2, where it
is apparent that the optimum number of nodes in the
hidden unit is five.
Figure 4 shows plots of both the actual and pre-
dicted outputs obtained from the autoencoder network
during the training process; while figure 5 shows plots
of both the actual and predicted outputs obtained from
the trained autoencoder network, when exposed to the
validation data set.
Autoencoder Networks for Water Demand Predictive Modelling
235

Table 2: The Results of the Hidden Nodes Experiment.
N
hidden
E
training
E
validation
∆E
1 4.9604% 4.9731% −0.0127%
2 4.6435% 3.9704% +0.6731%
3 2.5479% 2.1436% +0.4043%
4 1.7653% 1.4940% +0.2713%
5 1.3273% 1.2202% +0.1071%
Figure 4: Autoencoder network - predicted output (dotted
plot), from the training data set, on the same system of axes
with the target/actual output (solid plot).
Figure 5: Autoencoder network - predicted output (dotted),
from the validation data set, on the same system of axes
with the target/actual output (solid)
4.5 Performance Evaluation
Following the successful completion of the process of
determining the optimum number of nodes in the hid-
den unit, it then becomes necessary to evaulate the
performance of this optimized network under the ex-
posure of the testing data set. The average error in-
Figure 6: Autoencoder network - predicted output (dotted
plot), from the testing data set, on the same system of axes
with the target/actual output (solid plot).
troduced in equation 5, and the time taken by the op-
timized autoencoder network to produce an output –
given a single instance of input data – are readily us-
able as measures of perfomance. It is, however, nec-
essary to introduce an additional measure that should
indicate the accuracy of the optimized network.
The accuracy of an optimized network can – de-
pending on the application at hand – be evaluated in a
number of ways. This manuscript introduces a figure
of tolerance, T . If the predicted water demand value
is equal to the target value, plus or minus the figure
of tolerance, then it is counted as accurate. The total
of the counted accurate values is then divided by the
total number of data points (199) in the testing set and
multiply it by a hundred, to express it as a percentage.
This relationship is depicted in equation 6.
A =
∀
(y
p
− y
t
)
≤ T : Count(y
p
)
Count(y
p
)
× 100% (6)
According to the South African Department of
Water and Environmental Affairs (previously known
as the Department of Water Affairs and Forestry), the
water services sector represents an overall demand
that is 19% of the total water supplied (Msiza et al.,
2007). This implies that 19% of the water supplied
is consumed by the water supplier itself. An analy-
sis of the overall data set used in this study indicates
that the average annual water demand is 2 700 Mega
Litres, and 19% of this figure works out to 513 Mega
Litres. Using equation 6 – with the worked out value
of T = 513 Mega Litres – the optimized autoencoder
network, an accuracy of 100% is obtained. Figure 6
depicts – on the same system of axes – the autoen-
coder network predicted time series, versus the actual
time series.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
236
5 CONVENTIONAL NEURAL
NETWORK
IMPLEMENTATION
In order to benchmark the performance of this autoen-
coder network, a conventional neural network is im-
plemented and exposed to the same data sets.
5.1 Model Inputs and Outputs Selection
This conventional network – unlike the autoencoder
network – has a total of five inputs (water demand
values of the past four days and the population figure)
and one output (water demand value of the fifth day).
As mentioned before, the autoencoder network has an
additional input variable because the required output
(water demand figure of the fifth day) has to form part
of the input vector.
5.2 Hidden Nodes
With the autoencoder network, the optimum number
of hidden nodes was determined in an experimental
fashion, but with a conventional network that process
is done through the guidance of Kolmogorov’s the-
orem on multi-layer neural networks (Msiza et al.,
2011). This theorem suggests that, during the process
of training a conventional multi-layer neural network
model, the number of nodes in the hidden unit should
be twice the number of parameters in the input unit.
The conventional network, for that reason, ends up
with a total of ten nodes in the hidden unit (because
there is a total of five nodes in the input unit).
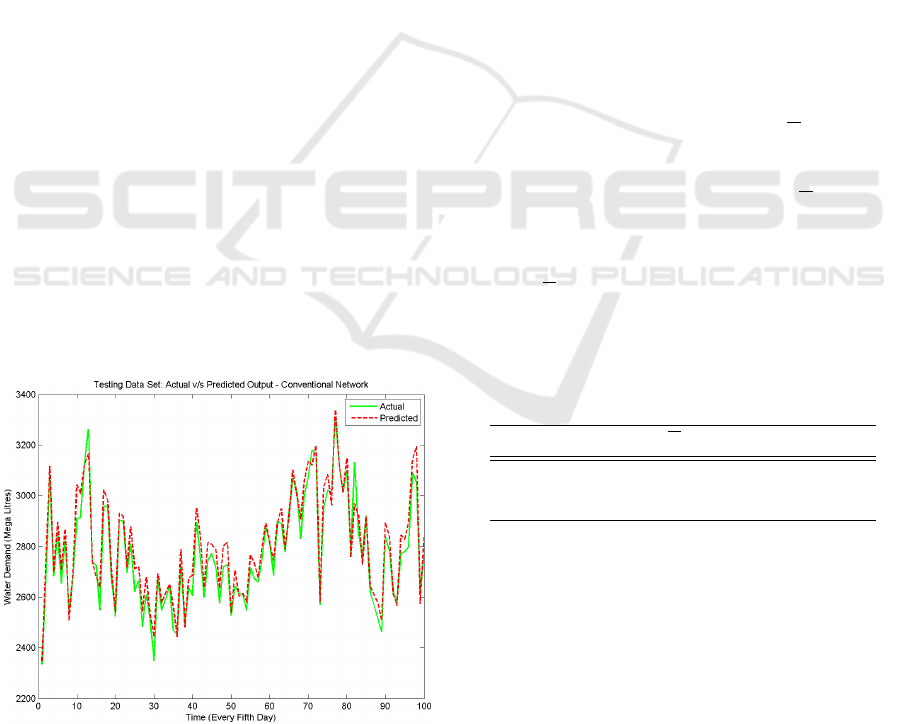
Figure 7: Conventional network - predicted output (dotted
plot), from the testing data set, on the same system of axes
with the target/actual output (solid plot).
5.3 Performance Evaluation
Like the autoencoder network, this conventional net-
work is trained through the use of the SCG algorithm
with a linear activation function, for 5 000 cycles.
This is after using the same data treatment techniques
used in the case of the autoencoder network. Figure 7
shows a time series predicted by the trained conven-
tional network, versus the actual time series, when
exposed to the testing data set. Using the same per-
formance indicators as in the case of the autoencoder
network, the next section carries out a comparison of
the two networks.
6 COMPARING THE
PERFORMANCE OF THE TWO
NETWORKS
Table 3 summarizes the comparison, in performance,
between the conventional and the autoencoder net-
work. These two networks are compared in terms of
accuracy (A), average prediction error (E), the time it
takes to generate a single output, and dimensionality
(D). Ideally, a better perfoming network should have
a higher value of A, and lower values of E, time, and
D. From table 3, it is easy to conclude that the autoen-
coder network is better than the conventional network.
This is due to the fact that the autoencoder has a lower
value of E and D, while they have the same value for
A. The conventional network only – slightly – outper-
foms the autoencoder network in terms of time.
Table 3: Comparison between the Conventional Network
(CN) and the Autoencoder Network (AN).
Model A E Time (s) D
CN 100% 1.99% 3.70 × 10
−5
10
AN 100% 1.25% 3.72 × 10
−5
5
7 CONCLUSIONS AND FUTURE
WORK
The purpose of the work presented in this manuscript
was to interrogate the usability of autoencoder neural
networks in predicting a water demand time series.
The choice of autoencoder networks was inspired by
the ideal of having a network that has low dimension-
ality, less complexity, high accuracy, and good gen-
eralization ability. This study was conducted using
Autoencoder Networks for Water Demand Predictive Modelling
237

real data obtained from Rand Water, a bulk water sup-
plier in South Africa. This data was split into three
sets: one to train the network, another to validate
the training process, and the last one to evaluate the
performance of the trained network. Using a simple
and computationally inexpensive approach to deter-
mine the optimum number of nodes in the hidden unit,
the autoencoder ended up with a dimensionality of 5.
This was exactly half of the dimensionality of the con-
ventional network – informed by Kolmogorov’s the-
orem – with which it was compared. Both networks
registered a prediction accuracy of 100%, however the
autoencoder network had a lower average prediction
error. The conventional network slightly outperfomed
the autoencoder network in terms of the time taken
to generate data in the output layer. However, the
fact that the autoencoder network has a dimension-
ality that is significantly less than that of the conven-
tional network, makes it a better performing model.
Because both models registered 100% accuracy, it
would be useful to introduce variations on the data,
then evaluate the performance of the two models. Ex-
posing both models to various combinations of train-
ing algorithms and activation functions could, could
also be helpful. In addition, it could be useful to in-
troduce more neural network architectures, in order
to have a rich pool of model comparison. All these
suggestions could form part of possible future work.
ACKNOWLEDGEMENTS
The authors hereby acknowledge and thank Thomas
Phetlha, from Rand Water, for the water demand data.
REFERENCES
Bougadis, J., Adamowski, K., and Diduch, R. (2005).
Short-term Municipal Water Demand Forecasting. In
Hydrological Processes 19. pp 137-148.
Cooks, J. (2004). 100 Years of Excellence 1903-2003. Rand
Water, Johannesburg, 1st edition.
Hessel, M., Borgatelli, F., and Ortalli, F. (2014). A Novel
Approach to Model Design and Tuning through Auto-
matic Parameter Screening and Optimisation - Theory
and Application to a Helicopter Flight Simulator Case
Study. In 4th Intl. Conf. on Simulation & Modelling
Methodologies, Technol., and Appl. pp 24–35.
Jain, A., Varshney, A. K., and Joshi, U. C. (2001). Short-
term Water Demand Forecast Modelling at IIT Kanpur
Using Artificial Neural Networks. In IEEE Trans. on
Water Resources Management 15. pp 299-321.
Leke-Betechuoh, B., Marwala, T., and Tettey, T. (2006).
Autoencoder Networks for HIV Classification. In
Current Science 91. pp 1467-1473.
Marivate, V. N., Nelwamondo, F. V., and Marwala, T.
(2008). Investigation into the Use of Autoencoder
Neural Networks, Principal Component Analysis and
Support Vector Regression in Estimating Missing HIV
Data. In 17th World Congress of the Intl. Federation
of Automatic Control. pp 682-689.
Marwala, T. (2016). Handbook of Machine Learning:
Foundation of Artificial Intelligence. Imperial College
Press, London, (Accepted for Publication) edition.
Msiza, I. S., Nelwamondo, F. V., and Marwala, T. (2007).
Water Demand Forecasting Using Multi-layer Percep-
tron and Radial Basis Functions. In IEEE Intl. Joint
Conf. on Neural Networks. pp 13-18.
Msiza, I. S., Nelwamondo, F. V., and Marwala, T. (2008).
Water Demand Prediction Using Artificial Neural
Networks and Support Vector Regression. In Journal
of Computers 3. pp 1–8.
Msiza, I. S., Szewczyk, M., Halinka, A., Pretorius, J. H.,
Sowa, P., and Marwala, T. (2011). Neural Net-
works on Transformer Fault Detection: Evaluating
the Relevance of the Input Space Parameters. In
IEEE PES Power Systems Conf. & Exposition. DOI:
10.1109/PSCE.2011.5772567.
Nabney, I. T. (2004). Algorithms for Pattern Recognition.
Springer, Heidelberg, 4th edition.
Nelwamondo, F. V., Golding, D., and Marwala, T. (2013).
A Dynamic Programming Approach to Missing Data
Estimation Using Neural Networks. In Information
Sciences 237. pp 49-58.
Solanki, A., Agrawal, H., and Khare, K. (2015). Predic-
tive Analysis of Water Quality Parameters using Deep
Learning. In Intl. Journal of Computer Appl. 125. pp
29-34.
Thompson, B. B., Marks, R. J., Choi, J. J., El-Sharkawi,
M. A., Huang, M.-Y., and Bunje, C. (2002). Implicit
Learning in Autoencoder Novelty Assessment. In
IEEE Intl. Joint Conf. on Neural Networks. pp 2878–
2883.
Utts, J. M. and Heckard, R. F. (2015). Mind on Statistics.
Cengage Learning, Stanford, 5th edition.
van Deventer, V. and Mojapelo-Batka, M. (2013). A Stu-
dent’s A-Z of Psychology. Juta & Company, South
Africa, 2nd edition.
Yuan, Y. and Jia, K. (2015). A Water Quality Assessment
Method Based on Sparse Autoencoder. In IEEE Intl.
Conf. on Signal Processing, Communications & Com-
puting. pp 1-4.
Zhiyin, W., Long, Y., and Shengwei, T. (2015). Water Body
Extraction Method Based on Stacked Autoencoder. In
Journal of Computer Appl. 35. pp 2706-2709.
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
238
