
The Dead Zone Determination for Exoskeleton Arm with Double
Mode Control System
I. L. Ermolov, M. M. Knyazkov, A. N. Sukhanov and A. A. Kryukova
Institute for Problems in Mechanics of the Russian Academy of Sciences,
Prospect Vernadskogo 101-1, Moscow, Russian Federation
Keywords: Exoskeleton Control, EMG Sensors, Dead Zone Definition, Multibody Dynamics.
Abstract: The main goal of this paper is to determine the dead zone of control signal to provide the modes shift in the
exoskeleton control system. The kinematic system consists of two subsystems for left and right hands. Each
subsystem has 4 DOF and it is controlled individually. The control system for the designed exoskeleton device
is based on bioelectric potentials processing. It uses the information about muscular activity to form the
rotation speed of exoskeleton drives. The exoskeleton’s servo drive system is based on the feedback technique
of acquiring information from the actuators and passing it to the control system via the HMI. The dead zone
of control signal allows shifting control modes to let the exoskeleton device running in two modes – the setting
speed mode and angle tracking mode. The dead zone of control signal also allows signal noise and positioning
error reduction. The proposed idea is the definition of the dead zone as nonlinear function of joint coordinates.
1 INTRODUCTION
Researches in the field of wearable robotics are held
in many research centers in different countries.
Studies of exoskeleton devices design allow us to
estimate perspectives of applying such devices in
human life: medicine, sports, space researches, virtual
reality etc. The main problem for researchers and
engineers who works with such devices is
development of a control technique suitable for
different human limbs and also describing the
interaction between human-operator and exoskeleton.
The first active prototypes of exoskeletons
designed to implement limb motion of paralyzed
higher or lower extremities of patients (Ward et al.,
2010, Gurfinkel et al., 1972) had a control system
with feedforward (no feedback) with minimum
information about operating parameters acquired
from integrated sensors. Pre-planned motion of the
exoskeleton limbs was introduced by an operator
before the motion had started. Most of these
exoskeletons were redundant in terms of degrees of
freedom at the joints (Mistry et al., 2005). Thus it was
necessary to research and develop prototypes of such
systems to study the interaction of the operator and
the exoskeleton system. To satisfy a user’s needs, it is
sometimes unnecessary to build a redundant system
and only a limited number of degrees of freedom are
required, which can be provided by using the modular
technique (Gradetsky et al., 2010). Motion control
and orientation system of the exoskeleton device is
based on different sensors.
2 EXOSKELETON CONTROL
SYSTEM
The exoskeleton device for upper human limbs was
designed in the Laboratory of robotics and
mechatronics of the Institute for Problems in
Mechanics RAS (Figure 1). It is a multibody active
system with drives in joints. Its kinematics and
dynamics were described in previous works
(Gradetsky et al., 2014, Vukobratovič and Stokič,
1982, Vukobratovič et al., 1989). The system consists
of two subsystems for left and right hands. Each
subsystem has 4 DOF and it is controlled
individually. Current work is devoted to control
technique for this device.
2.1 The Exoskeleton Control System
The proposed control technique uses EMG
information about bioelectric potentials of the
274
Ermolov, I., Knyazkov, M., Sukhanov, A. and Kryukova, A.
The Dead Zone Determination for Exoskeleton Arm with Double Mode Control System.
DOI: 10.5220/0005977302740279
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 274-279
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

operator. The operator controls exoskeleton limbs via
the control system by means of the human-computer
interface. This interface includes EMG sensors placed
on the operator’s skin. Each pair of EMG sensors
sends data to set of filters and then information about
muscle activity reaches control unit. After data
linearization and processing this unit forms control
signals for drive system.
Figure 1: The designed exoskeleton device for upper limbs.
The exoskeleton’s servo drive system is based on
the feedback technique of acquiring information from
the actuators and passing it to the control system via
the HMI. In this case, the feedback information
channel provides different data types. These data
show the amount of force-torque feedback, linear and
angular metric information to detect errors and
automatically reduce them to zero. The "human-
exoskeleton" system has direct influence of the
actuators on control elements. Thus it is necessary to
apply one more feedback information channel which
will contain data of the human presence effect. Such
data could be provided by noninvasive
electromyographic electrodes connected to human
skin. This will allow control system to determine the
presence of the human control action and adjust
actuators’ movement in a non-deterministic
environment under external force-torque impact.
Thus, a handle with a set of piezo-sensors will
transmit the force vector from human to control
system and exoskeleton will sense its operator and
will ignore any other force. Also averaging
algorithms applying to EMG sensor readings will
solve the problem of arm tremor during control.
The EMG-sensor system requires three electrodes
(Hidalgo et al., 2005). The ground electrode is needed
for providing a common reference to the differential
input of the preamplifier in the electrode. It is placed
on electrically neutral area of a skin. Other two
electrodes are placed then at two different points on
the muscle. The EMG signal amplitude is stochastic
in nature. It may be represented by a Gaussian
distribution function (Jain et al., 2012) and range
from 0 to 10 mV (peak-to-peak) (Saponas et al.,
2008.). EMG signal is sent to the preamplifier and
band pass filter. Then data goes to the analog input of
the microcontroller for processing. The amplified,
rectified, and smoothed signal is recorded for
analysis.
Experimental investigation showed that most
manipulations with objects can be divided into two
parts: moving and stabilization. Thus it was decided
to realize two control modes for the exoskeleton. The
first control mode is motion-mode. It activates when
the operator desires to move its limbs. This desire
effects on muscular activity and it is changing in time
(Zuniga and Simons, 1969.). The control signal from
the integrated controller forms velocity of limbs. The
second control mode is stabilization mode. It is
activated under absence of muscular activity. But
another research showed presence of muscular
activity even in quiescent state of the operator. It was
decided to perform a sort of dead zone for input data
to avoid noise and to provide feedback to the
operator.
Figure 2: Muscular activity in carrying a payload of
different masses.
The figure 2 shows muscular activity in carrying
a payload of different masses. It shows linear
dependence of normalized output data (voltage from
0 to 5 mV is scaled from 0 to 255 Points) from sensors
after processing from mass of the object in stable
mode. But further experiments shown that these
activity changes in different exoskeleton postures.
The Dead Zone Determination for Exoskeleton Arm with Double Mode Control System
275

Indeed current muscular activity (CMA) appeared to
be a function not only from carrying mass but current
joint coordinates. Figure 3 presents that statement.
Figure 3: Muscular activity in carrying a payload of
different masses in different postures.
Thus the control system should get information
about the current posture of the exoskeleton from
angular and linear sensors. The operator’s muscles
receive signals from nervous system (Figure 4).
These signals are being registered with EMG sensors.
After filtration, linearization and processing in
controller unit the drive controller unit sets speed of
drives of the exoskeleton. The links motion is
evaluated by operator.
Figure 4: The functional model of the exoskeleton control
system.
2.2 The Mathematical Simulation of
the Model
Let us discuss a plane stable system. Let M
3
and M
4
be torques in operator’s shoulder and elbow in sagittal
plane; L
3
be the length of the shoulder; L
4
be the
length of the forearm; m
3d
and m
4d
be masses of
motors in joints, m
3l
and m
4l
be masses of links in
joints; m
p
be the mass of the payload.
is reaction
force in the shoulder, g is acceleration of gravity
(Figure 5). We need to know torques in joints to form
desired control. The idea is to configure the control
system with known payload mass to find limits for
that torques in terms of dead zone. In other words we
have the source of control signals – muscles. In
different postures they provide different amplitude of
voltage. To reduce effects from noise and tremor we
should implement a dead zone that will be the
motivator for changing control modes.
Figure 5: The functional model of the exoskeleton control
system.
Signals with amplitude lower than the dead zone
should be ignored by the system and activate
stabilization mode. Signals with amplitude higher
than the dead zone will form the links’ torques. The
solution for the system is:
M
=gl
sin
(
φ
)
×
×m
гр
+m
зв
+m
дв
+
зв
+
gl
sin
(
β
)
m
гр
+
зв
M
=gl
sin
(
β
)
m
гр
+
зв
β=φ
−φ
, (1)
Thus we can calculate the numerical value of the
dead zone for the control system. Torques are formed
with motors under Processed EMG signals.
Figures 6 and 7 show that torques in given joints
are dependent from posture of the exoskeleton. These
surfaces are visual representation of the dead zone.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
276
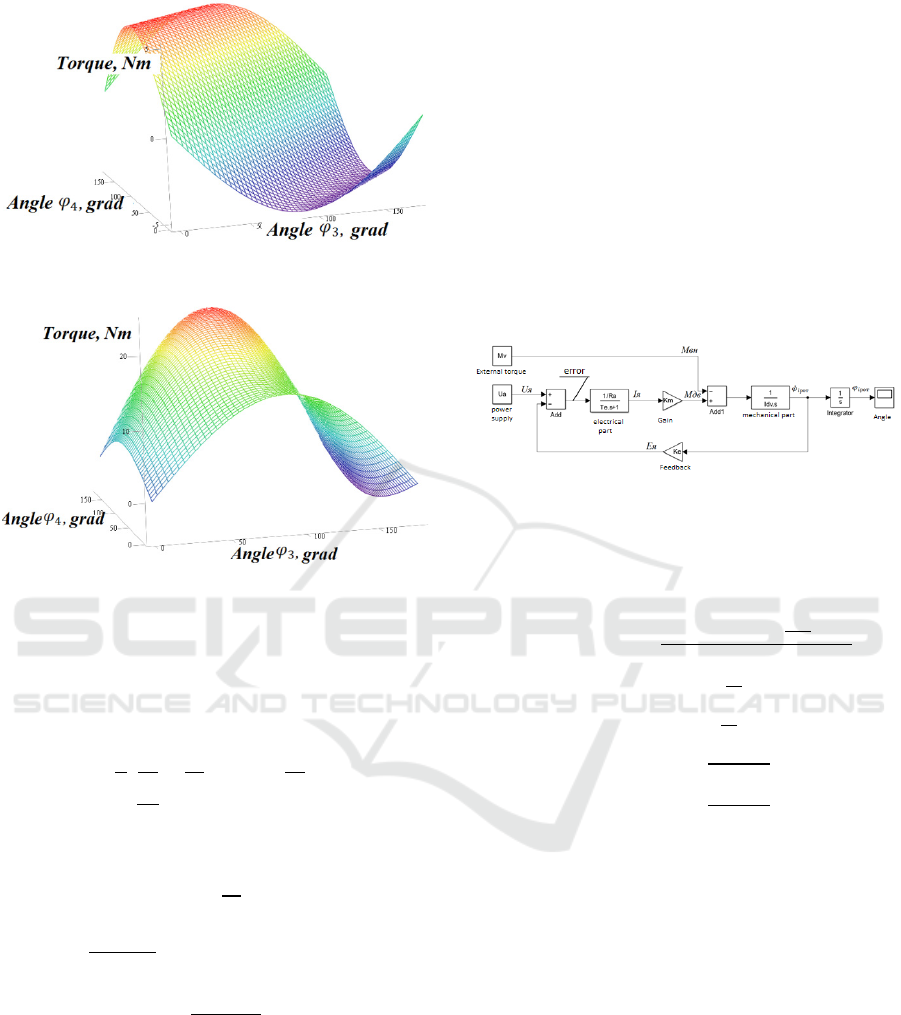
Figure 6: Dead zone for torque in the elbow.
Figure 7: Dead zone for torque in the shoulder in sagittal
plane.
For the whole design the control system solves
equations for every joint and finds dead zone for each
torque at a time. It forms speed for motors
.
in
joints under the next conditions:
−
к
=
−
+
=
−
=
=
=
=
.
(
)
=
=
(
)
,
|
|
>
|
|
|
,
,
(
)
+
(
)
,
|
|
≤
|
|
|
,
,
=
=1,4
,(2)
Here E
is kinetic energy of the system; E
is
potential energy of the system; M
is torque in each
joint;
is the gear ratio for each motor;
is joint
coordinate,
is joint speed;
is inductance of rotor;
is current in the rotor;
is resistance of rotor;
is supply voltage;
is back EMF;
,
are
electrical and mechanical factors of motors;
is
processed value of EMG signal;
is
normalization factor;
is numerical value of torque
for each joint corresponding with dead zone for the
current posture (Figures 6, 7),m
is payload mass,
φ
is joint coordinate from the memory of the
control system, k
is proportional speed factor, k
is integral speed factor.
The experiment for stabilization control involved
a servo drive (Figure 8). When the amplitude of the
control signal is lower than the dead zone’ value the
control system activates stabilization mode. It uses
angle, stored in memory for each joint as an initial
condition. In the motion mode the control system sets
required speed for drives and rewrites current angles
in the memory.
Figure 8: Servo drive control scheme
The discrete transfer function Ф
п
(
w
)
of the close
looped servo drive with three feedback loops is
presented in (3).
Ф
п
(
w
)
=
(
)
A
=T
+
+ω
A
=T
∙
+ω
A
=
∙
A
=
∙
.
∙
, (3)
Where T
is time-constant of the speed controller,
T
is sampling time in digital system, ω
is cut-off
frequency, ω
is speed cutoff frequency, T
.
is
equivalent time-constant.
3 EXPERIMENTS
The HMI program was designed to display EMG data
after filtration (De Luca, 2002, Day, 2002.) and
control signal from microcontroller unit on the screen
using Java language (Figure 9). Scaled information
about EMG-signal amplitude and the dynamics of the
signal in real-time was obtained.
The Dead Zone Determination for Exoskeleton Arm with Double Mode Control System
277

Figure 9: The Human-Machine Interface (HMI) for signal
data real-time testing.
Here the high level of the control signal returns
the “enable” command for the servo drive to start
rotation according the force sensors data readings.
Figure 10: Opening door with the key.
During the experiment a tool (a key) was attached
to the exoskeleton’s link (Figure 10). A keyhole has
been equipped with a limit switch. The experimental
research for the designed system shown that
application of the designed control system with two
control modes improves its efficiency. In motion with
using proposed control technique the position error of
the end effector of the exoskeleton was less than the
position error caused in the same conditions without
using control EMG signal in the experiment.
Thus, using the designed control algorithm for the
exoskeleton, based on a complex processing of sensor
information improves the quality of exoskeleton
movement control.
Figure 11: Results of the experiment.
Here (Figure 11) the left figure presents desired
angle and the right figures show the result of the
experiments with the suggested control technique
(top) and the old technique based on force sensors
data use only (bottom).
Figure 12: The virtual model of the exoskeleton.
The virtual mechanical model of the exoskeleton
has been examined in the SimMechanics. Variations
of angles between links were obtained. The obtained
data shows the desired flexion in the joints during the
control. The model is also provides joint torques and
moments of inertia of links. This model provided
desired torques M
for the current posture of the
operator that needs for dead zone estimation.
4 CONCLUSIONS
The main goal of this paper is to determine the dead
zone of control signal to provide the modes shift in
the exoskeleton control system. The control system
for the designed exoskeleton device is based on
bioelectric potentials processing. It uses the
information about muscular activity to form the
rotation speed of exoskeleton drives. It was shown
that current muscle activity is changing with posture
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
278

of the exoskeleton. Thus it was decided to implement
a nonlinear dead zone to the control system. The dead
zone of control signal allows shifting control modes
to let the exoskeleton device running in two modes –
the setting speed mode and angle tracking mode. The
dead zone of control signal also allows signal noise
and positioning error reduction.
ACKNOWLEDGEMENTS
This work is supported by RFBR grant № 14-08-
00537 A.
REFERENCES
Ward, J., Sugar, T., Standeven, J., and Engsberg, J., 2010.
Stroke Survivor Gait Adaptation and Performance
After Training on a Powered Ankle Foot Orthosis, 2010
IEEE International Conference on Robotics and
Automation, Anchorage Convention District, May 3-8,
Anchorage, Alaska, USA
Gurfinkel, V. S., Malkin, V. B., Cetlin, M. L., Shneider, A.
Yu., 1972. Bioelectricheskoe upravlenie (Bioelectric
control), Nauka, Moscow, 247p. (in Russian)
Mistry, M., Mohajerian, P., Schaal, S., 2005. Arm
Movement Experiments with Joint Space Force Fields
using an Exoskeleton Robot, Proceedings of the 2005
IEEE, 9th International Conference on Rehabilitation
Robotics June 28 - July 1, Chicago, IL, USA,
Gradetsky, V., Kalinichenko, S., Kravchuk, L., Lopashov,
V., 2010. “Modular Design and Mechatronic
Approaches to the Exoskeleton System”, Lecture Notes
of the ICB Seminars Biomechanics, Biomechanics of
the Musculoskeletal System
Gradetsky, V. G., Ermolov, I. L., Knyazkov, M. M.
Semyonov, E.A., Sukhanov, A.N. 2014. «Experimental
Investigation of Human Exoskeleton Model»,
Proceedings of ROMANSY 2014 XX CISM-IFToMM
Symposium on Theory and Practice of Robots and
Manipulators, Moscow, Russia, June 23, 2014 — June
26, published in the “Springer Verlag” №22, pp. 275-
281.
Vukobratovič, M., Stokič, D., 1982. Scientific
Fundamentals of Robotics, Control of Manipulation
Robots: Theory and Application, Springer-Verlag,
Vol.2.
Vukobratovič, M., Borovač, B., Surla, D., Stokič, D., 1989.
Scientific Fundamentals of Robotics, Biped
Locomotion: Dynamics, Stability, Control and
Application, Springer-Verlag, Vol.7.
Hidalgo, M., Sanchez, A., Tene, G., Fuzzy Control of a
2005, Robotic Arm Using EMG Signals, Department of
Automatization and Industrial Control,
Jain, R. K., Datta, S. and Majumder, S., 2012. Design and
Control of an EMG Driven IPMC Based Artificial
Muscle Finger, Second International Conference on
Innovative Computing Technology (INTECH 2012)
September 18-20, Casablanca, Morocco
Saponas, T. S., Tan, D. S., Morris, D. & Balakrishnan R.,
2008. Demonstrating the feasibility of using forearm
electromyography for muscle-computer Interfaces, CHI
2008, April 5-10, Florence, Italy
Zuniga, E. N., Simons, G. D., 1969. Nonlinear relations
between averaged electromyogram potential and
muscle tension in normal subjects. – Arch. Phys. Med.
And Rehabilit., pp.613-620.
De Luca, C. J., 2002. Surface Electromyography: Detection
and Recording, by DelSys Incorporated.
Day, S., 2002. Important Factors in Surface EMG
Measurement, Bortec Biomedical Ltd
The Dead Zone Determination for Exoskeleton Arm with Double Mode Control System
279
