
Development of Discrete Mechanics for Distributed Parameter
Mechanical Systems and Its Application to Vibration Suppression
Control of a String
Tatsuya Kai
1
, Kouhei Yamaki
1
and Shunpei Koike
2
1
Tokyo University of Science, 6-3-1 Niijuku, Katsushika-ku, Tokyo 125-8585, Japan
2
Simplex Inc., 1-23-1 Toranomon, Minato-ku, Tokyo 105-6319, Japan
Keywords:
Discrete Mechanics, Distributed Parameter Mechanical Systems, Nonlinear Optimization, Vibration Suppres-
sion Control, String.
Abstract:
In this study, a new stabilization method by blending discrete mechanics and nonlinear optimization for 1-
dimensional distributed parameter mechanical systems is developed. Discrete mechanics is a kind of numer-
ical solutions for distributed parameter mechanical systems and it is known that it has some advantages in
terms of numerical errors and preserving property of the original systems. First, for discrete Euler-Lagrange
equations with control inputs, we formulate a nonlinear optimal control problem with constraints by setting an
objective function, and initial and boundary conditions. Then, it is shown that the problem is represented as a
finite-dimensional nonlinear optimal problem with constraints and it can be solved by the sequential quadratic
programming method. After that, a vibration suppression control problem for a string is dealt with as a phys-
ical example. As a result, it can be confirmed that vibration of the string is suppressed and the whole of the
system is stabilized by the proposed new method.
1 INTRODUCTION
In general, when we control a given system, we
first derive its mathematical model represented by
continuous-time differential equations. Next, we an-
alyze the features of the model and then design a
continuous-time controller which can achieve a given
control purpose. Since computers deal with only dig-
ital signals, we have to consider “discretization” of
the mathematical model or the controller for the use
of computers. However, the discretization process
causes various problems such as loss of properties
of the original continuous-time model and controller,
debasement of control performances, and destabiliza-
tion of the system. Therefore, for controller design
and synthesis with computers, we haveto think a great
deal of the relationship between continuous and dis-
crete signals.
During recent years, for concentrated constant
systems, a new discretizing method called “discrete
mechanics” has been developed (Marsden et al.,
1998; Kane et al., 2000; Marsden and West, 2001;
Junge et al., 2005). In discrete mechanics, first,
some fundamental concepts and principles such as
Lagrangians, Hamiltonians, Hamilton’s principle, and
Lagrange-d’Alembert’s principle are discretized, and
then discrete equations of motion for systems are de-
rive and called “discrete Euler-Lagrange equations.”
It is known that discrete mechanics has some remark-
able advantages in comparison with other methods,
and thus it has great potential as a powerful numerical
solution. The authors have researched applications of
discrete mechanics to controltheory and derived some
results, for example, swing-up control of the cart-
pendulum system (Kai, 2012; Kai et al., 2012; Kai
and Shintani, 2014), and stable gait generation and
obstacle avoidance control for biped robots (Kai and
Shintani, 2011; Kai and Shibata, 2015; Kai, 2015).
It is expected that discrete mechanics has application
potentiality to not concentrated constant systems but
distributed parameter systems.
In this study, discrete mechanics for 1-
dimensional distributed parameter mechanical
systems is developed and its application to control
theory is considered. First, Section 2 describes de-
tails on discrete mechanics for distributed parameter
mechanical systems. Next, Section 3 shows a new
control method based on discrete mechanics and
nonlinear optimization. Then, in Section 4, we treat
the vibration suppression control of a string as a
492
Kai, T., Yamaki, K. and Koike, S.
Development of Discrete Mechanics for Distributed Parameter Mechanical Systems and Its Application to Vibration Suppression Control of a String.
DOI: 10.5220/0005978204920498
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 492-498
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
physical example, and some numerical simulations
are shown in order to confirm the new method.
2 DISCRETE MECHANICS FOR
DISTRIBUTED PARAMETER
MECHANICAL SYSTEMS
In this section, discrete mechanics for 1-dimensional
distributed parameter mechanical systems are pre-
sented.
Let us denote the time variable as t ∈ R and in
the position of the 1-dimensional space as x ∈ R. We
also refer a displacement of the system at the time t
and the position x as u(t,x) ∈ R, and u(t,x) with a
subscript indicates partial derivative of u(t, x) with re-
spect to the subscript, e.g. u
t
, u
x
, u
tt
, u
tx
, u
xx
. In this
paper, we deal with a continuous Lagrangian density
which includes through second-order partial deriva-
tive of u(t,x) as
L
c
(t, x,u, u
t
,u
x
,u
tt
,u
tx
,u
xx
) (1)
Next, we consider discretization of variables. As
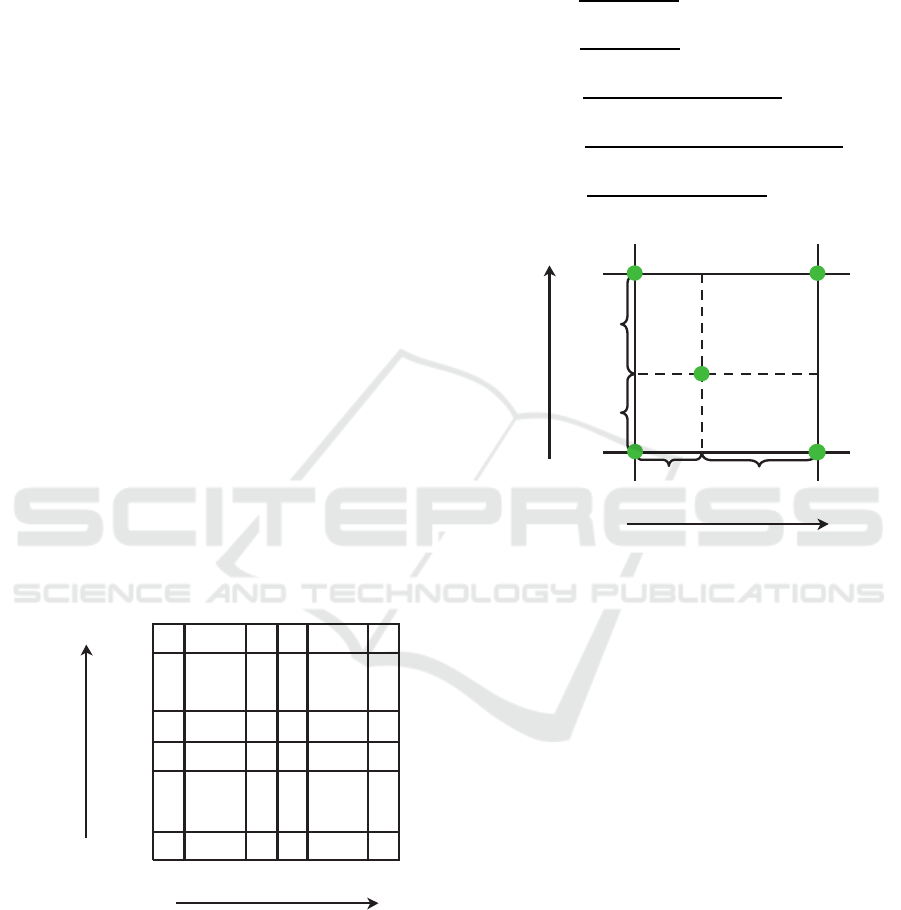
shown in Fig. , the time variable t and the position
x are discretized with sampling intervals h and d as as
t ≈ hk (k = 1, 2, ··· , K −1, K),
x ≈ dl (l = 1, 2,··· ,L−1,L),
(2)
respectively, where k ∈Z (1 ≤k ≤K) and l ∈ Z (1 ≤
l ≤ L) are indices of t and x, respectively.
time
position
1
2 k − 1 k k +1
K − 1 K
l +1
L − 1
L
l − 1
l
1
2
Figure 1: Discretization of Time and Position.
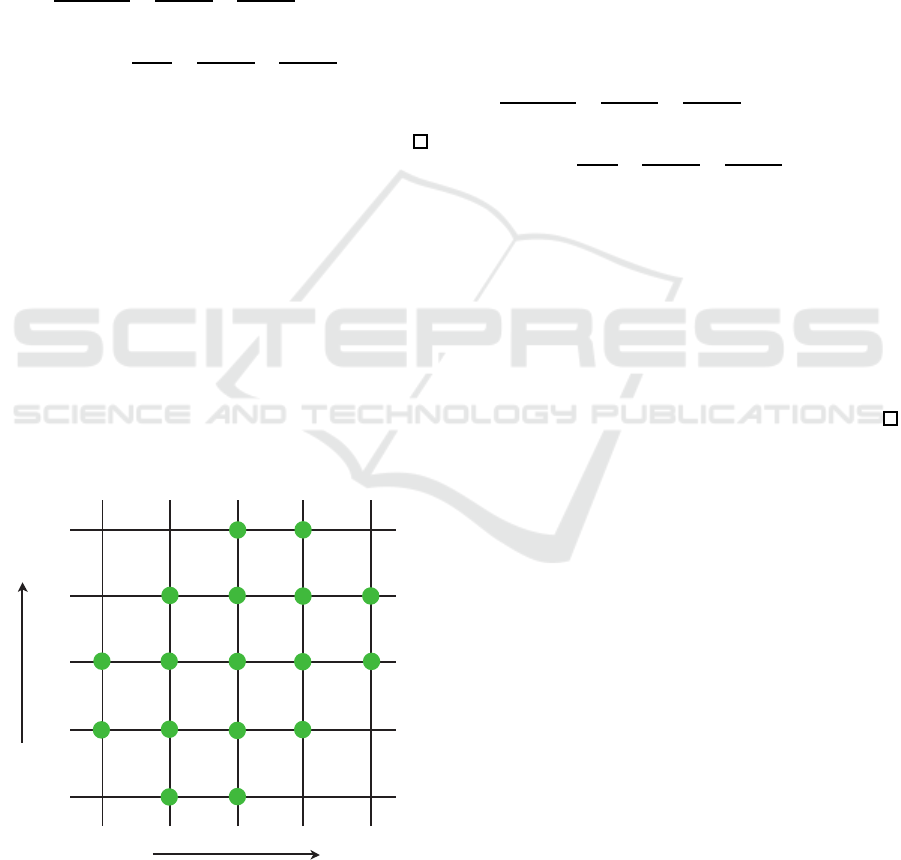
Now, we use a new notation U
k,l
∈ R as a discrete
version of the displacement of the system at the time
step k and the position l. Then, as shown in Fig. 2,
the displacement of the system at the time t and the
position x: u(t, x) is represented as
u(t, x) ≈ (1−α)(1−β)U
k,l
+ (1−α)βU
k,l+1
+ α(1−β)U
k+1,l
+ αβU
k+1,l+ 1
(3)
with four data U
k,l
, U
k,l+1
, U
k+1,l
, U
k+1,l+ 1
, where
α, β ∈ R are dividing parameters (0 < α, β < 1). Par-
tial derivatives of u(t, x) are also represented by
u
t
(t, x) ≈
U
k+1,l
−U
k,l
h
,
u
x
(t, x) ≈
U
k,l+1
−U
k,l
d
,
u
tt
(t, x) ≈
U
k+1,l
−2U
k+1,l
+U
k−1,l
h
2
,
u
tx
(t, x) ≈
U
k+1,l+ 1
−U
k,l+1
−U
k+1,l
+U
k,l
hd
,
u
xx
(t, x) ≈
U
k,l+1
−2U
k,l
+U
k,l−1
d
2
.
(4)
time
position
1 − β
β
u(t, x)
U
k,l
U
k,l+1
U
k+1,l
U
k+1,l+1
k +1
l
l
+1
k
α
1 − α
Figure 2: Discretization of u(t, x).
By substituting (2)–(4) into (1) and multiplying it
by hd, we here define “a discrete Lagrangian density”
as
L
d
k,l
=
L
d
(k, l,U
k−1,l
,U
k,l−1
,U
k,l
,U
k,l+1
,U
k+1,l
,U
k+1,l+ 1
).
(5)
We also define “a discrete action sum” as
S
d
(U) :=
K−1
∑
k=2
L−1
∑
l=2
L
d
k,l
, (6)
and consider “a discrete variation” as
δS
d
(U) := S
d
(U + δU) −S
d
(U), (7)
where δU is a variation of U and satisfies the bound-
ary conditions:
δU
1,l
= δU
2,l
= δU
K−1,l
= δU
K,l
= 0,
δU
k,1
= δU
k,2
= δU
k,L−1
= δU
k,L
= 0.
(k = 1, ···, K; l = 1, ··· , L)
(8)
As a analogy of Hamilton’s principle in the
continuous-time version, we consider “discrete
Development of Discrete Mechanics for Distributed Parameter Mechanical Systems and Its Application to Vibration Suppression Control of
a String
493
Hamilton’s principle” and it states that “only a mo-
tion such that the discrete action sum (6) is stationary,
that is, S
d
(U) = 0, can be realized.” By applying dis-
crete Hamilton’s principle to the discrete action sum
(6), and calculating in details, we can derive “discrete
Euler-Lagrange equations” as the following (due to
limitations of space, the proof is omitted).
Theorem 1 : For the discrete Lagrangian density L
d
k,l
(5), the discrete Euler-Lagrange equations that satisfy
discrete Hamilton’s principle is given by
∂L
d
k−1,l− 1
∂U
k,l
+
∂L
d
k−1,l
∂U
k,l
+
∂L
d
k,l−1
∂U
k,l
+
∂L
d
k,l
∂U
k,l
+
∂L
d
k,l+1
∂U
k,l
+
∂L
d
k+1,l
∂U
k,l
= 0.
(k = 3, 4, ··· , K −2; l = 3, 4,··· , L−2)
(9)
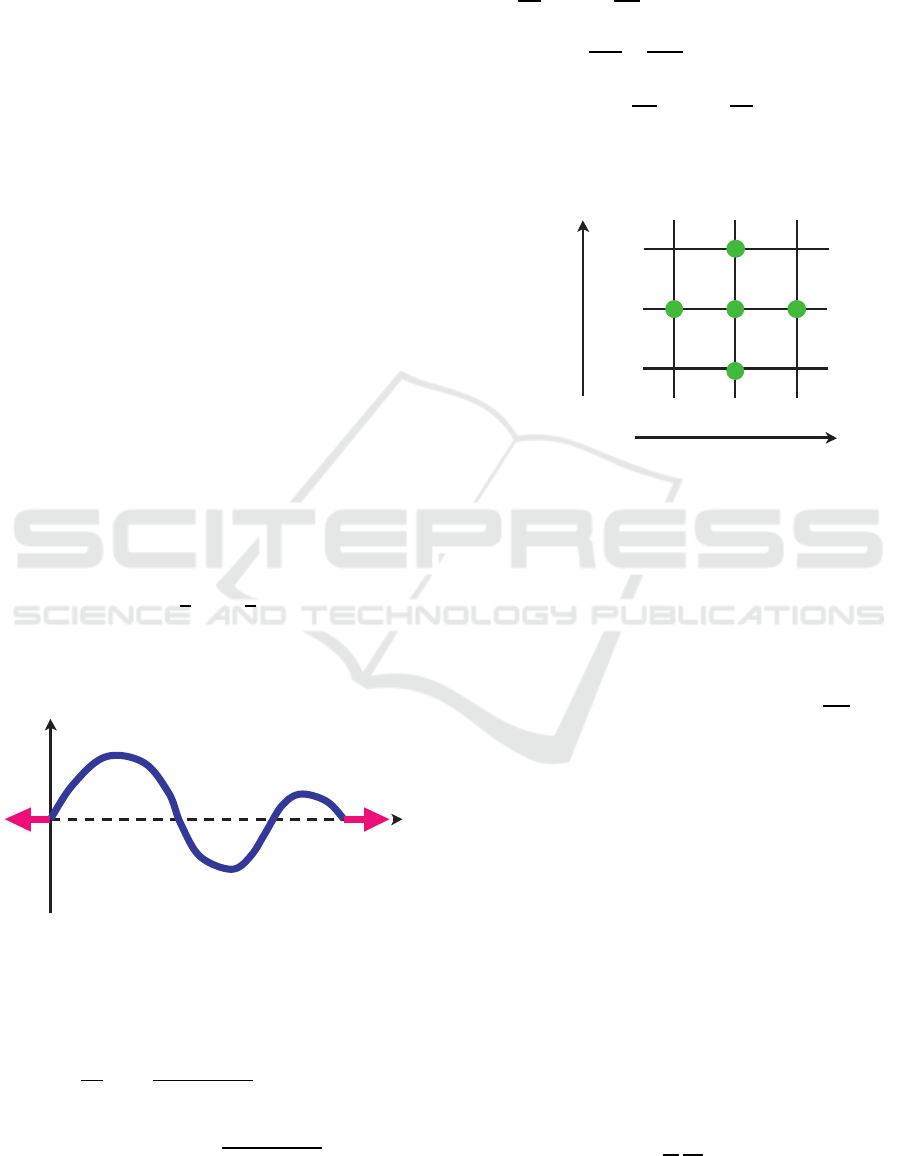
It is noted that the discrete Euler-Lagrange equa-
tions (9) are represented as a set of difference equa-
tions that include 17 variables: U
k−2,l− 1
, U
k−2,l
,
U
k−1,l− 2
, U
k−1,l− 1
, U
k−1,l
, U
k−1,l+ 1
, U
k,l−2
, U
k,l−1
,
U
k,l+1
, U
k,l+1
, U
k,l+2
, U
k+1,l− 1
, U
k+1,l
, U
k+1,l+ 1
,
U
k+1,l+ 2
, U
k+2,l
, U
k+2,l+ 1
as shown in Fig. 3, and
we calculate all the KL displacements U
k,l
(1 ≤ k ≤
K; 1 ≤ l ≤ L) by using the discrete Euler-Lagrange
equations (9) under suitable initial and boundary con-
ditions. In addition, the discrete Euler-Lagrange
equations (9) are generally nonlinear and implicit, and
hence we need some numerical solutions for nonlin-
ear equations such as Newton’s method in order to
calculate all the displacements of the system.
2 +2
time
position
k
k +1
k − 1
l − 1
l
l +1
l +2
l −2
U
k,l
U
k,l+1
U
k+1,l
U
k−1,l
U
k,l+2
U
k,l−2
U
k,l−1
k −
k
U
k− ,l2
U
k−1,l −1
U
k− ,l2
−1
U
k−1,l −2
U
k−1,l
+1
U
k+1,l
U
k+1,l
+1
+2
U
k ,l+1
+2
U
k ,l
+2
U
k+1,l −1
Figure 3: Discrete Euler-Lagrange Equation.
3 OPTIMAL CONTROL
PROBLEM FOR DISCRETE
MECHANICS MODEL
In this section, a nonlinear control problem for a
mathematical model derived by discrete mechanics
is formulated, and a solution method of the problem
is considered. First, the setting on control inputs is
shown. Denote a control input at the time step k and
the position l as F
k,l
∈R. If an actuator is not installed
at the position l, we set F
k,l
== 0 (k = 1, ···, K). We
also denote and a set of indices l such that actuators
are installed as ∆. Thus, the discrete discrete Euler-
Lagrange equations with control inputs are given by
∂L
d
k−1,l− 1
∂U
k,l
+
∂L
d
k−1,l
∂U
k,l
+
∂L
d
k,l−1
∂U
k,l
+
∂L
d
k,l
∂U
k,l
+
∂L
d
k,l+1
∂U
k,l
+
∂L
d
k+1,l
∂U
k,l
= F
k,l
.
(k = 3, 4,··· , K −2; l = 3, 4,··· ,L−2)
(10)
In this study, the next control problem is dealt with for
the discrete discrete Euler-Lagrange equations with
control inputs (10)
Problem 1: For the discrete Lagrangian density (5)
and the discrete Euler-Lagrange equation with control
inputs (10), find control inputs F
k,l
(k = 2, ··· , K −
1; l ∈ ∆) that make all the specified displacements
U
k,l
(k = κ, ··· ,K; l = 1, ··· , L) converge to 0.
In order to solve Problem 1, we consider an op-
timal control approach. Using weight parameters
a, b, c, we set an evaluation function as
J(U, F) = a
κ−1
∑
k=1
L
∑
l=1
U
2
k,l
+ b
K
∑
k=κ
L
∑
l=1
U
2
k,l
+ c
K−2
∑
k=3
∑
l∈∆
F
2
k,l
,
(11)
where the first and second terms evaluate the displace-
ments from k = 1 to k = κ −1 and ones from k = κ to
k = K, respectively, and the third term evaluates the
values of control inputs. It can be expect that we can
make all the specified displacements converge to 0.
by minimizing the evaluation function (11). The op-
timal control problem for the discrete Euler-Lagrange
equation with control inputs (10) can be formulated
as
min
U,F
(11),
subject to (10),
given initial conditions, boundary conditions.
(12)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
494
The optimal control problem (12) can be referred as
a finite-dimensional nonlinear optimization problem
with constraints, and hence we can solve it by numer-
ical solutions such as “the sequential quadratic pro-
gramming method” (Nocedal and Wright, 2006; Gur-
witz, 2015). It is known that the sequential quadratic
programming method can be applied to a relatively
large-scale problems and effectively obtain an opti-
mal or near-optimal solution.
4 APPLICATION TO VIBRATION
SUPPRESSION CONTROL OF
STRING
4.1 Problem Setting
This section treats an application to a physical system:
a string and confirms the proposed control method via
numerical simulations.
We deal with a string clamped at both ends as il-
lustrated in Fig. 4. Denote the position of the string as
x and the displacement of the string at time t and the
position x as u(t, x). physical parameters of the string
are set as ρ: a energy density of the string, N: ten-
sion of the string. Then, the continuous Lagrangian
density of the string is given by
L
c
=
1
2
ρu
2
t
−
1
2
Nu
2
x
. (13)
Note that the continuous Lagrangian density (13) con-
tains through first-order partial derivative u
t
, u
x
.
u(t, x)
x
N
N
Figure 4: String.
Discretization setting are the same as the one in
the previous section. From (13), we have the discrete
Lagrangian density:
L
d
k,l
=
hd
2
(
ρ
U
k+1,l
−U
k,l
h
2
−N
U
k,l+1
−U
k,l
d
2
)
,
(14)
and hence from (9) we obtain the discrete Euler-
Lagrange equation of the string as
−
ρd
h
U
k−1,l
+
Nh
d
U
k,l−1
+
2ρd
h
−
2Nh
d
U
k,l
+
Nh
d
U
k,l+1
−
ρd
h
U
k+1,l
= 0.
(15)
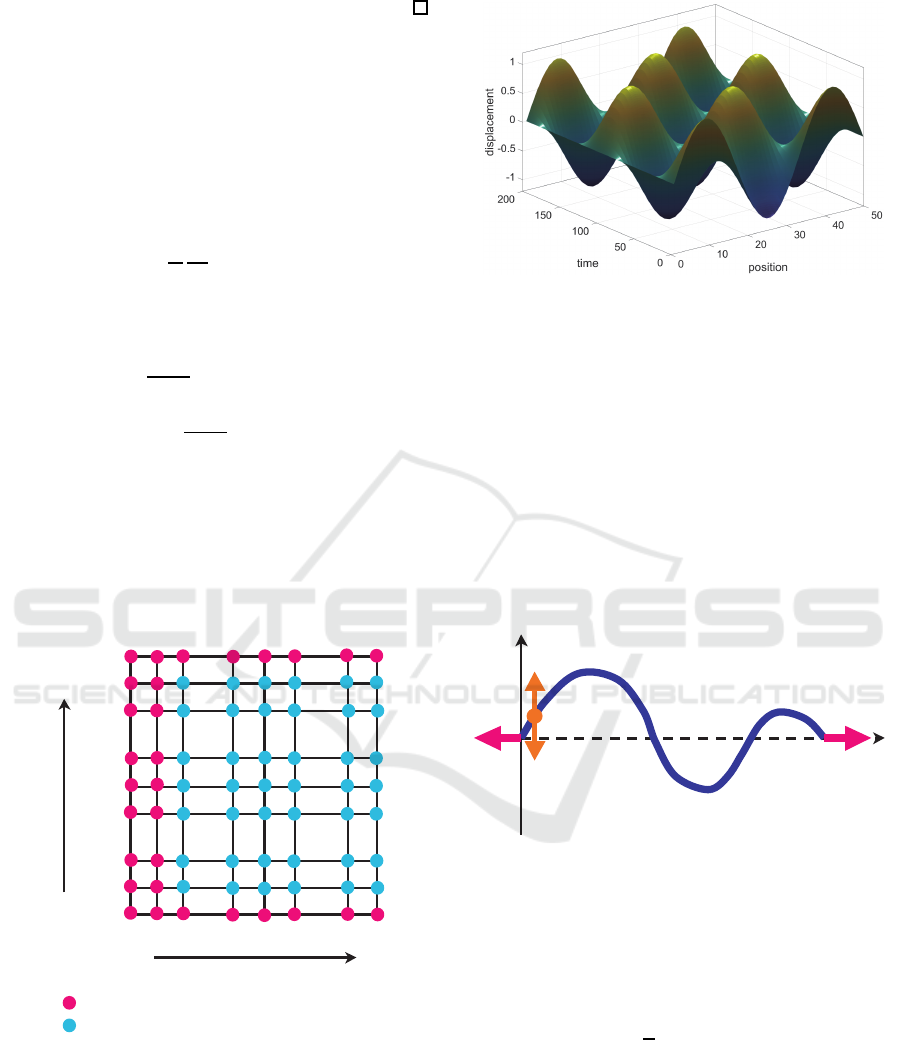
We see that (15) contains 5 displacement variables
U
k−1,l
, U
k,l−1
, U
k,l
, U
k,l+1
, U
k,l+1
as depicted in Fig.
5.
time
position
k
k +1
k − 1
l − 1
l
l +1
U
k,l
U
k,l+1
U
k+1,l
U
k−1,l
U
k,l−1
Figure 5: Discrete String Model.
Now, we shall investigate numerical stability of
(15). In computation of partial differential equations
by computers with numerical solutions, the concept
“numerical stability” is quite essential. Let us denote
a solution u(t,x) of the distributed parameter mechan-
ical system in the complex form:
u(t, x) = u(t)e
imx
, (16)
where m is the number of waves and i =
√
−1 is the
imaginary unit. That is to say, (16) shows a wave
whose amplitude is u(t) and wave number is m. Dis-
cretizing (16), we have
U
k,l
= U
k
e
imld
. (17)
If the amplitude U
k
is intensifying over time, it be-
comes numerically instable. A numerical stability
condition focused on amplification degrees is called
“a von Neumann condition” (Thomas, 1998; Quar-
teroni and Valli, 2008). The next proposition gives
a von Neumann condition for the discrete Euler-
Lagrange equation of the string (due to limitations of
space, the proof is omitted).
Proposition 1: A von Neumann condition such that
the discrete Euler-Lagrange equation of the string
(15) is numerically stable is given by
0 <
N
ρ
h
2
d
2
≤ 1. (18)
Development of Discrete Mechanics for Distributed Parameter Mechanical Systems and Its Application to Vibration Suppression Control of
a String
495
From the result of Proposition 1, It turns out that
for given a string with physical parameters ρ, N, we
set sampling intervals h, d such that (18) satisfies,
then numerical stability is guaranteed. In next subsec-
tions, some numerical simulations will be performed,
and physical parameters are set as ρ = 0.1, N = 1. For
this setting, we set sampling intervalsas h = 0.01, d =
0.1, and these parameters satisfies the von Neumann
condition (18):
N
ρ
h
2
d
2
= 0.1. (19)
In addition, we consider initial conditions of the
string as a sine curve:
U
1,l
= sin
3π
l −1
L−1
(l = 1,··· , L),
U
2,l
= 0.99sin
3π
l −1
L−1
(l = 1,··· , L),
(20)
and boundary conditions on clamp at both ends:
U
k,1
= U
k,L
= 0 (k = 1, ··· ,K). (21)
Therefore, for given initial and boundary conditions
(20), (21), all the displacement are calculated by the
discrete Euler-Lagrange equation of the string (15) as
shown in Fig. 6.
time
position
1
2
k
−
1
k k +1 K
−
1
K
l +1
L − 1
L
l − 1
l
1
2
3
3
L − 2
: known (initial and boundary conditions)
: unknown
Figure 6: Calculation of Discrete String Model.
In Fig.7, free vibration of the string with out con-
trol inputs is illustrated with K = 200, L = 50. From
this figure, we can see that the string is periodically
vibrating with the maximum amplitude 1 and this is
consistent with actual behavior of the string.
Figure 7: Free Vibration of String with No Control.
4.2 Simulation I
In this subsection, a numerical simulation is carried
out by the proposed control method in order to check
the effectiveness. We now assume that the number
of control inputs is 1, that is to say, the actuator that
can generate a control input is installed at only the
extreme left of the string as illustrated in Fig. 8. Pa-
rameters are set as steps: K = 400, L = 50, the set of
actuator indices: ∆ = {2}, the start time step of stabi-
lization: κ = 300, the weight parameters of evaluation
function: a = 1, b = 1000, c = 1.
l
1
50
ActuatorActuator
2
NN
N
U
k,l
Figure 8: Setting of Simulation I.
Figs. 9 and 10 shows simulation results. Fig. 9
shows a 3D plot of the displacements of the string
U
k,l
, and fig. 10 illustrates a time series on average of
the absolute value of U
k,l
:
1
L
L
∑
l=1
|U
k,l
|. (22)
From these results, it can be confirmed that all the
displacements of the string in the desired time step
k = 300−400 converge to 0, and hence vibration sup-
pression control is achieved. However, since the num-
ber of control inputs is 1, if the start time of stabiliza-
tion is set as a smaller one, the value of the control
input rises and the control performance is degraded.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
496
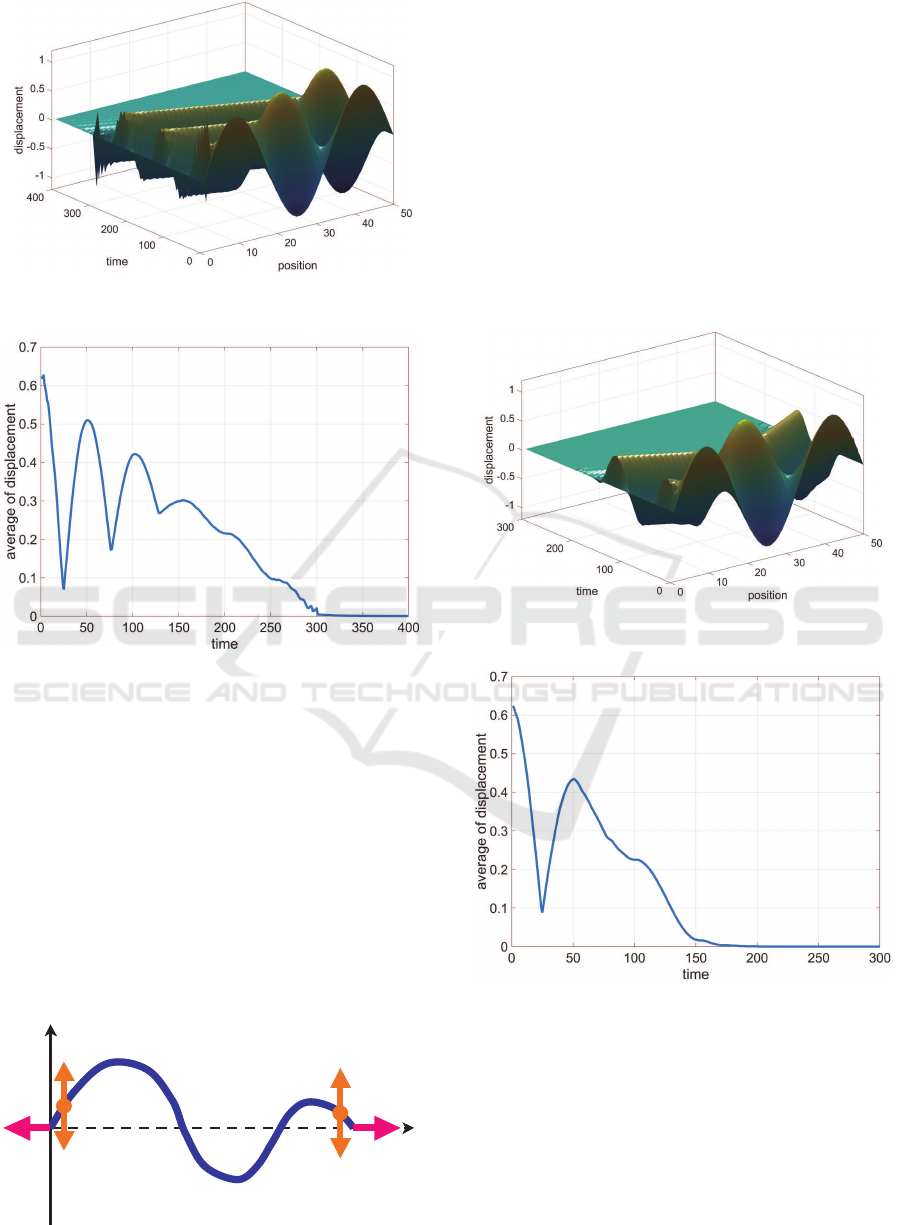
Figure 9: 3D Plot for Displacement of String (Simulation
I).
Figure 10: Time Series for Average of Displacement (Sim-
ulation I).
4.3 Simulation II
Next, this subsection shows another numerical simu-
lation. It is assumed that the number of control in-
puts is 2, that is to say, the actuator that can gen-
erate a control input is installed at both ends of the
string as illustrated in Fig. 11. Parameters are set
as steps: K = 300, L = 50, the set of actuator in-
dices: ∆ = {2, 49}, the start time step of stabilization:
κ = 200, the weight parameters of evaluation func-
tion: a = 1, b = 1000, c = 1.
l
NN
N
1
50
Actuator 1Actuator 1
Actuator 2Actuator 2
2
49
U
k,l
Figure 11: Setting of Simulation II.
In Figs. 12 and 13, simulation results are depicted.
Fig. 12 illustrates a 3D plot of the displacements
of the string U
k,l
, and fig. 13 shows a time series
on average of the absolute value of U
k,l
(22). From
these results, we can see that all the displacements
of the string converge to 0 in the desired time step
k = 200−300, and hence vibration suppression con-
trol is achieved in common with Simulation I. More-
over, since the number of control inputs is 2, the sys-
tem is stabilized at earlier time step (k = 200) than the
one in Simulation I (k = 300). It is also confirmed
that by setting the weight parameter of the evalua-
tion function b as a larger value, stabilization can be
started at earlier time step.
Figure 12: 3D Plot for Displacement of String (Simulation
II).
Figure 13: Time Series for Average of Displacement (Sim-
ulation II).
5 CONCLUSIONS
In this study, discrete mechanics for 1-dimensional
distributed parameter mechanical systems has been
developed and its application to control theory has
been considered. Vibration suppression control of a
string as an example of physical systems has been also
Development of Discrete Mechanics for Distributed Parameter Mechanical Systems and Its Application to Vibration Suppression Control of
a String
497

shown in order to verify the effectiveness of the pro-
posed method. As a result, this study derives a new
control approach to distributed parameter mechanical
systems.
The future work includes the following topics;
theoretical analysis on discrete Euler-Lagrange equa-
tions, Extension to 2-dimensional distributed pa-
rameter mechanical systems, and development of
feedback-type controllers.
REFERENCES
Gurwitz, C. B. (2015). Sequential Quadratic Programming
Methods Based on Approximating a Projected Hes-
sian Matrix. Andesite Press.
Junge, O., Marsden, J. E., and Ober-Blobaum, S. (2005).
Discrete mechanics and optimal control. in Proc. of
16th IFAC World Congress, Praha, Czech Republic,
Paper No. We-M14-TO/3.
Kai, T. (2012). Control of the cart-pendulum system based
on discrete mechanics - part i : Theoretical analysis
and stabilization control -. IEICE Transactions on
Fundamentals of Electronics, Communications and
Computer Sciences, Vol. E95-A, No. 2, Page 525-533.
Kai, T. (2015). Circular obstacle avoidance control of the
compass-type biped robot based on a blending method
of discrete mechanics and nonlinear optimization. In-
ternational Journal of Modern Nonlinear Theory and
Application, Vol. 4, No. 3, Page 179-189.
Kai, T., Bito, K., and Shintani, T. (2012). Control of the
cart-pendulum system based on discrete mechanics -
part ii : Transformation to continuous-time inputs and
experimental verification -. IEICE Transactions on
Fundamentals of Electronics, Communications and
Computer Sciences, Vol. E95-A, No. 2, Page 534-541.
Kai, T. and Shibata, T. (2015). Gait generation for
the compass-type biped robot on general irregular
grounds via a new blending method of discrete me-
chanics and nonlinear optimization. Journal of Con-
trol, Automation and Electrical Systems, Vol. 26, No.
5, Page 484-492.
Kai, T. and Shintani, T. (2011). A discrete mechanics ap-
proach to gait generation for the compass-type biped
robot. Nonlinear Theory and Its Applications, IEICE,
Vol. 2, No. 4, Page 533-547.
Kai, T. and Shintani, T. (2014). A new discrete mechan-
ics approach to swing-up control of the cart-pendulum
system. Communications in Nonlinear Science and
Numerical Simulation, Vol. 19, Page 230-244.
Kane, C., Marsden, J. E., Ortiz, M., and West, M. (2000).
Variational integrators and the newmark algorithm for
conservative and dissipative mechanical systems. Int.
J. for Numer. Meth. in Engineering, Vol. 49, Page
1295-1325.
Marsden, J. E., Patrick, G. W., and Shkoller, S. (1998).
Multisymplectic geometry, variational integrators and
nonlinear pdes. Comm. in Math. Phys., Vol. 199, Page
351-395.
Marsden, J. E. and West, M. (2001). Discrete mechanics
and variational integrators. Acta Numerica, Vol. 10,
Page 3571-5145.
Nocedal, J. and Wright, S. J. (2006). Numerical Optimiza-
tion. Springer.
Quarteroni, A. and Valli, A. (2008). Numerical Approxima-
tion of Partial Differential Equations. Springer.
Thomas, J. W. (1998). Numerical Partial Differential Equa-
tions: Finite Difference Methods. Springer.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
498
