Exploration of Unknown Map for Gas Searching and Picking Up Objects

using Khepera Mobile Robots

Sara Ashry Mohammed

1,3

and Walid Gomaa

1,2

Cyber-Physical Systems Lab (CPS), Computer Science and Engineering (CSE),

Egypt-Japan University of Science and Technology (E-JUST), Alexandria, Egypt

Faculty of Engineering, Alexandria University, Alexandria, Egypt

Computers and Systems Department, Electronic Research Institute (ERI), Giza, Egypt

Keywords:

Mobile Robots, Explore Unknown Map, Gas Detection, V-REP, Khepera III, Albers Algorithm.

Abstract:

In this paper, the integrated approach for searching, detecting the source of gas leakage and capturing object

using Khepera III mobile robot is introduced. It was tested in natural grid environments as shown in experi-

ments but it is usable in vast areas; e.g. houses and labs to pick up gas victims. Experiments are performed

using a master Khepera robot equipped with a gas sensor and two slave robots equipped with grippers to take

the best path to pick up the object. Moreover, this paper proposes an improvement of Albers exploration algo-

rithm to reduce the time required to explore an unknown map with different polygon obstacles. The proposed

approach aims at minimizing the overall exploration time, making it possible to localize gas source in an efﬁ-

cient way, as demonstrated in V-REP simulation as well as real world experiments. A comparison among both

algorithms has shown the effectiveness of the proposed one, where the percentage of performance speedup is

about 30% to 57% depending on the size of the map and number of obstacles.

1 INTRODUCTION

Nowadays, using robots instead of humans in risk op-

erations is an interesting point in the ﬁeld of robotics.

Autonomous Robots are typically designed to per-

form search operations in buildings, mines, and caves,

which are considered extremely challenging complex

environments. One of the ﬁrst such challenges is the

exploration of the environment. Robotic exploration

is an online problem for map building in which mo-

bile robots use their onboard sensors to discover grad-

ually the physical and layout structure of the initially

unknown environment.

The Evaluation of the current experimental explo-

ration methods is solely based on relative compar-

isons between the robots’ performance in some test

environments (Amigoni, 2008). Subsequently, it is

hard to evaluate the room size is available for improv-

ing on-line exploration strategies. The Whole com-

parison between on-line exploration strategies and op-

timal off-line performance in test maps is needed. It

can be done based on the competitive ratio. Mainly,

the competitive ratio is P

of the on-line algorithm

A, where P

is the performance of A in a test envi-

ronment while P

is the performance of the ofﬂine al-

gorithm which has knowledge of the map (Ghosh and

Klein, 2010). Lots of studies have been done in map-

ping and exploration; see for example, (Higashikawa

and Katoh, 2013), (Herrmann et al., 2010), (Icking

et al., 2010) and, (Doriya et al., 2015).

Recently, It received looking for olfactory targets

with mobile robots a great interest because of its im-

portance in the detection of a chemical leak, and

search and rescue operations. Many studies have been

done in this ﬁeld in (Marjovi and Marques, 2011) and

(Le Comte et al., 2012). In this paper, map explo-

ration and gas source detection are the main topics.

In the following discussion, we focus on improv-

ing Albers exploration algorithm to explore unknown

grid maps with obstacles for detecting gas leakage

source. Then, take the optimal path to the target nodes

(potential victims). The motivation of this work is to

give an explanatory prototype of a robotic system that

saves people from ﬁres and bottlenecks resulting from

gas leakage and the potential ignition of ﬁres. Us-

ing a multi-robot system in risk operations instead of

ﬁreﬁghters ensures the safety of their lives and helps

them to perform harder tasks. Motion planning is im-

plemented on two various levels: sensor based and

model based. At the model level (Bender et al., 2002),

294

Mohammed, S. and Gomaa, W.

Exploration of Unknown Map for Gas Searching and Picking Up Objects using Khepera Mobile Robots.

DOI: 10.5220/0005978402940302

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 294-302

ISBN: 978-989-758-198-4

planning depends on a priori knowledge of the envi-

ronment. There is a need to search for free paths be-

tween certain start and goal states. The Sensor path

planners deal with the unexpected items in the scene

and usually, they are perfect for obstacle avoidance

using robot sensors. Both models are employed in

our work where a sensor based module is utilized by

a master Khepera robot which is supplied with a gas

sensor circuit, and a model based module is used by

two slaves Khepera robots as shown in Section 4.

The paper is organized as follows. Section 1 is an

introduction. Section 2 gives the related work. Al-

bers algorithm is discussed in section 3. Section 4

describes the Khepera III robot and the types of used

sensors. Our proposed framework and algorithm are

also introduced. Section 5 shows the accuracy of our

approach in both real world and simulation experi-

ments. Section 6 concludes the paper.

2 RELATED WORK

Most of the research work on the single-robot explo-

ration of new maps relied on grid map using sensor

model. A Robot should construct a whole map us-

ing the shortest path as much as possible. This prob-

lem was studied previously by many researchers, e.g.,

(Betke et al., 1995), and (Rivest et al., 2015). The

general problem of exploring a room without obsta-

cles with a competitive ratio of examining places with

obstacles was introduced by (Deng et al., 1998). For

a simple polygon, (Hoffmann et al., 2001) achieved a

constant competitive ratio of c= 26.55, while (Albers

et al., 2002) showed that constant competitive factor

for maps with obstacles does not exist (Fekete and

Schmidt, 2010). For rectilinear polygons, (Hammar

et al., 2006) showed that the traveled distance accord-

ing to the Manhattan metric is c= 1.50 in the case of

having a starting point on the boundary. The original

Ray algorithm to explore grids with rectangular ob-

stacles is proposed by (Betke et al., 1995). In contrast

(Albers et al., 2002) proposed an algorithm for ex-

ploring grids with arbitrary obstacles. We improved

Albers algorithm with an average competitive ratio of

(c= 1.35), but there is no a constant competitive ratio.

A Wireless Sensor Network (WSN) of an olfac-

tion mobile robot to localize the odor source was

suggested by (Qi et al., 2015). (IS¸ILAK, 2010) De-

signed WSN to detect gas leakage and warns person

with sound and vibration especially for people of Al-

Zheimer disease who are more likely to forget to close

the gas in the kitchen. WSN based on smart home

for elder people to provide them with a safe living

was developed by (Ransing and Rajput, 2015). Res-

cue operation in mines is risky so (Chakkath et al.,

2012) proposed a prototype of a mobile robot with

a gas sensor, temperature sensor, and camera which

transmit the live video signal to monitor the status

in a tunnel. (Kim et al., 2015) proposed a method

to improve object identiﬁcation and also complement

sensor drawbacks of the infrared and radar sensor for

imaging through smoke by ﬁreﬁghter robot.

3 BACKGROUND

Albers Algorithm

Albers algorithm (Albers et al., 2002) can be called

Lower Ray Traversal Algorithm (LRT) to be easily

distinguished from the newly proposed one. The al-

gorithm assumed that the outer boundary of the grid

is rectangular and that no obstacles touch the outer

boundary. The LRT algorithm is summarized as:

1) The robot starts from point x

and moves along

the exterior boundary of the scene clockwise until it

reaches x

again. By this, the robot could know the di-

mension of the map and determine the exterior lower

open segment. 2) Let S be the lower open segment

of the exterior boundary. A Lower Open Segment of

any obstacle O is a maximal sequence of consecutive

horizontal edges on the boundary of O so that the inte-

rior of O is south of the robot. Fig. 1 shows the lower

open segment in the bold lines of the grid map with ar-

bitrary obstacles. 3) Start from node x

i+1

on the open

segment S to move up in vertical ray on the northern

direction until hitting the exterior boundary. Then, go

south till hitting the open segment and go one step

east on the segment and radiate another Up-Ray in a

recursive operation till hitting the exterior boundary

or obstacle O at point X . 4) If the up ray hits an ob-

stacle O, then go around the boundary of the obstacle

in a clockwise manner, detect the open segment of O

till it reaches X again Then take the shortest path to

the ﬁrst point on the segment and recursively do ray

traversal to continue exploring. If the robot faces an-

other obstacle at Y , repeat the same processes. It goes

for any new obstacle till exploring the latest obstacle,

then go back to explore the uncompleted open seg-

ment of previous constraints and so on till all the map

is entirely scanned as shown in ﬁgure 2. The obstacle

is planned thoroughly if all the nodes are explored.

A signiﬁcant advantage of the ray algorithm is that

it applies the depth-ﬁrst search strategy (DFS) which

traverses all edges and guarantees drawing a complete

map. However, Albers algorithm has some draw-

backs including the following: 1) The robot traverses

the same vertical ray twice because it goes up and

Exploration of Unknown Map for Gas Searching and Picking Up Objects using Khepera Mobile Robots

295

Figure 1: Left picture indicate open segment while right

picture indicate grid map with arbitrary obstacles.

Figure 2: The Lower Ray Traversal Algorithm.

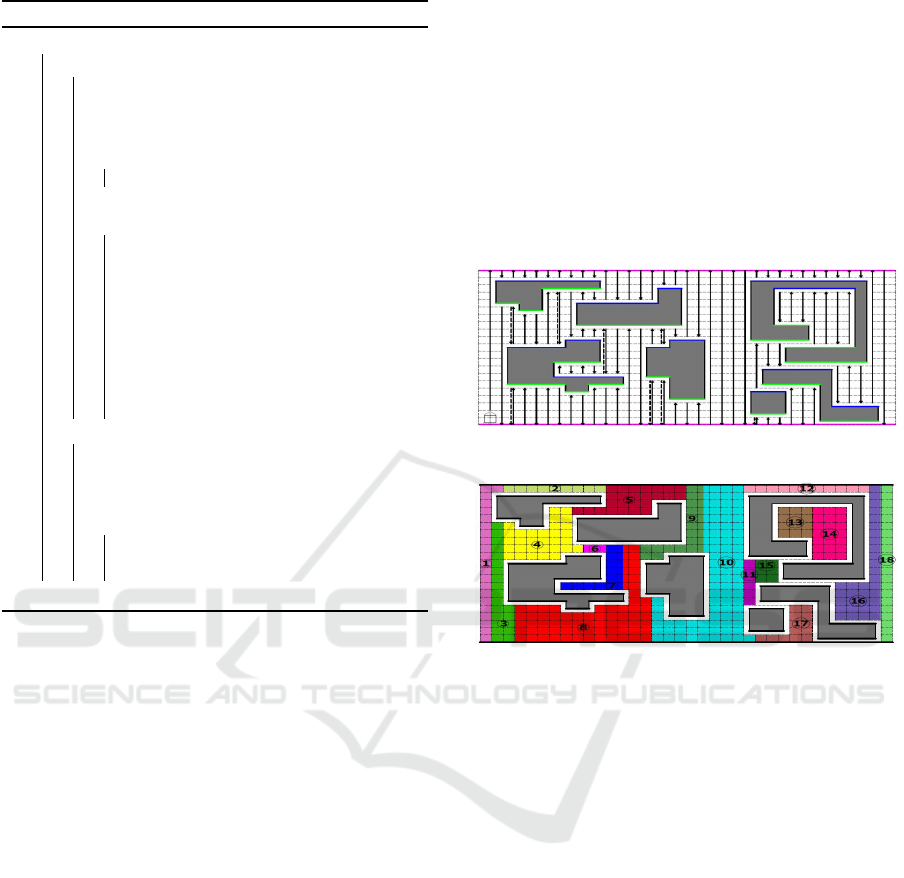
Figure 3: Exploring areas in non-ordered sections at 13, 14.

down on the same line to hit the lower open segment.

Hence, this algorithm doubles the time of exploration.

The newly proposed algorithm enhances this draw-

back; see section 4.2. 2) In case, the environment

is occupied by multiple obstacles, the segment of the

last obstacle is completely explored before the previ-

ous ones which mean that the robot would go back

till the ﬁrst obstacle is thoroughly explored which al-

lows some horizontal edges to be traversed more than

twice. This leads to exploring the map in a non-

ordered way where region 13 explored before region

14 as shown in ﬁgure 3.

4 PROPOSED APPROACH

In this section, we introduce the methodology of an

integrated approach to detect sources of gas leakage

and capture objects using mobile robots. Beides, we

propose an improvement to Albers algorithm.

4.1 Search and Picking Up Objects

Map exploration, gas source detection and picking up

objects (potential gas leakage victim) using Khepera

III robot are the main ideas in this paper. We de-

veloped a prototype integrated approach for the pur-

pose of saving people from gas bottlenecks where the

multi robot system consists of one master robot (R1)

equipped with the gas sensor to search a rectangular

grid map using our proposed zigzag ray traversal al-

gorithm and detects the source of gas leakage. Then,

It sends the environment map and the target point (ob-

ject found beside gas source node) to two slave robots

(R2,R3) by an intermediate computer with Ubuntu

12.04 operating system. Slave robots receive the map

as well as the target point from the an intermediate

computer through a Wireless compact ﬂash card Wi-

ﬁ B/G: Ambicom WL5400G-CF module for network

connection. They equipped with grippers to capture

the object in the face to face.

In experiments in section 5, the two robots took

the Dijkstra shortest path algorithm (E.W.Dijkstra,

1959) to the target point as shown in ﬁgure 8. R3

took the same path of R2 as it is the shortest one but

it’s path was increased with last three steps to face

R2. R3 was delayed with an edge from R2 to avoid

the collision between them. R2 reached before the

object with a node and then checked arriving of R3

each time by using three front ultrasound sensor with

threshold (T ≤ 55) where T is the edge length in cen-

timeter. R2 waited until R3 reach after the object with

a node in a face to face position. Then, both of them

began together to open the ﬁngers of the gripper, fall

to touch the ground, catch the object and go up.

4.2 Zigzag Ray Traversal Algorithm

(Proposed Algorithm)

Let’s call this algorithm lower upper ray traversal

(LURT) which avoids the defects of the previous

algorithm (LRT). The outline of the proposed LURT

algorithm is explained in details in the following

steps: 1) Start from any point on the corner of the

map (e.g. x

) and move along the exterior boundary

of the scene until the robot reaches to x

again. 2)

Let S be the upper and lower segments of the outer

boundary where An Upper Segment of any object O

is a consecutive horizontal edges on the boundary of

O so that the interior of O is north of the robot and

Lower Segment is deﬁned in Section 3. Fig. 4 shows

the lower/upper segment in the bold blue/green lines

respectively at the grid map with arbitrary obstacles.

3) Start from node x

i+1

on the lower segment S to

move up in a vertical ray in the northern direction

until hitting the exterior boundary or an obstacle.

When the ray hits the lower/upper exterior segment,

it executes the zigzag process. If the ray hits the

obstacle at point X

, then it executes the obstacle

boundary scan and explores segments. 4) At the end

of exploring all obstacles, complete the exploration

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

296

Algorithm 1: Search and capture Object.

switch RobotsState do

case Exploring do

Master robot starts working;

Apply zigzag ray traversal algorithm;

Check gas odor at each node;

if GasOdor == true then

Mark this node as gas source node;

if (ObjectBesideGasOdor == true)

then

Mark this node as a target point;

Send the environment map and the

target point to slave robots using

an intermediary computer;

Move the master robot to ﬁnal

corner on the boundary;

Stop the master robot;

RobotsState = TakingPath;

case TakingPath do

Slave robots start working;

Apply Dijkstra algorithm;

if (Robot1-ReachTarget == true) &

(Robot2-ReachTarget == true) then

Move gripper down;

Catch Object, move gripper up;

end

by the zigzag traversal process.

The zigzag process can be outlined as follows:

After radiating a ray to the north, move one step in

the east and emit a ray in the reverse direction from

the previous one (up/east/down).

The Obstacle boundary scan can be outlined as

follows: 1) Move around the ﬁrst obstacle clockwise

until reaching X

again. 2) While moving, detect

the up/down obstacle segment, store critical points

(points of rotation) for each segment in a queue and

mark them as visited. 3) After the boundary scan, go

to the ﬁrst point at the ﬁrst segment of the obstacle to

execute the exploration process.

The Segment exploration can be outlined as fol-

lows: 1) Start a zigzag ray traversal exploring from

the ﬁrst point at the ﬁrst segment detected by the cur-

rent obstacle. After exploring the ﬁrst segment, move

around the obstacle clockwise and go to the lowest

point of the contiguous segment (lowest sum of x and

y value of this point). 2) If any ray hits a new obstacle,

then execute the boundary scan of the new obstacle,

give priority to the new obstacle to be explored ﬁrst,

and execute the segment exploration. Recursively, do

that for each new obstacle and then take the short-

est path to the previous uncompleted obstacle to com-

plete exploring. 3) If the ray radiated from any obsta-

cle segment hits a visited point on a previous obstacle

(which its exploring process has not been completed

yet), then swap the priority of the exploration between

the two obstacles to complete exploring the previous

obstacle segments. 4) If the ray reaches the end-lock

state, go in the reverse direction of the same line and

execute a zigzag process. End-lock: If the right or the

left side of the ends of the ray is an obstacle, it ’s hard

to move to move one step east in the zigzag process.

Then, go in the reverse direction.

Figure 4: Zigzag Ray lines and lower/upper segment.

Figure 5: Exploring area in sequence at regions 13 and 14.

The following algorithm is the pusedo code of

Zigzag Ray Traversal where symbols S1 is the left

infrared sensor, S3 is the front sensor and S5 is the

right sensor. Rdir is the robot direction.

The main advantages of the proposed algorithm:

1) Exploring the map totally in (half the duration

achieved by the Albers algorithm + small factor σ ) as

will be showed in Section 5. σ factor is the same equal

time of the exterior boundary travel, obstacles bound-

ary travels and some vertical edge traverse of the two

algorithms. To simply understand the difference be-

tween Albers algorithm and the proposed algorithm:

assume the same map with obstacles as shown in Fig-

ures 2 and 4. The number of rays that passed the map

is 187 in ﬁgure 2. In contrast, the number of rays is

102 in ﬁgure 4. Thus, the LURT algorithm explores

the map in 0.545 + σ of the LRT. 2) The proposed

algorithm scans the whole map in contiguous areas

mostly as in ﬁgure 5. In contrast, Albers algorithm

scans the same map in mostly non-contiguous areas

as shown in ﬁgure 3. So, the main feature of the pro-

posed algorithm is saving the time of traversing the

map and saving the energy of the robot’s battery in

Exploration of Unknown Map for Gas Searching and Picking Up Objects using Khepera Mobile Robots

297

Algorithm 2: Zigzag Ray Traversal.

while true do

Execute Zigzag Ray Traversal Algorithm

end

switch state do

case Idle do

state=BoundaryScan

Explore Forward;

case BoundaryScan do

if (x==0) & (y==0) then

state=VerticalSweep

SetMapDimension

Explore Backward, Forward , Left

else if (S3==false) & (S1==true) then

Explore Forward

else if (S3==true) then Explore Right

case ObsMap do

if (x==ObsCell1.x)&(y==ObsCell1.y)

then state=BoundaryTravel

Explore Forward

else if (S3==false)&(S5==false) then

Explore Right, Forward

else if (S3==false) then

if Rdir==Forward then

Map(x+1,y)=obsIndex

if Rdir==Backword then

Map(x-1,y)=obsIndex

if Rdir==Right then

Map(x,y-1)=obsIndex

Fill UpSegment Array

if Rdir==Left then

Map(x,y+1)=obsIndex

Fill DownSegment Array

Explore Forward

else if (S3==true) then

if Rdir==Forward then

Map(x,y+1)=obsIndex

if Rdir==Backword then

Map(x,y-1)=obsIndex

if Rdir==Right then

Map(x+1,y)=obsIndex

Fill UpSegment Array

if Rdir==Left then

Map(x-1,y)=obsIndex

Fill DownSegment Array

Explore Left

case SegmentCheck do

if (Rdir==Right)&(S5==true) then

state=VerticalSweet; ExploreLeft;

else if (Rdir==Right)&(S5==false)

then

state=BoundaryTravel;

ExploreRight

else Explore Nothing

end

Algorithm 3: Complete Zigzag Ray Traversal.

switch state do

case BoundaryTravel do

if (x == ObsCell1.x)&(y ==

ObsCell1.y) then

state=VerticalSweep

Explore Left , Forward

else if (S3==false)&(S5==false) then

Explore Right, Forward

else if (S3==false)&(Rdir==Right)

then

state=SegmentCheck

Explore Forward

else if S3==false then

Explore Forward

else if S3==true then

Explore Left , Forward

case VerticalSweep do

if (S3==false) then Explore Forward

if (S3==true)&(Rdir==Forward) then

if (y≤ vertCells-1) &

Map(x,y+1)==0 then

state=ObsMap

obsIndex++

Map(x,y+1)=obsIndex

obsCell1.x= x

obsCell1.y= y

Explore Left , Forward

else if (S5 ==

true)&(Map(x,y+1)≥ 1) then

Explore Backward

else if (S5 == true)&(y

==vertCells) then

state=Finish

else Explore Right, Forward, Right

if (S3==true)&(Rdir==Backword)

then

if (y≥ 1)&(Map(x,y-1)==0) then

state=ObsMap

obsIndex++

Map(x,y-1)=obsIndex

obsCell1.x=x

obsCell1.y=y

Explore Left , Forward

else if (S1 == true)&(y ==0) then

state=Finish;

else if (S1==true)& Map(x,y-1)≥ 1

then

Explore Backward

else

state=BoundaryTravel

Explore Left , Forward

case Finish do

Explore Halt

Print explore all map

end

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

298

addition to usefulness for critical applications as res-

cue operations.

The disadvantage of the proposed algorithm is

that it needs higher space storage than the LRT to

store critical points for segments of any obstacle. The

storage space is the number of queues needed to store

critical points only. However, the storage cost is very

small compared to the double rays of traversing a map

in the real world.

4.3 Khepera Robot Platform

The Khepera III is a small mobile robot developed

by K-Team, it has two wheels. The features of this

robot could match the performance of much larger

robots. The robot consists of 9 infrared sensors to

detect an obstacle and ﬁve ultrasonic sensors to detect

long-range objects. It also has two infrared sensors

on its ground to follow the lines. Moreover, it allows

for expansion using the Korebot II extension board

for any external sensor, camera, or gripper as in ﬁgure

7 and 8. C/ C++ programming language are used to

program the robot (Lambercy and Bureau, 2007).

Architecture of the Khepera III Robot: To

reduce the compilation time of running the code on

khepera III processor, the following parameter should

be taken in consideration as explained in (XScale,

2002).

• Processor: Marvell PXA270 with XScale, 7

Stage pipeline and32 KB instruction cache.

• Dynamic Branch Prediction to reduce the penal-

ties of changing the ﬂow of program execution.

• Supports Write-back or write-through caching.

• Loop Unrolling: loop with a ﬁxed number of iter-

ations may be faster if the loop is unrolled rather

than trying to schedule prefetch instructions.

• SDRAM resources are typically: 4 memory

banks, 1 page buffer per bank referencing a 4k ad-

dress range and 4 transfer request buffers.

• Out of Order Completion: instructions may com-

plete out of order because there are no data depen-

dencies exist.

• Use of Bypassing: The pipeline makes extensive

use of bypassing to minimize data hazards. It

allows results forwarding from multiple sources,

eliminating the need to stall the pipeline.The

pipeline issues a single instruction per clock.

Calculate Real Speed in mm: In speed mode, the

controller has a speed value of the wheels as input,

and it controls the motor to keep this speed. The speed

value is a division of a constant factor (16776960) by

the time between encoder pulsations (Lambercy and

Bureau, 2007).

MotorSpeed =

16776960

Timer5value

Postscaler

osc

T mr5Prescaler

(1)

RealSpeed

= ConversionFactor ∗ MotorSpeed

RealSpeed

WheelCircumference

Time ∗ 2764

(2)

where ConversionFactor = 6.9439 ∗ 10

−3

, fosc =

20MHz, Tmr5Prescaler = 8, Postscaler = 4, Wheel-

Circumference is 128.8mm and 2764 corresponds to

the number of measures per a wheel revolution.

Odometry Distance and Orientation: The

equations that govern the dynamics of the robot are

as follows.

V =

W =

−V

WheelSpacing

θ =

∑

i=0

δt

r =

∑

i=0

δt[−sinθa

+ cosθa

]

(3)

Where V is the robot’s velocity, V

is the velocity of

the right wheel, and V

is the left wheel velocity. So

the resultant velocity is the average of the velocities

of the left and right wheels. W is the angular velocity

and WheelSpacing = 88.41mm. θ is the odometer

angle orientation, and r is the odometer distance, δt

is the timestamp difference, the a

is X direction, a

is Y direction.

The Direction of the Robot is Relative to its Initial

Position: Adjusting the robot’s movement direction

is relative to the initial position; we proposed this state

diagram as shown in the following ﬁgure 6.

Figure 6: Robot state diagram to adjust movement direc-

tion.

Exploration of Unknown Map for Gas Searching and Picking Up Objects using Khepera Mobile Robots

299

Sensors used in the Experiments: Infrared sensors

provide low range coverage, less than 0.5m in most

cases, this is because the emitted energy is not con-

centrated. However, infrared sensors are cheap and

reliable for many applications. For instance, they can

be used successfully to detect obstacles that are close

to the robot. The threshold of the two ground infrared

proximity sensors to distinguish between white and

black lines on the ﬂoor is 3000 while the threshold of

the IR sensors to detect obstacle is greater than 65.

It is better to use the ultrasound sensor to detect

obstacles in long distances. Each sonar sensor

measurement provides information about the empty

and occupied spaces in the cone in front of the

sensor. The multiple measurements are integrated

in a sonar sensor map, using a powerful tool that

combines information from sensors in such a way

to deal with errors and uncertainties in the data. We

propose to take the best sonar reading as follows;

take N measurements from each sensor, arrange them

in ascending order, and then take the median value.

This is probably the best reading.

Gas Sensor Circuit and Gripper: During explo-

ration and navigation, the master robot is equipped

with a gas sensor board developed manually by us as

shown in ﬁgure 7. It can be used for detecting leakage

gas equipment both in residential areas and industry.

The gas sensor module name is MQ-6. It is sen-

sitive to LPG, iso-butane gas, propane, natural gas

and town gas. It avoids the noise of alcohol, cook-

ing fumes and, cigarette smoke. The sensor needs a

resistor at the output to ground. Its value is ranging

from 2kOhm to 47kOhm, the lower the value is, the

less sensitive the sensor is. Also, the higher the value

is, the less accurate, it is for higher concentrations of

gas (Datasheet, ). We choose 12kOhm as a suitable

value in our designed circuit. The designed circuit

in ﬁgure 7 is composed of the MQ-6 gas module. It

has two leds; one of them is a power indicator, and

the other one is an indicator of sensing the gas odor.

Reading take digitally from bin number IO1 in Kor-

eIOLE Extension Board.

Figure 7: Gas sensor circuit combined with khepera III.

Figure 8: Two khepera III with grippers to capture object

(potentional victim).

5 EXPERIMENTS

5.1 V-REP Simulation

V-REP is a very nice tool for fast prototyping and ver-

iﬁcation, remote monitoring and swift algorithm de-

velopment. A V-REP plug-in was specially developed

to allow an axiomatical and realistic Khepera robot

simulation in (Rohmer et al., 2013).

Table 1: Comparison between the proposed approach and

Albers approaches in vrep simulation.

Test Map

Nodes

Obsta-

cles

Albers

in min

Zigzag

in min

Speed

T1 9*9 1 22.5 14.5 35%.

T2 9*9 2 25 17.25 30%

T3 19*39 5 326.16 191.76 41.2%

(a) (b)

Figure 9: (a) Map with one obstacle in test-1, (b) Map with

two obstacles in test-2.

(a) (b)

Figure 10: Left is a large map with ﬁve obstacles in test-3

and right shows the master robot track in green line, red and

yellow lines are the tracks of the two slave robots in test-4.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

300

The current section describes the experimental de-

tails, assumptions, and the obtained results tested by

V-REP where the Lua programming language is used.

Use a Khepera robot to explore a map consisting

of n × m nodes and N obstacles where n is the hori-

zonal nodes, and m is vertical nodes and N is the num-

ber of barriers in the environment. Table 1 compares

the result of Albers algorithm, and the Zigzag pro-

posed algorithm. Test-1, Test-2, and Test-3 are shown

in Figures 9 and 10 respectively.

Test-4: Use a master robot to explore a map that con-

sists of 7 × 7 nodes with one obstacle and two slave

robots to catch goal which demonstrates in Algorithm

1 as shown in ﬁgure 10.

5.2 Real World Experiment

Use a Khepera robot to explore a map consisting of

S ×R nodes and M obstacles where S is the horizonal

nodes, and R is vertical nodes and M is the number of

obstacles in the environment. Table 2 compares the

result of Albers algorithm, and the Zigzag proposed

algorithm. Test-1 and Test-2 are shown in Figure 11.

Table 2: Comparison between the proposed approach and

Albers approaches in Real World.

Test Map

Nodes

Obsta-

cles

Albers

in min

Zigzag

in min

Speed

T1 9*9 0 28 13 57%

T2 9*9 1 27 17 37%

T3 9*7 2 24 15 35%

(a) (b)

Figure 11: (a) Map with one obstacle in experiment-1 at

real world, (b) Map with two obstacles in experiment-2.

Figure 12: Master and slave robots in test-4 at real world.

Test-4: This experiment is a whole system where a

master robot with the gas sensor is used in searching,

and two slave robots with grippers are used for pick-

ing up the object as shown in ﬁgure 12.

6 CONCLUSIONS

This paper enhance Albers algorithm (LRT) by using

proposed Zigzag Ray Traversal algorithm (LURT).

The proposed (LURT) algorithm reduces the ex-

ploration time compared to the LRT. These algo-

rithms are tested using the V-REP simulation and

real world experiments. The percentage of per-

formance speedup is about 30% to 57% depend-

ing on the size of the map and the number of ob-

stacles as shown in ﬁgure 13, 14 . Also, this

paper developped an itegrated approach for using

Khepera robots in detecting gas leakage and captur-

ing objects. All experiment as shown in vedio list

link https://www.youtube.com/playlist?list=

PLzxdjgyt-2Qy6G-pAJ4zdXeK_V-OqDPM- .

In future work, we will develop algorithms for

multi-robot to explore large geometric maps without

an intermediate computer in order to reduce the ex-

ploration time and enhance the overall performance.

Dispensing an intermediate computer will make hard

challenging in cooperation between robots and how

much signals could transfer between them. Also, we

will use laser range ﬁnder to detect far obstacles and

objects easily and accurately.

Figure 13: Comparing the results of Albers with our pro-

posed algorithm in real world.

Figure 14: Comparing the results of Albers with our pro-

posed algorithm in V−REP.

Exploration of Unknown Map for Gas Searching and Picking Up Objects using Khepera Mobile Robots

301

ACKNOWLEDGMENTS

The author would like to thank Dr. Alaa sheta

from Electronic Research Institute, Dr. Mohammed

Hamdy from Fayoum University and Dr. Mohammed

Abdel-Aziz Khamis from E-JUST for their continu-

ous help. The ﬁrst author is supported by a scholar-

ship from the Mission Department, Ministry of Scien-

tiﬁc Research of Egypt which is gratefully thankful.

REFERENCES

Albers, S., Kursawe, K., and Schuierer, S. (2002). Explor-

ing unknown environments with obstacles. Algorith-

mica, 32(1):123–143.

Amigoni, F. (2008). Experimental evaluation of some ex-

ploration strategies for mobile robots. In Robotics

and Automation. ICRA, IEEE International Confer-

ence on, pages 2818–2823. IEEE.

Bender, M. A., Fern

andez, A., Ron, D., Sahai, A., and Vad-

han, S. (2002). The power of a pebble: Exploring and

mapping directed graphs. Information and Computa-

tion, 176(1):1–21.

Betke, M., Rivest, R. L., and Singh, M. (1995). Piecemeal

learning of an unknown environment. Machine Learn-

ing, 18(2-3):231–254.

Chakkath, M. S., Hariharansiddharath, S., and Hemalatha,

B. (2012). Mobile robot in coal mine disaster surveil-

lance. Transportation, 261:230.

Datasheet, M.-. L. S.

Deng, X., Kameda, T., and Papadimitriou, C. (1998). How

to learn an unknown environment. i: the rectilinear

case. Journal of the ACM (JACM), 45(2):215–245.

Doriya, R., Mishra, S., and Gupta, S. (2015). A brief sur-

vey and analysis of multi-robot communication and

coordination. In Computing, Communication & Au-

tomation (ICCCA), 2015 International Conference on,

pages 1014–1021.

E.W.Dijkstra (1959). A note on two problems in connexion

with graphs. Numerische mathematik, 1(1):269–271.

Fekete, S. P. and Schmidt, C. (2010). Polygon exploration

with time-discrete vision. Computational Geometry,

43(2):148–168.

Ghosh, S. K. and Klein, R. (2010). Online algorithms for

searching and exploration in the plane. Computer Sci-

ence Review, 4(4):189–201.

Hammar, M., Nilsson, B. J., and Persson, M. (2006). Com-

petitive exploration of rectilinear polygons. Theoreti-

cal computer science, 354(3):367–378.

Herrmann, D., Kamphans, T., and Langetepe, E. (2010).

Exploring simple triangular and hexagonal grid poly-

gons online.

Higashikawa, Y. and Katoh, N. (2013). Online vertex explo-

ration problems in a simple polygon. IEICE TRANS-

ACTIONS on Information and Systems, 96(3):489–

497.

Hoffmann, F., Icking, C., Klein, R., and Kriegel, K. (2001).

The polygon exploration problem. SIAM Journal on

Computing, 31(2):577–600.

Icking, C., Kamphans, T., Klein, R., and Langetepe, E.

(2010). Exploring grid polygons online. arXiv

preprint arXiv:1012.5240.

IS¸ILAK, A. H. (2010). Smart home applications for dis-

abled people by using wireless sensor network. Engi-

neering Project Report.

Kim, J.-H., Starr, J. W., and Lattimer, B. Y. (2015). Fire-

ﬁghting robot stereo infrared vision and radar sensor

fusion for imaging through smoke. Fire Technology,

51(4):823–845.

Lambercy, F. and Bureau, P. (2007). Khepera iii user man-

ual. User manual, K-Team.

Le Comte, B. R., Gupta, G. S., and Chew, M. T. (2012).

Distributed sensors for hazard detection in an urban

search and rescue operation. In Instrumentation and

Measurement Technology Conference (I2MTC), 2012

IEEE International, pages 2385–2390. IEEE.

Marjovi, A. and Marques, L. (2011). Multi-robot olfactory

search in structured environments. Robotics and Au-

tonomous Systems, 59(11):867–881.

Qi, Q., Cheng, L., Wu, H., Liu, N., Huang, J., and Wang,

Y. (2015). Mobile olfaction robot odor source local-

ization based on wireless sensor network. In Chinese

Automation Congress (CAC), 2015, pages 366–370.

Ransing, R. S. and Rajput, M. (2015). Smart home for

elderly care, based on wireless sensor network. In

Nascent Technologies in the Engineering Field (IC-

NTE), 2015 International Conference on, pages 1–5.

Rivest, R. L., Singh, M., and Betke, M. (2015). Piecemeal

learning of an unknown environment.

Rohmer, E., Singh, S. P., and Freese, M. (2013). V-rep:

A versatile and scalable robot simulation framework.

pages 1321–1326.

XScale, I. (2002). Core developer’s manual. 2007-10-10].

http://developer. intel. com/design/intelxscale.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

302