Automatic Compositional Verification of Probabilistic Safety Properties
for Inter-organisational Workflow Processes
Redouane Bouchekir
1
, Saida Boukhedouma
2
and Mohand Cherif Boukala
1
1
MOVEP, Computer Science Department, USTHB, BP 32 El-Alia, Algiers, Algeria
2
LSI, Computer Science Department, USTHB, BP 32 El-Alia, Algiers, Algeria
Keywords:
Verification, IOWF Process, BPEL4WS, Probabilistic Automata, Model Checking, Compositional Verifica-
tion, Assume-Guarantee Reasoning Rule.
Abstract:
For many complex systems, it is important to verify formally their correctness; the aim is to guarantee the
reliability and the correctness of such systems before their effective deployment. Several methods have been
proposed to this effect using different formal tools such as Probabilistic Automata (PA). In this paper we focus
on verification of service-based inter-organizational workflow (IOWF) processes which support collaboration
and cooperation between WF processes attached to several partners, and specified using the business process
execution language (BPEL4WS). Then, IOWF processes are translated to Probabilistic Automata (PA) models.
More than verification support, PA provides a numerical evaluation of the IOWF process. We also propose
the use of compositional verification to cope with the state space explosion problem. The IOWF behavior is
checked against probabilistic safety properties. The verification and the analysis are performed in an automated
way using the PRISM model checker and based on the assume-guarantee reasoning rule.
1 INTRODUCTION
A general characteristic of modern computing sys-
tems is their complexity where chances of introduc-
ing errors increase significantly. Detecting and fixing
these errors is a very important goal. Model checking
is an effective method to verify systems by exhaus-
tively searching the complete state space exhibited by
a system. A variant of model checking is probabilis-
tic model checking (Baier et al., 2008), (Baier and
Kwiatkowska, 1998).
Probabilistic model checking involves the con-
struction of a finite-state model augmented with prob-
abilistic information, such as Markov chain or PA
(Lehmann and Shelah, 1982), (Hart et al., 1984). This
model is then checked against properties specified in
probabilistic extensions of temporal logic, such as
PCTL (Hansson and Jonsson, 1994). This permits
quantitative notions of correctness to be checked, e.g.
“ The message will be delivered with probability 1”.
It also provides other classes of properties, such as
performance or reliability, e.g. “compute expected
probability for a successful transmission of a data
packet”.
As with any formal verification technique, one
of the main challenge for probabilistic model check-
ing when checking large/complex systems is the state
space explosion problem: the number of states grows
exponentially. A promising direction to combat this
problem is the compositional verification (Larsen
et al., 1995), (Feng et al., 2010), (Feng, 2013).
Compositional verification suggests a “divide and
conquer” strategy to reduce the verification task into
simpler subtasks. A popular approach is the assume-
guarantee paradigm (AG) (P
˘
as
˘
areanu et al., 2008),
(Chen et al., 2010), in which individual system com-
ponents are verified under assumptions about their
environment. Once it has been verified that all sys-
tem components do indeed satisfy these assumptions,
proof rules can be used to combine individual veri-
fication results, establishing correctness properties of
the overall system.
For systems modelled using PA, AG reasoning
proof rules are recently proposed in (He et al., 2015),
(Feng, 2013), (Feng et al., 2010).
Inter-Organisational Workflow (IOWF) processes
constitute a good example of complex systems in the
area of B2B cooperation. Indeed, with the emergence
of service oriented architecture (SOA) and Web ser-
vices standards (Alonso et al., 2004), many research
works have been directed towards WF composition,
mainly based on Web services (Sheng et al., 2014),
244
Bouchekir, R., Boukhedouma, S. and Boukala, M.
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes.
DOI: 10.5220/0005978602440253
In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 244-253
ISBN: 978-989-758-199-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Gabrel et al., 2013), (Gorton et al., 2009). Each part-
ner implements his local WF process as an orchestra-
tion of Web services. Then, an IOWF process can be
considered as a composition of orchestrations of Web
services, usually specified using BPEL4WS language
(Business Process Execution Language for Web Ser-
vices) (Jordan et al., 2007). This results in complex
WF process models. However, there is no guarantee
that the specification of a composite WF is free of er-
rors, even if all WF components are safe. Therefore,
analysing and verifying the correctness of the IOWF
process behaviour before it becomes operational is
important.
The work described in this paper focuses on the
formal modelling and verification of composite WF
(IOWF) processes by using an automatic AG reason-
ing approach. We need to analyse and verify the com-
position because each partner aims to be autonomous
and have the freedom to create or modify his own
WF process at any moment. In addition, this com-
position should not influence the current WF perfor-
mance. More precisely, our main goal is to verify the
logic correctness of a WF composition, e.g. avoid-
ance unsafe system states, satisfaction of certain busi-
ness constraints, e.g. a partner needs to receive always
a reply after a request. In addition, We use the AG
reasoning approach to cope with the the state space
explosion problem.
The remainder of the paper is organized as fol-
lows: Section 2 summarizes briefly some related
works and explains the motivation of this paper. In
Section 3, we provide some background on WF,
IOWF, PA, the L
∗
learning algorithm and probabilis-
tic model checking. Section 4 presents our approach
to modelling and verifying the IOWF behaviour and
finally, Section 5 concludes the paper and talks about
future works.
2 RELATED WORKS AND
MOTIVATION
Research on formal verification has attracted consid-
erable attention. In this section, we review some
research works related to formal verification of WF
composition, focusing on model checking and AG
reasoning approaches. Authors of (Sba
¨
ı et al., 2010)
present a method for verifying collaborative WF pro-
cesses based on model checking techniques. In par-
ticular, they propose to verify soundness properties
of these processes using SPIN model checker. First,
they translate the adopted specification of WFs (i.e.
the WF-net) to Promela, which is the description lan-
guage of models to be verified by SPIN, then express
the soundness properties in Linear Temporal Logic
(LTL) and use SPIN to test whether each property is
satisfied by the Promela model of the WF-net in ques-
tion. (Doshi et al., 2004) consider the issue of auto-
matic WF composition, they propose to use Markov
Decision Processes MDPs to model WF composi-
tion. They justify the use of MDPs by : (1) the un-
certainty over the true environmental model and, (2)
the dynamic environments. Another work (Braghetto
et al., 2011) propose to map business process models
to stochastic formalisms (Stochastic Automata Net-
work). The main contribution of this work is that
they consider both qualitative and quantitative anal-
ysis of WF composition; for performance informa-
tion, they refer to a set of probabilities values attached
to the states. In (Gallotti et al., 2008), the authors
used a model driven approach, which automatically
transforms a design model of service composition into
an analysis model, then feeds a probabilistic model
checker for quality prediction. The issue of verify-
ing if composite Web services design satisfies some
desirable properties was considered also in (Benta-
har et al., 2013), the behaviours of Web services are
modeled using automata-based techniques (Kripke
model). Authors of this work proposed a verification
technique based on the reduction of model checking
compositions to model checking LTL and CTL, by
verifying the operational behaviour against the prop-
erties specified by the control behaviour. For the AG
approaches, some works propose the use of composi-
tional verification approach (Feng et al., 2010), (Feng,
2013) to cope with the state space explosion problem.
An assume-guarantee reasoning rule for PA was pro-
posed in (Feng et al., 2010), (Feng, 2013), using the
L
∗
automatically generate assumptions. Many works
used the compositional verification to verify and anal-
yse complex systems, such as (Calinescu et al., 2012),
where they proposed to used AG proof rules to verify
complex IT systems.
Unlike previous works, in this paper, we state that
a well-defined WF schema can be modelled using PA.
This choice is advantage by: (1) PAs support the veri-
fication and provide a numerical quantitative analysis
of IOWF; (2) more large properties can be expressed,
e.g. computing the probability to reach unsafe system
states, verifying that a partner always receives a reply
after a request, with a certain probability value,...etc.
(3) PAs can be applied for modelling and verifying
large/complex systems (which is the case of the most
real-world IOWF processes) by the use of the compo-
sitional verification approach. We model, separately,
each WF process using PA; the composition of WF
is modelled by a synchronisation between PAs. The
separate modelling of WF processes composing the
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes
245

global IOWF process will let us to use the AG ap-
proach, where each WF is considered as a component.
3 PRELIMINARIES
We give some background knowledge about WF and
IOWF in Section 3.1, Section 3.2 presents the PA,
Section 3.3 describes the L
∗
learning algorithm and
Section 3.4 presents some basics on the probabilistic
model checking.
3.1 Workflow and Inter-organizational
Workflow
A workflow (WF) process is the automation of all
or part of a business process in which information
flows from one activity to another (respectively, one
participant to another) according to a set of prede-
fined rules WFMC
1
. The WF behaviour which is de-
fined, in WFMC, as: ”WF schema is used to repre-
sent the structure of an application in terms of tasks
as well as temporal and data dependencies between
tasks”. In practice, a WF schema can be described
using BPEL4WS which is an XML-based language
that allows composition of Web services in a service-
oriented architecture (SOA), for interconnection and
data-sharing. Programmers use BPEL4WS for speci-
fication and execution of a WF process based on Web
services. BPEL4WS messages are typically used to
invoke remote services, orchestrate process execution
and manage events and exceptions.
Inter-organizational WF (IOWF) can be defined
as a manager of activities involving two or more
WFs (affiliated with business partners), autonomous,
possibly heterogeneous and interoperable in order to
achieve a common business goal (Van Der Aalst,
1999).
3.2 Probabilistic Automata
In this paper, the PA model is used for modelling WF
(and IOWF) schemas. The choice of using PA in our
approach comes from the fact that they allow the mod-
elling of the most constructs of IOWF schema, in-
cluding, basic activities, structured activities and Web
service activities. It allows also both the verification
and the analysis of IOWF processes. In addition, PAs
are known to model concurrent probabilistic systems,
which are in our case, IOWF processes allowing con-
current execution of two or more Web services.
1
Workflow Management Coalition- http://www.wfmc.org
Definition 1. An automata is a tuple A =
(S,s
0
,Σ
A
,δ
A
,F) where S is a finite set of states, s
0
∈ S
is an initial state, Σ
A
is a finite set of actions, δ
A
⊆
S × Σ
A
× S is a transition relation and F ⊆ S is a set
of final or accepting states. A is a deterministic finite
automata if |δ
A
(s,a)| ≤ 1 for all s ∈ S and a ∈ Σ
A
,
where |δ
A
(s,a)| is the size of the set δ
A
. A is called a
complete DFA if |δ
A
(s,a)| = 1.
In the following, we use Dist(S) to denote the set
of all discrete probability distributions over a set S.
Definition 2. A labelled probabilistic automaton (PA)
is a tuple M = (S,s
0
,Σ
M
,δ
M
,L) where S,s
0
,Σ
M
are
defined as for DFA. δ
M
⊆ S × (Σ
M
∪ {τ}) × Dist(S) is
a probabilistic transition relation and L → 2
AP
is a la-
belling function, assigning atomic propositions form
a set AP to a state.
In a state s of PA M, one or more transitions, de-
noted s a
−→
µ, are available, where a ∈ Σ
M
is an action
label, µ is a probability distribution over states and
(s,a,µ) ∈ δ
M
. A path through a PA is a (finite or in-
finite) sequence s
0
a
0
,µ
0
−−−→
s
1
a
1
,µ
1
−−−→
.... To reason about
PAs, we use the notion of adversaries, which resolve
the non-deterministic choices in a PA, based on its
execution history. Formally, an adversary maps any
finite path to a distribution over the available transi-
tions in the last state on the path. In this paper, we use
also the notion of parallel composition of PAs, which
refers to standard definition of parallel composition of
PAs M
1
and M
2
, denoted M
1
k M
2
, where M
1
and M
2
synchronise over all common actions (Segala, 1995).
3.3 The L
∗
Algorithm
The L
∗
algorithm (Angluin, 1987) is a formal method
to learn a DFA with the minimal number of states that
accepts an unknown language L over an alphabet Σ.
During the learning process, the L
∗
algorithm inter-
acts with a Teacher to make two types of queries: (i)
membership queries and (ii) equivalence queries. A
membership queries are used to check whether some
word w is in the target language, we can see member-
ship queries as a function MQuery such that:
MQuery(w) =

1 if w ∈ L
0 otherwise
Equivalence queries are used to check whether a
conjectured DFA A accepts the target language. If the
conjectured DFA is not correct, the teacher would re-
turn a counterexample to L
∗
to refine the automaton
being learnt, also we can see equivalence queries as a
function EQuery such that:
EQuery(A) =

1 L(A) = L
0 and a counterexample otherwise
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
246

At the implementation level, L
∗
maintains an ob-
servation table (U,V ). Where U is a non-empty fi-
nite prefix-closed of words and V is a non-empty fi-
nite suffix-closed set of words. MQuery(w) = ((U ∪
U.Σ).V ) 7→ {+, −} for all w ∈ ((U ∪U.Σ).V ), where
Σ is the alphabet of the target language and {+, −}
represent whether or not a word is accepted by the
target language or not. The L
∗
checks at the end of
the membership queries whether the observation ta-
ble is closed and consistent. An observation table T
is closed if for all u ∈ U, v ∈ V and w ∈ Σ, there is a
u
0
∈ U such that T (uwv) = T (u
0
v). An observation ta-
ble T is consistent if for all u,u
0
∈ U , v ∈ V and w ∈ Σ,
T (uv) = T (u
0
v) ⇒ T (uwv) = T (u
0
wv).
3.4 Probabilistic Model Checking
A probabilistic safety properties are specified by
Probabilistic Computation Tree Logic PCTL (Hans-
son and Jonsson, 1994) in the form of P
≤p
[ψ] with
p ∈ [0,1] and
φ ::= true|a|φ
1
∧ φ
2
|¬φ
ψ ::= φUφ
where a is an atomic proposition, φ a state for-
mula, ψ a path formula and U the “until” temporal
operator.
We consider safety properties, which are often
characterized as “nothing bad should happen”. In
the context of probabilistic systems, safety proper-
ties also capture a wide range of useful properties,
e.g. “the maximum probability of an error occur-
ring is at most 0.01” is specified as P
≤0.01
[trueUφ
err
]
where φ
err
is a state formula indicating the occur-
rence of an error. We say that a state s ∈ S satis-
fies P (written M, s |= P
≤p
[trueUφ
err
]) if P
max
s
≤ p.
Model M satisfies P (written M |= P
≤p
[trueUφ
err
]) if
M,s
0
|= P
≤p
[trueUφ
err
].
In this paper, we focus on regular safety property.
Safety property P over AP is called regular if its set of
bad prefixes constitutes a regular language over 2
AP
,
so a regular safety property P can be represented as a
set of infinite words, that is characterised by regular
language of bad prefixes.
4 DESCRIPTION OF OUR
APPROACH
In this section, we describe our approach for composi-
tional probabilistic verification of IOWF schema. Fig-
ure 1 presents an overview of our approach. The first
step is to translate the BPEL4WS files to a PRISM
module, where each BPEL4WS file describes a WF
process attached to a given partner, by means of PA.
The output of the first step is a set of PAs, where each
PA models a WF schema. In the second step, we use
the AG approach to verify if the IOWF process satis-
fies the probabilistic safety property P. Indeed, this
will let us to check the correctness of the probabilistic
safety property P without constructing and analysing
the full model, which is M
W F
1
k M
W F
2
; instead, we
generate an assumption A which simulates one com-
ponent (let A simulates M
W F
1
). By using the assump-
tion A, if A is much smaller than the component M
W F
1
then we can expect significant gains in terms of mem-
ory space.
4.1 Translate IOWF to PA
In this section, we describe how we translate IOWF
schemas to PAs. This translation needs to consider
the compositional aspect, this means that we need to
model the set of WFs composing the IOWF as a set of
components (set of PAs), this will let us to use the AG
approach for verification of the global IOWF process.
In addition, for automatic translation from BPEL4WS
specification to PA model, we have implemented a
translator tool. Our translator accepts as input a set of
BPEL4WS and WSDL files, and generates a PRISM
model, which represents a set of PAs.
The translator translates each WF process to a
PRISM module. In the following, we describe how
we translate each activity of the WF process to its
equivalent in PA and in PRISM code. Also, we de-
scribe how we encode communication between WFs
invoked in a global IOWF process.
The initial (final) node of a WF, is modelled by an
initial (final) state of the PA.
4.1.1 Modelling Basic Activities
Basic BPEL4WS control flow activities, which are:
Assign, Empty, Wait, Throw and Exit, are mapped to
their equivalents in PAs as described in Table 1. We
model the wait activity using flags, since in this paper
we aim to model the logic behaviour of an IOWF pro-
cess. Therefore, we do not need to model time in wait
activity.
4.1.2 Modelling Structured Activities
Usual structured BPEL4WS activities are: Sequence,
Switch, While, Flow, Pick, we mapped each activity
to its equivalent in PAs as shown on Table 2.
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes
247

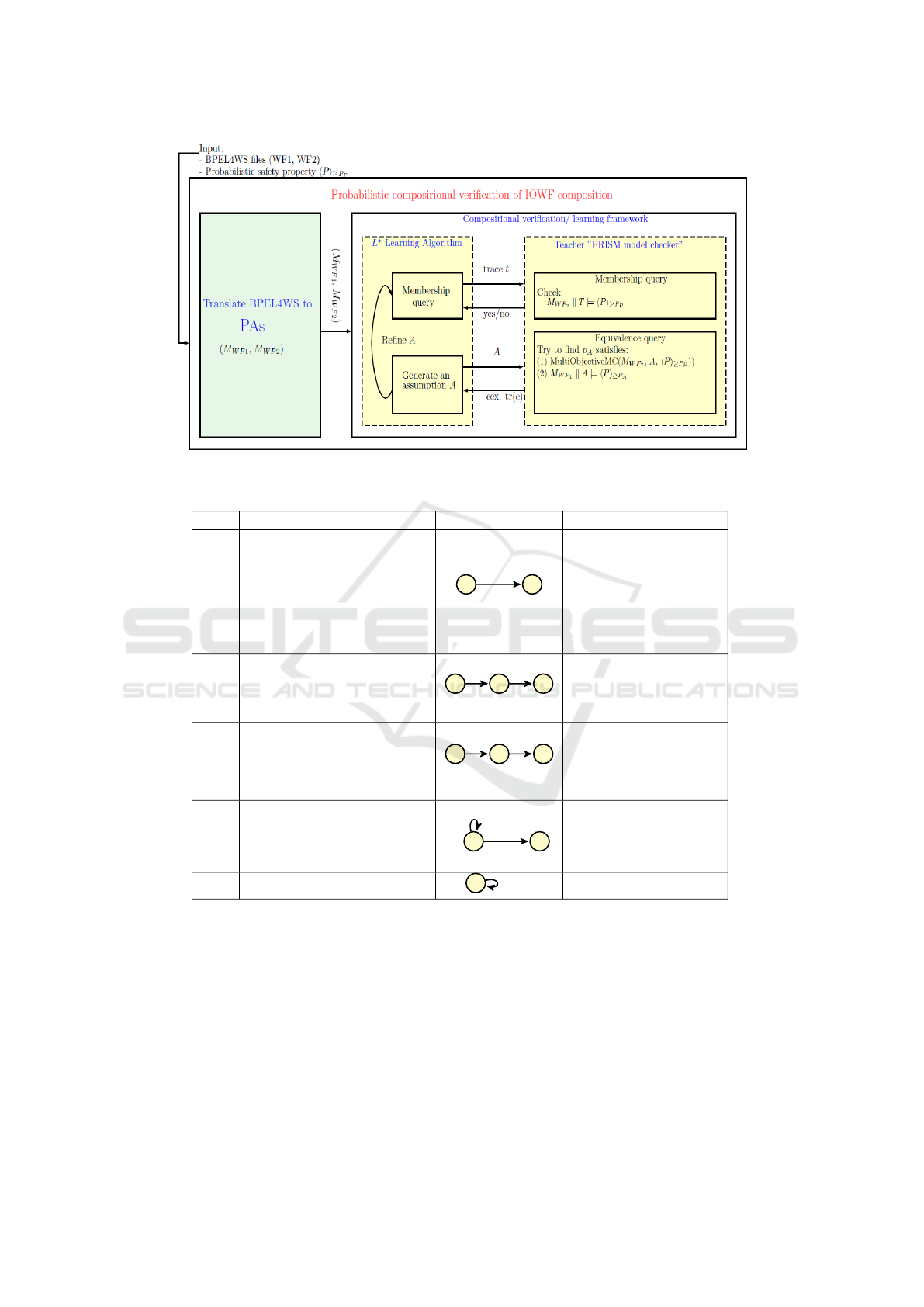
Figure 1: An overview of our approach.
Table 1: Translation of BPEL4WS’s basic activities to PRISM language.
Name BPEL4WS Syntax PAs PRISM language
Assign
a
0
< assignname = ”Assign1” >
< copy >
< f romvariable = ”Var1”/ >
< tovariable = ”Var2”/ >
< /copy >
< /assign >
a
1
a
0
a
1
Assign1 p = 1
[Assign1] a=0 → (a’=1);
Empty
a
0
< emptyname = ”Empty1”/ >
a
2
a
0
a
1
Empty1
a
2
p = 1 p = 1
[] a=0 → (a’=1);
[] a=1 → (a’=2);
....
label “Empty1”=a=1;
Throw
a
0
< throwname = ”T hrow1”
f aultName = ”sxeh : systemFault”
f aultVariable = ”Variable1”/ >
a
2
a
0
a
1
systemFault
a
2
p = 1 p = 1
[] a=0 → (a’=1);
[] a=1 → (a’=2);
....
label “systemFault”=a=1;
Wait
< waitname = ”Wait1” >
< f or >
0
10
0
< / f or >
< /wait >
a
0
a
1
f lagWait1
¬ f lagWait1
f ormula flagWait1;
[] a=0 and flagWait1 → (a’=0);
[] a=0 and ¬ flagWait1 → (a’=1);
Exit
< exit/ >
a
f
p = 1
[final] a=f → (a’=f);
4.1.3 Modelling Web Service Activities
In BPEL4WS specification, the ”partnerLink” spec-
ifies the partner from/to which a message is re-
ceived/sent. When the IOWF view is considered, the
partnerLink construct plays an important role since it
defines the communication channel between the inter-
nal/external WF or between WF processes involved in
cooperation. Common interactions patterns between
WF and external Web services (or external WF) are:
(1) One-way messages, (2) Synchronous interactions
and (3) Asynchronous interactions.
One-way Messages is considered when a WF
process sends a message to an external partner, and
this partner does not need to reply. The external part-
ner can be either an external Web service or an exter-
nal WF (encapsulated in a composite Web service).
The WF process sending the message does not wait
for a response, but continues executing immediately.
Figure 2 shows a one-way interaction. In the case
where the external partner is a Web service, we model
the one-way messages by a state in the PA, since we
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
248

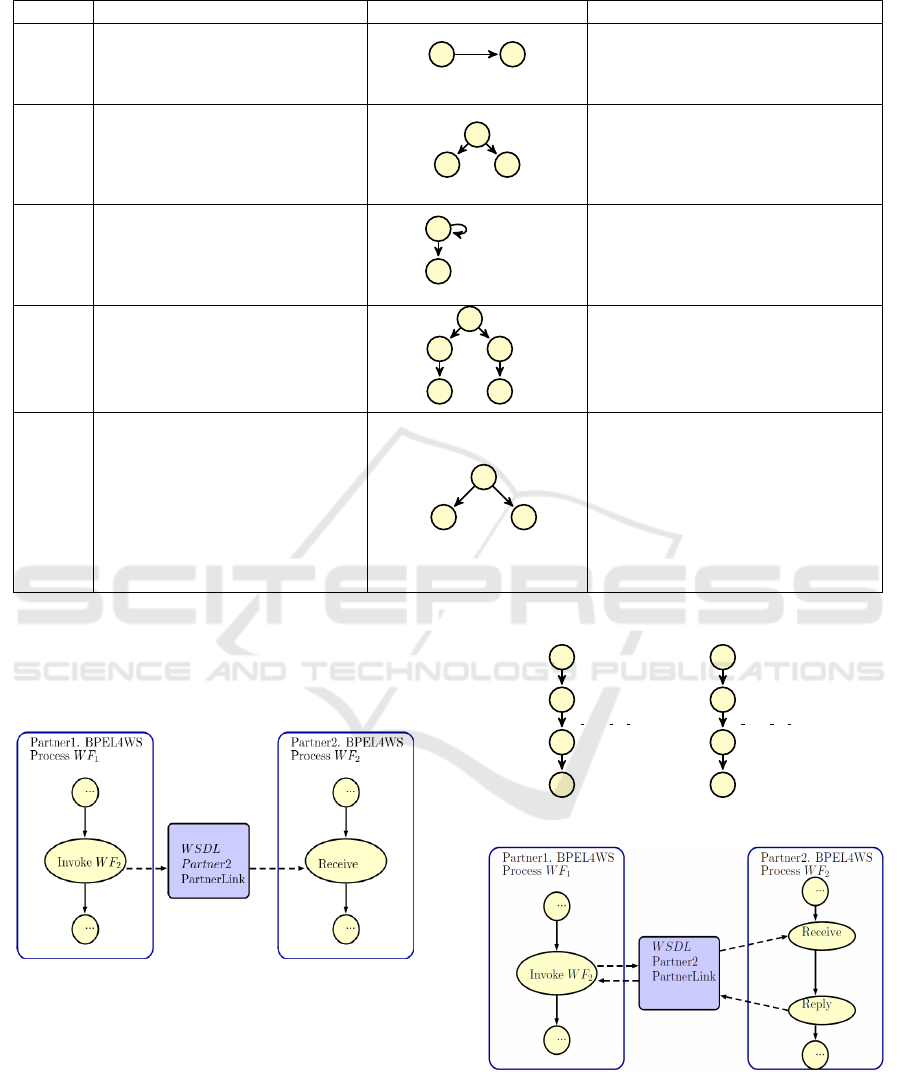
Table 2: Translation of BPEL4WS’s structured activities to PRISM language.
Activity BPEL4WS Syntax PAs PRISM language
Sequence
< sequence... >
a
0
a
1
< /sequence >
a
0
a
1
p = 1
[] a=0 → (a’=1);
Switch
a
0
< switch... >
a
1
a
2
< /switch >
a
0
a
1
a
2
p
1
p
2
[] a=0 → p
1
: (a’=1) + p
2
: (a’=2); //p
1
+ p
2
= 1
While
< whilename = ”While1” >
< condition > boolExp < /condition >
a
0
< /while >
a
1
a
0
a
1
boolExp
¬ boolExp
f ormula boolExp;
[] a=0 and boolExp → (a’=0);
[] a=0 and ¬ boolExp → (a’=1);
Flow
a
0
< f low... >
a
1
a
2
< / f low >
a
0
a
1
a
2
a
2
a
1
p
1
p
2
p
2
p
1
[] a=0 → p
1
: (a’=1) + p
2
: (a’=2); // p
1
= p
2
= 1
[] a=1 → p
2
: (a’=2);
[] a=2 → p
1
: (a’=1);
Pick
a
0
< pick... >
< onMessage... >
a
1
< /onMessage... >
< onAlarm... >
a
2
< /onAlarm... >
< /pick >
a
0
a
1
a
2
isMessage
isAlarm
f ormula isMessage;
f ormula isAlarm;
[] a=0 and isMessage → (a’=1);
[] a=0 and isAlarm → (a’=2);
do not model the external behaviour of the Web ser-
vice. Otherwise, we model the one-way interaction
between two WF processes by a synchronous interac-
tion between the PAs modelling the two WFs.
Figure 2: One-way interaction.
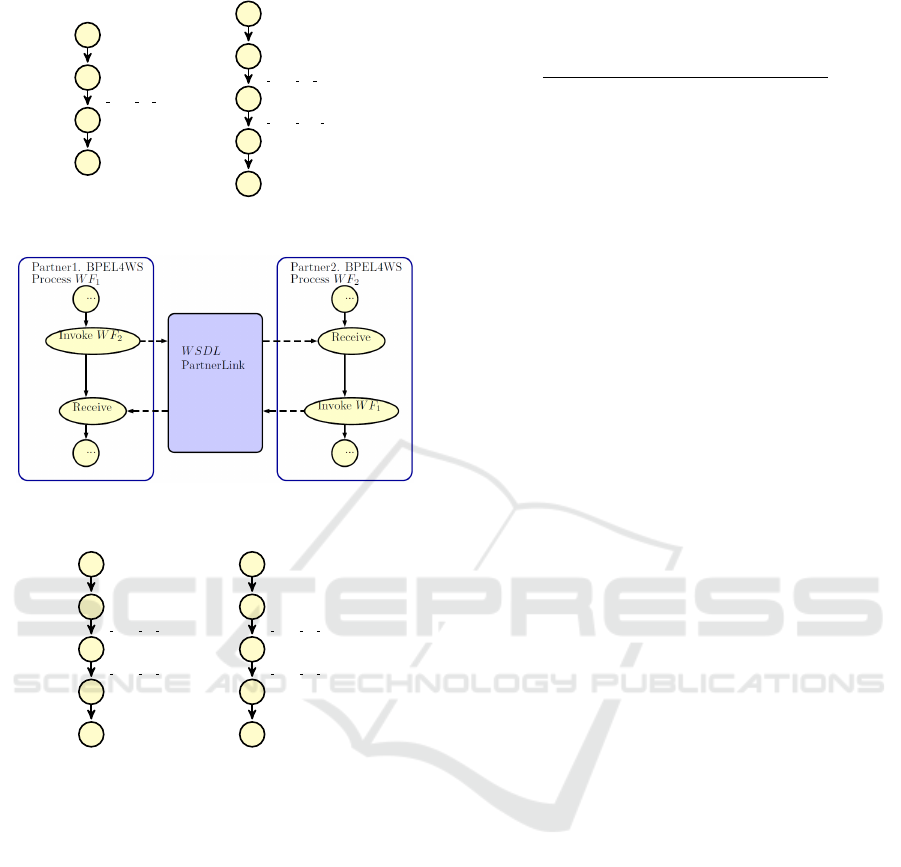
In a Synchronous Interaction, a WF process
sends a request to an external Web service or an ex-
ternal WF by using ”invoke” activity, and receives an
immediate reply. Figure 4 shows how we model the
synchronous interactions in an IOWF process model.
In an Asynchronous Interaction, a WF process
sends a request to an external Web service or exter-
nal WF by using the ”invoke” activity, and waits until
receiving a reply. Figure 6 shows how we model the
synchronous interactions in IOWF process model.
WFprocess1
...
s
0
s
i+1
...
I1 W F1 R1 W F2
WFprocess2
...
t
0
t
i+1
...
I1 W F1 R1 W F2
Figure 3: Modelling one-way interaction in PA.
Figure 4: Synchronous interaction.
4.2 Compositional Verification of
IOWFs
The second step in our framework is the composi-
tional verification of IOWF schema. This step is
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes
249

WFprocess1
...
s
0
s
i+1
...
I1 W F1 R1 W F2
WFprocess2
...
t
0
t
i+1
t
i+2
...
I1 W F1 R1 W F2
I1 W F1 RP1 W F2
Figure 5: Modelling synchronous interaction in PA.
Figure 6: Asynchronous interaction.
WFprocess1
...
s
0
s
i+1
s
i+2
...
I1 W F1 R1 W F2
I2 W F2 R2 W F1
WFprocess2
...
t
0
t
i+1
t
i+2
...
I1 W F1 R1 W F2
I2 W F2 R2 W F1
Figure 7: Modelling asynchronous interaction in PA.
based on an AG reasoning rule, which describes the
steps and the rules to infer the assumption A and how
to use it in the verification process. For clarity, it is
undicidable to infer assumption as PA under a version
of Angluin’s learning algorithm (L
∗
), and a learning
algorithms for general probabilistic systems may not
exist after all (Komuravelli et al., 2012). Given the
absence of learning algorithms for probabilistic sys-
tems, the authors of (Feng et al., 2010) propose to
represent assumption as DFA and use the L
∗
to infer
this assumption. In our work, we adapt the same proof
rule to verify the IOWF behaviour.
Theorem 1. Let M
W F
1
and M
W F
2
be PA modelling
WF W F1 and W F2, respectively. hAi
≥P
A
and hPi
≥P
P
are regular probabilistic safety properties such that
their alphabets satisfy Σ
A
⊆ Σ
M
W F
1
and Σ
P
⊆ Σ
M
W F
2
∪
Σ
A
,P
p
,P
A
∈ [0,1] are a rational probability bound,
then the following proof rule holds:
Table 3: AG rule for probabilistic systems (Feng et al.,
2010).
htrueiM
W F
1
hAi
≥P
A
(1)
hAi
≥P
A
M
W F
1
hPi
≥P
P
(2)
htrueiM
W F
1
k M
W F
2
hPi
≥P
P
(3)
This AG rule means that if we have two PA M
W F
1
and M
W F
2
modelling the local WFs W F
1
and W F
2
, re-
spectively, composed to build an IOWF process, we
can check the correctness of a probabilistic safety
property hPi
≥P
P
on the IOWF without constructing
and verifying the full model. Instead, we first infer
an appropriate assumption A by using the L
∗
learn-
ing algorithm; then check if we can use this assump-
tion to verify the IOWF by following the two premise
(1) and (2). Promise (1) can be checked by us-
ing a standard probabilistic model checking algorithm
(Kwiatkowska et al., 2009) and promise (2) can be
checked using multi-objective model checking algo-
rithm (Etessami et al., 2007).
4.3 Running Example
Example 1. We illustrate the formal modelling
and the compositional verification technique dis-
cussed in this paper by using the example of inter-
organisational process TA/AH shown in Figure 8. It
involves two business partners respectively called TA
for a Travel Agency and AH for a local airline com-
pany. TA provides an internet reservation system for
its customers. The TA sends the customer reservation
requests to its partner (AH) in case of a valid request;
otherwise, it closes the client session. When AH re-
ceives a reservation request, it checks if the number of
seats requested are available, if they are available, it
registers the reservation data and alocate additional
services such as seating, special meals ...etc. Other-
wise, if the number of seats requested are not avail-
able, it adds the request to the waiting list. In both
cases, AH company returns a notification to its part-
ner TA.
As described before, the first step in our approach
is to model the local WF of TA/AH by using PAs,
Figure 9 and 10 shown the PAs modelling the local
WF TA and AH, respectively.
For the IOWF AT/AH, we apply the compositional
verification to verify if M
W F
TA
k M
W F
AH
satisfies the
probabilistic safety property : P
min
≥0.985
[G¬(” f ail”)],
which means the minimum probability that the sys-
tem should never fails, over all possible adversaries,
is at least 0.985.
As described before, a probabilistic safety prop-
erty can be expressed using a regular language of bad
prefixes, this can be then represented by a DFA P
err
,
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
250

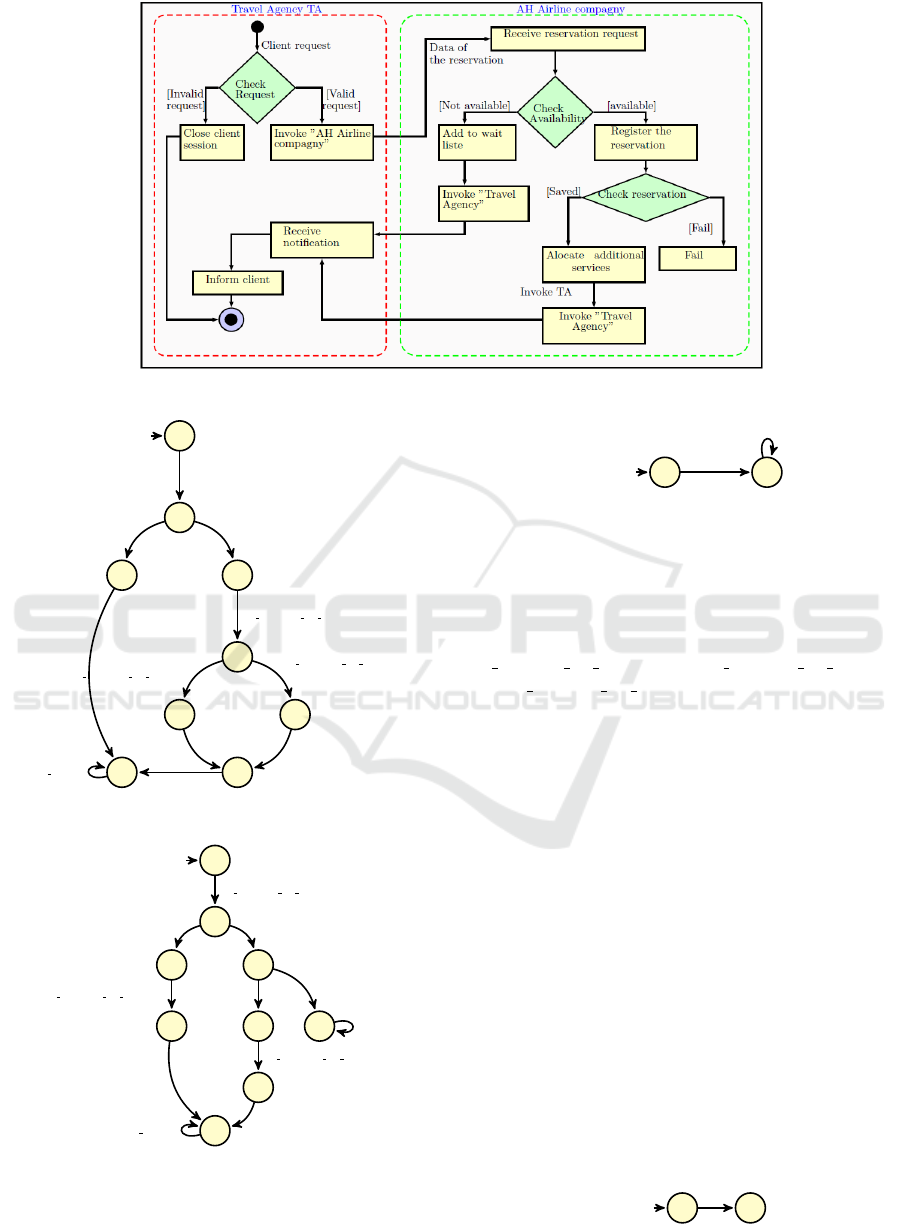
Figure 8: Activity diagram of the inter-organizational workflow schema of AT/AH.
s
0
start
s
1
s
2
s
3
s
4
s
5
s
6
s
7
s
8
ClientRequest
0.9 isValidRequest
0.1 isValidRequest
I1 MW F
TA
R1 MW F
AH
I2 MW F
AH
R2 MW F
TA
I3 MW F
AH
R3 MW F
TA
In f ormClient
In f ormClient
End W F
TA
Figure 9: PA M
W F
TA
Modelling the local WF ”TA”.
t
0
start
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
I1 MW F
TA
R1 MW F
AH
3/4 isAvailable
1/4 isAvailable
0.9 isReserved
0.1 isReserved
I2 MW F
AH
R2 MW F
TA
I3 MW F
AH
R3 MW F
TA
f ail
End W F
AH
Figure 10: PA M
W F
AH
Modelling the WF ”AH”.
in our case, the DFA specifies our probabilistic safety
property is shown in Figure 11.
p
0
start
p
1
f ail
f ail
Figure 11: DFA P
err
.
For instance, we initialize the set U = V = {ε},
where U and V are a set of actions used by the L
∗
learning algorithm to infer a conjecture assumption.
Σ
A
= {c,d,e}, where c,d and e are the actions
I1 MW F
TA
R1 MWF
AH
, I2 MW F
AH
R2 MWF
TA
and I3 MW F
AH
R3 MWF
TA
, respectively. Σ
A
repre-
sents the set of actions of the assumption and ε is an
empty word.
The L
∗
starts by applying membership queries,
which verify whenever a given trace T should be in-
cluded in the assumption. The trace T denotes a PA
representing a trace, i.e a linear, |T | + 1 state in which
each transition has probability 1 and labelled by an
action of an element of the set (U.U).Σ
A
. For in-
stance, the element (U.U).Σ
A
= {ε,c,e,d}. L
∗
starts
by checking if c should be included or not in the gen-
erated assumption, for this it builds a trace T (shown
in Figure 12). The criterion to check if the T should
be included in the assumption is checked by verifying
if T k M
W F
AH
k P
err
satisfies the probabilistic safety
property P. Consider the trace T shown in Figure
12, we have used the model checker PRISM to check
whenever T k M
W F
AH
k P
err
satisfies the property:
Pmin =?[G¬((”err
P
”)and(”err
T
”))], where ”err
P
”
and ”err
T
” are two atomic proposition labelling the
final states of P
err
and T , respectively.
h
0
start
h
1
c
Figure 12: PA representing the trace T for the action c.
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes
251

The results of the membership queries are stored
in an observation table, for the first set of membership
queries, the results are stored in the first observation
table T
0
(Table 4).
Table 4: The first observation tables T
0
.
T
0
V = {ε}
U = {ε} −
c +
e −
d −
The first observation table T
0
is not closed, since
there is no row in the table of T
0
that corresponds to
T
0
(c). To make T
0
closed, we add the action c to the
set U. For now, the set U and (U.U)Σ
A
are set to U =
{ε,c} and (U.U)Σ
A
= {ε,c,e,d, c.c,c.e,c.d}. The L
∗
learning algorithm repeats the same process as before
to check whenever c.c,c.e and c.d should be included
in the assumption. The second observation Table T
1
is
shown in Table 5. The observation table T
1
is closed
and consistent.
Table 5: The second observation tables T
1
.
T
1
V = {ε}
U = {ε} −
U = {c} +
e −
d −
c.c +
c.e +
c.d +
We generate the first conjecture assumption A
err
1
based on T
1
. The first conjecture assumption A
err
1
is
shown in Figure 13.
a
0
start
a
1
e,d
c
c,e,d
Figure 13: The first conjecture assumption A
err
1
.
Now, we need to analyse if the first conjecture as-
sumption A
err
1
can be used to establish the AG reason-
ing proof rule, this is done through verification of the
two promises of the AG (Feng et al., 2010):
• To verify htrueiM
W F
TA
hAi
≥P
A
, we first compute
M
W F
TA
k A
err
1
, then model checked M
W F
TA
k A
err
1
to
obtain 1 − P
A
, the maximum probability of reach-
ing the (undesirable) accepting states of A
err
.
• To verify hAi
≥P
A
M
W F
AH
hPi
≥P
P
, we first compute
M
W F
AH
k A
err
1
k P
err
. We used the multi-objective
model checking algorithm to check the second
promise because the satisfaction of A with prob-
ability P
A
and of P with probability P
P
must be
analysed together. Theses steps are described in
detail in (Feng et al., 2010). For our example
we have used the latest version of PRISM, where
probabilistic model checking algorithms and the
multi-objective model checking algorithm are au-
tomated.
In practice, we start by checking the second
promise, i.e, hAi
≥P
A
M
W F
AH
hPi
≥P
P
, by using the
model checker PRISM. This results an empty inter-
val, which indicates that, even under the assump-
tion hAi
≥1
, M
W F
AH
would still not satisfy P, there-
fore, we must refine A
err
1
. To refine A
err
1
we gen-
erate a probabilistic counterexample showing that
hAi
≥1
M
W F
AH
hPi
≥P
P
does not hold and then use this
to generate traces for the L
∗
learning algorithm.
More precisely, to generate this counterexample of
hAi
≥1
M
W F
AH
hPi
≥P
P
, we first computed the parallel
composition of A
err
1
k M
W F
AH
k P
err
, then we have
used COMICS
2
Tool to compute the minimal coun-
terexamples for PAs. After few iterations, follow-
ing the same process described in this example, our
framework returns that the M
W F
TA
k M
W F
AH
satisfies
the safety property P.
5 CONCLUSIONS
In this paper, we proposed an approach to formal
modelling and verification of IOWF processes result-
ing from composition of two or more WF processes.
The main aspects that characterise our approach are:
(1) it supports both the analysis and the verification
of both a standalone WF process schema or a compo-
sition of WF processes (IOWF), where each WF pro-
cess is modelled using PA, (2) it supports the specifi-
cation and verification of regular safety properties de-
scribed in PCTL, (3) it covers all activities of a given
WF process. To cope with the state space explosion
problem faces when verifying large/complex IOWF,
we proposed to use AG reasoning proof rule, and we
have shown how to apply our approach using a sim-
ple example. We plan to extend this work by applying
our approach to verify real life complex IOWF and
use other AG reasoning rule such as (He et al., 2015).
We moreover like to extend our translator to support
BPMN description language.
REFERENCES
Alonso, G., Casati, F., Kuno, H., and Machiraju, V. (2004).
Web services : concepts, architectures and applica-
2
http://www-i2.informatik.rwth-aachen.de/i2/comics/
SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
252

tions. Springer.
Angluin, D. (1987). Learning regular sets from queries
and counterexamples. Information and computation,
75(2):87–106.
Baier, C., Katoen, J.-P., et al. (2008). Principles of model
checking, volume 26202649. MIT press Cambridge.
Baier, C. and Kwiatkowska, M. (1998). Model checking
for a probabilistic branching time logic with fairness.
Distributed Computing, 11(3):125–155.
Bentahar, J., Yahyaoui, H., Kova, M., and Maamar, Z.
(2013). Symbolic model checking composite web ser-
vices using operational and control behaviors. Expert
Systems with Applications, 40(2):508–522.
Braghetto, K. R., Ferreira, J. E., and Vincent, J.-M. (2011).
Performance evaluation of business processes through
a formal transformation to san. In Computer Perfor-
mance Engineering, pages 42–56. Springer.
Calinescu, R., Kikuchi, S., and Johnson, K. (2012). Com-
positional reverification of probabilistic safety prop-
erties for large-scale complex it systems. In Large-
Scale Complex IT Systems. Development, Operation
and Management, pages 303–329. Springer.
Chen, Y.-F., Clarke, E. M., Farzan, A., Tsai, M.-H.,
Tsay, Y.-K., and Wang, B.-Y. (2010). Automated
assume-guarantee reasoning through implicit learn-
ing. In Computer Aided Verification, pages 511–526.
Springer.
Doshi, P., Goodwin, R., Akkiraju, R., and Verma, K. (2004).
Dynamic workflow composition using markov deci-
sion processes. In Web Services, 2004. Proceedings.
IEEE International Conference on, pages 576–582.
IEEE.
Etessami, K., Kwiatkowska, M., Vardi, M. Y., and Yan-
nakakis, M. (2007). Multi-objective model checking
of markov decision processes. In Tools and Algo-
rithms for the Construction and Analysis of Systems,
pages 50–65. Springer.
Feng, L. (2013). On Learning Assumptions for Composi-
tional Verification of Probabilistic Systems. PhD the-
sis, University of Oxford.
Feng, L., Kwiatkowska, M., and Parker, D. (2010). Com-
positional verification of probabilistic systems us-
ing learning. In Quantitative Evaluation of Systems
(QEST), 2010 Seventh International Conference on
the, pages 133–142. IEEE.
Gabrel, V., Manouvrier, M., and Murat, C. (2013). A new
linear program for qos-aware web service composi-
tion based on complex workflow.
Gallotti, S., Ghezzi, C., Mirandola, R., and Tamburrelli,
G. (2008). Quality prediction of service composi-
tions through probabilistic model checking. In Quality
of Software Architectures. Models and Architectures,
pages 119–134. Springer.
Gorton, S., Montangero, C., Reiff-Marganiec, S., and Sem-
ini, L. (2009). Stpowla: Soa, policies and workflows.
In Service-Oriented Computing-ICSOC 2007 Work-
shops, pages 351–362. Springer.
Hansson, H. and Jonsson, B. (1994). A logic for reasoning
about time and reliability. Formal aspects of comput-
ing, 6(5):512–535.
Hart, S. et al. (1984). Probabilistic temporal logics for fi-
nite and bounded models. In Proceedings of the six-
teenth annual ACM symposium on Theory of comput-
ing, pages 1–13. ACM.
He, F., Gao, X., Wang, B.-Y., and Zhang, L. (2015).
Leveraging weighted automata in compositional rea-
soning about concurrent probabilistic systems. In
Proceedings of the 42nd Annual ACM SIGPLAN-
SIGACT Symposium on Principles of Programming
Languages, pages 503–514. ACM.
Jordan, D., Evdemon, J., Alves, A., Arkin, A., Askary, S.,
Barreto, C., Bloch, B., Curbera, F., Ford, M., Goland,
Y., et al. (2007). Web services business process execu-
tion language version 2.0. OASIS standard, 11(120):5.
Komuravelli, A., Pasareanu, C. S., and Clarke, E. M.
(2012). Learning probabilistic systems from tree
samples. In Proceedings of the 2012 27th Annual
IEEE/ACM Symposium on Logic in Computer Sci-
ence, pages 441–450. IEEE Computer Society.
Kwiatkowska, M., Norman, G., and Parker, D. (2009).
Prism: probabilistic model checking for performance
and reliability analysis. ACM SIGMETRICS Perfor-
mance Evaluation Review, 36(4):40–45.
Larsen, K. G., Pettersson, P., and Yi, W. (1995). Composi-
tional and symbolic model-checking of real-time sys-
tems. In Real-Time Systems Symposium, 1995. Pro-
ceedings., 16th IEEE, pages 76–87. IEEE.
Lehmann, D. and Shelah, S. (1982). Reasoning with time
and chance. Information and Control, 53(3):165–198.
P
˘
as
˘
areanu, C. S., Giannakopoulou, D., Bobaru, M. G.,
Cobleigh, J. M., and Barringer, H. (2008). Learning to
divide and conquer: applying the l
∗
algorithm to au-
tomate assume-guarantee reasoning. Formal Methods
in System Design, 32(3):175–205.
Sba
¨
ı, Z., Missaoui, A., Barkaoui, K., and Ben Ayed, R.
(2010). On the verification of business processes by
model checking techniques. In Software Technol-
ogy and Engineering (ICSTE), 2010 2nd International
Conference on, volume 1, pages V1–97. IEEE.
Segala, R. (1995). Modelling and verification of random-
ized distributed real time systems. PhD thesis, Mas-
sachusetts Institute of Technology.
Sheng, Q. Z., Qiao, X., Vasilakos, A. V., Szabo, C., Bourne,
S., and Xu, X. (2014). Web services composition: A
decade’s overview. Information Sciences, 280:218–
238.
Van Der Aalst, W. M. (1999). Process-oriented architec-
tures for electronic commerce and interorganizational
workflow. Information systems, 24(8):639–671.
Automatic Compositional Verification of Probabilistic Safety Properties for Inter-organisationalWorkflow Processes
253