Local Ozone Prediction with Hybrid Model

Dejan Gradiˇsar

, Boˇstjan Graˇsiˇc

, Marija Zlata Boˇznar

, Primoˇz Mlakar

and Juˇs Kocijan

1,3

Joˇzef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia

MEIS d.o.o, Mali Vrh pri

Smarju 78, SI-1293

Smarje - Sap, Slovenia

University of Nova Gorica, Vipavska 13, SI-5000 Nova Gorica, Slovenia

Keywords:

Air Pollution, Ozone, Prediction of Ozone Concentration, Statistical Modelling.

Abstract:

Tropospheric ozone in high concentrations can cause health problems. A reliable alerting system is needed.

In this paper we present the hybrid model that can be used for ozone forecasting in urban microlocations.

The hybrid model is combined from meteorological and air-quality models (covering large geographical 3-

dimensional space), and empirical model (offering good local forecasts), implemented as a Gaussian-process

model. Prediction model for the city of Koper in Slovenia that has Mediterranean climate and problems with

the ozone pollution is presented and used for improved one-day-ahead forecasting of the maximum hourly

value within each day. The model validation results show that hybrid model improves ozone forecasts and

provides better alert systems for the selected location.

1 INTRODUCTION

Tropospheric ozone is an air pollutant that causes

health problems. Therefore, the EU directives were

established that regulate standards of air quality that

guarantee the protection of human health as well the

thresholds of ozone for informing and alerting the

public when they are violated. For this reason the

forecasting of the ozone is necessary.

In order to provide good forecast of ozone con-

centration, air-quality and meteorological models are

necessary. These models can be developed using

a variety of methods that contain the scientiﬁc un-

derstanding of the physical processes involved in air

quality and meteorology, i.e. ﬁrst principles models

(Im et al., 2015). These models provide prognostic

time- and spatially-resolved concentrations for vari-

ous scenarios (including atypical ones) and, above all,

provide insights into pollutant formation processes

(Zhang et al., 2012). Due to their complete spatial

coverage, these models also provide forecasts in loca-

tions which are not monitored (

Zabkar et al., 2015).

While air-quality and meteorological models cover

large geographical 3-dimensional space, their local

resolution is often not satisfactory. This is a disadvan-

tage in the case of topographically complex terrain.

On the other hand, models can be developed

empirically, using statistical methods that describe

the non-linear dynamics of air-quality components,

formed from available measurement data only. When

these models are developed correctly and well, they

provide forecasts of higher accuracy and with better

computational efﬁciency than ﬁrst principles models

(Zhang et al., 2012). Nevertheless, the physical pro-

cesses involved in air quality and meteorology can-

not be seen transparently in empirical models. Vari-

ous empirical models are used for air-quality forecast-

ing, ranging from Principal Component Regression to

Takagi–Sugeno fuzzy models, e.g., (Al-Alawi et al.,

2008), (Petelin et al., 2013), (Mlakar and Boˇznar,

2011).

The present paper deals with improving the ozone

forecasting in a selected micro-location, the city of

Koper in Slovenia, for the purpose of giving alerts,

which, in general, has a complex and geographically

diverse terrain (

Zabkar et al., 2015). Presented work

is part of extensive efforts to develop air-quality fore-

casting system for Slovenia. The main contribution

of the present work is the combination of ﬁrst prin-

ciples and empirical model as presented in (Gradiˇsar

et al., 2015) on the case of neural-network models,

while in this paper empirical model is developed us-

ing Gaussian-process (GP) model (Kocijan, 2016).

The integration of ﬁrst principles and empirical mod-

els for forecasting ozone with the aim of uniting ’the

best of both worlds’ in modelling, is to overcome the

problem of the low resolution of ﬁrst principles mod-

els while retaining their advantages.

262

Gradišar, D., Graši

c, B., Božnar, M., Mlakar, P. and Kocijan, J.

Local Ozone Prediction with Hybrid Model.

DOI: 10.5220/0005980002620269

In Proceedings of the 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2016), pages 262-269

ISBN: 978-989-758-199-1

The idea of using the hybrid model, i.e., the com-

bination of ﬁrst principles and empirical models is not

a novel one. It is quite common in ﬁelds like process

engineering, e.g., (von Stosch et al., 2014). GP mod-

els may complement ﬁrst principles models as a sup-

plement for parts of a model, e.g., in (Schmitt et al.,

2008), as a model of stochastic input, known as Latent

Force Model (LFM), e.g., in (

Alvarez et al., 2009), or

as a model of residuals from ﬁrst principles models,

e.g., in (Chen et al., 2013). However, hybrid mod-

els have rarely been employed in atmospheric science.

Applications in (Pelliccioni and Tirabassi, 2006) and

(Goyal and Kumar, 2012) are examples of integrating

ﬁrst principles and empirical models for the elimina-

tion of system errors in diagnostic investigation of the

air quality in ﬂat terrain case studies and for so-called

tracer experiments using nonreactive gasses.

The present report is structured as follows. The

problem is described in the next section. The pro-

posed methodology is introduced in Section 3. Sec-

tion 4 describes and discusses the results of the exper-

iments to showthe feasibility of the proposed method-

ology. The conclusions are drawn at the end.

2 PROBLEM DESCRIPTION

The problem considered in this paper is to improve

ozone forecasting and consequentlyto increase the re-

liability of alerts for the city of Koper. The location

is an urban location, and this is the kind of location

where alerts based on EU directives are necessary.

The solution shall circumvent a real-life problem that

is caused by the low resolution of the meteorologi-

cal and air-quality models, something which becomes

problematic at microlocations in complex terrain.

The on-line forecasting model is aimed at pre-

dictions of the daily maximum ozone concentrations

one-day ahead of the target day. The daily maximum

value is, in our case, deﬁned as the maximum value

of the hourly average ozone concentrations obtained

between 1 and 24 hours on a particular day. The pre-

dictions of the model for the next day are to be made

at 24:00 hours on the day before the target day.

3 METHODOLOGY

Our goal is to develop an hybrid ozone-forecasting

model, composed of ﬁrst principles and empirical

models. Such a model allows us to use the advan-

tages of both and produce more accurate forecasts.

Two ﬁrst principles models are used in our study: one

for air-quality predictions and another to predict the

meteorological variables. Besides those, we use a

database with various historical meteorological and

air-quality values measured in the city of Koper for

the training of the empirical model.

Three sets of ozone-concentrationpredictions will

be developed for the selected location. Two ﬁrst prin-

ciples models are used in our study: one to predict air

quality (QualeAria) and the other for meteorological

forecasts (WRF model). Prediction model based only

on these two models is denoted by Model 1. Predic-

tions based on an empirical model, i.e., a GP model

that has been developed based on air-quality and me-

teorological measurements for the target day. This

model is highly accurate for the microlocation from

where the measurements have been sampled. How-

ever, it is unrealistic, because in reality, the meteoro-

logical regressors for the time of prediction can be

based on meteorological forecasts only. Neverthe-

less, the predictions of such a model are in our case

used for comparison with the other model’s accuracy,

and the model will be referred to as the idealistic GP

model and denoted by Model 2. Predictions based on

an hybrid model for each of the selected microloca-

tions, which will integrate all available information,

i.e., the history of air-quality and meteorological mea-

surements from that speciﬁc location, and air-quality

and meteorological forecasts from the ﬁrst principles

models available for that region. The aim of the hy-

brid model, denoted by Model 3, is to attain the pre-

diction quality of the idealistic GP model and at the

same time retain the transparency of the ﬁrst princi-

ples model.

3.1 The Air-quality Model—QualeAria

Air quality predictions for selected locations are

obtained with the QualeAria forecasting system.

QualeAria implements three-dimensional state-of-

the-art models to describe the emission, dispersion,

and transformation of pollutants in the atmosphere. It

is based on the Flexible Air quality Regional Model—

FARM, a 3D Eulerian model simulating the disper-

sion and chemical reactions of atmospheric pollutants

(Kukkonen et al., 2012). The model is operationally

run by the ARIANET and is coupled with the mete-

orological model RAMS, (AriaNet Srl. and ENEA,

2015). It is part of the MINNI Italian national mod-

elling system (Zanini et al., 2005) and is based on the

same meteorological and air-quality models.

The QualeAria system is currently conﬁgured on

two nested computational grids, the wider one cover-

ing Europe at a horizontalresolution of 48 km, and the

smaller one covering Italy and its near neighbourhood

at 12 km resolution. Slovenia is placed in the inner

Local Ozone Prediction with Hybrid Model

263

part of the second modelling domain, far enough from

the domain’s border so that the results for Slovene ter-

ritory are not heavily affected by the boundary condi-

tions. QualeAria produces air pollution forecasts for

Slovenia for up to two days in advance at 1 h time

resolution and also at 12 km spatial resolution. The

predictions of the main pollutants from this conﬁgu-

ration are validated in (Boˇznar et al., 2014) and are

available on-line on a daily basis on the KOoreg web-

site (MEIS d.o.o., 2015).

3.2 The Meteorological Model—WRF

Meteorological predictions for selected locations are

obtained with the Weather Research & Forecast—

WRF model (Skamarock et al., 2008). The WRF

model is a numerical weather prediction system that is

used for operational forecasting and for atmospheric

research. The WRF model was developed coopera-

tively by the US institutions (NCEP and NCAR), and

the meteorological research community. There are

two dynamics solvers in the WRF software frame-

work: ARW and NNM, where the ARW solver, pri-

marily developed and maintained by NCAR, is used

in this study.

ARW model, which runs permanently on daily ba-

sis at the MEIS company,calculate predictionson two

geographical domains. A larger domain (central Eu-

rope) is covered with 101 by 101 cells in a resolution

of 12 km per 3 hours and a smaller domain (Slovenia

with surroundings) covered with 76 by 76 cells in a

resolution of 4 km per 30 min. The horizon of pre-

diction is two days and three hours. The model is run

at 5:00 UTC. The simulation runs for three to four

hours, and it is run again at 17:00 UTC. The model

with a given conﬁguration running over the terrain of

Slovenia was validated in (Boˇznar et al., 2012).

3.3 The Gaussian-process Model

GP models are probabilistic, non-parametric models

based on the principles of Bayesian probability. GPs

actually provide a Bayesian interpretation to the ker-

nel methods (Rasmussen and Williams, 2006). This

means that with a GP model we do not try to approxi-

mate the modelled system by ﬁtting the parameters of

the selected basis functions, but rather we search for

the relationship among the measured data. The mod-

elling properties of GP models are reviewed in (Ras-

mussen and Williams, 2006), (Kocijan, 2016), (Shi

and Choi, 2011).

GP models can be used for regression, where

the task is to infer a mapping from a set of N D-

dimensional regression vectors represented by the re-

gression matrix X = [x

,...,x

]

to a vector of

output data y = [y

,...,y

] forming the data D =

{(x

)|i = 1,... ,N} = {(X,y)}. The outputs are

usually assumed to be noisy realisations of the under-

lying function f(x

). A GP model assumes that the

output is a realisation of a GP with a joint probabil-

ity density function p(y) = N (m,K), with the mean

m and covariance K being functions of the inputs x.

Usually, the mean function is deﬁned as 0, while the

covariance function or kernel K

= C(x

) deﬁnes

the characteristics of the process to be modelled, i.e.,

the stationarity, smoothness, etc. The value of the

covariance function C(x

) expresses the correla-

tion between the individual outputs f(x

) and f(x

)

with respect to the inputs x

and x

. The covari-

ance function can be any function that generates a

positive, semi-deﬁnite covariance matrix. Assuming

the stationary data is contaminated with white noise,

the most commonly used covariance function is the

composition of the square exponential (SE) covari-

ance function with ‘automatic relevance determina-

tion’ (ARD) hyperparameters (MacKay, 1998) and a

constant covariance function assuming white noise.

The ARD property means that hyperparameters indi-

cate the importance of individual inputs. Description

of this and further covariance functions suitable for

various applications can be found in, e.g., (Kocijan,

2016).

The common aim of regression is to predict the

output y

∗

in an unobserved test location x

∗

given the

training data, a known mean function and a known co-

variance functionC. The posterior predictivedistribu-

tion can be obtained by constructing the joint poste-

rior distribution using the Bayes’ rule. The computa-

tion of posterior distribution integrals can be difﬁcult

due to the intractable nature of the non-linear func-

tions. In the case of GP inference a frequently used

approximate solution to the problem of intractable in-

tegrals is to estimate the hyperparameters with the

maximising of the marginal likelihood from Bayes’

rule (Rasmussen and Williams, 2006).

A prediction of the GP model, in addition to the

mean value, also provides information about the con-

ﬁdence of the prediction using the prediction vari-

ance. Usually, the conﬁdence in the prediction is

interpreted with a 2σ interval, which corresponds to

about 95% of the conﬁdence interval. The conﬁdence

interval highlights the areas of the input space where

the prediction quality is poor, due to the lack of data

or noisy data, by indicating a wider conﬁdence inter-

val around the predicted mean.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

264

3.4 Validation Methodology

The proposed hybrid model (Model 3) will be com-

pared to (i) the existing QualeAria system (Model 1)

and (ii) the idealistic GP model trained with inputs

based on measurements only (Model 2).

Koper is an industrial and port town on the Adri-

atic coast with a Mediterranean climate, with its air

quality strongly inﬂuenced by the river Po and the in-

dustrial Friuli region in Italy.

Both empirical models, including the hybrid mod-

els, have been trained on measurements from a period

of one year and tested on measurements from the pe-

riod of the two subsequent years. This was done for

the purpose of demonstrating the performance of the

forecasting models for a longer period.

4 RESULTS AND DISCUSSION

4.1 Measurements

The meteorological and air-quality variables at the se-

lected location were measured and then elaborated on

an hourly basis. The measured data in this study were

acquired for all the available variables for a period of

three years (from the beginning of 2012 to the end of

2014). Available variables’ measurements are: ozone

concentration (O

), solid particles (PM10), nitrogen

oxides concentration (NO

), nitrogen dioxide concen-

tration (NO

), carbon monoxide (CO), air tempera-

ture (AirTemp), relative humidity (RelHum), global

solar radiation (GlSolRad), wind speed (WindSpd),

wind direction (WindDir), air pressure (Pressure) and

precipitation (Precip).

Besides the measurements, one-day ahead pre-

dictions of meteorological variables obtained from

the WRF modelling system, and air-quality variables

forecast by the QualeAria system for the same period

of time are available.

4.2 Regressor Selection

To gain a credible ozone forecast, the model needs in-

put data of all inﬂuential variables. However, with the

number of available variables and their lagged values,

the size of the regression vector or input features and,

consequently, of the model, increases noticeably. For

this reason it is necessary to select only the regres-

sors that add the most information to the prediction.

Various methods for the selection of the regressors or

features are available.

In this paper, we use the same regressors as

they were used in similar neural-network based study

(Gradiˇsar et al., 2015). The method used in this study

was introduced in (Kocijan et al., 2016) and is as fol-

lows. It combines various regressor-selection algo-

rithms, where the rankings achieved are ﬁrst averaged

for various locations in Slovenia and these are later

grouped to obtain the ﬁnal sequence of regressors,

ordered in terms of their importance. In the second

stage, we determine how many of regressors should

be used in order to produce the best prediction, us-

ing 10-fold cross-validation. Note that the models in

the second stage were GP models. Further note, that

the hybrid model uses one additional regressor: the

value of ozone from the QualeAria system for the tar-

get day (O3(k+ 1)). As prediction for NO

needed in

hybrid model is not available from QualeAria model,

is used instead which is a reasonable substi-

tute for NO

. In the case that there are no measure-

ments for some regressors, the training and prediction

are performed without that time interval. The ﬁrst 9

regressors from the ﬁnal selection give the best re-

sults on average on all tested locations and measures.

These are: O3(k), GlSolRad(k+ 1), AirTemp(k+ 1),

AirTemp(k), GlSolRad(k), RelHum(k+ 1), NOx(k+

1), Pressure(k+1) and Pressure(k). All listed regres-

sors have been used for the empirical as well as for the

hybrid model, but forecasts are used instead of mea-

surements when necessary according to the type of

model.

This procedure makes it possible to obtain a sin-

gle uniform regression vector for a larger area, in our

case the urban parts of Slovenia, and to avoid having

to select the regressors every time we include a new

location.

4.3 Prediction Quality

In this section we compare all three different mod-

els used for one-day-ahead predictions of 1h O

daily

maxima in the selected location. The predictions

are validated with the following performance mea-

sures, which are described in the Appendix: the root

mean square error (RMSE), the standardised mean-

squared error (SMSE), the mean standardised log loss

- MSLL, Pearson’s correlation coefﬁcient (PCC), the

mean fractional bias (MFB), and the factor of the

modelled values within a factor of two of the obser-

vations (FAC2).

Firstly, we analyse the prediction quality of the

QualeAria system. As described in subsection 3.1, its

spatial resolution is 12 km. Therefore, we can expect

that its predictions are not equally accurate in every

location. The resulting performance measures for the

observed location are listed in Table 1.

Next, we introduce the idealistic GP model. The

Local Ozone Prediction with Hybrid Model

265

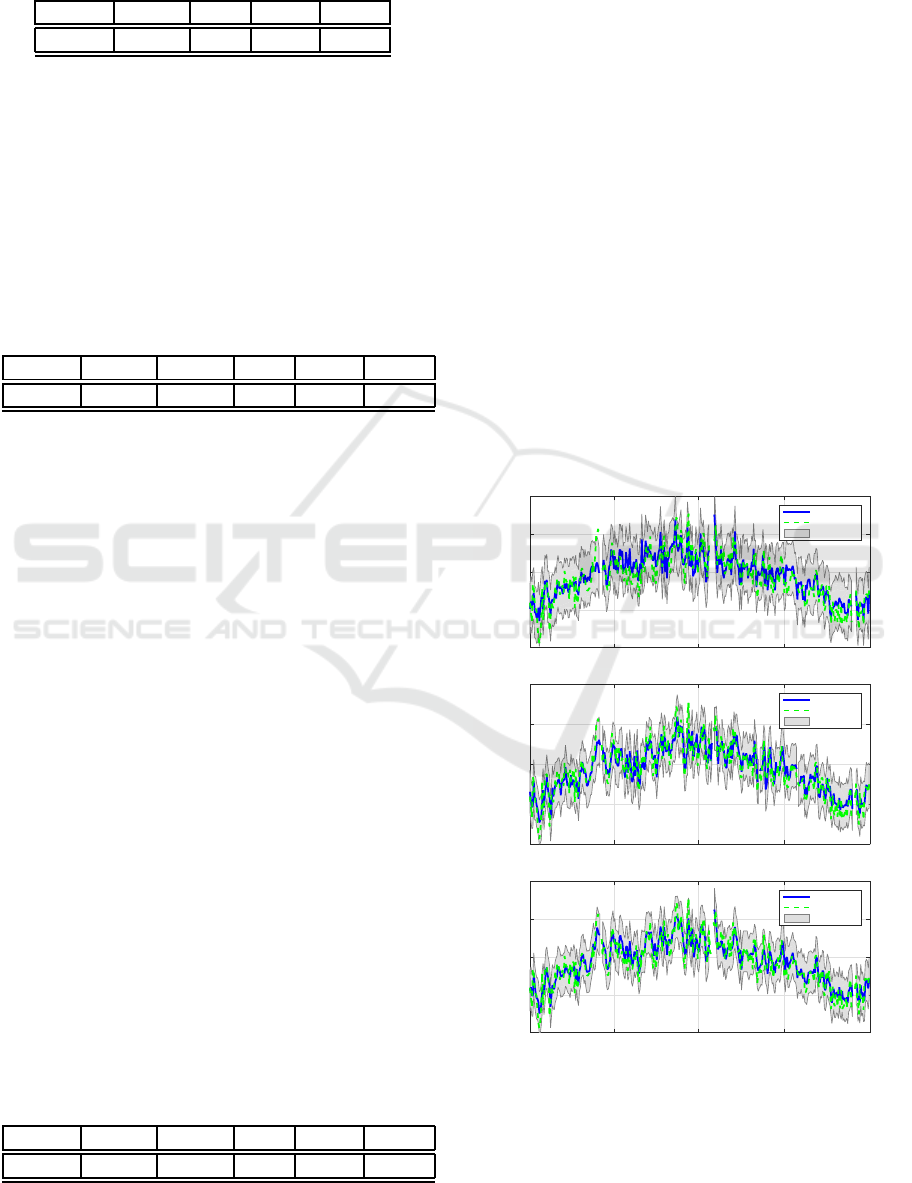
Table 1: Performance measures for predictions of daily

maximum O

concentrations: QualeAria predictions

(Model 1).

RMSE SMSE PCC MFB FAC2

16.40 0.26 0.86 0.033 0.987

regressors as selected in subsection 4.2 are used for

training and prediction of the ozone concentration

level. In this case we assume the ideal case, where

also the regressors corresponding to the time of pre-

diction (the target day) are taken from the database

of measurements as surrogates for a perfect forecast.

The evaluation of the model predictions is presented

in Table 2.

Table 2: Performance measures for predictions of daily

maximum O

concentrations: idealistic GP model using

measured data only (Model 2).

RMSE SMSE MSLL PCC MFB FAC2

13.06 0.17 -0.89 0.91 0.019 0.99

It can be seen from the table that the predictions

of the idealistic GP model are much better than those

from Table 1. Nevertheless, the idealistic model can-

not provide insights into the pollutant formation pro-

cesses.

Finally, we present the evaluation results for the

hybrid model (Model 3). The idea of the hybrid model

is to enhance the predictions from the ﬁrst principles

model with the empirical model. This can be seen

as the serial connection of the ﬁrst principles model

and the empirical model. This way, the addition of

the GP to the ﬁrst principles model compensates for

the model mismatch in microlocations due to resolu-

tion inaccuracies. The values of performance mea-

sures in this study exhibit slightly better results from

those presented in study (Gradiˇsar et al., 2015).

The hybrid model also uses predicted air-quality

regressors, including the ozone concentration, pro-

vided by the QualeAria forecast system. Conse-

quently, the regressors are combined from the his-

torical measured data of air-quality and meteorolog-

ical variables, from predicted meteorological regres-

sors obtained from the WRF model, and predicted air-

quality regressors for O

and NO

from the QualeAria

model for the target day.

The evaluation of the hybrid model predictions is

given in Table 3 and conﬁrms the improvement in the

Table 3: Performance measures for predictions of daily

max. concentrations: hybrid model predictions (Model 3).

RMSE SMSE MSLL PCC MFB FAC2

12.67 0.16 -0.92 0.92 0.026 0.99

quality of the predictions.

The results show that in our case the ﬁrst prin-

ciples air-quality models can be upgraded and their

results enhanced with a properly trained empirical

model. It is clear also that the predictions of the hy-

brid model are better than those of the idealistic GP

model, as it has additional information about ozone

prediction from ﬁrst principles air-quality model.

It is important to note that any suitable ﬁrst prin-

ciples and any properly trained empirical nonlinear

model can be used to pursue the proposed modelling

and forecasting method for complex terrain. The se-

lection at hand was conditioned by the availability of

the data and need to evaluate the prediction using GP

models.

Next, a visual comparison of the models’ predic-

tions, employing time responses and scatter plots, will

be given for the considered microlocation. In Figure

1, time-series plots of the measured and predicted val-

ues for one year (2014), out of two years that are used

for validation, are shown. It can be observed that the

predictions by the QualeAria forecasting system are

not up to the predictions of the hybrid model.

01-Jan-2014 01-Apr-2014 01-Jul-2014 01-Oct-2014 01-Jan-2015

Ozone [µg/m

]

100

150

200

Model 1: QualeAria

prediction (µ )

measurement

µ ± 2σ

01-Jan-2014 01-Apr-2014 01-Jul-2014 01-Oct-2014 01-Jan-2015

Ozone [µg/m

]

100

150

200

Model 2: GP model (measurements)

prediction (µ )

measurement

µ ± 2σ

01-Jan-2014 01-Apr-2014 01-Jul-2014 01-Oct-2014 01-Jan-2015

Ozone [µg/m

]

100

150

200

Model 3: Hybrid model

prediction (µ )

measurement

µ ± 2σ

Figure 1: Time-series plot of predictions for daily max-

imum ozone concentrations for Koper for year 2014:

QualeAria predictions (Model 1), GP using measured data

(Model 2) and hybrid model (Model 3).

The prediction values are shown also in scatter

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

266

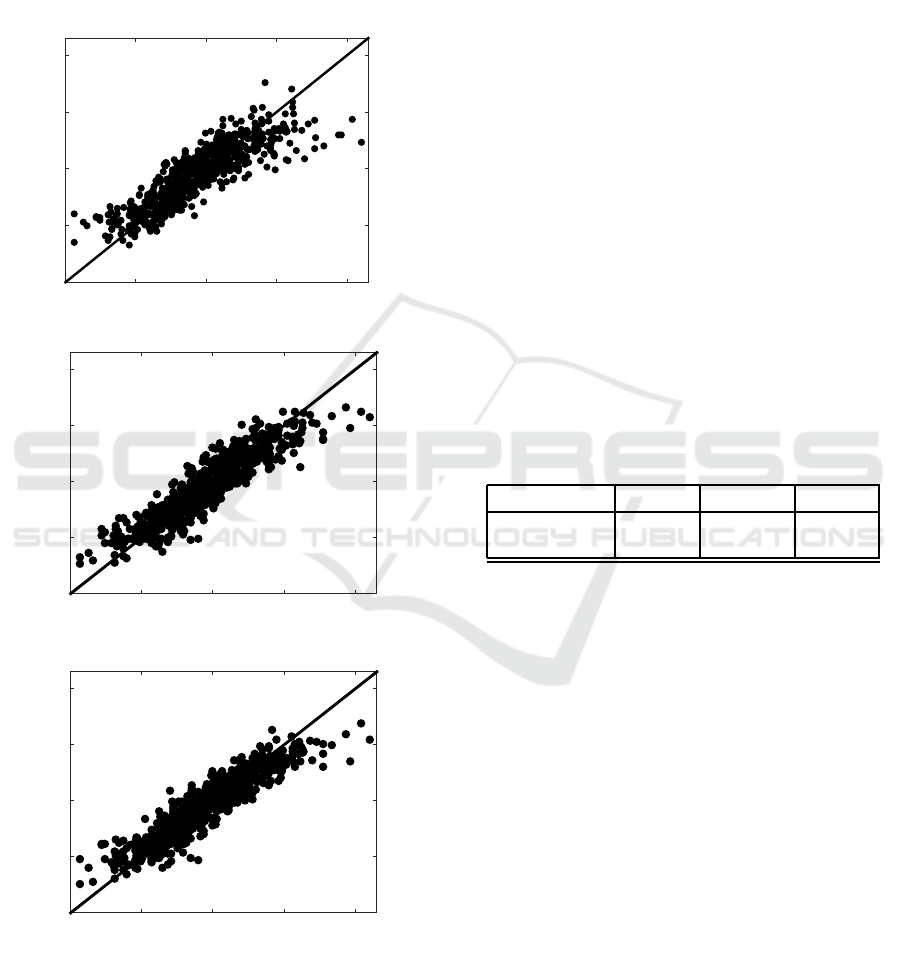
plots in Figure 2. The ﬁgures compare the predicted

and measured values. It can be seen that the predic-

tion quality for the location of interest improves when

GP models are used that use the information gained

from measurements at the location. It can be seen that

all developed models don’t provide good predictions

for higher values of ozone.

Measurements [µ g/m

]

0 50 100 150 200

Predictions [µg/m

]

100

150

200

Model 1: QualeAria

Measurements [µg/m

]

0 50 100 150 200

Predictions [µg/m

]

100

150

200

Model 2: GP model (measurements)

Measurements [µg/m

]

0 50 100 150 200

Predictions [µg/m

]

100

150

200

Model 3: Hybrid model

Figure 2: Predicted values versus observation values for

daily maximum ozone concentrations for Koper: QualeAria

predictions (Model 1), GP using measured data (Model 2),

hybrid model (Model 3).

The main purpose of the ozone-concentration

forecasting is to predict when concentration values

violate the prescribed thresholds. The European

Union’s Air Quality Directive sets four standards (Eu-

ropean Parliament and Council of the EU, 2010) to re-

duce air pollution by ozone and its impacts on health:

(i) information threshold: 1-hour average ozone con-

centration of 180 µg/m

, (ii) alert threshold: 1-hour

average ozone concentration of 240 µg/m

, (iii) long-

term objective: the maximum daily 8-hour mean con-

centration of ozone should not exceed 120 µg/m

, (iv)

target value: long-term objective (120 µg/m

) should

not be exceeded on more than 25 days per year, aver-

aged over three years.

We have analysed how successful our prediction

models would be when used to alert about cases of

1-hour ozone concentration. It never occurs that the

alert threshold (240 µg/m

) is violated in the observed

years. In Table 4, the number of information thresh-

old violations (180 µg/m

) is given, together with

the number of violations of additional—lowered—

informative threshold (140 µg/ m

). This threshold is

added in order to show the prediction capabilities of

our models.

In Table 4, all violations detected in 2013–2014

are listed, i.e., actual (correctly/failed forecasts).

Table 4: No. of threshold violations (Actual alarms/Correct

forecasts/False alarms).

Thr. [µg/m

] QA GP Hybrid

≥ 140 52/11/9 52/30/10 52/26/7

≥ 180 5/0/0 5/0/0 5/0/0

From the presented results it is clear that the de-

veloped hybrid model, based on local measured data

together with the available predictive meteorological

and air-quality values, predicts ozone concentrations

better than the currently available QualeAria system.

However, future work is needed in order to develop

methodologies, that would provide better predictions

for higher values of the ozone concentrations.

5 CONCLUSIONS

An application of an hybrid model for improving

ozone forecasting in the city of Koper, Slovenia is de-

scribed in the paper. Forecasting models have been

developed and validated for a period of three years.

The resulting model for this city is the com-

bination of the QueleAria air-quality model, the

WRF meteorological model, and empirical GP model.

QualeAria and WRF models do not provide enough

accurate ozone predictions for the purpose of issuing

alerts for this microlocation, because its horizontal

Local Ozone Prediction with Hybrid Model

267

resolution is too low and it misses a fair amount of

details. The integration of ﬁrst principles and empir-

ical model enables the combined model to maintain

the scientiﬁc insights into pollutant formation pro-

cesses and prognostic abilities for atypical scenarios,

but have an improved forecasting ability for the mi-

crolocation.

The analysis shows that the hybrid model under

realistic conditions provides improved forecasting re-

sults than used ﬁrst-principles models. An effective

methodology for the development of a model with an

increased reliability of ozone forecasting that can be

used for alerting the inhabitants according to regula-

tions has been demonstrated.

Work on improved alerts based on on-line air-

quality model will be continued for obtaining better

air-quality forecasting models using other strategies

on prediction.

ACKNOWLEDGEMENTS

This work was supported by the Slovenian Research

Agency with Grant Development and Implementa-

tion of a Method for On-Line Modelling and Fore-

casting of Air Pollution, L2-5475 and Grant Systems

and Control, P2-0001. The Slovenian Environment

Agency provided part of the data.

REFERENCES

Al-Alawi, S. M., Abdul-Wahab, S. A., and Bakheit, C. S.

(2008). Combining principal component regression

and artiﬁcial neural-networks for more accurate pre-

dictions of ground-level ozone. Environ Modell Softw,

23:396–403.

Alvarez, M. A., Luengo, D., and Lawrence, N. D. (2009).

Latent force models. In 12th Int. Conf. on Artiﬁcial

Intelligence and Statistics, volume 5, pages 5–9.

AriaNet Srl. and ENEA (2015). Qualearia - forecast system

for the air quality in italy and europe. http://www.aria-

net.eu/QualeAria.

Boˇznar, M. Z., Mlakar, P., and Graˇsiˇc, B. (2012). Short-

term ﬁne resolution WRF forecast data validation in

complex terrain in Slovenia. International journal of

environment and pollution, 50(1-4):12–21.

Boˇznar, M. Z., Mlakar, P., Graˇsiˇc, B., Calori, G., D’Allura,

A., and Finardi, S. (2014). Operational background

air pollution prediction over Slovenia by QualeAria

modelling system - validation. International journal

of environment and pollution, 54(2-4):175–183.

Chen, N., Qian, Z., Meng, X., and Nabney, I. (2013).

Short-term wind power forecasting using Gaussian

processes. In International joint conference on Ar-

tiﬁcial Intelligence IJCAI’13, pages 1771–1777.

European Parliament and Council of the EU (2010). Direc-

tive 2008/50/EC on ambient air quality and cleaner

air for Europe. Number L 152. Ofﬁcial Journal of the

European Union, Brussels.

Goyal, P. and Kumar, A. (2012). Air quality forecasting

throught integrated model using air dispersion model

and neural network. In Latest advances in systems sci-

ence and computational intelligence, pages 219–224.

WSEAS.

Gradiˇsar, D., Graˇsiˇc, B., Boˇznar, M., Mlakar, P., and Koci-

jan, J. (2015). Improved local-ozone forecasting using

the integrated model. Technical Report DP - 11958,

Jozef Stefan Institute, Ljubljana.

Im, U., Bianconi, R., Solazzo, E., Kioutsioukis, I., Badia,

A., Balzarini, A., , Bar, R., Bellasio, R., Brunner,

D., Chemel, C., Curci, G., Flemming, J., Forkel, R.,

Giordano, L., Jimnez-Guerrero, P., Hirtl, M., Hodzic,

A., Honzak, L., Jorba, O., Knote, C., Kuenen, J. J.,

Makar, P. A., Manders-Groot, A., Neal, L., Prez,

J. L., Pirovano, G., Pouliot, G., Jose, R. S., Savage,

N., Schroder, W., Sokhi, R. S., Syrakov, D., Torian,

A., Tuccella, P., Werhahn, J., Wolke, R., Yahya, K.,

Zabkar, R., Zhang, Y., Zhang, J., Hogrefe, C., and

Galmarini, S. (2015). Evaluation of operational on-

line-coupled regional air quality models over Europe

and North America in the context of AQMEII phase

2. Part I: Ozone. Atmospheric Environment, 115:404–

420.

Kocijan, J. (2016). Modelling and Control of Dynamic Sys-

tems Using Gaussian Process Models. Springer Inter-

national Publishing, Cham.

Kocijan, J., Gradiˇsar, D., Boˇznar, M. Z., Graˇsiˇc, B., and

Mlakar, P. (2016). On-line algorithm for ground-level

ozone prediction with a mobile station. Atmospheric

Environment, 131:326–333.

Kukkonen, J., Olsson, T., Schultz, D. M., Baklanov, A.,

Klein, T., Miranda, A. I., Monteiro, A., Hirtl, M.,

Tarvainen, V., Boy, M., Peuch, V.-H., Poupkou, A.,

Kioutsioukis, I., Finardi, S., Soﬁev, M., Sokhi, R.,

Lehtinen, K. E. J., Karatzas, K., San Jos´e, R., Astitha,

M., Kallos, G., Schaap, M., Reimer, E., Jakobs,

H., and Eben, K. (2012). A review of operational,

regional-scale, chemical weather forecasting mod-

els in Europe. Atmospheric Chemistry and Physics,

12(1):1–87.

MacKay, D. J. C. (1998). Introduction to Gaussian pro-

cesses. NATO ASI Series, 168:133–166.

MEIS d.o.o. (2015). KOoreg regional air pollution control

prognostic and diagnostic modelling system.

Mlakar, P. and Boˇznar, M. Z. (2011). Advanced air pollu-

tion, chapter Artiﬁcial neural networks: a useful tool

in air pollution and meteorological modelling, pages

495–508. InTech, Rijeka.

Pelliccioni, A. and Tirabassi, T. (2006). Air dispersion

model and neural network: A new perspective for inte-

grated models in the simulation of complex situations.

Environmental Modelling & Software, 21(4):539–546.

Petelin, D., Grancharova, A., and Kocijan, J. (2013). Evolv-

ing Gaussian process models for the prediction of

ozone concentration in the air. Simulation Modelling

Practice and Theory, 33(1):68–80.

SIMULTECH 2016 - 6th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

268

Rasmussen, C. E. and Williams, C. K. I. (2006). Gaussian

Processes for Machine Learning. MIT Press, Cam-

bridge, MA.

Schmitt, K., Madsen, J., Anitescu, M., and Negrut, D.

(2008). A Gaussian process based approach for han-

dling uncertainty in vehicle dynamics simulation. In

International Mechanical Engineering Congress and

Exposition (IMECE), volume 11, pages 617–628.

Shi, J. Q. and Choi, T. (2011). Gaussian process regression

analysis for functional data. Chapman and Hall/CRC,

Taylor & Francis group, Boca Raton, FL.

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O.,

Barker, M., Duda, K. G., Huang, X. Y., Wang, W., and

Powers, J. G. (2008). A description of the advanced

research WRF version 3. Technical report, National

Center for Atmospheric Research.

von Stosch, M., Oliveira, R., Peres, J., and de Azevedo, S. F.

(2014). Hybrid semi-parametric modeling in process

systems engineering: Past, present and future. Com-

puters & Chemical Engineering, 60:86 – 101.

Zabkar, R., Honzak, L., Skok, G., Forkel, R., Rakovec, J.,

Ceglar, A., and

Zagar, N. (2015). Evaluation of the

high resolution wrf-chem (v3.4.1) air quality forecast

and its comparison with statistical ozone predictions.

Geoscientiﬁc Model Development, 8(7):2119–2137.

Zanini, G., Pignatelli, T., Monforti, F., Vialetto, G., Vi-

tali, L., Brusasca, G., Calori, G., Finardi, S., Radice,

P., and Silibello, C. (December, 2005). The MINNI

project: An integrated assessment modeling system

for policy making. In Proceedings of MODSIM05,

International Congress on Modelling and Simulation,

Melbourne, Australia.

Zhang, Y., Bocquet, M., Mallet, V., Seigneur, C., and Bak-

lanov, A. (2012). Real-time air quality forecasting,

part i: History, techniques, and current status. Atmo-

spheric Environment, 60:632 – 655.

APPENDIX

The following are performance measures used in the

study.

• The root-mean-square error - RMSE,

RMSE =

∑

i=1

(E(ˆy

) − y

)

, (1)

where y

and ˆy

are the observation and the predic-

tion in the i-th step, respectively, E(·) denotes the

expectation, i.e., the mean value, of the random

variable, and N is the number of used observa-

tions.

• The standardised mean-squared error - SMSE

(Rasmussen and Williams, 2006):

SMSE =

∑

i=1

(E(ˆy

) − y

)

, (2)

where σ

is the variance of the observations.

• The mean standardised log loss - MSLL (Ras-

mussen and Williams, 2006):

MSLL =

∑

i=1



ln(σ

) +

(E(ˆy

) − y

)



−

∑

i=1

ln(σ

) +

− E(y))

(3)

where σ

is the prediction variance in the i-th step,

and E(y) is the expectation, i.e., the mean value,

of the vector of the observations.

• The Pearson’s correlation coefﬁcient - PCC:

PCC =

∑

i=1

(E(ˆy

) − E(

y))(y

− E(y))

Nσ

ˆy

, (4)

where E(

y) is the expectation, i.e., the mean

value, of the vector of predictions, and σ

,σ

ˆy

are

the standard deviations of the observationsand the

predictions, respectively.

• The mean fractional bias - MFB:

MFB =

∑

i=1

E(ˆy

) − y

(E(ˆy

) + y

)

. (5)

• The factor of the modelled values within a factor

of two of the observations - FAC2:

FAC2 =

∑

i=1

with

(

1 for 0.5 ≤ |

E( ˆy

)

| ≤ 2,

0 else.

(6)

RMSE and SMSE are frequently used measures for

the accuracy of the predictions’ mean values, which

are 0 in the case of perfect model. SMSE is the

standardised measure with values between 0 and 1.

MSLL is a standardised measure suited to predictions

in the form of random variables. It weights the pre-

diction error more heavily when it is accompanied by

a smaller prediction variance. The MSLL is approx-

imately zero for the simple models and negative for

the better ones. PCC is a measure of associativity and

is not sensitive to bias. Its value is between -1 and

+1, with ideally linearly correlated values resulting in

a value 1. MFB is the measure that bounds the max-

imum bias and gives additional weight to underesti-

mations and less weight to overestimations. Its value

is between -2 and +2, with the value 0 in the case of

a perfect model. FAC2 indicates the fraction of the

data that satisﬁes the condition from Equation (6). Its

value is between 0 and 1, with the perfect model re-

sulting in a value of 1.

Local Ozone Prediction with Hybrid Model

269