
Dynamic Model-based Control of Redundantly Actuated,
Non-holonomnic, Omnidirectional Vehicles
Christoph St¨oger, Andreas M¨uller and Hubert Gattringer
Institute of Robotics, Johannes Kepler University Linz, Altenberger Straße 69, 4040 Linz, Austria
Keywords:
Dynamic Modeling and Control, Redundant Actuation, Pseudo-omnidirectional, Singularities.
Abstract:
Vehicles with several centered orientable wheels have one of the highest maneuverability and are hence an
excellent choice for transportation tasks in narrow environments. However, they are non-holonomic, in general
redundantly actuated, and additionally suffer from configuration singularities, which makes their modeling and
control challenging. Existing control approaches only consider the vehicle kinematics whereas the required
torques are commonly controlled by classical PD motor controllers. However, this leads to considerable
tracking errors and a violation of the constraints especially during acceleration phases. Moreover, actuator
counteractions and an undefined torque distribution can be observed. This paper introduces a model-based
control concept that overcomes these issues. It resolves counteractions and distributes torques according to
physical limitations which significantly reduces slippage and the energy consumption and further reduces the
tracking error. To this end, an inverse dynamics solution of a redundantly parametrized model is used. The
method is robust to configuration singularities. This is confirmed by experimental results.
1 INTRODUCTION
Mobile platforms offer a large workspace for appli-
cations in service robotics as well as manufacturing.
Their main application is, especially in industry, still
the transportation of goods –a seemingly simple task
that can, however, become very complex given the
demand from industry for compact and cost-efficient
shop floor solutions. A consequence is that a pre-
cise locomotion with a mobile base offering the max-
imum degree of maneuverability δ
M
(Campion et al.,
1996), i.e. δ
M
= 3, is ever more relevant. Vehicles
with δ
M
= 3 are also called omnidirectional since they
are able to move in each direction and independently
change their orientation. Holonomic omnidirectional
vehicles, equipped with n ≥ 3 Mecanum or Swedish
wheels, are the most popular type of this class. They
need a small number of actuators, since they do not
need to steer, and are easy to control. However,
Mecanum wheels possess poor load capacities com-
pared to standard wheels, they introduce vibrations
to the actuators and chassis, and lead to much higher
slippage. Platforms with n ≥ 2 centered orientable
standard wheels overcome these problems. Center
orientable wheels are wheels which can be steered
about a vertical axis passing through the center of the
wheel. Such platforms are omnidirectional as well but
non-holonomic,i.e. they can independently attain any
position and orientation but may have to reorient their
wheels during the navigation. For this reason they are
often called pseudo-omnidirectional.
The number of driven wheels depends on the
transporter size, i.e. the payload, and is often higher
than 2. The driving motors are thereby acting in par-
allel which means that the vehicle is not only non-
holonomic but also redundantly actuated. There are
several publications about the higher-level kinematic
control of such vehicles (Giordano et al., 2009; Of-
tadeh et al., 2013; St¨oger et al., 2015), which results in
a feasible motion of the wheels and moves the vehicle
to a destination. However, there is hardly any lower-
level dynamic control scheme for actually achieving
this motion reported in the literature. It is mostly in-
dicated that a simple PD controller is used. Such a
control neither takes the dynamic of the vehicle into
account, nor the redundancy of the actuation. Consid-
erable errors in dynamic phases and unnecessary high
torques due to the actuator counteraction, which again
lead to slip, are the consequence.
Common approaches for controlling platforms
with δ
M
< 3 can be divided into two classes: 1) ro-
bust control and 2) model-based control strategies. In
the first class sliding mode controllers are widely used
(Yang and Kim, 1999). One and the same controller
Stöger, C., Müller, A. and Gattringer, H.
Dynamic Model-based Control of Redundantly Actuated, Non-holonomnic, Omnidirectional Vehicles.
DOI: 10.5220/0005980200690078
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 69-78
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
69

works for different loads quite well but the robust-
ness has to be paid by a high switching frequency of
the input torques. Thereby, the second class is more
promising for us. A model-based inverse dynam-
ics controller reduce the tracking error significantly
and can easily be adapted if the load of the vehicle
changes. So far there is hardly any dynamic con-
trol method for redundantly actuated platforms with
δ
M
= 3. In (Lee and Li, 2015) the authors use the in-
verse dynamics solution extended by a sliding mode
controller but have not addressed the redundancy res-
olution or counteraction avoidance. Methods for the
control of redundantly actuated systems can be found
in the field of parallel mechanisms (M¨uller and Huf-
nagel, 2012) and are adapted in this paper to the needs
of mobile robots. Our aim is to use only a minimal de-
mand of torque and to distribute this demand among
the actuators by considering their limitations as well
as differences in frictional conditions, e.g. due to an
unbalanced load, in order to increase the uptime of the
vehicle and reduce slippage in the resulting motion.
The result is a novel concept for the low-level control
of non-holonomic,omnidirectional vehicles equipped
with an arbitrary number n of wheels. The control
concept can be seen as building block which is inde-
pendent from the higher-level control scheme used for
motion planning.
Although there is a large number of dynamic mod-
els for other platform types, e.g. differential drives
(Fukao et al., 2000) or car like systems (De Luca
et al., 1998), only a few models are available for
omnidirectional, non-holonomic vehicles. Moreover,
those models either do not consider constraint forces
(Lee and Li, 2015) or neglect the wheels (Ploeg et al.,
2002) which results in a considerable model error.
However, such models can still be found in the lit-
erature since they bypass the resolution of the singu-
lar rolling constraints. Therefore, a novel dynamic
model is presented in this paper. It is redundantly
parametrized, which is especially also valid in sin-
gular configurations, and includes all relevant effects.
Constraining forces are numerically eliminated by a
null space projection method (M¨uller and Hufnagel,
2012). The null space projector is computed by a
novel semi-analytic orthogonalization method which
takes the structure of the constraints into account and
is computationally efficient. The latter is especially in
the context of the control crucial.
The paper is structured as follows. In Section
2 the description of the platforms kinematics is pre-
sented. The configuration variables are described and
the rolling constraints are formulated. In Section 3
the redundant parametrized dynamic model is derived
whereby an overview about the modeled effects in-
cluding friction is given and the constraint forces are
eliminated. In Section 4 the inverse dynamics is com-
puted and the torque distribution method presented.
Subsequently, the control concept is formulated and
its asymptotic stabilization is proofed. Experiments
which validate the theory are presented in Section 5.
The paper closes with a summary in Section 6 and
some remarks for future research.
2 PLATFORM KINEMATICS
The variables that parametrize the current configura-
tion of the platform, see Figure 1, can be divided into
two sets (Ostrowski and Burdick, 1996). The first set
describe the vehicle’s posture, i.e. displacement of
the chassis-fixed frame F
C
= {O
C
,
C
x
x
x,
C
y
y
y} relative to
an inertial frame F
I
= {O
I
,
I
x
x
x,
I
y
y
y}.
Assumption 1. The vehicles motion is assumed to be
restricted to the horizontal plane.
With Assumption 1 the pose can be parametrized us-
ing q
q
q
C
= (x,y,γ)
T
∈ SE(2). The vector (x,y) ∈ R
2
describes the reference point O
C
in the frame F
I
and
γ ∈ S
1
is the angle enclosed by
I
x
x
x and
C
x
x
x.
I
x
x
x
I
y
y
y
C
x
x
x
C
y
y
y
Wi
x
x
x
Wi
y
y
y
O
I
O
C
O
Wi
chassis
ϕ
si
ϕ
ri
x
y
γ
l
i
ϕ
0i
Figure 1: Non-holonomic, omnidirectional vehicle with n =
4 centered orientable wheels.
The second set of variables are called shape or inter-
nal variables. They describe the configuration of the
locomotion system and are given by n roll angles ϕ
ri
and n steer angles ϕ
si
, with i ∈ {1, .. .n}. They are
summarized in
q
q
q
ϕ
= (ϕ
r1
,... ϕ
rn
,ϕ
s1
,... ϕ
sn
)
T
∈ T
2n
. (1)
Here T
2n
is the 2n dimensional torus. For later pur-
pose additional frames F
Wi
= {O
Wi
,
Wi
x
x
x,
Wi
y
y
y} are at-
tached at each drive unit.
The configuration of the mobile platform is thus de-
scribed by the vector of generalized coordinates
q
q
q = (q
q
q
T
C
,q
q
q
T
ϕ
)
T
∈ Q = SE(2) × T
2n
. (2)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
70

Although ideal rolling is a simplified assumption
we can use it within the control in order to minimize
the resultant slippage and counteraction. Ideal rolling
means that the longitudinal velocity (
Wi
x
x
x direction) of
a certain wheel i is consistent with its rolling speed,
which requires
cos(ϕ
si
+ γ)˙x+ sin(ϕ
si
+ γ)˙y+ l
i
sin(ϕ
si
− ϕ
0i
)
˙
γ− r
˙
ϕ
ri
= 0, (3)
and that the lateral velocity (
Wi
y
y
y direction) is zero, i.e.
−sin(ϕ
si
+γ) ˙x+cos(ϕ
si
+γ) ˙y+l
i
cos(ϕ
si
−ϕ
0i
)
˙
γ = 0.
(4)
The polar coordinates l
i
and ϕ
0i
describe the position
of the ith wheel O
Wi
observed from F
C
, see Figure 1.
The following properties directly follow from the
rolling constraints, see Equation (3) and (4):
Property 1. The constraints can be written in Pfaf-
fian form, i.e. linear in velocities, as J
J
J(q
q
q)
˙
q
q
q = 0.
Property 2. The n steering velocities
˙
ϕ
si
are uncon-
strained. Hence, the columns of J
J
J which correspond
to them are zero.
The rank m of J
J
J ∈ R
2n,3+2n
determines the number
of independent constraints. Hence, the number of in-
dependent velocities respecting the constraints, also
referred to as generalized velocities, is
δ
v
= 3 + 2n− m. (5)
Another interesting property is that the n lateral con-
straints (4) only restrict the chassis twist ( ˙x, ˙y,
˙
γ). By
considering the corresponding rows in J
J
J, one can eas-
ily proof the following property.
Property 3. The number and set of independent lat-
eral constraints depends on the steering angles and is
between 1 and 3.
In the case of n > 2 wheels the minimum number of
generalized velocities is δ
v
= 3 + 2n − (n + 3) = n.
Referring to Property 2, they are given by the uncon-
strained steering angles. In this case, the vehicle can
not drive but only steer the wheels. Thus, vehicles
with n > 2 wheels have to drive in regions of reduced
rank. In this regions, only one particular twist, namely
the rotation about the instantaneous center of rotation,
is possible. Some wheel setups, especially for n = 2
wheels, permit the axial alignment of all wheel axes.
In this special configuration, the number m of inde-
pendent constraints further reduces by 1 since all lat-
eral constraints are equal. Such configurations allow
the vehicle to rotate about an arbitrary point on the
line specified by the wheel axes. This is summarized
by the following property.
Property 4. The constraint matrix J
J
J is either perma-
nent singular or can become singular. The number of
generalized velocities is thus δ
v
∈ {n+ 1,n + 2}.
3 DYNAMIC MODELING
3.1 Redundantly Parametrized
Equations of Motion
The equations of motion are derived using the Projec-
tion Equations
N
∑
b=1
h
∂
R
v
v
v
c,b
∂
˙
q
q
q
∂
R
ω
ω
ω
b
∂
˙
q
q
q
i
T
R
˙
p
p
p
c,b
+
R
˜
ω
ω
ω
IR R
p
p
p
c,b
−
R
f
f
f
c,b
R
˙
L
L
L
b
+
R
˜
ω
ω
ω
IR R
L
L
L
b
−
R
τ
τ
τ
b
= 0.
(6)
Projection Equations are based on the Newton-
Euler equations for body b which are evaluated in a
reference frame F
R
, and are projected onto the direc-
tion of the generalized coordinates q
q
q. Here
R
p
p
p
c,b
=
m
b
R
v
v
v
c,b
is the linear momentum of the center of grav-
ity (c) of body b.
R
L
L
L
b
=
R
Θ
b
R
ω
ω
ω
b
is the angular mo-
mentum, and
R
v
v
v
c,b
and
R
ω
ω
ω
b
are corresponding trans-
lational and angular velocities.
˜
ω
ω
ω is a skew symmet-
ric matrix representing the cross product
˜
ω
ω
ωp
p
p = ω
ω
ω× p
p
p.
R
f
f
f
c,b
and
R
τ
τ
τ
b
are total forces and torques acting on
the center of gravity / body. The Equations (6) are
used to model inertia effects, the influence of traction
and friction forces as well as motor torques.
Inertia is considered for N = 2n + 1 bodies:
• the chassis (c)
and n drive units including:
• n steer motors (si), which are mounted on the
chassis and are rigidly coupled with a drive unit
• n drive motors (ri), which are in turn mounted
on the drive unit and are rigidly coupled with the
wheel.
The inertia of the chassis is, in general, significantly
higher than the inertia of the drive unit. However,
since especially the orientation of the drive unit has
a much higher acceleration they are relevant too. The
velocities of the chassis are
c
v
v
v
c,c
=
˙xcos(γ)+ ˙ysin(γ) − ˙xsin(γ) + ˙ycos(γ) 0
T
c
ω
ω
ω
c
=
0 0
˙
γ
T
and the velocities of the steer axes and the rolling
wheels are
Wi
v
v
v
c,si
=
Wi
v
v
v
c,ri
=
˙xcos(γ+ ϕ
si
) + ˙ysin(γ+ ϕ
si
) + l
i
sin(ϕ
si
− ϕ
0i
)
˙
γ
− ˙xsin(γ+ ϕ
si
) + ˙ycos(γ+ ϕ
si
) + l
i
cos(ϕ
si
− ϕ
0i
)
˙
γ
0
Wi
ω
ω
ω
si
=
0 0
˙
γ+
˙
ϕ
si
T
Wi
ω
ω
ω
ri
=
0
˙
ϕ
ri
˙
γ+
˙
ϕ
si
T
,
Dynamic Model-based Control of Redundantly Actuated, Non-holonomnic, Omnidirectional Vehicles
71

all vectors are expressed in F
Wi
(Figure 1). It is as-
sumed that the center of gravity of the drive unit co-
incides with the steering axis O
Wi
.
There are two kinds of friction sources. The first
kind is bearing friction. It is commonly modeled as
a viscose and coulomb friction using a static model
(Bona and Indri, 2005). The model is computationally
inexpensive and the parameters can be easily identi-
fied since the model is linear w.r.t. the parameters.
The second kind of friction source is the tire/soil con-
tact. Since ideal rolling is assumed the generalized,
i.e. projected, traction forces Q
Q
Q
t
are imposed by the
constraints (3), (4):
Q
Q
Q
t
= J
J
J
T
λ
λ
λ, (7)
where λ
λ
λ ∈ R
2n
are the corresponding Langrange mul-
tipliers. The ground contact model must also take the
rolling resistance into account. The rolling resistance
is caused by elastic deformation of tire and soil, and
can again be modeled (within a certain velocity range)
by a Coulomb and viscous friction model (Hall and
Moreland, 2001). The applied driving (r) and steering
(s) torques are given by
Wi
τ
τ
τ
si
=
0 0 1
T
(τ
si
− µ
sci
sign(
˙
ϕ
si
) − µ
svi
˙
ϕ
si
)
Wi
τ
τ
τ
ri
=
0 1 0
T
(τ
ri
− µ
rci
sign(
˙
ϕ
ri
) − µ
rvi
˙
ϕ
ri
),
where µ are friction coefficients for the Coulomb (c)
and viscous (v) friction, τ
si
is the steering torque and
τ
ri
the rolling torque, respectively. The discontinuous
sign(x) function leads to chattering about zero veloc-
ity. In order to avoid that, this function is replaced in
the control law by the smooth tanh(x/ε) function. The
parameter ε is used to determine the region where the
force is reduced due to low speeds. The value of ε de-
pends on the application. In the experiment it was set
to 0.01rad/s, which corresponds to a driving speed of
≈ 1mm/s for the considered system.
The dynamics of the non-holonomic, omnidirec-
tional vehicle can be expressed by the system of dif-
ferential algebraic equations
M
M
M(q
q
q)
¨
q
q
q+C
C
C(q
q
q,
˙
q
q
q)
˙
q
q
q+ f
f
f(
˙
q
q
q) = B
B
B(q
q
q)u
u
u+J
J
J(q
q
q)
T
λ
λ
λ (8a)
J
J
J(q
q
q)
˙
q
q
q = 0. (8b)
Here M
M
M ∈ R
2n+3,2n+3
is the generalized inertia ma-
trix, C
C
C
˙
q
q
q ∈ R
2n+3
includes Coriolis and centrifugal
forces, f
f
f ∈ R
2n+3
Coulomb and viscous friction, u
u
u =
τ
r1
,... τ
rn
,τ
s1
,... τ
sn
∈ R
2n
, and B
B
B ∈ R
2n+3,2n
are
the input torques and matrix, and J
J
J
T
λ
λ
λ the generalized
constraining forces acting on the system.
Assumption 2. It is assumed that each wheel is fully
actuated, i.e. each wheel has a steering and driving
motor.
Then, the input matrix has the following structure
B
B
B =
B
B
B
r
0
n+3,n
0
n,n+3
I
n,n
(9)
where 0
i, j
∈ R
i, j
is a zero matrix, I
n,n
∈ R
n,n
a identity
matrix and
B
B
B
r
=
0
3,n
I
n,n
. (10)
The dimensions slightly change for vehicles where
this is not the case but the method is still valid.
3.2 Elimination of Constraint Forces
The Equations (8) form a differential algebraic sys-
tem, and their evaluation requires the determination
of the Lagrange multipliers λ
λ
λ. The computational ex-
pense of this computation is in particular problematic
since it should be used within the control law (M¨uller
and Hufnagel, 2012). Therefore, the constraint reac-
tions are not computed but eliminated instead. This
is commonly done by reformulating the equations of
motion with a set of generalized velocities that respect
the constraints. However, the subset of regular con-
straints depends on the configuration of the vehicle.
As a consequence, a set of different generalized ve-
locities and their corresponding dynamics equations
are often used. However, this leads to issues dur-
ing the transition between these models which can be
avoided by the following approach.
(M¨uller and Hufnagel, 2012) suggest to use one
redundantly parametrized model, as in (8), but elimi-
nate the constraining forces by projecting the dynam-
ics equation with a projector N
N
N to the null space of J
J
J.
This projector is not unique. The requirements are
J
J
JN
N
N = 0, (11)
i.e. N
N
N is an orthogonal complement of J
J
J, and
rank(N
N
N) = δ
v
, i.e. N
N
N
T
only removes constraining
forces. Projecting Equations (8) leads to
N
N
N
T
(M
M
M
¨
q
q
q+C
C
C
˙
q
q
q+ f
f
f) = N
N
N
T
B
B
Bu
u
u. (12)
There are two methods proposed by (M¨uller and
Hufnagel, 2012) for the analytic computation of N
N
N.
Both, however assume regular constraints and, as a
consequence of Property 4, are not directly applicable
for pseudo-omnidirectional vehicles. In this work a
semi-analytical approach is used which consist of an
analytical and a numerical step.
In the analytical step Property 2 is used
to determine n columns of N
N
N. The columns
k ∈ {4 + n,. .. 3 + 2n}, corresponding to the
steering velocities, of J
J
J are zero. Hence, unit
vectors u
k
, which are zero but have 1 at the
kth component, lie in the null space of the
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
72

Algorithm 1: Gram-Schmidt inspired projec-
tion method for the null space computation. k·k
is the Euclidean vector norm.
1 Function compute remaining null space vectors
input : Constraint matrix J
J
J
output: Remaining null space directions N
N
N
n
2 K
K
K = [J
J
J
T
], N
n
N
n
N
n
= [ ], i = 1
3 δ
v
= n
4 for i = 1,... 3 do
5
˙
q
q
q = u
i
6 i = i+ 1
7 eliminate
directions(
˙
q
q
q, K
K
K)
8 if k
˙
q
q
qk > ε then
9
˙
q
q
q =
˙
q
q
q/k
˙
q
q
qk
10 N
N
N
n
= [N
N
N
n
,
˙
q
q
q]
11 δ
v
= δ
v
+ 1
12 K
K
K = [K
K
K,
˙
q
q
q]
13 end
14 end
15 end
16 Function eliminate
directions
input :
˙
q
q
q vector under consideration, K
K
K column
vectors represent directions which
should be eliminated
output: n
n
n: remaining components of
˙
q
q
q
17 k = 1
18 repeat
19 j
j
j = column(K
K
K, k)
20 k = k + 1
21
˙
q
q
q =
˙
q
q
q−
˙
q
q
q
T
j
j
j
kj
j
jk
2
j
j
j
22 until k
˙
q
q
qk < ε or k >nr
of columns(K
K
K)
23 end
constraint Jacobian, i.e. J
J
Ju
k
= 0. Hence, the full rank
matrix
N
N
N
a
=
0
n+3,n
I
n,n
(13)
satisfies (11). This provides n columns of N
N
N.
In the numerical step the remaining δ
v
− n null
space vectors are computed. This is commonly done
by a singular value or full QR decomposition. These
algorithms, however, compute a basis for both, the
n + 2 (or n + 1) constrained and the remaining 1 (or
2) unconstrained directions and thereby add an un-
necessary high computational expense to the method-
ology. An algorithm that avoids this is introduced in
the following, see Algorithm 1. It is inspired by the
Gram-Schmidt orthogonalization (Bj¨orck, 1994).
The algorithm determines a non-trivial vector
˙
q
q
q
r
,
which is orthogonal to the constrained directions j
j
j,
where j
j
j is a transposed row of J
J
J and hence again
fulfills J
J
J
˙
q
q
q
r
= 0. The search starts with
˙
q
q
q = u
u
u
1
=
(1,0, .. . 0)
T
that correspond to a pure translation in
the x-direction of frame F
I
, see Figure 1 and (2). The
rolling constraints are obviously violated since the en-
tries that correspond to the drive velocities
˙
ϕ
ri
are
zero. However, since the column space of J
J
J
T
and the
allowed directions form an orthogonal complement,
this vector can always be split into allowed and con-
strained components. The constrained components
are removed in the elimination
directions phase by
means of a vector projection. This reveal whether
there is any motion possible which has a component
in the x-direction. If not, the y-direction or finally a
pure rotation is tried. The algorithm also works in
the case of aligned wheel axes, i.e. 2 missing vectors.
The only thing to do is to continue searching after one
admissible velocity is found, and to remove not only
the constrained directions but also the former found
admissible directions.
The computation is very efficient since the projec-
tion, which is needed for the elimination step, only
consists of simple arithmetical operations and the
number of projections is limited to 6n. J
J
J has only
zero columns in the last n entries, thus the result has
the following structure
N
N
N
n
=
N
N
N
r
0
n,δ
v
−n
(14)
where N
N
N
r
∈ R
n+3,δ
v
−n
is computed by the algorithm,
so that the columns of N
N
N
r
are orthonormal.
Combining the analytical N
N
N
a
and numerical N
N
N
n
null space bases finally result in
N
N
N =
N
N
N
n
N
N
N
a
=
N
N
N
r
0
n+3,n
0
n,δ
v
−n
I
n,n
. (15)
Property 5. The columns of the null space projection
matrix N
N
N are orthonormal. Hence the left inverse of
N
N
N is given by its transposed.
4 MODEL-BASED CONTROL
4.1 Inverse Dynamics and Redundancy
Resolution
At this point the inverse dynamics can be computed
by evaluating (12) with a desired motion q
q
q
d
(t)
N
N
N
T
M
M
M
¨
q
q
q
d
+N
N
N
T
C
C
C
˙
q
q
q
d
+N
N
N
T
f
f
f = Q
Q
Q
d
= N
N
N
T
B
B
Bu
u
u
ID
, (16)
which determines the required generalized forces Q
Q
Q
d
.
Resolving the last term in (16) yields required torques
u
u
u
ID
thus solving the inverse dynamics problem. The
computational effort of this task can be significantly
reduced if the structures of B
B
B, see (9), and N
N
N, see (15),
are taken into account
N
N
N
T
r
B
B
B
r
0
δ
v
−n,n
0
n,n+3
I
n,n
u
u
u
r
u
u
u
s
=
Q
Q
Q
r,d
Q
Q
Q
s,d
. (17)
Dynamic Model-based Control of Redundantly Actuated, Non-holonomnic, Omnidirectional Vehicles
73

Hence, the special choice of N
N
N decouples the driving
u
u
u
r
and steeringu
u
u
s
torques. The latter are directly given
by the last n elements Q
Q
Q
s,d
of the generalized torques
Q
Q
Q
d
.
The driving torques must be computed by the re-
maining equations
B
B
B
r
u
u
u
r
= Q
Q
Q
r,d
. (18)
By investigating the dimensions of the projected input
matrix
B
B
B
r
= N
N
N
T
r
B
B
B
r
∈ R
δ
v
−n,n
, where δ
v
− n is in gen-
eral 1 or 2, it follows that the equation is underdeter-
mined. Hence, there is an infinity number of driving
torquesu
u
u
r
which result in the sameQ
Q
Q
r,d
. The system is
therefore called redundantly actuated. To resolve this
redundancy, the solution is chosen which minimize
the following quadratic cost function (M¨uller, 2011)
u
u
u
∗
r
= arg min
u
u
u
r
1
2
u
u
u
T
r
W
W
Wu
u
u
r
(19a)
s.t.
B
B
B
r
u
u
u
r
= Q
Q
Q
r,d
, (19b)
with a positive definite weight matrix W
W
W ∈ R
n,n
. The
cost function ensures that only a minimal torque de-
mand is used to provide Q
Q
Q
r,d
. The distribution of this
demand can be done by choosing a proper weight ma-
trix. In our approach the following diagonal matrix is
used
W
W
W = diag
1/τ
2
r,max1
,... 1/τ
2
r,maxn
, (20)
whereby τ
r,maxi
are the maximum torques w.r.t. the
motor and friction limitations. The latter is approxi-
mated by the stall torques, that is the maximum torque
which can be applied to a single wheel, while accel-
erating the chassis against a stop, that does not result
in slippage. They are determined by experiments and
should include frictional differences due to an unbal-
anced load in the torque distribution.
The solution of (19) is given by
u
u
u
r
= W
W
W
−1
B
B
B
T
r
B
B
B
r
W
W
W
−1
B
B
B
T
r
−1
|
{z }
=: B
B
B
+
r
Q
Q
Q
r,d
. (21)
Where
B
B
B
+
r
is a right inverse of B
B
B
r
, i.e. B
B
B
r
B
B
B
+
r
= I
n,n
.
Summarizing, the inverse dynamics yields
u
u
u
ID
= (N
N
N
T
B
B
B)
+
Q
Q
Q
d
, (22)
with the right inverse
(N
N
N
T
B
B
B)
+
=
B
B
B
+
r
0
l−n,n
0
n,n+3
I
n,n
(23)
of the projected input matrix N
N
N
T
B
B
B .
4.2 Augmented PD-control
The inverse dynamics (22) provides the torque needed
to follow a given desired motion q
q
q
d
. However, there
is no feedback stabilization mechanism in this law.
Hence, model uncertainties and disturbances will in-
evitably lead to significant errors. The classical ap-
proach to eliminate these errors is a decentralized
strategy which independently controls the 2n actuated
degrees of freedom
τ
ri
= P
r
Z
t
0
(
˙
ϕ
ri,d
−
˙
ϕ
ri
)dτ + D
r
(
˙
ϕ
ri,d
−
˙
ϕ
ri
) (24)
τ
si
= P
s
(ϕ
si,d
− ϕ
si
) + D
s
(
˙
ϕ
si,d
−
˙
ϕ
si
). (25)
The rolling constraints instantaneously only admit
δ
v
∈ {n + 1,n + 2} independent velocities, hence the
result is a violation of the rolling constraints and a
counteraction of the control torques.
Our approach resolves this problem by a central-
ized model-based control
u
u
u
APD
= (N
N
N
T
B
B
B)
+
N
N
N
T
M
M
M
¨
q
q
q
d
+N
N
N
T
C
C
C
˙
q
q
q
d
+N
N
N
T
f
f
f
+D
D
DN
N
N
T
(
˙
q
q
q
d
−
˙
q
q
q)+P
P
P
Z
t
0
N
N
N
T
(
˙
q
q
q
d
−
˙
q
q
q)dτ
. (26)
The system matrices and vectors M
M
M,C
C
C, f
f
f are evalu-
ated by the vehicles current pose/velocity. The argu-
ments of them are suppressed due to the lack of space.
D
D
D,P
P
P ∈ R
δ
v
,δ
v
are positive definite gain matrices. The
idea behind (26) is to use the projected velocity error
and its integral
e
e
e
v
= N
N
N
T
(
˙
q
q
q
d
−
˙
q
q
q), e
e
e
p
=
Z
t
0
e
e
e
v
dτ, (27)
instead of the individual velocity error of each wheel
to stabilize the system. The counteraction is thereby
removed since the dimension of the error is equal to
the local degree of freedom δ
v
. The resulting torques
are finally again distributed in a minimal fashion over
the existing drives.
In the following it is proven that (26) asymptot-
ically stabilizes
˙
q
q
q along a desired motion
˙
q
q
q
d
. It is
therefore assumed that the desired velocity
˙
q
q
q
d
is pro-
vided by a higher-level controller and respects the
constraints. By applying (26) to (12) and project
it into unconstrained directions, the closed loop dy-
namic equations can be formulated as follows
N
N
N
T
M
M
M(
¨
q
q
q
d
−
¨
q
q
q)+N
N
N
T
C
C
C(
˙
q
q
q
d
−
˙
q
q
q)+D
D
De
e
e
v
+P
P
Pe
e
e
p
= 0. (28)
Moreover,
˙
q
q
q and
˙
q
q
q
d
respect the constraints. Hence,
they are lying in the null space of J
J
J and, as such, can
be expressed by a linear combination v
v
v
1
,v
v
v
2
of the ba-
sis N
N
N of this space
˙
q
q
q
d
−
˙
q
q
q = N
N
Nv
v
v
1
−N
N
Nv
v
v
2
= N
N
Ne
e
e
v
. (29)
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
74

It follows from Property 5 and Equation (27) that e
e
e
v
=
v
v
v
1
− v
v
v
2
. Inserting (29) in (28), yields the following
error system
˜
M
M
M
˙
e
e
e
v
+
˜
C
C
Ce
e
e
v
+D
D
De
e
e
v
+P
P
Pe
e
e
p
= 0 (30)
with the projected mass matrix
˜
M
M
M = N
N
N
T
M
M
MN
N
N and the
projected Coriolis and centrifugal forces
˜
C
C
Ce
e
e
v
where
˜
C
C
C = N
N
N
T
M
M
M
˙
N
N
N +N
N
N
T
C
C
CN
N
N. The stability can be proven by
introducing the following Lyapunov function
V =
1
2
e
e
e
T
v
˜
M
M
Me
e
e
v
+
1
2
e
e
e
T
p
P
P
Pe
e
e
p
. (31)
Differentiating V w.r.t. time along a solution
e
e
e
v
(t),e
e
e
p
(t) of (30) yields
˙
V =
1
2
e
e
e
T
v
(
˜
M
M
M − 2
˜
C
C
C)e
e
e
v
−e
e
e
T
v
D
D
De
e
e
v
= −e
e
e
T
v
D
D
De
e
e
v
≤ 0. (32)
Thereby, the following properties are used:
Property 6.
˜
M
M
M is positive definite,
Property 7.
˙
˜
M
M
M − 2
˜
C
C
C is skew symmetric.
The proof of them can be found in (Murray et al.,
1994). Referring to the Krasovskii-LaSalle invari-
ance principle, for a positive definite function V > 0
with a negative semi-definite derivative
˙
V ≤ 0 the
state converge to a rest position in the subset of
˙
V = 0. The only rest position of (30) in this subset
is (e
e
e
v
(t),e
e
e
p
(t)) = (0, 0) which proves the asymptotic
stabilization of the control law.
5 EXPERIMENTAL RESULTS
In this Section experimental results of the proposed
theory are presented. The used vehicle is equipped
with n = 2 actuated wheels and is shown in Figure
2. The wheels are diametrically mounted about the
reference point O
C
. The front wheel is indexed by
i = 1, the rear wheel by i = 2. The driving motors
are DC motors with a maximum torque of 25.6Nm.
They allow a maximum driving speed of 4.1rad/s
which equals a linear velocity of
˙
ϕ
ri
r = 0.41m/s
with a wheel radius r = 0.1m. The steering motors
are brushless DC motors with a maximum torque of
129Nm and a maximum steering speed of 195.95
◦
/s.
Selected parameters of the considered vehicle are
summarized in Table 1.
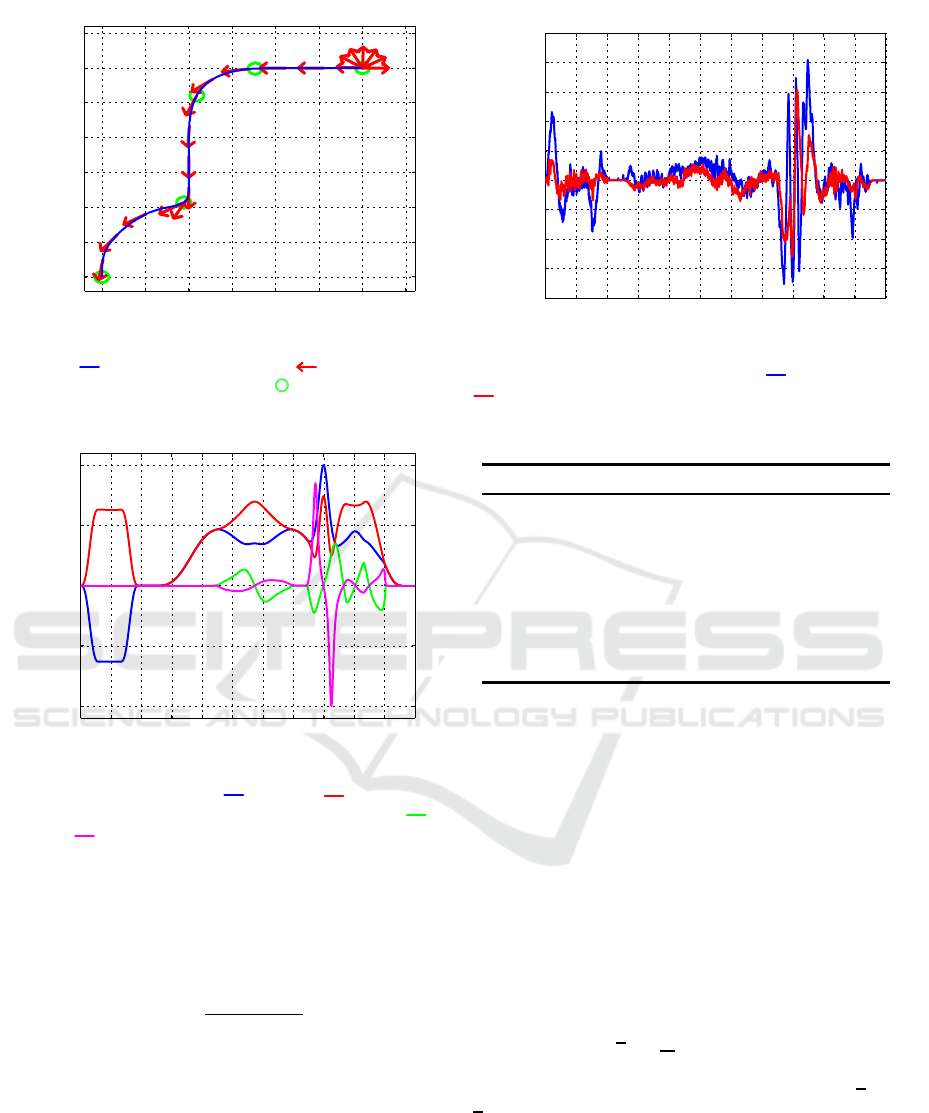
Figure 3 visualizes the driven maneuver. It can be
divided into two parts. The first part (t = 0.. .5s) is
a pure rotation by γ = 180
◦
about the reference point
O
C
. Therefore, the wheel axes have to be aligned,
hence it is a motion where the constraints are singu-
lar. In the second part, a mixed motion with transla-
tional and rotational components is done in a regular
Figure 2: Non-holonomic omnidirectional manipulator with
n = 2 actuated wheels. The laser scanner marks the front
side.
Table 1: Selected parameters of the equations of motion.
Inertias are given together with the corresponding rotation
axes.
symbol value description
m
C
93 kg chassis weight
C
C
4.51kgm
2
inertia chassis
Wi
z
z
z axis
B
i
20.5· 10
−3
kgm
2
inertia steering unit
Wi
y
y
y
C
i
0.2234kgm
2
inertia steering unit
Wi
z
z
z
µ
rci
0.88 Nm Coulomb, driving
µ
rvi
0.35Nms/rad viscous, driving
µ
sci
2.11 Nm Coulomb, steering
µ
svi
2.08Nms/rad viscous, steering
configuration. The orientation is chosen to be always
tangential to the desired (x
d
,y
d
) curve. The corre-
sponding steering and driving velocities are summa-
rized in Figure 4. The motion is firstly controlled by a
classic PD control approach (25) and secondly by the
proposed model-based control (26). A fair compari-
son between them is ensured by an independent op-
timization of the corresponding control coefficients.
The result of this optimization is summarized in Ta-
ble 2. The coefficients P
r
and D
r
corresponds to the
error component which is projected by N
N
N
r
while P
s
and D
s
correspond to the projection of N
N
N
s
.
Since the steering angles are unconstrained and
regularly actuated, both control concepts result in the
same error correction laws. Thus, the same control
coefficients can be used. Differences between the re-
sulting tracking errors, see Figure 6, are a result of the
inverse dynamics and can be primary seen in acceler-
ation phases t ∈ {11,15,. ..18}s. There, the model-
based control result in a significantly lower tracking
error. The tracking error of the driving velocities can
Dynamic Model-based Control of Redundantly Actuated, Non-holonomnic, Omnidirectional Vehicles
75
y in m
x in m
start
0
0.25
0.5 0.75 1 1.25 1.5 1.75
0
0.25
0.5
0.75
1
1.25
1.5
1.75
Figure 3:
replacements
Desired chassis position, sampled chas-
sis orientation and driving direction,
points in time t
i
∈
{0s,10s, 12s,16s,22s}.
0
t in s
0 2 4 6
8
10
12
14 16 18 20 22
−1
−0.5
0
0.5
1
˙
ϕ
d
/
˙
ϕ
max
Figure 4: Driving velocity of front and rear wheel
normalized by r
˙
ϕ
r,max
=0.4m/s, steering velocity of
front and rear wheel normalized by
˙
ϕ
s,max
=180
◦
/s.
be found for the front wheel i = 1 in Figure 5. Sig-
nificant differences can again mainly be found at ac-
celeration phases t ∈ {0,3,16,20}s. The differences
can also be seen in the total slip distance (constraint
violation)
∆
i
=
Z
T
t=0
q
˙
∆
2
longi
+
˙
∆
2
lati
dt. (33)
It is computed by integrating the left-hand side of
Equation (3) and (4). Due to violation they are not
zero but equal to some longitudinal
˙
∆
longi
and lateral
˙
∆
lati
slip. Along the 2.595m long path, the model-
based control leads to ∆
1
+ ∆
2
= 0.041m (1.58% of
total path length) slip distance, whereby classic PD
control leads ∆
1
+ ∆
2
= 0.137m (5.28% of total path
length) slip distance.
Significant differences can also be noticed in the
t in s
0 2 4 6 8 10 12 14 16 18 20 22
−40
−30
−20
−10
0
10
20
30
40
50
r(
˙
ϕ
r1d
−
˙
ϕ
r1
) in mm/s
Figure 5: Velocity tracking error for the classic PD and
model-based controlled front wheel i = 1.
Table 2: Control coefficients.
symbol value description
P
r
0.937Nm/rad driving classic
D
r
0.181Nms/rad driving classic
P
r
0.112Nm/rad driving model-based
D
r
0.238Nms/rad driving model-based
P
s
1.13 Nm/rad steering
D
s
0.3 Nms/rad steering
τ
r,max1
9.6Nm torque weight front
τ
r,max2
10.2Nm rear motor
resulting driving torques. They are presented for the
classic control in Figure 7 and for the model-based
PD control in Figure 8. Between t = 10s and 12s it
can be seen that the classic control result in signifi-
cant higher driving torques than the model-based ap-
proach. Moreover, the torques show an opposite sign.
Hence, one motor is accelerating while the other de-
celerates. This is a clear result of the counteraction
and an arbitrary distribution of the torque demand.
Further investigations show, that this higher demand
can be observed over the whole trajectory. As indi-
cator for the energy demand, the quadratic average of
the torques is used
τ
2
=
1
T
Z
T
t=0
τ
2
dt. (34)
For the model-based control this indicator is
τ
r1
+
τ
r2
= 3.039Nm which is 14.75% lower than the
3.565Nm for the classic control. The consequence
is a much lower energy demand for the model-based
control, and as a result a much higher uptime.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
76

t in s
0 2 4 6 8 10 12 14 16 18 20 22
−1.5
−1
−0.5
0
0.5
1
ϕ
s1d
− ϕ
s1
in
◦
Figure 6: Steering tracking error for the classic PD and
replacements
model-based controlled front wheel i = 1.
4
τ in Nm
t in s
0 2 4 6 8 10 12 14 16 18 20
22
−5
0
5
10
Figure 7: Driving torque for the classic DP control.
Front wheel i = 1 and rear wheel i = 2.
4
τ in Nm
t in s
0 2 4 6 8 10 12 14 16 18 20 22
−5
0
5
10
Figure 8: Driving torque for the model-based control.
Front wheel i = 1 and rear wheel i = 2.
6 SUMMARY AND OUTLOOK
In this work a model-based dynamic control con-
cept is introduced for redundantly actuated, non-
holonomic and omnidirectional vehicles with n cen-
tered orientable standard wheels.
The first part of this paper introduces a framework
for the dynamic modeling of such vehicles, including
friction and inertia effects. It turned out, that the kine-
matic constraints of the vehicle are permanently sin-
gular or can become singular. Therefore the dynam-
ics is modeled with a redundant set of coordinates.
This formulation does not eliminate unknown trac-
tion forces (constraint forces) in the dynamic equa-
tions but is in each configuration, especially in singu-
lar configurations, valid. The elimination of the con-
straint forces is done through projecting the dynamics
equation with a null space projector of the constraints.
This projector is computed in a highly efficient man-
ner by a semi-analytical approach.
The second part uses this model for an augmented
PD-control consisting of an inverse dynamics compo-
nent as well as a stabilizing feedback PD control law.
The distribution of the computed torque among the
different actuators is done through a weighted least
square approach. Whereby wheels with a higher stall
torque, which is the maximum motor torque that does
not result in slippage, during accelerating the chassis
against a mechanical stop, are less weighted. A PD
control is additionally used to asymptotically stabilize
the vehicle along a desired motion. The counteraction
is thereby avoided by using the projected velocity er-
ror instead of the individual wheel velocity errors.
Future work will focus on the online identification
of the load weight and the frictional conditions. This
knowledge can be used to adapt the parameters of the
inverse dynamics as well as the torque balancing law
which improves the robustness of the concept. Ad-
ditionally, the dynamic model will be used to moni-
tor the vehicles state enabling a higher-level logic to
detect faults on the drive units and unexpected colli-
sions.
ACKNOWLEDGEMENTS
This work has been supported by the Austrian
COMET-K2 program of the Linz Center of Mecha-
tronics (LCM), and was funded by the Austrian fed-
eral government and the federal state of Upper Aus-
tria.
Dynamic Model-based Control of Redundantly Actuated, Non-holonomnic, Omnidirectional Vehicles
77

REFERENCES
Bj¨orck,
˚
A. (1994). Numerics of gram-schmidt orthog-
onalization. Linear Algebra and Its Applications,
197:297–316.
Bona, B. and Indri, M. (2005). Friction compensation in
robotics: an overview. In Conference on Decision
and Control and European Control Conference, pages
4360–4367. IEEE.
Campion, G., Bastin, G., and D’Andr´ea-Novel, B. (1996).
Structural properties and classification of kinematic
and dynamic models of wheeled mobile robots. Trans-
actions on Robotics and Automation, 12:47–62.
De Luca, A., Oriolo, G., and Samson, C. (1998). Feed-
back control of a nonholonomic car-like robot. In
Robot motion planning and control, pages 171–253.
Springer.
Fukao, T., Nakagawa, H., and Adachi, N. (2000). Adap-
tive tracking control of a nonholonomic mobile robot.
Robotics and Automation, IEEE Transactions on,
16(5):609–615.
Giordano, P. R., Fuchs, M., Albu-Sch¨affer, A., and
Hirzinger, G. (2009). On the kinematic modeling and
control of a mobile platform equipped with steering
wheels and movable legs. In International Confer-
ence on Robotics and Automation, pages 4080–4087.
IEEE.
Hall, D. E. and Moreland, J. C. (2001). Fundamentals of
rolling resistance. Rubber chemistry and technology,
74(3):525–539.
Lee, M.-H. and Li, T.-H. S. (2015). Kinematics, dynamics
and control design of 4wis4wid mobile robots. In The
Journal of Engineering, volume 1. IET.
M¨uller, A. (2011). A robust inverse dynamics formula-
tion for redundantly actuated pkm. In 13th World
Congress in Mechanism and Machine Science, Gua-
najuato, Mexico, pages 19–25.
M¨uller, A. and Hufnagel, T. (2012). Model-based control of
redundantly actuated parallel manipulators in redun-
dant coordinates. Robotics and Autonomous Systems,
60(4):563–571.
Murray, R. M., Li, Z., Sastry, S. S., and Sastry, S. S. (1994).
A mathematical introduction to robotic manipulation.
CRC press.
Oftadeh, R., Ghabcheloo, R., and Mattila, J. (2013). A
novel time optimal path following controller with
bounded velocities for mobile robots with indepen-
dently steerable wheels. In International Conference
on Intelligent Robots and Systems, pages 4845–4851.
IEEE.
Ostrowski, J. and Burdick, J. (1996). Geometric perspec-
tives on the mechanics and control of robotic locomo-
tion. In Robotics Research, pages 536–547. Springer.
Ploeg, J., van der Knaap, A. C., Verburg, D. J., and Auto-
motive, T. (2002). Design, implementation and evalu-
ation of a high performance agv. In Intelligent Vehicle
Symposium. IEEE.
St¨oger, C., M¨uller, A., and Gattringer, H. (2015). Kine-
matic analysis and singularity robust path control of a
non-holonomic mobile platform with several steerable
driving wheels. In International Conference on Intel-
ligent Robots and Systems, pages 4140–4145. IEEE.
Yang, J.-M. and Kim, J.-H. (1999). Sliding mode control for
trajectory tracking of nonholonomic wheeled mobile
robots. Robotics and Automation, IEEE Transactions
on, 15(3):578–587.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
78
